2 求导法则与求导基本公式

y y
x = ϕ ( y)
β
( x, y )
y = f (x)
α
o
x
x
内单调、 定理 如果函数 x = ϕ( y)在某区间I y内单调、可导 且ϕ′( y) ≠ 0 , 那末它的反函数 = f ( x)在对应区间 I x内也可导 , 且有 1 f ′( x) = . ϕ′( y)
即
反函数的导数等于直接函数导数的倒数. 反函数的导数等于直接函数导数的倒数.
§2 求导法则和求导基本公式
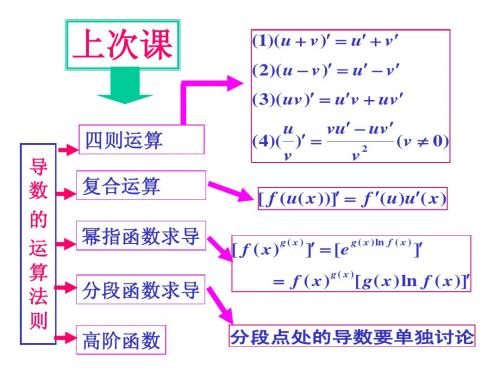
四则运算 反函数求导 复合函数求导 高阶导数
一. 四则运算
定理 如果函数u( x), v( x)在点x处可导,则它 们的和、 们的和、差、积、商(分母不为零)在点x处也 可导, 并且
(1) [u( x) ± v( x)]′ = u′( x) ± v′( x); (2) [u( x) ⋅ v( x)]′ = u′( x)v( x) + u( x)v′( x); u( x) u′( x)v( x) − u( x)v′( x) (3) [ ]′ = (v( x) ≠ 0). 2 v( x) v ( x)
= 2 cos x[ f ′(cos2 x ) − f ′(sin 2 x )]
dy dy + sin x = 0 dx du
小
2. 复合函数的求导法则
结
反函数的求导法则（注意成立条件） 1. 反函数的求导法则（注意成立条件）;
（注意函数的复合过程,合理分解正确使用链 注意函数的复合过程, 导法）; 导法） 已能求导的函数:可分解成基本初等函数, 已能求导的函数:可分解成基本初等函数,或 常数与基本初等函数的和、 常数与基本初等函数的和、差、积、商.
v v
Oct. 13 Wed.
Review
导数四则运算
(1) [u( x) ± v( x)]′ = u′( x) ± v′( x); (2) [u( x) ⋅ v( x)]′ = u′( x)v( x) + u( x)v′( x); u( x) u′( x)v( x) − u( x)v′( x) (3) [ ]′ = (v( x) ≠ 0). 2 v( x) v ( x)
= 2 sin x cos x[ f ′(sin 2 x ) − f ′(cos 2 x )]
又因 u = cos x 时，y = f (1 − u 2 ) + f ( u 2 )，
dy = f ′(1 − u 2 )( −2u) + f ′( u 2 )2u ∴ du
= 2u[ f ′( u 2 ) − f ′(1 − u 2 )]
定理 由函数 y = f (u)与 u = u( x) 复合而成的函数 y = f (u( x))。若 f ′(u) 与 u′( x) 存在，则 y = f (u( x) 存在， 可导， 在 x 可导，且 dy dy du = ⋅ . dx du dx 即 因变量对自变量求导,等于因变量对中间 因变量对自变量求导, 变量求导,乘以中间变量对自变量求导.( .(链式法 变量求导,乘以中间变量对自变量求导.(链式法 则)
1.常数和基本初等函数的导数公式 .
( C )′ = 0 (sin x )′ = cos x (tan x )′ = sec 2 x (sec x )′ = sec x tan x
( x µ )′ = µx µ −1 (cos x )′ = − sin x (cot x )′ = − csc 2 x (csc x )′ = − csc x cot x
一般地, 函数f ( x)的n − 1阶导数的导数称为
函数f ( x)的n阶导数, 记作
d n y d n f ( x) f ( n) ( x), y( n) , . 或 n n dx dx 二阶和二阶以上的导数统称为高阶导数 高阶导数. 二阶和二阶以上的导数统称为高阶导数
相应地 , f ( x )称为零阶导数 ; f ′( x )称为一阶导数 .
6 6 (n)
Hw：p101 1(9,10,11,12),3,4(1),8(2,4),9(1,3).
推广 设 y = f ( u), u = ϕ (v ), v = ψ ( x ),
则复合函数 y = f {ϕ [ψ ( x )]}的导数为 dy dy du dv = ⋅ ⋅ . dx du dv dx
为实数， 求证 xα = αxα −1，α 为实数， x > 0； 例1
例2 例3 例4
y = 1 − x 2； y = ln( x + 1 + x 2 )； y = ln | x |； x≠0 ， 0
d3 y . 二阶导数的导数称为三阶导数, 二阶导数的导数称为三阶导数 f ′′′( x), y′′′, 3 dx4 d y ( 4) ( 4) 三阶导数的导数称为四阶导数, 三阶导数的导数称为四阶导数 f ( x), y , . 4 dx
d 2 y d 2 f ( x) . 记作 f ′′( x), y′′, 2 或 2 dx dx
1 2 x sin 处可导， x 例5 设 f ( x ) 在 x = 0 处可导，又 g ( x ) = 0 处的导数。 求 f ( g ( x )) 在x = 0处的导数。
设 f ( x ) 为可导函数， y = f (sin 2 x ) + f (cos 2 x ), 为可导函数， 例6 若令 u = cos x，证明 dy dy + sin x = 0 dx du dy 证明： ∵ = f ′(sin 2 x )2 sin x cos x + f ′(cos 2 x )2 cos x ( − sin x ) dx
2. 二阶导数的力学意义： 例
瞬时加速度。
1. y = xα (α > 0)，求 y ( n )； 2. y = ln(1 + x )，求 y ( n )； 3. y = e ，求y ；
ax ( n)
4. y = a x (a > 0, a ≠ 1)，求y ( n )； 5. y = sin x，求y ( n )。
k =0 k n n ( n− k )
v
(k )
Leibniz莱布尼兹公式 莱布尼兹公式
例 1. y = x e ， 求 y ；
2 3x (n)
1+ x 2. y = ，求y ( n )； 1− x 1 3. y = 求y ( 50 )。 x (1 − x )
常用高阶导数公式
(1) ( a x ) ( n ) = a x ⋅ ln n a (a > 0) π ( n) n ( 2) (sin kx ) = k sin( kx + n ⋅ ) 2 π ( n) n ( 3) (cos kx ) = k cos( kx + n ⋅ ) 2
( 4) ( x α ) ( n ) = α( α − 1) ⋯ (α − n + 1) x α − n
(n)
(e x ) ( n ) = e x
(5) (ln x )
= ( −1)
n −1
( n − 1)! xn
1 (n) n n! ( ) = ( −1) n + 1 x x
例
设 y = sin x + cos x , 求y .
利用上述公式及法则初等函数求导问题可完全解 决. 注意:初等函数的导数仍为初等函数 注意:初等函数的导数仍为初等函数.
(sinh x)′ = cosh x
1 (tanh x)′ = cosh2 x
(cosh x)′ = sinh x
例
1.
y=e
sin 2
1 x
，求y′；
x v( x) tan x
阶导数时,求出 阶后,不要急于 注意 求n阶导数时 求出 或4阶后 不要急于 阶导数时 求出1-3或 阶后 合并,分析结果的规律性 写出n阶导数 分析结果的规律性,写出 阶导数.(数学归纳 合并 分析结果的规律性 写出 阶导数 数学归纳 法证明) 法证明
3. 运算规则
设函数 u和v具有n阶导数 , 则
i =1k=1 k≠i n n
例1 例2 例3 例4
cot 的导数； 求 tan x， x的导数； 的导数； 求函数 y = a + x + ln a (a > 0)的导数； cosh x的导数； 的导数； 求 sinh x，
x a
x + x−2 设y = ，求y′。 3 x +6
2
二. 反函数求导
(1) ( u ± v ) ( n ) = u ( n ) ± v ( n ) ( 2) (Cu) ( n ) = Cu ( n )
( 3) ( u ⋅ v )
(n)
= u v + nu
(n)
( n −1 )
n(n − 1) ( n− 2 ) (n u v ′′ v′ + 2!
n( n − 1) ⋯ ( n − k + 1) ( n− k ) ( k ) (n) u v + ⋯ + uv + k! = ∑C u
Hw：p96
2(1,3,6,7,9,10)，3(3),6(6,7,8)，
7(单),8(单),9,10(2),12(2,6,7, 8,9)。
四. 高阶导数
1. 概念 问题:变速直线运动的加速度 问题:变速直线运动的加速度.
∴ a ( t ) = v ′( t ) = [ f ′( t )]′ .
定义 如果函数f ( x)的导数f ′( x)在点x处可导,即 f ′( x + ∆x) − f ′( x) ( f ′( x))′ = lim ∆x→0 ∆x 存在,则称( f ′( x))′为函数f ( x)在点x处的二阶导数.
反函数求导 反函数的导数等于直接函数导数的倒数.