面心立方最密堆积
面心立方最密堆积半径和边长的关系

面心立方最密堆积半径和边长的关系
面心立方的最密堆积是学习几何学和化学时很常见的概念,它也
被广泛应用于科学、工程和工业研究中。
面心立方在化学中也有很重
要的作用,它是由六个均匀大小的正方形面和八个共面组成的立方体,每个六边形面上都有一个半径,其边长公式如下:
边长=2r
其中r为半径。
可以看出,边长和半径之间存在着直接的数学关系,而且在计算中也很容易证明:边长乘以2等于半径。
首先,在面心立方的最密堆积中,从未确定的八个共面垂直,形
成了立方体状的物体,其中每个面都是由六个均匀大小的正方形组成的。
然后,在其中的每个正方形面上,确定一个半径,以此作为直角
三角形的斜边,则在原型物体中形成特殊的立方体,比如,当r为1时,其边长就是2。
在实际应用中,面心立方最密堆积还具有很多独特的优势。
首先,它能够最大程度地凸显目标图形和结构,使得其形状变得均一性以及
牢固稳定,从而降低了实际应用中的干扰程度。
其次,由于在几何学
上有精确地定义,使得该结构在计算机上能够不断改进和优化,从而
最大程度地提高了其信息传递和处理的效率。
综上所述,面心立方最密堆积对于科学、工程和工业研究具有重
要的意义,它不仅能够节约物资,而且还能提高信息传递和处理的效率,并且边长和半径之间存在着较为明确的数学关系,可以根据其公
式来计算得到,这也更加地方便了实际的应用。
面心立方最密堆积的八面体空隙

面心立方最密堆积的八面体空隙摘要:I.引言- 面心立方最密堆积的背景- 八面体空隙的概念和重要性II.面心立方最密堆积的结构- 面心立方的定义- 最密堆积的概念- 面心立方最密堆积的晶胞结构III.八面体空隙的形成和性质- 八面体空隙的定义- 八面体空隙的形成过程- 八面体空隙的性质和特点IV.八面体空隙在材料科学中的应用- 八面体空隙与材料性能的关系- 八面体空隙在材料制备和应用中的作用- 八面体空隙对材料稳定性的影响V.总结- 八面体空隙对面心立方最密堆积的重要性- 未来研究方向和前景正文:面心立方最密堆积的八面体空隙在材料科学中具有重要的意义。
在面心立方最密堆积中,八面体空隙是一种特殊的晶体空隙,其结构特点是原子在晶胞中呈现出最紧密的堆积方式。
本文将从面心立方最密堆积的结构、八面体空隙的形成和性质以及其在材料科学中的应用等方面进行详细阐述。
首先,面心立方最密堆积是一种具有高度有序性的晶体堆积方式。
在面心立方最密堆积中,每个原子的周围都紧邻着12 个最近邻原子,呈现出高度的密排结构。
这种结构具有很高的空间利用率,使材料具有优异的力学性能和稳定性。
其次,八面体空隙是面心立方最密堆积中的一种特殊空隙。
八面体空隙的形成是由于在面心立方晶胞中,原子之间存在一定的间隙。
这些间隙在晶胞的堆积过程中,会形成八面体形状的空隙。
八面体空隙具有特定的空间结构,其数量与晶胞中原子数相等。
八面体空隙的性质和特点对其在材料科学中的应用具有重要的影响。
八面体空隙的大小和分布对材料的密度、孔隙率、抗压强度等性能指标有显著的影响。
此外,八面体空隙还可以作为材料的传输通道,影响材料的导电性、热传导性等物理性能。
在材料科学中,八面体空隙对面心立方最密堆积材料的应用具有重要意义。
例如,在金属材料中,八面体空隙与晶界、位错等缺陷密切相关,影响材料的塑性变形能力;在陶瓷材料中,八面体空隙可以影响材料的烧结性能和致密度;在催化剂材料中,八面体空隙可以作为活性中心的载体,提高催化剂的催化活性。
面心立方最密堆积的八面体空隙

面心立方最密堆积的八面体空隙(最新版)目录一、面心立方最密堆积的概念及特点二、八面体空隙的形成与分布三、八面体空隙的数量及计算方法四、八面体空隙在面心立方最密堆积中的应用五、结论正文一、面心立方最密堆积的概念及特点面心立方最密堆积(Face-centered cubic close-packed structure)是一种常见的晶体结构,它属于密堆积结构,具有较高的空间利用率。
在面心立方最密堆积中,每个晶胞包含 4 个原子,它们分别位于晶胞的顶点、面心和体内。
这种结构的特点是晶胞中原子之间的距离相等,空间利用率较高,达到 74%。
二、八面体空隙的形成与分布在面心立方最密堆积中,八面体空隙(octahedral voids)是指由 6 个相邻晶胞组成的空间区域,其中心是一个八面体。
八面体空隙在面心立方最密堆积中分布均匀,数量较少。
每个八面体空隙都与 8 个四面体空隙(tetrahedral voids)相邻。
三、八面体空隙的数量及计算方法在面心立方最密堆积中,八面体空隙的数量较少,每个晶胞平均含有1 个八面体空隙。
在计算八面体空隙的数量时,可以采用以下方法:首先统计一个晶胞中的原子数,然后根据原子数计算出与之相邻的八面体空隙的数量。
具体地,对于面心立方最密堆积,原子数为 4,因此相邻的八面体空隙数量为 8 个。
四、八面体空隙在面心立方最密堆积中的应用八面体空隙在面心立方最密堆积中具有重要的应用,它们可以作为填隙原子进入晶体的通道。
在晶体生长过程中,原子通过八面体空隙进入晶体,逐渐填充四面体空隙。
此外,八面体空隙还可以用来分析晶体的稳定性和力学性能。
五、结论面心立方最密堆积是一种具有较高空间利用率的晶体结构,其中八面体空隙分布均匀,数量较少。
八面体空隙在晶体生长、稳定性和力学性能分析等方面具有重要应用。
面心立方最密堆积的八面体空隙

面心立方最密堆积的八面体空隙介绍面心立方最密堆积是一种在立方体中排列球体的方法,使得球体之间的空隙最小化。
在这种排列中,八面体空隙是一种特殊的空隙形态,具有独特的几何特征和应用价值。
本文将深入探讨面心立方最密堆积的八面体空隙的特点、性质和应用。
八面体空隙的定义八面体空隙是指在面心立方最密堆积中,八个球体围成的空间。
它由六个面、八条边和八个顶点组成,形状呈八面体。
八面体空隙是一种特殊的空隙形态,具有高度对称性和紧密的结构。
八面体空隙的几何特征八面体空隙具有以下几何特征: 1. 对称性:八面体空隙的六个面和八条边具有高度的对称性,可以通过旋转和镜像操作得到相同的形状。
2. 紧密度:八面体空隙中球体之间的距离非常接近,最大程度地减小了空隙大小,实现了最密堆积的效果。
3. 稳定性:八面体空隙的结构稳定,不易发生变形或塌陷,可以承受一定的外力作用。
八面体空隙的应用八面体空隙在材料科学、物理学和化学等领域具有广泛的应用价值。
以下是一些典型的应用案例: 1. 催化剂载体:八面体空隙的结构稳定性和紧密度使其成为理想的催化剂载体。
通过在八面体空隙中引入催化剂,可以提高催化反应的效率和选择性。
2. 纳米材料合成:八面体空隙可以作为纳米材料的模板,在其中合成纳米颗粒或纳米晶体。
通过调控八面体空隙的大小和形状,可以控制合成材料的尺寸和形貌。
3. 能源存储:八面体空隙可以用于储存和释放能源,例如作为电池的电解质或储氢材料的载体。
八面体空隙的稳定性和紧密度可以提高能源存储的效率和安全性。
4. 光学材料:八面体空隙可以用于制备具有特殊光学性质的材料,例如光子晶体。
通过调控八面体空隙的结构和尺寸,可以实现对光的传播和控制。
八面体空隙的性质研究对八面体空隙的性质进行深入研究,可以帮助我们更好地理解其几何特征和应用价值。
以下是一些八面体空隙性质的研究方向: 1. 空隙大小:研究八面体空隙的大小可以帮助我们确定最密堆积的效果和空隙的容纳能力。
晶胞结构
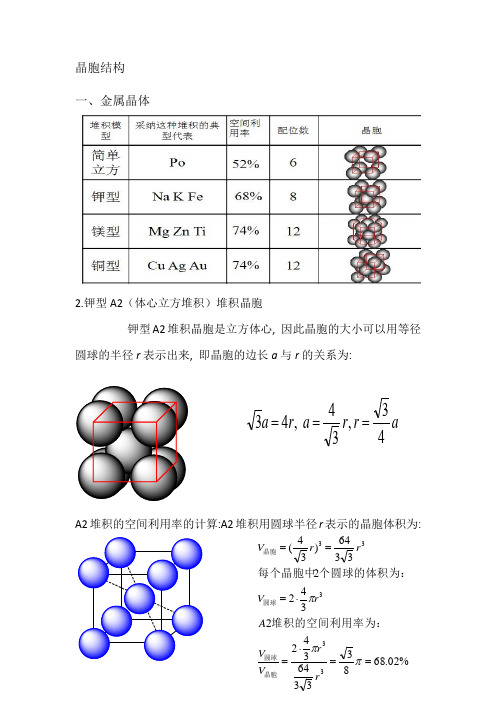
晶胞结构一、金属晶体2.钾型A2(体心立方堆积)堆积晶胞钾型A2堆积晶胞是立方体心, 因此晶胞的大小可以用等径圆球的半径r 表示出来, 即晶胞的边长a 与r 的关系为:A2堆积的空间利用率的计算:A2堆积用圆球半径r 表示的晶胞体积为:ar r a r a 43,34 ,43===%02.68833364342234223364)34(33333==⋅=⋅===πππr r V V A rV rr V 晶胞圆球圆球晶胞堆积的空间利用率为:个圆球的体积为:每个晶胞中3.六方最密堆积(4)A1(面心立方最密堆积)A1是ABCABCABC······型式的堆积,从这种堆积中可以抽出一个立方面心点阵,因此这种堆积型式的最小单位是一个立方面心晶胞。
A1堆积晶胞是立方面心, 因此晶胞的大小可以用等径圆球的半径r 表示出来, 即晶胞的边长a 与r 的关系为:A1堆积空间利用率的计算:A1堆积用圆球半径r 表示的晶胞体积为:(5)A4堆积形成晶胞A4堆积晶胞是立方面心点阵结构, 因此晶胞的大小可以用等径圆球的半径r 表示出来, 即晶胞的边长a 与r 的关系为:A4堆积的空间利用率的计算:A4堆积用圆球半径r 表示的晶胞体积为: ra r a 22 ,42==%05.742312163441344 4216)22(33333==⋅=⋅===πππr r V V A r V r r V 晶胞圆球圆球晶胞堆积的空间利用率为:个圆球的体积为:每个晶胞中ar r a r r a 83,38 ,8243===⨯=%01.34163335123484348 833512)38(33333==⋅=⋅===πππr r V V A r V r r V 晶胞圆球圆球晶胞堆积的空间利用率为:个圆球的体积为:每个晶胞中二、原子晶体1.金刚石立体网状结构,每个碳原子形成4个共价键,任意抽出2个共价键,每两个单键归两个六元环所有,而不是只归一个六元环所有(如图所示,红色的两个碳碳单键,可以构成蓝色和紫红色的两个六元环)。
面心立方最密堆积

面心立方最密堆积引言在固体领域中,堆积是指将多个颗粒排列在一起的过程,使它们能够紧密地堆放在一起。
在堆积的过程中,最密堆积是一种理想的堆积方式,其能够最大程度地减少颗粒之间的空隙,实现最高的紧密度。
而面心立方最密堆积则是最密堆积中最常见的一种形式。
本文将详细介绍面心立方最密堆积的特点、堆积过程以及其在实际应用中的重要性。
面心立方最密堆积的定义面心立方最密堆积是一种特殊的堆积结构,其颗粒以面心立方的方式进行排列,使得每个颗粒都与周围的六个颗粒紧密接触。
在面心立方结构中,每个颗粒都位于一个凹槽中,形成一个共享边(face)的堆积结构,这也是其名称的由来。
面心立方最密堆积的堆积过程面心立方最密堆积的堆积过程包括两个主要步骤:初始化和堆积。
1.初始化:在进行堆积之前,首先需要选择一种合适的颗粒进行堆积。
面心立方最密堆积中最常用的颗粒是小球状颗粒,如金属球、塑料球等。
在初始化步骤中,需要将这些颗粒根据一定的规则摆放在堆积空间的底部,以形成一个初始的面心立方结构。
2.堆积:在初始化步骤完成后,开始进行堆积过程。
在这个过程中,每个颗粒都根据一定的规则放置在底部的面心立方结构上方。
具体来说,每个颗粒都应该与周围的六个颗粒紧密接触,以最大程度地减少空隙。
通常情况下,这个过程是通过逐层堆积来完成的,即每层都按照面心立方的规则进行堆积,直到整个堆积结构达到所需的高度。
面心立方最密堆积的特点面心立方最密堆积具有以下几个主要特点:1.最高的紧密度:面心立方最密堆积是堆积中最紧密的一种结构,能够最大程度地减少颗粒之间的空隙,实现最高的紧密度。
这种紧密堆积结构在工程应用中具有重要的意义,可以提高材料的物理性能和力学性能。
2.高度规整:面心立方最密堆积的结构十分规整,每个颗粒都位于一个凹槽中,呈现出一定的有序性。
这种规整的结构使得面心立方最密堆积在一些需要精确堆积的应用中非常有用,比如微芯片生产、晶体管制造等。
3.良好的堆积稳定性:面心立方最密堆积的结构具有良好的堆积稳定性,颗粒之间通过紧密的接触互相支撑。
面心立方最密堆积的八面体空隙

面心立方最密堆积的八面体空隙面心立方最密堆积是指在一个面心立方晶胞中,最紧密地堆积同一种原子。
八面体空隙则是存在于该堆积结构中的一种特殊空隙。
本文将从深度和广度两个方面对面心立方最密堆积的八面体空隙进行探讨。
一、面心立方最密堆积的概述面心立方最密堆积是一种常见的晶体堆积方式,也被称为最密堆积或充分堆积。
在这种堆积结构中,每个原子与其周围的12个原子接触,形成一个正二十面体。
它有着高度的紧密度和稳定性,因此在许多晶体中都存在该堆积结构。
二、八面体空隙的定义与定位在面心立方最密堆积结构中存在八面体空隙,它是通过原子充分堆积形成的一种隐含的空隙。
具体来说,每个八面体空隙被六个紧邻的原子所包围,这些原子分别位于八面体的八个顶点和顶点上的原子的邻近位置。
八面体空隙是面心立方最密堆积结构的一个重要特征。
三、八面体空隙的性质和意义1. 八面体空隙的大小:八面体空隙的大小与原子半径有关,通常为较大原子半径的74%。
这意味着只有原子半径超过一定大小的原子才能占据这些空隙,如金属离子。
2. 八面体空隙的稳定性:由于八面体空隙被周围的原子紧密包围,因此具有较高的稳定性,可以容纳较大的离子或分子。
3. 八面体空隙的应用:八面体空隙在催化剂设计、吸附材料和气体储存等领域具有重要应用。
利用八面体空隙的特殊性质,可以实现对分子的选择性吸附、储存和转化。
四、个人观点和理解对于我来说,面心立方最密堆积的八面体空隙是一个非常有趣和重要的研究领域。
通过对八面体空隙的理解和探索,我们可以更好地理解晶体内部的结构和性质,并应用于不同领域的科学研究和工程应用中。
总结回顾:本文首先介绍了面心立方最密堆积的概念和特点,详细讲解了八面体空隙的定义和定位。
介绍了八面体空隙的性质和意义,包括空隙的大小、稳定性和应用。
分享了个人对于这个主题的观点和理解。
通过本文的学习,我们对面心立方最密堆积的八面体空隙有了更深入的了解,同时也开拓了我们的科学思维和应用能力。
立方最密堆积

配位多面体的极限半径比
配位多面体
平面三角形 四面体 八面体 立方体 立方八面体
配位数
3 4 6 8 12
半径比(r+/r-)min
0.155 0.225 0.414 0.732 1.000
构性判断
半径比(r+/r-) 0.225-0.414 0.414-0.732 >0.732
A
面心立方最密堆积(A1)分解图
A1 型最密堆积图片
将密堆积层的相对位置按照ABCABC……方式作 最密堆积,重复的周期为3层。这种堆积可划出 面心立方晶胞。
A3型最密堆积图片
将密堆积层的相对位置按照ABABAB…方式作 最密堆积,这时重复的周期为两层。
A1、A3型堆积小结
同一层中球间有三角形空隙,平均每个球摊列2个空隙。 第二层一个密堆积层中的突出部分正好处于第一层的空 隙即凹陷处,第二层的密堆积方式也只有一种,但这两
1 四方晶系(t):有1个四重对称轴(a=b, α=β=γ=90º) 2 三方晶系(h):有1个三重对称轴(a=b, α=β=90º,
γ=120º) 3 正交晶系(o):有3个互相垂直的二重对称轴或2个
互相垂直的对称面(α=β=γ=90º) 4 单斜晶系(m):有1个二重对称轴或对称面
(α=γ=90º) 5 三斜晶系(a):没有特征对称元素
74.05%
12 4 a 2 2r
六方最密 堆积(A3)
体心立方 密堆积(A2)
金刚石型 堆积(A4)
六方 体心立方 面心立方
74.05% 68.02% 34.01%
12 2 8(或14) 2
48
a b 2r c2 6a
3
r 3a 4
