最新人教版初二下册数学勾股定理的逆定理优秀PPT课件

(1) a＝15 , b ＝8 , c＝17
(2) a＝13 , b ＝14 , c＝15
分析：根据勾股定理的逆定理，一个三角形中两条较小边长的平方 和等于最大边长的平方，那么这个三角形是直角三角形
定理应用
解（1）152＋82＝225＋64＝289 172＝289 ∴ 152＋82＝172 ∴这个三角形是直角三角形 （2）132+142=169+196=365 152=225 因为132+142≠152，
a 5
b 12 c 26c 169 0
2
试判断△ABC的形状.
课堂小结
（1）勾股定理的逆定理的内容是什么？
（2）原命题、逆命题之间的关系.
（3）用什么方法证明勾股定理的逆定理?
目标检测设计
1.以长度分别为下列各组数的线段为边，能构成直 角三角形的有哪些？
Hale Waihona Puke (1) 1 , 2 , 3
问题2：按照这种做法真能得 到一个直角三角形吗？
实验观察
5 3
4 追问：这个三角形的三条边有什么关系吗? 3 + 4 = 5
2 2 2
实验操作 提出猜想 动手画一画
（1）下列各组数中两个数的平方和等于第三个数的平 方，分别以这些数为边长（单位：cm）画三角形：
①2.5，6，6.5；②4，7.5，8.5.
课堂练习
1 判断由a、b、c组成的三角形是不是直角三角形：
(1) a＝6.5 , b ＝7.5 , c＝4 (2) a＝11 , b ＝60 , c＝61
8 10 3a , b 2, c 3 3 3 1 4a 3 , b 2, c 4 4 4
2、 已知a ， b ， c 为△ ABC 的三边 , 且 满足 2
2 b
=
2 c
那么这个三角形是直角三角形。
勾股定理
互逆命题
如果直角三角形两直角边分别为a，b， 斜边为c，那么有a2 + b2 = c2
• 问题5 :请同学们举出一些互逆命题，并思考：是否原命题 正确，它的逆命题也正确呢？举例说明． • 追问1： 在我们大家举出的互逆命题中原命题和逆命题都成吗？
• 问题6 : 原命题正确，它的逆命题不一定正确.那么勾股定理
• 追问1： 你能把勾股定理的题设与结论交换得到一个新的命
题吗？
• 追问2： “如果三角形三边长a、b、c满足， a2
b2 c 2
那么这个三角形是直角三角形.”能否把它作为判定直角三 角形的依据呢？本节课我们一起来研究这个问题.
实验观察
古埃及人曾用下面的方法得到直角
实验观察
用13个等距的结,把一根绳子分 成等长的12段,然后以3个结，4 个结，5个结的长度为边长，用 木桩钉成一个三角形，其中一 个角便是直角。
（2）量一量：用量角器分别测量上述各三角形的 最大角的度数. （3）想一想：判断这些三角形的形状，提出猜想.
实验操作 提出猜想
问题2 由上面几个例子你发现了什么吗?请以命题的 形式说出你的观点!
命题2 如果三角形的三边长a、b、c满足
a2 + b 2 = c 2
那么这个三角形是直角三角形。
归纳概念
的逆命题正确吗？如果你认为是真确的，你能证明这个命题 “如果三角形的三边长、b、c满足，那么这个三角形是直角 三角形”吗？
勾股定理逆定理的证明
已知:在△ABC中，AB=c BC=a CA=b 且a2+b2=c2 A 求证:△ ABC是直角三角形. 证明:画一个△A’B’C’,使 ∠ C’=90°,B’C’=a, C’A’=b ∵ ∠ C/=900 ∴ A’B’2= a2+b2 ∵ a2+b2=c2 ∴ A’B’ 2=c2 ∵ 边长取正值 ∴ A’B’ =c
八年级
下册
第十七章
勾股定理
17.2 勾股定理的逆定理 （第1课时）
课件说明
课题内容
勾股定理的逆定理证明及简单应用；原命题、逆
命题的概念及相互关系.
学习目标

理解勾股定理的逆定理. 了解互逆命题、互逆定理.
创设情境，提出问题
• 问题1： 你能说出勾股定理吗？并指出定理的题设和结论.
勾股定理的题设：直角 三角形的两直角边长分 别为a, b，斜 边长为c，结论：a 2 b 2 c 2
A′
a
C
c
b
B
a
C′
b
B′
勾股定理逆定理的证明
在△ ABC和△ A’B’C’中 BC=a=B’C’ CA=b=C’A’ AB=c=A’B’
∴ △ ABC ≌△ A’B’C’（SSS）
∴ ∠ C= ∠ C/=90°
则 △ ABC是直角三角形 （直角三角形的定义）
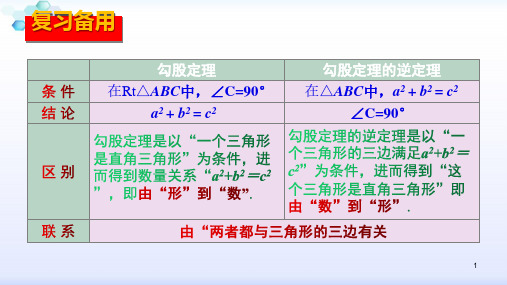
定理与逆定理
如果一个定理的逆命题经过证明是真命题,那么
(2) 6 , 8 , 14
(3) 2, 1.5 , 2.5
4
2,
2,
3
目标检测设计
2.说出下列命题的逆命题，这些命题的逆命题是真
命题吗？ （1）两条直线平行，内错角相等
（2）对顶角相等
（3）线段垂直平分线上的点到线段两端点的距离相等
目标检测设计
3.已知：如图，四边形ABCD中，∠B＝900，AB ＝ 3 ， BC ＝ 4 ， CD ＝ 12 ， AD ＝ 13, 求四边形 ABCD的面积?
它是一个定理,这两个定理称为互逆定理,其中一
个定理称另一个定理的逆定理.
我们已经学习了一些互逆的定理,如: (1)勾股定理及其逆定理；(2)两直线平行,内错角相等; (3) 内错角相等,两直线平行. (4)角的平分线的性质与判定； (5)线段的垂直平分线的性质与判定.
定理应用
例1 判断由a、b、c组成的三角形是不是直角三角形：
问题3：把勾股定理记着命题1，上面的结论作为命题2.
命题1和命题2的题设和结论分别是什么？
问题4：命题1和命题2的题设和结论有着什么的关系？
两个命题的题设和结论正好相反，象这样的两个命题叫
做互逆命题，如果其中一个叫原命题，那么另一个就叫
做它的逆命题.
归纳概念
如果三角形的三边长a、b、c满足
2 a
+
根据勾股定理，这个三角形不是三角形.
定理应用
解：因为a c b,
a c 1 ( 3) 4, b 2 4
2 2 2 2 2 2
所以b a c ,
2 2 2
所以这个三角形是直角三角形.
练习：同学们还知道哪些勾股数？请完成以下未完成的 勾股数.
（1）3, 4， （2）6, 8， （3）7, 24, （4）5, 12， （5）9, 12， ， ， ， ， .