2015中考真题训练二次函数
2015-2016年二次函数中考题 (三至七份)

九年级数学(下)二次函数中考题(三)1、(1)已知一元二次方程x2+px+q=0(p2﹣4q≥0)的两根为x1、x2;求证:x1+x2=﹣p,x1•x2=q.(2)已知抛物线y=x2+px+q与x轴交于A、B两点,且过点(﹣1,﹣1),设线段AB 的长为d,当p为何值时,d2取得最小值,并求出最小值.2、如图,在平面直角坐标系中,点A是抛物线()2-y=a x3+k与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为边的等边三角形ABC的周长为.3、抛物线2=++与x轴的交点坐标是(-l,0)和(3,0),则这条抛物线的对称y ax bx c轴是【】.A.直线x=-1 8.直线x=0 C.直线x=1 D.直线x= 34、已知点A(x1,y1)、B(x2,y2)在二次函数y=(x-1)2+1的图象上,若x1>x2>1,则y1y2.5、若抛物线y=ax2+bx+c的顶点是A(2,1),且经过点B(1,0),求抛物线的函数关系式.6、已知二次函数y=ax2+bx+c(a≠O)的图象如图所示,现有下列结论:①abc>0 ②b2-4ac<0 ⑤c<4b ④a+b>0,则其中正确结论的个数是【】A.1个B.2个C.3个D.4个第6题第7题7、如图,二次函数y=ax2+bx+c的图象过点(-1,1)、(2,-1).下列关于这个二次函数的叙述正确的是【】A.当x=0时,y的值大于1 B.当x=3时,y的值小于0C.当x=1时,y的值大于1 D.y的最大值小于08、已知二次函数y=a(x+1)2-b有最小值,则a,b的大小关系为【】A.a>b B.a<b C.a=b D.不能确定9、抛物线y=-2x2+1的对称轴是【】A.直线1x=2B.直线1x=2-C.y轴D.直线x=210、二次函数2y ax bx c=++的图象如图所示,则函数值y0<时x的取值范围是【】A.x1<-B.x>3 C.-1<x<3 D.x1<-或x>3第10题11、如图,抛物线y1=a(x+2)2-3与y2=12(x-3)2+1交于点A(1,3),过点A 作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:①无论x取何值,y2的值总是正数;②a=1;③当x=0时,y2-y1=4;④2AB=3AC;其中正确结论是【】A .①②B .②③C .③④D .①④12、抛物线2y ax bx 3=+-经过点(2,4),则代数式8a 4b 1++的值为【 】A .3B .9C .15D .15-13、已知二次函数y=2(x ﹣3)2+1.下列说法:①其图象的开口向下;②其图象的对称轴为直线x=﹣3;③其图象顶点坐标为(3,﹣1);④当x <3时,y 随x 的增大而减小.则其中说法正确的有【 】 A .1个 B .2个 C .3个 D .4个 14、已知二次函数()2y=ax +bx+c a 0≠的图象如图所示,下列结论错误的是【 】A.abc >0B.3a >2bC.m (am +b )≤a -bD.4a -2b +c <0第14题 第15题 第16题15、设A 1(2)y -,,B 2(1)y ,,C 3(2)y ,是抛物线2(1)y x a =-++上的三点,则1y ,2y ,3y 的大小关系为【 】A .213y y y >>B .312y y y >>C .321y y y >>D .312y y y >> 16、二次函数y=ax 2+bx +c(a≠0)的图象如图所示,给出下列结论:① b 2-4ac>0;② 2a +b<0;③ 4a -2b +c=0;④ a :b :c= -1:2:3.其中正确的是【 】 (A) ①② (B) ②③ (C) ③④ (D)①④ 17、抛物线234y x x =--+ 与坐标轴的交点个数是【 】 A .3 B .2 C .1 D .018、如图,二次函数y=ax 2+bx+c (a≠0)的图象与x 轴交于A 、B 两点,与y 轴交于点C ,点B 坐标(﹣1,0),下面的四个结论:①OA=3;②a+b+c <0;③ac >0;④b 2﹣4ac >0.其中正确的结论是【 】A .①④B .①③C .②④D .①② 19、对于二次函数y 2(x 1)(x 3)=+-,下列说法正确的是【 】A. 图象的开口向下B. 当x>1时,y 随x 的增大而减小C. 当x<1时,y 随x 的增大而减小D. 图象的对称轴是直线x=-1 20、设二次函数2y x bx c =++,当x 1≤时,总有y 0≥,当1x 3≤≤时,总有y 0≤, 那么c 的取值范围是【 】A.c 3=B.c 3≥C.1c 3≤≤D.c 3≤21、二次函数y=ax 2+bx+1(a≠0)的图象的顶点在第一象限,且过点(﹣1,0).设t=a+b+1,则t 值的变化范围是【 】A .0<t <1B .0<t <2C .1<t <2D .﹣1<t <122、如图,已知抛物线与x 轴的一个交点A (1,0),对称轴是x=﹣1,则该抛物线与x 轴的另一交点坐标是【 】A .(﹣3,0)B .(﹣2,0)C .x=﹣3D .x=﹣222题 23题 23、如图为二次函数y=ax 2+bx+c (a≠0)的图象,则下列说法:①a >0 ②2a+b=0 ③a+b+c >0 ④当﹣1<x <3时,y >0,正确的个数为【 】 A .1 B .2 C .3 D .4九年级数学(下) 二次函数中考题(四)1、已知抛物线y=ax 2﹣2x+1与x 轴没有交点,该抛物线的顶点所在的象限是【 】A .第四象限B .第三象限C .第二象限D .第一象限2、已知二次函数y=ax 2+bx+c 的图象如图所示,它与x 轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:①b ﹣2a=0;②abc <0;③a ﹣2b+4c <0;④8a+c >0.其中正确的有【 】A .3个B .2个C .1个D .0个3、关于x 的二次函数()()y=x+1x m -,其图象的对称轴在y 轴的右侧,则实数m 的取值范围是【 】A. m <1-B. 1<m<0-C. 0<m<1D. m >14、已知二次函数()()2y=a x 2+c a 0>-,当自变量x 3,0时,对应的值分别为123y y y ,,,则123y y y ,,的大小关系正确的是【 】A. 321y y y <<B. 123y y y <<C. 213y y y <<D. 312y y y << 5、已知二次函数y=﹣x 2﹣7x+,若自变量x 分别取x 1,x 2,x 3,且0<x 1<x 2<x 3,则对应的函数值y 1,y 2,y 3的大小关系正确的是【 】A .y 1>y 2>y 3B .y 1<y 2<y 3C .y 2>y 3>y 1D .y 2<y 3<y 16、已知二次函数)0(2≠++=a c bx ax y 的图象如图所示对称轴为21-=x 。
2015中考数学真题分类汇编:二次函数压轴题(含答案解析可打印)

2015中考数学真题汇编:二次函数1.(13分)(2015•福州)如图,抛物线y=x2﹣4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q.(1)这条抛物线的对称轴是,直线PQ与x轴所夹锐角的度数是;(2)若两个三角形面积满足S△POQ=S△PAQ,求m的值;(3)当点P在x轴下方的抛物线上时,过点C(2,2)的直线AC与直线PQ交于点D,求:①PD+DQ的最大值;②PD•DQ的最大值.解答:解:(1)∵y=x2﹣4x=(x﹣2)2﹣4,∴抛物线的对称轴是x=2,∵直线y=x+m,∴直线与坐标轴的交点坐标为(﹣m,0),(0,m),∴交点到原点的距离相等,∴直线与坐标轴围成的三角形是等腰直角三角形,∴直线PQ与x轴所夹锐角的度数是45°,故答案为x=2、45°.(2)设直线PQ交x轴于点B,分别过O点,A点作PQ的垂线,垂足分别是E、F,显然当点B在OA的延长线时,S△POQ=S△PAQ不成立;①当点B落在线段OA上时,如图①,==,由△OBE∽△ABF得,==,∴AB=3OB,∴OB=OA,由y=x2﹣4x得点A(4,0),∴OB=1,∴B(1,0),∴1+m=0,∴m=﹣1;②当点B落在线段AO的延长线上时,如图②,同理可得OB=OA=2,∴B(﹣2,0),∴﹣2+m=0,∴m=2,综上,当m=﹣1或2时,S△POQ=S△PAQ;(3)①过点C作CH∥x轴交直线PQ于点H,如图③,可得△CHQ是等腰三角形,∵∠CDQ=45°+45°=90°,∴AD⊥PH,∴DQ=DH,∴PD+DQ=PH,过P点作PM⊥CH于点M,则△PMH是等腰直角三角形,∴PH=PM,∴当PM最大时,PH最大,∴当点P在抛物线顶点出时,PM最大,此时PM=6,∴PH的最大值为6,即PD+DQ的最大值为6.②由①可知:PD+PH≤6,设PD=a,则DQ﹣a,∴PD•DQ≤a(6﹣a)=﹣a2+6a=﹣(a﹣3)2+18,∵当点P在抛物线的顶点时,a=3,∴PD•DQ≤18.∴PD•DQ的最大值为18.2.(10分)(2015•莆田)抛物线y=ax2+bx+c,若a,b,c满足b=a+c,则称抛物线y=ax2+bx+c 为“恒定”抛物线.(1)求证:“恒定”抛物线y=ax2+bx+c必过x轴上的一个定点A;(2)已知“恒定”抛物线y=x2﹣的顶点为P,与x轴另一个交点为B,是否存在以Q 为顶点,与x轴另一个交点为C的“恒定”抛物线,使得以PA,CQ为边的四边形是平行四边形?若存在,求出抛物线解析式;若不存在,请说明理由.解答:(1)证明:由“恒定”抛物线y=ax2+bx+c,得:b=a+c,即a﹣b+c=0,∵抛物线y=ax2+bx+c,当x=﹣1时,y=0,∴“恒定”抛物线y=ax2+bx+c必过x轴上的一个定点A(﹣1,0);(2)解:存在;理由如下:∵“恒定”抛物线y=x2﹣,当y=0时,x2﹣=0,解得:x=±1,∵A(﹣1,0),∴B(1,0);∵x=0时,y=﹣,∴顶点P的坐标为(0,﹣),以PA,CQ为边的平行四边形,PA、CQ是对边,∴PA∥CQ,PA=CQ,∴存在两种情况:①如图1所示:作QM⊥AC于M,则QM=OP=,∠QMC=90°=∠POA,在Rt△QMC和Rt△POA中,,∴Rt△QMC≌Rt△POA(HL),∴MC=OA=1,∴OM=2,∵点A和点C是抛物线上的对称点,∴AM=MC=1,∴点Q的坐标为(﹣2,﹣),设以Q为顶点,与x轴另一个交点为C的“恒定”抛物线的解析式为y=a(x+2)2﹣,把点A(﹣1,0)代入得:a=,∴抛物线的解析式为:y=(x+2)2﹣,即y═x2+4x+3;②如图2所示:顶点Q在y轴上,此时点C与点B重合,∴点C坐标为(1,0),∵CQ∥PA,∴∠OQC=∠OPA,在△OQC和△OPA中,,∴△OQC≌△OPA(AAS),∴OQ=OP=,∴点Q坐标为(0,),设以Q为顶点,与x轴另一个交点为C的“恒定”抛物线的解析式为y=ax2+,把点C(1,0)代入得:a=﹣,∴抛物线的解析式为:y=﹣x2+;综上所述:存在以Q为顶点,与x轴另一个交点为C的“恒定”抛物线,使得以PA,CQ为边的四边形是平行四边形,抛物线的解析式为:y=x2+4x+3,或y=﹣x2+.3.(13分)(2015•泉州)阅读理解抛物线y=x2上任意一点到点(0,1)的距离与到直线y=﹣1的距离相等,你可以利用这一性质解决问题.问题解决如图,在平面直角坐标系中,直线y=kx+1与y轴交于C点,与函数y=x2的图象交于A,B两点,分别过A,B两点作直线y=﹣1的垂线,交于E,F两点.(1)写出点C的坐标,并说明∠ECF=90°;(2)在△PEF中,M为EF中点,P为动点.①求证:PE2+PF2=2(PM2+EM2);②已知PE=PF=3,以EF为一条对角线作平行四边形CEDF,若1<PD<2,试求CP的取值范围.解答:解:(1)当x=0时,y=k•0+1=1,则点C的坐标为(0,1).根据题意可得:AC=AE,∴∠AEC=∠ACE.∵AE⊥EF,CO⊥EF,∴AE∥CO,∴∠AEC=∠OCE,∴∠ACE=∠OCE.同理可得:∠OCF=∠BCF.∵∠ACE+∠OCE+∠OCF+∠BCF=180°,∴2∠OCE+2∠OCF=180°,∴∠OCE+∠OCF=90°,即∠ECF=90°;(2)①过点P作PH⊥EF于H,Ⅰ.若点H在线段EF上,如图2①.∵M为EF中点,∴EM=FM=EF.根据勾股定理可得:PE2+PF2﹣2PM2=PH2+EH2+PH2+HF2﹣2PM2=2PH2+EH2+HF2﹣2(PH2+MH2)=EH2﹣MH2+HF2﹣MH2=(EH+MH)(EH﹣MH)+(HF+MH)(HF﹣MH)=EM(EH+MH)+MF(HF﹣MH)=EM(EH+MH)+EM(HF﹣MH)=EM(EH+MH+HF﹣MH)=EM•EF=2EM2,∴PE2+PF2=2(PM2+EM2);Ⅱ.若点H在线段EF的延长线(或反向延长线)上,如图2②.同理可得:PE2+PF2=2(PM2+EM2).综上所述:当点H在直线EF上时,都有PE2+PF2=2(PM2+EM2);②连接CD、PM,如图3.∵∠ECF=90°,∴▱CEDF是矩形,∵M是EF的中点,∴M是CD的中点,且MC=EM.由①中的结论可得:在△PEF中,有PE2+PF2=2(PM2+EM2),在△PCD中,有PC2+PD2=2(PM2+CM2).∵MC=EM,∴PC2+PD2=PE2+PF2.∵PE=PF=3,∴PC2+PD2=18.∵1<PD<2,∴1<PD2<4,∴1<18﹣PC2<4,∴14<PC2<17.∵PC>0,∴<PC<.4.(12分)(2015•福建)如图,在平面直角坐标系中,顶点为A(1,﹣1)的抛物线经过点B(5,3),且与x轴交于C,D两点(点C在点D的左侧).(1)求抛物线的解析式;(2)求点O到直线AB的距离;(3)点M在第二象限内的抛物线上,点N在x轴上,且∠MND=∠OAB,当△DMN与△OAB 相似时,请你直接写出点M的坐标.解答:解:(1)设抛物线的解析式为y=a(x﹣1)2﹣1,将B点坐标代入函数解析式,得(5﹣1)2a﹣1=3,解得a=.故抛物线的解析式为y=(x﹣1)2﹣1;(2)由勾股定理,得OA2=11+12=2,OB2=52+32=34,AB2=(5﹣1)2+(3+1)2=32,OA2+AB2=OB2,∴∠OAB=90°,O到直线AB的距离是OA=;(3)设M(a,b),N(a,0)当y=0时,(x﹣1)2﹣1=0,解得x1=3,x2=﹣1,D(3,0),DN=3﹣a.①当△MND∽△OAB时,=,即=,化简,得4b=a﹣3 ①M在抛物线上,得b=(a﹣1)2﹣1 ②联立①②,得,解得a1=3(不符合题意,舍),a2=﹣2,b=,M1(﹣2,),当△MND∽△BAO时,=,即=,化简,得b=12﹣4a ③,联立②③,得,解得a1=3(不符合题意,舍),a2=﹣17,b=12﹣4×(﹣17)=80,M2(﹣17,80).综上所述:当△DMN与△OAB相似时,点M的坐标(﹣2,),(﹣17,80).5.(14分)(2015•漳州)如图,抛物线y=﹣x2+2x+3与x轴交于A,B两点,与y轴交于点C,点D为抛物线的顶点,请解决下列问题.(1)填空:点C的坐标为(0,3),点D的坐标为(1,4);(2)设点P的坐标为(a,0),当|PD﹣PC|最大时,求α的值并在图中标出点P的位置;(3)在(2)的条件下,将△BCP沿x轴的正方向平移得到△B′C′P′,设点C对应点C′的横坐标为t(其中0<t<6),在运动过程中△B′C′P′与△BCD重叠部分的面积为S,求S与t 之间的关系式,并直接写出当t为何值时S最大,最大值为多少?解答:解:(1)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴C(0,3),D(1,4),故答案为:0;3;1;4;(2)∵在三角形中两边之差小于第三边,∴延长DC交x轴于点P,设直线DC的解析式为y=kx+b,把D、C两点坐标代入可得,解得,∴直线DC的解析式为y=x+3,将点P的坐标(a,0)代入得a+3=0,求得a=﹣3,如图1,点P(﹣3,0)即为所求;(3)过点C作CE∥x,交直线BD于点E,如图2,由(2)得直线DC的解析式为y=x+3,由法可求得直线BD的解析式为y=﹣2x+6,直线BC的解析式为y=﹣x+3,在y=﹣2x+6中,当y=3时,x=,∴E点坐标为(,3),设直线P′C′与直线BC交于点M,∵P′C′∥DC,P′C′与y轴交于点(0,3﹣t),∴直线P′C′的解析式为y=x+3﹣t,联立,解得,∴点M坐标为(,),∵B′C′∥BC,B′坐标为(3+t,0),∴直线B′C′的解析式为y=﹣x+3+t,分两种情况讨论:①当0<t<时,如图2,B′C′与BD交于点N,联立,解得,∴N点坐标为(3﹣t,2t),S=S△B′C′P﹣S△BMP﹣S△BNB′=×6×3﹣(6﹣t)×(6﹣t)﹣t×2t=﹣t2+3t,其对称轴为t=,可知当0<t<时,S随t的增大而增大,当t=时,有最大值;②当≤t<6时,如图3,直线P′C′与DB交于点N,立,解得,∴N点坐标为(,),S=S△BNP′﹣S△BMP′=(6﹣t)×﹣×(6﹣t)×=(6﹣t)2=t2﹣t+3;显然当<t<6时,S随t的增大而减小,当t=时,S=综上所述,S与t之间的关系式为S=,且当t=时,S 有最大值,最大值为.6.(12分)(2015•甘南州)如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c,经过A(0,﹣4),B(x1,0),C(x2,0)三点,且|x2﹣x1|=5.(1)求b,c的值;(2)在抛物线上求一点D,使得四边形BDCE是以BC为对角线的菱形;(3)在抛物线上是否存在一点P,使得四边形BPOH是以OB为对角线的菱形?若存在,求出点P的坐标,并判断这个菱形是否为正方形?若不存在,请说明理由.解答:解:(1)∵抛物线y=﹣x2+bx+c,经过点A(0,﹣4),∴c=﹣4又∵由题意可知,x1、x2是方程﹣x2+bx﹣4=0的两个根,∴x1+x2=b,x1x2=6由已知得(x2﹣x1)2=25又∵(x2﹣x1)2=(x2+x1)2﹣4x1x2=b2﹣24∴b2﹣24=25解得b=±,当b=时,抛物线与x轴的交点在x轴的正半轴上,不合题意,舍去.∴b=﹣.(2)∵四边形BDCE是以BC为对角线的菱形,根据菱形的性质,点D必在抛物线的对称轴上,又∵y=﹣x2﹣x﹣4=﹣(x+)2+,∴抛物线的顶点(﹣,)即为所求的点D.(3)∵四边形BPOH是以OB为对角线的菱形,点B的坐标为(﹣6,0),根据菱形的性质,点P必是直线x=﹣3与抛物线y=﹣x2﹣x﹣4的交点,∴当x=﹣3时,y=﹣×(﹣3)2﹣×(﹣3)﹣4=4,∴在抛物线上存在一点P(﹣3,4),使得四边形BPOH为菱形.四边形BPOH不能成为正方形,因为如果四边形BPOH为正方形,点P的坐标只能是(﹣3,3),但这一点不在抛物线上7.(10分)(2015•酒泉)如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C (5,0),其对称轴与x轴相交于点M.(1)求抛物线的解析式和对称轴;(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.解答:解:(1)根据已知条件可设抛物线的解析式为y=a(x﹣1)(x﹣5),把点A(0,4)代入上式得:a=,∴y=(x﹣1)(x﹣5)=x2﹣x+4=(x﹣3)2﹣,∴抛物线的对称轴是:x=3;(2)P点坐标为(3,).理由如下:∵点A(0,4),抛物线的对称轴是x=3,∴点A关于对称轴的对称点A′的坐标为(6,4)如图1,连接BA′交对称轴于点P,连接AP,此时△PAB的周长最小.设直线BA′的解析式为y=kx+b,把A′(6,4),B(1,0)代入得,解得,∴y=x﹣,∵点P的横坐标为3,∴y=×3﹣=,∴P(3,).(3)在直线AC的下方的抛物线上存在点N,使△NAC面积最大.设N点的横坐标为t,此时点N(t,t2﹣t+4)(0<t<5),如图2,过点N作NG∥y轴交AC于G;作AD⊥NG于D,由点A(0,4)和点C(5,0)可求出直线AC的解析式为:y=﹣x+4,把x=t代入得:y=﹣t+4,则G(t,﹣t+4),此时:NG=﹣t+4﹣(t2﹣t+4)=﹣t2+4t,∵AD+CF=CO=5,∴S△ACN=S△ANG+S△CGN=AM×NG+NG×CF=NG•OC=×(﹣t2+4t)×5=﹣2t2+10t=﹣2(t﹣)2+,∴当t=时,△CAN面积的最大值为,由t=,得:y=t2﹣t+4=﹣3,∴N(,﹣3).8.(12分)(2015•兰州)已知二次函数y=ax2的图象经过点(2,1).(1)求二次函数y=ax2的解析式;(2)一次函数y=mx+4的图象与二次函数y=ax2的图象交于点A(x1、y1)、B(x2、y2)两点.①当m=时(图①),求证:△AOB为直角三角形;②试判断当m≠时(图②),△AOB的形状,并证明;(3)根据第(2)问,说出一条你能得到的结论.(不要求证明)解答:(1)解:∵y=ax2过点(2,1),∴1=4a,解得a=,∴抛物线解析式为y=x2;(2)①证明:当m=时,联立直线和抛物线解析式可得,解得或,∴A(﹣2,1),B(8,16),分别过A、B作AC⊥x轴,BD⊥x轴,垂足分别为C、D,如图1,∴AC=1,OC=2,OD=8,BD=16,∴==,且∠ACO=∠ODB,∴△ACO∽△ODB,∴∠AOC=∠OBD,又∵∠OBD+∠BOD=90°,∴∠AOC+∠BOD=90°,即∠AOB=90°,∴△AOB为直角三角形;②解:△AOB为直角三角形.证明如下:当m≠时,联立直线和抛物线解析式可得,解得或,∴A(2m﹣2,(m﹣)2),B(2m+2,(m+)2),分别过A、B作AC⊥x轴,BD⊥x轴,如图2,∴AC=(m﹣)2,OC=﹣(2m﹣2),BD=(m+)2,OD=2m+2,∴==,且∠ACO=∠ODB,∴△ACO∽△OBD,∴∠AOC=∠OBD,又∵∠OBD+∠BOD=90°,∴∠AOC+∠BOD=90°,即∠AOB=90°,∴△AOB为直角三角形;(3)解:由(2)可知,一次函数y=mx+4的图象与二次函数y=ax2的交点为A、B,则△AOB恒为直角三角形.(答案不唯一).9.(12分)(2015•天水)在平面直角坐标系中,已知y=﹣x2+bx+c(b、c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),点C的坐标为(4,3),直角顶点B在第四象限.(1)如图,若抛物线经过A、B两点,求抛物线的解析式.(2)平移(1)中的抛物线,使顶点P在直线AC上并沿AC方向滑动距离为时,试证明:平移后的抛物线与直线AC交于x轴上的同一点.(3)在(2)的情况下,若沿AC方向任意滑动时,设抛物线与直线AC的另一交点为Q,取BC的中点N,试探究NP+BQ是否存在最小值?若存在,求出该最小值;若不存在,请说明理由.解答:解:(1)∵等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3)∴点B的坐标为(4,﹣1).∵抛物线过A(0,﹣1),B(4,﹣1)两点,∴,解得:b=2,c=﹣1,∴抛物线的函数表达式为:y=﹣x2+2x﹣1.(2)如答题图2,设顶点P在直线AC上并沿AC方向滑动距离时,到达P′,作P′M∥y轴,PM∥x轴,交于M点,∵点A的坐标为(0,﹣1),点C的坐标为(4,3),∴直线AC的解析式为y=x﹣1,∵直线的斜率为1,∴△P′PM是等腰直角三角形,∵PP′=,∴P′M=PM=1,∴抛物线向上平移1个单位,向右平移1个单位,∵y=﹣x2+2x﹣1=﹣(x﹣2)2+1,∴平移后的抛物线的解析式为y=﹣(x﹣3)2+2,令y=0,则0=﹣(x﹣3)2+2,解得x1=1,x=52,∴平移后的抛物线与x轴的交点为(1,0),(5,0),解,得或∴平移后的抛物线与AC的交点为(1,0),∴平移后的抛物线与直线AC交于x轴上的同一点(1,0).(3)如答图3,取点B关于AC的对称点B′,易得点B′的坐标为(0,3),BQ=B′Q,取AB中点F,连接QF,FN,QB′,易得FN∥PQ,且FN=PQ,∴四边形PQFN为平行四边形.∴NP=FQ.∴NP+BQ=FQ+B′Q≥FB′==2.∴当B′、Q、F三点共线时,NP+BQ最小,最小值为2.10.(10分)(2015•酒泉)如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.(1)求抛物线的解析式和对称轴;(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.解答:解:(1)根据已知条件可设抛物线的解析式为y=a(x﹣1)(x﹣5),把点A(0,4)代入上式得:a=,∴y=(x﹣1)(x﹣5)=x2﹣x+4=(x﹣3)2﹣,∴抛物线的对称轴是:x=3;(2)P点坐标为(3,).理由如下:∵点A(0,4),抛物线的对称轴是x=3,∴点A关于对称轴的对称点A′的坐标为(6,4)如图1,连接BA′交对称轴于点P,连接AP,此时△PAB的周长最小.设直线BA′的解析式为y=kx+b,把A′(6,4),B(1,0)代入得,解得,∴y=x﹣,∵点P的横坐标为3,∴y=×3﹣=,∴P(3,).(3)在直线AC的下方的抛物线上存在点N,使△NAC面积最大.设N点的横坐标为t,此时点N(t,t2﹣t+4)(0<t<5),如图2,过点N作NG∥y轴交AC于G;作AD⊥NG于D,由点A(0,4)和点C(5,0)可求出直线AC的解析式为:y=﹣x+4,把x=t代入得:y=﹣t+4,则G(t,﹣t+4),此时:NG=﹣t+4﹣(t2﹣t+4)=﹣t2+4t,∵AD+CF=CO=5,∴S△ACN=S△ANG+S△CGN=AM×NG+NG×CF=NG•OC=×(﹣t2+4t)×5=﹣2t2+10t=﹣2(t﹣)2+,∴当t=时,△CAN面积的最大值为,由t=,得:y=t2﹣t+4=﹣3,∴N(,﹣3).11.(10分)(2015•佛山)如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=﹣x2+4x刻画,斜坡可以用一次函数y=x刻画.(1)请用配方法求二次函数图象的最高点P的坐标;(2)小球的落点是A,求点A的坐标;(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积.请直接写出点M的坐标.解答:解:(1)由题意得,y=﹣x2+4x=﹣(x﹣2)2+4,故二次函数图象的最高点P的坐标为(2,4);(2)联立两解析式可得:,解得:,或.故可得点A的坐标为(,);(3)如图,作PQ⊥x轴于点Q,AB⊥x轴于点B.S△POA=S△POQ+S△梯形PQBA﹣S△BOA=×2×4+×(+4)×(﹣2)﹣××=4+﹣=;(4)过P作OA的平行线,交抛物线于点M,连结OM、AM,则△MOA的面积等于△POA的面积.设直线PM的解析式为y=x+b,∵P的坐标为(2,4),∴4=×2+b,解得b=3,∴直线PM的解析式为y=x+3.由,解得,,∴点M的坐标为(,).12.(14分)(2015•广州)已知O为坐标原点,抛物线y1=ax2+bx+c(a≠0)与x轴相交于点A(x1,0),B(x2,0),与y轴交于点C,且O,C两点间的距离为3,x1•x2<0,|x1|+|x2|=4,点A,C在直线y2=﹣3x+t上.(1)求点C的坐标;(2)当y1随着x的增大而增大时,求自变量x的取值范围;(3)将抛物线y1向左平移n(n>0)个单位,记平移后y随着x的增大而增大的部分为P,直线y2向下平移n个单位,当平移后的直线与P有公共点时,求2n2﹣5n的最小值.解答:解:(1)令x=0,则y=c,故C(0,c),∵OC的距离为3,∴|c|=3,即c=±3,∴C(0,3)或(0,﹣3);(2)∵x1x2<0,∴x1,x2异号,①若C(0,3),即c=3,把C(0,3)代入y2=﹣3x+t,则0+t=3,即t=3,∴y2=﹣3x+3,把A(x1,0)代入y2=﹣3x+3,则﹣3x1+3=0,即x1=1,∴A(1,0),∵x1,x2异号,x1=1>0,∴x2<0,∵|x1|+|x2|=4,∴1﹣x2=4,解得:x2=﹣3,则B(﹣3,0),代入y1=ax2+bx+3得,,解得:,∴y1=﹣x2﹣2x+3=﹣(x+1)2+4,则当x≤﹣1时,y随x增大而增大.②若C(0,﹣3),即c=﹣3,把C(0,﹣3)代入y2=﹣3x+t,则0+t=﹣3,即t=﹣3,∴y2=﹣3x﹣3,把A(x1,0),代入y2=﹣3x﹣3,则﹣3x1﹣3=0,即x1=﹣1,∴A(﹣1,0),∵x1,x2异号,x1=﹣1<0,∴x2>0∵|x1|+|x2|=4,∴1+x2=4,解得:x2=3,则B(3,0),代入y1=ax2+bx+3得,,解得:,∴y1=x2﹣2x﹣3=(x﹣1)2﹣4,则当x≥1时,y随x增大而增大,综上所述,若c=3,当y随x增大而增大时,x≤﹣1;若c=﹣3,当y随x增大而增大时,x≥1;(3)①若c=3,则y1=﹣x2﹣2x+3=﹣(x+1)2+4,y2=﹣3x+3,y1向左平移n个单位后,则解析式为:y3=﹣(x+1+n)2+4,则当x≤﹣1﹣n时,y随x增大而增大,y2向下平移n个单位后,则解析式为:y4=﹣3x+3﹣n,要使平移后直线与P有公共点,则当x=﹣1﹣n,y3≥y4,即﹣(﹣1﹣n+1+n)2+4≥﹣3(﹣1﹣n)+3﹣n,解得:n≤﹣1,∵n>0,∴n≤﹣1不符合条件,应舍去;②若c=﹣3,则y1=x2﹣2x﹣3=(x﹣1)2﹣4,y2=﹣3x﹣3,y1向左平移n个单位后,则解析式为:y3=(x﹣1+n)2﹣4,则当x≥1﹣n时,y随x增大而增大,y2向下平移n个单位后,则解析式为:y4=﹣3x﹣3﹣n,要使平移后直线与P有公共点,则当x=1﹣n,y3≤y4,即(1﹣n﹣1+n)2﹣4≤﹣3(1﹣n)﹣3﹣n,解得:n≥1,综上所述:n≥1,2n2﹣5n=2(n﹣)2﹣,∴当n=时,2n2﹣5n的最小值为:﹣.13.(2015•深圳)如图1,关于x的二次函数y=﹣x2+bx+c经过点A(﹣3,0),点C(0,3),点D为二次函数的顶点,DE为二次函数的对称轴,E在x轴上.(1)求抛物线的解析式;(2)DE上是否存在点P到AD的距离与到x轴的距离相等?若存在求出点P,若不存在请说明理由;(3)如图2,DE的左侧抛物线上是否存在点F,使2S△FBC=3S△EBC?若存在求出点F的坐标,若不存在请说明理由.解答:解:(1)∵二次函数y=﹣x2+bx+c经过点A(﹣3,0),点C(0,3),∴,解得,∴抛物线的解析式y=﹣x2﹣2x+3,(2)存在,当P在∠DAB的平分线上时,如图1,作PM⊥AD,设P(﹣1,m),则PM=PD•sin∠ADE=(4﹣m),PE=m,∵PM=PE,∴(4﹣m)=m,m=﹣1,∴P点坐标为(﹣1,﹣1);当P在∠DAB的外角平分线上时,如图2,作PN⊥AD,设P(﹣1,n),则PN=PD•sin∠ADE=(4﹣n),PE=﹣n,∵PM=PE,∴(4﹣n)=﹣n,n=﹣﹣1,∴P点坐标为(﹣1,﹣﹣1);综上可知存在满足条件的P点,其坐标为(﹣1,﹣1)或(﹣1,﹣﹣1);(3)∵S△EBC=3,2S△FBC=3S△EBC,∴S△FBC=,过F作FQ⊥x轴,交BC的延长线于Q,如图3,∵S△FBC=FQ•OB=FQ=,∴FQ=9,∵BC的解析式为y=﹣3x+3,设F(x0,﹣x02﹣2x0+3),∴﹣3x0+3+x02+2x0﹣3=9,解得:x0=或(舍去),∴点F的坐标是(,).14.(9分)(2015•珠海)如图,折叠矩形OABC的一边BC,使点C落在OA边的点D处,已知折痕BE=5,且=,以O为原点,OA所在的直线为x轴建立如图所示的平面直角坐标系,抛物线l:y=﹣x2+x+c经过点E,且与AB边相交于点F.(1)求证:△ABD∽△ODE;(2)若M是BE的中点,连接MF,求证:MF⊥BD;(3)P是线段BC上一点,点Q在抛物线l上,且始终满足PD⊥DQ,在点P运动过程中,能否使得PD=DQ?若能,求出所有符合条件的Q点坐标;若不能,请说明理由.解答:(1)证明:∵四边形ABCO为矩形,且由折叠的性质可知△BCE≌△BDE,∴∠BDE=∠BCE=90°,∵∠BAD=90°,∴∠EDO+∠BDA=∠BDA+∠DAB=90°,∴∠EDO=∠DBA,且∠EOD=∠BAD=90°,∴△ABD∽△ODE;(2)证明:∵=,∴设OD=4x,OE=3x,则DE=5x,∴CE=DE=5x,∴AB=OC=CE+OE=8x,又∵△ABD∽△ODE,∴==,∴DA=6x,∴BC=OA=10x,在Rt△BCE中,由勾股定理可得BE2=BC2+CE2,即(5)2=(10x)2+(5x)2,解得x=1,∴OE=3,OD=4,DA=6,AB=8,OA=10,∴抛物线解析式为y=﹣x2+x+3,当x=10时,代入可得y=,∴AF=,BF=AB﹣AF=8﹣=,在Rt△AFD中,由勾股定理可得DF===,∴BF=DF,又M为Rt△BDE斜边上的中点,∴MD=MB,∴MF为线段BD的垂直平分线,∴MF⊥BD;(3)解:由(2)可知抛物线解析式为y=﹣x2+x+3,设抛物线与x轴的两个交点为H、G,令y=0,可得0=﹣x2+x+3,解得x=﹣4或x=12,∴H(﹣4,0),G(12,0),①当PD⊥x轴时,由于PD=8,DM=DN=8,故点Q的坐标为(﹣4,0)或(12,0)时,△PDQ是以D为直角顶点的等腰直角三角形;②当PD不垂直与x轴时,分别过P,Q作x轴的垂线,垂足分别为N,I,则Q不与G重合,从而I不与G重合,即DI≠8.∵PD⊥DQ,∴∠QDI=90°﹣∠PDN=∠DPN,∴Rt△PDN∽Rt△DQI,∵PN=8,∴PN≠DI,∴Rt△PDN与Rt△DQI不全等,∴PD≠DQ,另一侧同理PD≠DQ.综合①,②所有满足题设条件的点Q的坐标为(﹣4,0)或(12,0).15(12分)(2015•河池)如图1,抛物线y=﹣x2+2x+3与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E(4,0).(1)写出D的坐标和直线l的解析式;(2)P(x,y)是线段BD上的动点(不与B,D重合),PF⊥x轴于F,设四边形OFPC的面积为S,求S与x之间的函数关系式,并求S的最大值;(3)点Q在x轴的正半轴上运动,过Q作y轴的平行线,交直线l于M,交抛物线于N,连接CN,将△CMN沿CN翻转,M的对应点为M′.在图2中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.解答:解:(1)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴D(1,4),当x=0时,y=﹣x2+2x+3=3,则C(0,3),设直线l的解析式为y=kx+b,把C(0,3),E(4,0)分别代入得,解得,∴直线l的解析式为y=﹣x+3;(2)如图(1),当y=0时,﹣x2+2x+3=0,解得x1=﹣1,x2=3,则B(3,0),设直线BD的解析式为y=mx+n,把B(3,0),D(1,4)分别代入得,解得,∴直线BD的解析式为y=﹣2x+6,则P(x,﹣2x+6),∴S=•(﹣2x+6+3)•x=﹣x2+x(1≤x≤3),∵S=﹣(x﹣)2+,∴当x=时,S有最大值,最大值为;(3)存在.如图2,设Q(t,0)(t>0),则M(t,﹣t+3),N(t,﹣t2+2t+3),∴MN=|﹣t2+2t+3﹣(﹣t+3)|=|t2﹣t|,CM==t,∵△CMN沿CN翻转,M的对应点为M′,M′落在y轴上,而QN∥y轴,∴MN∥CM′,NM=NM′,CM′=CM,∠CNM=∠CNM′,∴∠M′CN=∠CNM,∴∠M′CN=∠CNM′,∴CM′=NM′,∴NM=CM,∴|t2﹣t|=t,当t2﹣t=t,解得t1=0(舍去),t2=4,此时Q点坐标为(4,0);当t2﹣t=﹣t,解得t1=0(舍去),t2=,此时Q点坐标为(,0),综上所述,点Q的坐标为(,0)或(4,0).16.(10分)(2015•南宁)在平面直角坐标系中,已知A、B是抛物线y=ax2(a>0)上两个不同的点,其中A在第二象限,B在第一象限,(1)如图1所示,当直线AB与x轴平行,∠AOB=90°,且AB=2时,求此抛物线的解析式和A、B两点的横坐标的乘积.(2)如图2所示,在(1)所求得的抛物线上,当直线AB与x轴不平行,∠AOB仍为90°时,A、B两点的横坐标的乘积是否为常数?如果是,请给予证明;如果不是,请说明理由.(3)在(2)的条件下,若直线y=﹣2x﹣2分别交直线AB,y轴于点P、C,直线AB交y 轴于点D,且∠BPC=∠OCP,求点P的坐标.解答:解:(1)如图1,∵AB与x轴平行,根据抛物线的对称性有AE=BE=1,∵∠AOB=90°,∴OE=AB=1,∴A(﹣1,1)、B(1,1),把x=1时,y=1代入y=ax2得:a=1,∴抛物线的解析式y=x2,A、B两点的横坐标的乘积为x A•x B=﹣1(2)x A•x B=﹣1为常数,如图2,过A作AM⊥x轴于M,BN⊥x轴于N,∴∠AMO=∠BNO=90°,∴∠MAO+∠AOM=∠AOM+∠BON=90°,∴∠MAO=∠BON,∴△AMO∽△BON,∴,∴OM•ON=AM•BN,设A(x A,y A),B(x B,y B),∵A(x A,y A),B(x B,y B)在y=x2图象上,∴,y A=,y B=,∴﹣x A•x B=y A•y B=•,∴x A•x B=﹣1为常数;(3)设A(m,m2),B(n,n2),如图3所示,过点A、B分别作x轴的垂线,垂足为E、F,则易证△AEO∽△OFB.∴,即,整理得:mn(mn+1)=0,∵mn≠0,∴mn+1=0,即mn=﹣1.设直线AB的解析式为y=kx+b,联立,得:x2﹣kx﹣b=0.∵m,n是方程的两个根,∴mn=﹣b.∴b=1.∵直线AB与y轴交于点D,则OD=1.易知C(0,﹣2),OC=2,∴CD=OC+OD=3.∵∠BPC=∠OCP,∴PD=CD=3.设P(a,﹣2a﹣2),过点P作PG⊥y轴于点G,则PG=﹣a,GD=OG﹣OD=﹣2a﹣3.在Rt△PDG中,由勾股定理得:PG2+GD2=PD2,即:(﹣a)2+(﹣2a﹣3)2=32,整理得:5a2+12a=0,解得a=0(舍去)或a=﹣,当a=﹣时,﹣2a﹣2=,∴P(﹣,).16.(2015•北海)如图1所示,已知抛物线y=﹣x2+4x+5的顶点为D,与x轴交于A、B两点,与y轴交于C点,E为对称轴上的一点,连接CE,将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上.(1)直接写出D点和E点的坐标;(2)点F为直线C′E与已知抛物线的一个交点,点H是抛物线上C与F之间的一个动点,若过点H作直线HG与y轴平行,且与直线C′E交于点G,设点H的横坐标为m(0<m<4),那么当m为何值时,S△HGF:S△BGF=5:6?(3)图2所示的抛物线是由y=﹣x2+4x+5向右平移1个单位后得到的,点T(5,y)在抛物线上,点P是抛物线上O与T之间的任意一点,在线段OT上是否存在一点Q,使△PQT 是等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.解答:解:(1)∵抛物线y=﹣x2+4x+5=﹣(x﹣2)2+9∴D点的坐标是(2,9);∵E为对称轴上的一点,∴点E的横坐标是:﹣=2,设点E的坐标是(2,m),点C′的坐标是(0,n),∵将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上,∴△CEC′是等腰直角三角形,∴解得或(舍去),∴点E的坐标是(2,3),点C′的坐标是(0,1).综上,可得D点的坐标是(2,9),点E的坐标是(2,3).(2)如图1所示:令抛物线y=﹣x2+4x+5的y=0得:x2﹣4x﹣5=0,解得:x1=﹣1,x2=5,所以点A(﹣1,0),B(5,0).设直线C′E的解析式是y=kx+b,将E(2,3),C′(0,1),代入得,解得:,∴直线C′E的解析式为y=x+1,将y=x+1与y=﹣x2+4x+5,联立得:,解得:,,∴点F得坐标为(4,5),点A(﹣1,0)在直线C′E上.∵直线C′E的解析式为y=x+1,∴∠FAB=45°.过点B、H分别作BN⊥AF、HM⊥AF,垂足分别为N、M.∴∠HMN=90°,∠ADN=90°.又∵∠NAD=∠HNM=45°.∴△HGM∽△ABN∴,∵S△HGF:S△BGF=5:6,∴.∴,即,∴HG=5.设点H的横坐标为m,则点H的纵坐标为﹣m2+4m+5,则点G的坐标为(m,m+1),∴﹣m2+4m+5﹣(m+1)=5.解得:m1=,m2=.(3)由平移的规律可知:平移后抛物线的解析式为y=﹣(x﹣1)2+4(x﹣1)+5=﹣x2+6x.将x=5代入y=﹣x2+6x得:y=5,∴点T的坐标为(5,5).设直线OT的解析式为y=kx,将x=5,y=5代入得;k=1,∴直线OT的解析式为y=x,①如图2所示:当PT∥x轴时,△PTQ为等腰直角三角形,将y=5代入抛物线y=﹣x2+6x得:x2﹣6x+5=0,解得:x1=1,x2=5.∴点P的坐标为(1,5).将x=1代入y=x得:y=1,∴点Q的坐标为(1,1).②如图3所示:由①可知:点P的坐标为(1,5).∵△PTQ为等腰直角三角形,∴点Q的横坐标为3,将x=3代入y=x得;y=3,∴点Q得坐标为(3,3).③如图4所示:设直线PT解析式为y=kx+b,∵直线PT⊥QT,∴k=﹣1.将k=﹣1,x=5,y=5代入y=kx+b得:b=10,∴直线PT的解析式为y=﹣x+10.将y=﹣x+10与y=﹣x2+6x联立得:x1=2,x2=5∴点P的横坐标为2.将x=2代入y=x得,y=2,∴点Q的坐标为(2,2).综上所述:点Q的坐标为(1,1)或(3,3)或(2,2).17.(10分)(2015•贵港)如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y 轴交于点C(0,3),其对称轴I为x=﹣1.(1)求抛物线的解析式并写出其顶点坐标;(2)若动点P在第二象限内的抛物线上,动点N在对称轴I上.①当PA⊥NA,且PA=NA时,求此时点P的坐标;②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.解答:解:(1)∵抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴I为x=﹣1,∴,解得:.∴二次函数的解析式为y=﹣x2﹣2x+3=﹣(x+1)2+4,∴顶点坐标为(﹣1,4);(2)令y=﹣x2﹣2x+3=0,解得x=﹣3或x=1,∴点A(﹣3,0),B(1,0),作PD⊥x轴于点D,∵点P在y=﹣x2﹣2x+3上,∴设点P(x,﹣x2﹣2x+3)①∵PA⊥NA,且PA=NA,∴△PAD≌△AND,∴OA=PD即y=﹣x2﹣2x+3=2,解得x=﹣1(舍去)或x=﹣﹣1,∴点P(﹣﹣1,2);②∵S四边形BCPA=S△OBC+S△OAC=2+S△APC∵S△AOC=,S△OCP=x,S△OAP=•3•|y P|=﹣x2﹣3x+∴S△APC=S△OAP+S△OCP﹣S△AOC=x+(﹣x2﹣3x+)﹣=﹣x2﹣x=﹣(x﹣)2+,∴当x=﹣时,S△ACP最大值=,此时M(﹣,﹣),S四边形PABC最大=.18.(12分)(2015•桂林)如图,已知抛物线y=﹣x2+bx+c与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O 时,点C、D停止运动.(1)直接写出抛物线的解析式:y=﹣x2+3x+8;(2)求△CED的面积S与D点运动时间t的函数解析式;当t为何值时,△CED的面积最大?最大面积是多少?(3)当△CED的面积最大时,在抛物线上是否存在点P(点E除外),使△PCD的面积等于△CED的最大面积?若存在,求出P点的坐标;若不存在,请说明理由.解答:解:(1)将点A(0,8)、B(8,0)代入抛物线y=﹣x2+bx+c得:,解得:b=3,c=8,∴抛物线的解析式为:y=﹣x2+3x+8,故答案为:y=﹣x2+3x+8;(2)∵点A(0,8)、B(8,0),∴OA=8,OB=8,令y=0,得:﹣x2+3x+8=0,解得:x18,x2=2,∵点E在x轴的负半轴上,∴点E(﹣2,0),∴OE=2,根据题意得:当D点运动t秒时,BD=t,OC=t,∴OD=8﹣t,∴DE=OE+OD=10﹣t,∴S=•DE•OC=•(10﹣t)•t=﹣t2+5t,即S=﹣t2+5t=﹣(t﹣5)2+,∴当t=5时,S最大=;(3)由(2)知:当t=5时,S最大=,∴当t=5时,OC=5,OD=3,∴C(0,5),D(3,0),由勾股定理得:CD=,设直线CD的解析式为:y=kx+b,将C(0,5),D(3,0),代入上式得:k=﹣,b=5,∴直线CD的解析式为:y=﹣x+5,过E点作EF∥CD,交抛物线与点P,如图1,设直线EF的解析式为:y=﹣x+b,将E(﹣2,0)代入得:b=﹣,∴直线EF的解析式为:y=﹣x﹣,将y=﹣x﹣,与y=﹣x2+3x+8联立成方程组得:,解得:,,∴P(,﹣);过点E作EG⊥CD,垂足为G,∵当t=5时,S△ECD==,∴EG=,过点D作DN⊥CD,垂足为N,且使DN=,过点N作NM⊥x轴,垂足为M,如图2,可得△EGD∽△DMN,∴,即:,解得:DM=,∴OM=,由勾股定理得:MN==,∴N(,),过点N作NH∥CD,与抛物线交与点P,如图2,设直线NH的解析式为:y=﹣x+b,将N(,),代入上式得:b=,∴直线NH的解析式为:y=﹣x+,将y=﹣x+,与y=﹣x2+3x+8联立成方程组得:,解得:,,∴P(8,0)或P(,),综上所述:当△CED的面积最大时,在抛物线上存在点P(点E除外),使△PCD的面积等于△CED的最大面积,点P的坐标为:P(,﹣)或P(8,0)或P(,).19.(14分)(2015•安顺)如图,抛物线y=ax2+bx+与直线AB交于点A(﹣1,0),B(4,),点D是抛物线A,B两点间部分上的一个动点(不与点A,B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.(1)求抛物线的解析式;(2)设点D的横坐标为m,△ADB的面积为S,求S关于m的函数关系式,并求出当S 取最大值时的点C的坐标.解答:解:(1)由题意得,解得:,∴y=﹣x2+2x+.(2)设直线AB解析式为:y=kx+b,则有,解得:,∴y=x+,则D(m,﹣m2+2m+),C(m,m+),CD=(﹣m2+2m+)﹣(m+)=﹣m2+m+2,∴S=(m+1)•CD+(4﹣m)•CD=×5×CD=×5×(﹣m2+m+2)=﹣m2+m+5∵﹣<0,∴当m=时,S有最大值,当m=时,m+=×+=,∴点C(,).20.(16分)(2015•毕节市)如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,顶点M关于x轴的对称点是M′.(1)求抛物线的解析式;(2)若直线AM′与此抛物线的另一个交点为C,求△CAB的面积;(3)是否存在过A,B两点的抛物线,其顶点P关于x轴的对称点为Q,使得四边形APBQ 为正方形?若存在,求出此抛物线的解析式;若不存在,请说明理由.解答:解:(1)将A、B点坐标代入函数解析式,得,解得,抛物线的解析式y=x2﹣2x﹣3;(2)将抛物线的解析式化为顶点式,得y=(x﹣1)2﹣4,M点的坐标为(1,﹣4),M′点的坐标为(1,4),设AM′的解析式为y=kx+b,将A、M′点的坐标代入,得,解得,AM′的解析式为y=2x+2,联立AM′与抛物线,得,解得,C点坐标为(5,12).S△ABC=×4×12=24;(3)存在过A,B两点的抛物线,其顶点P关于x轴的对称点为Q,使得四边形APBQ 为正方形,由ABPQ是正方形,A(﹣1,0)B(3,0),得P(1,﹣2),Q(1,2),或P(1,2),Q(1,﹣2),①当顶点P(1,﹣2)时,设抛物线的解析式为y=a(x﹣1)2﹣2,将A点坐标代入函数解析式,得a(﹣1﹣1)2﹣2=0,解得a=,抛物线的解析式为y=(x﹣1)2﹣2,②当P(1,2)时,设抛物线的解析式为y=a(x﹣1)2+2,将A点坐标代入函数解析式,得a(﹣1﹣1)2+2=0,解得a=﹣,抛物线的解析式为y=﹣(x﹣1)2+2,综上所述:y=(x﹣1)2﹣2或y=﹣(x﹣1)2+2,使得四边形APBQ为正方形.21.(16分)(2015•六盘水)如图,已知图①中抛物线y=ax2+bx+c经过点D(﹣1,0),D (0,﹣1),E(1,0).(1)求图①中抛物线的函数表达式.(2)将图①中的抛物线向上平移一个单位,得到图②中的抛物线,点D与点D1是平移前后的对应点,求该抛物线的函数表达式.(3)将图②中的抛物线绕原点O顺时针旋转90°后得到图③中的抛物线,所得到抛物线表达式为y2=2px,点D1与D2是旋转前后的对应点,求图③中抛物线的函数表达式.(4)将图③中的抛物线绕原点O顺时针旋转90°后与直线y=﹣x﹣1相交于A、B两点,D2与D3是旋转前后如图④,求线段AB的长.解答:解:(1)将D、C、E的坐标代入函数解析式,得,解得.图①中抛物线的函数表达式y=x2﹣1;(2)将抛物线的函数表达式y=x2﹣1向上平移1个单位,得y=x2,该抛物线的函数表达式y=x2;(3)将抛物线的函数表达式y=x2绕原点O顺时针旋转90°,得x=y2,图③中抛物线的函数表达式x=y2;(4)将图③中抛物线的函数表达式x=y2绕原点O顺时针旋转90°,得y=﹣x2,联立,。
2015年中考数学压轴题精选—二次函数(16题)_附详细解答和评分标准

2015全国中考数学压轴题精选——二次函数1、(10广东茂名25题)(本题满分10分)如图,在平面直角坐标系中,抛物线y =-32x 2+b x +c 经过A (0,-4)、B (x 1,0)、 C (x 2,0)三点,且x 2-x 1=5. (1)求b 、c 的值;(4分)(2)在抛物线上求一点D ,使得四边形BDCE 是以BC 为对角线的菱形;(3分)(3)在抛物线上是否存在一点P ,使得四边形B P O H 是以OB 为对角线的菱形?若存在,求出点P 的坐标,并判断这个菱形是否为正方形?若不存在,请说明理由.(3分)解:解:(1)解法一: ∵抛物线y =-32x 2+b x +c 经过点A (0,-4), ∴c =-4 ……1分又由题意可知,x 1、x 2是方程-32x 2+b x +c =0的两个根, ∴x 1+x 2=23b , x 1x 2=-23c =6 ·························································· 2分 由已知得(x 2-x 1)2=25 又(x 2-x 1)2=(x 2+x 1)2-4x 1x 2=49b 2-24 ∴49b 2-24=25 解得b =±314···························································································· 3分当b =314时,抛物线与x 轴的交点在x 轴的正半轴上,不合题意,舍去.∴b =-314. ··························································································· 4分 解法二:∵x 1、x 2是方程-32x 2+b x +c=0的两个根, 即方程2x 2-3bx +12=0的两个根.(第25题图)x∴x =4969b 32-±b , ································································· 2分∴x 2-x 1=2969b 2-=5,解得 b =±314 ·················································································· 3分 (以下与解法一相同.)(2)∵四边形BDCE 是以BC 为对角线的菱形,根据菱形的性质,点D 必在抛物线的对称轴上, ···················································································· 5分又∵y =-32x 2-314x -4=-32(x +27)2+625····························· 6分 ∴抛物线的顶点(-27,625)即为所求的点D . ································· 7分(3)∵四边形BPOH 是以OB 为对角线的菱形,点B 的坐标为(-6,0),根据菱形的性质,点P 必是直线x =-3与抛物线y =-32x 2-314x -4的交点, ···················································· 8分 ∴当x =-3时,y =-32×(-3)2-314×(-3)-4=4,∴在抛物线上存在一点P (-3,4),使得四边形BPOH 为菱形. ··············· 9分 四边形BPOH 不能成为正方形,因为如果四边形BPOH 为正方形,点P 的坐标只能是(-3,3),但这一点不在抛物线上. ············································· 10分 2、(08广东肇庆25题)(本小题满分10分)已知点A (a ,1y )、B (2a ,y 2)、C (3a ,y 3)都在抛物线x x y 1252+=上. (1)求抛物线与x 轴的交点坐标; (2)当a =1时,求△ABC 的面积;(3)是否存在含有1y 、y 2、y 3,且与a 无关的等式?如果存在,试给出一个,并加以证明;如果不存在,说明理由.解:(1)由5x x 122+=0, ··································································· (1分)得01=x ,5122-=x . ······································································· (2分) ∴抛物线与x 轴的交点坐标为(0,0)、(512-,0). ································· (3分)(2)当a =1时,得A (1,17)、B (2,44)、C (3,81), ·························· (4分)分别过点A 、B 、C 作x 轴的垂线,垂足分别为D 、E 、F ,则有ABC S ∆=S ADFC 梯形 -ADEB S 梯形 -BEFC S 梯形 ············································· (5分) =22)8117(⨯+-21)4417(⨯+-21)8144(⨯+ ······························· (6分)=5(个单位面积) ······························································ (7分)(3)如:)(3123y y y -=. ······························································· (8分)事实上,)3(12)3(523a a y ⨯+⨯= =45a 2+36a . 3(12y y -)=3[5×(2a )2+12×2a -(5a 2+12a )] =45a 2+36a . ··········· (9分) ∴)(3123y y y -=. ········································································ (10分) 3、(08辽宁沈阳26题)(本题14分)26.如图所示,在平面直角坐标系中,矩形ABOC 的边BO 在x 轴的负半轴上,边OC 在y 轴的正半轴上,且1AB =,OB =ABOC 绕点O 按顺时针方向旋转60 后得到矩形EFOD .点A 的对应点为点E ,点B的对应点为点F ,点C 的对应点为点D ,抛物线2y ax bx c =++过点A E D ,,.(1)判断点E 是否在y 轴上,并说明理由; (2)求抛物线的函数表达式;(3)在x 轴的上方是否存在点P ,点Q ,使以点O B P Q ,,,为顶点的平行四边形的面积是矩形ABOC 面积的2倍,且点P 在抛物线上,若存在,请求出点P ,点Q 的坐标;若不存在,请说明理由.解:(1)点E 在y 轴上 ··············································································· 1分 理由如下:连接AO ,如图所示,在Rt ABO △中,1AB =,BO =,2AO ∴=1sin 2AOB ∴∠=,30AOB ∴∠=由题意可知:60AOE ∠=306090BOE AOB AOE ∴∠=∠+∠=+=点B 在x 轴上,∴点E 在y 轴上. ······························································· 3分x第26题图(2)过点D 作DM x ⊥轴于点M1OD = ,30DOM ∠=∴在Rt DOM △中,12DM =,2OM = 点D 在第一象限,∴点D 的坐标为12⎫⎪⎪⎝⎭, ············································································· 5分 由(1)知2EO AO ==,点E 在y 轴的正半轴上∴点E 的坐标为(02),∴点A的坐标为( ··············································································· 6分 抛物线2y ax bx c =++经过点E ,2c ∴=由题意,将(A ,12D ⎫⎪⎪⎝⎭,代入22y ax bx =++中得32131242a a ⎧-+=⎪⎨++=⎪⎩解得89a b ⎧=-⎪⎪⎨⎪=⎪⎩∴所求抛物线表达式为:2829y x x =-+ ················································ 9分 (3)存在符合条件的点P ,点Q . ······························································ 10分 理由如下: 矩形ABOC的面积AB BO == ∴以O B P Q ,,,为顶点的平行四边形面积为由题意可知OB 为此平行四边形一边,又OB =OB ∴边上的高为2 ···················································································· 11分依题意设点P 的坐标为(2)m ,点P在抛物线2829y x =-+上282299m m ∴--+=解得,10m =,28m =-1(02)P ∴,,228P ⎛⎫- ⎪ ⎪⎝⎭以O B P Q ,,,为顶点的四边形是平行四边形,PQ OB ∴∥,PQ OB == ∴当点1P 的坐标为(02),时, 点Q的坐标分别为1(Q,2Q ;当点2P的坐标为2⎛⎫⎪ ⎪⎝⎭时,点Q的坐标分别为32Q ⎛⎫ ⎪ ⎪⎝⎭,42Q ⎫⎪⎪⎝⎭. ········································ 14分4、(08辽宁12市26题)(本题14分)26.如图16,在平面直角坐标系中,直线y =与x 轴交于点A ,与y 轴交于点C ,抛物线2(0)y ax x c a =+≠经过A B C ,,三点.(1)求过A B C ,,三点抛物线的解析式并求出顶点F 的坐标;(2)在抛物线上是否存在点P ,使ABP △为直角三角形,若存在,直接写出P 点坐标;若不存在,请说明理由; (3)试探究在直线AC 上是否存在一点M ,使得MBF △的周长最小,若存在,求出M 点的坐标;若不存在,请说明理由.解:(1)直线y =x 轴交于点A ,与y 轴交于点C .(10)A ∴-,,(0C ············································································· 1分 点A C ,都在抛物线上,x0a c c⎧=++⎪∴⎨⎪=⎩a c ⎧=⎪∴⎨⎪=⎩ ∴抛物线的解析式为2y x x =················································· 3分 ∴顶点1F ⎛ ⎝⎭ ·················································································· 4分 (2)存在 ································································································ 5分1(0P ······························································································ 7分2(2P ····························································································· 9分 (3)存在 ······························································································ 10分理由: 解法一:延长BC 到点B ',使BC B C '=,连接B F '交直线AC 于点M ,则点M 就是所求的点.········································································· 11分 过点B '作B H AB '⊥于点H .B点在抛物线2y x x =(30)B ∴,在Rt BOC △中,tan OBC ∠=,30OBC ∴∠=,BC =在Rt BB H '△中,12B H BB ''==6BH H '=,3OH ∴=,(3B '∴--, ········································ 12分 设直线B F '的解析式为y kx b =+33k b k b ⎧-=-+⎪∴⎨-=+⎪⎩解得2k b ⎧=⎪⎪⎨⎪=-⎪⎩62y x ∴=-················································································· 13分xy y x ⎧=⎪∴⎨=⎪⎩解得37x y ⎧=⎪⎪⎨⎪=⎪⎩37M ⎛∴ ⎝⎭, ∴在直线AC 上存在点M ,使得MBF △的周长最小,此时37M ⎛ ⎝⎭,. ·· 14分 5、(08青海西宁28题)如图14,已知半径为1的1O 与x 轴交于A B ,两点,OM 为1O 的切线,切点为M ,圆心1O 的坐标为(20),,二次函数2y x bx c =-++的图象经过A B ,两点.(1)求二次函数的解析式;(2)求切线OM 的函数解析式;(3)线段OM 上是否存在一点P ,使得以P O A ,,为顶点的三角形与1OO M △相似.若存在,请求出所有符合条件的点P 的坐标;若不存在,请说明理由.解:(1) 圆心1O 的坐标为(20),,1O 半径为1,(10)A ∴,,(30)B ,……1分二次函数2y x bx c =-++的图象经过点A B ,,∴可得方程组10930b c b c -++=⎧⎨-++=⎩····································································· 2分 解得:43b c =⎧⎨=-⎩∴二次函数解析式为243y x x =-+- ······································· 3分 (2)过点M 作MF x ⊥轴,垂足为F . ······················································ 4分OM 是1O 的切线,M 为切点,1O M OM ∴⊥(圆的切线垂直于经过切点的半径). 在1Rt OO M △中,1111sin 2O M O OM OO ∠== 1O OM ∠ 为锐角,130OOM ∴∠= ························ 5分1cos3022OM OO ∴==⨯=图14在Rt MOF △中,3cos3022OF OM ===.1sin 3022MF OM ===. ∴点M 坐标为322⎛ ⎝⎭,············································································· 6分设切线OM 的函数解析式为(0)y kx k =≠32k =,k ∴=····· 7分∴切线OM 的函数解析式为y x =··························································· 8分 (3)存在. ····························································································· 9分 ①过点A 作1AP x ⊥轴,与OM 交于点1P .可得11Rt Rt APO MOO △∽△(两角对应相等两三角形相似)11tan tan 30P A OA AOP =∠==,11P ⎛∴ ⎝⎭····································· 10分 ②过点A 作2AP OM ⊥,垂足为2P ,过2P 点作2P H OA ⊥,垂足为H . 可得21Rt Rt APO O MO △∽△(两角对应相等两三角开相似)在2Rt OP A △中,1OA = ,2cos30OP OA ∴==在2Rt OP H △中,223cos 4OH OPAOP =∠== ,2221sin 2P H OP AOP =∠== ,234P ⎛∴ ⎝⎭ ································· 11分∴符合条件的P 点坐标有1⎛ ⎝⎭,34⎛ ⎝⎭·············································· 12分6、(08山东济宁26题)(12分)ABC △中,90C ∠= ,60A ∠= ,2AC =cm .长为1cm 的线段MN 在ABC △的边AB 上沿AB 方向以1cm/s 的速度向点B 运动(运动前点M 与点A 重合).过M N ,分别作AB 的垂线交直角边于P Q ,两点,线段MN 运动的时间为t s .(1)若AMP △的面积为y ,写出y 与t 的函数关系式(写出自变量t 的取值范围);(2)线段MN 运动过程中,四边形MNQP 有可能成为矩形吗?若有可能,求出此时t 的值;若不可能,说明理由;(3)t 为何值时,以C P Q ,,为顶点的三角形与ABC △相似?解:(1)当点P 在AC 上时,AM t = ,tg60PM AM ∴== .21(01)22y t t ∴==≤≤. ······························································ 2分当点P 在BC 上时,tan 30)PM BM t ==-.21)(13)2y t t t =-=≤≤. ··········································· 4分(2)2AC = ,4AB ∴=.413BN AB AM MN t t ∴=--=--=-.tan 30)3QN BN t ∴==- . ······························································ 6分由条件知,若四边形MNQP 为矩形,需PM QN =)t =-, 34t ∴=. ∴当34t =s 时,四边形MNQP 为矩形.························································ 8分 (3)由(2)知,当34t =s 时,四边形MNQP 为矩形,此时PQ AB ∥,PQC ABC ∴△∽△. ··············································································· 9分除此之外,当30CPQ B ∠=∠=时,QPC ABC △∽△,此时tan 30CQ CP ==1cos 602AM AP ==,22AP AM t ∴==.22CP t ∴=-. ························ 10分cos302BN BQ ==,)BQ t ∴==-.又BC =)CQ t ∴=-=·································· 11分322t ∴=-12t =. ∴当12t =s 或34s 时,以C P Q ,,为顶点的三角形与ABC △相似. ··············· 12分7、(08四川巴中30题)(12分)30.已知:如图14,抛物线2334y x =-+与x 轴交于点A ,点B ,与直线34y x b =-+相交于点B ,点C ,直线34y x b =-+与y轴交于点E .(1)写出直线BC 的解析式. (2)求ABC △的面积.(3)若点M 在线段AB 上以每秒1个单位长度的速度从A 向B 运动(不与A B ,重合),同时,点N 在射线BC 上以每秒2个单位长度的速度从B 向C 运动.设运动时间为t 秒,请写出MNB △的面积S 与t 的函数关系式,并求出点M 运动多少时间时,MNB △的面积最大,最大面积是多少?解:(1)在2334y x =-+中,令0y =23304x ∴-+=12x ∴=,22x =-(20)A ∴-,,(20)B , ········································· 1分又 点B 在34y x b =-+上302b ∴=-+32b =BC ∴的解析式为3342y x =-+ ··································································· 2分(2)由23343342y x y x ⎧=-+⎪⎪⎨⎪=-+⎪⎩,得11194x y =-⎧⎪⎨=⎪⎩222x y =⎧⎨=⎩ ············································· 4分 914C ⎛⎫∴- ⎪⎝⎭,,(20)B ,4AB ∴=,94CD =················································································· 5分 1994242ABC S ∴=⨯⨯=△ ············································································ 6分(3)过点N 作NP MB ⊥于点P EO MB ⊥ NP EO ∴∥BNP BEO ∴△∽△ ·················································································· 7分 BN NP BE EO ∴= ··························································································· 8分 由直线3342y x =-+可得:302E ⎛⎫ ⎪⎝⎭, ∴在BEO △中,2BO =,32EO =,则52BE = 25322t NP∴=,65NP t ∴= ··········································································· 9分 16(4)25S t t ∴=-2312(04)55S t t t =-+<< ········································································ 10分2312(2)55S t =--+ ················································································ 11分此抛物线开口向下,∴当2t =时,125S =最大∴当点M 运动2秒时,MNB △的面积达到最大,最大为125. ······················· 12分。
2015年中考数学汇总:二次函数真题

2015年中考数学汇总:二次函数真题练习一、选择题1.(2015,广西柳州,11,3分)如图,二次函数y=ax2+bx+c的图象与x轴相交于(﹣2,0)和(4,0)两点,当函数值y>0时,自变量x的取值范围是()A.x<﹣2B.﹣2<x<4C.x>0D.x>42.(2015,广西玉林,12,3分)如图,反比例函数y=的图象经过二次函数y=ax2+bx图象的顶点(﹣,m)(m>0),则有()A.a=b+2k B.a=b﹣2k C.k<b<0D.a<k<03.(2015,广西河池,8,3分)将抛物线y=x2向右平移2个单位,再向上平移3个单位后,抛物线的解析式为(B)A.y=(x+2)2+3B.y=(x-2)2+3C.y=(x+2)2﹣3D.y=(x-2)-34. (2015•齐齐哈尔,第9题3分)抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则下列结论:①4ac﹣b2<0;②2a﹣b=0;③a+b+c<0;④点M (x1,y1)、N(x2,y2)在抛物线上,若x1<x2,则y1≤y2,其中正确结论的个数是()A.1个B.2个C.3个D.4个5. (2015•内蒙古呼伦贝尔兴安盟,第11题3分)二次函数y=(x+2)2﹣1的图象大致为()A.B.C.6. (2015•天津,第12题3分)(2015•天津)已知抛物线y=﹣x2+x+6与x轴交于点A,点B,与y轴交于点C.若D为AB的中点,则CD的长为()A.B.C.D.7.(2015•贵州省贵阳,第10题3分)已知二次函数y=﹣x2+2x+3,当x≥2时,y的取值范围是()A.y≥3B.y≤3C.y>3D.y<38. (2015•贵州省黔东南州,第10题4分)如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0,②a+b+c>0,③a>b,④4ac﹣b2<0;其中正确的结论有()A.1个B.2个C.3个D.4个9. (2015•黑龙江省大庆,第9题3分)已知二次函数y=a(x﹣2)2+c,当x=x1时,函数值为y1;当x=x2时,函数值为y2,若|x1﹣2|>|x2﹣2|,则下列表达式正确的是()A.y1+y2>0 B.y1﹣y2>0 C.a(y1﹣y2)>0 D.a(y1+y2)>010. (2015•辽宁省盘锦,第8题3分)如图是二次函数y=ax2+bx+c=(a≠0)图象的一部分,对称轴是直线x=﹣2.关于下列结论:①ab<0;②b2﹣4ac>0;③9a﹣3b+c<0;④b﹣4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=﹣4,其中正确的结论有()A.①③④B.②④⑤C.①②⑤D.②③⑤11.(4分)(2015•黔西南州)(第9题)如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=6cm,动点P从点C沿CA,以1cm/s的速度向点A运动,同时动点O从点C沿CB,以2cm/s的速度向点B运动,其中一个动点到达终点时,另一个动点也停止运动.则运动过程中所构成的△CPO的面积y(cm2)与运动时间x(s)之间的函数图象大致是()A.B.C.D.二、填空题1. (2015•宁德第15题4分)二次函数y=x2﹣4x﹣3的顶点坐标是(,).2.(2015福建龙岩15,3分)抛物线y=2x2﹣4x+3绕坐标原点旋转180°所得的抛物线的解析式是3. (2015•辽宁省朝阳,第15题3分)一个足球被从地面向上踢出,它距地面的高度h(m)与足球被踢出后经过的时间t(s)之间具有函数关系h=at2+19.6t,已知足球被踢出后经过4s落地,则足球距地面的最大高度是m.三、解答题1. (2015•福建第22题10分)已知二次函数y=﹣x2+2x+m.(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标.2. (2015•甘南州第17题7分)已知抛物线y=ax2+bx+3的对称轴是直线x=1.(1)求证:2a+b=0;(2)若关于x的方程ax2+bx﹣8=0的一个根为4,求方程的另一个根..3. (2015•宁德第24题4分)已知抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,O是坐标原点,点A的坐标是(﹣1,0),点C的坐标是(0,﹣3).(1)求抛物线的函数表达式;(2)求直线BC的函数表达式和∠ABC的度数;(3)P为线段BC上一点,连接AC,AP,若∠ACB=∠PAB,求点P的坐标.4. (2015•福建第24题12分)如图,在平面直角坐标系中,顶点为A(1,﹣1)的抛物线经过点B(5,3),且与x轴交于C,D两点(点C在点D的左侧).(1)求抛物线的解析式;(2)求点O到直线AB的距离;(3)点M在第二象限内的抛物线上,点N在x轴上,且∠MND=∠OAB,当△DMN与△OAB相似时,请你直接写出点M的坐标.5. (2015•甘南州第22题9分)如图,折叠矩形OABC的一边BC,使点C落在OA边的点D处,已知折痕BE=5,且=,以O为原点,OA所在的直线为x轴建立如图所示的平面直角坐标系,抛物线l:y=﹣x2+x+c 经过点E,且与AB边相交于点F.(1)求证:△ABD∽△ODE;(2)若M是BE的中点,连接MF,求证:MF⊥BD;(3)P是线段BC上一点,点Q在抛物线l上,且始终满足PD⊥DQ,在点P运动过程中,能否使得PD=DQ?若能,求出所有符合条件的Q点坐标;若不能,请说明理由.考点:二次函数综合题..分析:(1)由折叠和矩形的性质可知∠EDB=∠BCE=90°,可证得∠EDO=∠DBA,可证明△ABD∽△ODE;(2)由条件可求得OD、OE的长,可求得抛物线解析式,结合(1)由相似三角形的性质可求得DA、AB,可求得F点坐标,可得到BF=DF,又由直角三角形的性质可得MD=MB,可证得MF为线段BD的垂直平分线,可证得结论;(3)过D作x轴的垂线交BC于点G,设抛物线与x轴的两个交点分别为M、N,可求得DM=DN=DG,可知点M、N为满足条件的点Q,可求得Q点坐标.解答:(1)证明:∵四边形ABCO为矩形,且由折叠的性质可知△BCE≌△BDE,∴∠BDE=∠BCE=90°,∵∠BAD=90°,∴∠EDO+∠BDA=∠BDA+∠DAB=90°,∴∠EDO=∠DBA,且∠EOD=∠BAD=90°,∴△ABD∽△ODE;(2)证明:∵=,∴设OD=4x,OE=3x,则DE=5x,∴CE=DE=5x,∴AB=OC=CE+OE=8x,又∵△ABD∽△ODE,∴==,∴DA=6x,∴BC=OA=10x,在Rt△BCE中,由勾股定理可得BE2=BC2+CE2,即(5)2=(10x)2+(5x)2,解得x=1,∴OE=3,OD=4,DA=6,AB=8,OA=10,∴抛物线解析式为y=﹣x2+x+3,当x=10时,代入可得y=,∴AF=,BF=AB﹣AF=8﹣=,在Rt△AFD中,由勾股定理可得DF===,∴BF=DF,又M为Rt△BDE斜边上的中点,∴MD=MB,∴MF为线段BD的垂直平分线,∴MF⊥BD;(3)解:由(2)可知抛物线解析式为y=﹣x2+x+3,设抛物线与x轴的两个交点为M、N,令y=0,可得0=﹣x2+x+3,解得x=﹣4或x=12,∴M(﹣4,0),N(12,0),过D作DG⊥BC于点G,如图所示,则DG=DM=DN=8,∴点M、N即为满足条件的Q点,∴存在满足条件的Q点,其坐标为(﹣4,0)或(12,0).点评:6. (2015•甘南州第28题12分)如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c,经过A(0,﹣4),B(x1,0),C(x2,0)三点,且|x2﹣x1|=5.(1)求b,c的值;(2)在抛物线上求一点D,使得四边形BDCE是以BC为对角线的菱形;(3)在抛物线上是否存在一点P,使得四边形BPOH是以OB为对角线的菱形?若存在,求出点P的坐标,并判断这个菱形是否为正方形?若不存在,请说明理由.考点:二次函数综合题.分析:(1)把A(0,﹣4)代入可求c,运用两根关系及|x2﹣x1|=5,对式子合理变形,求b;(2)因为菱形的对角线互相垂直平分,故菱形的另外一条对角线必在抛物线的对称轴上,满足条件的D点,就是抛物线的顶点;(3)由四边形BPOH是以OB为对角线的菱形,可得PH垂直平分OB,求出OB的中点坐标,代入抛物线解析式即可,再根据所求点的坐标与线段OB的长度关系,判断是否为正方形即可.解答:解:(1)∵抛物线y=﹣x2+bx+c,经过点A(0,﹣4),∴c=﹣4又∵由题意可知,x1、x2是方程﹣x2+bx﹣4=0的两个根,∴x1+x2=b,x1x2=6由已知得(x2﹣x1)2=25又∵(x2﹣x1)2=(x2+x1)2﹣4x1x2=b2﹣24∴b2﹣24=25解得b=±,当b=时,抛物线与x轴的交点在x轴的正半轴上,不合题意,舍去.∴b=﹣.(2)∵四边形BDCE是以BC为对角线的菱形,根据菱形的性质,点D必在抛物线的对称轴上,又∵y=﹣x2﹣x﹣4=﹣(x+)2+,∴抛物线的顶点(﹣,)即为所求的点D.(3)∵四边形BPOH是以OB为对角线的菱形,点B的坐标为(﹣6,0),根据菱形的性质,点P必是直线x=﹣3与抛物线y=﹣x2﹣x﹣4的交点,∴当x=﹣3时,y=﹣×(﹣3)2﹣×(﹣3)﹣4=4,∴在抛物线上存在一点P(﹣3,4),使得四边形BPOH为菱形.四边形BPOH不能成为正方形,因为如果四边形BPOH为正方形,点P的坐标只能是(﹣3,3),但这一点不在抛物线上点评:本题考查了抛物线解析式的求法,根据菱形,正7.(2015•辽宁铁岭)(第24题)某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.图,求出y与x之间的函数关系式;(3)若该蔬菜经销商每日销售此种蔬菜不低于75千克,且当日零售价不变,那么零售价定为多少时,该经销商销售此种蔬菜的当日利润最大?最大利润为多少元?考点:二次函数的应用;一次函数的应用.分析:(1)根据这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元,可得60×5=300元;若超过60千克时,批发的这种蔬菜全部打八折,则90×5×0.8=360元;(2)把点(5,90),(6,60)代入函数解析式y=kx+b(k≠0),列出方程组,通过解方程组求得函数关系式;(3)利用最大利润=y(x﹣4),进而利用配方法求出函数最值即可.解答:解:(1)由题意知:当蔬菜批发量为60千克时:60×5=300(元),当蔬菜批发量为90千克时:90×5×0.8=360(元).故答案为:300,360;(2)设该一次函数解析式为y=kx+b(k≠0),把点(5,90),(6,60)代入,得,解得.故该一次函数解析式为:y=﹣30x+240;(3)设当日可获利润w(元),日零售价为x元,由(2)知,w=(﹣30x+240)(x﹣5×0.8)=﹣30(x﹣6)2+120,当x=6时,当日可获得利润最大,最大利润为120元.点评:此题主要考查了一次函数的应用以及二次函数的应用,得出y与x的函数关系式是解题关键.8.(2015•辽宁铁岭)(第26题)如图,在平面直角坐标系中,抛物线y=ax2+bx+与x轴交于A(﹣3,0),B (1,0)两点.与y轴交于点C,点D与点C关于抛物线的对称轴对称.(1)求抛物线的解析式,并直接写出点D的坐标;(2)如图1,点P从点A出发,以每秒1个单位长度的速度沿A→B匀速运动,到达点B时停止运动.以AP为边作等边△APQ(点Q在x轴上方),设点P在运动过程中,△APQ与四边形AOCD重叠部分的面积为S,点P的运动时间为t秒,求S与t之间的函数关系式;(3)如图2,连接AC,在第二象限内存在点M,使得以M、O、A为顶点的三角形与△AOC相似.请直接写出所有符合条件的点M坐标.考点:二次函数综合题.分析:(1)直接代入求得函数解析式即可,由点D与C对称求得点D坐标即可;(2)由特殊角的三角函数值得出∠DAP=60°,则点Q一直在直线AD上运动,分别探讨当点P在线段AO上;点Q在AD的延长线上,点P在线段OB上以及点Q在AD的延长线上,点P在线段OB上时的重叠面积,利用三角形的面积计算公式求得答案即可;(3)由于OC=,OA=3,OA⊥OC,则△OAC是含30°的直角三角形,分两种情况探讨:当△AMO以∠AMO 为直角的直角三角形时;当△AMO以∠OAM为直角的直角三角形时;得出答案即可.解答:解:(1)∵抛物线y=ax2+bx+经过A(﹣3,0),B(1,0)两点,∴,解得,∴抛物线解析式为y=﹣x2﹣x+;则D点坐标为(﹣2,).(2)∵点D与A横坐标相差1,纵坐标之差为,则tan∠DAP=,∴∠DAP=60°,又∵△APQ为等边三角形,∴点Q始终在直线AD上运动,当点Q与D重合时,由等边三角形的性质可知:AP=AD==2.①当0≤t≤2时,P在线段AO上,此时△APQ的面积即是△APQ与四边形AOCD的重叠面积.AP=t,∵∠QAP=60°,∴点Q的纵坐标为t•sin60°=t,∴S=×t×t=t2.②当2<t≤3时,如图:此时点Q在AD的延长线上,点P在OA上,设QP与DC交于点H,∵DC∥AP,∴∠QDH=∠QAP=∠QHD=∠QPA=60°,∴△QDH是等边三角形,∴S=S△QAP﹣S△QDH,∵QA=t,∴S△QAP=t2.∵QD=t﹣2,∴S△QDH=(t﹣2)2,∴S=t2﹣(t﹣2)2=t﹣.③当3<t≤4时,如图:此时点Q在AD的延长线上,点P在线段OB上,设QP与DC交于点E,与OC交于点F,过点Q作AP的垂涎,垂足为G,∵OP=t﹣3,∠FPO=60°,∴OF=OP•tan60°=(t﹣3),∴S△FOP=×(t﹣3)(t﹣3)=(t﹣3)2,∵S=S△QAP﹣S△QDE﹣S△FOP,S△QAP﹣S△QDE=t﹣.∴S=t﹣﹣(t﹣3)2=t2+4t﹣.综上所述,S与t之间的函数关系式为S=.(3)∵OC=,OA=3,OA⊥OC,则△OAC是含30°的直角三角形.①当△AMO以∠AMO为直角的直角三角形时;如图:过点M2作AO的垂线,垂足为N,∵∠M2AO=30°,AO=3,∴M2O=,又∵∠OM2N=M2AO=30°,∴ON=OM2=,M2N=ON=,∴M2的坐标为(﹣,).同理可得M1的坐标为(﹣,).②当△AMO以∠OAM为直角的直角三角形时;如图:∵以M、O、A为顶点的三角形与△OAC相似,∴=,或=,∵OA=3,∴AM=或AM=3,∵AM⊥OA,且点M在第二象限,∴点M的坐标为(﹣3,)或(﹣3,3).综上所述,符合条件的点M的所有可能的坐标为(﹣3,),(﹣3,3),(﹣,),(﹣,).点评:此题考查二次函数的综合运用,图形的运动,待定系数法求函数解析式,特殊角的三角函数,三角形的面积,分类讨论是解决问题的关键.9.(16分)(2015•黔西南州)(第26题)如图,在平面直角坐标系中,平行四边形ABOC如图放置,将此平行四边形绕点O顺时针旋转90°得到平行四边形A′B′OC′.抛物线y=﹣x2+2x+3经过点A、C、A′三点.(1)求A、A′、C三点的坐标;(2)求平行四边形ABOC和平行四边形A′B′OC′重叠部分△C′OD的面积;(3)点M是第一象限内抛物线上的一动点,问点M在何处时,△AMA′的面积最大?最大面积是多少?并写出此时M的坐标.考点:二次函数综合题.分析:(1)利用抛物线与x轴的交点问题可求出C(﹣1,0),A′(3,0);计算自变量为0时的函数值可得到A (0,3);(2)先由平行四边形的性质得AB∥OC,AB=OC,易得B(1,3),根据勾股定理和三角形面积公式得到OB=,S△AOB=,再根据旋转的性质得∠ACO=∠OC′D,OC′=OC=1,接着证明△C′OD∽△BOA,利用相似三角形的性质得=()2,则可计算出S△C′OD;(3)根据二次函数图象上点的坐标特征,设M点的坐标为(m,﹣m2+2m+3),0<m<3,作MN∥y轴交直线AA′于N,求出直线AA′的解析式为y=﹣x+3,则N(m,﹣m+3),于是可计算出MN=﹣m2+3m,再利用S△AMA′=S△ANM+S和三角形面积公式得到S△AMA′=﹣m2+m,然后根据二次函数的最值问题求出△AMA′的面积最大值,同时刻△MNA′确定此时M点的坐标.解答:解:(1)当y=0时,﹣x2+2x+3=0,解得x1=3,x2=﹣1,则C(﹣1,0),A′(3,0);当x=0时,y=3,则A(0,3);(2)∵四边形ABOC为平行四边形,∴AB∥OC,AB=OC,而C(﹣1,0),A(0,3),∴B(1,3)∴OB==,S△AOB=×3×1=,又∵平行四边形ABOC旋转90°得平行四边形A′B′OC′,∴∠ACO=∠OC′D,OC′=OC=1,又∵∠ACO=∠ABO,∴∠ABO=∠OC′D.又∵∠C′OD=∠AOB,∴△C′OD∽△BOA,∴=()2=()2=,∴S△C′OD=×=;(3)设M点的坐标为(m,﹣m2+2m+3),0<m<3,作MN∥y轴交直线AA′于N,易得直线AA′的解析式为y=﹣x+3,则N(m,﹣m+3),∵MN=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m,∴S△AMA′=S△ANM+S△MNA′=MN•3=(﹣m2+3m)=﹣m2+m=﹣(m﹣)2+,∴当m=时,S△AMA'的值最大,最大值为,此时M点坐标为().点评:本题考查了二次函数的综合题:熟练掌握二次函数的性质、抛物线与x轴的交点和二次函数的最值问题;会运用旋转的性质和平行四边形的性质;会利用相似三角形的性质计算三角形的面积.10.(2015•辽宁抚顺)(第23题,12分)一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系(2)该批发商若想获得4000元的利润,应将售价定为多少元?(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?考点:二次函数的应用.分析:(1)根据图表中的各数可得出y与x成一次函数关系,从而结合图表的数可得出y与x的关系式.(2)根据想获得4000元的利润,列出方程求解即可;(3)根据批发商获得的总利润w(元)=售量×每件利润可表示出w与x之间的函数表达式,再利用二次函数的最值可得出利润最大值.解答:解:(1)设y与x的函数关系式为y=kx+b(k≠0),根据题意得,解得.故y与x的函数关系式为y=﹣x+150;(2)根据题意得(﹣x+150)(x﹣20)=4000,解得x1=70,x2=100>90(不合题意,舍去).故该批发商若想获得4000元的利润,应将售价定为70元;(3)w与x的函数关系式为:w=(﹣x+150)(x﹣20)=﹣x2+170x﹣3000=﹣(x﹣85)2+4225,∵﹣1<0,∴当x=85时,w值最大,w最大值是4225.∴该产品每千克售价为85元时,批发商获得的利润w(元)最大,此时的最大利润为4225元.点评:本题考查二次函数的应用,难度较大,解答本题的关键是根据题意列出方程,另外要注意掌握二次函数的最值的求法.11.(2015•辽宁抚顺)(第26题,14分))已知,△ABC在平面直角坐标系中的位置如图①所示,A点坐标为(﹣6,0),B点坐标为(4,0),点D为BC的中点,点E为线段AB上一动点,连接DE经过点A、B、C三点的抛物线的解析式为y=ax2+bx+8.(1)求抛物线的解析式;(2)如图①,将△BDE以DE为轴翻折,点B的对称点为点G,当点G恰好落在抛物线的对称轴上时,求G点的坐标;(3)如图②,当点E在线段AB上运动时,抛物线y=ax2+bx+8的对称轴上是否存在点F,使得以C、D、E、F为顶点的四边形为平行四边形?若存在,请直接写出点F的坐标;若不存在,请说明理由.考点:二次函数综合题.分析:(1)根据抛物线y=ax2+bx+8经过点A(﹣6,0),B(4,0),应用待定系数法,求出抛物线的解析式即可.(2)首先作DM⊥抛物线的对称轴于点M,设G点的坐标为(﹣1,n),根据翻折的性质,可得BD=DG;然后分别求出点D、点M的坐标各是多少,以及BC、BD的值各是多少;最后在Rt△GDM中,根据勾股定理,求出n的值,即可求出G点的坐标.(3)根据题意,分三种情况:①当CD∥EF,且点E在x轴的正半轴时;②当CD∥EF,且点E在x轴的负半轴时;③当CE∥DF时;然后根据平行四边形的性质,求出点F的坐标各是多少即可.解答:解:(1)∵抛物线y=ax2+bx+8经过点A(﹣6,0),B(4,0),∴解得∴抛物线的解析式是:y=﹣x2﹣x+8.(2)如图①,作DM⊥抛物线的对称轴于点M,,设G点的坐标为(﹣1,n),由翻折的性质,可得BD=DG,∵B(4,0),C(0,8),点D为BC的中点,∴点D的坐标是(2,4),∴点M的坐标是(﹣1,4),DM=2﹣(﹣1)=3,∵B(4,0),C(0,8),∴BC==4,∴,在Rt△GDM中,32+(4﹣n)2=20,解得n=4±,∴G点的坐标为(﹣1,4+)或(﹣1,4﹣).(3)抛物线y=ax2+bx+8的对称轴上存在点F,使得以C、D、E、F为顶点的四边形为平行四边形.①当CD∥EF,且点E在x轴的正半轴时,如图②,,由(2),可得点D的坐标是(2,4),设点E的坐标是(c,0),点F的坐标是(﹣1,d),则解得∴点F的坐标是(﹣1,4),点C的坐标是(1,0).②当CD∥EF,且点E在x轴的负半轴时,如图③,,由(2),可得点D的坐标是(2,4),设点E的坐标是(c,0),点F的坐标是(﹣1,d),则解得∴点F的坐标是(﹣1,﹣4),点C的坐标是(﹣3,0).③当CE∥DF时,如图④,,由(2),可得点D的坐标是(2,4),设点E的坐标是(c,0),点F的坐标是(﹣1,d),则解得∴点F的坐标是(﹣1,12),点C的坐标是(3,0).综上,可得抛物线y=ax2+bx+8的对称轴上存在点F,使得以C、D、E、F为顶点的四边形为平行四边形,点F的坐标是(﹣1,4)、(﹣1,﹣4)或(﹣1,12).点评:(1)此题主要考查了二次函数综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了数形结合思想的应用,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力.(2)此题还考查了平行四边形的性质和应用,以及待定系数法求函数解析式的方法,要熟练掌握.(3)此题还考查了直角三角形的性质和应用,以及勾股定理的应用,要熟练掌握.12.(2015•辽宁阜新)(第18题,12分)如图,抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).(1)求抛物线的函数表达式;(2)若点P在抛物线上,且S△AOP=4S BOC,求点P的坐标;(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.考点:二次函数综合题.分析:(1)把点A、C的坐标分别代入函数解析式,列出关于系数的方程组,通过解方程组求得系数的值;(2)设P点坐标为(x,﹣x2﹣2x+3),根据S△AOP=4S△BOC列出关于x的方程,解方程求出x的值,进而得到点P 的坐标;(3)先运用待定系数法求出直线AC的解析式为y=x+3,再设Q点坐标为(x,x+3),则D点坐标为(x,x2+2x ﹣3),然后用含x的代数式表示QD,根据二次函数的性质即可求出线段QD长度的最大值.解答:解:(1)把A(﹣3,0),C(0,3)代入y=﹣x2+bx+c,得,解得.故该抛物线的解析式为:y=﹣x2﹣2x+3.(2)由(1)知,该抛物线的解析式为y=﹣x2﹣2x+3,则易得B(1,0).∵S△AOP=4S△BOC,∴×3×|﹣x2﹣2x+3|=4××1×3.整理,得(x+1)2=0或x2+2x﹣7=0,解得x=﹣1或x=﹣1±.则符合条件的点P的坐标为:(﹣1,4)或(﹣1+,﹣4)或(﹣1﹣,﹣4);(3)设直线AC的解析式为y=kx+t,将A(﹣3,0),C(0,3)代入,得,解得.即直线AC的解析式为y=x+3.设Q点坐标为(x,x+3),(﹣3≤x≤0),则D点坐标为(x,﹣x2﹣2x+3),QD=(﹣x2﹣2x+3)﹣(x+3)=﹣x2﹣3x=﹣(x+)2+,∴当x=﹣时,QD有最大值.点评:此题考查了待定系数法求二次函数、一次函数的解析式,二次函数的性质以及三角形面积、线段长度问题.此题难度适中,解题的关键是运用方程思想与数形结合思想.13.(12分)(2015•葫芦岛)(第24题)小明开了一家网店,进行社会实践,计划经销甲、乙两种商品.若甲商品每件利润10元,乙商品每件利润20元,则每周能卖出甲商品40件,乙商品20件.经调查,甲、乙两种商品零售单价分别每降价1元,这两种商品每周可各多销售10件.为了提高销售量,小明决定把甲、乙两种商品的零售单价都降价x元.(1)直接写出甲、乙两种商品每周的销售量y(件)与降价x(元)之间的函数关系式:y甲=10x+40,y乙=10x+20;(2)求出小明每周销售甲、乙两种商品获得的总利润W(元)与降价x(元)之间的函数关系式?如果每周甲商品的销售量不低于乙商品的销售量的,那么当x定为多少元时,才能使小明每周销售甲、乙两种商品获得的总利润最大?考点:二次函数的应用.分析:(1)根据题意可以列出甲、乙两种商品每周的销售量y(件)与降价x(元)之间的函数关系式;(2)根据每周甲商品的销售量不低于乙商品的销售量的,列出不等式求出x的取值范围,根据题意列出二次函数的解析式,根据二次函数的性质求出对称轴方程,得到答案.解答:解:(1)由题意得,y甲=10x+40;y乙=10x+20;(2)由题意得,W=(10﹣x)(10x+40)+(20﹣x)(10x+20)=﹣20x2+240x+800,由题意得,10x+40≥(10x+20)解得x≤2,W=﹣20x2+240x+800=﹣20(x﹣6)2+1520,∵a=﹣20<0,∴当x<6时,y随x增大而增大,∴当x=2时,W的值最大.答:当x定为2元时,才能使小明每周销售甲、乙两种商品获得的总利润最大.点评:本题考查的是二次函数的应用,正确列出二次函数的关系式,掌握二次函数的性质是解题的关键.14.(14分)(2015•葫芦岛)(第26题)如图,直线y=﹣x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+ x+c经过B、C两点.(1)求抛物线的解析式;(2)如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标和△BEC面积的最大值?(3)在(2)的结论下,过点E作y轴的平行线交直线BC于点M,连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.考点:二次函数综合题.分析:(1)首先根据直线y=﹣x+3与x轴交于点C,与y轴交于点B,求出点B的坐标是(0,3),点C的坐标是(4,0);然后根据抛物线y=ax2+x+c经过B、C两点,求出a\c的值是多少,即可求出抛物线的解析式.(2)首先过点E作y轴的平行线EF交直线BC于点M,EF交x轴于点F,然后设点E的坐标是(x,﹣x2+x+3),则点M的坐标是(x,﹣x+3),求出EM的值是多少;最后根据三角形的面积的求法,求出S△ABC,进而判断出当△BEC面积最大时,点E的坐标和△BEC面积的最大值各是多少即可.(3)在抛物线上存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形.然后分三种情况讨论,根据平行四边形的特征,求出使得以P、Q、A、M为顶点的四边形是平行四边形的点P的坐标是多少即可.解答:解:(1)∵直线y=﹣x+3与x轴交于点C,与y轴交于点B,∴点B的坐标是(0,3),点C的坐标是(4,0),∵抛物线y=ax2+x+c经过B、C两点,∴解得∴y=﹣x2+x+3.(2)如图1,过点E作y轴的平行线EF交直线BC于点M,EF交x轴于点F,,∵点E是直线BC上方抛物线上的一动点,∴设点E的坐标是(x,﹣x2+x+3),则点M的坐标是(x,﹣x+3),∴EM=﹣x2+x+3﹣(﹣x+3)=﹣x2+x,∴S△ABC=S△BEM+S△MEC==×(﹣x2+x)×4=﹣x2+3x=﹣(x﹣2)2+3,∴当x=2时,即点E的坐标是(2,3)时,△BEC的面积最大,最大面积是3.(3)在抛物线上存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形.①如图2,,由(2),可得点M的横坐标是2,∵点M在直线y=﹣x+3上,∴点M的坐标是(2,),又∵点A的坐标是(﹣2,0),∴AM==,∴AM所在的直线的斜率是:;∵y=﹣x2+x+3的对称轴是x=1,∴设点Q的坐标是(1,m),点P的坐标是(x,﹣x2+x+3),则解得或,∵x<0,∴点P的坐标是(﹣3,﹣).②如图3,,由(2),可得点M的横坐标是2,∵点M在直线y=﹣x+3上,∴点M的坐标是(2,),又∵点A的坐标是(﹣2,0),∴AM==,∴AM所在的直线的斜率是:;∵y=﹣x2+x+3的对称轴是x=1,∴设点Q的坐标是(1,m),点P的坐标是(x,﹣x2+x+3),则解得或,∵x>0,∴点P的坐标是(5,﹣).③如图4,,由(2),可得点M的横坐标是2,∵点M在直线y=﹣x+3上,∴点M的坐标是(2,),又∵点A的坐标是(﹣2,0),∴AM==,∵y=﹣x2+x+3的对称轴是x=1,∴设点Q的坐标是(1,m),点P的坐标是(x,﹣x2+x+3),则解得,∴点P的坐标是(﹣1,).综上,可得在抛物线上存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形,点P的坐标是(﹣3,﹣)、(5,﹣)、(﹣1,).点评:(1)此题主要考查了二次函数综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了数形结合思想的应用,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力.(2)此题还考查了函数解析式的求法,以及二次函数的最值的求法,要熟练掌握.(3)此题还考查了三角形的面积的求法,要熟练掌握.15.(2015,广西柳州,23,8分)如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B 重合),过点F的反比例函数y=(k>0)的图象与BC边交于点E.(1)当F为AB的中点时,求该函数的解析式;(2)当k为何值时,△EFA的面积最大,最大面积是多少?考点:待定系数法求反比例函数解析式;反比例函数图象上点的坐标特征;二次函数的最值.分析:(1)当F为AB的中点时,点F的坐标为(3,1),由此代入求得函数解析式即可;(2)根据图中的点的坐标表示出三角形的面积,得到关于k的二次函数,利用二次函数求出最值即可.解答:解:(1)∵在矩形OABC中,OA=3,OC=2,∴B(3,2),∵F为AB的中点,∴F(3,1),∵点F在反比例函数y=(k>0)的图象上,∴k=3,∴该函数的解析式为y=(x>0);(2)由题意知E,F两点坐标分别为E(,2),F(3,),∴S△EFA=AF•BE=×k(3﹣k),=k﹣k2=﹣(k2﹣6k+9﹣9)=﹣(k﹣3)2+当k=3时,S有最大值.S最大值=.点评:此题属于反比例函数综合题,涉及的知识有:坐标与图形性质,待定系数法确定反比例解析式,以及二次函数的性质,熟练掌握待定系数法是解本题的关键.16.(2015,广西柳州,26,12分)如图,已知抛物线y=﹣(x2﹣7x+6)的顶点坐标为M,与x轴相交于A,B两点(点B在点A的右侧),与y轴相交于点C.(1)用配方法将抛物线的解析式化为顶点式:y=a(x﹣h)2+k(a≠0),并指出顶点M的坐标;(2)在抛物线的对称轴上找点R,使得CR+AR的值最小,并求出其最小值和点R的坐标;(3)以AB为直径作⊙N交抛物线于点P(点P在对称轴的左侧),求证:直线MP是⊙N的切线.考点:二次函数综合题.专题:综合题.分析:(1)利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,即可把一般式转化为顶点式,然后根据二次函数的性质求出抛物线的顶点坐标;(2)连接BC,则BC与对称轴的交点为R,此时CR+AR的值最小;先求出点A、B、C的坐标,再利用待定系数法求出直线BC的解析式,进而求出其最小值和点R的坐标;(3)设点P坐标为(x,﹣x2+x﹣3).根据NP=AB=列出方程(x﹣)2+(﹣x2+x﹣3)2=()2,解方程得到点P坐标,再计算得出PM2+PN2=MN2,根据勾股定理的逆定理得出∠MPN=90°,然后利用切线的判定定理即可证明直线MP是⊙N的切线.解答:(1)解:∵y=﹣(x2﹣7x+6)=﹣(x2﹣7x)﹣3=﹣(x﹣)2+,∴抛物线的解析式化为顶点式为:y=﹣(x﹣)2+,顶点M的坐标是(,);(2)解:∵y=﹣(x2﹣7x+6),∴当y=0时,﹣(x2﹣7x+6)=0,解得x=1或6,∴A(1,0),B(6,0),∵x=0时,y=﹣3,∴C(0,﹣3).连接BC,则BC与对称轴x=的交点为R,连接AR,则CR+AR=CR+BR=BC,根据两点之间线段最短可知此时CR+AR的值最小,最小值为BC==3.设直线BC的解析式为y=kx+b,∵B(6,0),C(0,﹣3),∴,解得,∴直线BC的解析式为:y=x﹣3,令x=,得y=×﹣3=﹣,∴R点坐标为(,﹣);(3)证明:设点P坐标为(x,﹣x2+x﹣3).∵A(1,0),B(6,0),∴N(,0),∴以AB为直径的⊙N的半径为AB=,∴NP=,即(x﹣)2+(﹣x2+x﹣3)2=()2,化简整理得,x4﹣14x3+65x2﹣112x+60=0,(x﹣1)(x﹣2)(x﹣5)(x﹣6)=0,解得x1=1(与A重合,舍去),x2=2,x3=5(在对称轴的右侧,舍去),x4=6(与B重合,舍去),∴点P坐标为(2,2).∵M(,),N(,0),∴PM2=(2﹣)2+(2﹣)2=,PN2=(2﹣)2+22==,MN2=()2=,∴PM2+PN2=MN2,∴∠MPN=90°,∵点P在⊙N上,∴直线MP是⊙N的切线.点评:本题是二次函数的综合题,其中涉及到二次函数的图象与性质、待定系数法求一次函数的解析式、轴对称﹣最短路线问题以及切线的判定等知识,综合性较强,难度适中.第(3)问求出点P的坐标是解题的关键.17.(2015,福建南平,24,分)如图,在平面直角坐标系中,已知抛物线y=ax2+bx的对称轴为x=,且经过点A(2,1),点P是抛物线上的动点,P的横坐标为m(0<m<2),过点P作PB⊥x轴,垂足为B,PB交OA于点C,点O关于直线PB的对称点为D,连接CD,AD,过点A作AE⊥x轴,垂足为E.(1)求抛物线的解析式;(2)填空:。
2015二次函数中考真题卷高难度专项练习及答案

组卷二次函数难题1-30一、选择题(共12小题)1.(2011•包头)已知二次函数y=ax2+bx+c同时满足下列条件:对称轴是x=1;最值是15;二次函数的图象与x轴有两个交点,其横坐标的平方和为15﹣a,则b的值是()A.4或﹣30 B.﹣30 C.4D.6或﹣20 2.(2011•玉溪)如图,函数y=﹣x2+bx+c的部分图象与x轴、y轴的交点分别为A(1,0),B(0,3),对称轴是x=﹣1,在下列结论中,错误的是()A.顶点坐标为(﹣1,4)B.函数的解析式为y=﹣x2﹣2x+3C.当x<0时,y随x的增大而增大D.抛物线与x轴的另一个交点是(﹣3,0)3.(2010•钦州)已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论:①ac>0;②a﹣b+c<0;③当x<0时,y<0;④方程ax2+bx+c=0(a≠0)有两个大于﹣1的实数根.其中错误的结论有()A.②③B.②④C.①③D.①④4.(2010•柳州)抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:x …﹣2 ﹣1 0 1 2 …y …0 4 6 6 4 …从上表可知,下列说法正确的个数是()①抛物线与x轴的一个交点为(﹣2,0);②抛物线与y轴的交点为(0,6);③抛物线的对称轴是x=1;④在对称轴左侧y随x增大而增大.A.1B.2C.3D.45.(2010•自贡)y=x2+(1﹣a)x+1是关于x的二次函数,当x的取值范围是1≤x≤3时,y在x=1时取得最大值,则实数a的取值范围是()A.a≤﹣5 B.a≥5 C.a=3 D.a≥36.(2010•十堰)方程x2+2x﹣1=0的根可看出是函数y=x+2与y=的图象交点的横坐标,用此方法可推断方程x3+x ﹣1=0的实根x所在范围为()A.﹣B.C.D.17.(2010•西宁)下列哪一个函数,其图象与x轴有两个交点()A.B.C.D.8.(2010•台州)如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x﹣m)2+n的顶点在线段AB上运动(抛物线随顶点一起平移),与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为﹣3,则点D的横坐标最大值为()A.﹣3 B.1C.5D.89.(2010•东营)二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx﹣ac 与反比例函数在同一坐标系内的图象大致为()A.B.C.D.10.(2010•广安)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②b<a+c;③2a+b=0;④a+b>m(am+b)(m≠1的实数).其中正确的结论有()A.1个B.2个C.3个D.4个11.(2010•丽水)如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD 的面积为y,则y与x之间的函数关系式是()A.y=B.y=C.y=D.y=12.(2011•兰州)如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是()A.B.C.D.二、填空题(共12小题)(除非特别说明,请填准确值)13.(2009•黄石)若抛物线y=ax2+bx+3与y=﹣x2+3x+2的两交点关于原点对称,则a、b 分别为_________、_________.14.(2010•成都)如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s 的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过_________秒,四边形APQC的面积最小.15.(2009•金华)如图,在第一象限内作射线OC,与x轴的夹角为30°,在射线OC上取一点A,过点A作AH⊥x 轴于点H.在抛物线y=x2(x>0)上取点P,在y轴上取点Q,使得以P,O,Q为顶点的三角形与△AOH全等,则符合条件的点A的坐标是_________.16.(2009•江津区)锐角△ABC中,BC=6,S△ABC=12,两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y>0),当x=_________,公共部分面积y最大,y最大值=_________.17.(2008•庆阳)兰州市“安居工程”新建成的一批楼房都是8层高,房子的价格y(元/平方米)随楼层数x(楼)的变化而变化(x=1,2,3,4,5,6,7,8);已知点(x,y)都在一个二次函数的图象上(如图所示),则6楼房子的价格为_________元/平方米.18.(2009•浙江)如图,抛物线y=ax2+bx+c与x轴的一个交点A在点(﹣2,0)和(﹣1,0)之间(包括这两点),顶点C是矩形DEFG上(包括边界和内部)的一个动点,则:(1)abc_________0(填“>”或“<”);(2)a的取值范围是_________.19.(2009•包头)已知二次函数y=ax2+bx+c的图象与x轴交于点(﹣2,0)、(x1,0),且1<x1<2,与y轴的正半轴的交点在(0,2)的下方.下列结论:①4a﹣2b+c=0;②a<b<0;③2a+c>0;④2a﹣b+1>0.其中正确结论的个数是_________个.20.(2010•兰州)如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为_________米.21.(2008•黄石)若实数a,b满足a+b2=1,则2a2+7b2的最小值是_________.22.(2009•包头)将一条长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长各做成一个正方形,则这两个正方形面积之和的最小值是_________cm2.23.(2008•长春)将抛物线y=ax2+bx+c(a≠0)向下平移3个单位,再向左平移4个单位得到抛物线y=﹣2x2﹣4x+5,则原抛物线的顶点坐标是_________.24.(2009•兰州)二次函数y=x2的图象如图所示,点A0位于坐标原点,A1,A2,A3,…,A2008在y轴的正半轴上,B1,B2,B3,…,B2008在二次函数y=x2第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2007B2008A2008都为等边三角形,请计算△A0B1A1的边长=_________;△A1B2A2的边长=_________;△A2007B2008A2008的边长=_________.三、解答题(共6小题)(选答题,不自动判卷)25.(2013•徐州)如图,二次函数y=x2+bx﹣的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.(1)请直接写出点D的坐标:_________;(2)当点P在线段AO(点P不与A、O重合)上运动至何处时,线段OE的长有最大值,求出这个最大值;(3)是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.26.(2013•雅安)如图,已知抛物线y=ax2+bx+c经过A(﹣3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.(1)求该抛物线的解析式;(2)若点P是该抛物线对称轴l上的一个动点,求△PBC周长的最小值;(3)如图(2),若E是线段AD上的一个动点(E与A、D不重合),过E点作平行于y轴的直线交抛物线于点F,交x轴于点G,设点E的横坐标为m,△ADF的面积为S.①求S与m的函数关系式;②S是否存在最大值?若存在,求出最大值及此时点E的坐标;若不存在,请说明理由.27.(2013•烟台)如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,二次函数y=ax2+bx+c的图象经过点A,B,与x轴分别交于点E,F,且点E的坐标为(﹣,0),以0C为直径作半圆,圆心为D.(1)求二次函数的解析式;(2)求证:直线BE是⊙D的切线;(3)若直线BE与抛物线的对称轴交点为P,M是线段CB上的一个动点(点M与点B,C不重合),过点M作MN∥BE交x轴与点N,连结PM,PN,设CM的长为t,△PMN的面积为S,求S与t的函数关系式,并写出自变量t的取值范围.S是否存在着最大值?若存在,求出最大值;若不存在,请说明理由.28.(2013•新疆)如图,已知抛物线y=ax2+bx+3与x轴交于A、B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,3).(1)求抛物线的解析式;(2)在(1)中抛物线的对称轴上是否存在点D,使△BCD的周长最小?若存在,求出点D的坐标,若不存在,请说明理由;(3)若点E是(1)中抛物线上的一个动点,且位于直线AC的下方,试求△ACE的最大面积及E点的坐标.29.(2013•宜宾)如图,抛物线y=ax2+bx﹣4a经过A(﹣1,0)、C(0,4)两点,与x轴交于另一点B.(1)求抛物线的解析式;(2)已知点D(m,m+1)在第一象限的抛物线上,求点D关于直线BC对称的点的坐标;(3)在(2)的条件下,连接BD,点P为抛物线上一点,且∠DBP=45°,求点P的坐标.30.(2013•宜宾)某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元).设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.(1)求y与x的函数关系式并直接写出自变量x的取值范围;(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?(3)每件商品的售价定为多少元时,每个月的利润恰为2200元?根据以上结论,请你直接写出售价在什么范围时,每个月的利润不低于2200元?【章节训练】第2章二次函数-3参考答案与试题解析一、选择题(共12小题)组卷二次函数难题61-90 难度 5 级1.(2011•包头)已知二次函数y=ax2+bx+c同时满足下列条件:对称轴是x=1;最值是15;二次函数的图象与x轴有两个交点,其横坐标的平方和为15﹣a,则b的值是()A.4或﹣30 B.﹣30 C.4D.6或﹣20抛物线与x轴的交点;二次函数的性质;二次函数的最值.专题:压轴题;函数思想.分析:由在x=1时取得最大值15,可设解析式为:y=a(x﹣1)2+15,只需求出a即可,又与x轴交点横坐标的平方和为15﹣a,可求出a,所以可求出解析式得到b的值.解答:解:解法一:∵x轴上点的纵坐标是0,∴由题可设抛物线与x轴的交点为(1﹣t,0),(1+t,0),其中t>0,∵两个交点的横坐标的平方和等于15﹣a即:(1﹣t)2+(1+t)2=15﹣a,可得t=,由顶点为(1,15),可设解析式为:y=a(x﹣1)2+15,将(1﹣,0)代入可得a=﹣2或a=15(不合题意,舍去)∴y=﹣2(x﹣1)2+15=﹣2x2+4x+13,∴b=4;解法二:∵对称轴是x=1,最值是15,∴设y=ax2+bx+c=a(x﹣1)2+15,∴y=ax2﹣2ax+15+a,设方程ax2﹣2ax+15+a=0的两个根是x1,x2,则x1+x2=﹣=2,x1•x2=,∵二次函数的图象与x轴有两个交点,其横坐标的平方和为15﹣a,(x1)2+(x2)2=(x1+x2)2﹣2x1x2=15﹣a,∴22﹣=15﹣a,a2﹣13a﹣30=0,a1=15(不合题意,舍去),a2=﹣2,∴y=﹣2(x﹣1)2+15=﹣2x2+4x+13;∴b=4.故选C.点评:本题考查了二次函数的最值及待定系数法求解析式,难度一般,关键算出a的值.组卷二次函数难题61-90 难度 4 级2.(2011•玉溪)如图,函数y=﹣x2+bx+c的部分图象与x轴、y轴的交点分别为A(1,0),B(0,3),对称轴是x=﹣1,在下列结论中,错误的是()A.顶点坐标为(﹣1,4)B.函数的解析式为y=﹣x2﹣2x+3C.当x<0时,y随x的增大而增大D.抛物线与x轴的另一个交点是(﹣3,0)考点:抛物线与x轴的交点;二次函数的性质.专题:计算题;压轴题.分析:由于y=﹣x2+bx+c的图象与x轴、y轴的交点分别为A(1,0),B(0,3),将交点代入解析式求出函数表达式,即可作出正确判断.解答:解:将A(1,0),B(0,3)分别代入解析式得,,解得,,则函数解析式为y=﹣x2﹣2x+3;将x=﹣1代入解析式可得其顶点坐标为(﹣1,4);当y=0时可得,﹣x2﹣2x+3=0;解得,x1=﹣3,x2=1.可见,抛物线与x轴的另一个交点是(﹣3,0);由图可知,当x<﹣1时,y随x的增大而增大.可见,C答案错误.故选C.点评:本题考查了抛物线与x轴的交点及二次函数的性质,利用待定系数法求出函数解析式是解题的关键,同时要注意数形结合.组卷二次函数难题61-90 难度 4 级3.(2010•钦州)已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论:①ac>0;②a﹣b+c<0;③当x<0时,y<0;④方程ax2+bx+c=0(a≠0)有两个大于﹣1的实数根.其中错误的结论有()A.②③B.②④C.①③D.①④考点:二次函数图象与系数的关系.专题:压轴题.分析:①由二次函数y=ax2+bx+c(a≠0)的图象开口方向知道a<0,与y轴交点知道c>0,由此即可确定ac的符号;②由于当x=﹣1时,y=a﹣b+c,而根据图象知道当x=﹣1时y<0,由此即可判定a﹣b+c的符号;③根据图象知道当x<﹣1时抛物线在x轴的下方,由此即可判定此结论是否正确;④根据图象与x轴交点的情况即可判定是否正确.解答:解:①∵二次函数y=ax2+bx+c(a≠0)的图象开口向下,∴a<0,∵与y轴交点在x轴上方,∴c>0,∴ac<0;②∵当x=﹣1时,y=a﹣b+c,而根据图象知道当x=﹣1时y<0,∴a﹣b+c<0;③根据图象知道当x<﹣1时抛物线在x轴的下方,∴当x<﹣1,y<0;④从图象可知抛物线与x轴的交点的横坐标都大于﹣1,∴方程ax2+bx+c=0(a≠0)有两个大于﹣1的实数根.故错误的有①③.故选C.点评:此题主要考查了利用图象求出a,b,c的范围,以及特殊值的代入能得到特殊的式子,如:当x=1时,y>0,a+b+c>0;x=﹣1时,y<0,a﹣b+c<0.组卷二次函数难题61-90 难度4.5级4.(2010•柳州)抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:x …﹣2 ﹣1 0 1 2 …y …0 4 6 6 4 …从上表可知,下列说法正确的个数是()①抛物线与x轴的一个交点为(﹣2,0);②抛物线与y轴的交点为(0,6);③抛物线的对称轴是x=1;④在对称轴左侧y随x增大而增大.A.1B.2C.3D.4考点:抛物线与x轴的交点.专题:压轴题;图表型.分析:从表中知道当x=﹣2时,y=0,当x=0时,y=6,由此可以得到抛物线与x轴的一个交点坐标和抛物线与y 轴的交点坐标,从表中还知道当x=﹣1和x=2时,y=4,由此可以得到抛物线的对称轴方程,同时也可以得到在对称轴左侧y随x增大而增大.解答:解:从表中知道:当x=﹣2时,y=0,当x=0时,y=6,∴抛物线与x轴的一个交点为(﹣2,0),抛物线与y轴的交点为(0,6),从表中还知道:当x=﹣1和x=2时,y=4,∴抛物线的对称轴方程为x=(﹣1+2)=0.5,同时也可以得到在对称轴左侧y随x增大而增大.所以①②④正确.故选C.点评:此题主要考查了抛物线与坐标轴的交点坐标与自变量和的函数值的对应关系,也考查了利用自变量和对应的函数值确定抛物线的对称轴和增减性.组卷二次函数难题61-90 难度4.5 级5.(2010•自贡)y=x2+(1﹣a)x+1是关于x的二次函数,当x的取值范围是1≤x≤3时,y在x=1时取得最大值,则实数a的取值范围是()A.a≤﹣5 B.a≥5 C.a=3 D.a≥3考点:二次函数的最值.专题:压轴题.分析:由于二次函数的顶点坐标不能确定,故应分对称轴不在[1,3]和对称轴在[1,3]内两种情况进行解答.解答:解:第一种情况:当二次函数的对称轴不在1≤x≤3内时,此时,对称轴一定在1≤x≤3的右边,函数方能在这个区域取得最大值,x=>3,即a>7,第二种情况:当对称轴在1≤x≤3内时,对称轴一定是在区间1≤x≤3的中点的右边,因为如果在中点的左边的话,就是在x=3的地方取得最大值,即:x=≥,即a≥5(此处若a取5的话,函数就在1和3的地方都取得最大值)综合上所述a≥5.故选B.点评:本题考查了二次函数的最值确定与自变量x的取值范围的关系,难度较大.组卷二次函数难题61-90 难度 4 级6.(2010•十堰)方程x2+2x﹣1=0的根可看出是函数y=x+2与y=的图象交点的横坐标,用此方法可推断方程x3+x ﹣1=0的实根x所在范围为()A.﹣B.C.D.1考点:二次函数的图象;反比例函数的图象.专题:压轴题.分析:首先根据题意推断方程x3+x﹣1=0的实根是函数y=x2+1与y=的图象交点的横坐标,再根据四个选项中x 的取值代入两函数解析式,找出抛物线的图象在反比例函数上方和反比例函数的图象在抛物线的上方两个点即可判定推断方程x3+x﹣1=0的实根x所在范围.解答:解:依题意得方程x3+x﹣1=0的实根是函数y=x2+1与y=的图象交点的横坐标,这两个函数的图象如图所示,∴它们的交点在第一象限,当x=1时,y=x2+1=2,y==1,此时抛物线的图象在反比例函数上方;当x=时,y=x2+1=1,y==2,此时反比例函数的图象在抛物线的上方;∴方程x3+x﹣1=0的实根x 所在范围为<x<1.故选C.点评:此题考查了学生从图象中读取信息的数形结合能力.解决此类识图题,同学们要注意分析其中的“关键点”,还要善于分析各图象的变化趋势.组卷二次函数难题61-90 难度 4 级7.(2010•西宁)下列哪一个函数,其图象与x轴有两个交点()A.B.C.D.考点:抛物线与x轴的交点.专题:计算题.分析:由题意得,令y=0,看是否解出x值,对A,B,C,D,一一验证从而得出答案.解答:解:A、令y=0得,,移项得,,方程无实根;B、令y=0得,,移项得,,方程无实根;C、令y=0得,,移项得,,方程无实根;D、令y=0得,,移项得,,方程有两个实根.故选D.点评:此题考查二次函数的性质及与一元二次方程根的关系.(利用开口方向和顶点坐标也可解答)组卷二次函数难题61-90 难度 4.5 级8.(2010•台州)如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x﹣m)2+n的顶点在线段AB上运动(抛物线随顶点一起平移),与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为﹣3,则点D的横坐标最大值为()A.﹣3 B.1C.5D.8考点:二次函数综合题.专题:压轴题;动点型.分析:当C点横坐标最小时,抛物线顶点必为A(1,4),根据此时抛物线的对称轴,可判断出CD间的距离;当D点横坐标最大时,抛物线顶点为B(4,4),再根据此时抛物线的对称轴及CD的长,可判断出D点横坐标最大值.解答:解:当点C横坐标为﹣3时,抛物线顶点为A(1,4),对称轴为x=1,此时D点横坐标为5,则CD=8;当抛物线顶点为B(4,4)时,抛物线对称轴为x=4,且CD=8,故C(0,0),D(8,0);由于此时D点横坐标最大,故点D的横坐标最大值为8;故选D.点评:能够正确地判断出点C横坐标最小、点D横坐标最大时抛物线的顶点坐标是解答此题的关键.组卷二次函数难题61-90 难度 4.5级9.(2010•东营)二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx﹣ac 与反比例函数在同一坐标系内的图象大致为()A.B.C.D.考点:二次函数的图象;一次函数的图象;反比例函数的图象.专题:压轴题.分析:先根据二次函数y=ax2+bx+c的图象判断出a、b、c、a﹣b+c的符号,再用排除法对四个答案进行逐一检验.解答:解:由二次函数y=ax2+bx+c的图象开口向上可知,a>0,因为图象与y轴的交点在y轴的负半轴,所以c<0,根据函数图象的对称轴x=﹣>0,可知b<0,∵a>0,b<0,c<0,ac<0,∴一次函数y=bx﹣ac的图象过一、二、四象限,故可排除A、C;由函数图象可知,当x=﹣1时,y>0,即y=a﹣b+c>0,∴反比例函数的图象在一、三象限,可排除D选项,故选B.点评:此题比较复杂,综合考查了二次函数、一次函数及反比例函数图象的特点,锻炼了学生数形结合解题的思想方法.组卷二次函数难题61-90 难度4.5 级10.(2010•广安)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②b<a+c;③2a+b=0;④a+b>m(am+b)(m≠1的实数).其中正确的结论有()A.1个B.2个C.3个D.4个考点:二次函数图象与系数的关系.专题:压轴题.分析:①由抛物线开口向下a<0,抛物线和y轴的正半轴相交,c>0,﹣=1>0,b>0,②令x=﹣1,时y<0,即a﹣b+c<0,③﹣=1,即2a+b=0,④把x=m代入函数解析式中表示出对应的函数值,把x=1代入解析式得到对应的解析式,根据图形可知x=1时函数值最大,所以x=1对应的函数值大于x=m对应的函数值,化简得到不等式成立,故④正确.解答:解:①根据图象,a<0,b>0,c>0,故①错误;②令x=﹣1,时y<0,即a﹣b+c<0,故②错误;③∵﹣=1,∴2a+b=0,故③正确;④x=m对应的函数值为y=am2+bm+c,x=1对应的函数值为y=a+b+c,又x=1时函数取得最大值,∴a+b+c>am2+bm+c,即a+b>am2+bm=m(am+b),故④正确.故选B.点评:主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.组卷二次函数难题61-90 难度 5 级11.(2010•丽水)如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD 的面积为y,则y与x之间的函数关系式是()A.y=B.y=C.y=D.y=考点:根据实际问题列二次函数关系式.专题:压轴题.分析:四边形ABCD图形不规则,根据已知条件,将△ABC绕A点逆时针旋转90°到△ADE的位置,求四边形ABCD的面积问题转化为求梯形ACDE的面积问题;根据全等三角形线段之间的关系,结合勾股定理,把梯形上底DE,下底AC,高DF分别用含x的式子表示,可表示四边形ABCD的面积.解答:解:作AE⊥AC,DE⊥AE,两线交于E点,作DF⊥AC垂足为F点,∵∠BAD=∠CAE=90°,即∠BAC+∠CAD=∠CAD+∠DAE∴∠BAC=∠DAE又∵AB=AD,∠ACB=∠E=90°∴△ABC≌△ADE(AAS)∴BC=DE,AC=AE,设BC=a,则DE=a,DF=AE=AC=4BC=4a,CF=AC﹣AF=AC﹣DE=3a,在Rt△CDF中,由勾股定理得,CF2+DF2=CD2,即(3a)2+(4a)2=x2,解得:a=,∴y=S四边形ABCD=S梯形ACDE =×(DE+AC)×DF=×(a+4a)×4a=10a2=x2.故选C.点评:本题运用了旋转法,将求不规则四边形面积问题转化为求梯形的面积,充分运用了全等三角形,勾股定理在解题中的作用.组卷二次函数难题61-90 难度4.5级12.(2011•兰州)如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是()A.B.C.D.考点:二次函数的应用;全等三角形的判定与性质;勾股定理.专题:压轴题.分析:根据条件可知△AEH≌△BFE≌△CGF≌△DHG,设AE为x,则AH=1﹣x,根据勾股定理EH2=AE2+AH2=x2+(1﹣x)2,进而可求出函数解析式,求出答案.解答:解:∵根据正方形的四边相等,四个角都是直角,且AE=BF=CG=DH,∴可证△AEH≌△BFE≌△CGF≌△DHG.设AE为x,则AH=1﹣x,根据勾股定理,得EH2=AE2+AH2=x2+(1﹣x)2即s=x2+(1﹣x)2.s=2x2﹣2x+1,∴所求函数是一个开口向上,对称轴是直线x=.∴自变量的取值范围是大于0小于1.故选B.点评:本题需根据自变量的取值范围,并且可以考虑求出函数的解析式来解决.二、填空题(共12小题)(除非特别说明,请填准确值)组卷二次函数难题61-90 难度5 级13.(2009•黄石)若抛物线y=ax2+bx+3与y=﹣x2+3x+2的两交点关于原点对称,则a、b 分别为、3.考点:二次函数图象与几何变换;关于原点对称的点的坐标.专题:压轴题.分析:有交点,可让两个抛物线组成方程组.解答:解:由题意可得,两个函数有交点,则y相等,则有ax2+bx+3=﹣x2+3x+2,得:(a+1)x2+(b﹣3)x+1=0.∵两交点关于原点对称,那么两个横坐标的值互为相反数;两个纵坐标的值也互为相反数.则两根之和为:﹣=0,两根之积为<0,解得b=3,a<﹣1.设两个交点坐标为(x1,y1),(x2,y2).这两个根都适合第二个函数解析式,那么y1+y2=﹣(x12+x 22)+3 (x 1+x2)+4=0,∵x1+x2=0,∴y1+y2=﹣(x1+x2)2+2x1x2+4=0,解得x1x 2=﹣2,代入两根之积得=﹣2,解得a=﹣,故a=﹣,b=3.另法:(若交点关于原点对称,那么在y=﹣x2+3x+2中,必定自身存在关于原点对称的两个点,设这两个点横坐标分别为k和﹣k,直接在y=﹣x2+3x+2代入k,然后相加两个式子﹣k2+3k+2=0与﹣k2﹣3k+2=0,可得出k为±,从而直接得到两个点,再待定系数法,将两点代入y=ax2+bx+3,直接可以得出a,b的值.点评:本题用到的知识点为:两个函数有交点,那么应让这两个函数图象组成方程组,而后根据根与系数的关系求解.组卷二次函数难题61-90 难度 4.5 级14.(2010•成都)如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s 的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不与点C重合).如果P、Q分别从A、B 同时出发,那么经过3秒,四边形APQC的面积最小.考点:二次函数的应用.专题:计算题.分析:根据等量关系“四边形APQC的面积=三角形ABC的面积﹣三角形PBQ的面积”列出函数关系求最小值.解答:解:设P、Q同时出发后经过的时间为ts,四边形APQC的面积为Smm2,则有:S=S△ABC﹣S△PBQ==4t2﹣24t+144=4(t﹣3)2+108.∵4>0∴当t=3s时,S取得最小值.点评:本题考查了函数关系式的求法以及最值的求法.组卷二次函数难题61-90 难度 5 级15.(2009•金华)如图,在第一象限内作射线OC,与x轴的夹角为30°,在射线OC上取一点A,过点A作AH⊥x 轴于点H.在抛物线y=x2(x>0)上取点P,在y轴上取点Q,使得以P,O,Q为顶点的三角形与△AOH全等,则符合条件的点A的坐标是(3,),(,),(2,2),(,).考点:二次函数综合题.专题:压轴题.分析:在△AOH中,因为∠AOH=30°,所以A的纵坐标是横坐标的倍,若设A的坐标为(t,t),则Q、P 点坐标均可求出,然后根据全等三角形的判定,对应求解即可.解答:解:由题可得A的横坐标是纵坐标的倍,故设A的坐标为(t,t);则Q的坐标为(0,2t)或(0,t);可求得P点对应的坐标,解可得t的值有4个,为,,2,;故点A的坐标是(3,)、(,)、(2,2)、(,).点评:本题考查二次函数的有关性质,涉及图象与点的坐标的求法.组卷二次函数难题61-90 难度 4 级16.(2009•江津区)锐角△ABC中,BC=6,S△ABC=12,两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y>0),当x=3,公共部分面积y最大,y最大值=6.考点:二次函数的应用.专题:压轴题;动点型.分析:公共部分分为三种情形:在三角形内;刚好一边在BC上,此时为正方形;正方形有一部分在三角形外,此时为矩形.显然在内部时的面积比刚好在边上时要小,所以需比较后两种情形时的面积大小.为正方形时可求出面积的值,为矩形时需求面积表达式再求最大值.解答:解:公共部分分为三种情形:在三角形内;刚好一边在BC上,此时为正方形;正方形有一部分在三角形外,此时为矩形.显然在内部时的面积比刚好在边上时要小,所以需比较后两种情形时的面积大小.(1)求公共部分是正方形时的面积,作AD⊥BC于D点,交MN于E点,∵BC=6,S△ABC=12,∴AD=4,∵MN∥BC,∴即,解得x=2.4,此时面积y=2.42=5.76.(2)当公共部分是矩形时如图所示:设DE=a,根据得=,所以a=4﹣x,公共部分的面积y=x(4﹣x)=﹣x2+4x,∵﹣<0,∴y有最大值,当x=﹣=3时,y最大值==6.综上所述,当x=3时,公共部分的面积y最大,最大值为6.点评:此题需分类讨论,综合比较后得结论.组卷二次函数难题61-90 难度4 级17.(2008•庆阳)兰州市“安居工程”新建成的一批楼房都是8层高,房子的价格y(元/平方米)随楼层数x(楼)的变化而变化(x=1,2,3,4,5,6,7,8);已知点(x,y)都在一个二次函数的图象上(如图所示),则6楼房子的价格为2080元/平方米.考点:二次函数的应用.专题:操作型;函数思想.分析:从图象中找出顶点坐标、对称轴,利用对称性即可解答.解答:解:由图象可知(4,2200)是抛物线的顶点,∵x=4是对称轴,∴点(2,2080)关于直线x=4的对称点是(6,2080).∴6楼房子的价格为2080元.点评:要求熟悉二次函数的对称性,并准确的找到所求的点与那个已知点是对称点,此题的关键是能找到顶点是(4,2200).组卷二次函数难题61-90 难度 5 级18.(2009•浙江)如图,抛物线y=ax2+bx+c与x轴的一个交点A在点(﹣2,0)和(﹣1,0)之间(包括这两点),顶点C是矩形DEFG上(包括边界和内部)的一个动点,则:(1)abc<0(填“>”或“<”);(2)a的取值范围是≤a≤.考点:二次函数综合题.专题:压轴题;动点型.分析:(1)观察图形发现,由抛物线的开口向下得到a<0,顶点坐标在第一象限得到b>0,抛物线与y轴的交点在y轴的上方推出c>0,由此即可判定abc的符号;(2)顶点C是矩形DEFG上(包括边界和内部)的一个动点,当顶点C与D点重合,可以知道顶点坐标为(1,3)且抛物线过(﹣1,0),则它与x轴的另一个交点为(3,0),由此可求出a;当顶点C与F点重合,顶点坐标为(3,2)且抛物线过(﹣2,0),则它与x轴的另一个交点为(8,0),由此也可求a,然后由此可判断a的取值范围.解答:解:(1)观察图形发现,抛物线的开口向下,∴a<0,∵顶点坐标在第一象限,∴﹣>0,∴b>0,而抛物线与y轴的交点在y轴的上方,∴c>0,∴abc <0;(2)顶点C是矩形DEFG上(包括边界和内部)的一个动点,当顶点C与D点重合,顶点坐标为(1,3),则抛物线解析式y=a(x﹣1)2+3,由,解得﹣≤a≤﹣;当顶点C与F点重合,顶点坐标为(3,2),则抛物线解析式y=a(x﹣3)2+2,由,解得﹣≤a≤﹣;∵顶点可以在矩形内部,∴﹣≤a≤﹣.点评:本题主要考查了抛物线的解析式y=ax2+bx+c中a、b、c对抛物线的影响,在对于抛物线的顶点在所给图形内进行运动的判定,充分利用了利用形数结合的方法,展开讨论,加以解决.组卷二次函数难题61-90 难度 5.5 级。
2015年中考数学真题训练二次函数_及答案
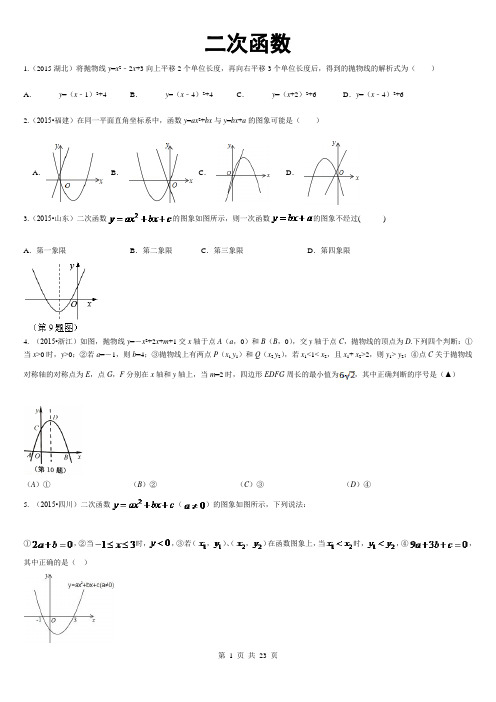
二次函数1.(2015湖北)将抛物线y=x2﹣2x+3向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线的解析式为()A.y=(x﹣1)2+4 B.y=(x﹣4)2+4 C.y=(x+2)2+6 D.y=(x﹣4)2+62.(2015•福建)在同一平面直角坐标系中,函数y=ax2+bx与y=bx+a的图象可能是()A.B.C.D.3.(2015•山东)二次函数的图象如图所示,则一次函数的图象不经过( )A.第一象限B.第二象限C.第三象限D.第四象限4. (2015•浙江)如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和B(B,0),交y轴于点C,抛物线的顶点为D.下列四个判断:①当x>0时,y>0;②若a=-1,则b=4;③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1< x2,且x1+ x2>2,则y1> y2;④点C关于抛物线对称轴的对称点为E,点G,F分别在x轴和y轴上,当m=2时,四边形EDFG周长的最小值为,其中正确判断的序号是(▲)(A)①(B)②(C)③(D)④5. (2015•四川)二次函数()的图象如图所示,下列说法:①,②当时,,③若(,)、(,)在函数图象上,当时,,④,其中正确的是()A .①②④B .①④C .①②③D .③④6.(2015•山东)如图是抛物线y 1=ax 2+bx +c (a ≠0)图象的一部分,抛物线的顶点坐标A (1,3),与x 轴的一个交点B (4,0),直线y 2=mx +n (m ≠0)与抛物线交于A ,B 两点,下列结论:①2a +b =0;②abc >0;③方程ax 2+bx +c =3有两个相等的实数根;④抛物线与x 轴的另一个交点是(﹣1,0);⑤当1<x <4时,有y 2<y 1,其中正确的是( )A . ①②③B . ①③④C . ①③⑤D . ②④⑤7.(2015·湖南省)若抛物线y =(x ﹣m )2+(m +1)的顶点在第一象限,则m 的取值范围为( )A . m >1B . m >0C . m >﹣1D . ﹣1<m <08.(2015•广东)对于二次函数y =﹣x 2+2x .有下列四个结论:①它的对称轴是直线x =1;②设y 1=﹣x 12+2x 1,y 2=﹣x 22+2x 2,则当x 2>x 1时,有y 2>y 1;③它的图象与x 轴的两个交点是(0,0)和(2,0);④当0<x <2时,y >0.其中正确的结论的个数为( )A . 1B . 2C . 3D . 49. (2015•浙江)二次函数)0(4)4(2≠--=a x a y 的图象在2<x <3这一段位于x 轴的下方,在6<x <7这一段位于x 轴的上方,则a 的值为【 】A . 1B . -1C . 2D . -210.(2015•安徽省)如图,一次函数y 1=x 与二次函数y 2=ax 2+bx +c 图象相交于P 、Q 两点,则函数y =ax 2+(b -1)x +c 的图象可能是( )11.(2015•四川)如图,抛物线y =ax 2+bx +c (c ≠0)过点(﹣1,0)和点(0,﹣3),且顶点在第四象限,设P =a +b +c ,则P 的取值范围是( )A . ﹣3<P <﹣1B . ﹣6<P <0C . ﹣3<P <0D . ﹣6<P <﹣3P Q OOO OO yy y y yx x x x xA .B .C .D .第10题图12.(2015·山东)已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(﹣1,0),下列结论:①abc<0;②b2﹣4ac=0;③a>2;④4a﹣2b+c>0.其中正确结论的个数是()A. 1 B. 2 C. 3 D. 413. (2015•浙江)如图,已知直线分别交轴、轴于点、,是抛物线上的一个动点,其横坐标为,过点且平行于轴的直线交直线于点,则当时,的值是▲ .14.(2015湖南)如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,顶点C的纵坐标为﹣2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是.(写出所有正确结论的序号)①b>0②a﹣b+c<0③阴影部分的面积为4④若c=﹣1,则b2=4A.15.(2015上海)如果将抛物线y=x2+2x-1向上平移,使它经过点A(0,3),那么所得新抛物线的表达式是_______________.16. (2015山东)二次函数的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积为.17. (2015•浙江)已知抛物线)()(2m x m x y ---=,其中m 是常数(1)求证:不论m 为何值,该抛物线与x 轴一定有两个公共点;(2)若该抛物线的对称轴为直线25=x ,①求该抛物线的函数解析式;②把该抛物线沿y 轴向上平移多少个单位长度后,得到的抛物线与x 轴只有一个公共点?18. (2015山东)如图隧道的截面由抛物线和长方形构成,长方形的长是12m ,宽是4m .按照图中所示的直角坐标系,抛物线可以用cbx x y ++-=261表示,且抛物线上的点C 到OB 的水平距离为3m ,到地面OA 的距离为217m 。
2015版武汉中考二次函数专题练习及答案
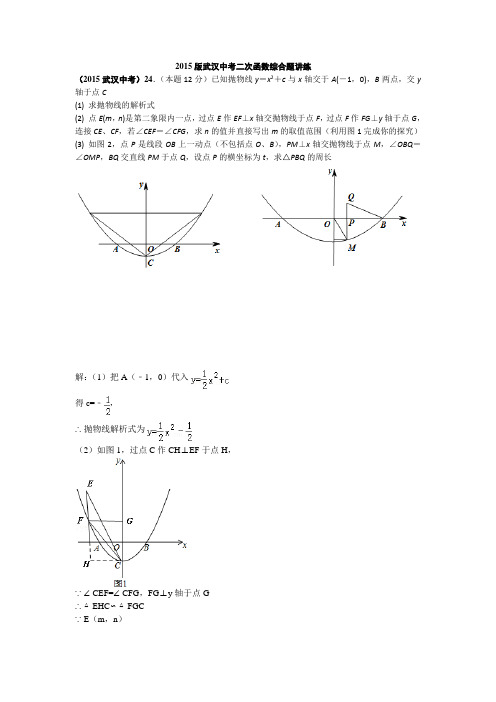
2015版武汉中考二次函数综合题讲练(2015武汉中考)24.(本题12分)已知抛物线y=x2+c与x轴交于A(-1,0),B两点,交y 轴于点C(1) 求抛物线的解析式(2) 点E(m,n)是第二象限内一点,过点E作EF⊥x轴交抛物线于点F,过点F作FG⊥y轴于点G,连接CE、CF,若∠CEF=∠CFG,求n的值并直接写出m的取值范围(利用图1完成你的探究)(3) 如图2,点P是线段OB上一动点(不包括点O、B),PM⊥x轴交抛物线于点M,∠OBQ=∠OMP,BQ交直线PM于点Q,设点P的横坐标为t,求△PBQ的周长解:(1)把A(﹣1,0)代入得c=﹣,∴抛物线解析式为(2)如图1,过点C作CH⊥EF于点H,∵∠CEF=∠CFG,FG⊥y轴于点G∴△EHC∽△FGC∵E(m,n)∴F(m,)又∵C(0,)∴EH=n+,CH=﹣m,FG=﹣m,CG=m2又∵,则∴n+=2∴n=(﹣2<m<0)(3)由题意可知P(t,0),M(t,)∵PM⊥x轴交抛物线于点M,∠OBQ=∠OMP,∴△OPM∽△QPB.∴.其中OP=t,PM=,PB=1﹣t,∴PQ=.BQ=∴PQ+BQ+PB=.∴△PBQ的周长为2.yQ FEO xO MDCB Axy6、如图1,抛物线23y ax bx =++经过点A (-3,0),B (-1,0)两点, (1)求抛物线的解析式;(2)设抛物线的顶点为M ,直线y=-2x+9与y 轴交于点C ,与直线OM 交于点D ,现将抛物线平移,保持顶点在直线OD 上,若平移的抛物线与射线CD (含端点C )只有一个公共点,求它的顶点横坐标的值或者取值范围;(3)如图2,将抛物线平移,当顶点至原点时,过点Q (0,3)作不平行于x 轴的直线交抛物线于E 、F 两点,问在y 轴的负半轴上是否存在点P ,使△PEF 的内心在y 轴上。
若存在,求出点P 的坐标;若不存在,请说明理由。
图 1图2答案:(1)抛物线32++=bx ax y 经过A(-3,0),B(-1,0)⎩⎨⎧=+-=+-∴030339b a b a ,解得⎩⎨⎧==41b a ∴抛物线的解析式:342++=x x y 。
2015年中考真题初中数学---二次函数(3)
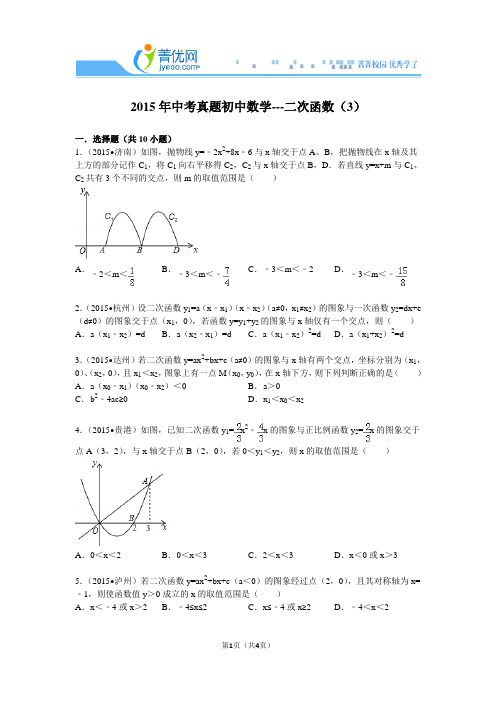
2015年中考真题初中数学---二次函数(3)一.选择题(共10小题)1.(2015•济南)如图,抛物线y=﹣2x2+8x﹣6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是()<﹣2.(2015•杭州)设二次函数y1=a(x﹣x1)(x﹣x2)(a≠0,x1≠x2)的图象与一次函数y2=dx+e3.(2015•达州)若二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点,坐标分别为(x1,4.(2015•贵港)如图,已知二次函数y1=x2﹣x的图象与正比例函数y2=x的图象交于点A(3,2),与x轴交于点B(2,0),若0<y1<y2,则x的取值范围是()5.(2015•泸州)若二次函数y=ax2+bx+c(a<0)的图象经过点(2,0),且其对称轴为x=6.(2015•六盘水)如图,假设篱笆(虚线部分)的长度16m,则所围成矩形ABCD的最大面积是()7.(2015•铜仁市)河北省赵县的赵州桥的桥拱是近似的抛物线形,建立如图所示的平面直角坐标系,其函数的关系式为y=﹣x2,当水面离桥拱顶的高度DO是4m时,这时水面宽度AB为()8.(2015•金华)图2是图1中拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可近似看成抛物线y=﹣(x﹣80)2+16,桥拱与桥墩AC的交点C恰好在水面,有AC⊥x轴,若OA=10米,则桥面离水面的高度AC为()16米米米9.(2015•潍坊)如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是()cm2B cm2cm2cm210.(2015•嘉兴)如图,抛物线y=﹣x2+2x+m+1交x轴与点A(a,0)和B(b,0),交y 轴于点C,抛物线的顶点为D,下列四个命题:①当x>0时,y>0;②若a=﹣1,则b=4;③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2;④点C关于抛物线对称轴的对称点为E,点G,F分别在x轴和y轴上,当m=2时,四边形EDFG周长的最小值为6.其中真命题的序号是()2015年中考真题初中数学---二次函数(3)参考答案一.选择题(共10小题)1.D 2.B 3.A 4.C 5.D 6.C 7.C 8.B 9.C 10.C。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题
1.(2014上海)如果将抛物线y=x 2
向右平移1个单位,那么所得的抛物线的表达式
3.(2014•新疆)对于二次函数
y =(x ﹣1)2
+2的图象,下列说法正确的是( )
4.(2014•滨州)下列函数中,图象经过原点的是( )
5. (2014江苏苏州)二次函数
y=ax +bx ﹣1(a ≠0)的图象经过点(1,1),则代数
B (8,3),则h 的值可以是( ) A . 6 B . 5
C . 4
D . 3
2
9.(2013河南省)在二次函数2
21y x x =-++的图像中,若y 随x 的增大而增大,则
x 的取值范围是( )
(A )1x < (B )1x >
(C )1x <- (D )1x >-
10. (2014年四川资阳)二次函数y =ax 2
+bx +c (a ≠0)的图象如图,给出下列四个结论:
①4ac ﹣b 2
<0;②4a +c <2b ;③3b +2c <0;④m (am +b )+b <a (m ≠﹣1), 其中正确结论的个数是( )
A . 4个
B .3个
C . 2个
D . 1个
姓名 成绩_____
二、填空题
11. (2013淮安)二次函数y=x 2
+1的图象的顶点坐标是 12.(2013年广东湛江)抛物线2
1y x =+的最小值是 13.(2014年云南)抛物线y =x 2
﹣2x +3的顶点坐标是
14.(2013年北京)请写出一个开口向上,并且与y 轴交于点(0,1)的抛物线的解析式_________(2014•珠海)对称轴平行于y 轴的抛物线与x 轴交于(1,0),(3,0)两点,則它的对称轴为
15.(2014安徽省)某厂今年一月份新产品的研发资金为a 元,以后每月新产品的研发资金与上月相比增长率都是x ,则该厂今年三月份新产品的研发资金y (元)关于
x 的函数关系式为y =
三、.解答题
16.(2014山东威海)已知抛物线y =ax 2
+bx +c (a ≠0)经过A (﹣1,0),B (4,0),C (0,2)三点.求这条抛物线的解析式;
17.(2014福建泉州)如图,已知二次函数y =a (x ﹣h )2
+的图象经过原点O (0,
0),A (2,0).
(1)求解析式并写出该函数图象的对称轴
(2)若将线段OA 绕点O 逆时针旋转60°到OA ′,试判断点A ′是否为该函数图象的顶点?
18.(2014•滨州)已知二次函数y=x2﹣4x+3.
(1)用配方法求其图象的顶点C的坐标,并描述该函数的函数值随自变量的增减而变化的情况;
(2)求函数图象与x轴的交点A,B的坐标,及△ABC的面积.
19.(2013浙江省嘉兴市)某汽车租赁公司拥有2O辆汽车。
据统计,当每辆车的日租金为400元时,可全部租出;当每辆车的日租金每增加50元,未租出的车将增加1辆;公司平均每日的各项支出共4800元.设公司每日租出x辆车时,日收益为y元.(日收益=日租金收入一平均每日各项支出)
(1)公司每日租出x辆车时,每辆车的日租金为_______元(用含x的代数式表示);
(2)当每日租出多少辆时,租赁公司日收益最大?最大是多少元?
(3)当每日租出多少辆时,租赁公司的日收益不盈也不亏?
20.(2013山东省青岛市)在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如图所示:
⑴试判断y与x 之间的函数关系,并求出函数关系式;
⑵若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润w(元)与销售单价x(元/个)之间的函数关系式;
⑶若许愿瓶的进货成本不超过900元,要想获得最大的利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.
21.(2014•益阳)如图,直线y=﹣3x+3与x轴、y轴分别交于点A、B,抛物线y=a
(x﹣2)2+k经过点A、B,并与X轴交于另一点C,其顶点为P.
(1)求a,k的值;
(2)抛物线的对称轴上有一点Q,使△ABQ是以AB为底边的等腰三角形,求Q点
的坐标;。
