弹性力学及有限元(1)
合集下载
弹性力学及有限元习题参考答案(赵均海、汪梦甫)汇编

2
(1,1)
4
(0,0)
5
(1,1)
(0,0)
(1,0)
号
③
2
(1,1)
5
(1,0)
6
(2,0)
④
2
(1,1)
3
(2,1)
6
(2,0)
元
②
1
2
1
2
1
2
cm
1
-1
-1
0
0
-1
1
0
-1
K11
K K 21
K31
1
2
K12
K 22
K32
0
1
-1
1
-1
0
1
0
-1
0
-1
1
K13
K 23 (i 1, j 2, m 3)
(3)主方向:
l( − ) + + = 0
+ ( − ) + = 0
+ + ( − ) = 0
2 + 2 + 2 = 1
第一主方向:将1 = −46 MPa 及个分量代入上式,有:
101l + 40 = 0
0
0
0
0
5 2
7 17
0
0
0
0
5 12
0
0
17
0 12 2
0
0
0
0
0
17
5
5
0
0
0
0 12 5
34
0 12 5
0
0
(1,1)
4
(0,0)
5
(1,1)
(0,0)
(1,0)
号
③
2
(1,1)
5
(1,0)
6
(2,0)
④
2
(1,1)
3
(2,1)
6
(2,0)
元
②
1
2
1
2
1
2
cm
1
-1
-1
0
0
-1
1
0
-1
K11
K K 21
K31
1
2
K12
K 22
K32
0
1
-1
1
-1
0
1
0
-1
0
-1
1
K13
K 23 (i 1, j 2, m 3)
(3)主方向:
l( − ) + + = 0
+ ( − ) + = 0
+ + ( − ) = 0
2 + 2 + 2 = 1
第一主方向:将1 = −46 MPa 及个分量代入上式,有:
101l + 40 = 0
0
0
0
0
5 2
7 17
0
0
0
0
5 12
0
0
17
0 12 2
0
0
0
0
0
17
5
5
0
0
0
0 12 5
34
0 12 5
0
0
弹性力学及有限元法1

弹性力学及有限元法
Elae Element Method
机械工程与自动化学院
现代设计与分析研究所
张瑞金 Rjzhang@
弹 性 力 学 及 有 限 元 法
第一章 绪论
了解弹性力学的定义;
了解弹性力学研究方法 ; 掌握有限单元法的基本思想; 了解常用有限元计算程序; 课程计划。
绪 论
现有网格基础上,根据有限元计算结果估计计算误差、重新划分网格和 再计算的一个循环过程。 3、由求解线性问题发展到求解非线性问题 许多工程问题如材料的破坏与失效、裂纹扩展等仅靠线性理论根本不能 解决,必须进行非线性分析求解,例如薄板成形就要求同时考虑结构的 大位移、大应变(几何非线性)和塑性(材料非线性);而对塑料、橡 胶、陶瓷、混凝土及岩土等材料进行分析,则必须考虑材料非线性。 4、由单一结构场求解发展到耦合场问题的求解 求解线性结构问题,只要离散单元足够小,所得的解就可足够逼近于精 确值。现在发展方向是结构非线性、流体动力学和耦合场问题的求解。 例如由于摩擦接触而产生的热问题,金属成形时由于塑性功而产生的热 问题,需要结构场和温度场的有限元分析结果交叉迭代求解,即“热力耦 合”的问题。 5、程序面向用户的开放性 商业化的提高要求给用户一个开放的环境。
解析法:得出精确的函数解
数值法: 差分法:采用差商代替微商,将弹力中导 出的微分方程及其边界条件化为差分方程 (代数方程)进行求解。 变分法:根据变形体的能量极值原理,导 出弹性力学的变分方程,并进行求解。 有限单元法:离散模型的数值解
绪 论
弹 性 3. 有限元法基本思想 力 学 及 有 将求解区域划分为有限个互不重叠的单元,单元 之间仅依靠节点连接,单元内部点的待求量可由 限 元 单元节点量通过选定的函数关系插值求得,建立 法
Elae Element Method
机械工程与自动化学院
现代设计与分析研究所
张瑞金 Rjzhang@
弹 性 力 学 及 有 限 元 法
第一章 绪论
了解弹性力学的定义;
了解弹性力学研究方法 ; 掌握有限单元法的基本思想; 了解常用有限元计算程序; 课程计划。
绪 论
现有网格基础上,根据有限元计算结果估计计算误差、重新划分网格和 再计算的一个循环过程。 3、由求解线性问题发展到求解非线性问题 许多工程问题如材料的破坏与失效、裂纹扩展等仅靠线性理论根本不能 解决,必须进行非线性分析求解,例如薄板成形就要求同时考虑结构的 大位移、大应变(几何非线性)和塑性(材料非线性);而对塑料、橡 胶、陶瓷、混凝土及岩土等材料进行分析,则必须考虑材料非线性。 4、由单一结构场求解发展到耦合场问题的求解 求解线性结构问题,只要离散单元足够小,所得的解就可足够逼近于精 确值。现在发展方向是结构非线性、流体动力学和耦合场问题的求解。 例如由于摩擦接触而产生的热问题,金属成形时由于塑性功而产生的热 问题,需要结构场和温度场的有限元分析结果交叉迭代求解,即“热力耦 合”的问题。 5、程序面向用户的开放性 商业化的提高要求给用户一个开放的环境。
解析法:得出精确的函数解
数值法: 差分法:采用差商代替微商,将弹力中导 出的微分方程及其边界条件化为差分方程 (代数方程)进行求解。 变分法:根据变形体的能量极值原理,导 出弹性力学的变分方程,并进行求解。 有限单元法:离散模型的数值解
绪 论
弹 性 3. 有限元法基本思想 力 学 及 有 将求解区域划分为有限个互不重叠的单元,单元 之间仅依靠节点连接,单元内部点的待求量可由 限 元 单元节点量通过选定的函数关系插值求得,建立 法
弹性力学边值问题及有限元法(PPT)

0
Ni y Ni x
N j x 0
N j y
0
N j y N j x
N m x 0
N m y
0
N m y N m x
ui
vi
u v
j j
um vm
1 2A
b0i ci
0 ci bi
bj 0 cj
0 cj bj
B Bi B j
ui
bm 0 cm
0 cm bm
a
u
v
N
ae
INi
I
1 0
0 1
IN j INm ae
位移模式需满足以下三个条件: 1、位移模式必须反映单元的刚体位移 2、位移模式必须反映单元的常量应变 3、位移模式应尽可能反映位移的连续性
单元应变函数
u
x y
xy
x u
y
u y
v x
Ni
x
0
Ni
y
) xy
x
E
1 2
( x
y)
y
E
1 2
(
x
y)
xy
2(1 E
)
xy
E
1 2
1
2
xy
x y
xy
E
1 2
1
0
1 0
1
0
0
xxyy
2
D DBae
D
E
1 2
1
0
1 0
0
0
1
2
在数学上,要将某个微分方程的定解问题 转化为一个变分问题求解,必须针对已给的定 解问题构造一个相应的泛函,并证明定解问题 的解与泛函极值问题的解等价。
弹性力学:平板弯曲问题的有限元分析(1)

其中为薄板的弯曲刚度9899薄板的弹性曲面微分方程薄板横截面上的内力称为薄板横截面上的内力称为薄板内力薄板内力是指薄板横截面的单是指薄板横截面的单位宽度上由应力合成的位宽度上由应力合成的主矢量主矢量和和主矩主矩
平板弯曲问题的有限元分析(1) Kirchhoff弹性薄板理论
参考文献: “弹性力学(下册)”第13章。徐芝纶
x
2w
2 (z2
2
2
)dz 4
E 3 12(1 2 )
x
2w
(c)
同样,在y为常量的截面上,每单位宽度内的 y , yx , yz
也分别合成如下的弯矩,扭矩,和横向剪力:
M y
2 2
z
y dz
E
12(1
3
2
)
(
2w y2
2w x2
)
(d)
M yx
2
2
z yxdz
E 3 12(1 2 )
(9-6)
( z )z q
(f)
2
将(9-6)式代入薄板上板面的边界条件:
得:
E
12(1
3
2
)
4
w
q
(9-7)
或 D4w q, (9-8)
其中
D
E
12(1
3
2
)
(9-9)
薄板的弹性曲面微分方程
为薄板的弯曲刚度
§9-3 薄板横截面上的内力
► 薄板横截面上的内力,称为薄板内力,是指薄板横截面的单 位宽度上,由应力合成的主矢量和主矩。
对z积分,得到: z
2(1 2 )
2
( 4
z
z2 )4w 3
F3 (x,
平板弯曲问题的有限元分析(1) Kirchhoff弹性薄板理论
参考文献: “弹性力学(下册)”第13章。徐芝纶
x
2w
2 (z2
2
2
)dz 4
E 3 12(1 2 )
x
2w
(c)
同样,在y为常量的截面上,每单位宽度内的 y , yx , yz
也分别合成如下的弯矩,扭矩,和横向剪力:
M y
2 2
z
y dz
E
12(1
3
2
)
(
2w y2
2w x2
)
(d)
M yx
2
2
z yxdz
E 3 12(1 2 )
(9-6)
( z )z q
(f)
2
将(9-6)式代入薄板上板面的边界条件:
得:
E
12(1
3
2
)
4
w
q
(9-7)
或 D4w q, (9-8)
其中
D
E
12(1
3
2
)
(9-9)
薄板的弹性曲面微分方程
为薄板的弯曲刚度
§9-3 薄板横截面上的内力
► 薄板横截面上的内力,称为薄板内力,是指薄板横截面的单 位宽度上,由应力合成的主矢量和主矩。
对z积分,得到: z
2(1 2 )
2
( 4
z
z2 )4w 3
F3 (x,
弹性力学教学课件-1-有限元位移法的基本概念
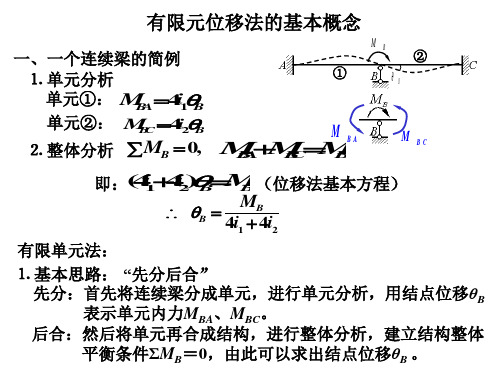
2i1
M3 0
2i1 4i1 4i2
2i2
②
M3
3
0阵:
M M M123420ii11
2i1 4i1 4i2
2i2
420ii22132
m(e) 1 m2
k k1 21 1
k12(e) k22
(e) 1
2
四、支承条件的引入
第一步:暂不引入支承条件,
0
1 1
2
3
2 i1 2
即: M M1242ii11112(4i1i1240i2)322i23 1
M3 012i224i23
0
或:
M M M123420ii11
2i1 4i1 4i2
2i2
420ii22132
1
(4i1 4i2)2 ② 2 i2 2
① 2 2
3
2 i2 3
3 4 i2 3
①2
②
3
M M M123420ii11
2i1 4i1 4i2
2i2
420ii22012M PP123
取出前面两个纯量方程:
4i112i12 P1 2i11(4i14i2)2
P2
即:
4i1 2i1
4i12i14i212P P12
1
①
M2
2
②
M3
3
4 i1 1
2 i1 1 ①
②
0
1 1
2
3
2 i1 2
即: M M1242ii11112(4i1i1240i2)322i23 1
M3 012i224i23
0
或:
M M M123420ii11
2i1 4i1 4i2
弹性力学及有限元法 ANSYS实例演示课件

有限元法是一种数值分析方法,通过 将连续的物理系统离散化为有限数量 的单元,利用这些单元的组合来逼近 真实系统的行为。
它广泛应用于工程领域,用于解决各 种复杂的力学、热学、电磁学等问题 。
有限元法的实现过程
01
离散化
将连续的物理系统划分为有限数量 的离散单元。
整体分析
将所有单元的数学模型组合起来, 形成整个系统的数学模型。
使用ANSYS的几何建模 功能,创建一个矩形薄 板模型。
选择适当的单位制,如 国际单位制(SI)。
为薄板指定弹性模量、 泊松比和密度等材料属 性。
通过与已知解进行比较 ,验证模型的正确性和 准确性。
材料属性设置与网格划分
01
02
03
材料属性
根据问题描述,为薄板设 置弹性模量、泊松比和密 度等材料属性。
局限性
ANSYS软件的学习曲线较陡峭,需要用户具备一定的专业背景和经验;同时,对于某些特殊问题,可 能需要结合其他软件或方法进行求解。
未来研究与发展的方向
多物理场耦合
进一步发展多物理场耦合的有限元分析方法 ,以模拟更复杂的工程问题。
智能化与自动化
研究有限元分析的智能化和自动化技术,提 高分析效率和精度。
网格划分
对薄板进行网格划分,选 择合适的网格密度以提高 求解精度。
网格质量检查
检查网格质量,确保网格 划分满足求解精度要求。
边界条件与载荷设置
边界条件
载荷与边界条件验证
根据实际情况,为薄板的边界设置约 束条件,如固定约束或简支约束。
通过有限元分析理论,验证所设置的 载荷和边界条件的正确性。
载荷设置
结构分析
有限元法能够模拟复杂结构的力学行为,为工程设计 和优化提供依据。
它广泛应用于工程领域,用于解决各 种复杂的力学、热学、电磁学等问题 。
有限元法的实现过程
01
离散化
将连续的物理系统划分为有限数量 的离散单元。
整体分析
将所有单元的数学模型组合起来, 形成整个系统的数学模型。
使用ANSYS的几何建模 功能,创建一个矩形薄 板模型。
选择适当的单位制,如 国际单位制(SI)。
为薄板指定弹性模量、 泊松比和密度等材料属 性。
通过与已知解进行比较 ,验证模型的正确性和 准确性。
材料属性设置与网格划分
01
02
03
材料属性
根据问题描述,为薄板设 置弹性模量、泊松比和密 度等材料属性。
局限性
ANSYS软件的学习曲线较陡峭,需要用户具备一定的专业背景和经验;同时,对于某些特殊问题,可 能需要结合其他软件或方法进行求解。
未来研究与发展的方向
多物理场耦合
进一步发展多物理场耦合的有限元分析方法 ,以模拟更复杂的工程问题。
智能化与自动化
研究有限元分析的智能化和自动化技术,提 高分析效率和精度。
网格划分
对薄板进行网格划分,选 择合适的网格密度以提高 求解精度。
网格质量检查
检查网格质量,确保网格 划分满足求解精度要求。
边界条件与载荷设置
边界条件
载荷与边界条件验证
根据实际情况,为薄板的边界设置约 束条件,如固定约束或简支约束。
通过有限元分析理论,验证所设置的 载荷和边界条件的正确性。
载荷设置
结构分析
有限元法能够模拟复杂结构的力学行为,为工程设计 和优化提供依据。
二、 弹性力学有限元法基本原理(一)

1 6 12 8
引入约束条件:u1 0
即划去第一个方程,解出其余三个方程得到:
u2 13 3 cL u3 23 u 3 AE 27 4
结合单元位移模式 u N d 就得到整体上近似位移场。
s 是插值基函数矩阵,称为“形函数”矩阵。 L
L s N L
u1 d 称为单元1的节点位移列阵。 u2
其它两个单元也有同样的插值位移试探函数:
单元2:
u N d u N d
u2 , d u3
1 T U d k d 2
1 DT K D DT R 2 p 0 应用势能驻值条件: D
简写为: p
得到有限元求解方程——系统平衡方程:
K D R
即:
1 1 0 0 u1 1 2 1 0 u AE 2 cL2 L 0 1 2 1 u3 6 0 0 1 1 u4
这个做法正体现了有限元法的实质。
上面形式的分片位移试探函数有下列缺点: 必须对它进行调整,使其满足连续条件和边界约束条件; 多项式系数作为广义坐标缺乏明显的物理意义。
1) 2)
因此,上述不是通常意义上标准的有限元形式,仍然具有
局限性,如对于二维以上的问题使各单元之间分片多项式
保持连续性很难处理。
下面用节点位移未知量作为待定参数(广义坐标),得到 其标准有限元形式。
重新构造单元内位移试探函数
离散结构中,节点位移分量是问 题的基本未知量。
在每个单元内通过对节点位移插 值,分片建立位移试探函数:
(同济大学)第1讲_弹性力学及有限元方法概述

有限元分析
的一般规律物体在空间的位置随时间的改变
对象内容
任务
对象内容
任务
概述
ANSYS 静力分析z起重机械有限元应用
整机模态分析
车辆安全性
工件淬火3.06 min 时的温度、组织分布(NSHT3D)
同济大学
同济大学
金属反挤压成型:温度分布和变化铸造成型:温度变化和气泡
速度
压力导流管分析
超音速飞行压力分布汽车气动分析
高速导弹气动
同济大学
两根热膨胀系数不同的棒焊接在一起,加热后的变形情况
子结构方法分析大型结构的早期应用法
梁单元
建模时充分利用重复性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
弹性力学及有限元
上海交通大学土木工程系 吴刚
本课程的地位和作用
弹性力学作为一门基础技术学科,是近代 工程建设的必要基础之一
➢土木工程(水利、土建及采矿工程)
将弹性力学作为计算、设计和应力-应变分析的理论基础
➢船舶工程
船体结构的强度、刚度计算
➢航空及航天工程
航空航天结构的强度、 刚度计算
➢机械工程
成为数值分析工具,而且成为设计分析工具 ➢ 有限单元法将计算数学与工程分析相结合,极大地
扩展和延伸了弹性力学理论与方法,取得了当代力 学理论应用的高度成就 ➢ 有限元方法作为一种数值计算方法已经在土木、机 械、航空航天、热传导、电磁场、原子工程、生物 医学工程等众多学科领域得到广泛应用,已成为科 技工作者进行科学研究、解决工程技术问题的强有 力的工具
学习本课程的目的
掌握确定一般工程结构物体在外荷载作 用下的弹性变形、内力分布规律及承载 能力的方法
为进一步研究工程结构的强度、振动、 稳定性、破坏与失效等力学问题打下必 要的理论基础
掌握有限元的基本概念,初步掌握有限 元解平面问题的基本步骤和方法
本课程的教学
教师
认真备课,努力讲透有关概念和难点问题
• Phillip L. Gould. Introduction to Linear Elasticity. Springer-Verlag Press, 1997.
第一章 绪 论
§1-1 弹性力学的内容
弹性力学的定义及其研究内容
弹性力学,全称弹性体力学,又称弹性理论,是固 体力学的一个分支学科。 弹性力学研究弹性体在外界因素(外力、温度变化 和边界约束变动等)作用下而产生的应力和变形。
弹性力学的发展初期主要是通过实践,尤其是通过实验 来探索弹性力学的基本规律。英国的胡克和法国的马略 特于1680年分别独立地提出了弹性体的变形和所受外力 成正比的定律,后被称为胡克定律。牛顿于1687年确立 了力学三定律。
同时,数学的发展,使得建立弹性力学数学理论的条件 已大体具备,从而推动弹性力学进入第二个时期。在这 个阶段除实验外,人们还用最粗糙的、不完备的理论来 处理一些简单构件的力学问题。这些理论在后来都被指 出有或多或少的缺点,有些甚至是完全错误的。
所谓弹性,是指物体的应力与应变之间有着一一对应的关系, 而且当外作用除去后,物体又恢复到原来的状态。 弹性力学是材料力学课程的延续。在这门课程中,仅限于讨 论理想弹性体,即应力与应变之间的关系为线性函数,也就 是满足大家所熟知的胡克定律。
弹性力学的求解方法
数学方法
一种数学方法就是用数学分析的工具对弹性力学边 值问题进行求解,从而得出物体的应力场和位移场 等。这种方法要解含未知量的偏微分方程,即采用 所谓的逆解法和半逆解法。对很多问题精确求解的 难度很大,故通常采用近似解法。如:基于能量原 理的变分方法,其中主要是里茨( Ritz,W.)法,伽 辽金( Galerkin,塑性力学解题指导及习 题集,高等教育出版社,1985.
• 黄文彬,曾国平. 弹·塑性力学难题分析,高 等教育出版社,1998.
• 刘小明等编. 弹性力学题解,华中科技大学出 版社,2003.
• Arthur P. Boresi, Ken P. Chong. Elasticity in Engineering Mechanics. Wiley Press, 1999.
实验与数学相结合的方法 这种方法常用于形状非常复杂的弹性结构。例如 对结构的持殊部位的应力状态难以确定,可以用 光弹性方法测定,作为已知量,置入数值计算中, 特别是当边界条件难以确定时,则需两种方法结 合起来,以求得可靠的解答。
本课程主要介绍数学方法。
弹性力学的发展简史
人类从很早时就已经知道利用物体的弹性性质了,比如 古代弓箭就是利用物体弹性的例子。当时人们还是不自 觉的运用弹性原理,而人们有系统、定量地研究弹性力 学,是从17世纪开始的。
学生
做到课前预习及课后复习 上课认真听讲 圆满完成布置的作业
◆考核方式
期终考试与平时成绩相结合 成绩比例 期终∶平时=7∶3
本课程的讲授
教材:
徐芝纶著《弹性力学简明教程》(第三版) 高等教育出版社,2002年
内容:
第一章~第六章 视具体情况,讲授时会作一定的增、删。
教学参考书
• 杨桂通. 弹性力学简明教程.清华大学出版社,2006. • 徐芝纶. 弹性力学(第三版). 高等教育出版社,
另一种数学方法是数值方法。特别是广泛应用计算 机以后,数值方法对大量的弹性力学问题十分有效。 在数值方法中,常见的有差分法及边界元法等。目 前已广泛应用于弹性力学的各类问题的计算中。
实验方法 利用机电方法、光学方法、声学方法等来测定结 构部件在外力作用下应力和应变的分布规律,如 光弹性法、云纹法等。
1990. • 钱伟长,叶开源. 弹性力学. 科学出版社,1956. • S.Timoshenko & J. N. Goodier. Theory of
Elasticity.(Third edition) McGraw-hill Book Co.,1970. • 丁科,陈月顺. 有限单元法.北京大学出版社,2006. • 龙驭球. 有限单元法概论. 人民教育出版社,1978.
空气动力学 有限单元法
弹性力学本身发展迅速,现已形成了一些专 门分支学科,如:
热弹性力学 弹性动力学 弹性系统的稳定理论
等等
有限单元法作为一种重要的数值方法, 已在理论研究和工程中得到广泛应用
➢ 数值解法是现代科学技术,特别是计算机技术的迅 速发展和广泛应用为基础
➢ 有限单元法以弹性力学为基础 ➢ 有限单元法为代表的计算力学 ➢ 以有限元为基础的CAD, CAE等技术,使计算机不仅
机器部件在各种工作条件下的强度研究
➢地震科学
计算出震源的位置并研究地震波传播的规律性
➢军事工程
防护工程与人防工程结构的设计和分析计算
弹性力学作为一门基础理论学科, 具有广阔的发展前景
物理学家在光波理论中引用弹性力学。
弹性波理论
弹性力学已应用于:
材料科学 生物力学 断裂力学 损伤力学
学科交叉形成新分支(边缘学科):
上海交通大学土木工程系 吴刚
本课程的地位和作用
弹性力学作为一门基础技术学科,是近代 工程建设的必要基础之一
➢土木工程(水利、土建及采矿工程)
将弹性力学作为计算、设计和应力-应变分析的理论基础
➢船舶工程
船体结构的强度、刚度计算
➢航空及航天工程
航空航天结构的强度、 刚度计算
➢机械工程
成为数值分析工具,而且成为设计分析工具 ➢ 有限单元法将计算数学与工程分析相结合,极大地
扩展和延伸了弹性力学理论与方法,取得了当代力 学理论应用的高度成就 ➢ 有限元方法作为一种数值计算方法已经在土木、机 械、航空航天、热传导、电磁场、原子工程、生物 医学工程等众多学科领域得到广泛应用,已成为科 技工作者进行科学研究、解决工程技术问题的强有 力的工具
学习本课程的目的
掌握确定一般工程结构物体在外荷载作 用下的弹性变形、内力分布规律及承载 能力的方法
为进一步研究工程结构的强度、振动、 稳定性、破坏与失效等力学问题打下必 要的理论基础
掌握有限元的基本概念,初步掌握有限 元解平面问题的基本步骤和方法
本课程的教学
教师
认真备课,努力讲透有关概念和难点问题
• Phillip L. Gould. Introduction to Linear Elasticity. Springer-Verlag Press, 1997.
第一章 绪 论
§1-1 弹性力学的内容
弹性力学的定义及其研究内容
弹性力学,全称弹性体力学,又称弹性理论,是固 体力学的一个分支学科。 弹性力学研究弹性体在外界因素(外力、温度变化 和边界约束变动等)作用下而产生的应力和变形。
弹性力学的发展初期主要是通过实践,尤其是通过实验 来探索弹性力学的基本规律。英国的胡克和法国的马略 特于1680年分别独立地提出了弹性体的变形和所受外力 成正比的定律,后被称为胡克定律。牛顿于1687年确立 了力学三定律。
同时,数学的发展,使得建立弹性力学数学理论的条件 已大体具备,从而推动弹性力学进入第二个时期。在这 个阶段除实验外,人们还用最粗糙的、不完备的理论来 处理一些简单构件的力学问题。这些理论在后来都被指 出有或多或少的缺点,有些甚至是完全错误的。
所谓弹性,是指物体的应力与应变之间有着一一对应的关系, 而且当外作用除去后,物体又恢复到原来的状态。 弹性力学是材料力学课程的延续。在这门课程中,仅限于讨 论理想弹性体,即应力与应变之间的关系为线性函数,也就 是满足大家所熟知的胡克定律。
弹性力学的求解方法
数学方法
一种数学方法就是用数学分析的工具对弹性力学边 值问题进行求解,从而得出物体的应力场和位移场 等。这种方法要解含未知量的偏微分方程,即采用 所谓的逆解法和半逆解法。对很多问题精确求解的 难度很大,故通常采用近似解法。如:基于能量原 理的变分方法,其中主要是里茨( Ritz,W.)法,伽 辽金( Galerkin,塑性力学解题指导及习 题集,高等教育出版社,1985.
• 黄文彬,曾国平. 弹·塑性力学难题分析,高 等教育出版社,1998.
• 刘小明等编. 弹性力学题解,华中科技大学出 版社,2003.
• Arthur P. Boresi, Ken P. Chong. Elasticity in Engineering Mechanics. Wiley Press, 1999.
实验与数学相结合的方法 这种方法常用于形状非常复杂的弹性结构。例如 对结构的持殊部位的应力状态难以确定,可以用 光弹性方法测定,作为已知量,置入数值计算中, 特别是当边界条件难以确定时,则需两种方法结 合起来,以求得可靠的解答。
本课程主要介绍数学方法。
弹性力学的发展简史
人类从很早时就已经知道利用物体的弹性性质了,比如 古代弓箭就是利用物体弹性的例子。当时人们还是不自 觉的运用弹性原理,而人们有系统、定量地研究弹性力 学,是从17世纪开始的。
学生
做到课前预习及课后复习 上课认真听讲 圆满完成布置的作业
◆考核方式
期终考试与平时成绩相结合 成绩比例 期终∶平时=7∶3
本课程的讲授
教材:
徐芝纶著《弹性力学简明教程》(第三版) 高等教育出版社,2002年
内容:
第一章~第六章 视具体情况,讲授时会作一定的增、删。
教学参考书
• 杨桂通. 弹性力学简明教程.清华大学出版社,2006. • 徐芝纶. 弹性力学(第三版). 高等教育出版社,
另一种数学方法是数值方法。特别是广泛应用计算 机以后,数值方法对大量的弹性力学问题十分有效。 在数值方法中,常见的有差分法及边界元法等。目 前已广泛应用于弹性力学的各类问题的计算中。
实验方法 利用机电方法、光学方法、声学方法等来测定结 构部件在外力作用下应力和应变的分布规律,如 光弹性法、云纹法等。
1990. • 钱伟长,叶开源. 弹性力学. 科学出版社,1956. • S.Timoshenko & J. N. Goodier. Theory of
Elasticity.(Third edition) McGraw-hill Book Co.,1970. • 丁科,陈月顺. 有限单元法.北京大学出版社,2006. • 龙驭球. 有限单元法概论. 人民教育出版社,1978.
空气动力学 有限单元法
弹性力学本身发展迅速,现已形成了一些专 门分支学科,如:
热弹性力学 弹性动力学 弹性系统的稳定理论
等等
有限单元法作为一种重要的数值方法, 已在理论研究和工程中得到广泛应用
➢ 数值解法是现代科学技术,特别是计算机技术的迅 速发展和广泛应用为基础
➢ 有限单元法以弹性力学为基础 ➢ 有限单元法为代表的计算力学 ➢ 以有限元为基础的CAD, CAE等技术,使计算机不仅
机器部件在各种工作条件下的强度研究
➢地震科学
计算出震源的位置并研究地震波传播的规律性
➢军事工程
防护工程与人防工程结构的设计和分析计算
弹性力学作为一门基础理论学科, 具有广阔的发展前景
物理学家在光波理论中引用弹性力学。
弹性波理论
弹性力学已应用于:
材料科学 生物力学 断裂力学 损伤力学
学科交叉形成新分支(边缘学科):
