希望杯100试题及答案
2011年小学希望杯数学邀请赛6年级培训题1、计算：4.8×17.4×6.25—37.5×0.174×5.•3=_________。
2、计算： 0.•6＋0.•1•8＋0.4•3•9=_________。
3、计算：120092008200920072008−××+＋120102009201020082009−××+＋120112010201120092010−××+＋120122011201220102011−××+=_________。
4、计算：212122×+＋323222×+＋…＋10110010110022×+=_________。
5、在 10个连续自然数中，最多有_________个质数。
6、一类自然数，从第三个数字开始，每个数字都恰好是它前面两个数字的和，如 123,235等等，这类三位数共有________个。
7、已知一串分数：31，32，61，62，63，64，65，91，92，93，94，95，96，97，98，121，122，…1211，151，152，…其中第 2011个分数是_________。
8、已知 A={1,3,5,7}，B={1,4,7}，C={2,5,7,8}。
规定： A∩B={1,3,5,7}∩{1,4,7}={1,7}； A ∪B={1,3,5,7}∪{1,4,7}={1,3,4,5,7}。
根据此规定，可求得（ A∪C）∩B={_________}．9、某月的日历如图 1所示。
若用 2×3（2行3列）的长方形框出 6个数，使它们的和是 81．那么这 6个数中最小的是_________。
10、某些数除以 11余 1，除以 13余 3，除以 15余 13，那么这些数中最小的数是_________． 11、已知：43201312111=+++x ，则x=_________。
12、在自然数 1—2011中，最多可以取出________个数，使得这些数中任意四个数的和都不能被 11整除。
13、在自然数中，1² =1，2²=4，3² =9，…，数 1,4,9,…称为完全平方数。
若自然数 N=4434421L 12121212个m +++ （1≤m ≤2011）是一个完全平方数，则这样的 N 有________个。
14、有 4个不同的自然数 a,b, c, d 而且 0＜a＜b＜c＜d．如果 b－a =5, d－c =7, a,b,c, d 的平均数是 17,那么 d 最大是________．15、在数学竞赛中取得前四名的方方、园园、宝宝、贝贝年龄依次是相差 1岁，而且他们年龄的乘积是 1180,则他们的年龄分别是________、________、________、________．16、一个多位数是 149162536496481…,从左向右数的第 100个数字是________．17、有 100个连续自然数，请你按某种顺序排列，然后计算相邻三个数的和，其中和为偶数的最多有________个。
18、已知 a,b 为质数( a＞b )，ab 表示 a 与 b 的乘积，若 a＋ab＋b =55，那么 a－b 的值是________．19、一个六位数，它的个位上的数字是 6。
如果把数字 6移到第一位，所得的数是原数的 4倍。
这个六位数是________．20、两个数的最小公倍数是 252,最大公约数是 7,并且两个数中的大数不是小数的倍数，则这两个数是________．21、小宝记得英语单词 “hello”是由三个不同的字母 h,e,o 和两个相同的字母 l 组成的，但不记得排列顺序，则小宝可能出现的拼写错误共有________种。
22、将一个两位数的个位数字与十位数字交换后得到一个新数，它与原数相加，得到的和恰好是某个自然数的平方，这个和是________．23、一批树苗，如果让男女一起栽，平均每人需栽 6棵．如果只让女生栽，平均每人需栽 10棵．若只让男生栽，平均每人需________棵．24、小明同学准备把自己的零花钱都捐献给舟曲灾区的小朋友．他共有三个储钱罐，A 储钱罐里的钱占全部零花钱的七分之五，B 储钱罐里有 33元钱，C 储钱罐里的钱占全部零花钱的五分之几，小明共有零花钱________元．25、将 1～9这九个数字分别填入下列算式中的□中，使等式成立：（每个数字只能用一次） □□□×□□＝□□×□□＝400226、福利种子店对某种子进行促销：购买 5千克以内按 2元/千克销售 ,超过 5千克时,超出部分按八折销售．下面四个图中的_______为购买种子数(千克)与所付钱数(元)的关系图．27、10减去它的21后,再减去剩下的31 ,再减去剩下的41 ,…,当最后减去剩下的101后,剩下的数是_______.28、已知一个五位数b a 751 能被 72整除,则这个五位数是_______．29、将一个数的所有的约数两两求和,在所有的和中,若最小的是4,最大的是180,则这个数是_______．30、有100种食品,其中含钙的有86种,含铁的有43种,含锌的有15种,那么,其中既含钙又含铁的食品最少有_______种,同时含钙、铁、锌的食品最多有_______种．31、今年，张老师与他的三个学生的年龄和为76岁，且三个学生的年龄比为5：5：6,六年后张老师的年龄和三个学生的年龄之和相等，今年三个学生中年龄最大的是_______岁． 32、小庆看一本故事书，第一天了全书的61多2页,第二天看了全书的91少5页，第三天看完剩下的133页．这本故事书共有_______页.33、某校有201人参加数学竞赛，按百分制计分且得分均为整数，若总分为9999分，则至少有_______人的分数相同．34、甲、乙、丙三杯盐水的浓度分别为38℅,87.5℅和43．已知三杯盐水共200克，其中甲与乙丙两杯盐水的质量和相等，三杯盐水混合后，盐水的浓度变为60℅,那么，丙杯中有盐水_______克．35、小宇过生日时，妈妈送给小宇一盒圆珠笔，他把好朋友小刚和小强找来，他把这盒圆珠笔的一半给了小刚，然后又给小刚加了1支．接着，他又把剩下的一半分给了小强，也同样给小强又加了 1支，最后剩下 5支圆珠笔，他自己留下了．这盒圆珠笔共有_______支． 36、毛毛和丫丫要到同一地方去旅游，乘船可直接到达该地，也可骑马沿河岸前进，但其中还有31 的路途必须下马步行，若骑马的速度是船速的3倍，步行的速度是船速的52，若毛毛、丫丫骑马同时出发，那么，先到达旅游地点的是_______．37、某建筑公司2010年元月1日签订某公路修筑工程合同，限定2010年12月31日完工，结果92名工人上半年（即元月2日到6月30日）只完成了工程的52．如果照此速度要在限期内全部完工，下半年（从7月1日到12月31日）应增加______名工人．38、某商场销售MP4,去年按定价的90℅出售，能获得20℅的利润，今年由于进价降低，按去年定价的80℅出售，能获得25℅的利润．今年进价是去年进价的______℅． 39、师徒俩人加工同样多的零件，当师傅完成21时，徒弟完成120个．当师傅完成任务时，徒弟完成54．则师傅加工零件______个． 40、某停车场中共有三轮摩托车，四轮小轿车和六轮大卡车30辆，各种轮子共116个．已知四轮小轿比六轮大卡车的5倍多2辆，那么这个停车场中共有______辆小轿车．41、小王和小张在假期进行勤工俭学，他们在印刷公司任打字员．有一次，他们共同输入一份书稿，完成任务时，小王输入了全部书稿的85，小张每小时输入6000个字．如果单独让小王输入这份书稿要24小时．这份书稿共有______个字．42、三块重量相等的锡与铁的比是1：5,第二块合金中锡与铁的比是2：7,第三块合金中锡与铁的比是 3：4,如果把三块合金溶合成一块，那么新溶合成的合金中锡与铁的比是______．43、从 1、2、3、4这四个数字中取一个，或两个，或三个，或四个组成的自然数共有＿＿＿个，将它们从小到大排列，第41个数是＿＿＿．44、狐狸、小熊、小鹿、小猴现在分它们得到的一千克饼，怎样分好呢？狡猾的狐狸说：“饼不多，我少分一点吧·！先把饼的 20℅给我，小猴从我分剩的饼中分25℅,小鹿从小猴分剩的饼中分30℅,小熊再从小鹿分剩的饼中分35℅,最后剩下的一点点给我，怎么样？”大家觉得狐狸分得最少，就同意了．可最后发现狐狸分得的饼最多，狐狸共分得到＿＿＿千克饼．45、上午8时，甲、乙两人同时出发，都从A 地到B 地，若两人匀速行进，甲用3小时走完全程，乙用 4小时走完全程，当乙所剩路程是甲所剩路程的2倍时，是＿＿＿时＿＿＿分．46、一项工程，第一天甲做，第二天乙做，第三天甲做，第四天乙做，这样交替轮流做，那么恰好用整数天完工，如果第一天乙做，第二天甲做，第三天乙做，第四天甲做，这样交替轮流做，那么完工时间要比前一种多半天．已知乙单独完成这项工程需要20天，则甲单独完成这项工程需要＿＿＿天．47、将一些棱长是1 的小正方体堆放成一个立体，图2 是这个立体的俯视图、正视图和左视图．这个立体的体积最小是＿＿＿．48、如图3,已知正方形ABCD 和正方形CEFG 的边长分别是8 厘米和6 厘米，那么阴影部分的面积是＿＿＿平方厘米．49、如图4 所示的两个同心圆的半径分别为R 和r，R 和r 都是自然数，若圆环（阴影部分）的面积是493π，则R－r＝＿＿＿.50、如图5所示的半圆的直径BC＝8cm,AB＝AC，D 是AC 的中点，则阴影部分的面积是＿＿＿cm²．51、园艺工人把一块正方形的草坪分成如图6所示的四个长方形种植不同的草，图中阴影部分是正方形，它包含在40m²的长方形之内，准备种植一种特殊植物，阴影部分的面积是＿＿＿m².52、图7中共有＿＿＿个长方体．53、图8是一个400米和跑道，两头是两个半圆，每一个半圆的弧长是 100米，中间是一个长方形，长为100米，那么400米跑道所围成的面积是＿＿＿平方米．54、一个大正方体，表面全涂上红色后，被分割成若干个体积都等于1的小正方体，如果在这些小正方体中，六个面都没有涂红色的小正方体的个数占全部小正方体个数的278，那么大正方体的边长是＿＿＿．55、一个底面半径是10厘米，高30厘米的圆柱形容器中，水深8厘米，要在容器中放入长和宽都是8厘米，高是15厘米的长方体状的铁块，铁块竖放在水中，那么水面上升＿＿＿厘米（π取3.14）．56、小丽的妈妈今年 35岁，她的年龄是小丽年龄的5倍，当妈妈的年龄是小丽年龄的3倍还多2岁时，小丽＿＿＿岁．57、如图9所示，某桌球桌面为长方形ABCD，小球从A 沿45°角击出，恰好经过5次碰撞到达B处．则 AB：BC＝＿＿＿．58、沪宁高铁通车后，一列动车早晨8时从南京开往上海，途中停靠5个车站，每站各停车2分钟．8时25分一列高速列车也从南京开往上海，途中不停车，高速列车的速度比动车快51，结果两车同时到达上海．高速列车从南京开到上海用时＿＿＿分钟．59、某次考试共有9道题，做对1～9题的人数占参加考试人数的82﹪，65﹪，92﹪，93﹪，68﹪， 98﹪,70﹪,60﹪,72﹪.如果做对5道或5道以上为及格，那么这次考试的及格率至少是＿＿＿．60、小明下午放学后在家看动画片，这时刚好是6点整，此刻钟面上的时针反向成一条直线，当他看完动画片后，时针和分针刚好又一次反向成一条直线，则此刻是＿＿＿时＿＿＿分．61、有两种酒精溶液，甲溶液的浓度是75﹪,乙溶液的浓度是15﹪，现在要将这两种溶液混合成浓度是50﹪的酒精溶液18升，应取甲溶液＿＿＿升，乙溶液＿＿＿升．62、已知2011年3月中，星期二的天数比星期一的天数多，那么植树节是星期＿＿＿.63、一项工程先由甲单独做18天，再由乙接着单独做8天可以完成；若甲乙二人合作，12天可以完成，现甲先单独做6天，然后由乙接着做完余下的工程，则乙需要做＿＿＿天．64、有6级台阶，小明从下向上走，若每次只能跨过一级或两级，他有＿＿＿种不同走法．65、某公司针对A、B、C三种岗位招聘了35人，其中只能上B岗位的人数等于只能上C岗位人数的 2倍．而只能上A岗位的人数比能兼职别的岗位的人多1人，在只能上一个岗位的人群中，有一半还能上A岗位，则招聘的35人中能兼职别的岗位的有＿＿＿人．66、某钢铁厂去年生产钢铁180万吨，今年前5个月的产量等于去年全年的产量，照这样计算，这个钢铁厂今年将比去年增产百分之＿＿＿.67、张家镇中心小学距离县城48千米，其中一部分是上坡路，其余是下坡路．张校长骑自行车从学校到县城，去时用了4.2小时，返回时用了3.8小时．已知张校长骑自车上坡每小时行10千米，则他骑自行车下坡每小时行＿＿＿千米．68、服装占买进一批童装，按每件获得40﹪的利润定价．按此定价卖出这批童装的90﹪时，由于换季，为了加快资金周转，服装店按定价的七折出售，将剩下的童装全部卖出，这样所得的利润比按原定价出售获得的利润少了15﹪.按规定，不论以什么价格出售，卖完这批童装必须上缴营业税300元．服装店买进这批童装花了＿＿＿元．69、甲、乙两辆清洁车负责东、西区间的公路清扫任务．甲车单独清扫需要8小时，乙车单独清扫需要12小时，两车同时从东、西区相向开出，相遇时甲车比乙车多清扫2千米，则东、西两区相距＿＿＿千米．70、甲、乙、丙三人在A、B两地植树，A地要植528棵，B地要植504棵．已知甲、乙、丙每天分别植树24,30,32棵，甲在A地植树，丙在B地植树，乙先在A地植树，然后转到B地植树．两地同时开始同时结束，乙应在开始后第＿＿＿天从A地转到B地．71、有三块草地，面积分别是5，15，25亩。
2023希望杯四年级数学思维训练100题(含答案)
2023希望数学——4年级培训100题1.已知：A※B=A×B+A+B，则1※9※9※9※9※9※9※9※9※9※9=________。
2.木木练习口算，她按照自然数的顺序从1开始求和，当计算到某个数时，和是888，但她重复计算了其中一个数。
那么木木重复计算的数是________。
3.把自然数从1开始，排列成如下的三角阵：第1列为1；第2列为2，3，4；第3列为5，6，7，8，9，以此类推，每一列比前一列多排两个数。
以1开头的行中，第2023个数是________。
4.将11~21分别填入下图中的圆圈内，使每条虚线上三个数之和都相等。
中心数有________种填法。
5.计算：（26÷25）×（27÷17）×（25÷9）÷（39÷17）=________。
6.计算：9＋99＋999＋9999＋99999=________。
7.定义运算：a☆b＝(a+b)÷6，若m☆8＝24，m＝________。
8.请把图中的除法竖式补充完整。
9.下面这个表有100行，这个表中所有数的和是________。
10.在空格内填入数字1～5，使得每行、每列数字都不重复。
图中格线上给出的数表示旁边两个数的和或者积。
11.计算：（1＋3＋5＋…＋2023）＋（2－4－6－…－2022）＝_______。
12.如果1△3＝1+11+111，2△5＝2+22+222+2222+22222，8△2＝8+88，那么6△4＝_______。
13.甲乙两人练习跑步，从同一地点同向出发。
若乙比甲先跑10米，则甲跑5秒追上乙；若乙比甲先跑2秒，则甲跑4秒追上乙。
甲每秒跑_________米，乙每秒跑________米。
14.甲、乙、丙三个班的人数和为194，乙班人数比甲班人数的5倍还多1，丙班人数比乙班人数的5倍还多2。
甲班有________人，乙班有________人，丙班有________人。
希望杯考前100题 (1)
37. 字母 W、M、T、C 分别代表 4 个不同的数字，并且WW × MM + WT + C = 2017 ， 求W + M + T + C 的值.
38. 字母 a，b，c 表示 3 个不同的非零数字，若 abc + bc + c = 724 ，求 a + b + c .
常州学而思 双师课堂
受益一生的能力
64. 如图，矩形 ABCD 中，F 为 BC 的中点，CE=2DE，矩形 ABCD 的面积为 3，求阴影部 分的面积.
D
E
C
F
A
B
65. 在边长是 1 米的正六边形内任意丢放 7 颗小石子，则总有两颗小石子的距离不大 1 米， 请说明理由.
常州学而思 双师课堂
受益一生的能力
66. 某次考试共有 10 道判断题．小张划了 5 个钩和 5 个叉，结果对了 8 道；小李划了 2 个 钩和 8 个叉．结果对了 6 道；小王一道都不会，索性全部打叉，那么他至少可以蒙对多 少道题？
12. 桌上有一些纸片，每张纸片上都有编号（不是按顺序编的），马小虎同学错把 6 和 69 拿倒了，导致这些编号的平均数多出 1，问这些纸片共有多少张？
常州学而思 双师课堂
受益一生的能力
13. 有一串数，最前面的 4 个数是 2，0，1，8，从第 5 个数起，每一个数都是它前面相邻 4 个数之和的个位数字，问在这一串数中，会依次出现 2，0，1，7 这 4 个数吗？
14. 某工人每小时内需先生产 2 个 A 产品，再生产 3 个 B 产品，最后生产 1 个 C 产品，则 第 725 个产品是哪种产品？
15. 著名的哥德巴赫猜想可以陈述为：任意大于 2 的偶数，都可表示成两个质数之和．将偶 数 88 表示成两个质数的和，有几种表示方法？（ a + b 和 b + a 视为同一种表示方法）
2023年六年级希望杯赛前培训100题答案
2023年六年级希望杯赛前培训100题答案这份文档是为2023年六年级希望杯赛前培训准备的100题答案。
在这个培训中，我们将会涵盖各种题型和知识点，以确保学生们在比赛中取得好成绩。
数学1. 36 ÷ 4 = ？- 答案：92. 187 + 293 = ？- 答案：4803. 982 - 594 = ？- 答案：3884. 85 × 2 = ？- 答案：1705. 953 ÷ 7 = ？- 答案：136英语1. What is the capital city of Australia?- 答案：Canberra2. Which of the following words is spelled incorrectly?I ___ to the cinema every week.A. goB. goesC. going- 答案：A (go)4. Fill in the blank with the correct form of the verb "to be": She ___ 10 years old.A. amB. isC. are- 答案：B (is)5. Which sentence is written in the passive voice?A. John built a house.B. The house was built by John.C. John is building a house.- 答案：B (The house was built by John)语文1. 下列每组成语中，加点的字的读音都不相同的一组是？A. 蒙羞，重峦叠嶂，借箭，右撇子B. 人声鼎沸，工程，自告奋勇，戒骄戒躁C. 绕梁三日，一专多能，集腋成裘，经纬万端- 答案：A2. 请写出：“薛涛初学笛， / 池上清风来。
/ 然后天真殊， / 怀抱亦纤弱。
(完整版)希望杯竞赛赛前培训100题(三年级)
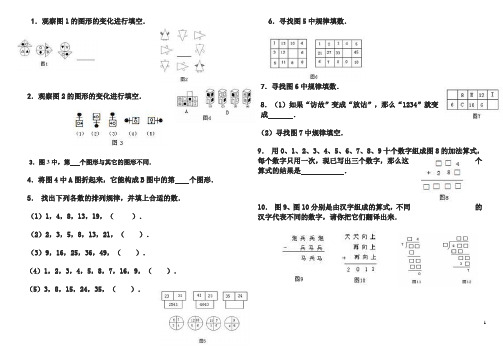
1．观察图1的图形的变化进行填空．2．观察图2的图形的变化进行填空．3．图3中，第个图形与其它的图形不同．4．将图4中A图折起来，它能构成B图中的第个图形．5．找出下列各数的排列规律，并填上合适的数．（1）1，4，8，13，19，（）．（2）2，3，5，8，13，21，（）．（3）9，16，25，36，49，（）．（4）1，2，3，4，5，8，7，16，9，（）．（5）3，8，15，24，35，（）．6．寻找图5中规律填数．7．寻找图6中规律填数．8．（1）如果“访故”变成“放诂”，那么“1234”就变成．（2）寻找图7中规律填空．9．用0、1、2、3、4、5、6、7、8、9十个数字组成图8的加法算式，每个数字只用一次，现已写出三个数字，那么这个算式的结果是．10．图9、图10分别是由汉字组成的算式，不同的汉字代表不同的数字，请你把它们翻译出来．11．在图11、图12算式的空格内，各填入一个合适的数字，使算式成立．12．已知两个四位数的差等于8765，那么这两个四位数和的最大值是．13．中午12点放学的时候，还在下雨．已经连续三天下雨了，大家都盼着晴天，再过36小时会出太阳吗？14．某年4月份，有4个星期一、5个星期二，问4月的最后一天是星期几？15．张三、李四、王五三位同学中有一个人在别人不在时为集体做好事，事后老师问谁做的好事，张三说是李四，李四说不是他，王五说也不是他．它们三人中只有一个说了真话，那么做好事的是16．小李，小王，小赵分别是海员、飞行员、运动员，已知：（1）小李从未坐过船；（2）海员年龄最大；（3）小赵不是年龄最大的，他经常与飞行员散步.则是海员，是飞行员，是运动员．17．用凑整法计算下面各题：（1）1997+66 （2）678+104 （3）967-598 （4）456-30718．用简便方法计算下列各题： 634+（266-137） 2011-（364+611）558-（369-342） 2010-（374-990-874）19．用基准法计算： 108+99+93+102+97+105+103+94+95+10420．用简便方法计算：899999+89999+8999+899+8921．求100以内的所有偶数的和是多少？22．有一数列3，9，15，…，153，159．请问：（1）这组数列共有多少项？（2）第15项是多少？（3）111是第几项的数？23．有10只盒子，54只乒乓球，把这54只乒乓球放到10只盒子中，要求每个盒子中最少放1只乒乓球，并且每只盒子中的乒乓球的只数都不相同，如果能放，请说出放的方法；如果不能放，请说明理由．24．如图13有一个宝塔算式，从上向下数，第一层的和为1，第二层的和为5，第三层的和为15，…，第十层的和为多少？25．甲、乙、丙三位同学参加希望杯数学竞赛的平均成绩是75分，甲、丙的平均成绩是71分，那么乙得了多少分？26． 6名同学在一起打乒乓球，两人轮流上；从上午9点打到上午11点；他们平均休息多少分钟？27．已知七个自然数的和是154，求这七个连续自然数各是什么数？28．张红、王莉、李月、赵兰四人的平均身高是158厘米，再加上刘辉，五人的平均身高是160厘米. 求刘辉的身高．29．从北京到上海的特快列车，中途要停靠7个大站. 这样，有几种不同价格的车票？30．1个五元纸币，2个五角硬币，3个一元硬币，一共可以组成多少种人民币值？31．从图14中O点出发又回到O点，每条线段不能重复走，共有几条不同路线？32．布袋里有五个彩色玻璃球，每次最多只能拿走一个或2个，可分多次取出．问取完五个球，有多少种不同的取法？33．简便计算下列各题.125165 3 12573225 （49+28+56）7 （43+35+20）7 （96-33-39） 3 3637+6437 225（94） 43045937．算式（）9=13…（）中，最大、最小的被除数分别是多少？38．30（）=（）…6中，除数和商各是多少？39．小胡在计算除法时，把除数87写成78，结果商是64，还余54，正确的商应该是多少？40．149除以一个两位数，余数是5，请写出所有这样的两位数。
小学“希望杯”培训100题(六年级)及解析
小学“希望杯”培训100题（六年级）一、解答题（共100小题）1．计算：=．2．计算：2012×2014×（）．3．．4．计算：（0.+0.3）×0.×0.7×=．5．计算：=．6．计算：=7．兄弟俩都有点傻，一位只有自己过一年长一岁而别人不会长．某天，哥哥对弟弟说：”再过3年我的年龄就是你的2倍．”弟弟说：”不对，再过3年我和你一样大．”今年，他们俩分别是岁，岁．8．有一堆黑白棋子，黑棋的粒数是白棋的2倍，每次从中取出白棋3粒黑棋5粒，白棋恰好取完时黑棋还剩20粒．则原来这堆棋子共有粒．9．如图，边长12cm的正方形与直径为16cm的圆部分重叠，若没有重叠的两空白部分的面积分别是S1，S2，则S1﹣S2=．（π取3）10．有一列数：8，18，24，49，55，60，65，77，81，98，100．它们的最小公倍数是．（以乘方形式表示，不用写出计算结果）11．王老师将200块糖分给了甲乙丙三个小朋友，甲比乙的2倍还要多，乙比丙的3倍还要多，那么甲最少有块糖，丙最多有块糖．12．建军路小学有钢琴，小提琴这两个兴趣班，这两个班的学员都是来自A班或者B班的．钢琴班有来自A班，小提琴班有来自B班，并且钢琴班的总人数是小提琴班总人数的倍，那么这两个兴趣班中来自B班的人数与总人数的比值是．13．定义：”如果一个数有12个约数，那么称这样的数为’好数’”．则将所有的”好数”由小到大依次排列，第三个是．14．有一口枯井，用一根绳子测井口到井底的深度，将绳对折后垂到井底，绳子超过井口9米；将绳子三折后垂到井底，绳子超过井口2米，则绳长米，井深米．15．将100个梨分给10个同学，每个同学的梨个数互不相同．分得梨个数最多的同学，至少得到个梨．16．31500的约数中与6互质的共有个．17．如图2，S△ABC=24，D是AB的中点．E在AC上，AE：EC=2：1．DC交BE于点O．若s△DBO=a，S△CEO=b，则a﹣b=．18．已知有三个连续的自然数，它们中最小的一个是9的倍数，中间一个是7的倍数，最大的一个是5的倍数，那么这些自然数最小分别是．19．快速公交3号线行驶于安定门与宏福苑小区之间，已知它的发车间隔时间是相等的，苏老师开车从宏福苑小区到安定门，每过3分钟她的迎面就驶来一辆快速公交，每隔12分钟她就超过一辆快速公交．快速公交全程是45分钟，假设公交车和苏老师开车的速度都不变，那么苏老师开车从宏福苑小区到安定门需要分钟．20．将自然数1，2，3，…，依次写下去，组成一个数：12345678910111213…，当写到2054时，这个大数除以9的余数是．21．地震时，地震中心同时向各个方向传播出纵波和横波．纵波的传播速度是3.96km/s，横波的传播速度是2.58km/s，某次地震，地震监测点用地震仪接收到地震的纵波之后，隔了18.5s，接收到这个地震的横波，那么这次地震的地震中心距离地震监测点km．22．对于非零自然数n，如果能找到非零自然数a，b使得n=a+b+ab，则称n是一个”联谊数”，如：3=1+1+1×1，则3就是一个”联谊数”，那么从1到20这20个自然数当中，”联谊数”共有个．23．甲乙丙丁四个人去购物，付账时每人都拿出一些钱，已知，乙丙丁三人付钱的总和是甲的5倍，甲丙丁三人付钱的总和是乙的4倍，甲乙丁三人付钱的总和是丙的3倍，丁付了46元，那么四个人共花了元．24．一个自然数，在3进制中的数字和是24．它在9进制中的数字和最小是，最大是．25．设N=1×2×…×209×210，则：（1）N的末尾一共出现个连续的数字”0”；（2）用N不断除以12，知道结果不能被12整除为止，一共可以除以次．26．如果长方形，正方形，正三角形分别有a，b，c条对称轴，则（a+b+c）2=．27．在数4，11，19，73，93，118，125，238中相邻若干个数之和是3的倍数而不是9的倍数的数组共有组．28．A，B两校的男、女生人数的比分别为8：7和30：31，两校合并后男、女生人数的比是27：26，则A，B两校合并前人数比是．29．甲、乙、丙、丁四人参加数学竞赛，赛后猜测他们之间的考试乘绩情况是：甲说：“我可能考的最差．”乙说：“我不会是最差的．”丙说：“我肯定考的最好．”丁说：“我没有丙考的好，但也不是最差的．”成绩公布后，只有一人猜错了，则此四人的实际成绩从高到低的次序是．30．若在同一斜坡上往返，上坡速度为5m/s，下坡速度为7m/s，则往返一次的平均速度是________米/秒．31．若三个连续偶数的最小公倍数是1008，则这三个自然数的和是．32．某数除以7余4，除以9余6，除以11余2，那么这个数的最小可能是．33．某店原来将一批羽绒服按100%的利润定价出售，淡季，商家按38%的利润重新定价，这样售出了其中的40%．旺季价格有所回升，售出了余下的全部羽绒服．结果，实际获得的总利润是原定利润的45.2%，那么旺季的价格是原定价格的%．（注：”按100%的利润定价”指的是”利润=成本×100%”）34．统计局统计了664座城市，按空气污染情况可分为三类：良好，轻度污染和严重污染．其中，空气质量良好的城市数比严重污染城市数的3倍多52座，轻度污染城市数是严重污染城市数的2倍．则空气严重污染城市有座．35．如图中三个正方形的边长分别为10，20，30，那么图中阴影部分的面积是．36．在1到2013这2013个数中，共有个数与四位数5678相加时不发生进位．37．如图，在正方形ABCD中，E，F分别是边AB，BC的中点．那么，以这6个点中的任意三个为顶点可组成的不同的三角形的个数是．38．若整数x满足不等式，则x=．39．如图，三个同心圆的半径分别是1厘米，3厘米，5厘米，AB，CD，EF，GH八等分这个圆，且都过圆心O．图中阴影部分的面积与非阴影部分的面积之比是．40．如下表，自然数以一定的规律排列，横为行，竖为列，如9在第3行第2列，记为9=（3，2），则2013=（，）．41．如图是由边长为1的25个小正方形拼成的图形，则阴影部分的面积是 ．42．生活中，有人习惯用1/2表示1月2日，也有人习惯用1/2表示2月1日，这样一来，如果遇到1/2，就不能明确这究竟是1月2日还是2月1日了．一年中这种容易混淆的日期表示共有 天．43．计算：．44．在下面的括号里填上不同的自然数，使等式成立．（答案不唯一，写出一个即可）．45．如图，在△ABC 中，，E ，G 分别是AD ，ED 的中点，若△EFG 的面积为1，则△ABC 的面积是 ．46．如图 （1），（2），（3），边长相等的三个正方形内分别紧排着9个，16个，25个等圆．设三个正方形内的阴影部分面积分别为S 1，S 2，S 3，则S 1，S 2，S 3的大小关系是 ．47．有甲乙两只圆柱形玻璃杯，其内直径分别是20厘米，24厘米，杯中盛有适量的水．甲杯中沉没着一铁块，当取出此铁块后，甲杯中的水位下降了6厘米；然后将铁块沉没于乙杯，且乙杯中的水没外溢，则这时乙杯中的水位上升了 厘米．48．建筑公司计划修一条隧道．当完成任务的时，公司引进新设备，修建速度提高了20%，每天的工作时间缩短为原来的80%，实际185天完成了任务．若按原计划，则 天可完成任务．49．如果一个自然数能表示成两个非零自然数的平方差，则称这个数为”吉祥数”，如：9=52﹣42，9是”吉祥数”．那么从1开始的自然数中，第2013个”吉祥数”是 ．50．有3个整数，如果第2个数的5倍是第1个数与1的差的4倍，第3个整数的5倍是第2个数与1的差的4倍，那么第1个数的最小值是．51．春蕊班的每位同学都参加了课外体操班或围棋班，有的同学还同时参加了两个班．如果同时参加两个班的人数是参加围棋班的，是参加体操班人数的．那么这个班只参加体操与只参加围棋班的人数之比是．52．甲乙两个硬盘的成本共1600元，甲按30%的利润定价，乙按40%的利润定价，甲按定价的90%出售，乙按定价的85%出售，供货的利润290元．那么甲的成本是元．53．已知，其中a，b，c，d，e都是整数，则其中最大的数的值是．54．咖啡店新推出一款杯子，定价是88元/个，实际销售时降了价，结果销量比预计的增加了，收入增加了，则每个杯子被降价元．55．若三个连续自然数的平方的和等于245，则这三个连续自然数的和是．56．已知长方体表面积是148cm2，底面面积是30cm2，底面的周长是22cm，则这个长方体的体积是cm3．57．用棱长为2厘米的小正方体，如图所示层层重叠放置．则当重叠了5层时，这个立方体的表面积是平方厘米．58．由长度分别为2，3，4，5，6的五条线段为边，可以组成个不同的三角形．59．若字母a，b，c分别表示不同的非零数字，则由a，b，c组成的各个数位上数字不同的三位数共有个，若除三位数外，其余几个的和为2874，则=．60．如图，边长为2a的正方形ABCD内有一个最大的圆圆O，圆O内有一个最大的正方形EFGH．用S1，S2，S3依次表示△EOF的面积，弓形EmF的面积，带弧边EmF的△EBF的面积，则S1*S2*S3=．（圆周率π取3）61．从12点开始，经过分钟，时针与分针第一次成90°角；12点之后，时针与分针第二次成90°角的时刻是．62．已知一列数：1，1，2，3，5，8，13，21，34，55，89，144，233，…，若第n个数比第n+2个数小233，则n=．63．一只蚂蚁沿边长为240cm的等边三角形ABC的三条边由A点顺时针爬行一周．它在三条边上的速度分别是每秒3cm，4cm，5cm（如图）．且当它到达拐点（A，B，C）时会休息26秒，当它爬完一周回到点A时，行程结束．这期间，蚂蚁的平均速度是cm/s．64．至多含有一个奇数数字且能被25整除的四位数共有个．65．观察下面的数表：（横排为行，竖排为列）表中第1列都是单位分数，分母依次为1，2，3…，每行自第2个分数起，每个分数的分子等于左边分数的分子加1，分母等于左边分数的分母减1，直到分数的分母等于1．则位于第行，第列．66．从最小的质数算起，若连续n（n是大于1的自然数）个质数的和是完全平方数，则n 最小是．67．现有3个互不相等的数，甲说是2，a+1，b+2；乙说是2b﹣1，3，a．若两人都说对了，则这三个数的乘积是．68．若×=6657，其中x，y，z都代表非零数字，则=．69．两个直角三角板如图放置，则∠BFE的度数是∠CAF的倍．70．一个长方体相邻的两个面的面积之和是130，它的长，宽，高都是不超过13的整数，且均为互不相等的质数，则这个长方体的体积是．71．如图，一个物体由2个圆柱组成，它们的半径分别是3厘米和6厘米，而高分别是5厘米和10厘米，则这个物体的表面积是平方厘米．72．植树节，5名小朋友给5棵树浇水，每个小朋友至少浇一棵树，但一个小朋友不能重复给同一棵树浇水，一桶水也只能浇一棵树．活动结束后，5个小朋友分别浇了2，2，3，5，x桶水，5棵树分别被浇了1，1，2，4，y 桶水，那么x=，y=．73．小明出去散步前看了一下手表，回来时又看了一下手表，发现此时手表的时针，分针的位置正好与出去时的分针，时针位置相同．若他在外逗留的时间不足一小时，则他在外待了分钟．74．如图所示，共有个三角形．75．一个长为4，宽为3的长方形如图竖直放置，在其右上角有一个红点A，长方形绕右下角旋转90°，成为一个横放的长方形，再绕右下角旋转90°，成为一个竖放的长方形，…，当小红点A第一次回到右上角时所走过的路程是．76．书架第一层有依次排列的10本不同的故事书，现将2本不同的漫画书也放入第一层，则不同的放法共有种．77．分母是385的所有最简真分数的和等于．78．有价值总和为174万元的三批货物，这三批货物的质量比是3：4：5，单位质量的价格比是6：5：4．这三批货物各价值万元．79．将分数化成小数后，如果小数点后第一位起连续N个数位上数字之和等于2013，那么N=．80．如图所示是一个边长为120m的等边三角形，甲乙同时分别从A点，B点按顺时针方向出发，甲每分钟走120m，乙每分钟走180m，但经过每个顶点时，因转弯都要耽误5s，则乙出发s后第一次追上甲．81．原来，单独打开进水管3小时能将水池注满，单独打开出水管4小时可排完一池水．后来，这个水池漏水了，同时打开进水管与出水管14小时才能将水池注满，则只打开进水管需要小时可以注满这个漏的水池．82．图书馆，游泳馆，少年宫三个站在一条笔直的公路上，且游泳馆到图书馆，少年宫两站的距离相等．小明和小华分别从图书馆，少年宫两站同时出发相向而行．小明超过游泳馆站100米后与小华相遇．然后二人继续前进．小明到达少年宫站后立即沿原路返回，经过游泳馆站后300米追上小华．则图书馆，少年宫两站相距米．83．马和狗约好去牛哥家做客，牛哥说他忘了去超市买面包，狗说他去，一会儿，马到了牛哥家，听说狗去买东西了，他急了，他说，狗跑5步的时间我能跑6步，我跑4步的距离相当于狗跑7步．而且我比他力气大，买东西的活儿我去，于是马也奔超市去了，此时狗已跑出550米了．超市离牛哥家有2000米，则马要跑米才能追上狗，此时离超市还有米．84．12和60是很有趣的两个数，这两个数的积恰好是这两个数的和的10倍：12×60=720=10×（12+60）．满足这两个条件的非零自然数对还有：．85．明明，亮亮，军军三人都参加了数学竞赛，他们共解出了100道题，每人都解出了其中的60道题目，若三个人都解出来的题称为基础题；只有两个人解出来的题称为中等题；只有一个人解出来的题称为难题，则在他们解出的100道题中，难题的数量比基础题的数量（填：多或少）道．86．一块木片沿河漂流，从河边的A地到B地，用了24小时．一只快艇在静水中的速度是18千米/小时，它从A驶到B所用的时间是从B驶到A所用时间的．则AB间的距离是千米．87．如图，AB∥CE，AC∥DE，且CE=DE=2AB=2AC，则=．88．小明和小林是两个集邮爱好者，他们共有邮票400多张，如果小明给小林a张邮票，小明就比小林少；如果小林给小明a张邮票，则小林就比小明少．那么小明原有张邮票，小林原有张邮票．89．用底面内半径和高分别是12cm，20cm的空心圆锥和空心圆柱各一个组成如图所示竖放的容器，在这个容器内注入一些细沙，能填满圆锥，还能填部分圆柱，经测量，圆柱部分的沙子高5cm，若将这个容器倒立，则沙子的高度是cm．90．为确保信息安全，信息需加密传输，发送方将明文加密成密文，接收方收到密文后解密可得明文．已知有一种加密方式是将英文26个小写字母a，b，c，…，依次对应0，1，2，…，25这26个整数（见下表），当明文中的字母对应的序号为a时，将a+10除以26后所得的余数作为密文中的字母对应的序号，例如明文”a”对应密文”k”．””91．如图，在正方形场地ABCD的四周有32个洞（每边9个洞），一个工人扛着32面旗子，从A洞开始插旗，按顺时针方向，每隔5个洞就插一面旗，当他绕着正方形走完5圈时，发现有n个洞不能插旗，求n．92．某校有960套桌凳需要维修．现有甲乙两个木工，甲单独修理这批桌凳比乙多用20天；乙每天比甲多修8套；甲乙每天的修理费分别是80元，120元．在修理桌凳过程中，学校要委派一名维修工进行质量监督，并由学校负担他每天10元的生活补助．现有以下三种修理方案共选择：①由甲单独修理；②由乙单独修理；③由甲乙共同合作修理．你认为哪种方案即省时又省钱？试比较说明．93．甲乙丙三辆汽车分别从A地开往千里之外的B地．乙比甲晚出发40分钟，出发后160分钟后能追上甲；丙比乙晚出发20分钟，出发后5小时追上乙．那么如果甲比乙先出发10分钟，乙比丙先出发10分钟，那么乙追上甲之后过多久丙能追上甲？94．已知甲乙丙三位同学在北京，广州，上海的大学学习软件设计，服装设计，城市规划．有下列判断：①甲不在北京学习；②乙不在广州学习；③在北京学习的同学不学城市规划；④在广州学习的同学是学软件设计的；⑤乙不学服装设计．三位同学各在什么城市学习什么专业？95．如图，长方形ABCD，ABEF，AGHF的长与宽的比相同，且，长方形BEHG的周长是22，求长方形ECDF的面积．96．在小于30的所有质数中，是否存在差与平方和都是质数的两个质数？若存在，有几组？若不存在，请说明理由．97．甲容器内有物质A和物质B，其质量比是2：3，乙容器内有物质B和物质C，其质量比是1：2，丙容器内有物质A和物质C．现将甲乙丙三容器中的物质以1：2：3的比例取出，混合，则所得新的混合物中，A，B，C三种物质的质量比是183：152：385．求丙容器内物质A和物质C的质量比．98．程序员设计了一款新游戏，共20级．小刚一次晋级2级游戏，或一次晋级3级游戏，那么他从入门（0级）晋级到第20级共有多少种不同的方法？10月份，小强的家里用了23m的居民用水，他开的餐厅，用了102m的餐饮用水，则这个月他应该交多少元水费？100．0．买一盒牙膏，一瓶沐浴露和一瓶洗发露共付款100元．若1瓶沐浴露比2盒牙膏贵，2瓶洗发露比7瓶沐浴露贵，8盒牙膏比1瓶洗发露贵，且每个产品的单价都是整数元，分别求一盒牙膏，一瓶沐浴露，一瓶洗发露的价格．小学“希望杯”培训100题（六年级）参考答案与试题解析一、解答题（共100小题，满分0分）1．计算：=．2．计算：2012×2014×（）=2．3．（2010•成都校级自主招生）．解：++…+，=×（﹣+﹣+…+﹣），=×（﹣）=×（）=×=．4．计算：（0.+0.3）×0.×0.7×=．+0.3）×0.7×，（+×××，×××（×××，=××=×=5．=102．解：，=（1+3+5+..+19）+3×=102+3×（1﹣）=100+=102．6．=．解：设n=++，m=，则：（1+++）×（+++）﹣（1++++）×（++），=（1+n）×m﹣（1+m）×n=m+mn﹣n﹣mn=m﹣n，=（）﹣（++）=．7．兄弟俩都有点傻，以为只有自己过一年长一岁而别人不会长．某天，哥哥对弟弟说：”再过3年我的年龄就是你的2倍．”弟弟说：”不对，再过3年我和你一样大．”今年，他们俩分别是6岁，9岁．解：弟弟：（3+3）÷（2﹣1）=6（岁）；哥哥：6+3=9（岁）．8．有一堆黑白棋子，黑棋的粒数是白棋的2倍，每次从中取出白棋3粒黑棋5粒，白棋恰好取完时黑棋还剩20粒．则原来这堆棋子共有180粒．解：取了：20÷（6﹣5）=20（次），共有：20×3×（1+2）=180（粒）；9．如图，边长12cm的正方形与直径为16cm的圆部分重叠，若没有重叠的两空白部分的面积分别是S1，S2，则S1﹣S2=48cm2．（π取3）S1﹣S2=（S1+S阴）﹣（S2+S阴）=S圆﹣S正=3×（16÷2）2﹣122=192﹣144=48（平方厘米）；10．有一列数：8，18，24，49，55，60，65，77，81，98，100．它们的最小公倍数是23×34×52×72×11×13．（以乘方形式表示，不用写出计算结果）11．王老师将200块糖分给了甲乙丙三个小朋友，甲比乙的2倍还要多，乙比丙的3倍还要多，那么甲最少有121块糖，丙最多有19块糖．12．建军路小学有钢琴，小提琴这两个兴趣班，这两个班的学员都是来自A班或者B班的．钢琴班有来自A班，小提琴班有来自B班，并且钢琴班的总人数是小提琴班总人数的倍，那么这两个兴趣班中来自B班的人数与总人数的比值是．）×=3﹣×=3班的人数与总人数的比值是；故答案为：．13．定义：”如果一个数有12个约数，那么称这样的数为’好数’”．则将所有的”好数”由小到大依次排列，第三个是84．14．有一口枯井，用一根绳子测井口到井底的深度，将绳对折后垂到井底，绳子超过井口9米；将绳子三折后垂到井底，绳子超过井口2米，则绳长42米，井深12米．对应的分率的差额是：﹣）（）15．将100个梨分给10个同学，每个同学的梨个数互不相同．分得梨个数最多的同学，至少得到15个梨．16．31500的约数中与6互质的共有8个．17．如图2，S△ABC=24，D是AB的中点．E在AC上，AE：EC=2：1．DC交BE于点O．若s△DBO=a，S△CEO=b，则a﹣b=4．S=S18．已知有三个连续的自然数，它们中最小的一个是9的倍数，中间一个是7的倍数，最大的一个是5的倍数，那么这些自然数最小分别是153，154，155．19．快速公交3号线行驶于安定门与宏福苑小区之间，已知它的发车间隔时间是相等的，苏老师开车从宏福苑小区到安定门，每过3分钟她的迎面就驶来一辆快速公交，每隔12分钟她就超过一辆快速公交．快速公交全程是45分钟，假设公交车和苏老师开车的速度都不变，那么苏老师开车从宏福苑小区到安定门需要27分钟．则苏老师与公车速度和为问题；苏老师与公车速度差为，因为这时是相遇问题；那么苏老师速度（+），所以苏老师与公车速度比：，，+），公车速度（﹣），苏老师与公车速度比：=520．将自然数1，2，3，…，依次写下去，组成一个数：12345678910111213…，当写到2054时，这个大数除以9的余数是3．21．地震时，地震中心同时向各个方向传播出纵波和横波．纵波的传播速度是3.96km/s，横波的传播速度是2.58km/s，某次地震，地震监测点用地震仪接收到地震的纵波之后，隔了18.5s，接收到这个地震的横波，那么这次地震的地震中心距离地震监测点136.96km．t=﹣，22．对于非零自然数n，如果能找到非零自然数a，b使得n=a+b+ab，则称n是一个”联谊数”，如：3=1+1+1×1，则3就是一个”联谊数”，那么从1到20这20个自然数当中，”联谊数”共有12个．23．甲乙丙丁四个人去购物，付账时每人都拿出一些钱，已知，乙丙丁三人付钱的总和是甲的5倍，甲丙丁三人付钱的总和是乙的4倍，甲乙丁三人付钱的总和是丙的3倍，丁付了46元，那么四个人共花了120元．=，丙占总数的；；﹣﹣）÷，24．一个自然数，在3进制中的数字和是24．它在9进制中的数字和最小是24，最大是72．25．设N=1×2×…×209×210，则：（1）N的末尾一共出现51个连续的数字”0”；（2）用N不断除以12，知道结果不能被12整除为止，一共可以除以102次．26．如果长方形，正方形，正三角形分别有a，b，c条对称轴，则（a+b+c）2=81．27．在数4，11，19，73，93，118，125，238中相邻若干个数之和是3的倍数而不是9的倍数的数组共有6组．28．A，B两校的男、女生人数的比分别为8：7和30：31，两校合并后男、女生人数的比是27：26，则A，B两校合并前人数比是45：61．29．（2011•成都）甲、乙、丙、丁四人参加数学竞赛，赛后猜测他们之间的考试乘绩情况是：甲说：“我可能考的最差．”乙说：“我不会是最差的．”丙说：“我肯定考的最好．”丁说：“我没有丙考的好，但也不是最差的．”成绩公布后，只有一人猜错了，则此四人的实际成绩从高到低的次序是乙丙丁甲．30．若在同一斜坡上往返，上坡速度为5m/s，下坡速度为7m/s，则往返一次的平均速度是米/秒．，那么上坡的时间就是，下坡的时间就是；用总路程+）÷，（米故答案为：．31．若三个连续偶数的最小公倍数是1008，则这三个自然数的和是48．32．某数除以7余4，除以9余6，除以11余2，那么这个数的最小可能是123．33．某店原来将一批羽绒服按100%的利润定价出售，淡季，商家按38%的利润重新定价，这样售出了其中的40%．旺季价格有所回升，售出了余下的全部羽绒服．结果，实际获得的总利润是原定利润的45.2%，那么旺季的价格是原定价格的75%．（注：”按100%的利润定价”指的是”利润=成本×100%”）34．统计局统计了664座城市，按空气污染情况可分为三类：良好，轻度污染和严重污染．其中，空气质量良好的城市数比严重污染城市数的3倍多52座，轻度污染城市数是严重污染城市数的2倍．则空气严重污染城市有102座．35．如图中三个正方形的边长分别为10，20，30，那么图中阴影部分的面积是600．36．在1到2013这2013个数中，共有51个数与四位数5678相加时不发生进位．37．如图，在正方形ABCD中，E，F分别是边AB，BC的中点．那么，以这6个点中的任意三个为顶点可组成的不同的三角形的个数是18．38．若整数x满足不等式，则x=3．因为不等式，＜3，2，39．如图，三个同心圆的半径分别是1厘米，3厘米，5厘米，AB，CD，EF，GH八等分这个圆，且都过圆心O．图中阴影部分的面积与非阴影部分的面积之比是1：3．厘米的圆面积的厘米的圆面积的，圆中，据此40．如下表，自然数以一定的规律排列，横为行，竖为列，如9在第3行第2列，记为9=（3，2），则2013=（4，60）．41．如图是由边长为1的25个小正方形拼成的图形，则阴影部分的面积是18．42．生活中，有人习惯用1/2表示1月2日，也有人习惯用1/2表示2月1日，这样一来，如果遇到1/2，就不能明确这究竟是1月2日还是2月1日了．一年中这种容易混淆的日期表示共有132天．43．计算：．2+））﹣，）2+）2+），．，2012+．44．在下面的括号里填上不同的自然数，使等式成立．（答案不唯一，写出一个即可）．的分子、分母同时扩大倍，变成的分子、分母同时扩大倍，变成===﹣=﹣﹣，==++++，==﹣﹣=+，45．如图，在△ABC中，，E，G分别是AD，ED的中点，若△EFG的面积为1，则△ABC的面积是18．中，，且，据此利用分数除法的意义即可解答问题．中，的面积的，÷=1846．如图（1），（2），（3），边长相等的三个正方形内分别紧排着9个，16个，25个等圆．设三个正方形内的阴影部分面积分别为S1，S2，S3，则S1，S2，S3的大小关系是相等．47．有甲乙两只圆柱形玻璃杯，其内直径分别是20厘米，24厘米，杯中盛有适量的水．甲杯中沉没着一铁块，当取出此铁块后，甲杯中的水位下降了6厘米；然后将铁块沉没于乙杯，且乙杯中的水没外溢，则这时乙杯中的水位上升了厘米．。
六年级希望杯培训试题100题
希望杯六年级培训题1、211⨯+321⨯+431⨯+…+200720061⨯＝ 。
2、〔1＋20021＋20041＋20061〕×〔20021＋20041＋20061＋20081〕－〔1＋20021＋20041＋20061＋20081〕×〔20021＋20041＋20061〕3、〔220071×3.6＋353×720072006〕÷43÷534、从21＋41＋61＋81＋101＋121 中去掉 和 ，余下的分数之和为1.5、99…9×55…5乘积的各位数字之和是 。
6、20031200412005120061 200711±±±±的整数局部是 。
〔分母中只有加号〕7、除法算式：÷它的计算结果的小数点后的前三位分别是 。
8、一个整数与它的倒数和等于20.05，这个数是 ，它的倒数是 。
2007个9 2007个59、在如图1的加法算式中，每个汉字分别代表1至9中的一个数字，且一样的汉字代表一样的数字，不同的汉字代表不同的数字，那么这个加法算式的和是 。
我 爱 希 望 杯 数 学 竞 赛＋ 8 6 4 1 9 7 5 3 2赛 竞 学 数 杯 望 希 爱 我10、有一个分数，它的分子加2,可以约简为74；它的分母减2,可以约简为2514。
这个分数是 。
11、四个非零自然数的和为38,这四个自然数的乘积的最小值是 ，最大值是 。
12、a 是质数，b 是偶数，且a 2+b=2022,那么a+b+1= 。
13、当a ＝2007时，a-1,a,a+1,a+2中的合数有 个。
14、从1到30这30个自然数连乘各的末尾共 个连续的数码0.15、一个质数p ，使得p+2,p+4同时都是质数，那么p 1＋21±p ＋41±p = .16、三个质数的倒数之和是20061155，那么这三个质数中最大的是17、彼此不等且大于0的偶数a,b,c,d 满足a+b+c+d=20，样的偶数组〔a,b,c,d 〕共有 组。
2024年希望杯六年级竞赛数学试卷培训题+答案
2024年希望杯竞赛六年级数学培训题1 .计算： ．2 . 计算： ．3 .计算： ．4 .计算：．5 .等式中的和都是自然数，．6 . ．7 .的积不到，里最大填 ．8 .以表示不超过的最大整数，若要，则自然数的最小值是 ．9 .如果正整数使得，则为 ．（其中表示不超过的最大整数） 10 .的整数部分是 ．11 .不等式，时的解为 ，时的解为 ，时的解为 ．12 .甲、乙两个两位数，甲数的等于乙数的，这两个数的和最大是 ． 13 .一个三位数加或者乘的结果都是完全平方数，这个三位数是 ． （注：一个自然数与自身相乘的积叫做完全平方数．） 14 .已知是数字到中的一个，若循环小数，则．15 .下面竖式中，相同的图标表示相同的数字，不同的图标表示不同的数字．那么，．， ．17 .将至填入右图的网格中，要求每个格子填一个整数，不同格子填的数字不同，且每个格子周围的格子（即与该格子有公共边的格子）所填数字之和是该格子中所填数字的整数倍，已知左右格子已经填有数字和，问：标有字母的格子所填的数字最大是 ．18 .各位数字均不大于，且能被整除的六位数共有 个. 19 .八位数（中的数字可重复出现）是的倍数，这样的八位数共有 个．20 .把的所有自然数连写在一起，可以得到这样的一个多位数，它是 位数．21 .某日，可可到动物园里去观赏动物，他看了猴子，熊猫和狮子三种动物，这三种动物的总量在到只之间，根据下面的情况： ①猴子和狮子的总数要比熊猫的数量多， ②熊猫和狮子的总数要比猴子的两倍还多， ③猴子和熊猫的总数要比狮子的三倍还多，④熊猫的数量没有狮子数量的两倍那么多，可知猴子有 只，熊猫有 只，狮子有 只．22 .儿童节的早上，方玲去图书馆看了一会儿书后到游泳馆游泳．她每天去一次图书馆，每天去游泳一次．方玲下一次既到图书馆看书，又到游泳馆游泳的时间是 月 日．23 .五名选手在一次数学竞赛中共得分，每人得分互不相等且都是整数，并且得分最高的选手得了分，那么得分最低的选手至少得 分，至多得 分． 24 .被除余，被除余，被除余的最小两位数是 。
2022 奥赛希望杯五年级培训 100题——答案版
2022希望少年俱乐部-五年级培训100题（解析）1.【答案】395【解析】原式=75÷30× 4.67×30+17.9×2.5=2.5×140.1+17.9×2.5=2.5×140.1+17.9=2.5×158=3952.【答案】579557.95【解析】原式=5795.5795×579.5÷5.795=5795.5795×579.5÷5.795=5795.5795×100=579557.953.【答案】27.25【解析】分两段计算，前一段5个数，后一段项数：0.99− 0.11 ÷0.02+1=45原式=0.5× 5 +0.11 + 0.99 × 45 ÷ 2=2.5+1.1 × 45 ÷ 2=2.5 + 24.75=27.254.【答案】5【解析】原式=（0.81+0.83+⋯⋯+0.99）× 0.6=（0.81+0.99）× 10 ÷2× 0.6=1.8× 10 ÷2×0.6=9×0.6=5.4所以结果的整数部分是5。
5.【答案】13【解析】首先考虑商的十位，6□□×□=□□7，商的十位只能是1，可知除数是6□7，接着考虑商的个位，6□7×□=□□61得知，商的个位只能是3，反推可知除数是687，剩下就可以正常推算。
6.【答案】2754【解析】首先□□□×7=□1□，可知前一个乘数百位是1因为结果是2□□□，可知第2行乘积最高位是2接着是1□□×□=20□，可知，前一个乘数的十位是0，后一个乘数是2再回头可知10□×7=□1□，一定是102×7=714，剩下就容易填了。
2021年希望杯100题四年级组(含答案)
希望杯 100 题四1．计算：9+99+999+9999+99999．2．计算：2016÷28÷4×7．3．计算：2014×2015+2013×2015-2012×2015-2011×2015．4．定义运算：a⊕b=a-b+8,a⊗b=a⨯b-5．求⎡⎣25⊕(4⊗7)⎤⎦⊗3．5．定义运算：a ⊕b =(a +b)÷ 6 ，若m ⊕ 8 = 24 ，求m 的值．6．在下面的□中填入运算符号“ +, -,⨯, ÷”使等式成立．12□4□4=7□7□37．不求最后结果，将以下三个乘法运算按从大到小排列：a = 2014 ⨯2016 ，b = 2013⨯2017 ，c = 2015⨯2015 ．8．把48 写成两个质数的和，有几种写法?9．已知4 个连续奇数的平均数是20，求最小的奇数．10．已知4 个连续奇数的平均数是20，求最小的奇数．11．五个数9，17，x，x+5，34 的平均数是24，求x．12．小杰从27 起写了26 个连续奇数，小强从26 起写了27 个连续自然数，然后他们分别将自己写的数求和，求这两个和的差．13．已知两个数的和是555，且较大数除以较小数得商12 余9，求较大数与较小数的差．14．在一个带余除法的算式中，如果把被除数152 写成125，则商会比原来的结果小3，且余数不发生变化，求余数．15．小明在做一道带余除法的运算时，把除数18 看作15，结果商没有改变，但余数增加了12．求商的值．16．求一切除以6 后余2 的两位数的和．17．一个数被5 除余1，被7 除余3，被11 除余7，这个数最小是多少？18．abc 表示一个各位数字互不相同的三位数，若这个数是6 的倍数，且a +c = 13 ，则称这个数为“金六点”，三位数中“金六点”有多少个?19．六位数a2016c 能被12 整除，求这样的六位数中最大的一个．20 一个八位数，它有前四位数和后四位数相同，而且它能被某个比1 大，比这个八位数小的数a 整除，求a．21．若x 和(2016 - 7x)÷ 9 都是大于0 的自然数，求满足条件的x 的个数．22．a，b 都是自然数，若a ⨯b = 2015 ，且a >b ，求a -b 的最大值．23．M、N 都是自然数，M ⨯N = 2015 ，且M >N ．问：M+N 最小是多少?24．连续写123 个123，得到一个庞大的数：123123123…，这个数能被3 整除吗？说明理由．25．已知六位数2□012□，万位上无论填入0~9 中哪一个数，都不能被11 整除，求这个六位数的个位数字．26．数一数，图1 中有多少个三角形？27．数一数，图2 中有多少个正方形？28．堆成图3 的几何体需要多少个正方体?29．求2016 的约数的个数．30．把22 个小球装到一些盒子中，要使每个盒子中小球的数量不同，最多可以装几个盒子？31．从5×6 的方格中选两个方格分别涂成红色和黄色，要求这两个方格不同行且不同列，共有多少种涂色方案?32．用2，0，1，5 这4 个数字可以组成多少个不同的两位数？33．从1 到100 的所有自然数中，不含有数字4 和5 的自然数有多少个?34．有6 个编有不同号码的小椅子，6 位小朋友要坐在椅子上，共有多少种坐法?（一个椅子只能坐一位小朋友）35．过年了，妈妈买了7 件不同的礼物，要送给亲朋好友的5 个孩子每人一件．其中姐姐的儿子小强想从智力拼图和遥控汽车中选一个，朋友的女儿小玉想从学习机和遥控汽车中选一件．那么妈妈送出这5 件礼物共有几种方法？36．如图4 所示，若大正方形的周长是48，小正方形的周长是16，求阴影部分的面积．37．长方形的长是宽的2 倍，面积是288，求长方形的周长．38．图5 由36 个边长是1 的小正方形组成，求 ABC 的面积．39．图6 由25 个边长是1 的小正方形组成，求阴影部分的面积．40．用一根长100 厘米的铁丝围成一个长方形，若长方形的宽是8 厘米的倍数，求所围成的长方形面积的最大值．41．如图7，长方形ABCD 与正方形EFGH 部分重合，已知AB=9 厘米，BC=6 厘米，EF=5 厘米，图中两部分阴影部分的面积分别记为S1 , S2，求S1-S2．42．用一根长34 厘米的铁丝围成长方形，使它的长和宽都是整数厘米，求围成的长方形面积的最大值．43．如图8 所示，在正方形中ABCD，BC=4BM．若梯形AMCD 的周长比∆ABM 的周长大12，求正方形的边长．44．某正方形草坪扩展成长方形后，一边增加了5 米，另一边增加了4 米，总面积增加了92 平方米，求原草坪的面积．45．一根绳子，若截去5 米，刚可绕花坛6 圈，若增加13 米，则可绕花坛8 圈，求这根绳子的长度．46．如图9，四个长方形和一个边长是5 的正方形纸片围成一个风车型的图案，图案的外轮廓的长是52，求长方形的长．47．求图10 的周长．（单位：厘米）48．如图11，从长方形纸片上裁掉两个正方形ABCD 和正方形CEFG，其中正方形ABCD 的面积是49 平方厘米，求余下的长方形纸片DGFH 的周长．49．有两个正方形，它们的周长相差8 厘米，面积相差32 平方厘米，求大正方形的面积．50．如图12，已知两相同的长方形ABCD 和DFEG 的长是6，求阴影部分的面积．51．如图13，大正六边形的面积是24 平方厘米，其中放了三个一样的小正六边形，求阴影部分的面积．52．2016 个3 相乘，乘积的个位数字是几？53．有n 个数：5，8，11，14，…，2015，求n．54．有一根木条，从最左端开始，每隔3 厘米做一个记号，每隔4 厘米也做一个记号，然后从有标记的地方截断，这样木条一共被截成了75 段，求木条原来的长．55．算式66 6 99 9 的结果有多少个3?2015个2015 个56．已知图14 中任意一个“田”字格中的四个数的和相等，求A、B、C、D 中最大数和最小数的差．57．已知图15 中任意相邻的三个格子中的数字之和都相等，这六个数字之和是30，求A+E+F．59．a，b 是1 至200 中的两个不相等的自然数，求(a +b)÷(a -b)的最大值．60．一把钥匙只能开一把锁，现在有8 把钥匙，7 把锁，最多要试多少次能把7 把锁和相应的钥匙搭配起来？61．甲、乙、丙、丁、戊五人参加100 米比赛，比赛结束后，甲说：“我的名次排在丁前面，丙后面．”丙说：“戊在我前面冲过终点．”丁说：“我比乙跑的快．”请根据他们的说法排出他们比赛的名次．整除的感应灯按一下．问：此时，有几个感应灯还亮着？63．小超从1 至9 的9 个数中选出5 个数求和，得23；小明也从1 至9 的9 个数中选出5 个数求和，得24．如果两人选的数中只有一个是相同的，求这个相同的数．64．某年7 月恰有4 个星期一和4 个星期四，这月的15 号是星期几?65．在长是156 米的小路的一侧等距离地种植13 棵树，路的两端都要植，求相邻两棵树之间的距离．66．某正方形操场四周等距离地种植了108 棵杨柳，小红从操场某角处的树下开始绕操场跑步，当她跑过第500 棵树时，这棵树是她所在操场边上跑过的树中的第几棵?（正方形操场四个顶点处都种了树）67．小林3 岁的时候，爷爷53 岁，那么小林10 岁时，爷爷年龄是小林的多少倍?68．晶晶比哥哥小3 岁，且2 年后哥哥的年龄是4 年前晶晶的年龄的2 倍，问晶晶今年几岁？69．今年，丹丹和父亲、母亲的年龄和是100 岁，若6 年前母亲的年龄是丹丹年龄的4 倍，11 年前，父亲的年龄是丹丹年龄的8 倍，问：丹丹今年几岁？70．某课外兴趣小组共有30 人，他们每个人都在暑假期间采集了一些生物标本，其中21 人采集了植物标本，16 人采集了动物标本，既采集了植物标本又采集了动物标本的有多少人？71．光明小学四年级（1）班35 人，他们的数学平均成绩为90 分，其中男生的平均成绩为88 分，女生的平均成绩为95 分，求女生的人数．72．一堆模具中长方形模具的数量是圆形模具的2 倍，现要将它们装箱出售，每24 个长方形模具和9 个圆形模具合装一箱，如此装了若干箱后，长方形模具还剩8 个，圆形模具还剩37 个，求长方形模具共有多少个？73．小芳读本故事书，若每天读16 页，22 天恰好读完，实际上读时，她前若干天每天读20 页，此后每天都比前一天少读1 页，又经过7 天，她恰好读完这本书，求小芳之前读了几天？74．某班共有45 人，在一次歌唱与朗诵的比赛中，参加唱歌比赛的同学有30 人，参加朗诵比赛的同学有25 人，若每个同学至少参加一项比赛，问两项比赛都参加的同学有多少人？75．某班举办回收旧书的活动，将收到的书放到几个箱子里．如果每个箱子放160 本，恰好放完：如果每个箱子多放10 本书，则剩下20 本书和两个空箱子．问：一共有多少个箱子，多少本书？76．有三堆棋子，从第一堆拿出15 个棋子放到第二堆，再从第二堆拿出18 个放到第三堆，最后从第三堆拿出12 个放到第一堆，这时每堆都有180 个棋子．求原来每堆棋子的个数．77．一名商人购进1000 个万花筒，每销售一个可以获得2 元的利润，每遇到一个残次品则会损失6 元，全部售完后，商人共获得1904 元利润，问：这批万花筒中有多少个残次品？78．体育老师带来一些排球，同学们分成若干组使用，6 人一组则缺1 个球，8 人一组则多1 个球，问：共有多少名同学？79．四年级其中考试科目包括语文、数学、英语三门功课，四（1）班总成绩的平均分为85 分，语文成绩的平均分为90 分，数学成绩的平均分比英语成绩的平均分少25 分，求英语成绩的平均分．80．不透明的箱子里面有红白两色的小球共120 个，且红球是白球的5 倍，问：红球比白球多几个?81．一个书架有两层，若从第一层拿出14 本书放到第二层，那么第二层上的书的数量是第一层的3 倍，若从第二层拿出12 本书放到第一层，则两层所放的书数量相等，书架上有多少本书？82．某天清晨，容器中有380 个细菌，在白天有光时，容器中的细菌减少70 个，夜间无光时，容器中的细菌将增加30 个，则经过8 个白天7 个夜间后，容器中还剩多少个细菌．83．矩形的边长是自然数，它的面积是3003，求矩形的最小周长．84．幼儿园的老师给班里的小朋友领来40 只桔子，200 块饼干，120 块奶糖，平均分发完毕，还剩4 只桔子，20 块饼干，12 粒奶糖．问：班里共有多少位小朋友？85．如果一个自然数从右往左看和从左往右看都一样，则称这个数为“回文数”．例如：343,2002 都是回文数现在一个十六位数2001200220032004 请你在这个数的两端或这些数字中加上一些数字，使它变成回文数．新得到的回文数的数字和最小是多少？86．水果店有菠萝、橙子、桃三种水果，桃的质量最大，是橙子质量的3 倍，是菠萝的质量的5 倍，已知橙子比菠萝多80 千克，这三种水果共重多少千克？87．有一牧场，假设牧场上的草是不断生长的．若养牛27 头，6 天把草吃尽；若养牛23 头，9 天把草吃尽．如果养牛21 头，那么几天能把牧场上的草吃尽？88．A、B 两队分别有队员35 人、42 人，若从A 队调出x 人到B 队，则B 队队员数比A 队队员数的2 倍多5，求x 的值．89．有两堆棋子，若从第一堆拿出30 枚放到第二堆，则第二堆的棋子数是第一堆棋子数的3 倍；若从第二堆拿出45 枚放到第一堆，则第一堆的棋子数是第二堆的棋子数的2 倍．求这两堆棋子共有多少枚?90．若6 名工人6 小时可生产零件720 个，则5 名工人生产900 个零件要用多少小时？91．一项工程，15 人每天工作6 小时，20 天可以完成任务．若在工作效率相同的情况下，改用25 人，每天工作8 小时，则现在完成这项工程需多少天．92．甲和乙每人各加工300 个零件，甲每小时加工50 个．当甲完成任务时，乙还有60 个零件没加工，那么乙每小时加工多少个零件?93．甲、乙两人分别从A、B 两地同时出发，相向而行，并在A、B 两地往返运动．甲每分钟行120 米，乙每分钟行80 米．若两人第一次相遇点C 与第二次相遇点D 之间的距离是100 米．求A、B 两地间的距离．94．甲、乙两人同时从A、B 两地相向而行，甲每分钟行80 米，乙每分钟比甲少行10 米，甲行完全程的一半后停下来等乙，又过了4 分钟才赶到，求这条路的总长．95．明明和奇奇从A、B 两地同时出发，相向而行，他们第一次相遇时，相遇点距A 地200 米，相遇后，他们继续前行，走到对方出发点后立即返回，第二次相遇时，相遇点距B 地120 米．求A、B 两地间的距离．96．一列货车从甲地开往乙地，平均每小时行60 千米，1 小时后，一列客车从乙地开往甲地，平均每小时行80 千米，又经过3 小时后，两车相遇，并继续前行，问：当客车到达甲地时，货车离乙地还有多少千米？97．甲、乙二人在泳池里游泳，同时同地同向出发，都要游1000 米．甲先以每4 分钟游100 米的速度游了600 米，接着以每4 分30 秒游100 米的速度游了后面的400 米．乙先以4 分15 秒游100 米的速度游了400 米，接着以每4 分5 秒游100 米的速度游了300 米，然后以每3 分55 秒游100 米的速度游了300 米．问：甲和乙谁先到达终点？98．一列火车通过260 米的隧道需要10 秒，通过330 米的隧道需要12 秒，求火车车身的长．99．甲火车长370 米，每秒钟行15 米，乙火车长350 米，每秒钟行21 米，两车同向行驶．乙车从追上甲车到完全超过共需几秒？100．早上8 点，小明和小强从甲、乙两地同时出发，以不变的速度相向而行．9 点20时两人相距10 千米，10 点时，两人相距还是10 千米．11 点时，速度较快的小明到达乙地，这时小强距甲地多少千米？答·提示1．原式=（10-1）+（100-1）+（1000-1）+（10000-1）+（100000-1）=10+100+1000+10000+100000-5=111110-5=111105．2．原式=2016÷（28×4÷7）=2016÷［（28÷7）×4］=2016÷16=126．3．原式=2015×（2014+2013-2012-2011）=2015×［（2014-2012）+（2013-2011）］=2015×（2+2）=8060．4．原式=［25○一（4×7-5）］⊗3=（25○一23）⊗3=（25-23+8）⊗3=10 ⊗3=10×3-5=25．5．因为 a ⊕b =( a +)b6÷,m⊕8=2，所以m ⊕8 =(m + 8)÷ 6 = 24 ，于是m = 24⨯6 -8 =136 ．6．12+4×4=7+7×3（答案不唯一）．7．a=2014×2016=（2015-1）×（2015+1）=2015×2015+2015-2015-1=c-1，所以 c >a >b ．8．48=5+43=7+41=11+37=17+31=19+29，共5 种．9．因为44×44=1936.45×45=2025，所以最小的自然数a=2015-2015=10．10．因为4 个连续奇数的平均数是20，所以这4 个连续奇数的和是20×4=80，设最小的奇数是a，则这4 个连续奇数的和可以表示为a +(a + 2)+(a + 4)+(a + 6)= 4a +12 ，所以最小的奇数是(80 -12)÷ 4 =17 ．11．依题意，有9+17+x+x+5+34=5×21即2x+65=105，得x=20．12．将两个人写的数按如下方式排列：27 29 31 33 …77．26 27 28 29 30 …52．观察可知，这两个和的差是1+2+3+…+25-26=299．13．因为较大数除以较小数得商12 余9，两个数的和是555，所以两个数的和减去9 后是较小数的13 倍，于是较小数=（555-9）÷13=42，较大数=555-42=513，较大数与较小数的差是513-42=471．14．两个算式比较，被除数减少了152-125=27，商减少了3，且余数不发生变化，可知除数是27÷3=9，152÷9=16……8，所以余数是8．15．把除数18 看作15 后，因为商没变，所以余数的增加量为商的18-15=3 倍，故商的值为12÷3=4．16．除以6 后余2 的两位数有15 个：14，20，26，32，38，44，50，56，62，68，74，80，86，92，98．它们的和是（14+98）×15÷2=840．17．因为这个数被5 除余1，被7 除余3，被11 除余7，所以这个数加4 后能被5，7，11 整除，能被5，7，11 整除的最小数是5×7×11=385，385-4=381．所以这个数最小是381．18．因为这个数是6 的倍数，所以它既是2 的倍数，又是3 的倍数，故 c 是偶数，且a +b +c 是3 的倍数，又 a +c =13 ，所以 b = 2 ，或5，或8，c = 0 ，或2，或4，或6，或8，因为这个数个倍数字互不相同，所以当c = 0 或2 时，a > 9 ，不满足条件，舍去；当c = 4 时，a = 9 ，则b = 2 ，或5，或8，这个三位数是924，或954，或984；当c = 6 时，a = 7 ，则b = 2 ，或5，或8，这个三位数是726，或756，或786；当c = 8 时， a = 5 ，则b = 2 ，这个三位数是528；故三位数中共有7 个“金六点”．19．记这个六位数为M，M 可被12 整除，则M 可被3，4 整除，M 可被4 整除，即M 的末两位数6b 可被4 整除．则 b = 0 ，或，4，或8，又因为M 可被3 整除，所以M 的各位数字之和a + 2 + 0 +1+ 6 +b =a +b + 9 可被3 整除．则 a +b 可被3 整除．当b = 0 时，a 可取3，6，9；当b = 4 时，a 可取2，5，8；当b = 8 时，a 可取1，4，7所以这样的六位数中最大的是920160．20．设这个八位数为abcdabcd ，则abcdabcd =a ⨯107 +b ⨯106 +c ⨯105 +d ⨯104 +a ⨯103 +b ⨯102 +c ⨯101 +d= a⨯103(104+1)+b⨯102(104+1)+c⨯10(104+1)+d(104+1)=(104+1)(a⨯103+b⨯102+c⨯10+d)= 10001(a ⨯102 +b ⨯102 +c ⨯10 +d)．所以，这个数肯定可以被10001 整除，即 a =10001．21．因为(2016 - 7x)÷9 = 224 - 7x ÷9和x 都是大于0 的自然数，所以7x ÷ 9 是小于224 的自然数．因为224÷7=32，所以x 可以是9 的1，2，3，…，31 倍，所以满足条件的x 共有31 个．22．因为a，b 都是自然数，a ⨯b = 2015, a >b ．则当a = 2015,b = 1时，a -b 的值最大，故 a -b 的最大值是20158-1=2014．23．由于M、N 都是自然数，M×N=2015，M>N，又2015=5×13×31．则当M 与N 最接近，即M=65，N=31 时，M+N 最小，为65+31=96．24．这个庞大的数的各个数位上的数字之和为（1+2+3）×123=738，由于738÷3=246，所以这个庞大的数能被3 整除．25．能被11 整除的数的特点是：奇数位上的数字和与偶数位的数字和的差是11 的倍数．当个位分别填入0，1，2，3，5，6，7，8，9 时，万位数字分别是：3，2，1，0，9，8，7，6，5，而当个位数字是4 时，万位数应为10，这不可能，所以这个六位数的个位数字是4．26．由1 个小三角形组成的三角形有20 个．由2 个小三角形组成的三角形有20 个，由4 个小三角形组成的三角形有4 个，由4 个小三角形和1 个小正方形组成的三角形有4 个，由5 个小三角形和1 个小正方形组成的三角形有1 个，所以图中共有49 个三角形．27．最小的正方形有12 个．由4 个小正方形构成的正方形有5 个，正中心还有1 个斜放的正方形．所以图中共有正方形18 个．28．可以分层来数，从上到下的4 层，每层需要正方体的个数分别是：1，1，4，6，1+1+4+6=12（个）．所以需要小正方体12 个．29．因为2016 = 25 ⨯32 ⨯7 ．所以2016 的约数有（5+1）×（2+1）×（1+1）=36（个）．30．因为1+2+3+4+5+6=21．把多出的一个球放到已装6 个球的盒子中，这样22 个球可以装6 个盒子．另外如果装7 个盒子，要使每个盒子中小球的数量不同，至少需要1+2+3+4+5+6+7=28 个小球．所以最多可以装6 个盒子．31．先任选一个方格涂成红色，有5×6=30 种方法．除去与选中方格同行同列的方格，还剩（5-1）×（6-1）=20 个方格．所以不同的方案有5×6×（5-1）×（6-1）=600（种）．32．因为0 不能出现在首位，所以十位数字可能是2，1，5 三种情况．因定十位数字后，个位数字可能是2，0，1，5 四种情况．由分步乘法原理得3×4=12，所以用2，0，1，5 这 4 个数字可以组成12 个不同的两位数．33．从1 到100 的所有自然数可分为三类：一位数，两位数，三位数．一位数中，不含4、5 的有7 个，它位是1、2、3、6、7、8、9；两位数中，不含量4、5 的可以这样考虑：十位上，不含4、5 的有1、2、3、6、7、8、9 这7 种情况．个位上，不含4、5 的有0、1、2、3、6、7、8、9 这8 种情况．要确定一个两位数，可以先取十位数，再取个位数，应用乘法原理．不含4 和5 的数有7×8=56（个）．三位数只有100．7+56+1=64（个），所以一共有64 个不含4、5 的自然数．34．第一位小朋友有6 个座位可以选，第二位小朋友有5 个座位可以选，第三位小朋友有4 个座位可以选，第四位小朋友有3 个座位可以选，第五位小朋友有2 个座位可以选，第六位小朋友只剩1 个座位，于是共有6×5×4×3×2×1=720（种）坐法．35．假如给小强的是智力拼图，则有方法2×5×4×3=120（种）．假如给小强的是遥控汽车，则有方法1×5×4×3=60（种）．总共有方法120+60=180（种）．36．因为大正方形的周长是48．所以大正方形的边长是48÷4=12，又因为小正方形的周长是12，所以小正方形的边长是16÷4=4，故阴影部分的面积是12×12-4×4=128．37．因为长方形的长是宽的2 倍，面积是288．所以宽×宽×2=288，即宽×宽=144．因为12×12=144，所以长方形的宽是12，长是24，周长是（12+24）×2=72．38．恰好含有∆ABC 的正方形的面积是4×4=16，此正方形内，∆ABC 之外的图形面积之和是3×1+4×4÷2+1×1=12，所以∆ABC 的面积=16-12=4．39．阴影部分的面积S=5×5-（3×2+2×1+2×1+2×2+3×1+5×1）÷2=25-11=14．40．因为长方形的周长是100 厘米，所以长方形的长+宽÷2=50（厘米）．又因为长方形的宽是8 厘米的倍数，则它的长和宽可能出现的情况如下表所示：所以围成的长方形的面积可以是42×8=336（平方厘米），34×16=544（平方厘米），26×24=624（平方厘米），故围成的长方形面积的最大值是624 平方厘米．41．记长方形与正方形形重合部分的面积为S，则S 1 -S2=(S长方形ABCD -S )-(S正方形EFGH -S )=S长方形ABCD-S正方形EFGH=9×6-5×5=29（平方厘米）．42．因为长方形的长与宽的和是34÷2=17（厘米）．所以用这根铁丝可围成的长方形的长、宽与面积的关系如下：所以，围成的长方形面积的最大值是72 平方厘米．43．因为AB =CD ，AM 是梯形AMCD 与∆ABM 共有的边，所以梯形AMCD 的周长- ∆ABM 的周长=CM+AD-BM=12．又因为MC=4BM，则CM=3BM，AD=BC=4BM，于是6BM=12，解得BM=2，所以AB=8．44．由题得原正方形的草坪的边长为（92-5×4）÷（5+4）=8（米）．所以原草坪的面积为8×8=64（平方米）．45．两次绕花坛所用绳子的长度差为5+13=18（米）．第二次比第一次多绕2 圈，则绕花坛一圈需用绳子18÷2=9（米），所以这条绳子的长度是9×6+5=59（米）．46．图形的外轮廊的长=4×（长+宽）+4×（长-宽-5）=8×长-20．所以8×长=52+20=72，可知长方形的长是72÷8=9．47．平移图中的部分线段后，可得到如图16 长方形，长方形的周长就是所求图形的周长．则图可得，长方形的宽是19 厘米，长是10+12=22（厘米）．故所求图形的周长是2×（19+22）=82（厘米）．48．长方形纸片DGFH 的周长=2（DG+GF）=2CD，恰好是正方形ABCD 的边长的2 倍．因为正方形ABCD 的面积是49 平方厘米，所以正方形ABCD 的边长是7 厘米，2×7=14（厘米）．故长方形纸片DGFH 的周长是14厘米．49．因为大正方形和小正方形的周长相差8 厘米，所以它们的边长相差8÷4=2（厘米）．图17如图 17，则有阴影部分的面积是 32 平方厘米．阴影部分的面积由 3 部分组成，其中 BEHC 和 DCIG 是两个相同的长方形，CGFI 是边长为 2 的正方形．所以 BC =（32-2×2）÷2÷2=7（厘米）．于是正方形 AEFG 的边长是 7+2=9（厘米）． 故大正方形的面积是 9×9=81（厘米）．50．因为长方形 ABCD 和 DFEG 相同，所以对角线 FD 和 AC 将两个长方形分成的 4 部分也相同，将 DC 右侧的阴影部分移到图形的左上角，则阴影部分的面积就是正方形 HGDC 的面积，为6×6=36．51．三个空白部分可以拼成一个小正六边形，所以阴影面积是24×3÷4=18（平方厘米）． 52．只有 1 个 3，个位数字是 3．2 个3 相乘，个位数字是 9， 3 个 3 相乘，个位数字是 7，4 个 3 相乘，个位数字是 1，5 个 3 相乘，个位数字是 3， …个位数字随 3 的个数周期变化，且周期是 4． 因为 2016÷4=504．所以 2016 个 3 相乘，个位数字和 4 个 3 相乘的个位数字相同，是 1．53．观察前几个数的规律，可知：从第二个数起每个数都比前一个数大 3，（2015-5+3）÷3=671，所以 n 的值是 671．54．因为 3 和 4 的最小公倍数是 12，所以每隔 12 厘米两种记号会重合一次．如图 18， 每 12 厘米长的木条都会被截成 6 段．75÷6=12……3．由图可知要多截出 3 段，需要 6 厘米木条． 所以木条原长 12×12+6=150（厘米）．55．原式= 66 6 ⨯ (100 0 -1)2015个= 2015个2015个2015个2015个2014个2014个故算式的结果中有 2014 个 3．56．由题得 A +5+E +8=5+B +6+ E= 66 6533 334 ． 66 6 ⨯ 00 0 - 66 6=E+6+C+7=8+E+7+D．即A+13=B+11=C+13=D+15．故最大数为B，最小数为D．且B-D=15-11=4．57．因为图中任意相邻的三个格子中的数字之和都相等，所以A+B+C=B+C+D=C+D+E=D+E+F=30÷2=15．即A=D，B=E，C=F，故A+E+F=D+E+F=15．58．整个过程中一共转了1+2+3+…+36=666（次）．每转过72 人次所有同学的朝向就会和原来一样，那么666÷72=9……18，所以，应该有18 名同学面朝里．59．要使(a +b)÷(a -b)的值最大，则需(a +b)的值最大，(a -b)的值最小．因为a，b 是1 至200 中的两个不相等的自然数．所以(a +b)的最大值是200+199=399，(a -b)的最小值是200-199=1，故(a +b)÷(a -b)的最大值是399÷1=399．60．开第一把锁，从最坏的情况考虑，试了7 把钥匙还未成功，则第8 把不用再试，一定能打开这把锁，此时还剩7 把钥匙，6 把锁；开第2 把锁时，同样从最坏的情况考虑，试了6 把钥匙还未成功，则第7 把不用再试，一定能打开这把锁，此时还剩6 把钥匙，5 把锁；同理，开第3 把锁时，最多要试5 次；开第4 把锁时，最多要试4 次；开第5 把锁时，最多要试3 次；开第 6 把锁时，最多要试2 次；开第7 把锁时，最多要试1 次．所以要把7 把锁全部打开最多要试7+6+5+4+3+2+1=28（次）．61．由甲说：“我的名次排在丁前面，丙后面．”可知：甲、丙、丁三人的名次是：丙、甲、丁．又由丙说：“戊在我前面冲过终点．”可知：戊跑的比丙快，即戊的名次要高于丙．又由丁说：“我比乙跑的快．”可知：丁的名次要高于乙．所以，这五个人的比赛名次为：戊、丙、甲、丁、乙．由于一开始感应灯是关的，所以只有那些被按过奇数次的感应灯才是亮的．因为只有平方数才有奇数个约数．63．这9 个数的和是：1+2+3+4+5+6+7+8+9-（1+9）×9÷2=45．由小刚和小明选的数中只有一个是相同的，可知他们正好把这9 个数全部都取到了，且有一个数取了两遍．所以他们取的数的总和比这9 个数的和多出来的部分就是所求的数．可知这个数是23+24-45=2．64．因为7 月有31 天，31÷7=4……3．所以一周中的7 天中，有4 天出现4 次，有3 天出现5 次，又因为周一和周四都出现4 次，所以出现5 次的是周五，周六和周日．所以7 月1 日只能是周五，可知7 月15 日也是周五．65．因为路的两端都要植树，所以156 米的小路一侧被分割成13-1=12（段），每段长度是156÷12=13（米）．即相邻两棵树之间的距离是13 米．66．因为500÷108=4（圈）……68（棵），所以小红绕操场跑了4 圈后又跑过68 棵树，又108÷4=27（棵），所以操场每边种27+1=28 棵树，考虑操场每条边最后一棵树是下一条边的第一棵树，且68÷（28-1）=2（边）……14（棵），故第500 棵树是她所在操场边上跑过的树中的第14 棵．67．因为小林3 岁的时候，爷爷53 岁，所以爷爷比小林53-3=50（岁），故小林10 岁时，爷爷为10+50=60（岁），因为60÷10=6，故小林10 岁时，爷爷的年龄是小林的 6 倍．68．2 年后哥哥的年龄比晶晶4 年前的年龄大4+2+3=9（岁）．所以晶晶4 年前的年龄是9÷（2-1）=9（岁），9+4=13（岁），即晶晶今年13 岁．69．设丹丹今年x 岁，则母亲今年（x-6）×4+6=4x-18（岁），父亲今年（x-11）×8+11=8x-77（岁）,于是x+（4x-18）+（8x-77）=100．解得x=15．所以丹丹今年15 岁．70．21+16-30=7（人），所以既采集了植物标本，又采集了动物标本的有7 人．71．假设全班都是男生，则总分比实际少35×（90-88）=70（分），每个女生比男生平均多95-88=7（分），所以这班女生的人数是70÷7=10（人）．72．若每箱装24 个长方形模具和12 个圆形模具，则依题意，当剩下8 个长方形模具时，应剩下4 个圆形模具，比实际少37-4=33（个），33÷（12-9）=11，所以共装了11 箱，故长方形模具共有24×11+8=272（人）．73．这本故事书共有16×22=352（页）．小芳后面7 天共读了⎡⎣20-1+(20-7)⎤⎦÷2⨯7=112（页），所以小芳之前读了（352-112）÷20=12（天）．74．因为30+25=55，55>45，所以必有同学两项比赛都参加了．由于每个同学至少参加一项比赛，根据包含排除法可知：全组人数=30+25-参加两项比赛的人数，即45=55-参加两项比赛的人数．所以，参加两项比赛的人数是55-45=10．75．两个箱子原来可放160×=320（本）书，每个箱子多放10 本后，这320 本书除20 本外全部分散到其他箱子，所以共有箱子（320-20）÷10+2=32（个），32×160=5120（本）．所以一共有32 个箱子，5120 本书．76．只考虑第一堆棋子，共发生了两次变化：拿出去15 个棋子，放入了12 个棋子．两次变化的结果是：第一堆减少了3 个棋子，剩余180 个棋子，所以第一堆原有180+3=183（个）棋子．同理，第二堆原有183 个棋子，第三堆原有174 个棋子．77．假设1000 个万花筒中没有残次品，则应获利润1000×2=2000（元），实际少获得利润2000-1904=96（元）．每遇到一件残次品商人少获得利润6+2=8（元），所以一共有残次品96÷8=12（件）．78．一共有排球（6+8）÷（8-6）=7（个），所以共有学生6×7+6=48（人）．79．由题得数学成绩的平均分+英语成绩的平均分=85×3-90=165．所以英语成绩的平均分=（165+25）÷2=95．80．因为红球是白球5 倍，所以小球的总个数是白球个数的5+1=6（倍）．所以白球的个数为120÷6=20，。
2019年“希望杯”四年培训题100题汇总(含答案)
小学“希望杯”全国数学邀请赛四年级培训题1.计算：2017×2071+2077×2017－2037×2017－2111×2017.2.计算：9999×2222+3333×3334.3.比较大小：A=2016×2018，B=2017×2017，C=2015×2019.4.定义新运算：a⊗⊗ b= a ⨯⋅⋅⋅⨯⨯b b b 个，求(1 ⊗ 4) ⊗ (2 ⊗ 3).5.一个自然数，各个数位上的数字之和是74，这个数最小是多少?6.一个三位数被3 除余1，被5 除余3，被7 除余5，这个数最大是多少?7.一个整除算式，被除数比商大126，除数是7，求被除数.8.一个三位数，它的各位数字之和是20，十位数字比个位数字大1，如果将百位数字与个位数字对调，得到的三位数比原三位数大198，求原数.9.在从1 开始的n 个连续的自然数中，去掉其中的一个数，余下各数的和是2017，求去掉的数.10.若干个数的平均数是17，加入一个新数2017 后，这组数的平均数变成21，原来共有多少个数?11.用2，0，1，7 这四个数字可以组成多少个没有重复数字的四位偶数?12.已知a，b，c 是三个质数，且a < b < c，a + b ×c = 93，求a，b，c.13.a，b，c 是彼此不同的非0 自然数，若a + b + c = 6，求四位奇数aabc 中最小的那个.14.a，b，c 是彼此不同的非0 自然数，若a + b + c = 6，求四位数aabc 中最大的那个.15.三位数abc 是质数，a，b，c 也是质数，cba 是偶数，ab 是5 的倍数，求三位数abc .16.求被7 除，余数是3 的最小的三位数.17.求被7 除，余数是4 的最大的四位数.18.将分别写有数字3，7，8 的三张卡片排成三位数abc，使它是43 的倍数，求abc .19.已知a，b，c 是不同的质数，且三位数abc 能同时被3，7 整除，求abc .20.用写有2，3，5，7 的四张纸片可以排成多少个小于1000 的质数?21.四位数abbc 可被两位数ac 整除，若a < c，a + c = 5，求b.22.在下面的算式里加上一对括号，使算式成立. 1×2×3+4×5+6+7+8+9=100.23.在等号左边添上适当的运算符号、括号，使等式成立.9 9 9 9 = 8.24.从1 至9 的自然数中选择8 个数填入下面的方框中，使得计算结果尽量大，那么这个结果最大是多少?25.在图1 的算式中，A，B，C，D 代表0~9 中四个各不相同的数字，且A 是最小的质数，求四位数ABCD。