振动位移速度加速度
何谓振幅振动速度振速振动加速度

何谓振幅振动速度振速振动加速度振动一般可以用以下三个单位表示:mm、mm/s、mm/s2。
振幅、振动速度(振速)、振动加速度。
振幅是表象,速度和加速度是转子激振力的程度。
mm振动位移:一般用于低转速机械的振动评定; mm/s振动速度:一般用于中速转动机械的振动评定;mm/s2 振动加速度:一般用于高速转动机械的振动评定。
工程实用的振动速度是速度的有效值,表征的是振动的能量;加速度是用的峰值,表征振动中冲击力的大小。
振幅理解成路程,单位是mm;把振速理解成速度,单位是mm/s;振动加速度理解成运动加速度,单位mm/s2。
速度描述的是运动快慢;振速就是振动快慢,一秒内能产生的振幅。
振幅相同的设备,它的振动状态可能不同,所以引入了振速。
位移、速度、加速度都是振动测量的度量参数。
就概念而言,位移的测量能够直接反映轴承固定螺栓和其它固定件上的应力状况。
例如:通过分析透平机上滑动轴承的位移,可以知道其轴承内轴杆的位置和摩擦情况。
速度反映轴承及其它相关结构所承受的疲劳应力。
而这正是导致旋转设备故障的重要原因。
加速度则反映设备内部各种力的综合作用。
表达上三者均为正弦曲线,分别有90度,180度的相位差。
现场应用上,对于低速设备(转速小于1000RPM)来说,位移是最好的测量方法。
而那些加速度很小,其位移较大的设备,一般采用折衷的方法,即采用速度测量,对于高速度或高频设备,有时尽管位移很小,速度也适中,但其加速度却可能很高的设备采用加速度测量是非常重要的手段。
另外还需要了解传感器的工作原理及应用选择,提及一点,例如采用涡流传感器测量的位移和应用加速度传感器通过两次积分输出的位移所得到的东西是完全不一样的。
涡流传感器测量轴承与轴杆之间的相对运动,加速度传感器测量轴承顶部的振动,然后转换成位移。
如整个轴承振动的很厉害,轴与轴承的相对运动很小,涡流传感器就不能反应出这样的状态,而加速度传感器则可以。
两种传感器测量两种不同的现象。
振动单位换算表
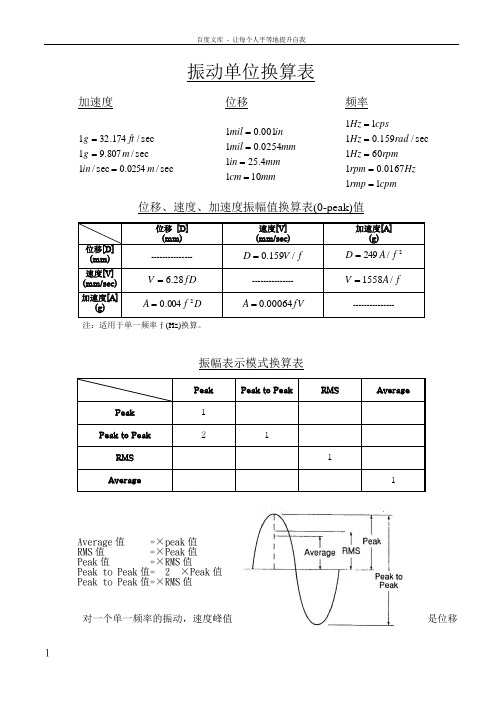
振动单位换算表加速度位移频率sec/0254.0sec /1sec /807.91sec /174.321m in m g ft g ===mmcm mm in mm mil inmil 1014.2510254.01001.01==== cpmrmp Hz rpm rpm Hz rad Hz cpsHz 110167.01601sec/159.0111=====位移、速度、加速度振幅值换算表(0-peak)值位移 [D] (mm) 速度[V] (mm/sec)加速度[A](g)位移[D] (mm) ---------------fV D /159.0=2/249f A D =速度[V] (mm/sec) fD V 28.6= ---------------f A V /1558=加速度[A](g)D f A 2004.0=fV A 00064.0=---------------注:适用于单一频率f (Hz)换算。
振幅表示模式换算表Peak Peak to PeakRMS AveragePeak 1 Peak to Peak2 1 RMS 1 Average1Average 值 =×peak 值 RMS 值 =×Peak 值 Peak 值 =×RMS 值Peak to Peak 值= 2 ×Peak 值 Peak to Peak 值=×RMS 值对一个单一频率的振动,速度峰值是位移峰值的2πf倍,加速度峰值又是速度峰值的2πf倍。
当然要注意位移一般用的峰峰值,速度用有效值,加速度用峰值。
还要注意现场测量的位移是轴和轴瓦的相对振动,速度和加速度测的是轴瓦的绝对振动。
假设一个振动的速度一定,是5mm/s,大家可以自己算下如果是低频振动,其位移会很大,但加速度很小。
高频振动位移则极小,加速度很大。
所以一般在低频区域都用位移,高频区域用加速度,中频用速度。
振动加速度计算公式

振动加速度计算公式
振动是物体在固定点或轴线周围做有规律地往复运动。
振动加速度是描述物体振动情况的一个物理量,表示单位时间内物体所获得的速度变化量。
首先,简谐振动的运动方程可以表示为:
x = Acos(ωt + φ)
其中,x为物体的位移,A为振幅,ω为角频率,t为时间,φ为相位常数。
其次,速度是位移对时间的导数,即
v = dx/dt = -Aωsin(ωt + φ)
再次,加速度是速度对时间的导数,即
a = dv/dt = -Aω^2cos(ωt + φ)
根据上述推导,振动加速度计算公式为:
a = -Aω^2cos(ωt + φ)
在上述公式中,A表示振幅,ω表示角频率,t表示时间,φ表示相位常数。
振幅决定了振动的幅度大小,角频率则影响振动的周期,相位常数则决定了振动的起始位置。
此外,还有一种计算振动加速度的方法是使用泰勒级数。
泰勒级数是一种将函数在其中一点展开成无穷级数的方法,通过求取一定阶数的导数来逼近其中一函数的值。
对于振动加速度,可以使用泰勒级数展开cos函数来计算。
根据泰勒
级数展开可得到:
cos(x) = 1 - (x^2/2!) + (x^4/4!) - (x^6/6!) + ...
通过对cos(x)函数进行泰勒级数展开,并截取一定阶数的项,可以
计算出振动加速度的近似值。
综上所述,振动加速度的计算公式可以根据物体振动特性得出,根据
简谐振动的运动方程和泰勒级数展开可以求得振动加速度的精确或近似值。
这些计算方法能够帮助我们更好地理解和描述振动现象。
第二章 旋转机械振动分析基础汇总
第二章 旋转机械振动分析基础振动在设备故障诊断中占了很大的比重,是影响设备安全、稳定运行的重要因素。
振动又是设备的“体温计”,直接反映了设备的健康情况,是设备安全评估的重要指标。
一台机组正常运行时,其振动值和振动变化值都应该比较小。
一旦机组振动值变大,或振动变的不稳定,都说明设备出现了一定程度的故障。
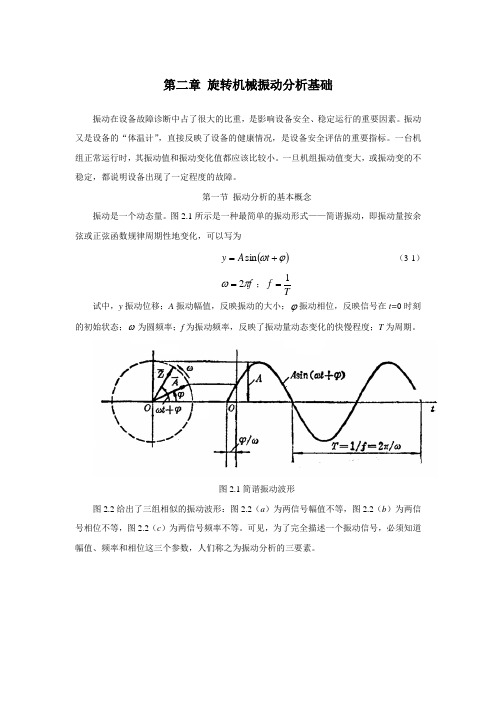
第一节 振动分析的基本概念振动是一个动态量。
图2.1所示是一种最简单的振动形式——简谐振动,即振动量按余弦或正弦函数规律周期性地变化,可以写为()ϕω+=t A y sin (3-1)f πω2=;Tf 1= 试中,y 振动位移;A 振动幅值,反映振动的大小;ϕ振动相位,反映信号在t=0时刻的初始状态;ω为圆频率;f 为振动频率,反映了振动量动态变化的快慢程度;T 为周期。
图2.1简谐振动波形图2.2给出了三组相似的振动波形:图2.2(a )为两信号幅值不等,图2.2(b )为两信号相位不等,图2.2(c )为两信号频率不等。
可见,为了完全描述一个振动信号,必须知道幅值、频率和相位这三个参数,人们称之为振动分析的三要素。
(a)幅值不等;(b)相位不等;(c)频率不等图2.2 三组相似的振动波型简谐振动时最简单的振动形式,实际发生的振动要比简谐振动复杂的多。
但是根据付立叶变换理论知道,不管振动信号多复杂,都可以将其分解为若干具有不同频率的简谐振动。
图2.3 付立叶变换图解旋转机械振动分析离不开转速,为了方便和直观起见,常以1x表示与转动频率相等的频率,又称为工(基)频,分别以0.5x、2x、3x等表示转动频率的0.5倍、2倍、3倍等相等的频率,又称为半频、二倍频、三倍频。
采用信号分析理论中的快速傅立叶变换可以很方便地求出复杂振动信号所含频率分量的幅值和相位。
目前频谱分析已成为振动故障诊断领域最基本的工具。
频谱分析所起的作用可以概括为以下两点:1)特定故障的频率特征具有必然性。
例如,转子不平衡的频率为工频,气流基振和油膜振荡等故障的频率为低频,电磁激振等故障为高频。
《振动测试》实验讲义
实验一 简谐振动幅值测量一、实验目的1.了解振动信号位移、速度、加速度之间的关系。
2.学会用各种传感器测量简谐振动的位移、速度、加速度幅值。
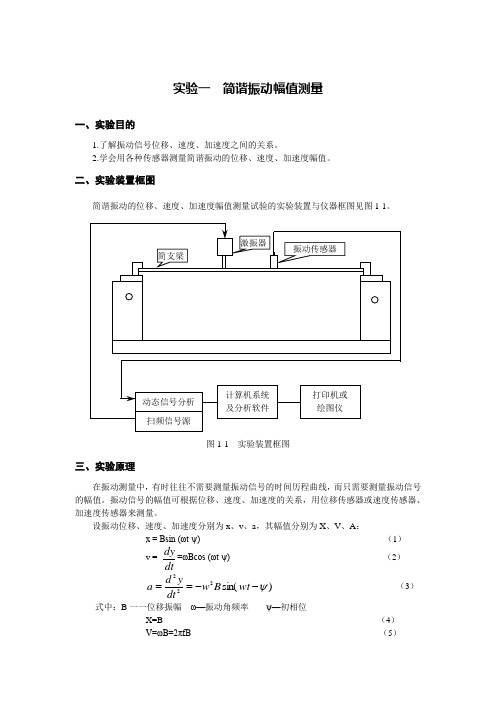
二、实验装置框图简谐振动的位移、速度、加速度幅值测量试验的实验装置与仪器框图见图1-1。
图1-1 实验装置框图三、实验原理在振动测量中,有时往往不需要测量振动信号的时间历程曲线,而只需要测量振动信号的幅值。
振动信号的幅值可根据位移、速度、加速度的关系,用位移传感器或速度传感器、加速度传感器来测量。
设振动位移、速度、加速度分别为x 、v 、a ,其幅值分别为X 、V 、A :x = Bsin (ωt -ψ) (1)v =dtdy =ωBcos (ωt -ψ) (2) )sin(222ψ--==wt B w dtyd a (3)式中:B 一一位移振幅 ω—振动角频率 ψ—初相位X=B (4) V=ωB=2πfB (5)A=ω2B=(2πf)2B (6)振动信号的幅值可根据式(6)中位移、速度、加速度的关系,分别用位移传感器、速度传感器或加速度传感器来测量。
也可利用动态分析仪中的微分、积分功能来测量。
四、实验方法1、安装激振器把激振器安装在支架上,将激振器和支架固定在实验台基座上,并保证激振器顶杆对简支梁有一定的预压力(不要超过激振杆上的标识),用专用连接线连接激振器和DH1301扫频信号源输出接口。
2、连接仪器和传感器把加速度传感器安装在简支梁的中部,输出信号接到电荷放大器的输入端,并将电荷放大器的输出接到数采分析仪的1通道。
3、仪器参数设置打开数采仪器的电源开关,开机进入DAS2003数采分析软件的主界面,设置采样率(2kHz)、量程范围,输入加速度传感器的灵敏度。
打开一个窗口,分别显示三个通道的信号。
4、采集并显示数据调节扫频信号源的输出频率,使梁产生振动。
分别调整电荷放大器为加速度、速度、位移状态,同时在窗口中读取当前振动的最大值(位移、速度、加速度)。
5、计算数据与实验数据比较按公式计算位移、速度或加速度值,并与实验数据比较。
振动计算力学公式

振动计算力学公式一、简谐振动(Simple Harmonic Motion)简谐振动指的是一个物体在一个平衡位置附近做低幅度的周期性振动。
简谐振动的一些重要的力学公式如下:1. 位移(Displacement):x = A * cos(ωt + φ)其中,x表示位移,A表示振幅,ω表示角频率,t表示时间,φ表示相位。
2. 速度(Velocity):v = -A * ω * sin(ωt + φ)其中,v表示速度。
3. 加速度(Acceleration):a = -A * ω^2 * cos(ωt + φ)其中,a表示加速度。
4. 动能(Kinetic Energy):K = 0.5 * m * v^2其中,K表示动能,m表示质量。
5. 势能(Potential Energy):P = 0.5 * k * x^2其中,P表示势能,k表示弹性系数。
6. 总机械能(Total Mechanical Energy):E = K + P其中,E表示总机械能。
7. 振动周期(Vibration Period):T = 2π/ω其中,T表示振动周期。
二、阻尼振动(Damped Vibration)阻尼振动指的是振动过程中受到了阻尼力的影响,导致振幅逐渐减小。
阻尼振动的一些重要的力学公式如下:1. 位移(Displacement):x = A * e^(-βt) * cos(ωdt + φ)其中,x表示位移,A表示振幅,β表示阻尼系数,ωd表示阻尼角频率,t表示时间,φ表示相位。
2. 速度(Velocity):v = -A * β * e^(-βt) * cos(ωdt + φ) - A * ωd * e^(-βt) * sin(ωdt + φ)其中,v表示速度。
3. 加速度(Acceleration):a = A * (β^2 * e^(-βt) *cos(ωdt + φ) + 2β * ωd * e^(-βt) * sin(ωdt + φ)) - A *ωd^2 * e^(-βt) * cos(ωdt + φ)其中,a表示加速度。
振动监测参数及标准

振动监测参数及标准
振动监测参数主要包括振动的振幅、频率、相位、振动速度、振动加速度、振动位移等。
1. 振幅:振幅是指振动的最大偏离量,通常用峰值或峰-峰值
表示。
2. 频率:频率是指振动的周期性重复次数,通常以赫兹(Hz)表示。
3. 相位:相位是指振动波形相对于特定参考点的时间偏移角度或时间延迟量。
4. 振动速度:振动速度是指振动物体通过空气、液体或固体传导的振动能量的速度。
5. 振动加速度:振动加速度是指振动物体加速度的大小,通常以米每秒平方(m/s^2)表示。
6. 振动位移:振动位移是指物体振动时从平衡位置到最大偏移的距离。
振动监测的标准通常采用国家或行业制定的振动监测标准,例如ISO10816标准。
该标准将振动级别划分为四个等级:I级
表示良好状态,II级表示可接受状态,III级表示存在问题或
需要进行进一步检查,IV级表示严重故障。
除ISO10816标准外,还有许多其他振动监测标准,如API 670、VDI 2056和ASME PTC 19.3等。
这些标准通常根据不
同的应用领域和设备类型提供了不同的振动限制值和评估方法。
正弦振动加速度与速度与振幅与频率关系

正弦振动加速度与速度与振幅与频率关系Prepared on 24 November 2020正弦振动一共有四个参数来描述,即:加速度(用a表示)m/s^2速度(用v表示) m/s位移(用D表示)行程(2倍振幅)m频率(用f表示)Hz公式:a=2πfvv=2πfd(其中d=D/2)a=(2πf)2d (2为平方)说明:以上公式中物理量的单位均为国际单位制例如频率为10HZ,振幅为10mmV=2**10*10/1000=0.628m/sa=(2**10)^2*10/1000=m/s^2正弦运动振幅5mm 频率200HZ我想你是在做一个弹簧振子,加速度是变化的,我想你需要的应该是弹簧的弹性系数k首先写出振动方程Y=5sin(x/200)根据设计要求,弹簧要使振子在1/200s的时候运动距离达到5mm,速度由最大的V0变为0,在这个过程中属于变力做功,(不知道你会积分不)如果不会也没有关系,我们知道弹簧的弹性势能为^2(式中H是弹簧的伸长量),在达到振幅时,H=5mm=5×10^(-3)m应用动能定理:^2=1/2mV0^2同时,应满足时间频率要求,应用动量定理,就必须用积分了,弹力在1/800(完成1/4周期需要的时间)时间内的冲量为I,I是以函数kHt为被积函数,对H由0到5,t由0到1/800的定积分,即I=×10^(-5)k由动量定理I=mV1-mV0,得,mV0=×10^(-5)k联立两式解得:k=256m(式中m不是单位,是振子得质量)而且初速度为400米每秒振动台上放置一个质量m=10kg的物体,它们一起上下作简谐振动,其频率ν=10Hz、振幅A=2×10-3m,求:(1)物体最大加速度的大小;(2)在振动的最高位置、最低位置,物体分别对台面的压力。
解:取x轴竖直向下,以振动的平衡位置为坐标原点,列运动方程x=Acos(2πνt+φ)于是,加速度a=-4π2ν2Acos(2πνt+φ)(1)加速度的最大值|a m|=4π2ν2A=m·s-2(2)由于物体在振动过程中仅受重力mg及竖直向上的托力f,按牛顿第二定律在最高位置mg-f=m|a m|f=m(g-|a|)=m这时物体对台面的压力最小,其值即在最低位置mg-f=m(-|a m|)f=m(g+|a|)=177Nm这时物体对台面的压力最大,其值即177N频率为60HZ,振幅为0.15mm的正弦振动,换算成加速度是多少只要了解一下其物理方法就不难得到结果了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
