第七讲 矩形波导
电磁波与天线---矩形波导

mπ 当x=0时,A2=0.当x=a时, k x = a 同理可得, nπ 当y=0时,B2=0,当y=b时, y = k b
最后得: 最后得
mπ x nπ y − j β z H z = H 0 cos e cos a b
ˆ ax ∂ ∂x Hx ˆ ay ∂ ∂y Hy
(9) ( n = 0 ,1, 2 , L )
(1) TE10 模的场结构
• 在(10)式中,令 m=1, n=0, 并注意到 )式中, • 那么, 那么,
mπ 2 nπ 2 π 2 kc = ( ) +( ) =( ) a b a
2
H z = H 0 cos( x)e− j β z a π a H x = j β H 0 sin( x)e − j β z π a a π E y = − jωµ H 0 sin( x)e − j β z π a
−
∂H
y
= jω ε E
x
同理,可得 在直角坐标系中展开可得 在直角坐标系中展开可得: 同理,可得E在直角坐标系中展开可得:
解式中的变量Z因 解式中的变量 因 − jβ z 为e ,所以上面 的两式可以对Z的偏 的两式可以对 的偏 导数化解。 导数化解。我们仅 对其中的4个式子进 对其中的 个式子进 行化解
2 2
∇ H =0
利用公式:∇×(∇×H) =∇∇•H)−∇ H (
2
• 得:
∇ H + ω µε H = ∇ H + k H = 0
2
2
2
2
• 式中: • 同理
k = ω µε
2
∇ E+k E =0
2 2
• 导波系统中,我们用直角坐标系,在 直角坐标系中,我们以E为例分解:
矩形波导的模式(3篇)

第1篇一、矩形波导的模式分类矩形波导中的电磁波模式主要分为TE(横电磁波)模式和TM(纵电磁波)模式。
1. TE模式TE模式是指电场只在波导的横向(垂直于传播方向)分量存在,而磁场则在纵向(沿传播方向)分量存在。
根据电场和磁场在波导横截面上的分布,TE模式又可以分为TE10、TE20、TE01等模式。
(1)TE10模式:TE10模式是矩形波导中最基本、最常用的模式。
其电场分布呈矩形,磁场分布呈椭圆。
TE10模式的截止频率最高,适用于高频传输。
(2)TE20模式:TE20模式的电场分布呈矩形,磁场分布呈圆形。
其截止频率低于TE10模式,适用于中频传输。
(3)TE01模式:TE01模式的电场分布呈矩形,磁场分布呈椭圆。
其截止频率最低,适用于低频传输。
2. TM模式TM模式是指磁场只在波导的横向分量存在,而电场则在纵向分量存在。
根据电场和磁场在波导横截面上的分布,TM模式又可以分为TM01、TM11、TM21等模式。
(1)TM01模式:TM01模式的电场分布呈矩形,磁场分布呈圆形。
其截止频率最高,适用于高频传输。
(2)TM11模式:TM11模式的电场分布呈矩形,磁场分布呈椭圆。
其截止频率低于TM01模式,适用于中频传输。
(3)TM21模式:TM21模式的电场分布呈矩形,磁场分布呈圆形。
其截止频率最低,适用于低频传输。
二、矩形波导的模式特性1. 截止频率截止频率是矩形波导中一个重要的参数,它决定了电磁波在波导中能否有效传输。
不同模式的截止频率不同,其中TE10模式的截止频率最高,适用于高频传输。
2. 相速度相速度是指电磁波在波导中传播的速度。
不同模式的相速度不同,TE模式的相速度比TM模式快。
3. 模式损耗模式损耗是指电磁波在波导中传播时,由于波导壁的吸收和辐射等原因,能量逐渐衰减的现象。
不同模式的损耗不同,TE模式的损耗比TM模式小。
4. 传输特性矩形波导中不同模式的传输特性不同,如TE模式的传输特性较好,适用于高频传输;TM模式的传输特性较差,适用于低频传输。
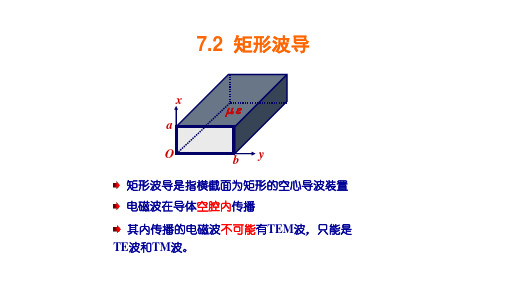
7.2.1矩形波导中的场分布
n z x sin y e b
由纵向场法,可得: m m n z Ex k 2 a Em cos a x sin b y e c E n E sin m x cos n y e z y m kc2 b a b m n z H x j n Em sin x cos y e 2 kc b a b m m n z H y j 2 Em cos x sin ye kc a a b
再加上边界条件
Ez |x 0 0 Ez |x a 0 E z | y 0 0 E z | y b 0
可以解得:
m k x a f ( x) A sin m x a
故
n k y b g ( y ) C sin n y b
两个常微分方程的通解为:f ( x)
A sin k x x B cos k x x,
g ( y ) C sin k y y D cos k y y
4
f ( x) A sin k x x B cos k x x, g ( y ) C sin k y y D cos k y y
③ 由于对相同的 m 和 n , TMmn 模和 TEmn 模的截止波数 kcmn 相同,
这种情况称为模式的简并; ④ 对于 TEmn 模,其 m 和 n 可以为 0 ,但不能同时为 0 ;而对于 TMmn 模, 其m 和n不能为0,即不存在TM0n 模和TMm0模。
7
振幅Em=AC,其大小由激励源强度决定。
2.2 矩形波导

H10(即TE10)波的截止波长最大,它最容易在波导中传播。
为了保证单一的H10波传输,波导尺寸必须满足:
(c ) H20 (c ) H10
a 2a
(c ) H01
2b
§2.2 矩形波导
2.2.4 矩形波导的主模—TE10
1.场表达式
Ez 0
电力线只分布在波导的横截面内
基模:TE10(a>b)
a
横截面图
y z
Hx 窄边纵切面 Ey
§2.2 矩形波导
x z
g
立体图见图2-5
基模:TE10(a>b) 宽边纵切面
§2.2 矩形波导
3.传输参量
波导波长
g
vp f
1 ( / c )2
相移常数
2 2 g
1 ( / c )2
§2.2 矩形波导
相速
vp
v
1 ( / c )2
群速 vg v 1 ( / c )2
(3) 场量沿z轴为行波,沿x轴和y轴为纯驻波
(4) 主模:最低次模
TE10模
一般来说,用a表示波导宽边,b表示窄边,a>b,K10=π/a是所 有波型中波数最小的,因此TE波型的最低次波型是TE10模。
§2.2 矩形波导
3.传输条件
波导中不同模式的截止波长是不同的,对于特定尺寸的波导,
只有满足 c 的模才能得到传输。
§2.2 矩形波导
TE10单模传输条件:
a 2a
2b
兼顾所能够承受一定的传输功率:图(2-8)
a 1.8a
(2-97)
兼顾最小功率损耗:
a=0.7λ
b=(0.4~0.5)a
§2.2 矩形波导
第七讲 矩形波导[详版课资]
![第七讲 矩形波导[详版课资]](https://img.taocdn.com/s3/m/4aac1a405ef7ba0d4a733beb.png)
2 Z 2
课堂优质
(12-3)
(12-4) (12-5)
2
一、矩形波导的求解思路
代入可知
t2E(x, y) E(x, y)
1 Z(z)
2Z (z)
z2
k2
0
(12-6)
由于其独立性,上式各项均为常数
1 Z (z)
2Z (z)
z2
2
t2
E
(
x,
y
)
E(x, y)
kc2
0
(12-7)
课堂优质
kc2 2 k 2
Ez E(x, y)ez
H z
H (x, y)ez
3
一、矩形波导的求解思路
并有
Ex
Ex
Ey
1
0
H H
x y
kc2
0
j
0
j
0
0
j
j
0
x Ex y
0
0
Hx x Hx
y
注意到Ez和Hz的横向函数课要堂优依质 赖具体的边界条件。 4
x
x
)cos(k y
y
y
)ez
课堂优质
9
二、矩形波导的横向解
边界条件
x=0, x=a, Ey=0 y=0, y=b, Ex=0
x 0, Ey 0, 可得x 0 x a, Ey 0, 可得kxa m
y 0, Ex 0, 可得 y 0 y a, Ex 0, 可得k y a n
kx
课堂优质
21
六、矩形波导中的简正波
Maxwell 方程通解
矩形波导
TEmn 波
TM
mn
波
矩形波导

(二)壁电流分布
J s n Ht
JS
x 0
n H t x z H z y H z y j E0 cos a a
x e j (t z ) x 0
y j E0 e j (t z ) J y a j (t z ) J S x a n H t x z H z y H z y j a E0 cos a x e x a
2 c
• 根据TE波的边界条件 • x=0 , ( x, y ) 0 ,得:C2=0
x • x=a , ( x, y ) 0 ,得: k x x
m (m=0,1,2,┄) a
• y=0 , ( x, y ) 0 ,得:C4=0 y n ( x, y ) • y=b , (n=0,1,2,┄) 0 ,得: k y y b
TE01 TE11 TM11 TE20
TE30 TE21 TM21 TE31 TM31
TE40
lc(cm) 图3-2 BJ-100型波导不同波型截止波长的分布图
在矩形波导中实现TE10单模传输,则要求电磁 波的工作波长必须满足下列条件
lc (TE20 ) l lc (TE10 ) l lc (TE01 )
k 2 k
1 2 2 c
2 2 2 m n a b
1 2
H T I ( z ) T ( x, y )
ET U ( z ) T ( x, y ) z
z E0 sin a
矩形波导 PPT

m 场量沿x轴[0,a]出现的半周期(半个纯驻波)的数目;
n 场量沿y轴[0,b]出现的半周期的数目。
④j 相位关系 Ey-Hx、Ex-Hy
z轴有功率传输
Ez-Hx、Ez-Hy
x、y轴无功率传输
所以行波状态下,沿波导纵向(z轴)传输有功功率、横向(x、
y轴)无功功率。
2) 场结构
为了能形象和直观的了解场的分布(场结构),可以 利用电力线和磁力线来描绘它。电力线和磁力线遵循 的规律:
力线上某点的切线方向
该点处场的方向
力线的疏密程度
场的强弱
电力线 发自正电荷、止于负电荷,也可以环绕着交变磁场构 成闭合曲线,电力线之间不能相交。在波导壁的内表面(假设为 理想导体)电场的切向分量为零,只有法向分量(垂直分量), 即在波导内壁处电力线垂直边壁。
磁力线 总是闭合曲线,或者围绕载流导体,或者围绕交变电 场而闭合,磁力线之间不能相交,在波导壁的内表面上只能存在 磁场的切向分量,法向分量为零。
3)相速和群速
TMmn和TEmn波型的相速和群速表示式相同:
vp
v
1(/c)2
vg v 1-c2
4)波型阻抗
TMmn和TEmn波型阻抗为:
ZTE
1
1c2
g
ZTM
1c2
g
5)尺寸选择——矩形波导的工作波型图
基于前面的定义,根据波导横截面尺寸、工作波长、 截止波长之间关系,构成矩形波导工作波型图。根据不 同要求,可利用波型图对波导的横截面尺寸和波导波长 作出选择。
TE0n和TEm0是非简并模;其余的TEmn和TMmn都存在简并模: 若a=b, 则TEmn 、TEnm、TMmn和TMnm是简并模;若a=2b,则TE01与TE20,TE02和 TE40,TE50、TE32和TM32是简并模。
电磁场与电磁波

2 Ez 2 Ez k c2 E z 0 x 2 y 2
分离变量法求解,即 E z ( x , y , z ) X Y e
j t z
1 Ex 2 kc Ey 1 k c2
E z H z x j y
电磁场与电磁波 第8章 导行电磁波 ------- 矩形波导 波导中电磁波传播的 截止现象
电磁场与电磁波 第8章 导行电磁波 ------- 矩形波导 截止波长和截止频率 将
2
EE e j t z ( x , y)
a b
k c2 k 2 0
E ex E x e jt z e y E y e jt z ez E( e jt z z x , y) (x , y) (x , y)
eT ET(x , y) e jt z ET(x , y) e j t z
[ ET(x , y) E ( ]e jt z z x , y)
E z H z y j x
1 k c2
E z H z j x y
电磁场与电磁波 第8章 导行电磁波 ------- 矩形波导 TM波纵向场分量的求解:求通解
电磁场与电磁波 第8章 导行电磁波 ------- 矩形波导 TM波纵向场分量的求解:应用边界条件,确定待定系数
(亥姆霍兹方程)
电磁场与电磁波 第8章 导行电磁波 ------- 矩形波导 算子和场矢量的横 向和纵向分离
电磁场与电磁波 第8章 导行电磁波 ------- 矩形波导 所谓纵横分离就是根据波的传播方向,将对横向和纵向 的偏微分进行分离,即
电磁场与电磁波 第8章 导行电磁波 ------- 矩形波导 同理,也可以将场矢量也表示成横向场分量和纵向分 量分离叠加的形式,即
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
五、TE10波的参数
(3)相速υp
p
C 1 2a
2
>C
(12-25)
(4)群速υg
g c 1 <C 2a p c
2 2
g p C 2
五、TE10波 的参数
(5)波型阻抗
Ey g Et 0 Ht Hx
六、矩形波导中的简正波
简正模(或简正波)理论包含三个方面: 1. 完备性 矩形波导中不论放置什么障碍物和边界条件,它 们里边存在的是 TEmn和 TMmn模式,而且,它们也只 能存在 TEmn和 TMmn模式,具体情况所不同的仅仅是 各种模式的比例与组合。
六、矩形波导中的简正波
2. 正交性
简正模中各个模式是相互正交的,也就是说, 它们之间没有功率和能量交换,即各模式相互独立, 在Fourier分析中表明
2 t
量只须讨论Hz,计及
t2 H ( x, y ) k c2 0 H ( x, y )
二、矩形波导的横向解
则矩形波导的横向解是
2 H ( x, y ) 2 H ( x, y ) 2 k c H ( x, y ) 2 2 x y
y
(12-17)
z b x em a 0
(12-18)
2 2 2 kx ky kc
二、矩形波导的横向解
一般可写出:
X A cos(k x x x )
Y B cos( k y y y )
总的可写出
H z H0 cos(k x x x )cos(k y y y )ez
(12-19)
下面的主要任务是利用边界条件确定kx,ky,和kc。 请注意:H0与激励强度有关。
H z H 0 cos x cos(t z ) a Ey
H sin x sin(t z ) 0 2 a a k
H x 2 H 0 sin x sin(t z ) a kc a
(12-3)
假定Ez(或Hz)可分离变量,也即
E z E ( x , y )Z ( z ) H z H ( x, y )W ( z )
(12-4)
(12-5)
且
2 2 t2 2 Z
一、矩形波导的求解思路
代入可知
t2 E ( x, y) 1 2 Z ( z) 2 k 0 2 E ( x, y ) Z (z) z
2 2
六、矩形波导中的简正波
传输模
e jz 2 1 c
2
E z 0
<cmn
雕落模
e z
>cmn
2
c
1 c
2
六、矩形波导中的简正波
注意到雕落模 ( 也称截止模 ) ,它是一种快速衰 减的振荡模式。也就是说,在不同的z处,有同一相 位。 当然,雕落模式没有功率和能量传播。 当模式不同,但却有相同的kc,我们称为简并模 式。最后显示的是TEmn和TMmn是简并(Degeneration) 的。
四、TE10波
场结构的画法上要注意: • 场存在方向和大小两个不同概念,场的大小是以 力线密度表示的 • 同一点不能有两根以上力线 • 磁力线永远闭合,电力线与导体边界垂直 • 电力线和磁力线相互正交
四、TE10波
y b a
x
y
x
x
0 Ey
0
z
0
z
Hx
x
a
0
0
z H
0
z
图 12-4 TE10波场结构
一、矩形波导的求解思路
并有
Ex E 0 1 y H x kc2 0 H j y 0 j 0 0 j 0 Ex x j Ex y 0 0 H x x H x y
七、TE10波单模存在条件
a m cos l x x dx 0 m l 0 sin a sin a b sin n y cos p y dy 0 m p 0 b sLeabharlann n b (12-20)
通过对偶可得到 TM 波的解:
三、矩形波导的解
其中,
m n k k k a b
2 c 2 x 2 y 2 2
(12-21)
上面称为TEmn波 m——表示x方向变化的半周期数 (即小→大→小) n——表示y方向变化的半周期数。
三、矩形波导的解
关于简正波的讨论: 以矩形波导为例,尽管在z方向它们只可能是入 射波加反射波 ( 即还是广义传输线 ) ,但是由于横向 边界条件它们由 TEmn 和 TMmn 波组成并且它们只能由 TEmn 和 TMmn 波组成 ( 后者,我们称之为完备性 ) ,矩形 波导中这些波的完备集合——即简正波。 任何情况的可能解,只能在简正波中去找,具 体场合所不同的仅仅是比例和组合系数,事实上, 这样就把求复杂场函数的问题变换成求各个模式的 系数。
注意到Ez和Hz的横向函数要依赖具体的边界条件。
二、矩形波导的横向解
在矩形波导中存在 TE 和 TM 两类波,请注意矩形波 导中不可能存在 TEM 波 ( 推而广之,任何空心管中都不 可能存在TEM波)。 这里以 TE 波为例作出讨论,即 Ez=0,对于纵向分
2 2 2 2 x y
二、矩形波导的横向解
边界条件
x=0, x=a, Ey=0 y=0, y=b, Ex=0
x 0, x a, E y 0, E y 0, 可得 x 0 可得k x a m
m kx , a
n ky , a
m整数
y 0, y a,
E x 0, E x 0,
1 1 2a
2
(12-29)
注记:在TE10波各参数中唯独波型阻抗要特别讨论。
六、矩形波导中的简正波
Maxwell 方程通解
矩形波导 TE mn 波 TM mn 波
传输波 雕落波
六、矩形波导中的简正波
矩形波导的求解是典型的微分方程法,通解表明: 在 z 方向它有广义传输线功能,即是入射波和反射波 的迭加;在xy方向由于边界条件限制形成很多分立的 TEmn波(Ez=0)和 TMmn波( Hz=0)。在物理上称之为离 散谱。有限边界构成离散谱。 m—x方向变化的半周期数; n—y方向变化的半周期数。 矩形波导中 TE 波和 TM 波的全部集体构成简正波 。
二、矩形波导的横向解
根据横向分量可以用纵向分量表示,有
Ex j H z j z H k cos( k x )sin( k y ) e 0 y x x y y 2 2 y kc kc
j H z j Ey 2 H 0 2 k x sin( k x x x )cos( k y y y )e z k c x kc
由于其独立性,上式各项均为常数
2
(12-6)
2 2 2 1 Z ( z) 2 k k c Z ( z) z 2 (12-7) z 2 E E ( x , y ) e z E ( x , y ) 2 t z kc 0 H H ( x , y ) e z E ( x , y )
(14-1)
这就保证了每一模的独立性。
六、矩形波导中的简正波
3. 传输模和雕落模
由于频率的选择,每一种模都有可能成为传输模 或雕落模。
2 m n 截止波数 kc k k a b
2 x 2 y 2 2
截止波长
c
2 m n a b
矩形波导中频率最低模式,也即我们要工作的传输 主模式即TE10波,m=1,n=0,若传播常数无耗γ=jβ。
H z H 0 cos x e jz a E y j 2 H 0 sin x e jz a kc a j H x 2 H 0 sin a kc a x e jz
可得 y 0 可得k y a n
n整数
三、矩形波导的解
最后得到TE波的解
m n z H H cos cos e 0 z a b n m n z H 0 cos x sin y e E x j 2 a b kc b m m n z H 0 sin x cos y e E y j 2 a b kc a E 0 z m m n z H H sin x cos y e 0 x k2 a a b c n m n z H H cos x sin y e y 0 2 a b kc b
三、矩形波导的解
这种思想,最早起源于矢量分析,任何空间矢量 方向与大小均 z 不相同,但是 (x,y,z) 建立x,y,z r 坐标系之后, 任一(三维)矢 0 y 量即归结为三 个系数 x
yj zk r xi
图 12-3 Vector Analysis
四、TE10波
0
Hz
五、TE10波的参数
(1) TE10波的截止特性 截止波数
2 2 2
m n k k k a b a
2 c 2 x 2 y
截止波长
2 c 2a kc
fc kc 2
截止频率
2
其它分量用 E z , H , 表示 Ex Ey Hx H y f1 E z , H
