高中数学抛物线求三角形面积最大值
二次函数求三角形面积最大值的典型题目

二次函数求三角形面积最大值的典型题目篇一:哎呀呀,说到二次函数求三角形面积最大值的题目,这可真是让我头疼了好一阵子呢!就比如说有这么一道题:在平面直角坐标系中,有一个二次函数图像,然后给了一堆点的坐标,让咱们求由这些点构成的三角形面积的最大值。
这可咋整?我一开始看到这题,那真是脑袋都大了!心里就想:“这啥呀?怎么这么难!”我瞪大眼睛,死死地盯着题目,手里的笔都快被我捏出汗来了。
我同桌小明呢,他倒是挺自信,还跟我说:“这有啥难的,看我的!”我心里暗暗不服气,哼,你就吹吧!然后老师开始讲题啦,老师说:“同学们,咱们得先找到这个二次函数的顶点坐标,这就好比是找到宝藏的钥匙!”我一听,宝藏?这比喻还挺有意思的。
老师接着说:“然后再看看那些给定的点,能不能通过一些巧妙的方法把三角形的面积表示出来。
”我就在那拼命点头,好像听懂了,其实心里还是有点迷糊。
我扭头看看后面的学霸小红,她一脸轻松,好像这题对她来说就是小菜一碟。
我忍不住问她:“小红,你咋这么厉害,这题你都懂啦?”小红笑了笑说:“多做几道类似的题,你也能懂!”我又埋头苦想,想着要是能像玩游戏一样,一下子就找到解题的秘诀该多好啊!经过一番折腾,我终于有点明白了。
原来求这个三角形面积最大值,就像是爬山,得找到那个最高的山峰,而我们要找的就是能让面积最大的那个点或者那条线。
你说,数学咋就这么难呢?但我就不信我搞不定它!我一定要把这些难题都攻克下来,让数学成为我的强项!总之,我觉得做这种二次函数求三角形面积最大值的题目,虽然过程很艰难,但只要我们不放弃,多思考,多练习,就一定能找到解题的窍门,取得胜利!篇二:哎呀!说起二次函数求三角形面积最大值的题目,这可真是让我又爱又恨呀!有一次上课,数学老师在黑板上出了一道这样的题:已知一个二次函数图像,还有三角形的三个顶点坐标都在这个函数图像上,让我们求三角形面积的最大值。
当时我一看,脑袋就嗡嗡响,这啥呀?我就开始在草稿纸上乱画,心里想着:“这咋这么难呢?”同桌小明凑过来,瞅了瞅我的草稿纸,说:“你这算的啥呀,思路都不对!”我瞪了他一眼,回道:“那你行你上啊!”然后我俩就你一句我一句地争论起来。
【经典压轴题】三角形面积最值问题30题含详细答案

试卷第1页,总14页………外…………○…………订…………○……学:___________考号:___________………内…………○…………订…………○……三角形面积最值问题30题含详细答案1.如图,抛物线2y ax bx c =++与x 轴交于点(1,0)A -,点(3,0)B ,与y 轴交于点C ,且过点(2,3)D -.点P 、Q 是抛物线2y ax bx c =++上的动点.(1)求抛物线的解析式;(2)当点P 在直线OD 下方时,求POD ∆面积的最大值.(3)直线OQ 与线段BC 相交于点E ,当OBE ∆与ABC ∆相似时,求点Q 的坐标.2.如图,在平面直角坐标系xOy 中,已知抛物线22y ax x c =-+与直线y kx b =+都经过(0,3)A -、(3,0)B 两点,该抛物线的顶点为C . (1)求此抛物线和直线AB 的解析式;(2)设直线AB 与该抛物线的对称轴交于点E ,在射线EB 上是否存在一点M ,过M 作x 轴的垂线交抛物线于点N ,使点M 、N 、C 、E 是平行四边形的四个顶点?若存在,求点M 的坐标;若不存在,请说明理由;(3)设点P 是直线AB 下方抛物线上的一动点,当PAB ∆面积最大时,求点P 的坐标,并求PAB ∆面积的最大值.3.如图,抛物线25(0)y ax bx a =+-≠经过x 轴上的点A (1,0)和点B 及y 轴上的点C ,经过B 、C 两点的直线为y x n =+.试卷第2页,总14页……订…………○……※※内※※答※※题※※……订…………○……①求抛物线的解析式.②点P 从A 出发,在线段AB 上以每秒1个单位的速度向B 运动,同时点E 从B 出发,在线段BC 上以每秒2个单位的速度向C 运动.当其中一个点到达终点时,另一点也停止运动.设运动时间为t 秒,求t 为何值时,△PBE 的面积最大并求出最大值. ③过点A 作AM BC ⊥于点M ,过抛物线上一动点N (不与点B 、C 重合)作直线AM 的平行线交直线BC 于点Q .若点A 、M 、N 、Q 为顶点的四边形是平行四边形,求点N 的横坐标.4.如图,在平面直角坐标系中,已知抛物线22(0)y ax bx a =++≠与x 轴交于()1,0A -),()3,0B 两点,与y 轴交于点C ,连接BC .(1)求该抛物线的解析式,并写出它的对称轴;(2)点D 为抛物线对称轴上一点,连接CD BD 、,若DCB CBD ∠=∠,求点D 的坐标;(3)已知()1,1F ,若(),E x y 是抛物线上一个动点(其中12x <<),连接CE CF EF 、、,求CEF ∆面积的最大值及此时点E 的坐标.(4)若点N 为抛物线对称轴上一点,抛物线上是否存在点M ,使得以,,,B C M N 为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点M 的坐标;若不存在,请说明理由.试卷第3页,总14页…○…………外………………订…………………线…………○……___________考号:______…○…………内………………订…………………线…………○……5.如图1,在Rt △ABC 中,∠A =90°,AB =AC ,点D ,E 分别在边AB ,AC 上,AD =AE ,连接DC ,点M ,P ,N 分别为DE ,DC ,BC 的中点.(1)观察猜想:图1中,线段PM 与PN 的数量关系是 ,位置关系是 ; (2)探究证明:把△ADE 绕点A 逆时针方向旋转到图2的位置,连接MN ,BD ,CE ,判断△PMN 的形状,并说明理由;(3)拓展延伸:把△ADE 绕点A 在平面内自由旋转,若AD =4,AB =10,请直接写出△PMN 面积的最大值.6.已知抛物线y =a (x ﹣1)2过点(3,4),D 为抛物线的顶点. (1)求抛物线的解析式;(2)若点B 、C 均在抛物线上,其中点B (0,1),且∠BDC =90°,求点C 的坐标: (3)如图,直线y =kx +1﹣k 与抛物线交于P 、Q 两点,∠PDQ =90°,求△PDQ 面积的最小值.7.如图,抛物线y =ax 2+bx+c 经过A (0,3)、B (﹣1,0)、D (2,3),抛物线与x试卷第4页,总14页装…………○……………○…………线※要※※在※※装※※订※答※※题※※装…………○……………○…………线轴的另一交点为E ,点P 为直线AE 上方抛物线上一动点,设点P 的横坐标为t . (1)求抛物线的表达式;(2)当t 为何值时,△PAE 的面积最大?并求出最大面积;(3)是否存在点P 使△PAE 为直角三角形?若存在,求出t 的值;若不存在,说明理由.8.如图,四边形ABCD 是边长为2,一个锐角等于60°的菱形纸片,小芳同学将一个三角形纸片的一个顶点与该菱形顶点D 重合,按顺时针方向旋转三角形纸片,使它的两边分别交CB 、BA (或它们的延长线)于点E 、F ,∠EDF=60°,当CE=AF 时,如图1小芳同学得出的结论是DE=DF .(1)继续旋转三角形纸片,当CE≠AF 时,如图2小芳的结论是否成立?若成立,加以证明;若不成立,请说明理由;(2)再次旋转三角形纸片,当点E 、F 分别在CB 、BA 的延长线上时,如图3请直接写出DE 与DF 的数量关系;(3)连EF ,若△DEF 的面积为y ,CE=x ,求y 与x 的关系式,并指出当x 为何值时,y 有最小值,最小值是多少?9.已知ABC 和ADE 都是等腰三角形,AB AC =,AD AE =,DAE BAC ∠=∠. (初步感知)(1)特殊情形:如图①,若点D ,E 分别在边AB ,AC 上,则DB __________EC .(填>、<或=)试卷第5页,总14页…………○………………○………………○…………………○……学校:____:___________班级:____:___________…………○………………○………………○…………………○……(2)发现证明:如图②,将图①中的ADE 绕点A 旋转,当点D 在ABC 外部,点E 在ABC 内部时,求证:DB EC =.(深入研究)(3)如图③,ABC 和ADE 都是等边三角形,点C ,E ,D 在同一条直线上,则CDB ∠的度数为__________;线段CE ,BD 之间的数量关系为__________.(4)如图④,ABC 和ADE 都是等腰直角三角形,90BAC DAE ∠=∠=︒,点C 、D 、E 在同一直线上,AM 为ADE 中DE 边上的高,则CDB ∠的度数为__________;线段AM ,BD ,CD 之间的数量关系为__________.(拓展提升)(5)如图⑤,ABC 和ADE 都是等腰直角三角形,90BAC DAE ∠=∠=︒,将ADE 绕点A 逆时针旋转,连结BE 、CD .当5AB =,2AD =时,在旋转过程中,ABE △与ADC 的面积和的最大值为__________.试卷第6页,总14页…○…………外………订…………○………………○……※内※※答※※题※※…○…………内………订…………○………………○……10.如图,在平面直角坐标系xOy 中,反比例函数(0)m y x x =>的图像经过点34,2A ⎛⎫⎪⎝⎭,点B 在y 轴的负半轴上,AB 交x 轴于点C ,C 为线段AB 的中点.(1)m =________,点C 的坐标为________;(2)若点D 为线段AB 上的一个动点,过点D 作//DE y 轴,交反比例函数图像于点E ,求ODE 面积的最大值.11.如图,直线l :y =﹣3x +3与x 轴、y 轴分别相交于A 、B 两点,抛物线y =ax 2﹣2ax +a +4(a <0)经过点B ,交x 轴正半轴于点C . (1)求该抛物线的函数表达式;(2)已知点M 是抛物线上的一个动点,并且点M 在第一象限内,连接AM 、BM ,设点M 的横坐标为m ,△ABM 的面积为S ,求S 与m 的函数表达式,并求出S 的最大值及此时动点M 的坐标;(3)将点A 绕原点旋转得点A ′,连接CA ′、BA ′,在旋转过程中,一动点M 从点B 出发,沿线段BA ′以每秒3个单位的速度运动到A ′,再沿线段A ′C 以每秒1个单位长度的速度运动到C 后停止,求点M 在整个运动过程中用时最少是多少?12.(问题提出)试卷第7页,总14页……○…………外装…………○……姓名:___________班级:____……○…………内装…………○……(1)如图①,在等腰Rt ABC 中,斜边4AC =,点D 为AC 上一点,连接BD ,则BD 的最小值为 .(问题探究)(2)如图2,在ABC 中,5AB AC ==,6BC =,点M 是BC 上一点,且4BM =,点P 是边AB 上一动点,连接PM ,将BPM △沿PM 翻折得到DPM △,点D 与点B 对应,连接AD ,求AD 的最小值.(问题解决)(3)如图③,四边形ABCD 是规划中的休闲广场示意图,其中135BAD ADC ∠=∠=︒,30DCB ∠=︒,AD =,3AB km =,点M 是BC 上一点,4MC km =.现计划在四边形ABCD 内选取一点P ,把DCP 建成商业活动区,其余部分建成景观绿化区.为方便进入商业区,需修建小路BP 、MP ,从实用和美观的角度,要求满足PMB ABP ∠=∠,且景观绿化区面积足够大,即DCP 区域面积尽可能小.则在四边形ABCD 内是否存在这样的点P ?若存在,请求出DCP 面积的最小值;若不存在,请说明理由.13.在平面直角坐标系中,点O 是原点,四边形AOBC 是矩形,点(5,0)A ,点(0,3)B .以点A 为中心,顺时针旋转矩形AOBC ,得到矩形ADEF ,点O B C ,,的对应点分别为D E F ,,.(1)如图①,当点D 落在BC 边上时,求点D 的坐标;(2)如图②,当点D 落在线段BE 上时,AD 与BC 交于点H .求点H 的坐标; (3)记K 为矩形AOBC 对角线的交点,S 为KDE 的面积,求S 的取值范围(直接写出结果即可).试卷第8页,总14页……外…………○……………订…………○…※※请※※线※※内※※答※※题※※……内…………○……………订…………○…14.(1)如图1,四边形ABCD 中,//AD BC ,点E 为DC 边的中点,连接AE 并延长交BC 的延长线于点F ,求证:ABF ABCD S S ∆=四边形.(S 表示面积)(2)如图2,在ABC ∆中,过AC 边的中点P 任意作直线EF ,交BC 边于点F ,交BA 的延长线于点E ,试比较EBF ∆与ABC ∆的面积,并说明理由.(3)如图3,在平面直角坐标系中,已知一次函数y kx b =+的图像过点()2,4P 且分别于x 轴正半轴,y 轴正半轴交于点A 、B ,请问AOB ∆的面积是否存在最小值?若存在,求出此时一次函数关系式;若不存在,请说明理由.15.△ABC 为等边三角形,AB =8,AD ⊥BC 于点D ,E 为线段AD 上一点,AE =.以AE 为边在直线AD 右侧构造等边三角形AEF ,连接CE ,N 为CE 的中点. (1)如图1,EF 与AC 交于点G ,连接NG ,求线段NG 的长;(2)如图2,将△AEF 绕点A 逆时针旋转,旋转角为α,M 为线段EF 的中点,连接DN ,MN .当30°<α<120°时,猜想∠DNM 的大小是否为定值,并证明你的结论; (3)连接BN .在△AEF 绕点A 逆时针旋转过程中,当线段BN 最大时,请直接写出△ADN 的面积.16.如图,已知A ,B 是线段MN 上的两点,4MN =,1MA =,1MB >,以A 为中心顺时针旋转点M ,以B 为中心逆时针旋转点N ,使M ,N 两点重合成一点C ,构成ABC ,设AB x =.试卷第9页,总14页…外…………○………………○…………订………○……学校:_____名:___________班级:___________考号…内…………○………………○…………订………○……(1)求x 的取值范围; (2)求ABC 面积的最大值.17.在平面直角坐标系中,抛物线265y x mx =-+与y 轴的交点为A ,与x 轴的正半轴分别交于点B (b ,0),C (c ,0).(1)当b =1时,求抛物线相应的函数表达式;(2)当b =1时,如图,E (t ,0)是线段BC 上的一动点,过点E 作平行于y 轴的直线l 与抛物线的交点为P .求△APC 面积的最大值;(3)当c =b + n .时,且n 为正整数.线段BC (包括端点)上有且只有五个点的横坐标是整数,求b 的值.18.如图,抛物线2y ax bx c =++与坐标轴交于点()()()0, 31,03,0A B E --、、,点P 为抛物线上动点,设点P 的横坐标为t .(1)若点C 与点A 关于抛物线的对称轴对称,求C 点的坐标及抛物线的解析式; (2)若点P 在第四象限,连接PA PE 、及AE ,当t 为何值时,PAE ∆的面积最大?最大面积是多少?(3)是否存在点P ,使PAE ∆为以AE 为直角边的直角三角形,若存在,直接写出点P试卷第10页,总14页…外…………○…※…内…………○…的坐标;若不存在,请说明理由. 19.综合与实践问题情境:在综合与实践课上,老师让同学们以“两个大小不等的等腰直角三角板的直角顶点重合,并让一个三角板固定,另一个绕直角顶点旋转”为主题开展数学活动,如图1,三角板ABC 和三角板CDE 都是等腰直角三角形,90C ∠=︒,点D ,E 分别在边BC ,AC 上,连接AD ,点M ,P ,N 分别为DE ,AD ,AB 的中点.试判断线段PM 与PN 的数量关系和位置关系.探究展示:勤奋小组发现,PM PN =,PM PN ⊥.并展示了如下的证明方法:∵点P ,N 分别是AD ,AB 的中点,∴PNBD ,12PN BD =. ∵点P ,M 分别是AD ,DE 的中点,∴PM AE ∥,12PM AE =.(依据1)∵CA CB =,CD CE =,∴BD AE =,∴PM PN =. ∵PNBD ,∴DPN ADC ∠=∠.∵PM AE ∥,∴DPM DAC ∠=∠.∵90BCA ∠=︒,∴90ADC CAD ∠+∠=︒.(依据2)∴90MPN DPM DPN CAD ADC ∠=∠+∠=∠+∠=︒.∴PM PN ⊥. 反思交流:(1)①上述证明过程中的“依据1”,“依据2”分别是指什么? ②试判断图1中,MN 与AB 的位置关系,请直接回答,不必证明;(2)创新小组受到勤奋小组的启发,继续进行探究,把CDE △绕点C 逆时针方向旋转到如图2的位置,发现PMN 是等腰直角三角形,请你给出证明;(3)缜密小组的同学继续探究,把CDE △绕点C 在平面内自由旋转,当4CD =,10CB =时,求PMN 面积的最大值.20.如图,在平面直角坐标系中,四边形 OABC 为菱形,点 C 的坐标为(4,0),∠AOC = 60°,垂直于 x 轴的直线 l 从 y 轴出发,沿 x 轴正方向以每秒 1 个单位长度的速度运动,设直线 l 与 菱形 OABC 的两边分别交与点 M 、N (点 M 在点 N 的上方).○…………外…………订………………○……级:___________考号:__○…………内…………订………………○……(1)求 A 、B 两点的坐标;(2)设 OMN 的面积为 S ,直线 l 运动时间为 t 秒(0 ≤t ≤6 ),试求 S 与 t 的函数表达 式;(3)在题(2)的条件下,t 为何值时,S 的面积最大?最大面积是多少.21.如图,抛物线y=ax 2+bx+c 经过点A (﹣1,0),C (0,3),抛物线的顶点在直线1x =上.(1)求抛物线的解析式;(2)若点P 为第一象限内抛物线上的一点,设△PBC 的面积为S ,求S 的最大值并求出此时点P 的坐标; 22.综合与探究如图,已知抛物线()20y ax bx c a =++≠与x 轴交于A 、()20B ,两点,与y 轴交于点C ,顶点坐标为点1924D ⎛⎫⎪⎝⎭,. (1)求此抛物线的解析式;(2)点P 为抛物线对称轴上一点,当PA PC +最小时,求点P 坐标;(3)在第一象限的抛物线上有一点M ,当BCM ∆面积最大时,求点M 坐标; (4)在x 轴下方抛物线上有一点H ,ABH ∆面积为6,请直接写出点H 的坐标.○…………装………○…………线…………※※请※※不※※要※※在※※○…………装………○…………线…………23.如图,已知抛物线23y ax bx =++与x 轴交于A 、B 两点,过点A 的直线l 与抛物线交于点C ,其中A 点的坐标是(1,0),C 点坐标是(4,3).(1)求抛物线的解析式;(2)抛物线的对称轴上是否存在点D ,使△BCD 的周长最小?若存在,求出点D 的坐标,若不存在,请说明理由;(3)点P 是抛物线上AC 下方的一个动点,是否存在点p ,使△PAC 的面积最大?若存在,求出点P 的坐标,若不存在,请说明理由.二、填空题24.如图,直线AB 交坐标轴于A(-2,0),B(0,-4),点P 在抛物线1(2)(4)2y x x =--上,则△ABP 面积的最小值为__________.25.如图,在平面直角坐标系xOy 中,半径为2的O 与x 轴的正半轴交于点A ,点B 是O 上一动点,点C 为弦AB 的中点,直线334y x =-与x 轴、y 轴分别交于点D 、E ,则CDE △面积的最小值为________.………○…………装………………订……………线…………○……学校:___________姓名:_级:___________考号:………○…………装………………订……………线…………○……26.如图,30AOB ∠=,C 是BO 上的一点,4CO =,点P 为AO 上的一动点,点D 为CO 上的一动点,则PC PD +的最小值为 ________,当PC PD +的值取最小值时,则OPC ∆的面积为________.27.如图,已知直线433y x =-与x 轴、y 轴分别交于A ,B 两点,P 是以(0,1)C 为圆心,1为半径的圆上一动点,连接PA ,PB ,当PAB ∆的面积最大时,点P 的坐标为__________.28.如图,在Rt ABC ∆中,90ACB ∠=︒,4AB =,点D ,E 分别在边AB ,AC 上,且2DB AD =,3AE EC =连接BE ,CD ,相交于点O ,则ABO ∆面积最大值为__________.…………装…………○…订…………○……线…………○……※请※※不※※要※※在※※装※※订内※※答※※题※※…………装…………○…订…………○……线…………○……29.如图,在△ABC 中,∠ACB =120°,AC =BC =2,D 是AB 边上的动点,连接CD ,将△BCD 绕点C 沿顺时针旋转至△ACE ,连接DE ,则△ADE 面积的最大值=_____.30.如图,∠AOB=45°,点M 、N 分别在射线OA 、OB 上,MN=7,△OMN 的面积为14,P 是直线MN 上的动点,点P 关于OA 对称的点为P 1,点P 关于OB 对称点为P 2,当点P 在直线NM 上运动时,△OP 1P 2的面积最小值为_____参考答案1.(1)抛物线的表达式为:223y x x =--;(2)POD S ∆有最大值,当14m =时,其最大值为4916;(3) Q -或(或1122⎛-+- ⎝⎭或⎝⎭. 【分析】(1)函数的表达式为:y=a (x+1)(x-3),将点D 坐标代入上式,即可求解; (2)设点()2,23P m m m --,求出32OG m =+,根据()12POD D P S OG x x ∆=⨯-1(32)(2)2m m =+-2132m m =-++,利用二次函数的性质即可求解; (3)分∠ACB=∠BOQ 、∠BAC=∠BOQ ,两种情况分别求解,通过角的关系,确定直线OQ 倾斜角,进而求解. 【详解】解:(1)函数的表达式为:(1)(3)y a x x =+-,将点D 坐标代入上式并解得:1a =, 故抛物线的表达式为:223y x x =--…①;(2)设直线PD 与y 轴交于点G ,设点()2,23P m m m --,将点P 、D 的坐标代入一次函数表达式:y sx t =+并解得,直线PD 的表达式为:32y mx m =--,则32OG m =+, ()12POD D P S OG x x ∆=⨯-1(32)(2)2m m =+-2132m m =-++,∵10-<,故POD S ∆有最大值,当14m =时,其最大值为4916; (3)∵3OB OC ==,∴45OCB OBC ︒∠=∠=,∵ABC OBE ∠=∠,故OBE ∆与ABC ∆相似时,分为两种情况:①当ACB BOQ ∠=∠时,4AB =,BC =AC = 过点A 作AH ⊥BC 与点H ,1122ABC S AH BC AB OC ∆=⨯⨯=⨯,解得:AH =,∴CH 则tan 2ACB ∠=,则直线OQ 的表达式为: 2 y x =-…②,联立①②并解得:x =故点Q -或(; ②BAC BOQ ∠=∠时,3tan 3tan 1OC BAC BOQ OA ∠====∠, 则直线OQ 的表达式为: 3 y x =-…③,联立①③并解得:x =故点13,22Q ⎛⎫-+- ⎪ ⎪⎝⎭或1322⎛⎫-+ ⎪ ⎪⎝⎭;综上,点Q -或(或1122⎛-+- ⎝⎭或13,22⎛-+ ⎝⎭. 【点睛】本题考查的是二次函数综合运用,涉及到解直角三角形、三角形相似、面积的计算等,其中(3),要注意分类求解,避免遗漏.2.(1)抛物线的解析式为223y x x =--,直线AB 的解析式为3y x =-,(2)(2,1)-或33(22+-+.(3)当32m =时,PAB∆面积的最大值是278,此时P 点坐标为33(,)22-. 【解析】 【分析】(1)将(0,3)A -、(3,0)B 两点坐标分别代入二次函数的解析式和一次函数解析式即可求解;(2)先求出C 点坐标和E 点坐标,则2CE =,分两种情况讨论:①若点M 在x 轴下方,四边形CEMN 为平行四边形,则CE MN =,②若点M 在x 轴上方,四边形CENM 为平行四边形,则CE MN =,设(,3)M a a -,则2(,23)N a a a --,可分别得到方程求出点M 的坐标;(3)如图,作//PG y 轴交直线AB 于点G ,设2(,23)P m m m --,则(,3)G m m -,可由12PAB S PG OB ∆=,得到m 的表达式,利用二次函数求最值问题配方即可. 【详解】解:(1)∵抛物线22y ax x c =-+经过(0,3)A -、(3,0)B 两点,∴9603a c c -+=⎧⎨=-⎩,∴13a c =⎧⎨=-⎩,∴抛物线的解析式为223y x x =--, ∵直线y kx b =+经过(0,3)A -、(3,0)B 两点,∴303k b b +=⎧⎨=-⎩,解得:k 1b 3=⎧⎨=-⎩,∴直线AB 的解析式为3y x =-,(2)∵2223(1)4y x x x =--=--,∴抛物线的顶点C 的坐标为(1,4)-, ∵//CE y 轴, ∴(1,2)E -, ∴2CE =,①如图,若点M 在x 轴下方,四边形CEMN 为平行四边形,则CE MN =, 设(,3)M a a -,则2(,23)N a a a --,∴223(23)3MN a a a a a =----=-+, ∴232a a -+=,解得:2a =,1a =(舍去), ∴(2,1)M -,②如图,若点M 在x 轴上方,四边形CENM 为平行四边形,则CE MN =,设(,3)M a a -,则2(,23)N a a a --,∴2223(3)3MN a a a a a =----=-, ∴232a a -=,解得:a =,a =(舍去),∴M ,综合可得M 点的坐标为(2,1)-或33(22+-+. (3)如图,作//PG y 轴交直线AB 于点G ,设2(,23)P m m m --,则(,3)G m m -, ∴223(23)3PG m m m m m =----=-+, ∴22211393327(3)3()2222228PAB PGA PGB S S S PG OB m m m m m ∆∆∆=+==⨯-+⨯=-+=--+, ∴当32m =时,PAB ∆面积的最大值是278,此时P 点坐标为33(,)22-.【点睛】本题是二次函数综合题,考查了待定系数法求函数解析式,二次函数求最值问题,以及二次函数与平行四边形、三角形面积有关的问题.3.①265y x x =-+-;②当2t =时,△PBE 的面积最大,最大值为;③点N 的横坐标为:4或52+或52.【解析】 【分析】①点B 、C 在直线为y x n =+上,则B (﹣n ,0)、C (0,n ),点A (1,0)在抛物线上,所以250505a b an bn n +-=⎧⎪+-=⎨⎪=-⎩,解得1a =-,6b =,因此抛物线解析式:265y x x =-+-; ②先求出点P 到BC 的高h为sin 45)BP t ︒=-,于是211)22)22PBE S BE h t t t ∆=⋅=-⨯=-+2t =时,△PBE 的面积最大,最大值为③由①知,BC 所在直线为:5y x =-,所以点A 到直线BC的距离d =N 作x轴的垂线交直线BC 于点P ,交x 轴于点H .设()2,65N m m m -+-,则(,0)H m 、(,5)P m m -,易证△PQN为等腰直角三角形,即NQ PQ ==4PN =,Ⅰ.4NH HP +=,所以265(5)4m m m -+---=解得11m =(舍去),24m =,Ⅱ.4NH HP +=,()25654m m m ---+-=解得152m +=,252m =(舍去),Ⅲ.4NH HP -=,()265[(5)]4m m m --+----=,解得152m =(舍去),252m =.【详解】解:①∵点B 、C 在直线为y x n =+上, ∴B(﹣n ,0)、C (0,n ), ∵点A (1,0)在抛物线上,∴250505a b an bn n +-=⎧⎪+-=⎨⎪=-⎩, ∴1a =-,6b =,∴抛物线解析式:265y x x =-+-;②由题意,得,4PB t =-,2BE t =,由①知,45OBC ︒∠=,∴点P 到BC 的高h 为sin 45)2BP t ︒=-,∴211(4)2(2)2222PBE S BE h t t t ∆=⋅=⨯-⨯=-+当2t =时,△PBE 的面积最大,最大值为③由①知,BC 所在直线为:5y x =-,∴点A 到直线BC 的距离d =过点N 作x 轴的垂线交直线BC 于点P ,交x 轴于点H .设()2,65N m m m -+-,则(,0)H m 、(,5)P m m -,易证△PQN 为等腰直角三角形,即NQ PQ ==∴4PN =,Ⅰ.4NH HP +=,∴265(5)4m m m -+---=解得11m =,24m =,∵点A 、M 、N 、Q 为顶点的四边形是平行四边形,∴4m =;Ⅱ.4NH HP +=,∴()25654m m m ---+-=解得152m =,252m =, ∵点A 、M 、N 、Q 为顶点的四边形是平行四边形,5m >,∴m =,Ⅲ.4NH HP -=,∴()265[(5)]4m m m --+----=,解得1m =,2m = ∵点A 、M 、N 、Q 为顶点的四边形是平行四边形,0m <,∴52m =,综上所述,若点A 、M 、N 、Q 为顶点的四边形是平行四边形,点N 的横坐标为:4或52或52-. 【点睛】本题考查了二次函数,熟练掌握二次函数的性质、平行四边形的判定与性质是解题的关键.4.(1)224233y x x =-++,对称轴1x =;(2)11,4D ⎛⎫ ⎪⎝⎭;(3)面积有最大值是4948,755,424E ⎛⎫ ⎪⎝⎭;(4)存在点M 使得以,,,B C M N 为顶点的四边形是平行四边形,()2,2M 或104,3M ⎛⎫- ⎪⎝⎭或102,3M ⎛⎫-- ⎪⎝⎭. 【解析】【分析】(1)将点A (-1,0),B (3,0)代入y=ax 2+bx+2即可;(2)过点D 作DG ⊥y 轴于G ,作DH ⊥x 轴于H ,设点D (1,y ),在Rt △CGD 中,CD 2=CG 2+GD 2=(2-y )2+1,在Rt △BHD 中,BD 2=BH 2+HD 2=4+y 2,可以证明CD=BD ,即可求y 的值; (3)过点E 作EQ ⊥y 轴于点Q ,过点F 作直线FR ⊥y 轴于R ,过点E 作FP ⊥FR 于P ,证明四边形QRPE 是矩形,根据S △CEF =S 矩形QRPE -S △CRF -S △EFP ,代入边即可;(4)根据平行四边形对边平行且相等的性质可以得到存在点M 使得以B ,C ,M ,N 为顶点的四边形是平行四边形,点M (2,2)或M (4,-103)或M (-2,-103); 【详解】 解:(1)将点()()1,0,3,0A B -代入22y ax bx =++, 可得24,33a b =-=, 224233y x x ∴=-++; ∴对称轴1x =;(2)如图1:过点D 作DG y ⊥轴于G ,作DH x ⊥轴于H ,设点()1,D y ,()()0,2,3,0C B ,∴在Rt CGD ∆中,()222221CD CG GD y =+=-+,∴在Rt BHD ∆中,22224BD BH HD y =+=+,在BCD ∆中,DCB CBD ∠=∠CD BD ∴=,22CD BD ∴=()22214y y ∴-+=+14y ∴=, 11,4D ⎛⎫∴ ⎪⎝⎭;(3)如图2:过点E 作EQ y ⊥轴于点Q ,过点F 作直线FR y ⊥轴于R ,过点E 作FP FR ⊥于P ,90EQR QRP RPE ︒∴∠=∠=∠=,∴四边形QRPE 是矩形,CEF CRF EFP QRPE S S S S ∆∆∆=--矩形,()()(),,0,2,1,1E x y C F ,111•222CEF SEQ QR EQ QC CR RF FP EP ∴=⋅-⨯⋅-⋅- ()()()()111121111222CEF S x y x y x y ∆∴=----⨯⨯--- 224233y x x =-++, 21736CEF S x x ∆∴=-+ ∴当74x =时,面积有最大值是4948, 此时755,424E ⎛⎫ ⎪⎝⎭; (4)存在点M 使得以,,,B C M N 为顶点的四边形是平行四边形,设()()1,,,N n M x y ,①四边形CMNB 是平行四边形时,1322x += 2x ∴=-102,3M ⎛⎫∴-- ⎪⎝⎭ ②四边形CNBM 时平行四边形时,3122x += 2x ∴=,()2,2M ∴;③四边形CNNB 时平行四边形时,1322x +=, 4x ∴=,104,3M ⎛⎫∴- ⎪⎝⎭; 综上所述:()2,2M 或104,3M ⎛⎫-⎪⎝⎭或102,3M ⎛⎫-- ⎪⎝⎭; 【点睛】本题考查了待定系数法求二次函数解析式,二次函数的图象及性质,勾股定理,平行四边形的判定与性质,及分类讨论的数学思想.熟练掌握二次函数的性质、灵活运用勾股定理求边长、掌握平行四边形的判定方法是解题的关键.5.(1)PM =PN ,PM ⊥PN ;(2)△PMN 是等腰直角三角形.理由见解析;(3)S △PMN 最大=492. 【分析】(1)由已知易得BD CE =,利用三角形的中位线得出12PM CE =,12PN BD =,即可得出数量关系,再利用三角形的中位线得出//PM CE 得出DPM DCA ∠=∠,最后用互余即可得出位置关系;(2)先判断出ABD ACE ∆≅∆,得出BD CE =,同(1)的方法得出12PM BD =,12PN BD =,即可得出PM PN =,同(1)的方法由MPN DCE DCB DBC ACB ABC ∠=∠+∠+∠=∠+∠,即可得出结论;(3)方法1:先判断出MN 最大时,PMN ∆的面积最大,进而求出AN ,AM ,即可得出MN 最大AM AN =+,最后用面积公式即可得出结论.方法2:先判断出BD 最大时,PMN ∆的面积最大,而BD 最大是14AB AD +=,即可得出结论.【详解】解:(1)点P ,N 是BC ,CD 的中点,//PN BD ∴,12PN BD =, 点P ,M 是CD ,DE 的中点, //PM CE ∴,12PM CE =, AB AC =,AD AE =,BD CE ∴=,PM PN ∴=,//PN BD ,DPN ADC ∴∠=∠,//PM CE ,DPM DCA ∴∠=∠,90BAC ∠=︒,90ADC ACD ∴∠+∠=︒,90MPN DPM DPN DCA ADC ∴∠=∠+∠=∠+∠=︒,PM PN ∴⊥,故答案为:PM PN =,PM PN ⊥;(2)PMN ∆是等腰直角三角形.由旋转知,BAD CAE ∠=∠,AB AC =,AD AE =,()ABD ACE SAS ∴∆≅∆,ABD ACE ∴∠=∠,BD CE =, 利用三角形的中位线得,12PN BD =,12PM CE =, PM PN ∴=,PMN ∴∆是等腰三角形,同(1)的方法得,//PM CE ,DPM DCE ∴∠=∠,同(1)的方法得,//PN BD ,PNC DBC ∴∠=∠,DPN DCB PNC DCB DBC ∠=∠+∠=∠+∠,MPN DPM DPN DCE DCB DBC ∴∠=∠+∠=∠+∠+∠BCE DBC ACB ACE DBC =∠+∠=∠+∠+∠ACB ABD DBC ACB ABC =∠+∠+∠=∠+∠,90BAC ∠=︒,90ACB ABC ∴∠+∠=︒,90MPN ∴∠=︒,PMN ∴∆是等腰直角三角形;(3)方法1:如图2,同(2)的方法得,PMN ∆是等腰直角三角形,MN ∴最大时,PMN ∆的面积最大,//DE BC ∴且DE 在顶点A 上面,MN ∴最大AM AN =+,连接AM ,AN ,在ADE ∆中,4AD AE ==,90DAE ∠=︒,AM ∴=在Rt ABC ∆中,10AB AC ==,AN =MN ∴==最大,22211114922242PMN S PM MN ∆∴==⨯=⨯=最大.方法2:由(2)知,PMN ∆是等腰直角三角形,12PM PN BD ==, PM ∴最大时,PMN ∆面积最大,∴点D 在BA 的延长线上,14BD AB AD ∴=+=,7PM ∴=,2211497222PMN S PM ∆∴==⨯=最大. 【点睛】此题属于几何变换综合题,主要考查了三角形的中位线定理,等腰直角三角形的判定和性质,全等三角形的判断和性质,直角三角形的性质的综合运用;解(1)的关键是判断出12PM CE =,12PN BD =,解(2)的关键是判断出ABD ACE ∆≅∆,解(3)的关键是判断出MN 最大时,PMN ∆的面积最大.6.(1)y =(x ﹣1)2;(2)点C 的坐标为(2,1);(3)1【分析】(1)将点(3,4)代入解析式求得a 的值即可;(2)设点C 的坐标为(x 0,y 0),其中y 0=(x 0﹣1)2,作CF ⊥x 轴,证△BDO ∽△DCF 得BO DF DO CF=,即1=00x 1y -=()01x 1-,据此求得x 0的值即可得; (3)过点D 作x 轴的垂线交直线PQ 于点G ,则DG =4,根据S △PDQ =12DG•MN 列出关于k 的等式求解可得.【详解】解:(1)将点(3,4)代入解析式,得:4a =4,解得:a =1,所以抛物线解析式为y =(x ﹣1)2;(2)由(1)知点D 坐标为(1,0),设点C 的坐标为(x 0,y 0),(x 0>1、y 0>0),则y 0=(x 0﹣1)2,如图1,过点C 作CF ⊥x 轴,∴∠BOD =∠DFC =90°,∠DCF+∠CDF =90°,∵∠BDC =90°,∴∠BDO+∠CDF =90°,∴∠BDO =∠DCF ,∴△BDO ∽△DCF , ∴BO DF DO CF=, ∴1=00x 1y -=()01x 1-,解得:x 0=2,此时y 0=1,∴点C 的坐标为(2,1).(3)设点P 的坐标为(x 1,y 1),点Q 为(x 2,y 2),(其中x 1<1<x 2,y 1>0,y 2>0), 如图2,分别过点P 、Q 作x 轴的垂线,垂足分别为M 、N ,由y=(x-1)2 ,y=kx+1-k ,得x 2﹣(2+k )x+k =0.∴x 1+x 2=2+k ,x 1•x 2=k .∴MN =|x 1﹣x 2|=|2﹣k|.则过点D作x轴的垂线交直线PQ于点G,则点G的坐标为(1,1),所以DG=1,∴S△PDQ=12DG•MN=12×1×|x1﹣x2|=12|2﹣k|,∴当k=0时,S△PDQ取得最小值1.【点睛】本题主要考查二次函数的综合问题,解题的关键是熟练掌握待定系数法求函数解析式、相似三角形的判定与性质及一元二次方程根与系数的关系等知识点.7.(1)y=﹣x2+2x+3;(2)t=32时,△PAE的面积最大,最大值是278;(3)t的值为1.【分析】(1)由A、B、C三点的坐标,利用待定系数法可求得抛物线解析式;(2)由抛物线的对称性可求得E点坐标,从而可求得直线EA的解析式,作PM∥y轴,交直线AE于点M,则可用t表示出PM的长,从而可表示出△PAE的面积,再利用二次函数的性质可求得其最大值即可;(3)由题意可知有∠PAE=90°或∠APE=90°两种情况,当∠PAE=90°时,作PG⊥y轴,利用等腰直角三角形的性质可得到关于t的方程,可求得t的值;当∠APE=90°时,作PK⊥x 轴,AQ⊥PK,则可证得△PKE∽△AQP,利用相似三角形的性质可得到关于t的方程,可求得t的值.【详解】解:(1)由题意得:0 4233a b ca b cc-+=⎧⎪++=⎨⎪=⎩,解得:123abc=-⎧⎪=⎨⎪=⎩,∴抛物线解析式为y=﹣x2+2x+3;(2)∵A(0,3),D(2,3),∴抛物线对称轴为x=1,∴E(3,0),设直线AE的解析式为y=kx+3,∴3k+3=0,解得,k=﹣1,∴直线AE的解析式为y=﹣x+3,如图1,作PM∥y轴,交直线AE于点M,设P(t,﹣t2+2t+3),M(t,﹣t+3),∴PM=﹣t2+2t+3+t﹣3=﹣t2+3t,∴12PAE PMA PMES S S PM OE=+=⋅=()21332t t⨯⨯-+=23327228t⎛⎫--+⎪⎝⎭,∴t=32时,△PAE的面积最大,最大值是278.(3)由图可知∠PEA≠90°,∴只能有∠PAE=90°或∠APE=90°,①当∠PAE=90°时,如图2,作PG⊥y轴,∵OA=OE,∴∠OAE=∠OEA=45°,∴∠PAG=∠APG=45°,∴PG=AG,∴t =﹣t 2+2t+3﹣3,即﹣t 2+t =0,解得t =1或t =0(舍去), ②当∠APE =90°时,如图3,作PK ⊥x 轴,AQ ⊥PK ,则PK =﹣t 2+2t+3,AQ =t ,KE =3﹣t ,PQ =﹣t 2+2t+3﹣3=﹣t 2+2t , ∵∠APQ+∠KPE =∠APQ+∠PAQ =90°, ∴∠PAQ =∠KPE ,且∠PKE =∠PQA , ∴△PKE ∽△AQP , ∴PK KEAQ PQ=, ∴222332t t t t t t-++-=-+,即t 2﹣t ﹣1=0,解得:t 或t 0(舍去),综上可知存在满足条件的点P ,t 的值为1或12+. 【点睛】本题考查了待定系数法求二次函数解析式、二次函数与几何面积最值问题以及二次函数与特殊三角形的问题,解题的关键是灵活运用二次函数的性质及几何知识.8.(1)成立,证明见解析;(2)DF=DE .(3)当x=0时,y 最小值 【分析】(1)如图1,连接BD .根据题干条件首先证明∠ADF=∠BDE ,然后证明△ADF ≌△BDE (ASA ),得DF=DE ;(2)如图2,连接BD .根据题干条件首先证明∠ADF=∠BDE ,然后证明△ADF ≌△BDE(ASA ),得DF=DE ;(3)根据(2)中的△ADF ≌△BDE 得到:S △ADF =S △BDE ,AF=BE .所以△DEF 的面积转化为:y=S △BEF +S △ABD .据此列出y 关于x 的二次函数,通过求二次函数的最值来求y 的最小值. 【详解】(1)DF=DE .理由如下: 如图1,连接BD .∵四边形ABCD 是菱形, ∴AD=AB . 又∵∠A=60°,∴△ABD 是等边三角形, ∴AD=BD ,∠ADB=60°, ∴∠DBE=∠A=60° ∵∠EDF=60°, ∴∠ADF=∠BDE . ∵在△ADF 与△BDE 中,ADF BDE AD BDA DBE ∠=⎧∠=∠=∠⎪⎨⎪⎩, ∴△ADF ≌△BDE (ASA ), ∴DF=DE ;(2)DF=DE .理由如下: 如图2,连接BD .∵四边形ABCD 是菱形, ∴AD=AB . 又∵∠A=60°,∴△ABD 是等边三角形, ∴AD=BD ,∠ADB=60°, ∴∠DBE=∠A=60° ∵∠EDF=60°, ∴∠ADF=∠BDE . ∵在△ADF 与△BDE 中,ADF BDE AD BDA DBE ∠=⎧∠=∠=∠⎪⎨⎪⎩, ∴△ADF ≌△BDE (ASA ), ∴DF=DE ;(3)由(2)知,△ADF ≌△BDE .则S △ADF =S △BDE ,AF=BE=x . 依题意得:y=S △BEF +S △ABD =12(2+x )xsin60°+12×2×2sin60°x+1)2.即x+1)20, ∴该抛物线的开口方向向上, ∴当x=0即点E 、B 重合时,y 最小值=29.(1)=;(2)证明见解析;(3)60°,BD=CE ;(4)90°,AM+BD=CM ;(5)7【分析】(1)由DE ∥BC ,得到DB ECAB AC=,结合AB=AC ,得到DB=EC ; (2)由旋转得到的结论判断出△DAB ≌△EAC ,得到DB=CE ;(3)根据等边三角形的性质和全等三角形的判定定理证明△DAB ≌△EAC ,根据全等三角形的性质求出结论;(4)根据全等三角形的判定和性质和等腰直角三角形的性质即可得到结论;(5)根据旋转的过程中△ADE 的面积始终保持不变,而在旋转的过程中,△ADC 的AC 始终保持不变,即可. 【详解】[初步感知](1)∵DE ∥BC , ∴DB ECAB AC=, ∵AB=AC , ∴DB=EC , 故答案为:=, (2)成立.理由:由旋转性质可知∠DAB=∠EAC , 在△DAB 和△EAC 中AD AE DAB EAC AB AC ⎪∠⎪⎩∠⎧⎨===, ∴△DAB ≌△EAC (SAS ), ∴DB=CE ;[深入探究](3)如图③,设AB ,CD 交于O ,∵△ABC 和△ADE 都是等边三角形, ∴AD=AE ,AB=AC ,∠DAE=∠BAC=60°,∴∠DAB=∠EAC , 在△DAB 和△EAC 中AD AE DAB EAC AB AC ⎪∠⎪⎩∠⎧⎨===, ∴△DAB ≌△EAC (SAS ), ∴DB=CE ,∠ABD=∠ACE , ∵∠BOD=∠AOC , ∴∠BDC=∠BAC=60°;(4)∵△DAE 是等腰直角三角形, ∴∠AED=45°, ∴∠AEC=135°, 在△DAB 和△EAC 中AD AE DAB EAC AB AC ⎪∠⎪⎩∠⎧⎨===, ∴△DAB ≌△EAC (SAS ), ∴∠ADB=∠AEC=135°,BD=CE , ∵∠ADE=45°,∴∠BDC=∠ADB-∠ADE=90°,∵△ADE 都是等腰直角三角形,AM 为△ADE 中DE 边上的高, ∴AM=EM=MD , ∴AM+BD=CM ;故答案为:90°,AM+BD=CM ; 【拓展提升】 (5)如图,由旋转可知,在旋转的过程中△ADE 的面积始终保持不变, △ADE 与△ADC 面积的和达到最大, ∴△ADC 面积最大,∵在旋转的过程中,AC 始终保持不变, ∴要△ADC 面积最大, ∴点D 到AC 的距离最大, ∴DA ⊥AC ,∴△ADE 与△ADC 面积的和达到的最大为2+12×AC×AD=5+2=7, 故答案为7. 【点睛】此题是几何变换综合题,主要考查了旋转和全等三角形的性质和判定,旋转过程中面积变化分析,解本题的关键是三角形全等的判定.10.(1)m=6,()2,0;(2)当a=1时,ODE 面积的最大值为278【分析】(1)将点34,2A ⎛⎫ ⎪⎝⎭代入反比例函数解析式求出m ,根据坐标中点公式求出点C 的横坐标即可;(2)由AC 两点坐标求出直线AB 的解析式为3342y x =-,设D 坐标为33,(04)42D a a a ⎛⎫-<≤ ⎪⎝⎭,则6,E a a ⎛⎫⎪⎝⎭,进而得到2327(1)88ODESa =--+,即可解答【详解】解:(1)把点34,2A ⎛⎫ ⎪⎝⎭代入反比例函数(0)m y x x=>,得:324m =,解得:m=6,∵A 点横坐标为:4,B 点横坐标为0,故C 点横坐标为:4022+=, 故答案为:6,(2,0);(2)设直线AB 对应的函数表达式为y kx b =+.将34,2A ⎛⎫ ⎪⎝⎭,(2,0)C 代入得34220k b k b ⎧+=⎪⎨⎪+=⎩,解得3432k b ⎧=⎪⎪⎨⎪=-⎪⎩. 所以直线AB 对应的函数表达式为3342y x =-. 因为点D 在线段AB 上,可设33,(04)42D a a a ⎛⎫-<≤ ⎪⎝⎭, 因为//DE y 轴,交反比例函数图像于点E .所以6,E a a ⎛⎫ ⎪⎝⎭. 所以221633333273(1)2428488ODESa a a a a a ⎛⎫=⋅⋅-+=-++=--+ ⎪⎝⎭. 所以当a =1时,ODE 面积的最大值为278. 【点睛】本题考查了函数与几何综合,涉及了待定系数法求函数解析式、三角形面积、坐标中点求法、二次函数的应用等知识点,解题关键是用函数解析式表示三角形面积.11.(1)y =﹣x 2+2x +3;(2)S 与m 的函数表达式是S =252m m --,S 的最大值是258,此时动点M 的坐标是(52,74);(3)点M在整个运动过程中用时最少是3秒. 【分析】(1)首先求出B 点的坐标,根据B 点的坐标即可计算出二次函数的a 值,进而即可计算出二次函数的解析式;。
二次函数之三角形面积最大-教师版
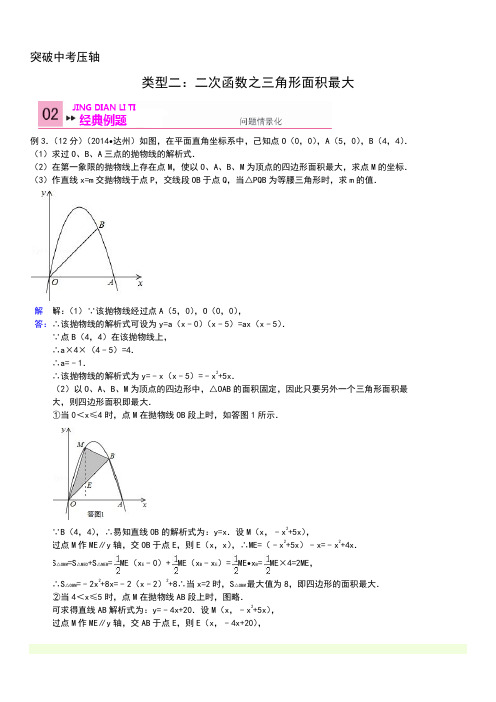
突破中考压轴类型二:二次函数之三角形面积最大例3.(12分)(2014•达州)如图,在平面直角坐标系中,己知点O (0,0),A (5,0),B (4,4). (1)求过O 、B 、A 三点的抛物线的解析式.(2)在第一象限的抛物线上存在点M ,使以O 、A 、B 、M 为顶点的四边形面积最大,求点M 的坐标. (3)作直线x=m 交抛物线于点P ,交线段OB 于点Q ,当△PQB 为等腰三角形时,求m 的值.解答: 解:(1)∵该抛物线经过点A (5,0),O (0,0), ∴该抛物线的解析式可设为y=a (x ﹣0)(x ﹣5)=ax (x ﹣5).∵点B (4,4)在该抛物线上, ∴a×4×(4﹣5)=4. ∴a=﹣1.∴该抛物线的解析式为y=﹣x (x ﹣5)=﹣x 2+5x .(2)以O 、A 、B 、M 为顶点的四边形中,△OAB 的面积固定,因此只要另外一个三角形面积最大,则四边形面积即最大.①当0<x≤4时,点M 在抛物线OB 段上时,如答图1所示.∵B (4,4),∴易知直线OB 的解析式为:y=x .设M (x ,﹣x 2+5x ),过点M 作ME ∥y 轴,交OB 于点E ,则E (x ,x ),∴ME=(﹣x 2+5x )﹣x=﹣x 2+4x . S △OBM =S △MEO +S △MEB =ME (x E ﹣0)+ME (x B ﹣x E )=ME •x B =ME×4=2ME,∴S △OBM =﹣2x 2+8x=﹣2(x ﹣2)2+8∴当x=2时,S △OBM 最大值为8,即四边形的面积最大. ②当4<x≤5时,点M 在抛物线AB 段上时,图略.可求得直线AB 解析式为:y=﹣4x+20.设M (x ,﹣x 2+5x ), 过点M 作ME ∥y 轴,交AB 于点E ,则E (x ,﹣4x+20),∴ME=(﹣x2+5x)﹣(﹣4x+20)=﹣x2+9x﹣20.S△ABM=S△MEB+S△MEA=ME(x E﹣x B)+ME(x A﹣x E)=ME•(x A﹣x B)=ME×1=ME,∴S△ABM=﹣x2+x﹣10=﹣(x﹣)2+∴当x=时,S△ABM最大值为,即四边形的面积最大.比较①②可知,当x=2时,四边形面积最大.当x=2时,y=﹣x2+5x=6,∴M(2,6).(3)由题意可知,点P在线段OB上方的抛物线上.设P(m,﹣m2+5m),则Q(m,m)当△PQB为等腰三角形时,①若点B为顶点,即BP=BQ,如答图2﹣1所示.过点B作BE⊥PQ于点E,则点E为线段PQ中点,∴E(m,).∵BE∥x轴,B(4,4),∴=4,解得:m=2或m=4(与点B重合,舍去)∴m=2;②若点P为顶点,即PQ=PB,如答图2﹣2所示.易知∠BOA=45°,∴∠PQB=45°,则△PQB为等腰直角三角形.∴PB∥x轴,∴﹣m2+5m=4,解得:m=1或m=4(与点B重合,舍去)∴m=1;③若点P为顶点,即PQ=QB,如答图2﹣3所示.∵P(m,﹣m2+5m),Q(m,m),∴PQ=﹣m2+4m.又∵QB=(x B﹣x Q)=(4﹣m),∴﹣m2+4m=(4﹣m),解得:m=或m=4(与点B重合,舍去),∴m=.综上所述,当△PQB为等腰三角形时,m的值为1,2或.例4.(12分)(2013•雅安)如图,已知抛物线y=ax2+bx+c经过A(﹣3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.(1)求该抛物线的解析式;(2)若点P是该抛物线对称轴l上的一个动点,求△PBC周长的最小值;(3)如图(2),若E是线段AD上的一个动点( E与A、D不重合),过E点作平行于y轴的直线交抛物线于点F,交x轴于点G,设点E的横坐标为m,△ADF的面积为S.①求S与m的函数关系式;②S是否存在最大值?若存在,求出最大值及此时点E的坐标;若不存在,请说明理由.解答:解:(1)由题意可知:解得:∴抛物线的解析式为:y=﹣x2﹣2x+3;(2)∵△PBC的周长为:PB+PC+BC∵BC是定值,∴当PB+PC最小时,△PBC的周长最小,∵点A、点B关于对称轴I对称,∴连接AC交l于点P,即点P为所求的点∵AP=BP∴△PBC的周长最小是:PB+PC+BC=AC+BC∵A(﹣3,0),B(1,0),C(0,3),∴AC=3,BC=;(3)①∵抛物线y=﹣x2﹣2x+3顶点D的坐标为(﹣1,4)∵A(﹣3,0)∴直线AD的解析式为y=2x+6 ∵点E的横坐标为m,∴E(m,2m+6),F(m,﹣m2﹣2m+3)∴EF=﹣m2﹣2m+3﹣(2m+6)=﹣m2﹣4m﹣3∴S=S△DEF+S△AEF=EF•GH+EF•AC=EF•AH=(﹣m2﹣4m﹣3)×2=﹣m2﹣4m﹣3;②S=﹣m2﹣4m﹣3=﹣(m+2)2+1;∴当m=﹣2时,S最大,最大值为1此时点E的坐标为(﹣2,2).1.(12分)(2013•攀枝花)如图,抛物线y=ax2+bx+c经过点A(﹣3,0),B(1.0),C(0,﹣3).(1)求抛物线的解析式;(2)若点P为第三象限内抛物线上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;(3)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.解答:解:(1)由于抛物线y=ax2+bx+c经过A(﹣3,0),B(1,0),可设抛物线的解析式为:y=a,解得,∴直线AC的解析式为:y=﹣x﹣3.设P点坐标为(x,x2+2x﹣3),则点N的坐标为(x,﹣x﹣3),∴PN=PE﹣NE=﹣(x2+2x﹣3)+(﹣x﹣3)=﹣x2﹣3x.∵S△PAC=S△PAN+S△PCN,∴S=PN•OA=×3(﹣x2﹣3x)=﹣(x+)2+,∴当x=﹣时,S有最大值,此时点P的坐标为(﹣,﹣);(3)在y轴上是否存在点M,能够使得△ADE是直角三角形.理由如下:∵y=x2+2x﹣3=y=(x+1)2﹣4,∴顶点D的坐标为(﹣1,﹣4),∵A(﹣3,0),∴AD2=(﹣1+3)2+(﹣4﹣0)2=20.设点M的坐标为(0,t),分三种情况进行讨论:①当A为直角顶点时,如图3①,由勾股定理,得AM2+AD2=DM2,即(0+3)2+(t﹣0)2+20=(0+1)2+(t+4)2,解得t=,所以点M的坐标为(0,);②当D为直角顶点时,如图3②,由勾股定理,得DM2+AD2=AM2,即(0+1)2+(t+4)2+20=(0+3)2+(t﹣0)2,解得t=﹣,所以点M的坐标为(0,﹣);③当M为直角顶点时,如图3③,由勾股定理,得AM2+DM2=AD2,即(0+3)2+(t﹣0)2+(0+1)2+(t+4)2=20,解得t=﹣1或﹣3,所以点M的坐标为(0,﹣1)或(0,﹣3);综上可知,在y轴上存在点M,能够使得△ADE是直角三角形,此时点M的坐标为(0,)或(0,﹣)或(0,﹣1)或(0,﹣3).2.(12分)(2013•泸州)如图,在直角坐标系中,点A的坐标为(﹣2,0),点B的坐标为(1,﹣),已知抛物线y=ax2+bx+c(a≠0)经过三点A、B、O(O为原点).(1)求抛物线的解析式;(2)在该抛物线的对称轴上,是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由;(3)如果点P是该抛物线上x轴上方的一个动点,那么△PAB是否有最大面积?若有,求出此时P点的坐标及△PAB 的最大面积;若没有,请说明理由.(注意:本题中的结果均保留根号)解:(1)将A(﹣2,0),B(1,﹣),O(0,0)三点的坐标代入y=ax2+bx+c(a≠0),可得:,解得:,故所求抛物线解析式为y=﹣x2﹣x;(2)存在.理由如下:如答图①所示,∵y=﹣x2﹣x=﹣(x+1)2+,∴抛物线的对称轴为x=﹣1.∵点C在对称轴x=﹣1上,△BOC的周长=OB+BC+CO;∵OB=2,要使△BOC的周长最小,必须BC+CO最小,∵点O与点A关于直线x=﹣1对称,有CO=CA,△BOC的周长=OB+BC+CO=OB+BC+CA,∴当A、C、B三点共线,即点C为直线AB与抛物线对称轴的交点时,BC+CA最小,此时△BOC的周长最小.设直线AB的解析式为y=kx+t,则有:,解得:,∴直线AB的解析式为y=﹣x﹣,当x=﹣1时,y=﹣,∴所求点C的坐标为(﹣1,﹣);(3)设P(x,y)(﹣2<x<0,y<0),则y=﹣x2﹣x ①如答图②所示,过点P作PQ⊥y轴于点Q,PG⊥x轴于点G,过点A作AF⊥PQ轴于点F,过点B作BE⊥PQ 轴于点E,则PQ=﹣x,PG=﹣y,由题意可得:S△PAB=S梯形AFEB﹣S△AFP﹣S△BEP=(AF+BE)•FE﹣AF•FP﹣PE•BE=(y++y)(1+2)﹣y•(2+x)﹣(1﹣x)(+y)=y+x+②将①代入②得:S△PAB=(﹣x2﹣x)+x+=﹣x2﹣x+=﹣(x+)2+∴当x=﹣时,△PAB的面积最大,最大值为,此时y=﹣×+×=,∴点P的坐标为(﹣,).3.(2012眉山)已知:如图,直线与x轴交于C点,与y轴交于A点,B点在x轴上,△OAB是等腰直角三角形.(1)求过A.B.C三点的抛物线的解析式;(2)若直线CD∥AB交抛物线于D点,求D点的坐标;(3)若P点是抛物线上的动点,且在第一象限,那么△PAB是否有最大面积?若有,求出此时P点的坐标和△PAB 的最大面积;若没有,请说明理由.解答:解:(1)令y=3x+3=0得:x=﹣1,故点C的坐标为(﹣1,0);令x=0得:y=3x+3=3×0+3=3故点A的坐标为(0,3);∵△OAB是等腰直角三角形.∴OB=OA=3,∴点B的坐标为(3,0),设过A.B.C三点的抛物线的解析式y=ax2+bx+c,解得:∴解析式为:y=﹣x2+2x+3;(2)设直线AB的解析式为y=kx+b,∴解得:∴直线AB的解析式为:y=﹣x+3∵线CD∥AB∴设直线CD的解析式为y=﹣x+b∵经过点C(﹣1,0),∴﹣(﹣1)+b=0解得:b=﹣1,∴直线CD的解析式为:y=﹣x﹣1,令﹣x+1=﹣x2+2x+3,解得:x=﹣1,或x=4,将x=4代人y=﹣x2+2x+3=﹣16+2×4+3=﹣5,∴点D的坐标为:(4,﹣5);(3)存在.如图1所示,设P(x,y)是第一象限的抛物线上一点,过点P作PN⊥x轴于点N,则ON=x,PN=y,BN=OB﹣ON=3﹣x.S△ABP=S梯形PNOA+S△PNB﹣S△AOB=(OA+PN)•ON+PN•BN﹣OA•OB=(3+y)•x+y•(3﹣x)﹣×3×3=(x+y)﹣,∵P(x,y)在抛物线上,∴y=﹣x2+2x+3,代入上式得:S△ABP=(x+y)﹣=﹣(x2﹣3x)=﹣(x﹣)2+,∴当x=时,S△ABP取得最大值.当x=时,y=﹣x2+2x+3=,∴P(,).所以,在第一象限的抛物线上,存在一点P,使得△ABP的面积最大;P点的坐标为(,).4.(2012•乐山)如图,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,﹣n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(m<n)分别是方程x2﹣2x﹣3=0的两根.(1)求抛物线的解析式;(2)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E两点(点D在y轴右侧),连接OD、BD.①当△OPC为等腰三角形时,求点P的坐标;②求△BOD 面积的最大值,并写出此时点D的坐标.解答:解(1)解方程x2﹣2x﹣3=0,得 x=3,x2=﹣1.∵m<n,∴m=﹣1,n=3…(1分)1∴A(﹣1,﹣1),B(3,﹣3).∵抛物线过原点,设抛物线的解析式为y=ax2+bx.∴解得:,∴抛物线的解析式为.…(4分)(2)①设直线AB的解析式为y=kx+b.∴解得:,∴直线AB的解析式为.∴C点坐标为(0,).…(6分)∵直线OB过点O(0,0),B(3,﹣3),∴直线OB的解析式为y=﹣x.∵△OPC为等腰三角形,∴OC=OP或OP=PC或OC=PC.设P(x,﹣x),(i)当OC=OP时,.解得,(舍去).∴P1(,).(ii)当OP=PC时,点P在线段OC的中垂线上,∴P2(,﹣).(iii)当OC=PC时,由,解得,x2=0(舍去).∴P3(,﹣).∴P点坐标为P1(,)或P2(,﹣)或P3(,﹣).…(9分)②过点D作DG⊥x轴,垂足为G,交OB于Q,过B作BH⊥x轴,垂足为H.设Q(x,﹣x),D(x,).S△BOD=S△ODQ+S△BDQ=DQ•OG+DQ•GH,=DQ(OG+GH),=,=,∵0<x<3,∴当时,S取得最大值为,此时D(,﹣).…(13分)5.(2012攀枝花)如图,在平面直角坐标系xOy中,四边形ABCD是菱形,顶点A.C.D均在坐标轴上,且AB=5,sinB=.(1)求过A.C.D三点的抛物线的解析式;(2)记直线AB的解析式为y1=mx+n,(1)中抛物线的解析式为y2=ax2+bx+c,求当y1<y2时,自变量x的取值范围;(3)设直线AB与(1)中抛物线的另一个交点为E,P点为抛物线上A.E两点之间的一个动点,当P点在何处时,△PAE的面积最大?并求出面积的最大值.解答:解:(1)∵四边形ABCD是菱形,∴AB=AD=CD=BC=5,sinB=sinD=;Rt△OCD中,OC=CD•sinD=4,OD=3;OA=AD﹣OD=2,即:A(﹣2,0)、B(﹣5,4)、C(0,4)、D(3,0);设抛物线的解析式为:y=a(x+2)(x﹣3),得:2×(﹣3)a=4,a=﹣;∴抛物线:y=﹣x2+x+4.(2)由A(﹣2,0)、B(﹣5,4)得直线AB:y1=﹣x﹣;由(1)得:y2=﹣x2+x+4,则:,解得:,;由图可知:当y1<y2时,﹣2<x<5.(3)∵S△APE=AE•h,∴当P到直线AB的距离最远时,S△ABC最大;若设直线L∥AB,则直线L与抛物线有且只有一个交点时,该交点为点P;设直线L:y=﹣x+b,当直线L与抛物线有且只有一个交点时,﹣x+b=﹣x2+x+4,且△=0;求得:b=,即直线L:y=﹣x+;可得点P(,).由(2)得:E(5,﹣),则直线PE:y=﹣x+9;新课标第一网则点F (,0),AF=OA+OF=;∴△PAE的最大值:S△PAE=S△PAF+S△AEF=××(+)=.综上所述,当P(,)时,△PAE的面积最大,为.。
第五讲+抛物线中三角形的面积问题
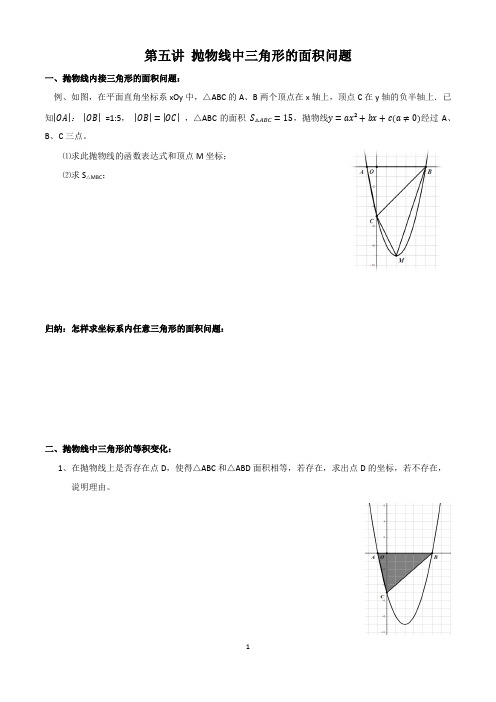
第五讲抛物线中三角形的面积问题一、抛物线内接三角形的面积问题:例、如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax²+bx+c(a≠0)经过A、B、C三点。
⑴求此抛物线的函数表达式和顶点M坐标;⑵求S△MBC;归纳:怎样求坐标系内任意三角形的面积问题:二、抛物线中三角形的等积变化:1、在抛物线上是否存在点D,使得△ABC和△ABD面积相等,若存在,求出点D的坐标,若不存在,说明理由。
2、在抛物线上是否存在点E,使得△ABC和△BCE面积相等,若存在,求出点E的坐标,若不存在,说明理由。
S△ABC。
若存在,求出点M的坐标;若不存在,请说明理由3、在抛物线上是否存在点M,使S△MBC= 134、(2011成都)在抛物线上是否存在异于B、C的点M,使△MBC中BC边上的高为7√?若存在,求出点M的坐标;若不存在,说明理由.5、点P(2,-3)是抛物线对称轴上的一点,在线段OC上有一动点M,以每秒2个单位的速度从O向C 运动,(不与点O,C重合),过点M作MH∥BC,交X轴于点H,设点M的运动时间为t秒,试把△PMH 的面积S表示成t的函数,当t为何值时,S有最大值,并求出最大值;6、在抛物线的对称轴上有一点P的纵坐标为5,在直线上BC求一点M使得S△PBM∶S△ABC=1:5.7、在直线BC下方抛物线上是否存在一个点F,使得△BCF的面积最大,若存在,求出点F的坐标,并求出最大面积,若不存在,说明理由。
练习:1、如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2,与y轴交于点C(0,-4),其中x1,x2是方程x2-4x-12=0的两个根.(1)求A、B两点坐标;(2)求抛物线的解析式;(3)点M是线段AB上的一个动点(不与A、B两点重合),过点M作MN∥BC,交AC于点N,连接CM,在M点运动时,△CMN的面积是否存在最大值?若存在,求出△CMN面积最大时点M的坐标;若不存在,请说明理由.2、(2010玉溪)如图,在平面直角坐标系中,点A的坐标为(1,△AOB(1)求点B的坐标;(2)求过点A、O、B的抛物线的解析式;(4)在(2)中x轴下方的抛物线上是否存在一点P,过点P作x轴的垂线,交直线AB于点D,线段OD 把△AOB分成两个三角形.使其中一个三角形面积与四边形BPOD面积比为2:3 ?若存在,求出点P的坐标;若不存在,请说明理由.yAB。
(完整版)高中数学经典50题(附答案)

高中数学题库1. 求下列函数的值域:解法2 令t =sin x ,则f (t )=-t 2+t +1,∵ |sin x |≤1, ∴ |t |≤1.问题转化为求关于t 的二次函数f (t )在闭区间[-1,1]上的最值.本例题(2)解法2通过换元,将求三角函数的最值问题转化为求二次函数在闭区间上的最值问题,从而达到解决问题的目的,这就是转换的思想.善于从不同角度去观察问题,沟通数学各学科之间的内在联系,是实现转换的关键,转换的目的是将数学问题由陌生化熟悉,由复杂化简单,一句话:由难化易.可见化归是转换的目的,而转换是实现化归段手段。
2. 设有一颗慧星沿一椭圆轨道绕地球运行,地球恰好位于椭圆轨道的焦点处,当此慧星离地球相距m 万千米和m 34万千米时,经过地球和慧星的直线与椭圆的长轴夹角分别为32ππ和,求该慧星与地球的最近距离。
解:建立如下图所示直角坐标系,设地球位于焦点)0,(c F -处,椭圆的方程为12222=+by a x (图见教材P132页例1)。
当过地球和彗星的直线与椭圆的长轴夹角为3π时,由椭圆的几何意义可知,彗星A 只能满足)3(3/ππ=∠=∠xFA xFA 或。
作m FA FB Ox AB 3221B ==⊥,则于故由椭圆第二定义可知得⎪⎪⎩⎪⎪⎨⎧+-=-=)32(34)(22m c c a a c m c ca a c m两式相减得,23)4(21.2,3231c c c m c a m a c m =-==∴⋅=代入第一式得 .32.32m c c a m c ==-∴=∴答:彗星与地球的最近距离为m 32万千米。
说明:(1)在天体运行中,彗星绕恒星运行的轨道一般都是椭圆,而恒星正是它的一个焦点,该椭圆的两个焦点,一个是近地点,另一个则是远地点,这两点到恒星的距离一个是c a -,另一个是.c a +(2)以上给出的解答是建立在椭圆的概念和几何意义之上的,以数学概念为根基充分体现了数形结合的思想。
抛物线上动点p的三角形面积-定义说明解析

抛物线上动点p的三角形面积-概述说明以及解释1.引言1.1 概述在数学中,抛物线是一种具有特定形状的曲线,其形状类似于开口向上的U形。
它是由一个定点和一条直线(称为准线或直线段)确定的曲线,其中定点被称为焦点,准线表示为直线段AB。
抛物线是一种非常重要的曲线,广泛应用于物理学、工程学等领域。
本文将围绕着抛物线上的动点P展开讨论。
在抛物线上,动点P具有自由运动的能力,并且可以在曲线上任意选择不同的位置。
我们将重点研究动点P所形成的三角形的面积,并探究如何计算这个面积。
通过研究动点P在抛物线上的运动以及三角形的面积计算方法,我们可以深入理解抛物线曲线的几何特征,并且可以应用这些知识解决实际问题。
同时,对抛物线上动点P的三角形面积的意义和应用也将在文章中进行探讨。
最后,在总结部分我们将对本文的内容进行总结,并展望未来对抛物线相关问题的研究方向。
本文旨在提供一个清晰的抛物线上动点P三角形面积的计算方法,并希望读者通过阅读本文能够对抛物线的几何特性有更深入的了解。
【1.2 文章结构】本文将分为以下几个部分来探讨抛物线上动点P的三角形面积的计算方法。
每个部分的内容如下:(1)引言:在引言部分,我们将概述本文的主题和研究对象,并介绍文章的结构和目的。
同时,我们也将对抛物线的定义和性质进行简要介绍。
(2)正文:在正文部分,我们将分为三个小节来详细阐述抛物线上动点P的三角形面积的计算方法。
首先,我们会介绍抛物线的定义和性质,包括其数学表达和几何特征。
然后,我们会讨论动点P在抛物线上的运动规律,这一部分将包括动点P在不同位置的情况下的三角形面积的变化规律。
最后,我们将介绍具体的计算方法,包括利用向量、坐标和参数方程等不同的方法来计算动点P的三角形面积。
(3)结论:在结论部分,我们将对前面的研究结果进行总结,并探讨抛物线上动点P的三角形面积的一些意义和应用。
同时,我们也会展望未来可能的研究方向和可进一步发展的领域。
通过以上的安排,我们旨在全面而系统地介绍抛物线上动点P的三角形面积的计算方法,并探讨其应用的可能性,为相关领域的研究和实践提供一定的参考和指导。
椭圆抛物线中有关三角形面积的最值问题

椭圆抛物线中有关三角形面积的最值问题
1.已知点(,0)(0)E m m >是抛物线24y x =内一个定点,过E 作斜率分别为1k 的直线交抛物线于点,A B ,过E 作斜率分别为2k 的直线交抛物线于点,C D ,且,M N 分别为,AB CD 的中点
(1)若121,1m k k ==-,求EMN ∆面积最小值
(2)若121k k +=,求证直线MN 过定点(,2)m
2.已知椭圆C
的中心在原点,一个焦点F
.
(Ⅰ)求椭圆C 的方程;
(Ⅱ)若椭圆C 在第一象限的一点P 的横坐标为1,过点P 作倾斜角互补的两条不同的直线PA ,PB 分别交椭圆C 于另外两点A ,B ,求证:直线AB 的斜率为定值;
(Ⅲ)求PAB ∆面积的最大值.
3. 已知椭圆的离心率为,长轴长为,直线交椭圆于不同的两点A 、B 。
(1)求椭圆的方程;
(2)求的值(O 点为坐标原点);
(3)若坐标原点O 到直线的距离为
,求面积的最大值。
4. 已知椭圆2222:1x y M a b +=(0)a b >>
的离心率为3
,且椭圆上一点与椭圆的两个焦点构成的三角形周长为246+.
(Ⅰ)求椭圆M 的方程;
(Ⅱ)设直线l 与椭圆M 交于,A B 两点,且以AB 为直径的圆过椭圆右顶点C ,求ABC ∆面积最大值. )0(122
22>>=+b a b
y a x 3632m kx y l +=:k OB OA m 求且,0,1=⋅=l 2
3AOB ∆。
【高考数学经典题型】抛物线与圆,求三角形面积最值(一题多解)

1/ 5试题出处:2020届湖北省“荆、荆、襄、宜”四地七校联考(改编)抛物线与圆,求三角形面积最值若点P 是抛物线22x y =上的动点,点,M N 在x 轴上,圆22(1)1x y +−=内切于,PMN ∆求PMN ∆面积的最小值. 答案:8解法一:动点设一个参数,利用勾股定理列等式如图,不妨设点2(2,2)P t t (1)t >,圆心为C ,两切点为,D E .分别过点P 作PH x ⊥,作PG x 轴,过点M 作x 轴垂线与PG 交于点G ,且,OM m ON n ==. 在Rt PCE ∆中,由勾股定理得,22222244(21)14PE PC CE t t t =−=+−−=,即22PE t =.在Rt PNH ∆中,由勾股定理得222,PN PH NH =+ 即()224224(2)t n t t n +=+−,可得1t n t =+. 在Rt PMG ∆中,由勾股定理得222,PM PG GM =+ 即()224224(2)t m t t m +=++,可得1t m t =−. 42224122()21121PMNt S m n t t t t ∆∴=⋅+⋅==−− 又2242111111()244t t t −=−−+≥ ∴当22t =时,PMN S ∆有最小值8.2 / 5解法二:动点设两个参数,利用直线与圆相切列等式 设00(,),(,0),(,0)P x y M a N b ,其中02y >且a b <.∴直线PN 的方程为:00()y y x b x b=−−, 直线PN 与圆相切,∴圆心(0,1)到直线PN 的距离为1, ∴1=∴()2000220y b x b y −+−= 同理可得,()2000220y a x a y −+−=.∴实数,a b 是关于x 的一元二次方程()2000220y x x x y −+−=的两根, ∴0000222x a b y y a b y −⎧+=⎪−⎪⎨−⎪⋅=⎪−⎩, ∴()()()22220002044842x y y a b a b ab y +−−=+−=−,2002x y =∴()()2202042y a b y −=−,0022y a b y −=− 20000014()248222PMNy S b a y y y y ∆∴=⋅−⋅==−++≥−− ∴当04y =时,PMN S ∆有最小值8.解法三:动点设两个参数,利用内切圆性质列等式 设点00(,),(,0),(,0)P x y M a N b −圆心为(0,1)C ,两切点为,D E . 在Rt PCD ∆中,PD =2002x y =,∴0PD y = PM PD DM PD MO =+=+3 / 5∴0y a =+,化简得20000002()x y MO a y x y x ===−−同理,可得20000002()x y NO b y x y x ===++0000000011()()22PMN y y S MO NO y y y x y x ∆∴=⋅+⋅=+⋅−+ 32000220000424822PMNy y S y y x y y ∆∴===−++≥−−− ∴当04y =时,PMN S ∆有最小值8.解法四:动点设一个参数、再设直线斜率,利用直线与圆相切列等式 设21(,)(2)2P m m m >,直线,PM PN 的斜率一定存在,分别设其为12,k k ,则直线PM 的方程为:211()2y m k x m −=−,1=,化简得:22342111(1)(2)04m k m m k m m −+−+−=……..① 同理可得:22342221(1)(2)04m k m m k m m −+−+−=……..②∴实数12,k k 是关于x 的一元二次方程223421(1)(2)04m x m m x m m −+−+−=的两根, ∴31224212221141m m k k m m m k k m ⎧−+=⎪−⎪⎨−⎪⋅=⎪−⎩, 分别令方程①,②中的0y =,得21,2M m x m k =−22,2N m x m k =−222112121122M N k k m m MN x x k k k k −=−=⋅−=2412121228PMNk k m m S MN k k ∆−∴=⋅⋅=⋅48m =4/ 5化简得4222116(48)82824PMNm S m m m ∆==−++≥−− ∴当28m =时,PMN S ∆有最小值8.解法五:动点设两个参数,利用内切圆性质列等式如图,设00(,),P x y 切点分别为,D E 且PMN ∆的内切圆半径1r = 则011()22PMN S MN y PM PN MN r ∆=⋅=++⋅1()2PM PN MN =++ 1()2PMN S OM PE ON PE MN MN PE ∆∴=++++=+MN MN ==0MN y MN =+≥012y MN ∴⋅≥ 016y MN ∴⋅≥0182PMN S y MN ∆∴=⋅≥ ∴PMN S ∆有最小值8.评论与赏析:圆锥曲线中求三角形面积的最值一直是考试的热点、难点问题.解法1跳出了解析几何的大量计算,两次用勾股定理将线段长用动点中的参数表示出.解法2利用直线与圆相切的性质及韦达定理找到线段整体与动点中的参数的关系.解法3利用三角形内切圆的性质和坐标运算将线段长用动点中的参数表示出来.解法4设切线斜率利用韦达定理找到线段与动点中的参数的关系.解法5巧妙利用三角形内切圆性质、这一题的数量特点及基本不等式直接得出面积的最值.5 / 5推广:过抛物线22(0)x py p =>上一点000(,)(2)P x y y p ≥作圆222:()C x y p p +−=的两条切线,分别与x 轴交于,M N 两点,则PMN ∆的最小值为28p .相似题:在平面直角坐标系xoy 中,过点2(2,21)P t t +作圆22:(1)(1)1E x y −+−=的两条切线,PM PN ,切点分别为,M N .当(1,)t ∈+∞时,设切线,PM PN 与y 轴分别交于点,,B C 求PBC ∆面积的最小值. 答案:8。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
已知抛物线y=ax2+bx+c的顶点A(2,0),与y轴的交点为
B(0,-1).
(1)求抛物线的解析式;
(2)在对称轴右侧的抛物线上找出一点C,使以BC为直径的圆经过抛物线的顶点A.并求出点C的坐标以及此时圆的圆心P点的坐标.
(3)在(2)的基础上,设直线x=t(0<t<10)与抛物线交于点N,当t为何值时,△BCN的面积最大,并求出最大值.
解析:(1)已知抛物线的顶点坐标,可直接设抛物线的解析式为顶点式进行求解.
(2)设C点坐标为(x,y),由题意可知.过点C作轴于点D,连接AB,AC.易证,根据对应线段成比例得出的关系式,再根据点C在抛物线上得,联立两个关系式组成方程组,求出
的值,再根据点C所在的象限确定点C的坐标。
P为BC的中点,取OD中点H,连PH,则PH为梯形OBCD的中位线.可得,故点H的坐标为(5,0)
再根据点P在BC上,可求出直线BC的解析式,求出点P的坐标。
(3)根据,得,所以求的最大值就是求MN的最大值,而M,N两点的横坐标相同,所以MN就等于点N的纵坐标减去点M的纵坐标,从而形成关于MN长的二次函数解析式,利用二次函数的最值求解。
解:(1) ∵抛物线的顶点是A(2,0),设抛物线的解析式为.
由抛物线过B(0,-1) 得,∴.
∴抛物线的解析式为.
即.
(2)设C的坐标为(x,y).
∵A在以BC为直径的圆上.∴∠BAC=90°.
作CD⊥x轴于D ,连接AB、AC.
∵,∴
∴△AOB∽△CDA.∴
∴OB·CD=OA·AD.
即1·=2(x-2).∴=2x-4.
∵点C在第四象限.
∴
由解得.
∵点C在对称轴右侧的抛物线上.
∴点C的坐标为(10,-16).∵P为圆心,∴P为BC中点.
取OD中点H,连PH,则PH为梯形OBCD的中位线.
∴PH=(OB+CD)=.
∵D(10,0)∴H(5,0)∴P (5, ).
故点P坐标为(5,).
(3)设点N的坐标为,直线x=t(0<t<10)与直线BC交于点M.
,
所以
设直线BC的解析式为,直线BC经过B(0,-1)、C (10,-16)
所以成立,解得:
所以直线BC的解析式为,则点M的坐标为.
MN==
==
所以,当t=5时,有最大值,最大值是.
点拨:(1)已知抛物线的顶点坐标(h,k)一般可设其解析式为.(2)求最值问题一般考虑根据已知条件构造二次函数求解.。
