湘教版数学九年级下册3.3画几何体的三视图(第1课时)课堂练习(含答案)
度湘教版数学九年级下册课堂练习第3章 由三视图计算物体的表面积与体积

度湘教版数学九年级下册课堂练习第3章由三视图计算物体的表面积与体积班级姓名第3章投影与视图由三视图计算物体的外表积与体积1.一个物体的三视图如图,其中主视图和左视图都是腰长为3、底边为2的等腰三角形,依据三视图求这个物体的外表积,并画出该物体的正面展开图.答图解:该几何体是一个底面半径为1,母线长为3的圆锥,正面展开图如答图.正面积为12=π,2×2π×3=3π,底面积为π×1∴外表积为3π+π=4π.2.一个长方体的左视图、仰望图及相关数据如下图,那么其主视图的面积为(B)左视图仰望图A.6 B.8 C.12 D.24【解析】左视图可失掉长方体的宽和高,仰望图可失掉长方体的长和宽,主视图可失掉长方体的长和高,长方体的高为2,长为4,∴主视图的面积为2×4=8.3.一个如下图的长方体的三视图如下图.假定其仰望图为正方形,那么这个长方体的外表积为(A)A.66 B.48C.482+36 D.57【解析】设长方体的底面边长为x,那么2x2=(32)2,∴x=3,∴该长方体的外表积为3×4×4+32×2=66.4.[2021·东营]如图,一个圆锥体的三视图如下图,那么这个圆锥体的正面积为__20π__.【解析】依据三视图失掉圆锥的底面圆的直径为8,即底面圆的半径r为4,圆锥的高为3,所以圆锥的母线长l=32+42=5,所以这个圆锥的正面积是π×4×5=20π.5.[2021·孝感]如图是一个几何体的三视图(图中尺寸单位:cm),依据图中数据计算,这个几何体的外表积为__16π__cm2.【解析】由主视图和左视图为三角形判别出是锥体,由仰望图是圆形可判别出这个几何体应该是圆锥.依据三视图知:该圆锥的母线长为6 cm,底面半径为2 cm,故外表积=πrl+πr2=π×2×6+π×22=16π(cm2).6.[2021·齐齐哈尔]如图,三棱柱的三视图如下图,△EFG中,EF=8 cm,EG=12 cm,∠EFG=45°,那么AB的长为【解析】如答图,过点E作EQ⊥FG于点Q,答图由题意可得出:EQ=A B.∵EF=8 cm,∠EFG=45°,∴EQ=AB=22×8=42(cm).7.如下图是一个食品包装盒的三视图(单位:cm),其中主视图是一个等边三角形.(1)请写出这个包装盒的几何体称号;(2)计算这个几何体的外表积.(结果保管根号)解:(1)由包装盒的三视图可得出包装盒是正三棱柱.(2)如答图,∵△ABC是等边三角形,答图∴∠B=60°.∵AD= 3 cm,∴AB=BC=2 cm,∴S底面积=12×2×3=3(cm2),S正面积=3×6×2=36(cm2),∴S外表积=S正面积+2S底面积=(36+23)cm2.8.一个几何体的三视图的有关尺寸如下图,请写出这个几何体的称号,并计算这个几何体的外表积.解:称号:直三棱柱.主视图为直角三角形,直角边长区分为4 cm和3 cm,依据勾股定理得斜边长为5 cm,S侧=3×2+4×2+5×2=24(cm2),S表=2S底+S侧=2×12×3×4+24=36(cm2),故这个几何体的外表积为36 cm2.9.某工厂要加工一批密封罐,设计者给出了密封罐的三视图(如图,单位:mm),请你依照三视图确定制造每个密封罐所需钢板的面积.(结果保管根号)解:由三视图可知,密封罐的外形是正六棱柱(如答图1).答图1答图2密封罐的高为50 mm,底面正六边形的直径为100 mm,边长为50 mm,答图2是它的外表展开图.由展开图可知,制造一个密封罐所需钢板的面积为6×50×50+2×6×12×50×50×sin 60°=(15 000+7 5003)mm2.。
湘教版九年级数学下册同步练习题画几何体的三视图
3.3 三视图
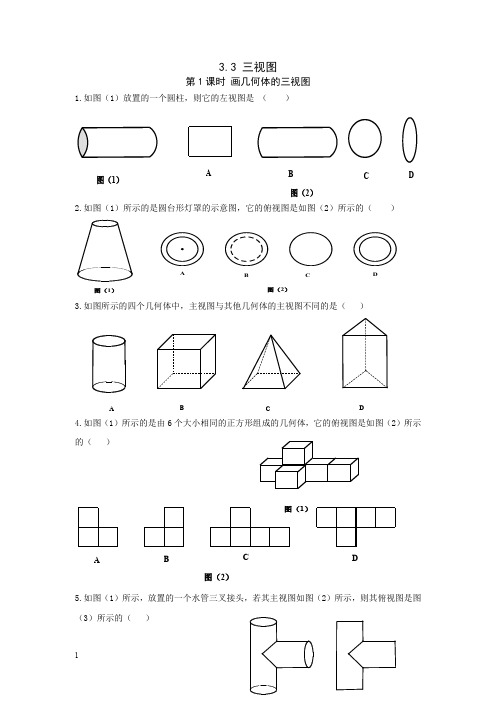
第1课时画几何体的三视图1.如图(1)放置的一个圆柱,则它的左视图是()
2.如图(1)所示的是圆台形灯罩的示意图,它的俯视图是如图(2)所示的()
3.如图所示的四个几何体中,主视图与其他几何体的主视图不同的是()
4.如图(1)所示的是由6个大小相同的正方形组成的几何体,它的俯视图是如图(2)所示的()
5.如图(1)所示,放置的一个水管三叉接头,若其主视图如图(2)所示,则其俯视图是图(3)所示的()
D
C
B
A
图(2)
D
C
B
A
图(1)
图(2)
D
C
B
A
图(2)
D
C
B
A
图(1)
图(1)
6.在水平的讲台上放置圆柱形水杯和长方形粉笔盒,如图(1)所示,则它的主视图是图(2)所示的( )
7.沿圆柱体上面直径截去一部分的物体如图所示,画出它的三视图.
图(3)D
C B A 图(2)D
C B A (第3题)。
【湘教版】九年级数学下册:配套教案设计(Word版,含反思)3.3 第1课时 画几何体的三视图
3.3三视图第1课时画几何体的三视图1.理解并掌握视图的概念,会判断简单几何体的三视图;2.会画圆柱、圆锥、球、棱柱的三视图.(重点)一、情境导入思考:在正午的太阳光下,一个物体在地面上的影子是一个圆,你能确定这个物体的形状吗?如图所示的几何体,在正午的太阳光下,在地面的影子分别是什么?它们的影子都是圆,这说明单凭在地上的影子,不可以确定物体的形状,即从一个方向看物体,不能确定物体的形状.二、合作探究探究点一:几何体的三视图的判断【类型一】简单几何体的三视图中心对称图形的是()解析:A.圆柱的主视图是长方形,是中心对称图形;B.圆锥的主视图是等腰三角形,不是中心对称图形;C.球的主视图是圆,是中心对称图形;D.正方体的主视图是正方形,是中心对称图形.故选B.方法总结:本题考查了简单几何体的三视图以及中心对称图形,先找出各个几何体的主视图,再根据中心对称图形的定义判断.变式训练:见《学练优》本课时练习“课堂达标训练”第3题【类型二】组合体的三视图将两个大小完全相同的杯子(如图甲)叠放在一起(如图乙),则图乙中实物的俯视图是()解析:根据三视图的概念,结合俯视图,观察该物体,看得见的画实线,看不见的画虚线.故选C.方法总结:正确理解主视图、左视图、俯视图的概念,充分发挥空间想象能力和动手操作能力.变式训练:见《学练优》本课时练习“课堂达标训练”第2题探究点二:作几何体的三视图作出下面物体的三视图.解析:此物体下面是一个六棱柱,上面是一个圆柱体.解:如图:方法总结:三视图中,主视图与俯视图等长,主视图与左视图等高,俯视图与左视图等宽.变式训练:见《学练优》本课时练习“课后巩固提升”第9题三、板书设计本节课由正午太阳光下的物体的影子引入视图及三视图的概念,接着介绍三视图的画法,通过作图巩固三视图的概念.培养了学生动手、动脑和空间想象能力,增加学生对美学的了解,激发了他们的求知欲望,从而加强了学生的学习兴趣.。
湘教版九年级数学下册《332由三视图到立体图形》同步练习(含答案解析).docx
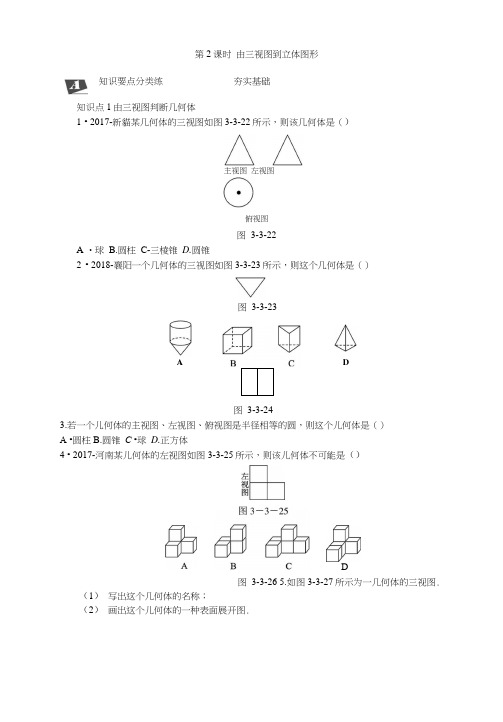
第2课时 由三视图到立体图形知识点1由三视图判断几何体1 • 2017-新貓某几何体的三视图如图3-3-22所示,则该几何体是()主视图 左视图俯视图图 3-3-22A •球 B.圆柱 C-三棱锥 D.圆锥2 • 2018-襄阳一个几何体的三视图如图3-3-23所示,则这个几何体是()图 3-3-243.若一个儿何体的主视图、左视图、俯视图是半径相等的圆,则这个儿何体是()A •圆柱B.圆锥 C •球 D.正方体4 • 2017-河南某儿何体的左视图如图3-3-25所示,则该儿何体不可能是()图 3-3-26 5.如图3-3-27所示为一几何体的三视图.(1) 写出这个几何体的名称;(2) 画出这个儿何体的一种表面展开图.知识要点分类练夯实基础A图 3-3-23DD△俯视图图3-3-27知识点2根据三视图进行计算6•若一个长方体的左视图、俯视图及相关数据如图3-3-28所示,则其主视图的面积为()2 4A. 6 B・8 C. 12 D. 247・2018-威海如图3-3-29是某圆锥的主视图和左视图‘该圆锥的侧而积是()A. 25 乃B. 24 乃C • 20 " D. 158 • 2018・日照如图3-3-30是一个几何体的三视图(图屮尺寸单位:CM),根据图中所示数据计算这个几何体的表面积是___________ .口 规律方法综合练 提升能力• 2017•常德如图3—3 — 31是一个儿何体的兰视图'则这个几何体是( )俯视图图 3-3-31A B C D图 3-3-3210.如图3 — 3—33是由若干个大小相同的正方体搭成的儿何体的三视图,则组成该儿何 体所用的正方体的个数是()A. 6B. 4C. 3D. 211 - 2017•青岛已知某几何体的三视图如图3-3-34所示,其中俯视图为正六边形,则 该几何体的表面积为 __________ .图 3-3-3412.图3-3-35①是一个组合几何体,它的下面是一个长方体,上面是一个圆柱.主视图 左视图冬视方向①4主视图 左视图俯视图2② —视图③⑴图②和图③是它的两个视图,在横线上分别填写两种视图的名称(填“主欄左”或“俯”);(2)根据两个视图中的尺寸,计算这个组合几何体的体积.(结果保留刀)图 3-3-36拓广探究创新练 冲刺满分13 •己知如图3 — 3—36①所示的儿何体.(1)图②所画的此几何体的三视图有错误吗?如果有错误,错在哪里?并画出正确的视 图; (2)根据图中的尺寸,求出几何体的表面积.(注:长方体的底面为正方形’单位:cm)视方向① ②教师详解详析1. D [解析]由于主视图与左视图是三角形,俯视图是带有圆心的圆,故该几何体是圆锥.故选D.2C [解析]根据主视图和左视图为矩形判断出该几何体是柱体,根据俯视图是三角形判断出这个儿何体是三棱柱.3• C [解析]三视图是半径相等的圆的几何体只有球.4• D5・解:(1)三棱柱.(2)答案不唯一‘如图所示:6• B [解析]主视图反映物体的长和高,左视图反映物体的宽和高,俯视图反映物体的长和宽.结合三者之间的关系从而确定主视图的长和宽分别为4,2,所以面积为8.故选B.7• C8-4JI cm2[解析]观察三视图确定此儿何体为圆锥,由左视图知此圆锥的底面半径为1,高为2也,由勾股定理得母线长为3,所以此圆锥的表面积=侧面积+底面积=兀rl+ n r= JI X1X3+ 兀X12=3JI + 兀=4 JT(cm2).9• B [解析]结合三个视图发现,应该是一个正方体在一个角上挖去一个小正方体,且小正方体的位置应该在右上角,故选B.10• A [解析]综合三视图可知,这个儿何体的底层有3个小正方体,第2层有1个小正方体,第3层有1个小正方体,第4层有1个小正方体,因此搭成这个几何体所用小正方体的个数是34-1 + 1 + 1=6.故选A.11・48+12羽[解析]观察该儿何体的三视图发现该儿何体为正六棱柱,其底面是边长为2的正六边形,高为4,故其底面中心到边的距离为羽,所以其表面积为2X4X6+2X5X6X2X^3=48+12 羽.12•解:⑴左俯(2)2X5X84-兀X(2三2尸><6=80+ 兀XlX6=80+6n. 答:这个组合儿何体的体积是80+6 n.13•解:(1)左视图错误,圆锥的左视图是三角形,左视图应为下图.(2)几何体的表面积=圆锥的侧面积+长方体的表面积一圆锥底面圆的面积=*>< 10兀X ^/152 +52 + 20 X 20 X 2 + 20 X 5 X 4- X52=25 71 +1200-25 =[1200 + (25 帧一25)兀]cm •。
湘教版九年级下册数学 第3章 三视图

知3-讲
特别警示:圆锥与棱锥的三视图的区别:圆锥的俯视图 的外轮廓线是圆;棱锥的俯视图的外轮廓线是多边形.
三视图
主视图 左视图
三视图
画法
俯视图
应用
课后作业
作业1 必做:请完成教材课后习题 补充:
作业2
知2-讲
例3 一种机器上有一个进行转动的零件叫燕尾槽(如图 3.3-7),请画出它的三视图.
解:这个燕尾槽的三视图如图3.3-8.
知2-讲
知识点 3 由三视图确定几何体
知3-讲
1. 由三视图描述几何体的方法:由三视图想象几何体的形 状,首先分别根据主视图、俯视图和左视图想象几何体
的正面、上面和左面,然后综合起来考虑整体形状. 特别提醒:由三视图描述几何体的形状时,要对三视图进
方画出左视图,与主视图 高平齐,与俯视图宽相等, 图3.3-3①中的几何体的三 视图如图3.3-3②所示.
速记口诀: 视图位置要摆明, 画图规则要记清. 主俯视图长对正, 左俯视图宽相等, 主左视图高平齐, 实线虚线应分清.
知2-讲
知2-讲
3. 画三视图的规定:画三视图时,看得见的部分的轮廓线 画成实线,因被其他部分遮挡而看不见的部分的轮廓线 画成虚线.
(4)利用由三视图画几何体与由几何体画三视图的互逆过程,反
复练习,不断总结方法.
3. 常见几何体的三视图
知3-讲
知3-讲
1. 几何体的三视图和展开图是平面图形,几何体、三视 图和展开图中,三者知其一,就能确定另外两种图形, 即三者之间可以互相转化.
2. 对于稍复杂的视图,可先将其化成几个简单的图形, 再综合分析.
视图在主视图的右边. 主视图反映物体的长和高,俯视
图反映物体的长和宽,左视图反映物体的高和宽.
2019年度湘教版数学九年级下册课堂练习第3章3.3第1课时画几何体的三视图

20佃-2 0佃学年度湘教版数学九年级下册课堂练习班级________ 姓名 ____________第3章投影与视图3.3三视图第1课时画几何体的三视图1. [2019广安]下列图形中,主视图为如图所示的是(B )□ ©AB2. [2019沈阳]如图是由五个相同的小立方块搭成的几何体,这个几何体的左视图是(D )3 .从一个棱长为3 cm的大立方体的角上挖去一个棱长为1 cm的小立方体,得到的几何体如图所示,则该几何体的左视图是4. 如图,正三棱柱的底面周长为9,在这个正三棱柱中截去一第1页0 A) B) D)BC个底面周长为3的正三棱柱,所得几何体的俯视图的周长是8/ _________________________________________________________________________________________________________________________________________________________________ ■5. [2019扬州]如图所示的几何体的主视图是(B )6. [2019 •新疆]如图是由三个相同的小正方体组成的几何体, 则该几何体的左视图是(C )8. [2019临安]小明同学从正面观察如图所示的两个物体,看到9. 如图,有四个几何体:其中俯视图是四边形的几何体个数是(B )A. 1B. 2C. 3D. 410. 如图是由一些大小相同的小正方体组合成的简单几何体.(1)图中有_6—个小正方体;⑵分别画出它的主视图和左视图.匚二I A「二I B C^DB LJLJC LJ DD的是(解:(2)如答图所示:11. 如图是一粮仓,其顶部是一圆锥,底部是一圆柱.(1) 画出粮仓的三视图;(2) 若圆柱的底面圆的半径为1 m,高为2 m,求圆柱的侧面积;(3) 假设粮食最多只能装到与圆柱同样高,贝憬多可以存放多少立方米的粮食?解:(1)如答图所示:答图(2) 2 淤1X 2= 4n (m).(3) 氷12X 2 = 2n (请.12. 将棱长是1 cm的小正方体组成如图所示的几何体,该几何体共由10个小正方体组成.(1) 画出这个几何体的三视图;(2) 求该几何体的表面积.解:(1)如答图所示:主视图俯视图主视图 左观闍第4页答图 (2)2 X (1+2+3) + 2X (1 + 2+3)+ 2X (1 + 2+ 3)= 36(cm 2).俯视图。
2017春九年级数学下册3.3第1课时画几何体的三视图试题新版湘教版
3.3 三视图
第1课时 画几何体的三视图
知识要点 画几何体的三视图
在下面的四个几何体中,它们各
自的左视图与主视图不相同的是( )
分析:分别确定出所给物体的左视图与主视图,再找出符合条件的结果即可.
方法点拨:对一些特殊几何体的三视图要熟记,在确定三视图时,要注意主视方向对三视图的影响.
(教材P111习题T1变式)作出下
面物体的三视图.
分析:此物体下面是一个六棱柱,上面是一个圆柱体.
方法点拨:三视图中,主视图与俯视图等长,主视图与左视图等高,俯视图与左视图等宽.
1.将两个大小完全相同的杯子(如图甲)叠放在一起(如图乙),则图乙中实物的俯视图是( )
参考答案:
要点归纳
知识要点:主视图左视图俯视图主视图左视图俯视图长高宽垂直实虚
典例导学
例1 B
例2 解:如图:
当堂检测
1.C。
【教育资料】20182019学年度湘教版数学九年级下册课堂练习第3章 3.3第1课时 画几何体的三视图学习精品
2019-2019学年度湘教版数学九年级下册课堂练习班级姓名第3章投影与视图3.3三视图第1课时画几何体的三视图1.[2019·广安]下列图形中,主视图为如图所示的是(B)ABCD2.[2019·沈阳]如图是由五个相同的小立方块搭成的几何体,这个几何体的左视图是(D)ABCD3.从一个棱长为3 cm的大立方体的角上挖去一个棱长为1 cm 的小立方体,得到的几何体如图所示,则该几何体的左视图是(C)C) 4.如图,正三棱柱的底面周长为9,在这个正三棱柱中截去一个底面周长为3的正三棱柱,所得几何体的俯视图的周长是__8__.5.[2019·扬州]如图所示的几何体的主视图是(B)A B C D6.[2019·新疆]如图是由三个相同的小正方体组成的几何体,则该几何体的左视图是(C)A B C D7.[2019·黄石]如图,该几何体的俯视图是(A)A B CD8.[2019·临安]小明同学从正面观察如图所示的两个物体,看到的是(C)A B C D9.如图,有四个几何体:其中俯视图是四边形的几何体个数是(B)A.1 B.2 C.3 D.410.如图是由一些大小相同的小正方体组合成的简单几何体.(1)图中有__6__个小正方体;(2)分别画出它的主视图和左视图.解:(2)如答图所示:答图11.如图是一粮仓,其顶部是一圆锥,底部是一圆柱.(1)画出粮仓的三视图;(2)若圆柱的底面圆的半径为1 m,高为2 m,求圆柱的侧面积;(3)假设粮食最多只能装到与圆柱同样高,则最多可以存放多少立方米的粮食?解:(1)如答图所示:答图(2)2π×1×2=4π(m2).(3)π×12×2=2π(m3).12.将棱长是1 cm的小正方体组成如图所示的几何体,该几何体共由10个小正方体组成.(1)画出这个几何体的三视图;(2)求该几何体的表面积.解:(1)如答图所示:答图(2)2×(1+2+3)+2×(1+2+3)+2×(1+2+3)=36(cm2).。
【湘教版九年级数学下册教案】3.3第1课时画几何体的三视图
3.3三视图第 1 课时画几何体的三视图1.理解并掌握视图的看法,会判断简单几何体的三视图;2.会画圆柱、圆锥、球、棱柱的三视图. (要点 )一、情境导入思虑:在中午的太阳光下,一个物体在地面上的影子是一个圆,你能确立这个物体的形状吗?以下列图的几何体,在中午的太阳光下,在地面的影子分别是什么?它们的影子都是圆,这说明单凭在地上的影子,不可以确立物体的形状,即从一个方向看物体,不可以确立物体的形状.二、合作研究研究点一:几何体的三视图的判断【种类一】简单几何体的三视图(2015 东·海县模拟)其主视图不是中心对称图形的是()分析: A. 圆柱的主视图是长方形,是中心对称图形; B. 圆锥的主视图是等腰三角形,不是中心对称图形; C.球的主视图是圆,是中心对称图形; D. 正方体的主视图是正方形,是中心对称图形.应选 B.方法总结:本题观察了简单几何体的三视图以及中心对称图形,先找出各个几何体的主视图,再依据中心对称图形的定义判断.变式训练:见《学练优》本课时练习“课堂达标训练” 第 3 题【种类二】组合体的三视图将两个大小完整同样的杯子(如图甲 )叠放在一起 (如图乙 ) ,则图乙中实物的俯视图是()分析:依据三视图的看法,结合俯视图,观察该物体,看得见的画实线,看不见的画虚线.应选 C.方法总结:正确理解主视图、左视图、俯视图的看法,充发散挥空间想象能力和动手操作能力.变式训练:见《学练优》本课时练习“课堂达标训练” 第 2 题研究点二:作几何体的三视图作出下边物体的三视图.分析:此物体下边是一个六棱柱,上边是一个圆柱体.解:如图:变式训练:见《学练优》本课时练习“课后牢固提高”第9 题三、板书设计本节课由中午太阳光下的物体的影子引入方法总结:三视图中,主视图与俯视图视图及三视图的看法,接着介绍三视图的画法,经过作图牢固三视图的看法.培育了学等长,主视图与左视图等高,俯视图与左视生着手、动脑和空间想象能力,增添学生对美学的认识,激发了他们的求知欲念,从而图等宽.增强了学生的学习兴趣.。
湘教版初中九年级下册数学课时同步练习 第3章 投影与视图 3.3《三视图》同步练习卷
湘教版数学九年级下册3.3《三视图》同步练习卷一、选择题1.下列几何体中,俯视图为四边形的是()2.如图所示几何体的左视图是( )3.由几个相同的小正方形搭成的一个几何体如图所示,这个几何体的主视图是()4.如图是某几何体的三视图及相关数据,则判断正确的是()A.a>cB.b>cC.4a2+b2=c2D.a2+b2=c25.一个几何体的三视图如图所示,则该几何体的表面积为()A.4π B.3π C.2π+4 D.3π+46.如图是某几何体的三视图,则该几何体的全面积等于()A.112B.136C.124D.847.如图是将正方体切去一个角后形成的几何体,则该几何体的左视图为()A. B. C. D.8.如图,箭头表示投影线的方向,则图中热水瓶的正投影是( )9.如图,由5个完全相同的小正方体组合成一个立体图形,它的左视图是( )A. B. C. D.10.如图①是由大小相同的小正方体搭成的几何体,将上层的小正方体平移后得到图②.关于平移前后几何体的三视图,下列说法正确的是( )A.主视图相同 B.左视图相同 C.俯视图相同 D.三种视图都不相同二、填空题11.如图是由一些完全相同的小正方体搭成的几何体的俯视图和左视图,组成这个几何体的小正方体的个数是________.12.如果一个圆锥的主视图是等边三角形,俯视图是面积为4π的圆,那么这个圆锥的左视图的面积是.13.如图是某几何体的三视图,则该几何体的表面积为14.如图是由几个小立方块搭成的几何体的主视图与左视图,这个几何体最多可能有________个小立方块.15.一个几何体的三视图如图,很据图示的数据计算该几何体的表面积为______(结果保留π).16.如图,是由10个完全相同的小正方体堆成的几何体.若现在你还有若干个相同的小正方体,在保证该几何体的从上面、从正面、从左面看到的图形都不变的情况下,最多还能放个小正方体.三、作图题17.由一些大小相同,棱长为1的小正方体搭成的几何体的俯视图如图所示,数字表示该位置的正方体个数.(1)请画出它的主视图和左视图;(2)给这个几何体喷上颜色(底面不喷色),需要喷色的面积为(3)在不改变主视图和俯视图的情况下,最多可添加块小正方体.18.画图题:①由大小相同的小立方块搭成的几何体如左图,请在右图的方格中画出该几何体的俯视图和左视图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018-2019学年度湘教版数学九年级下册课堂练习
班级姓名
第3章投影与视图
3.3三视图
第1课时画几何体的三视图
1.[2018·广安]下列图形中,主视图为如图所示的是(B)
A B C D
2.[2018·沈阳]如图是由五个相同的小立方块搭成的几何体,这个几何体的左视图是(D)
A
B
C
D
3.从一个棱长为3 cm的大立方体的角上挖去一个棱长为1 cm 的小立方体,得到的几何体如图所示,则该几何体的左视图是(C)
C)
4.如图,正三棱柱的底面周长为9,在这个正三棱柱中截去一个底面周长为3的正三棱柱,所得几何体的俯视图的周长是__8__.
5.[2018·扬州]如图所示的几何体的主视图是(B)
A B C D
6.[2018·新疆]如图是由三个相同的小正方体组成的几何体,则该几何体的左视图是(C)
A B C D
7.[2018·黄石]如图,该几何体的俯视图是(A)
A B C D
8.[2018·临安]小明同学从正面观察如图所示的两个物体,看到的是(C)
A B C D
9.如图,有四个几何体:
其中俯视图是四边形的几何体个数是(B)
A.1 B.2 C.3 D.4
10.如图是由一些大小相同的小正方体组合成的简单几何体.
(1)图中有__6__个小正方体;
(2)分别画出它的主视图和左视图.
解:(2)如答图所示:
答图
11.如图是一粮仓,其顶部是一圆锥,底部是一圆柱.
(1)画出粮仓的三视图;
(2)若圆柱的底面圆的半径为1 m,高为2 m,求圆柱的侧面积;
(3)假设粮食最多只能装到与圆柱同样高,则最多可以存放多少立方米的粮食?
解:(1)如答图所示:
答图
(2)2π×1×2=4π(m2).
(3)π×12×2=2π(m3).
12.将棱长是1 cm的小正方体组成如图所示的几何体,该几何体共由10个小正方体组成.
(1)画出这个几何体的三视图;
(2)求该几何体的表面积.
解:(1)如答图所示:
答图
(2)2×(1+2+3)+2×(1+2+3)+2×(1+2+3)=36(cm2).。
