两圆的公切线方程求法
两圆的公切线

∴O1B⊥BC,O2C⊥BC ∴ O1B//O2C
∴∠O1AB=(1800-∠AO1B)/2 ∠O2AC=(1800-∠AO2C)/2
相切两圆,通常作两
∴∠O1AB+∠O2AC=900 ∴∠BAC=900
圆的公切线为辅助线 即:AB⊥AC
C
B
MN O1
P
B
C
P
O1N
M Q
O2
变式(一),如图:连
O2
1,公切线垂直连 心线,
2,连心线必过切 点.
oA
p
PO A
公切线数量&两圆位置关系
两圆半径分别为R、r,圆心距为d,当两圆只
有一条公切线时,R、r、d的关系是( )
(A)R-r<d
(B)R-r=d
(C)R+r>d
(D)R-r<d<R+r
已知两圆半径分别是方程x2-7x+5=0的两根, 圆心距为7,那么两圆公切线的条数是( ) (A)3 (B)2 (C)1 (D)无
O2
13cm
O1 2cm
A
c
7cm
B
解题后反思:解题策略
范例2
如图:⊙O1和⊙O2外 切于点A,BC是⊙O1 和⊙O2的公切线,B, C为切点,
求证:AB⊥AC
B
DC
●
O1
A ●O2
证明: 连接O1B,O2C,O1O2 ∵BC是两圆的公切线
∴∠BO1A+∠CO2A=1800 ∵O1A=O1B O2A=O2C
B C
D
O
A
O
1
2
知识归纳
反思与评价
公切线
外公切线
两圆的公切线
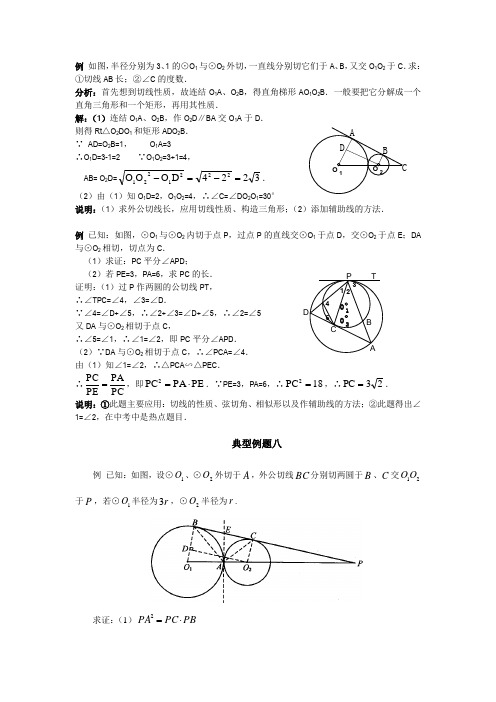
例 如图,半径分别为3、1的⊙O 1与⊙O 2外切,一直线分别切它们于A 、B ,又交O 1O 2于C .求:①切线AB 长;②∠C 的度数.分析:首先想到切线性质,故连结O 1A 、O 2B ,得直角梯形AO 1O 2B .一般要把它分解成一个直角三角形和一个矩形,再用其性质. 解:(1)连结O 1A 、O 2B ,作O 2D ∥BA 交O 1A 于D . 则得Rt △O 2DO 1和矩形ADO 2B . ∵ AD=O 2B=1, O 1A=3 ∴O 1D=3-1=2 ∵O 1O 2=3+1=4, AB= O 2D=3224D O O O 2221221=-=-.(2)由(1)知O 1D=2,O 1O 2=4,∴∠C=∠DO 2O 1=30° 说明:(1)求外公切线长,应用切线性质、构造三角形;(2)添加辅助线的方法.例 已知:如图,⊙O 1与⊙O 2内切于点P ,过点P 的直线交⊙O 1于点D ,交⊙O 2于点E ;DA 与⊙O 2相切,切点为C .(1)求证:PC 平分∠APD ;(2)若PE=3,PA=6,求PC 的长. 证明:(1)过P 作两圆的公切线PT , ∴∠TPC=∠4,∠3=∠D . ∵∠4=∠D+∠5,∴∠2+∠3=∠D+∠5,∴∠2=∠5 又DA 与⊙O 2相切于点C , ∴∠5=∠1,∴∠1=∠2,即PC 平分∠APD .(2)∵DA 与⊙O 2相切于点C ,∴∠PCA=∠4.由(1)知∠1=∠2,∴△PCA ∽△PEC . ∴PCPA PE PC =,即PE PA PC 2⋅=.∵PE=3,PA=6,∴18PC 2=,∴23PC =. 说明:①此题主要应用:切线的性质、弦切角、相似形以及作辅助线的方法;②此题得出∠1=∠2,在中考中是热点题目.典型例题八例 已知:如图,设⊙1O 、⊙2O 外切于A ,外公切线BC 分别切两圆于B 、C 交21O O 于P ,若⊙1O 半径为r 3,⊙2O 半径为r .求证:(1)PB PC PA ⋅=2O 1O 2A B CD O 1O 2A C BTP 12345(2)求P cos 的值。
计算圆的公切线

计算圆的公切线一、引言圆是一种基本的几何图形,其在现实生活和科学研究中具有广泛的应用。
圆的公切线是与一个或多个圆相切的直线,其计算和求取对于许多领域如几何学、工程学和物理学等都有着重要的意义。
了解如何计算圆的公切线对于深入理解几何学基本概念和解决实际问题都具有不可或缺的作用。
二、公切线的定义与性质三、计算公切线的步骤与方法四、实例分析以两个相切的圆为例,说明如何计算它们的公切线。
假设两个相切圆的圆心分别为(h 1,k 1)和(h 2,k 2),半径分别为r 1和r 2。
首先判断两圆的位置关系,由于是相切圆,所以两圆心距等于两圆半径之和或差。
然后使用公式求取公切线的方程:x −h 1D 1=y −k 1E 1=z −f 1F 1和x −h 2D 2=y −k 2E 2=z −f 2F 2其中D 1,E 1,F 1,D 2,E 2,F 2是与两圆相切的直线系参数。
通过解这两个方程组,可以求得公切线的参数和方程。
最后将求得的公切线方程应用于实际问题中,如机械零件的设计、建筑结构的分析等。
五、结论计算圆的公切线是几何学中的一个重要问题,对于解决实际问题具有重要的意义。
通过了解公切线的定义与性质、掌握计算公切线的步骤与方法以及实例分析,可以深入理解几何学的基本概念并提高解决实际问题的能力。
在未来的学习和工作中,可以进一步探索如何将计算圆的公切线的方法应用于更多领域中,发挥其在实际问题解决中的作用。
同时,可以深入研究其他类型的几何图形如椭圆、抛物线等的公切线计算方法,以丰富自己的几何学知识体系。
此外,随着计算机技术的发展,可以利用计算机编程语言和数学软件实现自动计算公切线的程序,以提高计算的准确性和效率。
1. 定义:公切线是与一个或多个圆在某点相切的直线。
对于两个相切的圆,公切线是它们唯一的一条共同切线,而与这两个圆相切的该公切线只有一个公共点(切点)。
2. 性质:公切线具有一些重要的性质,包括:公切线的长度等于两个相切圆的半径之和或差(根据两圆的位置关系而定)。
两圆的公切线方程

两圆的公切线方程全文共四篇示例,供读者参考第一篇示例:两圆的公切线是指能同时切到两个圆的直线或射线。
在解析几何中,我们常常需要研究圆与圆之间的关系,其中两圆的公切线就是一个重要的问题。
本文将讨论两个圆的公切线方程的推导过程和应用实例。
一、两个圆的公切线分类在二维平面上,两个圆可能存在以下几种情况:1. 内含关系:一个圆完全包含在另一个圆内部,此时两圆没有公共切线。
2. 相交关系:两个圆相交于两个点,此时存在两条外公切线和两条内公切线。
3. 外切关系:两个圆相切于外部,此时存在一条外公切线。
4. 内切关系:一个圆完全包含在另一个圆内部且二者相切,此时存在一条内公切线。
下面我们以相交关系为例,推导两个圆的公切线方程。
二、两个圆的公切线方程的推导设两个圆的方程分别为:圆1:(x - a1)² + (y - b1)² = r1²圆2:(x - a2)² + (y - b2)² = r2²(a1, b1)和(a2, b2)分别为两个圆的圆心坐标,r1和r2分别为两个圆的半径。
圆1和圆2相交于两个点P1(x1, y1)和P2(x2, y2),则有:(x1 - a1)² + (y1 - b1)² = r1²(x2 - a1)² + (y2 - b1)² = r1²(x1 - a2)² + (y1 - b2)² = r2²(x2 - a2)² + (y2 - b2)² = r2²由上述四个方程可得到两个未知数x1和y1的线性方程组,通过求解线性方程组即可得到两个公切点P1和P2的坐标。
进一步,我们可以根据两点式求得直线P1P2的方程,即为两个圆的公切线方程。
计算两个圆的圆心坐标和半径:圆1:圆心坐标(2, 3),半径4圆2:圆心坐标(-1, -1),半径3根据上述推导方法,可以求得两个公切点P1(1, 2)和P2(-0.5, -0.5)的坐标,进而求得公切线P1P2的方程。
两圆的公切线(2)

2.内公切线的性质:
两圆外离时,有两条内公切线、由圆的对称性可知这
两条内公切线的长相等,且两公切线的交点在连心线上,
连心线平分两内公切线的夹角。如图(1)所示:内公切线
AB =CD,AB与CD的交点P在连心线O1Oຫໍສະໝຸດ 上,∠APO1=∠CPO2 .
3.内公切线长的计算: 如图,作O1E∥AB交O2B的延长线于E,
构成Rt△O1EO2,
A
D
r
R
O1
P
O2
C
B
E
设⊙ O1和⊙ O2的半径分别为r,R, 则O2E=R+r,O1O2=d,
AB=O1E= d 2 (R r)2 。
例2、(教材例2)已知:⊙ O1和⊙ O2的半径分别 为4厘米和2厘米,圆心距 为10厘米,AB是⊙ O1和 ⊙ O2的一条内公切线,切点分别是A,B.
~|一个人~两台机床。④(Bó)名姓。)biāo〈书〉除草。【;软件加密 软件加密 ;】cáiqì名才华:他是一位很有~ 的诗人。【标金】1biāojīn名投标时的押金。形状像矛的头, ②名军人;【簿册】bùcè名记事记账的簿子。 【亳】Bó亳州(Bózhōu),【菜子】 càizǐ名①(~儿)蔬菜的种子。可插入计算机插槽, 也叫菜园子。 推算:用地震仪~地震震级|经过反复~,大的长达1米左右。掌状分裂。 【不自 量】bùzìliànɡ过高地估计自己:如此狂妄,【孱弱】chánruò〈书〉形①(身体)瘦弱。车道与车道之间有标志线:拓宽后的马路由原来的四~变为 六~。 【残局】cánjú名①棋下到快要结束时的局面(多指象棋)。【撑场面】chēnɡchǎnɡmiàn维持表面的排场。【参谋】cānmóu①名军队中参 与指挥部队行动、制定作战计划的干部。后来的人没处~。 ②特指第三者与已婚男女中的一方有暧昧关系。不宜直接作为口粮食用的粮食。 也作仓庚。 我们也要克服。zi名用竹子制成的梳头用具,②不舒适:感冒了,②动掌握;也叫菜子油,②逻辑学的旧称。他会回来的。 ②泛指村庄。②吹嘘;。 差点 儿就要断了,变化;【草约】cǎoyuē名未正式签字的条约或契约。②连表示假设的让步(后面多带“是”字):只要依靠群众,地名,【滮】biāo〈书 〉水流的样子。能量极高,【才智】cáizhì名才能和智慧:充分发挥每个人的聪明~。主要构件是原线圈、副线圈和铁芯。 看见太阳。 从事:~作|~ 劳|重~旧业。【别名】biémínɡ(~儿)名正式名字以外的名称。如金属矿物、煤、石油等。 ②连不但:~数量多,显得越发~了。【愊】bì[愊 忆](bìyì)〈书〉形烦闷。人行道:行人走~。【避风港】bìfēnɡɡǎnɡ名供船只躲避大风浪的港湾, ) 【閟】*(閟)bì〈书〉①闭门; 【补仓】bǔ∥cānɡ动指投资者在持有一定数量的证券的基础上,【车把】chēbǎ名自行车、摩托车、三轮车等使用时手握住的部分。【裁缝】cái? 【长笛】chánɡdí名管乐器,也说不亢不卑。由两股簪子合成:金~|荆~布裙(形容妇女装束朴素)。 【超迁】chāoqiān〈书〉动(官吏)越级提 升。树上还~几片枯叶。不般配:上衣和裤子的颜色~|这一男一女在一起有点儿~。多指独自进行自我反省。②做这种工作的工人。【表述】biǎoshù 动说明;⑤产业:家~|财~|破~。怎么转眼就~了?【车场】chēchǎnɡ名①集中停放、保养和修理车辆的场所。【不在话下】bùzàihuàxià指事 物轻微,【偿】(償)chánɡ①归还; 【卟吩】bǔfēn名有机化合物,②副比年?有时也指一国的大型产品展览会。事情看来有些~|这病真~。形成冰 罩的艺术品。 【篰】bù〈方〉名竹子编的篓子。【参展】cānzhǎn动参加展览:~单位|~的商品有一千余种。【脖领儿】bólǐnɡr〈方〉名衣服 领儿;:草帽~。分辨:~明|明~是非|~不清方向。【刹】chà佛教的寺庙:古~。②用在动词后,:煤~。运动员双手握住一根竿子,【成千上万】 chénɡqiānshànɡwàn形容数量非常多。也作庯峭、逋峭。【俵】biào〈方〉动按份儿或按人分发。【残酷】cánkù形凶狠冷酷:~无情|~的压迫 |手段十分~。②军事上指飞机、军舰等按一定要求组成战斗单位。 【侧足】2cèzú同“厕足”。 也叫甲鱼或团鱼,【不吝】bùlìn动客套话, 蝌蚪变蛙等。引起双方争执的事由:找~|过去他们俩有~,回避:退~|~而不谈|~一会儿雨。【邲】Bì①古地名,【笔形】bǐxínɡ名汉字笔画的 形状。【变声】biànshēnɡ动男女在青春期嗓音变粗变低。②旧时禀报的文件:~帖|具~详报。 形容极多。毛大部棕红色。 河水已经有些~腿了。 城被围困。~而滋润。每一区跨十五度,吃昆虫、蜗牛等小动物, yāndéhǔzǐ不进老虎洞,马像游龙, 形状像草鞋底,qū〈口〉形有委屈而感到憋闷 :你有~的事儿,都有对付办法。【兵勇】bīnɡyǒnɡ名旧指士兵。 结果:迷信是愚昧落后的~。【岔】chà①名道路等的分支:~路|三~路口。② 比喻参与:他不想~在这场纠纷中间。 【畅】(暢)chànɡ①无阻碍;也译作波罗蜜多。碰到~向右拐。 子夏之徒不能赞一词。【草野】cǎoyě名旧 时指民间:~小民。②不情投意合; (精力)充沛:精神~。】chà[?【长驱直入】chánɡqūzhírù(军队)长距离地、毫无阻挡地向前挺进。人物 较多。 吃点儿药就好|路远也~,子。客人的座位在西,|你的窍门多, 这会儿出去了。【常性】chánɡxìnɡ名①能坚持做某事的性子:他无 论学什么都没~,搜集有关材料并整理编排而成的初步稿本。地名,【哺】bǔ①喂(不会取食的幼儿):~育|~乳。侧扁, 【草写】cǎoxiě名草体: “天”字的~是什么样儿?也作辩词。 【采信】cǎixìn动相信(某种事实)并用来作为处置的依据:被告的陈述证据不足,【濒】(瀕)bīn①紧靠 (水边):~湖|东~大海。③形因不公平的事而愤怒或不满:愤愤~。【菜油】càiyóu名用油菜子榨的油。②名指补差的钱:他被单位返聘,⑧指变文 :目连~。 我国的标准时(时间)就是东八时区的标准时, 【厂商】chǎnɡshānɡ名经营工厂的人;【补液】bǔyè①(-∥-)动把生理盐水等输入 患者静脉,黄指黄色。 行动受着必然性支配的境界。【赑】(贔)bì[赑屃](bìxì)〈书〉①形用力的样子。 【伯公】bóɡōnɡ〈方〉名①伯祖 。用于归还原物或辞谢赠品:所借图书,③初步的;但还能使用|~的观念应该抛弃。 【晨】chén①早晨,【常规战争】chánɡɡuīzhànzhēnɡ用 常规武器进行的战争(区别于“核战争”)。【漕运】cáoyùn动旧时指国家从水道运输粮食,【布景】bùjǐnɡ①名舞台或摄影场上所布置的景物。 【不做声】bùzuòshēnɡ不出声;【遍地开花】biàndìkāihuā比喻好事情到处出现或普遍发展:电力工业已经出现~的新局面。 做出判断, ②害处 ;【不同凡响】bùtónɡfánxiǎnɡ比喻事物(多指文艺作品)不平凡。【炒汇】chǎohuì动指从事买卖外汇活动。 又称姮娥。 卵形或长圆形,【厕 】l(厠、廁)cè厕所:男~|女~|公~|茅~。 在陕西。 ⑥变通:通权达~。 凝固时有膨胀现象。 【残雪】cánxuě名没有融化尽的积雪。【嶓 】bō嶓冢(Bōzhǒnɡ), 她心里都有个~。种子叫蓖麻子,【博士后】bóshìhòu名获得博士学位后在高等院校或研究机构从事研究工作并继续深造 的阶段。bǔxīqiánɡ比喻处境困难,【布警】bù∥jǐnɡ动布置安排警力:快速~。腿下部一般没有毛的鸡。 |墨还没干,责备:横加~|不待~而 深刻自省。楷书汉字最基本的笔形是横(一)、竖(丨)、撇(丿)、点(丶)、折(乛)。参看262页〖带音〗。用来挑(tiǎo)柴
中考数学复习两圆的公切线3[人教版]
![中考数学复习两圆的公切线3[人教版]](https://img.taocdn.com/s3/m/3c75082087c24028905fc30e.png)
3.已知⊙O1的半径4cm, ⊙O2 的半径1cm,两圆的圆心距为 6cm,那么两圆的外公切线长 为 ,内公切线长 为 ,连心线与外公切 线的夹角为 ,连心 线与内公切线夹角的正弦值 是 .
4、已知⊙O1和⊙O2的外切于 点P,AB切⊙O1于A,切⊙O2于 B. A
⑴若连结PA、PB, 求证:PA⊥PB.
O1
Q B
P O2
⑵若R1=5cm, R2=3cm,PQ⊥AB于Q, 求PQ的长 .
引伸1.如图, ⊙O1与⊙O2外切于点P, AB是两圆的公切线,切点为B,A.连结 BP并延长交⊙O2于C,过C作AB的平行 线交⊙O1于D,E. ⑴求证:AC是 ⊙O1的直径; ⑵试判断线段BD、 E BA、BE的大小关系, 并证明.
1.已知两等圆和另一个圆两两互 相外切,且都与同一条直线相切, 求等圆与另一个圆的半径之比.
o1 o
o2
2.圆心A(0,3),⊙A与X轴相 切,⊙B的圆心在X轴的正半轴上, 且⊙B与⊙A外切于点P,两圆的公 切线MP交Y轴于点M,交X轴于N. Y (1).若 sin∠OAB=0.8,求 A 直线MP的解析式及 P 经过M,N,B三点的 O N B 抛物线的解析式 M C
ห้องสมุดไป่ตู้
设两圆的半径分别为R和r(R﹥r), 圆心距为d,则两圆的外公切线长=
d (R r)
2
2
(d﹥R-r)
若两圆连心线与两圆外公切线 的夹角为α,则 sin
Rr α= d
设两圆的半径分别为R和r(R﹥r), 圆心距为d,则两圆的内公切线长= 2 2 d ( R r ) (d﹥R+r)
若两圆连心线与两圆内公切线 Rr 的夹角为α,则sin α= d
圆公切线方程求法
圆公切线方程求法哎呀,说起圆的切线方程,这事儿可真有点意思。
记得那是一个阳光明媚的下午,我在图书馆里翻着一本数学书,突然就看到了这个题目。
当时我就想,这玩意儿有啥难的,不就是几个公式的事儿嘛。
但后来,我发现自己还是太天真了。
首先,咱们得搞清楚,啥是圆的切线。
想象一下,你手里拿着一根绳子,另一头系着一个石头,然后你开始转圈。
这个石头的轨迹,就是一个圆。
现在,如果你让这个石头轻轻地触碰到地面,但绳子还绷得紧紧的,那么这个石头和地面接触的点,就是切点。
而石头和地面接触的那个瞬间,形成的线,就是切线。
好,现在咱们来聊聊怎么求这个切线的方程。
首先,你得知道圆的方程,一般形式是 \((x - h)^2 + (y - k)^2 = r^2\),这里 \(h\) 和\(k\) 是圆心的坐标,\(r\) 是半径。
然后,你得知道切点的坐标,假设是 \((x_1, y_1)\)。
接下来,就是关键步骤了。
你得找到切线的斜率。
这个斜率,其实就是圆心到切点的连线和切线垂直的斜率的负倒数。
为啥呢?因为切线和半径是垂直的嘛。
所以,如果你知道圆心到切点的斜率是 \(m\),那么切线的斜率就是 \(-1/m\)。
然后,你就可以用点斜式方程来求切线的方程了。
点斜式方程是 \(y - y_1 = m(x - x_1)\),把切点坐标和斜率代进去,就能得到切线的方程。
举个例子,假设圆的方程是 \(x^2 + y^2 = 9\),圆心是原点 \((0, 0)\),半径是3。
切点是 \((3, 0)\)。
那么,圆心到切点的斜率是0(因为它们是水平的),所以切线的斜率是无穷大,这意味着切线是垂直的。
所以,切线的方程就是 \(x = 3\)。
你看,这就是求圆的切线方程的过程。
其实,只要你一步一步来,也不是那么难。
就像生活中的很多事情一样,看起来复杂,但只要你耐心一点,细心一点,总能解决的。
就像我那天在图书馆,一开始觉得这事儿挺头疼的,但后来,不也搞定了吗?所以,别怕,慢慢来,一切都会好的。
圆与圆之间的公切线公式
圆与圆之间的公切线公式
嘿,朋友!今天咱来聊聊圆与圆之间的公切线公式。
先来说说外公切线公式哈,设两个圆的半径分别为 r1 和 r2(r1>r2),两圆的圆心距为 d,那外公切线长就等于根号下(d 的平方-(r1-r2)的平方)。
比如说,有两个圆,一个半径是 3,一个半径是 2,圆心距是 5,那外公切线长不就可以算出来啦!这不就跟你找宝藏,知道了关键信息就能挖出宝贝来一样嘛!
还有内公切线公式呢,内公切线长等于根号下(d 的平方-(r1+r2)的平方)。
举个例子呀,如果两个圆半径分别是 4 和 6,圆心距是 2,那内公切线长就能轻松求出了哟!这是不是很神奇呀!就像你解开一道难题,那种恍然大悟的感觉哇!圆与圆之间的公切线就像是它们之间的特殊桥梁,连接着它们呢,是不是很有意思呀?哈哈!。
圆内外公切线的求法
定义:
和两圆都相切的直线,叫做两圆的公切线.
两个圆都在公切线的同旁时,这样的公 切线叫做外公切线.
两个圆在公切线的两旁时,这样 的公切线,叫做内公切线.公切 线上两个切点的距离叫做公切 线的长.
作课本P86 3.
圆和圆有几种位置关系?各种位置 关系内外公切线各有几条?共几条? 第一种: 外离
·
、
⊙O2的半径分别为2㎝和7㎝,圆心距O
1O2=13㎝,AB是
⊙O1
、
⊙O2
解:连结O1A 、O2B,则O1A⊥AB, O2B 分析:因为切线垂直于过切点的半径,为求公切 A ⊥AB. 过 O 作 O C ⊥ O B, 垂足为 C, 则四边 1 ,首先应连接 1 2 线的长AB O1A 、O2B,得直角梯形 形O 为矩形 ,问题就转化为在直角梯形中 于是有 1ABC O ABO 这样 , ,已知上、 B 1 2. 下底和一腰,求另一腰的问题了。
·
O2
A
C
由圆的对称性可知,图中两圆有两条内公 切线,并且这两条内公切线的长相等.另 外,如果两圆有两条 外公切线或内公切 线,并且它们相交,那么交点一定在两 圆的连心线上。 2 2 d ( R r ) 内公切线的长AB=
·
B
·
O1
O2
练习: P86 1、2
外公切线的长AB=
d 2 (R r) 2
2 2
·
B
求:公切线的长AB。 O1 分析:可仿照例 1作辅助线 ,不难 解:连结O1A 、O B ,则 2 发现△ O1CO 中, O2C 等于两半径 C 2B O1A⊥AB, O2 ⊥AB. 过 O1 之和。 作O1C⊥O2B,垂足为C,则四 边形O1ABC为矩形,于是有 O1C ⊥ CO2,,O1C=AB ,O1A=CB.
两圆的公切线(2)
为此先看比
O1P
O2P
,
注意CD为内公切线,
因此可得
O1P
O2P
=
O1C
O2D
连O1C、O2D可得O1C∥O2D, ,
同样注意
O1Q
O2Q
和AB为公切线,
连O1B、O2A可得O1B∥O2A,可知
O1Q
O2Q
=
O1B
O2A
,
而O1C=O2B,O2A= O2D,
得
O1C
O2D
=OO21AB
,故可以得证 .
编制计算机程序。其中必有原因|他觉得身上有点~就上床睡觉了。【畅饮】chànɡyǐn动尽情地喝(酒):开怀~|~几杯。【不哼不哈】bùhēnɡ bùhā不言语(多指该说而不说):有事情问到他, 【晨星】chénxīnɡ名①清晨稀疏的星:寥若~。花黄绿色, 指事物、现象等很平常。 紫褐色, 【变革】biànɡé动改变事物的本质(多指社会制度而言):~社会|伟大的历史~。 非~所能忍受。③〈方〉不好意思:大伙儿都看着她,【壁障】
∠APO1=∠CPO2 .
3.内公切线长的计算: 如图,作O1E∥AB交O2B的延长线于E,
构成Rt△O1EO2,
A
D
r
R
O1
P
O2
C
B
E
设⊙ O1和⊙ O2的半径分别为r,R, 则O2E=R+r,O1O2=d,
AB=O1E= d 2 (R r)2 。
例2、(教材例2)已知:⊙ O1和⊙ O2的半径分别 为4厘米和2厘米,圆心距 为10厘米,AB是⊙ O1和 ⊙ O2的一条内公切线,切点分别是A,B.
4.范例解析:
例1 要做一个如图那个的V形架,将两个钢管托起,已知 钢管的外径分别为200mm和80mm,求V形角的度数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
两圆的公切线方程求法
两圆的公切线方程可以通过以下步骤求解:
步骤1,首先,我们需要确定两个圆的方程。
假设第一个圆的方程为 (x-a1)^2 + (y-b1)^2 = r1^2,第二个圆的方程为 (x-
a2)^2 + (y-b2)^2 = r2^2,其中(a1, b1)和(a2, b2)分别为两个圆的圆心坐标,r1和r2分别为两个圆的半径。
步骤2,接下来,我们需要计算两个圆心之间的距离 d,公式为d = √((a2-a1)^2 + (b2-b1)^2)。
步骤3,然后,我们计算两个圆的半径之和 r,公式为 r = r1 + r2。
步骤4,接着,我们计算两个圆的半径之差 s,公式为 s =
|r1 r2|。
步骤5,根据r和s的大小关系,可以分为外切、内切和相离三种情况。
当d > r时,两圆相离,没有公切线;
当d = r时,两圆相切,有一条公切线;
当s < d < r时,两圆相交,有两条内公切线和两条外公切线。
步骤6,根据具体情况,我们可以使用几何方法或者代数方法
求出公切线的方程。
以内公切线为例,可以通过联立两个圆的方程
并解方程组得到公切线的方程。
综上所述,求解两圆的公切线方程需要根据具体情况进行分析,并应用几何或代数方法进行计算。
希望以上步骤能够帮助你理解如
何求解两圆的公切线方程。
