棱台结构特征
棱锥棱台的结构特征

棱锥棱台的结构特征
棱锥和棱台是几何图形中的一种,它们有着特殊的结构特征。
棱锥是
一种三维图形,由一个多边形的底面和与底面连接的直线段(称为侧面)
组成。
而棱台则是一种棱锥的特殊情况,它的底面和顶面是相同的多边形。
下面将对棱锥和棱台的结构特征进行详细描述。
1.棱锥的结构特征:
棱锥的底面是一个多边形,它可以是任意形状的多边形,如三角形、
四边形、五边形等。
棱锥的顶点称为顶点,它是由底面直线段的所有端点
连接而成。
棱锥的侧面由顶点和底面上的各个点以直线段连接而成,每个
侧面都是一个三角形。
2.棱台的结构特征:
棱台是一种特殊的棱锥,它的底面和顶面是相同的多边形。
棱台的底
面和顶面可以是任意形状的多边形,如三角形、四边形、五边形等。
棱台
的侧面是由底面和顶面上的各个点以直线段连接而成,每个侧面都是一个
梯形或者矩形。
总结:
棱锥和棱台的结构特征可以归纳为以下几点:
1.棱锥由一个底面和连接底面和顶点的直线段组成,侧面为三角形。
2.棱台是一种特殊的棱锥,其底面和顶面相同,侧面为梯形或矩形。
3.棱锥和棱台的底面可以是任意形状的多边形,如三角形、四边形等。
4.棱锥和棱台的顶点为连接底面各个点的直线段的交点。
5.棱锥和棱台的侧面为由底面和顶面上的各个点以直线段连接而成的三角形、梯形或矩形。
棱锥和棱台在几何学中有着广泛的应用,例如在建筑设计、工程测量和计算几何等领域。
他们的结构特征使得它们成为解决空间问题的重要工具,并且在实际应用中具有较高的实用价值。
棱台的结构特征

棱台的结构特征
棱台是一种几何体,由一个上底面和一个下底面组成,中间有若干个
侧面连接两个底面。
其结构特征主要包括以下几个方面:
1. 底面形状:棱台的上底面和下底面可以是任意多边形,如三角形、
四边形、五边形等。
不同的底面形状会影响到棱台的稳定性和美观度。
2. 侧面数量:棱台的侧面数量取决于其底面的边数。
例如,一个三角
形作为上下底面的棱台只有三个侧面,而一个六边形作为上下底面的
棱台则有六个侧面。
3. 侧棱长度:棱台的侧棱长度可以相等也可以不等,这取决于设计者
的要求。
如果所有侧棱长度相等,则该棱台称为正棱台;否则称为斜
棱台。
4. 顶点高度:顶点高度是指从上底面到顶点的垂直距离。
不同顶点高
度会导致不同大小和比例的侧面。
5. 对称性:如果上下底面相等并且对称,则该棱台具有轴对称性。
具
有轴对称性的棱台可以看作是由两个相同的三角形或多边形沿着它们
的公共边旋转而成。
6. 稳定性:棱台的稳定性取决于其底面和侧面的形状以及侧面与底面
的夹角。
如果侧面与底面夹角小于90度,则棱台更稳定;否则,棱台容易倾斜或倒塌。
总之,棱台具有多样化的结构特征,不同的设计要求会导致不同形状、大小和比例的棱台。
理解这些结构特征对于设计和制造高质量的棱台
至关重要。
高中数学知识点:棱台和圆台的结构特征

高中数学知识点:棱台和圆台的结构特征
1、定义:用一个平行于棱锥(圆锥)底面的平面去截棱锥(圆锥),底面和截面之间的部分叫做棱台(圆台);原棱锥(圆锥)的底面和截面分别叫做棱台(圆台)的下底面和上底面;原棱锥(圆锥)的侧面被截去后剩余的曲面叫做棱台(圆台)的侧面;原棱锥的侧棱被平面截去后剩余的部分叫做棱台的侧棱;原圆锥的母线被平面截去后剩余的部分叫做圆台的母线;棱台的侧面与底面的公共顶点叫做棱台的顶点;圆台可以看做由直角梯形绕直角边旋转而成,因此旋转的轴叫做圆台的轴.
2、棱台的表示方法:用各顶点表示,如四棱台1111ABCD A B C D -;
3、圆台的表示方法:用表示轴的字母表示,如圆台OO ';
要点诠释:
(1)棱台必须是由棱锥用平行于底面的平面截得的几何体.所以,棱台可还原为棱锥,即延长棱台的所有侧棱,它们必相交于同一点.
(2)棱台的上、下底面是相似的多边形,它们的面积之比等于截去的小棱锥的高与原棱锥的高之比的平方.
(3)圆台可以看做由圆锥截得,也可以看做是由直角梯形绕其直角边旋转而成.
(4)圆台的上、下底面的面积比等于截去的小圆锥的高与原圆锥的高之比的平方.。
教学设计1:1.1.2 棱柱、棱锥和棱台的结构特征
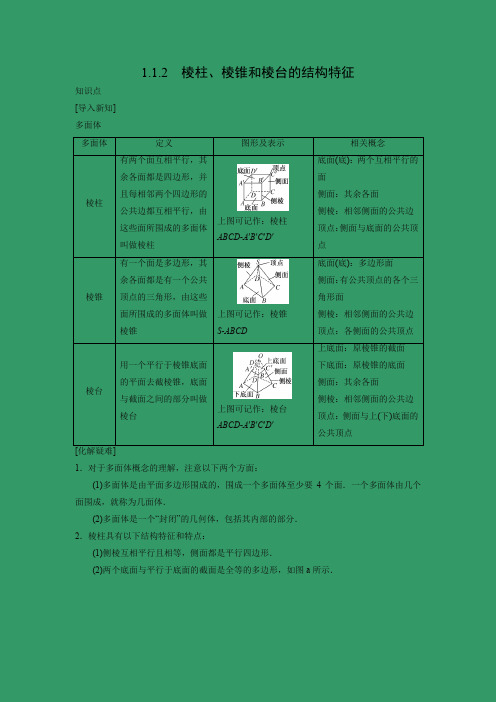
1.1.2棱柱、棱锥和棱台的结构特征知识点[导入新知]多面体多面体定义图形及表示相关概念棱柱有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱上图可记作:棱柱ABCDA′B′C′D′底面(底):两个互相平行的面侧面:其余各面侧棱:相邻侧面的公共边顶点:侧面与底面的公共顶点棱锥有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥上图可记作:棱锥SABCD底面(底):多边形面侧面:有公共顶点的各个三角形面侧棱:相邻侧面的公共边顶点:各侧面的公共顶点棱台用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分叫做棱台上图可记作:棱台ABCDA′B′C′D′上底面:原棱锥的截面下底面:原棱锥的底面侧面:其余各面侧棱:相邻侧面的公共边顶点:侧面与上(下)底面的公共顶点[化解疑难]1.对于多面体概念的理解,注意以下两个方面:(1)多面体是由平面多边形围成的,围成一个多面体至少要4个面.一个多面体由几个面围成,就称为几面体.(2)多面体是一个“封闭”的几何体,包括其内部的部分.2.棱柱具有以下结构特征和特点:(1)侧棱互相平行且相等,侧面都是平行四边形.(2)两个底面与平行于底面的截面是全等的多边形,如图a所示.(3)过不相邻的两条侧棱的截面是平行四边形,如图b所示.(4)有两个面平行,其余各面都是平行四边形的几何体不一定是棱柱,如图c所示.3.对于棱锥要注意有一个面是多边形,其余各面都是三角形的几何体不一定是棱锥,必须强调其余各面是共顶点的三角形,如图d所示.4.棱台中各侧棱延长后必相交于一点,否则不是棱台.题型一棱柱的结构特征[例1]下列关于棱柱的说法:(1)所有的面都是平行四边形;(2)每一个面都不会是三角形;(3)两底面平行,并且各侧棱也平行;(4)被平面截成的两部分可以都是棱柱.其中正确说法的序号是________.【答案】(3)(4)[类题通法]有关棱柱的结构特征问题的解题策略(1)紧扣棱柱的结构特征进行有关概念辨析.①两个面互相平行;②其余各面是四边形;③相邻两个四边形的公共边互相平行.求解时,首先看是否有两个平行的面作为底面,再看是否满足其他特征.(2)多注意观察一些实物模型和图片便于反例排除.[活学活用]下列说法正确的是()A.有两个面平行,其余各面都是四边形的几何体叫棱柱B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱C.各个侧面都是正方形的四棱柱一定是正方体D.九棱柱有9条侧棱,9个侧面,侧面均为平行四边形【答案】D题型二棱锥、棱台的结构特征[例2]下列关于棱锥、棱台的说法:(1)用一个平面去截棱锥,底面和截面之间的部分组成的几何体叫棱台;(2)棱台的侧面一定不会是平行四边形;(3)棱锥的侧面只能是三角形;(4)由4个面围成的封闭图形只能是三棱锥;(5)棱锥被平面截成的两部分不可能都是棱锥.其中说法正确的序号是________.【答案】(2)(3)(4)[类题通法]判断棱锥、棱台形状的两个方法(1)举反例法:结合棱锥、棱台的定义举反例直接判断关于棱锥、棱台结构特征的某些说法不正确.(2)直接法:判定方法棱锥棱台定底面只有一个面是多边形,此面即为底面两个互相平行的面,即为底面看侧棱相交于一点延长后相交于一点[活学活用]下列说法正确的有()①由5个面围成的多面体只能是四棱锥;②仅有两个面互相平行的五面体是棱台;③两个底面平行且相似,其余各面都是梯形的多面体是棱台;④有两个面互相平行,其余4个面都是等腰梯形的六面体是棱台.A.0个B.1个C.2个D.3个【答案】A题型三多面体的平面展开图[例3]如下图是三个几何体的侧面展开图,请问各是什么几何体?解由几何体的侧面展开图的特点,结合棱柱,棱锥,棱台的定义,可把侧面展开图还原为原几何体,如图所示:所以①为五棱柱,②为五棱锥,③为三棱台.[类题通法]1.解答此类问题要结合多面体的结构特征发挥空间想象能力和动手能力.2.若给出多面体画其展开图时,常常给多面体的顶点标上字母,先把多面体的底面画出来,然后依次画出各侧面.3.若是给出表面展开图,则可把上述程序逆推.[活学活用]水平放置的正方体的6个面分别用“前面、后面、上面、下面、左面、右面”表示,如图是一个正方体的表面展开图(图中数字写在正方体的外表面上),若图中“0”上方的“2”在正方体的上面,则这个正方体的下面是()A.1B.5C.快D.乐【答案】B易错易误辨析1.柱、锥、台结构特征判断中的误区[典例]如下图所示,下列关于这个几何体的正确说法的序号为________.①这是一个六面体;②这是一个四棱台;③这是一个四棱柱;④此几何体可由三棱柱截去一个三棱柱得到;⑤此几何体可由四棱柱截去一个三棱柱得到.【解析】①正确,因为有6个面,属于六面体的范围;②错误,因为侧棱的延长线不能交于一点,所以不正确;③正确,如果把几何体放倒就会发现是一个四棱柱;④⑤都正确,如下图所示.【答案】①③④⑤[易错防范]1.解答过程中易忽视侧棱的延长线不能交于一点,直观感觉是棱台,而不注意逻辑推理.2.解答空间几何体概念的判断题时,要注意紧扣定义,切忌只凭图形主观臆断.[成功破障]如图所示,将装有水的长方体水槽固定底面一边后倾斜一个小角度,则倾斜后水槽中的水形成的几何体是()A.棱柱B.棱台C.棱柱与棱锥的组合体D.不能确定【答案】A当堂检测1.下列图形中,不是三棱柱的展开图的是()【答案】C2.如图所示,在三棱台ABCA′B′C′中,截去三棱锥A′ABC,则剩余部分是()A.三棱锥B.四棱锥C.三棱柱D.组合体【答案】B3.面数最少的棱柱为________棱柱,共有________个面围成.【答案】三54.如图所示,M是棱长为2 cm的正方体ABCDA1B1C1D1的棱CC1的中点,沿正方体表面从点A到点M的最短路程是________ cm.【答案】135.如图所示,长方体ABCD A1B1C1D1.(1)这个长方体是棱柱吗?如果是,是几棱柱?为什么?(2)用平面BCNM把这个长方体分成两部分,各部分形成的几何体还是棱柱吗?如果是,是几棱柱,并用符号表示;如果不是,请说明理由.解:(1)是棱柱,并且是四棱柱,因为长方体相对的两个面是互相平行的四边形(作底面),其余各面都是矩形(作侧面),且相邻侧面的公共边互相平行,符合棱柱的定义.(2)截面BCNM的上方部分是三棱柱BB1MCC1N,下方部分是四棱柱ABMA1DCND1.。
棱柱、棱锥、棱台的结构特征

A
B
侧面与底面的公共顶点. 底面
C顶 点
棱柱的结构特征
棱柱的分类 1、按侧棱与底面是否垂直可分为: 1) 侧棱不垂直于底的棱柱叫做斜棱柱。
2)侧棱垂直于底的棱柱叫做直棱柱。
3) 底面是正多边形的直棱柱叫做正棱 柱。
2、按底面的边数分为:
棱柱的底面可以是三角形、四边形、 五边形、……
把这样的棱柱分别叫做三棱柱、四棱 柱、五棱柱、……
长方体:侧面和底面都是矩形的棱柱. 正方体:侧面和底面都是正方形的棱柱.
1.1 棱柱、棱锥、棱台的结构特征
棱柱 棱锥 棱台
棱锥结构特征
有一个面是多
边形,其余各面都
是有一个公共顶点
的三角形。
侧棱
A
顶点 S
侧面
D
C
底面
B
棱锥的结构特征
1.棱锥的概念:
一般地,有一个面是 多边形,其余各面都是 有一个公共顶点的三角 形,由这些面所围成的 几何体叫做棱锥.
四棱锥
五棱锥
棱柱 棱锥 棱台
棱台结构特征
用一个平行于棱
D’
锥底面的平面去截棱
D
锥,底面与截面之间 A’
的部分是棱台.
A
C’
B’
C
B
棱台的结构特征
1.棱台的概念:
棱台的底面:
原棱锥的底面和截
面分别叫做棱台的下底
面和上底面。
侧
棱
上底面
侧 面
下底面 顶 点
棱台的结构特征
1.棱台的概念:
用一个平行于棱锥底 面的平面去截棱锥,底 面与截面之间的部分, 这样的多面体叫做棱台.
图形
相关 概念
面:围成多面体的各个
棱台的结构特征-高中数学知识点讲解

棱台的结构特征
1.棱台的结构特征
【知识点的认识】
1.棱台:棱锥被平行于底面的平面所截,截面和底面间的部分叫做棱台.
2.认识棱台
棱台的上底面:原棱锥的截面叫做棱台的上底面.
棱台的下底面:原棱锥的底面叫做棱台的下底面.
棱台的侧面:棱台中除上、下底面外的所有面叫做棱台的侧面.
棱台的侧棱:相邻两侧面的公共边叫做棱台的侧棱.
棱台的高:当棱台的底面水平放置时,铅垂线与两底面交点间的线段或距离叫做棱台的高.
棱台的斜高:棱台的各个侧面的高叫做棱台的斜高.
3.棱台的结构特征
1.底面是多边形
棱台{
2.侧面是梯形
3.两底面互相平行
4.平行于底面的截面与底面相似
正棱台的性质:
(1)侧棱相等,侧面是全等的等腰梯形,斜高相等.
(2)两底面中心连线、相应的边心距和斜高组成一个直角梯形;两底面中心连线、侧棱和两底面相应的半径也组成一个直角梯形.
(3)棱台各棱的反向延长线交于一点.
4.棱台的分类
由三棱锥,四棱锥,五棱锥,…等截得的棱台,分别叫做三棱台,四棱台,五棱台,…等.
正棱台:由正棱锥截得的棱台叫做正棱台.
5.棱台的体积公式
设棱台上底面面积为S,下底面面积为S′,高为h,
1/ 2
V 棱台=1
3×(푆+푆′+푆×푆′)
×ℎ.
2/ 2。
课件9:1.1.2 棱柱、棱锥和棱台的结构特征

题型二:简单几何体中的计算问题 [典例] 正三棱锥的底面边长为 3,侧棱长为 2 3,求正三棱锥的高.
[解] 作出正三棱锥如图,SO 为其高,连接 AO,作 OD⊥AB 于 点 D,则点 D 为 AB 的中点. 在 Rt△ADO 中,AD=32,∠OAD=30°,
3 故 AO=cos∠2OAD= 3. 在 Rt△SAO 中,SA=2 3,AO= 3, 故 SO= SA2-AO2=3,其高为 3.
延长线交于一点;④有两个面互相平行,其余各面都是梯形,则此几何体是棱台.
A.①
B.②
C.③
D.④
(2)下列命题:
①各侧面为矩形的棱柱是长方体;②直四棱柱是长方体;
③侧棱与底面垂直的棱柱是直棱柱;④各侧面是矩形的直四棱柱为正四棱
柱.其中正确的是________(填序号).
[解析] (1)棱锥的侧面是有公共顶点的三角形,但是各侧棱不一定相等,故 ①②不正确;棱台是由平行于棱锥底面的平面截棱锥底面得到的,故各个侧 棱的延长线一定交于一点,③正确;棱台的各条侧棱必须交于一点故④错误. (2)①中一定为直棱柱但不一定是长方体;②直四棱柱的底面可以是任意的四 边形不一定是矩形;③符合直棱柱的定义;④中的棱柱为一般直棱柱,它的 底面不一定为正方形. [答案] (1) C (2) ③
(3) 凸 多 面 体 : 把 一 个 多 面 体 的 任 意 一 个 面 延 展 为 平 面 , 如 果 其 余 的 各
面 都在这个平面的同一侧 ,则这样的多面体就叫做凸多面体.
2.棱柱、棱锥、棱台
名称
棱柱
棱锥
棱台
定义
条件:①有两个
互相平行 的面;
条件:①有一个 棱锥被 平行于
面是 多边形 ;
高中数学《棱柱、棱锥、棱台的结构特征 》课件

17
课前自主预习
课堂互动探究
课堂达标自测
课后课时精练
数学 ·必修2
解析 棱柱是由一个平面多边形沿某一方向平移而形 成的几何体,因而侧面是平行四边形,故①对.
棱锥是由棱柱的一个底面收缩为一个点而得到的几何 体,因而其侧面均是三角形,且所有侧面都有一个公共点, 故②对.
棱台是棱锥被平行于底面的平面所截后,截面与底面之 间的部分,因而其侧面均是梯形,且所有的侧棱延长后均相 交于一点(即原棱锥的顶点),故③错④对.⑤显然正确.
所以(1)为五棱柱,(2)为五棱锥,(3)为三棱台.
29
课前自主预习
课堂互动探究
课堂达标自测
课后课时精练
数学 ·必修2
拓展提升 空间几何体的展开图
(1)解答空间几何体的展开图问题要结合多面体的结构 特征发挥空间想象能力和动手能力.
(2)若给出多面体画其展开图,常常给多面体的顶点标 上字母,先把多面体的底面画出来,然后依次画出各侧面.
数学 ·必修2
第一章 空间几何体
1.1 空间几何体的结构 1.1.1 棱柱、棱锥、棱台的结构特征
1
课前自主预习
课堂互动探究
课堂达标自测
课后课时精练
数学 ·必修2
课前自主预习
2
课前自主预习
课堂互动探究
课堂达标自测
课后课时精练
数学 ·必修2
知识点一 空间几何体的定义、分类及相关概念 1.空间几何体的定义
(3)若是给出表面展开图,则按上述过程逆推.
30
课前自主预习
课堂互动探究
课堂达标自测
课后课时精练
数学 ·必修2
【跟踪训练 3】 根据如下图所给的平面图形,画出立 体图.
