电路原理相量法

合集下载

(完整版)电路原理课后习题答案

答：(a）关联——同一元件上的电压、电流的参考方向一致，称为关联参考方向；
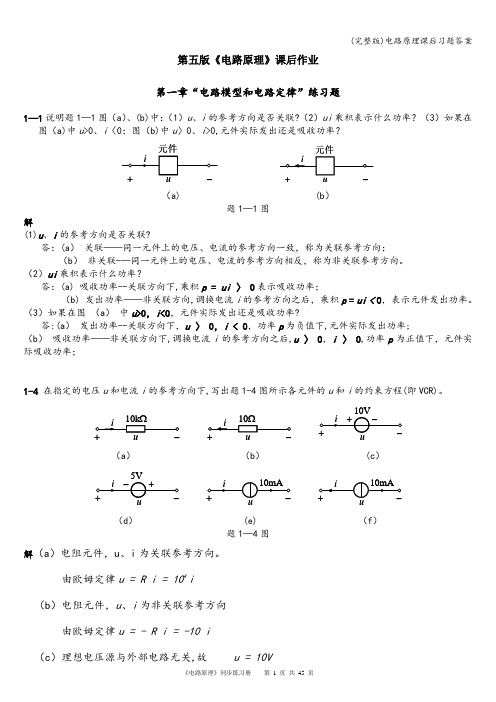
（b）非关联-—同一元件上的电压、电流的参考方向相反，称为非关联参考方向。
（2）ui乘积表示什么功率？
答：(a)吸收功率--关联方向下,乘积p=ui〉 0表示吸收功率；
（b)发出功率——非关联方向,调换电流i的参考方向之后，乘积p=ui<0，表示元件发出功率。
行列式解方程组为
所以
3-11用回路电流法求解题3—11图所示电路中电流I。
题3—11图
解由题已知，
其余两回路方程为
代人整理得
所以
3—12用回路电流法求解题3-12图所示电路中电流及电压 .
题3—12图
3-15列出题3—15图(a)、(b）所示电路的结点电压方程。
（a）(b）
题3-15图
解：图(a)以④为参考结点，则结点电压方程为：
电压源功率（发出30W）
(b）由基尔霍夫电压定律和电流定律可得各元件的电压电流如解1-5图(b)
故电阻功率（吸收45W）
电流源功率（发出30W)
电压源功率（发出15W）
（c)由基尔霍夫电压定律和电流定律可得各元件的电压电流如解1—5图（c）
故电阻功率 (吸收45W)
电流源功率 (吸收30W）
独立的KVL方程数分别为
(1) （2）
3—7题3—7图所示电路中，， , ，， ,用支路电流法求解电流。
题3-7图
解由题中知道， , 独立回路数为由KCL列方程:
对结点①
对结点②
对结点③
由KVL列方程：
对回路Ⅰ
对回路Ⅱ
对回路Ⅲ
联立求得
3—8用网孔电流法求解题3—7图中电流。

正弦量与相量法的基本概念

正弦量与相量法的基本概念
目
CONTENCT
录
• 正弦量定义与性质 • 相量法基础 • 正弦量与相量法的转换 • 交流电路中的相量法应用 • 相量法在电机控制中的应用 • 正弦量与相量法的实验验证
01
正弦量定义与性质
定义
总结词
正弦量是随时间按正弦规律变化的量，通常用复数表示。
详细描述
正弦量是随时间变化的物理量，如交流电电压、电流等。在数学上，正弦量通常用复数表示，其实部表示幅值大小，虚部表示相位。
THANK YOU
感谢聆听
相量法在电机控制中的应用
利用相量法可以简化电机控制中的数学模型，方便分析和设计控制策略。通过将交流电机等效为直流电机，可以使用成熟的直流电机控制方法进行控制。
控制算法
利用相量法，可以设计出各种控制算法，如PI控制器、模糊控制器等，实现对电机的精确控制。
案例分析：无刷直流电机控制
无刷直流电机
无刷直流电机是一种采用电子换向器的直流电机，具有高效、调速范围宽、维护方便等优点。
乘法运算
两个正弦量的乘法运算可以通过复数乘法实现，即对应相量直接相乘。
除法运算
两个正弦量的除法运算可以通过复数除法实现，即对应相量直接相除。
运算规则
在进行相量运算时，应遵循复数的运算法则和运算顺序。
03
正弦量与相量法的转换
转换公式
正弦量与相量法转换公式
$I = I_m angle theta$，其中 $I$ 是正弦量，$I_m$ 是相量，$theta$ 是初相角。
信号处理
在信号处理领域，相量法可用于分析信号的频谱和滤波器的设计。
04
交流电路中的相量法应用

正弦稳态分析--相量法

第6章正弦稳态分析--相量法 (186)学习重点 (186)6.1 正弦量 (186)6.2 复数 (188)6.3正弦交流电的相量表示 (190)6.3.1问题的引入 (190)6.3.2正弦量的相量式表示 (190)6.3.3正弦量的相量图表示 (192)6.3.正弦量的相量表示的应用 (192)6.4 KCL、KVL相量形式 (194)6.5 电阻、电感和电容元件VCR的相量形式 (195)6.6正弦交流电路的阻抗、导纳及等效 (198)6.6.1阻抗的概念 (198)6.6.2 导纳的概念 (200)6.7 正弦稳态电路的一般分析方法 (201)6.7.1 相量法的原理 (201)6.7.2 相量法的一般分析过程 (202)6.7.3 相量图法 (205)6.8 有功功率、无功功率、视在功率和复功率 (206)6.9 正弦稳态电路的功率守恒 (208)6.10 正弦稳态电路的最大功率传输 (212)6.11 仿真实验 (214)习题六 (216)185186第6章正弦稳态分析--相量法学习要点（1）正弦量的三要素及相量表示；（2）复阻抗；（3）KCL 、KVL 的相量形式；（4）有功功率、无功功率、视在功率和复功率。

电路的正弦稳态分析是重要的基础性问题，相量法是分析正弦稳态电路的简便有效的方法，重点理解为什么要引入相量法？相量法与正弦量的关系？引入相量法后，还是利用电路的两大约束，应用电路的基本分析方法，求解电路的相量响应，然后进行相量反变换求出时域响应。

本章涉及到的主要概念：三要素、有效值、相量、阻抗、有功功率、无功功率、视在功率、功率因数、复功率和最大功率传输等问题。

6.1 正弦量在经典电路理论中，一般把方向和大小均呈现周期性变化（交变）的电压、电流等周期函数（信号）作为基本的分析对象。

其中最重要的周期函数就是按正弦规律变化的正弦量。

可以采用sine 或cos 函数描述正弦量，本书采用cos 函数描述正弦量。

电路原理(上)_ 相量法_

2U 2
e
j t
)
Re(
2U1
e
j t
2U
2
e
j
t
)
Re[
2(U1U 2) e
j t ]
相量关系为：
U
U U1 U2
结论：同频正弦量的加减运算变为对应相量的加减运算。
8
相量法的基础
电路原理
i1 i2= i3
I1 I2 I3
例3 u1(t) 6 2cos(314t 30 ) V
u2(t) 4 2cos(314t 60 o) V
u 311.1cos(314t 67) V
试用相量表示i, u。
解
I 100 50A, U 220 67V
例2 已知I 60 30 A , f 50Hz , 试写出电流的瞬时值表达式。
解
i 60 2cos(314t 30) A
6
相量法的基础
相量图
在复平面上用矢量表示相量的图。
u(t) 2Ucos( t θ) U U
j t
Re 2Ie dt Re 2
I j t e
j
dij
dt
IIi
+π
2
II idt j
i 2
11
相量法的基础
电路原理
例4 用相量运算：
i(t)
+R
u(t)
L
-
C
i(t) 2I cos( t i)
u(t) Ri L di 1 idt dt C
| F |
a2 b2
b
或
θ
arctan( ) a
二. 复数运算
Im
b
F

电路原理-相量法

周期电流、电压有效值(effective value)定义
物理意义
直流I
Rห้องสมุดไป่ตู้
交流i
R
W RI T
2
W Ri (t )dt
2 0
T
电流有效值定义为
1 T 2 I i (t )dt T 0
def
有效值也称均方根值 (root-mean-square)
1 同样，可定义电压有效值： U T
8.1 复数
1. 复数的表示形式
Im b 向量 0 a Re 0 F
F=a+jb
( j 1 为虚单位）
Im b F |F|

①代数形式 ②三角形式
F a jb F | F | (cos j sin )
F | F | e j
F | F |
a
Re
③指数形式
④极坐标形式
除法：模相除，角相减
(3.41 j3.657) (9.063 j 4.226)
12.47 j 0.569 12.48 2.61
③ 旋转因子
Im
复数 ejθ =cosθ +jsinθ =1∠θ
F• e j 相当于F逆时针旋转一个角度θ ， ejθ 称为旋转因子。
j >0， u超前i，或i 落后u ，u 比i先到达最大值。 u, i u i
u i
j
O
t
j <0， i 超前 u，或u 滞后 i ，i 比 u 先到达最大值。
特殊相位关系：
①j ＝ 0，同相 u, i u i ②j = (180 ) ，反相 u, i u 0 u, i u i 0 i t

电路原理第八章_相量法

复数复数
—
孙惠英 shy@
上页
下页
返回
第8章
4、正弦量的相量表示法(续）
—
已知正弦量 220√ 2 cos ( ω t－35° ) 有效值相量最大值相量 220/ －35° — 220√ 2 /－35°
已知相量 10/45° and 正弦量的角频率ω 相应的正弦量 — 10 √ 2 cos( ωt + 45° )
0 ωt1
ωt2
ωt
φ
图8-5 用旋转矢量表示的正弦量
孙惠英 shy@
上页
下页
返回
第8章
4、正弦量的相量表示法 F = ⎪F⎪e j(ω t + ϕ )
ejθ = cosθ + jsinθ
设：有一复数
欧拉公式
F = ⎪F⎪ej(ωt + ϕ ) = ⎪F⎪cos(ωt + ϕ) + j⎪F⎪sin(ωt +ϕ) Re [F] = ⎪F⎪cos(ωt + ϕ ) Im [F] = ⎪F⎪sin(ωt + ϕ )
返回
第8章
三、旋转因子
/ϕ 旋转因子: e jϕ = 1 — A = ⎪A⎪ejα Aejϕ = ⎪A⎪ejαejϕ = ⎪A⎪ej(α+ϕ ) ejπ/2 = j1 e－jπ/2 = − j1
+j
Aejϕ
ϕ α
0
A
+1
e－jπ = − 1
孙惠英 shy@
上页
下页
返回
第8章
ϕ 12 = ϕ 1－ ϕ 2 —— u1 超前于 u2 的相角 ϕ 21 = ϕ 2－ ϕ 1 —— u2 超前于 u1 的相角

电路原理-正弦稳态电路的分析

对记录的数据进行分析，验证正弦稳态电路的原理和性质。
实验结果与讨论
实验结果
通过实验观察和数据记录，可以得出正弦稳态电路中电压和电流的波形关系，以及元件参数对波
形的影响。
结果分析
对实验结果进行分析，验证正弦稳态电路的基本原理，如欧姆定律、基尔霍夫定律等。
实验讨论
讨论实验中可能存在的误差来源，如电源稳定性、示波器的测量误差等。同时，可以探讨如何减小误差、提高实验精度的方法。
04 正弦稳态电路的分析实例
单相交流电路分析
总结词
分析单相交流电路时，需要计算电流、电压的有效值以及功率等参数，并考虑阻抗、导纳和相位角等因素。
详细描述
在单相交流电路中，电压和电流都是时间的正弦函数。为了分析电路，我们需要计算电流和电压的有效值，以及功率等参数。此外，还需要考虑阻抗、导纳和相位角等因素，以便更准确地描述电路的性能。
实验步骤与操作
3. 观察波形
2. 连接电源
将电源连接到电路中，为电路提供稳定的交流电压。
使用示波器观察电路中各点的电压和电流波形，并记录数据。
4. 调整元件参数
通过调整电阻器、电容器和电感器的参数，观察波形变化，并记录数据。
1. 搭建正弦稳态电路
5. 分析数据
根据实验要求，使用电阻器、电容器和电感器搭建正弦稳态电路。
相量法
1
相量法是一种分析正弦稳态电路的方法，通过引入复数相量来表示正弦量，将时域问题转化为复数域问题，简化计算过程。
2
相量法的核心思想是将正弦电压和电流表示为复数形式的相量，并利用相量图进行电路分析。
3
相量法的优点在于能够直观地表示正弦量的相位关系和幅度关系，简化计算过程，提高分析效率。

第六章-电路原理-张燕君-清华大学出版社

5. 相序：各相电源经过同一值(如正最大值)的先后顺序
正序(顺序)：A—B—C—A
C
B
A
负序(逆序)：A—C—B—A
B
A C
6. 对称三相电源连接
A +
•
UA
–N
•
C UC
•
UB
•
IA A
•
•
UAB UCA
N
•
B IB
B
I U •
•
C
BC
C
A
•
UC
•
UA
C
– •
+
B
UB
•
IA
A
•
•
U U •
A B CA
U bc
Z
2Iab
•
•
I ca
U ca
Z
Iab
即，相电流对称。
讨论（接）线电流和相电流的关系
•
IA
令
•
I ab
I0o
•
I bc
I 120o
•
I ca
I1 2 0o
a
•
IB
b
•
IC
•
I ab
Z •
Z
I ca
•Z I bc
线电流：
c
•
•
•
I A I ab I ca
3
•
I ab
30o
•
•
•
I B I bc I ab
(3) 线电压大小等于相电的压 3倍, 即Ul 3U p .
(4) 线电压相位领先对应相电压30o。
•
•
UAB U AN

第四章-正弦交流电路的相量法

.
原理：
+.
I
.
U
IC
.
.
I1
IC
R
jL
j 1 C
12
.
U
.
I
.
IC
-
a）
.
b） I 1
图4-11 功率因数的提高
根据图4-11分析如下:
a）电路图； b）相量图
并联电容前，总电流
I
I1
,电压超前电流的相位差为
; 1
并联电容后，总电流
I
I1
IC
,电压超前电流的相位差为 2
因 2 1 故 cos 2 cos 1 首页
U
Z1
+
Z2
•
U2
-
1053.13 -
图4-2 例4-1图
首页
U 2 Z2I (1 j7)1036.87V 7.07 81.87 1036.87 V 70.7 45 V
U1 Z1I (5 j15)1036.87V 15.8171.57 1036.87 V 158.1108.44 V
Y Y
对比可得
Y 1 Z
•
•
当电压、电流关联参考方向时，相量关系式U Z I
也可表示为 U I 或 I YU
Y
首页
二、用复导纳分析并联电路
图4-6所示是多支路并联电路，根据相量形式的基尔霍
夫电流定律，总电流
.
.
.
.
I I1 I2 In
.
.
.
Y1 U1 Y2 U2 Yn Un
因并联电容前后电路消耗的有功功率是相等的,故
并联电容前
P UI1 cos 1

相量分析法

正弦交流电路的分析和计算I U 、若正弦量用相量表示，电路参数用复数阻抗（)表示，则直流电路中介绍的基本定律、定理及各种分析方法在正弦交流电路中都能使用。

Cω C L ωL R R 1jj -→→→、、相量形式的基尔霍夫定律0 KCL ∑=IKVL ∑=U 电阻电路RI U =)(j L X I U =纯电感电路)j (CX I U -= 纯电容电路一般电路ZI U =相量（复数）形式的欧姆定律有功功率P有功功率等于电路中各电阻有功功率之和，或各支路有功功率之和。

iii R I P ∑=12无功功率等于电路中各电感、电容无功功率之和，或各支路无功功率之和。

)(12Ci Li ii X X I Q -=∑的相位差与为ii i I U ϕ无功功率QiQ ϕsin i ii I U ∑=1或iii i I U Pϕcos 1∑= 或一般正弦交流电路的解题步骤1、根据原电路图画出相量模型图(电路结构不变)e I i Uu X C X L R R CL →→→-→→→j j 2、根据相量模型列出相量方程式或画相量图3、用相量法或相量图求解4、将结果变换成要求的形式例1：已知电源电压和电路参数，电路结构为串并联。

求电流的瞬时值表达式。

一般用相量式计算:21212)i ,i I I I→→ 、i IZ Z Z →→→ 21 1)、分析题目：已知:V sin 2220t ωu =Ω400,Ω200Ω100,Ω501====C L X X ,R R 求: i 21i i ,+U-1R CX LX RI1I 2I解：用相量式计算V 0220︒∠=UΩj200100j 11+=+=L X R Z Ω140j j 2-=-=C X Z Ω33440240j 32050j400j200100j400)(j200)(10050︒∠=++=-+-++=Z +U-50ΩI1I 2I 100Ωj200Ωj400Ω-A 330.5334400220︒-∠=︒∠︒∠==Z U I A59.6-0.89330.5j400j200100j4002121︒∠=︒-∠⨯-+-=+=I Z Z Z IA93.80.5330.5j400j200100j2001002112︒∠=︒-∠⨯-++=+=IZ Z Z I )A33(sin 20.5︒-=∴t ωi )A 59.6(sin 20.891︒-=t ωi )A93.8(sin 20.52︒+=t ωi 同理：+U-50ΩI1I 2I 100Ωj200Ωj400Ω-例2：下图电路中已知：I 1=10A 、U AB =100V ，求：总电压表和总电流表的读数。

电路原理6用相量法分析电路的正弦稳态响应

相量图绘制
通过将相量按照比例放置在复平面内，可以直观地表示出各相量之间的关系。
相量图分析
通过观察相量图，可以分析出电路的阻抗、功率和相位差等参数。
相量法的应用场景
01
正弦稳态电路分析
相量法主要用于分析正弦稳态电路，包括交流电路和含有正弦激励的动态电路。
02
交流电路参数计算
03
控制系统分析
利用相量法可以方便地计算交流电路的阻抗、功率和相位差等参数。
03
对于多输入多输出系统，相量法可能无法给出完整的描述。
04
相量法不能处理瞬态响应或非正弦激励的问题。
未来研究方向与展望
01
研究方向
02
深入研究相量法的数学基础和物理意义，提高其理论水平。
探索相量法与其他电路分析方法的结合，如频域分析、时域分
03
析等。
未来研究方向与展望
• 研究如何将相量法应用于非线性系统和时变系统。
实例三：RLC电路的正弦稳态响应分析
总结词
RLC电路的正弦稳态响应具有谐振特性，其频率由L、C和R的比值决定。
详细描述
RLC电路的正弦稳态响应表现为一个具有谐振峰的波形，其频率由电感L、电容C和电阻R的比值决定，即谐振频率f=1/2π√(LC/R^2)。在RLC电路中，当频率f等于谐振频率时，电路的阻抗最小，电流最大；当频率f远离谐振频率时，电路的阻抗增大，电流减小。
相量法简介
定义
01
相量法是一种将正弦稳态的时域问题转化为复数02
通过相量法，可以更方便地分析交流电路的响应，包括电压、
电流和阻抗等。
优势
03
相量法简化了计算过程，使得复杂问题变得简单直观。

电路原理课件第8章相量法

三. 相位差：
两个同频率正弦量相位角之差。
i(t) 0
Im um
设 u(t)=Umcos(w t+ u)
2
i(t)=Imcos(w t+ i)
0
wt
则相位差j : j = (w t+ u)- (w t+ i)
u- i
同频率正弦量的相位差等于它们的初相之差。不同频率的两个正弦量之间的相位差不再是一个常数，而是随时间变动。
j u与i正交; j u与i反相;
2
§8 - 3相量法的基础
1. 正弦量的相量表示
复函数 F F ej(wt)
没有物理意义
F cos(wt ) j F sin(wt Ψ )
若对F取实部：
Re[F] F cos(ωt Ψ ) 是一个正弦量，有物理意义。
对于任意一个正弦时间函数都可以找到唯一的与其对应的复指数函数：
F e j
4、极坐标形式：
F F ej
=|F|
二复数运算
(1)加减运算——代数形式
+j F2
若 F1=a1+jb1
F2=a2+jb2 O
则 F1±F2= (a1±a2) +j (b1±b2)
F= F1 +F1
F1 +1
+j
O - F2
F2 F1
F= F1 - F2 +1
(2) 乘除运算——指数形式或极坐标形式
⑶∫i2dt。
解： ⑴设 i i1 i2 2I cos(wt i ), 其相量为 I=I/Ψi
I I1 I2 10/600A+22/-1500A=（5+j8.66）A+（-19.05-j11）A

第八章相量法

Um U= = 0.707U m 2
1 T u2dt （8-14） T 0
或者： Um = 2U
#
（8-15）
u = 2U cos(t + u )
§8.2 正弦量相位差：两正弦量间的相位之差称为相位差。线性电路中，如果全部激励都是同一频率的正弦量，则电路中的响应一定是同一频率的正弦量。因此，在正弦交流电路中， u,i 常常遇到同频率的正弦量，设任意两个同频率的正弦量 Im u =Umcos(ωt+φu ) Um i = Imcos(ωt+φi ) 从波形图中可看出u和i的频率相同，而振幅、初相不同。
T
V
R
i 在一T内所产生的热量为： Q~= i2Rdt (J)
0
-
I 在一T内所产生的热量为： Q-= I2RT (J)
T
按定义两者的Q应相等，即
0
i2Rdt= I2RT
+ uS -
i
R
由此得有效值定义式：
I=
1 T i2dt T 0
（8-12）
§8.2 正弦量将有效值定义用于正弦电流。设：i =Imcos(ωt+φi )，由（8-12）式得：
§8.3 相量法基础 Im= Ime jφi = Im φi 有效值相量为： I= Ie jφi = I φi （8-18）
（e jφi为旋转因子）（8-19）
任何一个正弦量通过上述变换都可以对应得到（8-19）式。有效值相量与最大值相量的关系为：I = 2I m 例如：已知正弦电压 u = 220 2 cos( 314t + 450 )V 所对应的有效值相量为： U= 220 450
．
．

大学电路第五版知识总结第八章

返回上页下页
②测量中，交流测量仪表指示的电压、电流读测量中，交流测量仪表指示的电压、数一般为有效值。数一般为有效值。 ③区分电压、电流的瞬时值、最大值、有效值的区分电压、电流的瞬时值、最大值、符号。符号。
i , Im , I , u, Um , U
返回
上页
下页
8-3 相量法的基础
i(t) = Im cos(ω t +φ ) = 2I cos(ω t +φ )
返回上页下页
同理，同理，可得正弦电压有效值与最大值的关系
1 U = Um 2
或
Um = 2U
若交流电压有效值为 U=220V ，
注意
U=380V 其最大值为 Um≈311V Um≈537V
工程上说的正弦电压、电流一般指有效值， ① 工程上说的正弦电压、电流一般指有效值，如设备铭牌额定值、电网的电压等级等。但绝缘水平、设备铭牌额定值、电网的电压等级等。但绝缘水平、耐压值指的是最大值。因此，在考虑电器设备的耐耐压值指的是最大值。因此，压水平时应按最大值考虑。压水平时应按最大值考虑。
规定： |ϕ | <π (180°) 规定：
等于初相位之差
返回
上页
下页
ϕ >0， u超前 ϕ 角，或i 滞后 u ϕ 角 (u 比 i 先超前i ，超前
到达最大值) 到达最大值)。
ϕ <0， i 超前 u ϕ 角，或u 滞后 i ϕ 角（ i 比 u 先，
到达最大值）。到达最大值）。 u, i u i
大学电路第五版知识总结第八章电路第五版知识点国际结算第五版第八章电流和电路知识点总结电路基础知识点总结电路知识点总结数字电路知识点总结大学电路知识点总结模拟电路知识点总结电路原理知识点总结

电路原理(邱关源)习题答案第八章相量法

第八章相量法求解电路的正弦稳态响应,在数学上是求非齐次微分方程的特解.引用相量法使求解微分方程特解的运算变为复数的代数运运算,从儿大大简化了正弦稳态响应的数学运算.所谓相量法,就是电压、电流用相量表示, RLC元件用阻抗或导纳表示,画出电路的相量模型,利用KCL,KVL和欧姆定律的相量形式列写出未知电压、电流相量的代数方程加以求解,因此,应用相量法应熟练掌握：(1)正弦信号的相量表示；(2) KCL,KVL的相量表示；(3) RLC元件伏安关系式的相量形式；(4) 复数的运算.这就是用相量分析电路的理论根据.8-1将以下复数化为极坐标形式：(1) Fi=-5-j5；⑵ F2 =-4+ j3；⑶ F3 =20+j40；(4) F4=j10; (5) F5=-3; (6) F6=2.78 +j9.20o解：(1) F1 =-5-j5 = a Z0a = (-5)2 (-5)2 =5.2-5 v1-arctan ——=-135 -5 (因F1在第三象限)故F1的极坐标形式为F1=5%'2/ -135-(2) F2 =—4 + j3=C(Y)2+32/arctan⑶—4)=52143.13：(F2在第二象限)(3)F3 =20+ j40 = J202 +402N arctan(40/20) =44.72/63.43二(4) F4 =10j =10/90 二⑸ F5=-3 = 3/180 二(6)F6 =2.78 + j 9.20 = 32.782+9.202/arctan(9.20/2.78) = 9.61,73.19 ：注：一个复数可以用代数型表示,也可以用极坐标型或指数型表示,即F=a1+ j a2 =a/e =ae ja它们相互转换的关系为：2 2 1-arctan—a〞0 a2 a i和a1 = acosi a2= asin?需要指出的,在转换过程中要注意F在复平面上所在的象限,它关系到日的取值及实部a i和虚部a2的正负.8-2将以下复数化为代数形式：〔1〕F i=10/—73；〔2〕F2 =15/112.6：；〔3〕F3 =1.2/152；〔4〕F4=10/-90 :〔5〕F i =5Z-180=;〔6〕 F i =10/ -1351解：〔1〕 F i =10/— 73°=10xcos〔—73二〕十j10xsin〔—73〕= 2.92 —j9.56⑵ F2=15/112.6〞 = 15cos112.6、15sin112.6' = -5.76+j13.85〔3〕 F3 =1.2/152 口=1.2cos152' + 1.2sin152 0 = —1.O6 + jO.56〔4〕F4 =10=-90*=-jIO〔5〕F1 =5/-180口= -5〔6〕 F i =10/-135,0cos〔-135：〕+10sin〔-135二〕=-7.07-j7.078 —3假设IO./.“十A260 °= 175/中.求A和中.解：原式=100+ Acos600+ ja sin600=175c o s9 + j175s in中根据复数相等的定义,应有实部和实部相等,即Acos60 100 =175cos虚部和虚部相等Asin60 =175sin「把以上两式相加,得等式A2 100 A -20625 -0-100主,1002+4乂20625 1 102.07A = ---------------------------------- 二+解得 2 「202.069.3102.07 ——Asin602sin =-------------- = --------------- — 175 175=30.348-4求8—1题中的F ,F6和F 2/F6.解：F 2 F6=(—4 j3) (2.78 j9.20) =5 143.13 9.61 73.19= 48.05. 216.32 =48.05. -143.684 j3 5. 143.13F 2 F6 = ------------ --- = ----------------- = 0.52 69.942.78 j9.20 9.61 73.198 — 5求8 —2题中的F 1 +巳和E/F 5 o解：F 1 F 5 - 10. - 73 5. - 180= 10cos(-73 ) j10sin(-73 ) -5 =-2.08 - j9.56 =9.78 -102.2710. -73F 1 F 5= ---------------------------- = 2 -73180 =2 1075/-1808 —6 假设.i 1 = -5cos(314t +60)Ai 2 = 10sin(314t + 60)A,i 3 =4cos(314t 60 )A(1)写出上述电流的相量,并绘出它们的相量图； (2)1与心和i1与)的相位差；(3)绘出3的波形图；(4)假设将3表达式中的负号去掉将意味着什么？ (5)求的周期T 和频率f .解：(1) i 1 二一5cos(314t+601 =5cos(314t+60 = —180=) =5cos(314t —120bi 2 =10sin(314t 60 ) = 10cos(314t - 30 )=0.505 所以故i 1 , i 2和i 3的相量表达式为(4)假设将i i (t)中的负号去掉,意味着i i 的初相位超前了 180二.即i i 的参考方向反向.(5) i i (t)的周期和频率分别为2 二 2 二T =——= ------ =0.02s = 20ms314 .1■ ■1f =一 =——= ---- =50 HzT 2 二 0.02注：定义两个同频率的正弦信号的相位差等于它们的初相之差,因此在比拟相位差时,两个正弦量必须满足(1)同频率；(2)同函数,即都是正弦或都是余弦；(3)同符合,即都为正号或都为负号,才能进行比拟.8-7 假设两个同频正弦电压的相量分别为U i =50/30 V ,5 =T00/-150 V ,其频率 f=100Hz .求：5I i ：一 120 A,1210 4:——30 A,13 ：——60 A2 2(3) i i (t)的波形图见题解图(b)所示.13 =1 - 3 - -120 -60 - -180其相量图如题解图(a)所示.(1)写出u i,出的时域形式；(2) 3与弘的相位差.(1)u1(t) = 50.. 2 cos(2 ft 30 ) = 50 .. 2 cos(628t 30 )Vu2(t) =-100.2cos(2二ft-150 ) =100..2cos(628t-150 =180 )V 二100,2cos(628t 30 )V(2)由于U1=50. 30 V ,U2=-100/-150 V =100. 30 V故相位差为中=30<30' = 0：即u1与u2同相位.8-8 ：3(t) =22072cos(314t—120 1Vu2(t) =220,2 cos(314t 30 )V(1)画出它们的波形图,求出它们的有效值、频率f和周期T;(2)写出它们的相量和画出其相量图,求出它们的相位差；(3)如果把电压电的参考方向反向,重新答复(1), (2).解：(1)波形如题解8—8图(a)所示.有效值为u1 =u2 = 220V u2314f1 = f2 =——= ---------------------- =50Hz频率2二2二1 1T1 = T2 0.02 s周期 f 50(2) 5和弘的相量形式为U1 =220 -120 V U2=220 30 V故相位差为 =i - ：2 =-120 -30 <-150 相量图见题解图(b)所示.(3)U2的参考方向反向,u2 (t)变为一u2 (t),有效值、频率和周期均不变,—U 2(t )的相量为 U'2 =220/30—180口=200/—150V故U1和U2的相位差为*=91-中2=-120 -(-150)=30 波形图和向量图见题解图(a)和(b).8 — 9一段电路的电压、电流为：3,u =10sin(10 t - 20 )V i =2cos(103t -50 )A(1)画出它们的波形图和向量图；(2)求出它们的相量差.33解：(1) u =10s lM10 t—20 )=10cos10 t —110 )V ,故 u 和 i 的相量分别为U a =22072cos 侬t +10)V , U b =22045cosgt -110 =)V , U c = 220 2 cos( t 130 )V求：(1) 3个电压的和；(2) U ab ,U bc ； (3)画出它们的相量图--------- ------------- 0 .2 I =-50 A210U =-110 V60 o8-10图示三个电压源的电压分别为:u(a) +1 -------处+e ; c ~ +题解8—10图解：“,u b, U c的相量为U a = 220 10 VU b=220. -110VU c =220. 130 V(1)应用相量法有U a U b U c=220 10 220/ -110 220 130a c=0即三个电压的和u a⑴u b(t) u c⑴=0⑵ U ab =U a -U b =220/10 220/-110 ：= 220 3 40 VU bc =U b -U c =220 -110 -220 130= 220.3 -80 V(3)相量图如题解8—10图所示u c(a)中电压表读数为V 1：30V ； V 2:60V ；图(b)中的V 1 :15V ； 100V .(电压表的读数为正弦电压的有效值.)求图中电压U s .题8—11图解法一：(a)图：设回路中电流「=1/0：根据元件的电压、电流相量关系,可得题8-11图U R = RI = RI 0 =3.0 V U L = jX L l = X L I 90 =6.90 V那么总电压 U S =U R -U L =30 • j60V所以U s 的有效值为US =痴2 +602 = 67.08V(b)图：设回路中电流相量I =1/0二A,由于U R = RI = RI 0 =15 0 VU L —X L I =X L I 90 =80 90 V8-11 图 V 2 :80V . V 3 :题解8—10图元件相量关系后效值关系相位关系相量图电阻R UR = RI R U R =RI R仇=%U C=-jX C I =X C I -90 =100 -90 V所以总电压U S =U R U L U C =15 j80 -100j =15-j 20V故U s的有效值为U S=J132+202=25V解法二：利用相量图求解.设电流「=1/0 '为参考相量,电阻电压U R与「同相位,电感电压U L超前I'90 :电容电压U c要滞后「90［总电压U s与各元件电压向量构成一直角三角形.题解8-11图〔a〕和〔b〕为对应原图〔a〕和〔b〕的相量图.由题解图〔a〕可得U S = . U R U L = 302 602 = 67.08V由题解图〔b〕可得U S = ,U R 〔U C-U L〕2 = 152〔100 -80〕2 = 258V题解8—11图注：这一题的求解说明,R, L, C元件上电压与电流之间的相量关系、有效值和相位关系〔如下表所示〕是我们分析正弦稳态电路的根底,必须很好地理解和掌握.电感LU L = jX L I LU L = jX L 「仇=仇+90二电容CU C = - jX C I C U C = X C I C仇=d -90二1 -----------------------------8—12图示正弦电流电路中,电流表的读数分别为 A ：5A ； A 2：2°A；A 3 :25A o 求：〔1〕图中电流表A 的读数；〔2〕如果维持A 的读数不变,而把电源的频率提升一倍,再求电流表 A 的读数.解法一:〔1〕 R, L, C 并联,设元件的电压为U R 二二U L 二U C 二U 二U 0根据元件电压、电流的相量关系,可得U U I R5/0 AR RU UI L =——=——-90 A - - j20A jXL X L应用KLC 的相量形式,总电流相量为I = I R I L I C =5-j20 j25 = 5 j5 =5' 2 45 A故总电流表的读数.・' =I =5、.2 =7.07A(2)设U R ==U L =U C =U -U — 0U U,,…—『一 ,、一 , I R =- =— =5,0 A. 当电流的频率提图一倍后,由于 R R不变,所以UR -U不I CU- jX C90 = 25 90 = j 25A题8—12图U UIc == = 2 25. 90 =50. 90 A一jX C _j ； 2 cI =I R I L 1c =5-j10 j50 =5 j40即,电流表的读数解法二：利用相量图求解.设U =U /00=U R =U L =Uc 为参考向量,根据元件电压、电流的相位关系知,I R 和U 同相位,1c 超前90： I L 滞后U 901 ■ ■ ■ 相量图如题解8—12图所示,总电流「与I R, I c 和I L 组成一个直角三角形.故电流表的读数为... =\IR(I c -I L )2A即 (1)@ =,52 +(25 -20)2 =7.07A⑵ @ =,52 +(25 -10)2 =40.31A注：从8—11题的解法二,可以体会到应用向量图分析电路的要点,那就是首先要选好一个参考相量,这个参考相量的选择,必须能方便地将电路中其它电变,而X L =2^L 增大一倍,26C 减小一倍,因此,有U 1 ——=—20.jX L j2 L 2所以A - -52 402 -40.31A题解8—12图压、电流相量,根据电路的具体结构及参数特点逐一画出,把所给的条件转化成相量图中的几何关系.最后根据相量图中的相量关系,使问题得到解决.一般对串联电路,选电流作参考方向较方便,如 8-11题.对并联电路,那么选电压作参考相量较方便,如8-12题.有些问题通过相量图分析将很直观和简便.8-13 对RL 串联电路作如下两次测量：(1)端口加90V 直流电压=0)时, 输入电流为3A; (2)端口加f =50H z 的正弦电压90V 时,输入电流为1.8A .求R 和L 的值.题解8—13图解：由题意画电路如题解8—13图所示.(1)当u s 为90V 直流电压时,电感L 看作短路,那么电阻RU-(2)当u s 为90V 交流电压时,设电流「=1/0口=1.8/0二A,根据相量法,U S = RI jX L I =30 1.8 jX L 1.8 U S =90 = 1.8 , 302 X i 2X L= (90)2 -302 =40 】1.8, X L X L 40L = ----- = ------- = -------- 解得 • 2开 100二8-14某一元件的电压、电流(关联方向)分别为下述 4种情况时,它可能是U0.127H 庆什么元件?'u =10cos(10t 十 45 1V (D i =2sin(10t +135)AU = 10. 45 V2即电压、电流同相位,根据元件电压、电流相位关系可知这是一个 5建的电阻元件.(1)把电压变为余弦形式有u=cos(100t - j 90 )V102 U 45 I =0 A(2) u 和i 的相量为J 2V 2U5一二5 45 (1 j); R jX L 那么I.. 255R : ---- ：. iX L ：--- :. i即这是一个「2 的电阻和v 2 的电感的串联组合.3,、.,8—15电路由电压源u s n 00 cos(10 t)V 及R 和L= 0.025H 串联组成.电感端电压的有效值为25V .求R 值和电流的表达式.解：由题意画电路的相量模型如题解 8—15图(a)所示,相量图如题解图 (b)所示.由于100U.2 0X L = L=103 0.025= 25」u =10sin(100t)V(2) i =2cos(100t)AU = -10costV (3) 、i=-sintA；u = 10cos(314t+451V (4)、 i =2cos(314t)A解：(1)把电流变为余弦形式有= 2cos(10t +135、901=2cos(10t + 45°)A,u和i 的相量为题解8—15图由图〔b〕知电阻电压的有效值为U R 66.144R = —R = -------- =66.144' 1所以电阻为I 1「滞后U S的角度(由于是感性电路)为.U L . 25Z= arcsin——=arcsin -------- -- - 20.70U S100 2因此电流的瞬时表达式为i(t) = 2cos(103t -20.70 )A100■ _________I U S— = ------------------------ 2—— =1 -20.70 A也可根据R jX L 66.144 j25得i(t) = 2cos(103t -20.70 )A8-16图示电路I1 =I2 =10A.求I和U S.■ ■ ■ ■ ■解：设U S为参考相量.I1与U S同相位,I2超前U S901相量图如题解8-题解8—16图题解8—16图I = J l2-12 = J102・ 102 =10、,2 A12Z= arctan = arctanl = 4511由电路图知U S = RI1 =10 10 = 100V故U s和「分别为U S -100. 0 VI = I. :Z =10,2 45 A8-17图示电路中1s=2/0 A.求电压u o■■' u u1s = I R ' I L =二 '解：R jX Lu - I S -2 0= 2 45V1 .2 —451即j题8—17图。

第三章相量法

= I m cos(ωt + ψ i ) 则代入上式求得: I =
Em Um ,E = 2 2
（只适合于正弦波）
Im 2
同理:
U=
表达式又可以写成：
i (t ) =
2 I cos( ω t + ψ i ) （A）, u ( t ) =
2 U cos( ω t + ψ u ) （V）
《电路原理》教案
=
∫ Re[
I& m ⋅ e
] ⋅ dt = Re[
∫ I&
m
⋅ e j ω t ⋅dt ]
e jω t & = Re[ I m ⋅ ] jω
& I & Fm = m jω
3. 微分运算：设： i (t )
& = I ∠ψ = I m cos(ωt + ψ i ) ⎯表示为 ⎯⎯→ I m m i
《电路原理》教案
第三章相量法
任课教师：贾玉福
共 10 页
第7页
则：
∑U &
k =1 P
km
=0
或
& ∑U
k =1
P
k
=0
其它定理、方法均由 KCL、KVL 得来,故均可用相量形式表示. 二.R、L、C 元件 VAR 的相量形式 1. 纯电阻：
u R = R ⋅ iR
设： iR
表示为 & = I ∠ψ = 2 I R cos(ωt + ψ i ) ⎯⎯ ⎯→ I R R i
直流产生的热量:
交流产生的热量：
WD = I 2 RT （J）
当 WD = W A 时则： I =
W A = ∫ i 2 Rdt （J）

《电路原理相量法》课件

05 相量法的实验验证
CHAPTER
实验设备与器材
电源
提供稳定的交流电，模拟真实电路中的电源。
电阻、电容和电感
用于构建各种电路，验证相量法的理论。
示波器
用于观察和记录实验中的电压和电流波形。
数据采集器和计算机
用于实时采集和处理实验数据。
实验步骤与操作
3. 开启电源
2. 设置测量参数
设定示波器的采样率、电压范围等参数，确保能够准确记录波形。
音频处理
相量法用于分析声音信号的频率和相位，以进行音频处理和编辑。
谢谢
THANKS
电阻元件的相量模型
总结词
描述电阻元件在相量法中的数学模型和特性。
详细描述
电阻元件的相量模型是一个实数，表示其纯实部的阻抗。在相量图中，电阻元件的相量位于实轴上。
04 相量法的电路分析
CHAPTER
简单电路的相量分析
总结词：简单明了
详细描述：对于简单的电阻、电容、电感电路，可以使用相量法进行直观分析，通过相量图和公式计算得出结果。
《电路原理相量法》ppt课件
目录
CONTENTS
• 相量法简介 • 相量法的数学基础 • 电路元件的相量模型 • 相量法的电路分析 • 相量法的实验验证 • 相量法在日常生活中的应用
01 相量法简介
CHAPTER
相量法的定义
相量法是一种分析正弦稳态电路的方法，通过引入相量来描述正弦量，将时域中的正弦稳态电路转换为复平面上的向量图，从而简化计算过程。
CHAPTER
复数及其运算
复数的定义
由实部和虚部组成的数，表示为 a + bi，其中 a 是实部，b 是虚部，i 是虚数单位。

chapter08相量法电路原理

N
线性
w1
w2
N
线性
w非
线性
不适用 ③ 相量法可以用来求强制分量是正弦量的任意常系数线
性微分方程的特解，即可用来分析正弦稳态电路。
8.3 电阻、电感和电容元件上电压和电流的相量关系
一. 电阻
i(t)
+ uR(t) -
已i知 (t)2Isiw n ty ()
wy 则 u R (t) R (t) i2 R sI itn )(
L
iR
jw L
+ iL
iC
uS
C
-
+ IL
R
US
-
IR
IC
1/jw C R
时域电路
iL iC iR
LdiL1
dt C
iCdt uS
1
RiR C iCdt
时域列写微分方程
相量模型
IL I C IR
jwLILjw1CI C US
RIR
1
jwC
IC
相量形式代数方程
相量模型：电压、电流用相量；元件用复数阻抗或导纳。
画相量图：选电流为参考向量(w L > 1/w C )
ULUUCj来自URIU
j
UX
UR
电压三角形
U UR 2 UX 2
.
IR
+
.
+ UR-
请看演示
三. 相量图
ωy y i(t)2 I sitn i() I I i
wy y u (t)2 U sitn u ( ) U U u
•
U
•
I
yu yi
四. 相量运算
(1) 同频率正弦量相加减

电路原理6.1.1正弦量及其相量表示 - 正弦量及其相量表示1

若j 0，则称 u 超前 i (或称 i 滞后 u )；若j 0，则称 u 滞后 i (或称 i 超前 u )；若j 0，则称 u 和 i 同相；若 j ，则称 u 和 i 反相；若 j 2，则称 u 和 i 正交。同频率正弦量的相位差可通过观察波形确定，在同一个周期内两个波形的极大值(或极小值)间的角度值( 180°)，即为两者的相位差。超前者先达到极值点。相位差与计时零点的选取、变动无关。1Fra bibliotek2Im2
=
Im 2
= 0.707Im
第6章正弦交流电路的稳态分析
四、复数的运算 1.复数的表示形式
1)代数形式 F = a jb
(j = 1)
在数学中虚单位常用i表示，如F=a+bi，但由于在电路
中已用i表示电流，故虚单位改用j表示。
实部虚部
Re[F ] a
Im[F ] = b
复数可用复平面上的向量表示：
imax imin=2Im 称为正弦量的峰－峰值。
第6章正弦交流电路的稳态分析
i = Imcos(ωt + i )
2.角频率
随时间变化的角度(ωt ψi)为正弦量的相位(或相角)。ω
为正弦量的角频率，是正弦量的相位随时间变化的角速度，
即
d
ω = dt (ωt + ψi )
角频率的单位为rad/s。它与正弦量的周期 T 和频率 f 之间的关系为：
F1 F2
j
2 |F2 | F1
F1
1 F2 2 0
+1
j F1
F1
|F2 | 2FF12
0
1 2 F2 +1
第6章正弦交流电路的稳态分析