从几个无穷级数看整数、圆周率和自然对数之底的不寻常的关系公式中没有中文
(完整版)《数学文化赏析》mooc答案

第一章一、多选题(共100.00 分)1.以下关于数学的描述,正确的有(A B)。
A.数学是研究现实世界的空间形式与数量关系的科学。
B.数学是研究模式与秩序的科学C.数学研究事物的物质属性D.数学只是研究数的科学2.以下表述中正确的有(A B C)。
A.数与形是数学科学的两大柱石;B.数与形是万物共性和本质;C.数与形是一个事物的两个侧面,二者有密切联系;D.数与形是不同的事物,也没有关系。
3.下列运动或变换中,属于拓扑变换的有(A C)。
八.橡皮筋拉伸;B.电风扇旋转;C.纸张折叠;D.投影。
4.以下各选项属于数学的特点的有(A C D)。
A.概念的抽象性;B.公式的简洁性;C.推理的严密性;D.结论的确定性。
5.以下选项中,属于数学关注的内容的部分有(A B C D)。
A.一种对象的内在性质;B.不同对象的联系;C.多种对象的共性;D.一组对象的变化规律。
6.数学中概念或定义的形成主要是(A B C)的结果。
A.分类;B.抓本质;C.抓共性;D.推理。
7.按照结构数学的观点,以下对象属于代数结构的有(A C)。
A.加法运算;8.比较大小;C.乘方运算;D.数轴。
8.以下关于公理系统的描述中,正确的有(A B D)。
A.公理之间应该相容;8.公理之间应该独立;C.公理需要证明;D.公理是数学理论正确性的前提。
9.以下推理形式中,属于合情推理的有(A B D)。
C.演绎;D.联想。
10.以下关于归纳推理的叙述中,正确的是(A B D)。
A.归纳推理是从个体认识群体的推理;B.归纳推理是从特殊到一般的推理;C.归纳推理是从一个个体认识另一个个体的推理;D.归纳推理不能保证结论的正确性。
11.以下关于类比推理的叙述中,正确的是(A C D)。
A.类比推理是发散性思维;B.类比推理是从一般到特殊的推理;C.类比推理是从一个个体认识另一个个体的推理;D.类比推理不能保证结论的正确性。
12.以下关于演绎推理的叙述中,正确的是(A B C D)。
级数与派

π=圆周÷直径
1706年,英国人琼斯(William Jones)首 次使用π代表圆周率,原来π是希腊文 πειφερεια(圆周)的字头。
圆周率的起源
最早应用圆周率 的记载,是在公 元前1650年埃及 人写的『赖因德 古本』(Rhind Papyrus)。
破记录的人
直至十六世纪,法国律师韦达(Francois Viete)利 用393216边形,计算出π精确到十个小数位 3.1415926536。 •最后一个用该方法算圆周率的是 德国人科伦(Ludolf van Ceulen), 他的多边形边数已超过三百二十亿 (60×229)。 •他用了几十年时间,在1610年计 算出35个小数位的π。 •因此德国人称圆周率为鲁道夫数 (Rudolfian number)
这样下去,有意义吗?还有研 究π的数学家吗?
拉玛奴江(Ramanujan)
•1887年生于印度一个贫穷的 小镇。
•他没有进过大学,读过的数 学书也不多,全凭自己研究和 发现。 •1913年英国数学家哈地 (G.H.Hardy)认为他是罕有天 才,便帮他到英国去做研究。 •他身体甚差,33岁便死于肺 病。
惊人的计算
利用以往数学家的方法,1853年,英国 的尚克斯(William Shanks)计算出π的607 位小数,打破一切记录。 二十年后,1873年,尚克斯再计算至707 位小数位。 可是他原来在第528位开始算错了,在七 十二年之后才有人发现。 这是血肉之驱计算π值的最后故事了。
1945年,英国教师弗格森 (D.F.Ferguson)花了一年时 间,用纸证明了七十二年 前尚克斯的错误。
中国晚清数学家曾纪鸿(曾国藩之子)曾运 用格雷果里级数,算出π的一百个小数位。
你觉得最经典的数学公式是什么?
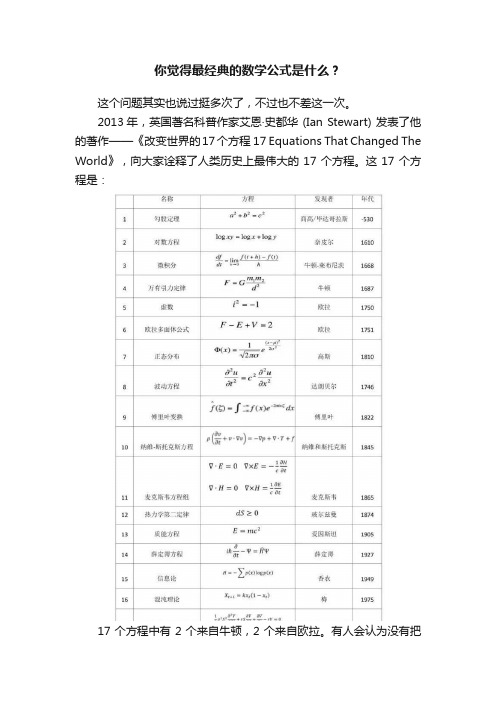
你觉得最经典的数学公式是什么?这个问题其实也说过挺多次了,不过也不差这一次。
2013年,英国著名科普作家艾恩·史都华 (Ian Stewart) 发表了他的著作——《改变世界的17个方程 17 Equations That Changed The World》,向大家诠释了人类历史上最伟大的17个方程。
这17个方程是:17个方程中有2个来自牛顿,2个来自欧拉。
有人会认为没有把欧拉恒等式e^iπ+ 1 = 0 纳入是一大疏忽,欧拉把数学中最基本的5个常数——0、1、圆周率π、自然对数的底e和虚数单位i,以及数学中最基本的两个符号,等号和加号,通过一个简单的恒等式联系在了一起,实在是让人叹服,欧拉恒等式被誉为世界上最美丽的公式。
史都华选中了i^2= -1,可能在《改变世界》和《美》之间他更注重前者。
如果把《改变世界》和《美》折中一下,并且只选择100年前的数学方程,同时抛开在物理、信息论等方面应用的话,可以得到以下10个方程或等式:人类花了千万年来从数量转向数字,数字概念的诞生是一个漫长的思维抽象的过程。
至少3万年以前,人类就已经会计数了,这是人之所以为人的重要转折点,是人类与动物的根本区别之一。
公元前8千年左右,算术诞生了,人类渐渐走上了科学之路,虽然路漫漫其修远兮,但上下求索,一发不可收拾。
1+ 1 = 2 对世界的改变是巨大的,故把它选入放于首位。
至于《爱情曲线》,它源于一个传说:法国数学家笛卡尔在1649年欧洲大陆爆发黑死病时流浪到瑞典,在斯德哥尔摩的街头,52岁的笛卡尔邂逅了18岁的瑞典公主克里斯汀。
几天后,他意外的接到通知,国王聘请他做小公主的数学老师。
跟随前来通知的侍卫一起来到皇宫,他见到了在街头偶遇的女孩子。
从此,他当上了小公主的数学老师。
小公主的数学在笛卡尔的悉心指导下突飞猛进,笛卡尔向她介绍了自己研究的新领域——直角坐标系。
每天形影不离的相处使他们彼此产生爱慕之心,公主的父亲国王知道了后勃然大怒,下令将笛卡尔处死,小公主克里斯汀苦苦哀求后,国王将其流放回法国,克里斯汀公主也被父亲软禁起来。
《从一到无穷大》读后感(精选23篇)

《从一到无穷大》读后感(精选23篇)当品味完一本著作后,相信大家都积累了属于自己的读书感悟,让我们好好写份读后感,把你的收获和感想记录下来吧。
那么你会写读后感吗?下面是小编为大家收集的《从一到无穷大》读后感(精选23篇),仅供参考,希望能够帮助到大家。
《从一到无穷大》读后感篇1花了两个多小时的时间,今日终于把第一部分内容读完了,这部分内容让我收获挺多的。
在我以前的认知中,无穷大的数就是无法计算出具体的大小,而对无穷大与无穷大的数大小的比较没有清晰的认识,只错误的认为无穷大的数中部分无穷数的集合是要少些的,比如错误的认为偶数的个数是要小于整数的个数的。
作者用一种通俗的描述方法说明了无穷大的数如何比较大小。
即寻找一种一一对应的关系,并举了多个常见的无穷大数的例子,比如所有的偶数、整数、普通分数的个数都是相等的。
其实这应该就是我们函数里面学过的一一映射,如果两个集合存在一一映射的关系,这两个集合元素的个数肯定是相等的。
但我想,如果作者用这种方法去说明的话,估计能看懂本书的人将会少很多。
无穷大数比较大小的方法解释清楚后,接着,作者抛出问题,是不是所有的无穷大数都相等呢?——层层深入。
由此引出了第二级无穷数列,前面的为第一级无穷数列。
作者用反证法说明了线段点的个数是要大于整数的个数。
首先把每一个点看做一个无穷小数,这样才方便于建立对应关系。
然后假设这两种间存在前面所说的一一对应的关系,那么很容易找出一个无穷小数(这个小数的第n位不等于第n个整数对应的小数的第n位)不在这样的对应关系中,所有不存在这样的对应关系,也就是线段的点的个数要大于整数的个数。
作者又说明了任何线、面、体上的点的个数都是相等的。
而到现今,数学家们已经找到第三级无穷数列,所有几何曲线的数目。
虽然作者没有给出证明,但应用前面的方法很容易证明,假如线段上的点与几何曲线的数目存在这样的一一对应关系,那么同样,我们也很容易找出一条几何曲线不在这样的对应关系中,比如这样一条曲线,它等于前面一一对应的所有曲线从开始到无穷的和。
高中数学数学五大常数

高中数学数学五大常数在高中数学学习中,有一些重要的常数被广泛地使用。
这些常数具有特殊的性质和意义,在数学领域中发挥着重要的作用。
本文将介绍高中数学中的五大常数:自然对数的底数e、圆周率π、黄金比例φ、虚数单位i以及欧拉常数γ。
自然对数的底数e自然对数的底数e是一个无理数,它的值约等于2.71828。
e出现在许多数学和科学问题中,比如指数函数、复利计算等。
它具有无限不循环小数的特点,是一个非常重要的数学常数。
圆周率π圆周率π是一个无理数,其值约等于3.14159。
π是一个关于圆的重要常数,它的定义是圆的周长与直径之比。
在高中数学中,π经常出现在计算圆的面积、周长以及弧长等问题中。
黄金比例φ黄金比例φ是一个无理数,它的值约等于1.618。
黄金比例是指两个数的比例等于它们之和与较大数之比,即(a+b)/a = a/b = φ。
黄金比例在数学、美学、艺术等领域中有着广泛的应用,被认为是一种最理想、最和谐的比例关系。
虚数单位i虚数单位i是一个特殊的数,它定义为满足 i^2 = -1 的数。
虚数单位在复数运算中起到重要的作用,扩展了实数域,使得复数的运算更加完备。
在高中数学中,虚数单位i常常与复数、方程以及三角函数等概念相关。
欧拉常数γ欧拉常数γ是数学家欧拉(Euler)命名的一个重要常数,它的值约等于0.5772。
欧拉常数出现在许多数学问题中,比如调和级数、贝塞尔函数等。
它在数论、解析数论等领域中也有广泛的应用。
这五个常数在数学中有着独特的地位和作用,它们的发现和研究为数学的发展做出了巨大的贡献。
在高中数学的学习过程中,了解这些常数的性质和应用将有助于我们更好地理解数学的本质和应用。
总结高中数学中的五大常数:自然对数的底数e、圆周率π、黄金比例φ、虚数单位i以及欧拉常数γ,虽然在数学概念和应用上各有不同,却都具有独特的数学意义和作用。
它们丰富了数学的世界,为我们理解和应用数学提供了重要的工具和思维方式。
对于高中数学学习者而言,了解这些常数的性质和应用,将有助于我们更好地掌握数学知识,提高数学思维能力。
高中数学代数部分常用公式及常用结论

高中数学代数部分常用公式及常用结论1.2.3.四种命题的相互关系:4.充要条件:(1)充分条件:若p q ⇒,则p 是q 充分条件.(2)必要条件:若q p ⇒,则p 是q 必要条件.(3)充要条件:若p q ⇒,且q p ⇒,则p 是q 充要条件. 注:如果甲是乙的充分条件,则乙是甲的必要条件;反之亦然.5.函数的单调性:(1)设[]2121,,x x b a x x ≠∈⋅那么[]1212()()()0x x f x f x -->⇔[]b a x f x x x f x f ,)(0)()(2121在⇔>--上是增函数;[]1212()()()0x x f x f x --<⇔[]b a x f x x x f x f ,)(0)()(2121在⇔<--上是减函数. (2)设函数)(x f y =在某个区间内可导,如果0)(>'x f ,则)(x f 为增函数;如果0)(<'x f ,则)(x f 为减函数.6. 如果函数)(x f 和)(x g 都是减函数,则在公共定义域内,和函数)()(x g x f +也是减函数; 如果函数)(u f y =和)(x g u =在其对应的定义域上都是减函数,则复合函数)]([x g f y =是增函数.7.奇偶函数的图象特征:奇函数的图象关于原点对称,偶函数的图象关于y 轴对称;反过来,如果一个函数的图象关于原点对称,那么这个函数是奇函数;如果一个函数的图象关于y 轴对称,那么这个函数是偶函数.8.函数()y f x =的图象的对称性:函数()y f x =的图象关于直线x a =对称()()f a x f a x ⇔+=-(2)()f a x f x ⇔-=.9.两个函数图象的对称性:(1)函数()y f x =与函数()y f x =-的图象关于直线0x =(即y 轴)对称. (2)函数)(x f y =和)(1x f y -=的图象关于直线y=x 对称.10.互为反函数的两个函数的关系:a b f b a f =⇔=-)()(1.11. 若函数)(b kx f y +=存在反函数,则其反函数为])([11b x f ky -=-,并不是)([1b kx f y +=-], 而函数)([1b kx fy +=-]是])([1b x f ky -=的反函数.12.几个常见的函数方程:(1)正比例函数()f x cx =,()()(),(1)f x y f x f y f c +=+=.(2)指数函数()x f x a =,()()(),(1)0f x y f x f y f a +==≠.(3)对数函数()log a f x x =,()()(),()1(0,1)f xy f x f y f a a a =+=>≠.(4)幂函数()f x x α=,'()()(),(1)f xy f x f y f α==.(5)余弦函数()cos f x x =,正弦函数()sin g x x =,()()()()()f x y f x f y g x g y -=+,()(0)1,lim1x g x f x→==.13.根式的性质:(1)n a =.(2)当n a =;当n ,0||,0a a a a a ≥⎧==⎨-<⎩.14.有理指数幂的运算性质:(1) (0,,)r s r sa a aa r s Q +⋅=>∈.(2) ()(0,,)r s rsa a a r s Q =>∈.(3)()(0,0,)r r rab a b a b r Q =>>∈.注: 若a >0,p 是一个无理数,则a p表示一个确定的实数.上述有理指数幂的运算性质,对于无理数指数幂都适用.15.指数式与对数式的互化式:log b a N b a N =⇔=(0,1,0)a a N >≠>.16.对数的换底公式 :log log log m a m NN a=(0a >,且1a ≠,0m >,且1m ≠, 0N >).推论 log log m na a nb b m =(0a >,且1a >,,0m n >,且1m ≠,1n ≠, 0N >).17.对数的四则运算法则:若a >0,a ≠1,M >0,N >0,则 (1)log ()log log a a a MN M N =+;(2) log log log a a a MM N N=-; (3)log log ()n a a M n M n R =∈.18.等差数列的通项公式:*11(1)()n a a n d dn a d n N =+-=+-∈;其前n 项和公式为1()2n n n a a s +=1(1)2n n na d -=+211()22d n a d n =+-.19.等比数列的通项公式:1*11()n nn a a a q q n N q-==⋅∈; 其前n 项的和公式为11(1),11,1n n a q q s q na q ⎧-≠⎪=-⎨⎪=⎩ 或11,11,1n n a a qq q s na q -⎧≠⎪-=⎨⎪=⎩.20.常见三角不等式:(1)若(0,)2x π∈,则sin tan x x x <<.(2) 若(0,)2x π∈,则1sin cos x x <+≤(3) |sin ||cos |1x x +≥.21.同角三角函数的基本关系式:22sin cos 1θθ+=, tan θ=θθcos sin , tan 1cot θθ⋅=.22.正弦、余弦的诱导公式:212(1)sin ,sin()2(1)s ,nn n co απαα-⎧-⎪+=⎨⎪-⎩212(1)s ,s()2(1)sin ,nn co n co απαα+⎧-⎪+=⎨⎪-⎩23.和角与差角公式:sin()sin cos cos sin αβαβαβ±=±;cos()cos cos sin sin αβαβαβ±= ;tan tan tan()1tan tan αβαβαβ±±= .22sin()sin()sin sin αβαβαβ+-=-(平方正弦公式);22cos()cos()cos sin αβαβαβ+-=-.sin cos a b αα+)αϕ+(辅助角ϕ所在象限由点(,)a b 的象限决定,tan baϕ=).24.二倍角公式:sin 2sin cos ααα=.2222cos 2cos sin 2cos 112sin ααααα=-=-=-.22tan tan 21tan ααα=-.25. 三倍角公式:3sin 33sin 4sin 4sin sin()sin()33ππθθθθθθ=-=-+.3cos34cos 3cos 4cos cos()cos()33ππθθθθθθ=-=-+.323tan tan tan 3tan tan()tan()13tan 33θθππθθθθθ-==-+-.26.三角函数的周期公式:函数sin()y x ωϕ=+,x ∈R 及函数cos()y x ωϕ=+,x ∈R (A , ω,ϕ为常数,且A ≠0,ω>0)的周期2T πω=;函数tan()y x ωϕ=+,,2x k k Z ππ≠+∈(A ,ω,ϕ为常数,且A ≠0,ω>0)的周期T πω=.27.正弦定理 :2sin sin sin a b cR A B C===. 余弦定理2222cos a b c bc A =+-; 2222cos b c a ca B =+-; 2222cos c a b ab C =+-.28. 简单的三角方程的通解:sin (1)arcsin (,||1)kx a x k a k Z a π=⇔=+-∈≤. s 2arccos (,||1)co x a x k a k Z a π=⇔=±∈≤.tan arctan (,)x a x k a k Z a R π=⇒=+∈∈.特别地,有sin sin (1)()k k k Z αβαπβ=⇔=+-∈. s cos 2()co k k Z αβαπβ=⇔=±∈.tan tan ()k k Z αβαπβ=⇒=+∈.29.最简单的三角不等式及其解集:sin (||1)(2arcsin ,2arcsin ),x a a x k a k a k Z πππ>≤⇔∈++-∈.sin (||1)(2arcsin ,2arcsin ),x a a x k a k a k Z πππ<≤⇔∈--+∈. cos (||1)(2arccos ,2arccos ),x a a x k a k a k Z ππ>≤⇔∈-+∈.cos (||1)(2arccos ,22arccos ),x a a x k a k a k Z πππ<≤⇔∈++-∈.tan ()(arctan ,),2x a a R x k a k k Z πππ>∈⇒∈++∈.tan ()(,arctan ),2x a a R x k k a k Z πππ<∈⇒∈-+∈.30.组合数公式:m n C=m n mmA A =m m n n n ⨯⨯⨯+-- 21)1()1(=!!!)(m n m n -⋅(n ∈N *,m N ∈,且m n ≤).31.组合数的两个性质:(1)m n C =mn n C - ; (2) m n C +1-m n C =m n C 1+. 注:规定10=n C .32.组合恒等式:(1)11mm n n n m C C m --+=; (2)1m mn n n C C n m -=-; (3)11mm n n n C C m--=;(4)∑=nr r nC0=n2;(5)1121++++=++++r n r n r r r r r rC C C C C .(6)nn n r n n n n C C C C C 2210=++++++ . (7)1425312-+++=+++n n n n n n n C C C C C C .(8)1321232-=++++n nn n n n n nC C C C .(9)rn m rn rm n r m n rm C C C C C C C +-=+++011. (10)nn n n n n n C C C C C 22222120)()()()(=++++ . 二项展开式的通项公式rr n r n r b a C T -+=1)210(n r ,,,=.33.复数的相等:,a bi c di a c b d +=+⇔==.(,,,a b c d R ∈)34.复数z a bi =+的模(或绝对值):||z =||a bi +35.复数的四则运算法则:(1)()()()()a bi c di a c b d i +++=+++;(2)()()()()a bi c di a c b d i +-+=-+-; (3)()()()()a bi c di ac bd bc ad i ++=-++; (4)2222()()(0)ac bd bc ada bi c di i c di c d c d +-+÷+=++≠++.36.实系数一元二次方程的解:实系数一元二次方程20ax bx c ++=,①若240b ac ∆=->,则1,2x =②若240b ac ∆=-=,则122b x x a==-;③若240b ac ∆=-<,它在实数集R 内没有实数根;在复数集C 内有且仅有两个共轭复数根240)x b ac =-<.。
高等数学(三)第11章 无穷级数

无穷级数是高等数学的一个重要内容,是无限个常量或变量之和的数学模型,它是表示函数、研究函数性态以及进行数值计算的一种有效工具,在数学理论以及工程技术中都有广泛的应用.11.1 数项级数的概念及性质11.1.1 数项级数的概念 实例1 小球运动的时间小球从1米高处自由落下, 每次跳起的高度减少一半, 问小球运动的总时间. 解 由自由落体运动方程221gt s =知g s t 2=.设k t 表示第k 次小球落地的时间, 则小球运动的总时间为+++++=k t t t t T 222321.这里出现了无穷多个数依次相加的式子.在物理、化学等许多学科中,也常能遇到这种无穷多个数或函数相加的情形,在数学上称之为无穷级数.上述级数的定义只是一个形式上的定义,怎样理解无穷级数中无穷多个数相加呢?我们可以从有限项出发,观察它们的变化趋势,由此来理解无穷多个数量相加的含义.令n n u u u S +++= 21,称n S 为级数(11.1.1)的部分和.当n 依次为1,2,3,…,时,得到一个数列1S ,2S ,…,n S ,…,称为级数(11.1.1)的部分和数列.从形式上不难知道∑∞=1n n u =n n S ∞→lim ,所以我们可以根据部分和数列的收敛与发散来定义级数的敛散性. 当级数∑∞=1n n u 收敛于S 时,常用其部分和S n 作为和S 的近似值,其差∑∑∑∞+==∞==-=-111n k knk k k k n u u u S S叫做该级数的余项,记为n r .用部分和S n 近似代替和S 所产生的绝对误差为| r n |.例11.1.1 判定级数 ++⋅++⋅+⋅)1(1321211n n 的敛散性.解 所给级数的一般项为111)1(1+-=+=n n n n u n ,部分和)1(1321211+⋅++⋅+⋅=n n S n 111)111()3121()211(+-=+-++-+-=n n n ,所以1)111(lim lim =+-=∞→∞→n S n n n ,故该级数收敛于1,即1)1(11=+∑∞=n n n . 例11.1.2 考察波尔察诺级数∑∞=--11)1(n n 的敛散性.解 它的部分和数列是1, 0, 1, 0, … ,显然n n S ∞→lim 不存在,∑∞=--11)1(n n 发散.例11.1.3 讨论几何级数(也称等比级数)∑∞=0n naq +++++=n aq aq aq a 2的敛散性,其中a ≠ 0, q 称为级数的公比.解 该几何级数前n 项的部分和21(1),11 ,1n n n a q q qS a aq aq aq na q -⎧-≠⎪-=++++=⎨⎪=⎩, 当q = 1时,由于lim lim n n n S na →∞→∞==∞,所以级数发散;当q = -1时,级数变为 +-+-a a a a ,显然lim n n S →∞不存在,所以级数发散;当| q | > 1时,由于lim n n S →∞=∞,所以级数发散;当| q | < 1时,由于lim 1n n a S q →∞=-,所以级数收敛于1a q-.因此,几何级数0n n aq ∞=∑当| q | < 1时收敛于qa-1;当| q | ≥ 1时发散. 几何级数的敛散性非常重要,许多级数敛散性的判别,都要借助几何级数的敛散性来实现.11.2 .2 数项级数的性质根据级数敛散性的概念,可以得到级数的几个基本性质.12()n n n ku k u u u kS ++=+++=,112)()k k k n k u u u u u u +++++++-+++S S -lim .从性质1的证明可以看出,如果n S 没有极限且k ≠0,则n σ也不可能有极限.换句话说,级数的每一项同乘以一个非零常数,其敛散性不改变.例如,47412)31(1313213231(32(3)1(2111=-=---+-=-+=-+∑∑∑∞=∞=∞=nn nn n n n n .由性质4知,若级数加括号后发散,则原级数必发散.但加括号后收敛的级数,去括号后未必收敛.例如,级数⋅⋅⋅+-+-+-)11()11(11()收敛,但去括号后级数⋅⋅⋅+-+-+-111111却发散.由级数收敛的必要条件可知,如果0lim ≠∞→n n u 或不存在,则级数一定发散.因此可用性质5判定级数∑∞=1n n u 发散性,有时性质5也称为“级数发散的第n 项判别法”.例11.1.4 判定级数∑∞=+112n n n 的敛散性.解 由于02112limlim ≠=+=∞→∞→n n u n n n ,故此级数发散.例11.1.5 证明调和级数 +++++n131211发散. 证明 将调和级数的两项、两项、四项、…、2m 项、… 加括号,得到一个新级数++++++++++++++++)21221121()81716151()4131()211(1m m m .因为 2141414131 ,21211=+>+>+, ,218181818181716151=+++>+++,21212121212211211111=+++>+++++++++m m m m m m , 所以新级数前m + 1项的和大于21+m ,故新级数发散.由性质4知,调和级数发散. 由于调和级数的一般项)(01∞→→=n nu n ,因此例5说明:级数的一般项u n 趋于零仅仅是级数收敛的必要条件,并非充分条件.所以,不可用性质5来判定级数的收敛性.例11.1.6 有甲,乙,丙三人按以下方式分一个苹果:先将苹果分成4份,每人各取一份;然后将剩下的一份又分成4份,每人又取一份;按此方法一直下去.那么最终每人分得多少苹果?解 依题意,每人分得的苹果为+++++n 4141414132. 它是41==q a 的等比级数,因此其和为 3141141=-=S . 即最终每人分得苹果的31.习题 11.11.写出下列级数的一般项.(1) -+-+-5645342312; (2) +-+-97535432a a a a .2.判断下列级数的敛散性. (1))1(1n n n -+∑∞=; (2)∑∞=16sinn n π; (3) ++⋅-++⋅+⋅)12()12(1531311n n ; (4) +++++++41312110021;(5)n n n n-∞=-+-∑)11()1(11; (6))31(1n n n+∑∞=.11.2 数项级数的审敛法11.2.1正项级数及其审敛法对于正项级数∑∞=1n n u ,其部分和S n = S n -1 + u n ≥ S n -1 (n = 2, 3, …),即部分和数列{S n }单调递增.若数列{S n }有界,则由单调有界数列必有极限的准则知,数列{S n }收敛,所以正项级数∑∞=1n n u 必收敛,设其和为S ,则有S n ≤ S .反之,若正项级数∑∞=1n n u 收敛于S ,则由收敛数列必有界的性质知,数列{S n }必有界.于是我们得到下述重要结论:例11.2.1证明正项级数 +++++=∑∞=!1!21!111!10n n n 收敛.证明 因为),2,1( 2122211211!11 ==⋅⋅⋅⋅≤⋅⋅⋅=-n n n n , 于是对任意的n ,有2221212111)!1(1!21!111-+++++≤-++++=n n n S,3213211211121<-=--+=--n n即正项级数∑∞=0!1n n 的部分和数列有界,故级数∑∞=0!1n n 收敛.利用定理11.2.1,可导出正项级数的若干审敛法,这里只介绍其中较为重要的两个.例11.2.2讨论广义调和级数(又称p —级数) +++++=∑∞=pppn pn n13121111 (其中p为常数)的敛散性.解 当 p ≤ 1时,有n n p 11≥,由于∑∞=11n n发散,由定理2.2知,p 级数发散. 当p >1时,取n x n ≤<-1,有ppx n 11≤,得到11111d d (2,3,)n n p pp n n x x n n n x --=≤=⎰⎰ 于是p 级数的部分和111123n p p p S n=++++231211111d d d np p pn x x x x x x -≤++++⎰⎰⎰1111111d 1(11,11n p p x x p n p -=+=+-<+--⎰即部分和数列{S n }有界,由定理11.2.1知,p 级数收敛.综上所述,当p > 1时,p 级数收敛 ;当p ≤ 1时,p 级数发散,以后我们常用p 级数作为比较审敛法时使用的级数.例11.2.3 判定下列级数的敛散性. (1) 2111n n ∞=+∑; (2)n ∞=. 解 (1) 因为22111n n u n ≤+=,而级数∑∞=121n n为p = 2 > 1的p 级数,故收敛,所以由比较审敛法知,级数∑∞=+1211n n 也收敛. (2) 因为n n n u n 111122=≥-=,而调和级数∑∞=11n n 发散,故级数∑∞=-1211n n 也发散.使用比较审敛法时,需要找到一个敛散性已知的正项级数来与所给正项级数进行比较,这对有些正项级数来说是很困难的.自然提出这样的问题:能否仅通过级数自身就能判定级数的敛散性呢?如果正项级数的一般项中含有乘积、幂或阶乘时,常用比值审敛法判定其敛散性. 例11.2.4 判定下列级数的敛散性:(1) 2132nnn n ∞=∑; (2) 11(1)!n n ∞=-∑; (3)11(21)n n n ∞=+∑. 解 (1) 因为123)1(23lim 322)1(3lim lim 2221211>=+=⋅+=∞→++∞→+∞→n n n n u u n n n n n n nn n ,所以级数∑∞=1223n n n n 发散.(2) 因为101lim !)!1(lim lim1<==-=∞→∞→+∞→n n n u u n n nn n ,所以级数∑∞=-1)!1(1n n 收敛. (3) 因为1)32)(1()12(lim lim1=+++=∞→+∞→n n n n u u n nn n ,此时比值审敛法失效,必须改用其他方法判别此级数的敛散性.由于22121)12(1n n n n u n <<+=,而级数∑∞=121n n为p = 2 > 1的p 级数,故收敛,所以由比较审敛法可知,级数∑∞=+1)12(1n n n 也收敛.11.2.2 交错级数及其审敛法交错级数的特点是正负项交替出现.关于交错级数敛散性的判定,有如下重要定理. 例11.2.5 判定交错级数 +-++-+--nn 1)1(41312111的敛散性.解 此交错级数的n u n 1=,且满足 1111+=+>=n n u n n u 且01lim lim ==∞→∞→n u n n n ,由定理11.2.4知,该交错级数收敛,其和小于1.11.2.3 任意项级数及其审敛法设有级数∑∞=1n n u ,其中u n ( n = 1, 2,…)为任意实数,称此级数为任意项级数.对于任意项级数,如何来研究其敛散性?除了用级数定义来判断外,还有什么办法?为此要介绍绝对收敛与条件收敛概念.1,2,)的级数,称为交错级例如,级数2111)1(n n n ∑∞=--绝对收敛,级数n n n 1)1(11∑∞=--条件收敛.定理11.2.5说明,对于任意项级数∑∞=1n n u ,如果它所对应的级数∑∞=1||n n u 收敛,则该级数必收敛,从而将任意项级数的敛散性判别问题转化为正项级数来讨论.但应注意,如果级数∑∞=1||n n u 发散,不能判定级数∑∞=1n n u 也发散.例11.2.6 判定级数∑∞=12)sin(n nn α的敛散性,其中α为常数. 解 由于n nn 212)sin(0≤≤α,而级数∑∞=121n n 是收敛的,由比较审敛法可知,级数∑∞=12)sin(n n n α收敛,即级数∑∞=12)sin(n n n α绝对收敛,由定理11.2.5知,级数∑∞=12)sin(n n n α收敛. 例11.2.7讨论交错p-级数p n n n 1)1(11∑∞=--的绝对收敛与条件收敛性,其中p 为常数.解 当p ≤ 0时,pn n nu 1)1(1--=不趋于)(0∞→n ,故该级数发散.当p >1时,有ppn n n11)1(1=--,且级数∑∞=11n p n收敛,故该级数绝对收敛.当0<p ≤ 1时,级数∑∞=11n p n 发散,但p n n n 1)1(11∑∞=--是交错级数,且满足定理11.2.4的条件,故所给级数条件收敛.习题11.21.用比较审敛法判定下列级数的敛散性. (1) ∑∞=-+133)1(n n n ;(2) )0(111>+∑∞=a an n .2.用比值审敛法判定下列级数的敛散性.(1) ∑∞=⋅1!2n n nnn ; (2) ∑∞=123n n n .3.判定下列级数是否收敛?若收敛,是条件收敛还是绝对收敛?(1) ;3)1(111-∞=-∑-n n n n (2) ∑∞=13sin n nn α. 11.3 幂 级 数11.3.1函数项级数的概念 实例1存款问题设年利率为r (实际上其随时间而改变),依复利计算,想要在第一年末提取1元,第二年末提取4元,第三年末提取9元,第n 年末提取2n 元,要能永远如此提取,问至少需要事先存入多少本金?分析:这里本金为存入的钱,设为A ,则一年后本金与利息之和为一年的本利和,即为)1(r A +,两年后的本利和为2)1(r A +,n 年后的本利和为n r A )1(+.解 若本金A 为n r -+)1(元,n 年后可提取本利和1)1()1(=+⋅+-n n r r (元).从而 若要n 年后提取本利和2n 元,则本金应为n r n -+)1(2元.所以为使第一年末提1元本利和,则要有本金1)1(-+r ;第二年末能提取本利和22=4元,则要有本金22)1(2-+r 元;第三年末能提取本利和32=9元,则要有本金32)1(3-+r 元,…第n 年末能提取2n 元本利和,则要有本金n r n -+)1(2元;如此下去,所需本金总数为∑∞=-+12)1(n n r n.令r x +=11,得∑∑∞=∞=-=+1212)1(n n n nx n r n .实例2中的∑∞=12n n x n 即为一个无穷级数,但通项不再是我们前面所学的常数,而是函数,称为函数项无穷级数.对于区间I 上的任意确定值x 0,函数项级数(3.1)便成为数项级数++++)()()(00201x u x u x u n . (11.3.2) 如果数项级数(11.3.2)收敛,则称点x 0为函数项级数(11.3.1)的收敛点;如果数项级数 (11.3.2)发散,则称点x 0为函数项级数(3.1)的发散点.函数项级数(11.3.1)的全体收敛点(或发散点)的集合叫做该级数的收敛域(或发散域).设函数项级数(11.3.1)的收敛域为D ,则对于任意的x ∈D ,函数项级数(11.3.1)都收敛,其和显然与x 有关,记作S (x ),称为函数项级数(11.3.1)的和函数,并记作D x x u x u x u x S n ∈++++=,)()()()(21 .例如,级数201n n n x x x x ∞==+++++∑的收敛域为(-1,1),和函数为x-11,即 01(1, 1)1n n x x x ∞==∈--∑.把函数项级数(11.3.1)的前n 项的和记作S n (x ),则在收敛域上有)()(lim 1x S x S un n n n==∞→∞=∑.将 r n (x ) = S (x ) -S n (x )称作该函数项级数的余项,则0)(lim =∞→x r n n .11.3.2 幂级数及其收敛性特别地,当x 0 = 0时,+++++=∑∞=n n n nn x a x a x a a x a 22100(11.3.4)称为关于x 的幂级数.本节主要讨论幂级数(11.3.4),幂级数(11.3.3)可通过代换t = x – x 0化成幂级数(11.3.4)来研究.下面首先讨论幂级数(11.3.4)的收敛域问题,即x 取数轴上哪些点时幂级数(11.3 .4) 收敛.0,1,2,),因此.定理11.3.1表明,如果幂级数(11.3.4)在x= x0处收敛(发散),则对于开区间(-| x0 |, | x0 |)内(闭区间[-| x0 |, | x0 |]外)的一切x,幂级数(11.3.4)都收敛(发散) .这样的正数R称为幂级数(11.3.4)的收敛半径.由于幂级数(11.3.4 )在区间(-R, R)一定是绝对收敛的,所以我们把(-R, R)称为幂级数(11.3.4)的收敛区间.幂级数在收敛区间内部有很好的性质.幂级数(11.3.4)在区间(-R, R)的两个端点x = ±R处可能发散也可能收敛,需要把x = ±R代入幂级数(11.3.4),化为数项级数来具体讨论.一旦知道了x =±R处幂级数(3.4)的敛散性,则幂级数(11.3.4)的收敛域为下面四个区间(-R, R), [-R, R) , (-R, R ], [-R, R ]之一.若幂级数(11.3.4)仅在x = 0处收敛,则规定收敛半径R = 0,此时收敛域退缩为一点,即原点;若对一切实数x,幂级数(11.3.4)都收敛,则规定收敛半径R = +∞,此时收敛区间与收敛域都是(-∞, +∞).下面给出幂级数(11.3.4)的收敛半径的求法.例11.3.1求下列幂级数的收敛半径.(1) 1(1)31nn n n x ∞=-+∑ (2) 0!n n x n ∞=∑; (3) 202n n n x ∞=∑.解 (1) 因311313lim 13)1(13)1(lim lim1111=++=+-+-==+∞→++∞→+∞→n n n n n n n n nn n a a ρ,故收敛半径31==ρR . (2) 因011lim !1)!1(1lim lim1=+=+==∞→∞→+∞→n n n a a n n nn n ρ,故收敛半径R = + ∞.(3) 因为该级数缺少奇次幂的项,定理3.2失效,换用比值审敛法求收敛半径.由于2(1)121212limlim 22n n n n n n nnx u x x u +++→∞→∞==,因此,由正项级数的比值审敛法知,当2112x <,即2||<x 时该幂级数绝对收敛;当2112x >,即2||>x 时该幂级数发散.故收敛半径2=R . 例11.3.2 求下列幂级数的收敛区间和收敛域.(1) 11(1)n nn x n +∞=-∑; (2) 21(2)n n x n ∞=-∑. 解 (1) 因为11lim )1(1)1(lim lim121=+=-+-==∞→++∞→+∞→n nnn a a n n n n nn n ρ, 所以收敛半径11==ρR ,收敛区间是(-1, 1),即该级数在(-1, 1)内绝对收敛.在端点x = 1处,级数成为交错级数∑∞=+-11)1(n n n ,这是收敛的级数.在端点x = -1处,级数成为∑∞=-11n n,这是发散的级数,故该级数的收敛域为(-1, 1].(2) 令t = x -2,则所给级数变成∑∞=12n n nt .因为 ,1)1(lim 1)1(1lim lim22221=+=+==∞→∞→+∞→n n n n a a n n nn n ρ故级数∑∞=12n n n t 的收敛半径11==ρR ,即级数∑∞=12n n nt 在区间(-1, 1)内绝对收敛.在端点t = 1处,级数∑∞=12n n n t 变成p 级数∑∞=121n n ,故收敛;在t = -1处,级数∑∞=12n n n t 变成交错级数∑∞=-121)1(n n n 也收敛.因此,幂级数∑∞=12n n n t 的收敛区间为(-1,1),收敛域为[-1, 1],从而级数∑∞=-12)1(n nn x 的收敛区间为(1,3),收敛域为[1, 3].(因为-1 ≤ t ≤ 1,即-1 ≤ x - 2 ≤ 1,所以13x ≤≤).11.3.3幂级数的运算 1. 四则运算设幂级数∑∞=0n n n x a 和∑∞=0n n n x b 的收敛半径分别为R 1和R 2,它们的和函数分别为S 1(x )和S 2( x ),令R = min{ R 1, R 2},则在(-R , R )内有(1) 加法运算(2) 乘法运算2. 分析运算设幂级数∑∞=0n n n x a 的收敛半径为(0)R R >),在(-R , R )内的和函数为S (x ),则有(1) 幂级数∑∞=0n n n x a 的和函数S ( x )在其收敛区间 (-R , R ) 内连续.(2) 幂级数∑∞=0n n n x a 的和函数S ( x )在其收敛区间 (-R , R ) 内可导,且有逐项求导公式:(3) 幂级数∑∞=0n n n x a 的和函数S ( x )在其收敛区间 (-R , R ) 内可积,且有逐项积分公式:注意:逐项求导和逐项积分前后,两幂级数具有相同的收敛半径和收敛区间. 例11.3.3 求下列幂级数的和函数. (1)11(11)n n nx x ∞-=-<<∑; (2)10(11)1n n x x n ∞+=-<<+∑.解 (1) 设11(), (1, 1)n n S x nx x ∞-==∈-∑,两端积分,得111()d d 1xxn n n n xS x x nx x x x∞∞-=====-∑∑⎰⎰, 上式两端对x 求导,得21(), (1, 1)(1)S x x x =∈--.(2) 设10(), (1, 1)1n n x S x x n ∞+==∈-+∑,两端对x 求导,得 ∑∑∞=∞=+-=='+='10111)1()(n n n n x x n n x S .上式两端从0到x 积分,得01()(0)d ln(1)1xS x S x x x-==---⎰, 而S ( 0 ) = 0,所以()ln(1), (1, 1)S x x x =∈---.例11.3.4求幂级数20, (1, 1)21nn x x n ∞=∈-+∑的和函数,并计算()2011212nn n ∞=+∑的值.解 设20(), (1, 1)21nn x S x x n ∞==∈-+∑,两端同时乘以x ,得,12)(012∑∞=++=n n n x x xS 两端对x 求导,得 ,1112])([202012x x n x x xS n nn n -=='⎪⎭⎫ ⎝⎛+='∑∑∞=∞=+ 上式两端从0到x 积分,得 20111()ln ,211xx x x x xx S +==--⎰d 所以 11()ln , (1, 1)21x S x x x x+=∈--.因为21=x 在(-1, 1)内部,代入上式,得 3ln 211211ln21212112120=-+⨯=⎪⎭⎫ ⎝⎛+∑∞=nn n . 习题 11.31.求下列幂级数的收敛区间.(1) +⋅⋅+⋅+64242232x x x ; (2)∑∞=++-11212)1(n n nn x ;(3)∑∞=--122212n n nx n ; (4)∑∞=-1)5(n n n x .2.利用逐项求导或逐项积分,求下列级数在收敛区间内的和函数. (1) )11( 14014<<-+∑∞=+x n x n n ; (2)∑∞=+<<-+0)1(2)11( )1(2n n x x n ,并求级数∑∞=-+01221n n n 的和. 11.4 函数展开成幂级数前面我们讨论了幂级数在收敛域内求和函数的问题,在实际应用中常常遇到与之相反的问题,就是对一个给定的函数,能否在一个区间内展开成幂级数?如果可以,又如何将其展开成幂级数?其收敛情况如何?本节就来解决这些问题.11.4.1泰勒(Taylor)级数如果函数f (x )在点x 0的某邻域U ( x 0, δ )内有定义,且能展开成x - x 0的幂级数,即对于任意的x ∈U ( x 0, δ ),有+-++-+-+=n n x x a x x a x x a a x f )()()()(0202010 . (11.4.1)由幂级数的分析性质知,函数f (x )在该邻域内一定具有任意阶导数,且 ),2,1( )()!1(!)(01)( =+-++=+n x x a n a n x fn n n . (11.4.2)在式(11.4.1)和式(11.4.2)中,令x = x 0,得)(00x f a =,!1)(01x f a '=,,!2)(02x f a ''= ,!)(,0)(n x f a n n =. (11.4.3) 将式(11.4.3)代入式(11.4.1)中,有+-++-''+-'+=n n x x n x f x x x f x x x f x f x f )(!)()(!2)()(!1)()()(00)(200000.这说明,如果函数f (x )在x 0的某邻域U ( x 0, δ )内能用形如式(11.4.1)右端的幂级数表示,则其系数必由式(11.4.3)确定,即函数f (x )的幂级数展开式是唯一的.函数f (x )的泰勒级数(11.4.4)的前n + 1项之和记为S n +1(x ),即n n n x x n x f x x x f x x x f x f x S )(!)()(!2)()(!1)()()(00)(2000001-++-''+-'+=+ ,并把差式f (x )- S n +1(x )叫做泰勒级数(4.4)的余项,记作R n ( x ),即)()()(1x S x f x R n n +-=.显然,只要函数f (x )在点x 0的某邻域U ( x 0,δ )内具有任意阶导数,则它的泰勒级数(11.4.4) 就已经确定,问题是级数(11.4.4)是否在x 0的某邻域内收敛?若收敛,是否以f (x )为其和函数?为此有下面的定理.显然,使用定理11.4.1来进行收敛性的判定是困难的.下面直接给出余项R n (x )的表达式称上式为拉格朗日型余项.在实际应用,若取常数x 0 = 0,此时泰勒级数(11.4.4)变成称为f (x )的麦克劳林(Maclaurin)级数,其余项为11.4.2函数展开成幂级数将函数)(x f 展开成0x x -或x 的幂级数,就是用其泰勒级数或麦克劳林级数表示)(x f .下面结合例题来研究如何将函数展开成幂级数.1. 直接展开法直接利用麦克劳林公式将函数f (x )展开为x 的幂级数的方法称为直接展开法,可以按照下列步骤进行(展开为(x -x 0)的幂级数与之类似):第一步 求出函数f ( x )在x = 0处的各阶导数 ),0(,),0(),0(),0()(n ff f f '''.若函数在x = 0处的某阶导数不存在,就停止进行,该函数不能展开为x 的幂级数.例如,在点x = 0处,37)(x x f =的三阶导数不存在,它就不能展开为x 的幂级数.第二步 写出幂级数+++''+'+nn x n f x f x f f !)0(!2)0()0()0()(2并求出收敛半径R 及收敛区间(-R , R ).第三步 在收敛区间(-R , R )内,考察余项R n ( x )的极限1)1()!1()(lim )(lim ++∞→∞→+=n n n n n x n f x R ξ(ξ介于0与x 之间), 是否为零?如果为零,第二步所写出的幂级数就是函数f ( x )在(-R , R )内的展开式,即),(,!)0(!2)0()0()0()()(2R R x x n f x f x f f x f nn -∈+++''+'+= .如果不为零,第二步写出的幂级数虽然收敛,但它的和并不是所给的函数f ( x ). 例11.4.1将下列函数展开为x 的幂级数.(1) ()e x f x =; (2) x x f sin )(=; (3) m x x f )1()(+=(m 为任意常数). 解 (1) 因为f (x ) = e x ,故f (n )(0 ) = 1( n = 0,1, 2,…).从而e x 的麦克劳林级数为++++++!!3!2132n x x x x n . 容易求得它的收敛半径R = +∞,下面考察余项1e ()(1)!n n R x x n ξ+=+, (ξ介于0与x 之间). 因为ξ介于0与x 之间,所以||e e x ξ<,因而有||11e e |()|||||(1)!(1)!x n n n R x x x n n ξ++=<++. 对于任一确定的x 值,e |x |是一个确定的常数,而级数++++++!!3!2132n x x x x n是绝对收敛的,由级数收敛的必要条件可知0)!1(||lim 1=++∞→n x n n , 所以 1||||lime 0(1)!n x n x n +→∞=+.由此可得,0)(lim =∞→x R n n ,这表明级数收敛于e x ,所以23e 1 ()2!3!!n x x x x x x n =++++++-∞<<+∞.(2) 因为x x f sin )(=,所以),2,1( )2sin()()( =+=n n x x f n π,则 ,)1()0(,0)0(,,1)0(,0)0(,1)0(,0)0()12()2(n n n ff f f f f -==-='''=''='=+.于是sin x 的麦克劳林级数为++-++-+-+)!12()1(!7!5!312753n x x x x x n n .它的收敛半径R = + ∞,考察余项的绝对值)(0)!1(||)!1()21sin()(11∞→→+≤+++=++n n x n x n x R n n n πξ.于是得展开式)( )!12()1(!5!3sin 1253+∞<<-∞++-+-+-=+x n x x x x x n n.(3) 用同样的方法,可以推得牛顿二项展开式)11( !)1()1(!2)1(1)1(2<<-++--++-++=+x x n n m m m x m m mx x nm .这里m 为任意实数.当m 为正整数时,就退化为中学所学的二项式定理.最常用的是12m =±的情形,读者可自己写出这两个式子.2.间接展开法以上几个例子是用直接展开法把函数展开为麦克劳林级数,直接展开法虽然步骤明确,但运算常常过于繁琐,尤其最后一步要考察n →∞时余项R n ( x )是否趋近于零,这不是一件容易的事.下面我们从一些已知函数的幂级数展开式出发,利用变量代换或幂级数的运算求得另外一些函数的幂级数展开式,这种将函数展开成幂级数的方法叫间接展开法.例11.4.2将下列函数展开为x 的幂级数. (1) x x f cos )(=; (2) )1ln()(x x f +=.解(1) 由例1中的(2)知,)( )!12()1(!5!3sin 1253+∞<<-∞++-+-+-=+x n x x x x x n n,两边对x 逐项求导,得).( !2)1(!4!21cos 242+∞<<-∞+-+-+-=x n x x x x nn )( (2) 由牛顿二项展开式得)11( )1(11132<<-+-++-+-=+x x x x x xn n .上式两端从0到x 逐项积分,得)11( 1)1(432)1ln(1432<<-++-++-+-=++x n x x x x x x n n . 又因为当x = -1时该级数发散,当x = 1时该级数收敛,故有)11(11)1()1ln(10≤<-+-=++∞=∑x x n x n n n.例11.4.3将下列函数展开为x - 1的幂级数: (1) x x f ln )(=; (2) 2)(2--=x x x x f . 解 (1) )]1(1ln[ln )(-+==x x x f ,利用)1ln(x +的展开式得),111( 1)1()1(3)1(2)1()1(ln 132≤-<-++--+--+---=+x n x x x x x n n 即 )20(1)1()1(ln 1≤<+--=+∞=∑x n x x n n n.(2) ⎪⎭⎫ ⎝⎛--+=--=--=x x x x x x x x x f 221131)1)(2(2)(2 ][)1(12)211(2131----+=x x . 由)11( )1(110<<--=+∑∞=x x x n n n ,得 )1211( 21)1(212112111 2<-<-+⎪⎭⎫ ⎝⎛--+-⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛--=-+x x x x x nn . )111( )1()1()1(1)1(112<-<-+-++-+-+=--x x x x x n . 于是⎥⎦⎤⎢⎣⎡----=--∑∑∞=∞=002)1(2)21()1(21312n n n n n x x x x x n n n n x )1(22)1(3101-⎥⎦⎤⎢⎣⎡--=∑∞=+,)20(<<x . 习题 11.41.将下列函数展开成x 的幂级数,并指出其收敛区间. (1) xx f -=31)(; (2) x x f 2cos )(=; (3) x x f arcsin )(=. 2.将函数231)(2++=x x x f 展开成(x + 4)的幂级数.11.5幂级数展开式的应用利用函数的幂级数展开式,可以进行近似计算,即展开式成立的区间内,函数值用级数的部分和按规定的精度要求近似计算.例11.5.1计算2的近似值( 精确到小数点四位,即误差不超过0.0001).解 由于 ++--++-+⋅+=+n x n n x x x !)1()1(!2)1(!11)1(2ααααααα21)211(2242-=-=根据上一节二项式展开式,取21-=x ,21=α 21)211(2242-=-=)21!453121!33121!21211(28642 -⋅⋅-⋅---=取前四项的和作为近似值,其差(称截断误差)为4r )21!5753121!4531(2108 +⋅⋅⋅+⋅⋅=0098.025225))21()21(211(21!45312910328≈=⋅=++++⋅⋅< 于是,近似值为≈24219.1)21!33121!21211(2642≈⋅---=.由“四舍五入”引起的误差叫做舍入误差. 计算时取五位小数,四舍五入后误差不会超过小数点后四位.本题如果用下面做法,展开的级数收敛很快,同样取前四项计算,误差很小.2150114.12-⎪⎭⎫ ⎝⎛-⨯=⎥⎦⎤⎢⎣⎡+⋅+⋅+⋅+⋅+⨯= 43250112835501165501835012114.1取前四项来作计算, 则4142.1]50116550183501211[4.1232≈⋅+⋅+⋅+⨯≈前四项的截断误差⎪⎭⎫ ⎝⎛++⨯⨯< 544501*********.1r ⎪⎭⎫ ⎝⎛+++⨯⨯⨯= 245015011501128354.1 83341025.65012814950128354.14950501128354.1-⨯≈⨯=⨯⨯⨯=⨯⨯⨯=例11.5.2 计算2ln 的近似值(精确到小数点后第4位). 解 将展开式)11()1(432)1ln(1432≤<-+-++-+-=+-x nx x x x x x nn 中的x 换成x -,得)11(432)1ln(432<≤--------=-x nx x x x x x n两式相减,得到不含有偶次幂的展开式)11(7531211ln 753<<-⎪⎪⎭⎫ ⎝⎛+++=-+x x x x x x x令211=-+xx ,解出31=x .以31=x 代入得⎪⎭⎫⎝⎛+⋅+⋅+⋅+⋅= 753317131513131311122ln若取前四项作为2ln 的近似值,则误差为0001.0700001341911132])91(911[32)31131311113191(2||911211131194<<⨯=-⨯=+++<+⨯+⨯+⨯= r于是取 6931.0317131513131311122ln 753≈⎪⎭⎫⎝⎛⋅+⋅+⋅+⋅≈.例11.5.3 利用x sin 求12sin 的近似值(精确到小数点后第6位). 解 由于展开式+--+-+-=--!)12()1(!5!3sin 12153n x x x x x n n (+∞<<∞-x ) 是交错级数,取前n 项部分和做近似估计,误差!)12(!)12()(1212+=+≤++n x n x x R n n n (+∞<<∞-x )151801212ππ=⨯== x ,取前三项能满足精度要求,于是53)15(!51)15(!311515sin12sin ππππ+-≈= 20791170.0)20943951.0(1201)20943951.0(6120943951.053≈+-≈ 精确到六位小数,207912.012sin ≈.例11.5.4 计算定积分⎰=10sin dx x xI 的近似值,精确到0.0001.解 因1sin lim0=→xxx ,所给积分不是广义积分,若定义函数在0=x 处的值为1,则它在区间]1,0[上连续.由前一节知,被积函数的展开时为+--+-+-=--!)12()1(!5!31sin )1(2142n x x x x x n n (∞<<∞-x ) 在区间]1,0[上逐项积分,得⎰10sin dx x x+-⋅--++⋅-⋅+⋅-=-!)12()12(1)1(!771!551!33111n n n这是交错级数,因为第四项5109.2352801!771-⨯<=⋅,所以取前三项的和作为积分的近似值就能满足精度要求.0.9461!551!3311≈⋅+⋅-≈I 例11.5.5 在爱因斯坦(Einstein )的狭义相对论中,速度为v 的运动物体的质量为220/1cv m m -=其中0m 为静止着的物体的质量,c 为光速.物体的动能是它的总动能与它的静止能量之差202c m mc K -=(1)证明在v 与c 相比很小时,关于K 的表达式就是经典牛顿物理学中的动能公式2021v m K =(2)估计s m v /100≤时,这两个动能公式的差别.解 (1)]1)1[(212220202--=-=-cv c m c m mc K ,记22c v x -=,展开成泰勒级数,有]1)16583211[(66442220-+⋅+⋅+⋅+= cv c v c v c m K)1658321(66442220 +⋅+⋅+⋅=cv c v c v c m当cv 很小时,2022202121v m c v c m K =⋅⋅≈.(2) 由解(1)可见,泰勒公式中一阶余项为(22cv x -=)252240225202252021)-(83)1(83)1(83!2)()(v c cv m x x c m x x c m x x f x r =+≤+=''=θθ(10<<θ).因为s m c /1038⨯=,s m v /100≤,则252240225201)(83)1(83)(v c cv m x x c m x r +=-≤010252283840)107.4(]100-103[8)103(1003m m -⨯<⨯⨯⨯⨯≤)()(.可见,误差极小,说明两个公式极为接近.习题 11.51.利用函数的幂级数展开式求下列各函数的近似值: (1)ln 3(误差不超过0.0001); (2)cos2︒(误差不超过0.0001);2.利用函数的幂级数展开式求下列定积 分的近似值:(1)0.54011dx x +⎰(误差不超过0.0001); (2)0.5arctan xdx x⎰(误差不超过0.001); 11.6傅里叶级数实例1振动问题一根弹簧受力后产生振动,如不考虑各种阻尼,其振动方程为)sin(ϕω+=t A y ,其中A 为振幅,ω为频率,ϕ为初相,t 为时间,称为简谐振动.人们对它已有充分的认识.如果遇到复杂的振动,能否把它分解为一系列简谐振动的叠加,从而由简谐振动去认识复杂的振动呢?实例2正弦波问题在电子线路中,对一个周期性的脉冲)(t f ,能否把它分解为一系列正弦波的叠加,从而由正弦波去认识脉冲)(t f 呢?实际上科学技术中其他一些周期运动也有类似的问题,这些问题的解决都要用到一类重要的函数项级数―傅里叶级数.为了研究傅里叶级数,我们先来认识下面一个概念—三角级数.它在数学与工程技术中有着广泛的应用.三角级数的一般形式是)sin cos (210nx b nx a a n n n ++∑∞=, 其中n n b a a ,,0 ( n = 1,2,…)都是常数,称为三角级数的系数.特别地,当a n = 0 ( n = 0,1,2,…)时,级数只含正弦项,称为正弦级数;当b n = 0 ( n = 1,2,…)时,级数只含常数项和余弦项,称为余弦级数.对于三角级数,我们讨论它的收敛性以及如何把一个周期为2l 的周期函数展开为三角级数的问题.11.6.1 以2π为周期的函数展开成傅里叶级数 1三角函数系 函数列,sin cos , ,2sin ,2cos ,sin ,cos 1nx nx x x x x ,, (11.6.1)称作三角函数系.三角函数系(11.6.1)有下列重要性质.这个定理的证明很容易,只要通过积分的计算即可验证,请读者自己进行.设两个函数ϕ和φ在[,]a b 上可积,且满足⎰=bax x x 0d )()(φϕ,则称函数ϕ和φ在[,]a b 上正交.由定理11.6.1,三角函数系(11.6.1)在[,]ππ-上具有正交性,称为正交函数系.-π2 周期为2π的函数的傅里叶级数设函数f (x )是周期为2π的周期函数,且能展开成三角级数,即设)sin cos (2)(10nx b nx a a x f n n n++=∑∞= (11.6.2)为了求出式(11.6.2)中的系数,假设式(11.6.2)可逐项积分,把它从-π到π逐项积分,得1()(cos sin ),2n n k a f x x x a nx x b nx x ππππππππ∞----==++∑⎰⎰⎰⎰d d d d 由三角函数系的正交性知,上式右端除第一项外均为0,所以0(),2a f x x x a πππππ--==⎰⎰d d 于是得01(),a f x x πππ-=⎰d 为求a n ( n = 1,2,…),先用cos kx 乘以式(5.2)两端,再从-π到π逐项积分,得1()cos cos (cos cos sin cos )2n n k a f x kx x kx x a nx kx x b nx kx x ππππππππ∞----==++∑⎰⎰⎰⎰d d d d .由三角函数系正交性知,上式右端除k = n 的一项外其余各项均为0,所以2()cos cos ,n n f x nx x a nx x a πππππ--==⎰⎰d d于是得1()cos (1,2,3,) n a f x nx x n πππ-==⎰d .类似地,为求b n ( n = 1,2,…),用sin kx 乘以式(11.6.2)两端,再从-π到π逐项积分,得1()sin (1,2,3,). n b f x nx x n πππ-==⎰d显然,当f (x )为奇函数时,公式(5.3)中的a n = 0 (n = 0, 1, 2, 3,…);当f (x )为偶函数时,公式(11.6.3)中的b n = 0 (n = 1, 2, 3,…),所以有(1) 当f (x )是周期为2π的奇函数时,其傅里叶级数为正弦级数nx b n n sin 1∑∞=,其中2()sin (1,2,3,) n b f x nx x n πππ-==⎰d ;(2) 当)(x f 是周期为2π的偶函数时,其傅里叶级数为余弦级数nx a a n n cos 21∑∞=+,其中 2()cos (1,2,3,) n a f x nx x n πππ-==⎰d .3 傅里叶级数的收敛性对于给定的函数)(x f ,只要)(x f 能使公式(5.3)的积分可积,就可以计算出)(x f 的傅里叶系数,从而得到)(x f 的傅里叶级数.但是这个傅里叶级数却不一定收敛,即使收敛也不一定收敛于)(x f .为了确保得出的傅里叶级数收敛于)(x f ,还需给)(x f 附加一些条件.对此有下面的定理.2,3,)2,3,)例11.6.1 正弦交流电i (x ) = sin x 经二极管整流后变为(如图11.6.1)⎩⎨⎧+<≤<≤-=ππππ)12(2,sin 2)12(,0)(k x k x k x k x f ,其中k 为整数.把函数f (x )展开为傅里叶级数.解 函数)(x f 满足收敛定理的条件,且在整个数轴上连续,因此)(x f 的傅里叶级数处处收敛于)(x f .函数f (x )的傅里叶系数为00112()sin a f x x x x ππππππ-===⎰⎰d d ,图11.6.120,11()cos d sin cos d 2,1)n n a f x nx x x nx x n n ππππππ-⎧⎪===⎨-⎪-⎩⎰⎰为奇数为偶数(, 00,111()sin d sin sin d 1, 12n n b f x nx x x nx x n πππππ-≠⎧⎪===⎨=⎪⎩⎰⎰.所以)(x f 的傅里叶展开式为)142cos 356cos 154cos 32cos (2sin 211)(2 +-++++-+=k kx x x x x x f ππ,)(+∞<<-∞x . 例11.6.2 如图11.6.2所示,一矩形波的表达式为⎩⎨⎧+<≤<≤--=ππππ)12(2,12)12(,1)(k x k k x k x f ,k 为整数.求函数)(x f 的傅里叶级数展开式.图11.6.2解 函数)(x f 除点x = k π ( k 为整数)外处处连续,由收敛定理知,在连续点(x ≠ k π)处,)(x f 的傅里叶级数收敛于)(x f .在不连续点(x = k π)处,级数收敛于02)1(1=-+.又因)(x f 是周期为2π的奇函数,因此,函数)(x f 的傅里叶系数为0 (0,1,2,3,)n a n ==,004,22()sin d 1sin d 0, n n n b f x nx x nx x n πππππ⎧⎪==⋅=⎨⎪⎩⎰⎰为奇数为偶数.所以)(x f 的傅里叶展开式为)( )12)12sin(55sin 33sin (sin 4)(为整数,k k x k xk x x x x f ππ≠+--++++= .该例中)(x f 的展开式说明:如果把)(x f 理解为矩形波的波函数,则矩形波可看作是由一系列不同频率的正弦波叠加而成.4 [-,]ππ或[0,]π上的函数展开成傅里叶级数在实际应用中,经常会遇到函数)(x f 只在[-π, π]上有定义,或虽在[-π, π]外也有定义但不是周期函数,而且函数)(x f 在[-π, π]上满足收敛定理的条件,要求把其展开为傅里叶级数.由于求)(x f 的傅里叶系数只用到)(x f 在[-π, π]上的部分,所以我们仍可用公式(11.6.3)求()f x 的傅里叶系数,至少)(x f 在(-π,π)内的连续点处傅里叶级数是收敛于)(x f的,而在x =±π处,级数收敛于)]0()0([21+-+-ππf f .类似地,如果)(x f 只在[0, π]上有定义且满足收敛定理条件,要得到)(x f 在[0, π]上的傅里叶级数展开式,可以任意补充)(x f 在[-π, 0]上的定义(只要公式(11.6.3)中的积分可积),称为函数的延拓,常用的两种延拓办法是把)(x f 延拓成偶函数或奇函数(称为奇延拓或偶延拓),然后将奇延拓或偶延拓后的函数展开成傅里叶级数,再限制x 在[0, π]上,此时延拓后的函数F (x )≡f (x ),这个级数必定是正弦级数或余弦级数,这一展开式至少在(0, π)内的连续点处是收敛于)(x f 的.这样做的好处是可以把)(x f 展开成正弦级数或余弦级数.例11.6.3 将函数f (x ) = x, x ∈[0, π ]分别展开成正弦级数和余弦级数.解 为了把)(x f 展开成正弦级数,先把)(x f 延拓为奇函数F (x ) = x, x ∈[-π, π],如图11.6.3所示,则1222()sin sin (1)n n b F x nx x x nx x nππππ+==⋅=-⎰⎰d d . 由此得F (x )在(-π, π)上的展开式,也即)(x f 在[0, π)上的展开式为)0( )sin )1(33sin 22sin (sin 21π<≤+-+-+-=+x nnxx x x x n . 在x = π处,上述正弦级数收敛于 图11.6.30)(21)]0()0([21=+-=-++-ππππf f . 为了把)(x f 展开成余弦级数,把)(x f 延拓为偶函数||)(x x F =, x ∈[-π, π],如图11.6.4所示,则0022()a F x x x x πππππ===⎰⎰d d ,222()cos d cos d 4, (1,2,)0,n a F x nx x x nx xn n n n πππππ==-⎧⎪==⎨⎪⎩⎰⎰为奇数时为偶数时 于是得到)(x f 在[0, π]上的余弦级数展开式为 图11.6.4。
北师大版七年级数学上册教案:2.1认识无理数

-无理数在实际问题中的应用:培养学生将无理数应用于解决实际问题的能力,如计算圆形面积、周长等。
举例:在讲解无理数与有理数的区别时,可以通过比较√2和1.414(√2的近似值)的关系,让学生明白无理数是无限不循环的,而有理数是有限或循环的。此外,通过实际例子,如计算圆的面积,让学生体会无理数在实际问题中的应用,并学会如何处理无理数的近似值。
直接输出以下内容:
四、教学流程
1.导入新课:以提问方式引导学生思考日常生活中遇到的与无理数相关的问题,激发学生的兴趣和好的定义、特点及其与有理数的区别。
-案例分析:通过具体实例,展示无理数在实际问题中的应用。
3.重点难点解析:
-强调无理数与有理数的本质区别,通过对比分析,帮助学生理解难点。
-掌握无理数的表示方法:介绍根号表示、无限不循环小数等,让学生熟练掌握无理数的表达方式。
-常见无理数的性质:分析π、e、√2等无理数的性质,强调它们的特点和应用。
举例:讲解√2是无理数时,可以通过实际计算说明它不能表示为两个整数之比,从而加深学生对无理数定义的理解。
2.教学难点
-无理数与有理数的区别:解释无理数与有理数的本质区别,如无限不循环小数与有限小数、循环小数的区别,这是学生容易混淆的地方。
2.学会无理数的表示方法,提高学生数学表达和符号意识。
3.通过探索无理数的性质和应用,发展学生的逻辑推理和数学建模能力。
4.培养学生勇于探索、积极思考的学习态度,提高数学素养和解决问题的能力。
5.激发学生对数学学科的兴趣,增强学生的数学情感,为后续学习奠定基础。
三、教学难点与重点
1.教学重点
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
从几个无穷级数看整数、圆周率和自然对数之底的不寻常的关系数学创生之初,只是一些简单的图形与计数,经过历史的堆积,历经萌芽,常量,变量等等阶段,发展到现代,已由数千年前的懵懂初开,化而为如今的枝繁叶茂,其内部存在的一切事物必有其存在的意义,互相关联,相辅相成,它能由最基本的自然数发展成实数理论,又扩展为多维数,并能自成一体,这本身就是一个奇迹,有时候想,也许宇宙本身就是数学性的,只有数学才是先验的。
站在数学浪花之尖,不住地向往,向往那历史上似乎渐渐逝去的光辉思维,向往古希腊的几何盛世,向往18世纪崇尚数感的年代,向往20世纪初期迸发的现代数学思想……Euclid 在写《原本》时是如何敏锐地选择了那几个定义公理公设并公理化地建立起整个欧氏几何,发展出公理化方法;Archimedes 又是如何将他的杠杆原理天才的与几何相结合并直觉地推导出一个个精妙的结论,从而引出微积分最原始的思想?Newton 又是怎样敏锐觉察到微分与积分的互逆关系?Euler 是在怎样的心境下将他的三角函数与复指数联系起来?Gauss 又是如何利用他的同余思想建立起一种研究数论的方法得到一个个不可思议的结论并开创了代数数论;Riemann 又是依据怎样的直觉断言ζ函数的非无聊零点都在直线ReZ=0.5上?Cantor 又是如何想到自然数集合与实数集合的基数存在本质的差别从而提出连续统假说而且建立起现代数学的基石---集合论……这一切,美妙如万花筒般,却又让人产生敬畏之心,一个理论的诞生,甚至一种奇思妙想的产生,若它确实对以往的难处产生了作用,那么在其中必能感受到一种强烈的反差,这种反差往往是由于体系扩大带来的,或许这叫做:领悟。
若是可能,我愿意遇见所有的那些反差……就让我们从Euler 公式,开始这一切的故事。
众所周知,1sin cos 22=+x x ,由此分解因式可有1,1)sin )(cos sin (cos -==-+i x i x x i x它形式上暗合于f(x)f(-x)=1,而x i x x f sin cos )(+=,我们将f(x)f(y)形式地展开有:)sin cos cos (sin )sin sin cos (cos )sin )(cos sin (cos y x y x i y x y x y i y x i x ++-=++也就是说:)sin()cos()sin )(cos sin (cos y x i y x y i y x i x +++=++ 换句话:)()()(y x f y f x f +=,这相当于暗示:f(x)是指数函数。
反复利用上式可有:nx i nx x i x nsin cos )sin (cos ±=±,故而得到两个式子:2)sin (cos )sin (cos cos nn x i x x i x nx -++=和ix i x x i x nx nn 2)sin (cos )sin (cos sin --+=现在让x 取无穷小量,n 取无穷大量,而nx=v 为有限数,x=v/n ,这样,就有:n vx x ==sin 与1cos =x ,代入以上两个式子,得到: i n iv n iv v n iv n iv v n n nn 2)1()1(sin 2)1()1(cos --+=-++=由熟知的结论: )∞==+n ()1(tn e n t ,得到:ie e v e e v iviv iviv 2sin 2cos ---=+=由此二式可有:v i v e ivsin cos +=至此,我们得到ix e x i x x f =+=sin cos )( ○1 此即Euler 公式。
即虚指数量可以用余弦和正弦来共同表示,这个公式非常重要,从它可以感受到:三角与指数同出一源,正弦余弦是复指数的两个方面,一个反一个正。
顺便提一句,在○1里令π=x 可得1-=πi e ,可以写成01=+πi e这个公式是数学里最美丽的公式,它把数学中最重要的几个常数:自然对数之底,圆周率,虚数单位,自然数的单位,0结合起来,我们只能欣赏它而不能解释它的存在到底意味着什么……另外,我们可以有i ei=2π,从而得到22)(ππ-==ee i iii,这样,ii 居然是一个实数2π-e。
觉得在兔子洞里走得够深了吗……现在我们用te 的麦克劳林级数∞++++=......!3!2132t t t e t展开○1的右边: ∞++--+=......!5!4!3!215432ix x ix x ix e ix并分离出实部和虚部,可得到余弦和正弦的幂级数:∞+-+-=......!6!4!21cos 642x x x x ○2 ∞+-+-=......!7!5!3sin 753x x x x x ○3 由○3有∞+-+-=......!7!5!31sin 642x x x x x ,令2x w =并考虑方程 0......!7!5!3132=∞+-+-w w w事实上就是xxsin 0=,故而,......3,2,πππ±±±=x ,那么此方程的所有根就是: ,......3,2,22222πππ=w将多项式零点与系数的关系类比于此,多项式所有零点的倒数之和等于它一次项系数与常数项之比的相反数,所以得到:!313121122222=⋯⋯+++πππ,两边每项都乘以圆周率的平方,得到反平方级数: 63121112222π=⋯⋯+++这表明数列}1{2n 的前n 项之和不会超过62π,而且这是最佳的上界。
设关于w 的方程的所有根为,......)3,2,1(=k w k 则有:901!512)!31(12)1(12212=-=-=∑∑∑<∞=j i ji k k kw w w w,这表明: 903121114444π=⋯⋯+++ 这个过程可以无休止进行下去,现在记:∞⋯⋯+++=s s 312111)(s s ζ(这就叫Riemann ζ函数,事实上,解析延拓后,s 可以在一切1Re ≠s 的复数上取值)经过计算,我们有:⋯⋯======,,,,,,638512875691)12(93555)10(9450)8(945)6(90)4(6)2(12108642πζπζπζπζπζπζ然而我们只能得到一切正偶数的函数值,关于奇数的,比如)3(ζ的具体答案,我们一无所知……我们再以另外一个角度看正弦的幂级数,既然∞+-+-=......!7!5!3sin 753x x x x x ,故而此多项式的一切零点为0,,......3,2,πππ±±±所以必然能成立:∞⋯⋯---=)31)(21)(1(sin 22222222πππx x x x x (每个因式包含两个零点) ○4 同理可以得到:∞⋯⋯---=)541)(341)(41(cos 22222222πππx x x x ○5 在○4里面令2π=x ,得到:∞⋯⋯---=)611)(411)(211(21222π, ∞⋯⋯⨯⨯⨯⨯∞⋯⋯⨯⨯⨯⨯⨯⨯⨯⨯=222286429775533121π这样就得到:∞=+-⨯⋯⋯⨯⨯⨯⨯⨯⋯⋯⨯⨯⨯⨯⨯=n n n n ,)12()12(9531)2(864222222222222π, 由这个式子可以看到圆周率和整数之间有着不寻常的关系!由前叙有2cos ixix e e x -+=,现在我们形式地将x 换成ix ,于是有:2cos xx e e ix -+=我们解方程:02=+-xx e e ,即0cos =ix ,故而: ⋯⋯±±±=,25,23,2πππix ,即方程的一切根为⋯⋯±±±=,25,23,2i i i x πππ于是可以写∞⋯⋯+++=+-)541)(341)(41(222222222πππx x x e e x x 这又是一个初看不可思议的公式,我们可以在其中让x 取1或者π来得到一些恒等式。
π和e 都包含在这个恒等式中。
另外,由ie e x ixix 2sin --=也可以得到一个无穷乘积,就留给读者自己完成吧。
我们知道,每一个不小于2的正整数都可以唯一的分解为若干个素数的乘积:+∈≠∈⋯⋯=Z p p imeNumber p p p p a k j i k n n αααα,,Pr ,2121这叫做算术基本定理,它并不是不证自明的,在此我们不作证明了。
由此,我们可以有: (4)131211......)551......)(331......)(221(511311211222++++=⋯⋯+++++++++=⋯⋯------------s s s s s s s s s ss s 上式最左端的分母中的2,3,5,……是一切素数,当那些括号被展开后,由于算术基本定理,每个正整数都将出现且只出现一次,故而得到最右端。
故而得到恒等式:∞⋯⋯---=---ss s s 511311211)(ζ 由之前的结论有:......111)......511)(311)(211(511311211511311211)90()6(23222122244422242+++=+++=⋯⋯---⋯⋯---=------m m m ππ 易见,最后一个等号后面的k m 是所有那些不含重素因子的正整数的全体。
前几个是:1,2,3,5,6,7,10,13,15,……由此可见所有这种数的平方的倒数和为215π. 以上得到的级数63121112222π=⋯⋯+++在历史上很有名,一般叫做反平方级数,下面我们来探索一下如果它每一项的分母都有一个扰动会如何呢?即:∞++++++++ (41)3121112222cc c c 先借用复变指数导出两个不定积分: 形式地,有C bia e dx eI xbi a xbi a ++==++⎰)()(,但是又:dx bx e i dx bx e I ax ax ⎰⎰+=sin cos用Euler 公式将第一个积分式的实部和虚部分开,和第二个积分式对比,可以得到:C ba bxb bx a e dx bx e C ba bxb bx a e dx bx e axaxax ax++-=+++=⎰⎰2222)cos sin (sin )sin cos (cos 利用这两个式子,将函数)2,0[,)(π∈=x e x f tx作周期为T=2π的延拓,将定义域扩大到R ,再将其展开为Fourier 级数:]sin )sin )((1cos )cos )((1[)(21)(20201202kx dx kx x f kx dx kx x f dx x f x f k T ⎰⎰∑⎰++−−→−∞==πππππππ得到:)sin 1cos 1(121)(222122222kx k tk e kx t t k e t e x f t k t t T +-++-+-−−→−∑∞==ππππππ)(x f 在x=0时间断,它的Fourier 级数在x=0时收敛到)(x f 在x=0处的左右极限的算术平均值:212)0()0(2+=++-t e f f π.所以得到:)t tk e t e e k t t t ∑∞=+-+-=+1222221(12121πππππ,整理后得到: 2222222221)(2)(312111te e t e e t t t t t t t t --+=⋯⋯++++++--πππππ 若引入记号:xxx e e x e e x x x x x sinh cosh coth ,2sinh ,2cosh =-=+=--(它们分别叫做双曲余弦函数,双曲正弦函数,双曲余切函数),则可以将上式写成:222222221)coth(312111tt t t t t -=⋯⋯++++++ππ ○6 事实上令右边的t 趋向于0取极限便是62π,这就是反平方级数;两边对t 求导数,还能得到更多的级数。
