静电场的能量...
第十章静电场中的能量

第十章静电场中的能量1电势能和电势一、静电力做功的特点1.静电力做功:在匀强电场中,静电力做功W=qEl cos θ.其中θ为静电力与位移方向之间的夹角.2.特点:在静电场中移动电荷时,静电力所做的功与电荷的起始位置和终止位置有关,与电荷经过的路径无关.(1)静电力做的功与电荷的起始位置和终止位置有关,但与具体路径无关,这与重力做功特点相似.(2)无论是匀强电场还是非匀强电场,无论是直线运动还是曲线运动,静电力做功均与路径无关.二、电势能1.电势能:电荷在电场中具有的势能,用E p表示.2.静电力做功与电势能变化的关系:静电力做的功等于电势能的减少量.表达式:W AB=E p A-E p B.(1)静电力做正功,电势能减少;(2)静电力做负功,电势能增加.3.电势能的大小:电荷在某点(A点)的电势能,等于把它从这点移动到零势能位置时静电力做的功E p A=W A0.4.电势能具有相对性电势能零点的规定:通常把电荷在离场源电荷无限远处或把电荷在大地表面的电势能规定为零.(1)电势能E p是由电场和电荷共同决定的,是电荷和电场所共有的,我们习惯上说成电荷在电场中某点的电势能.(2)电势能是相对的,其大小与选定的参考点有关。
确定电荷的电势能,首先应确定参考点,也就是零势能点的位置。
(3)电势能是标量,有正负但没有方向。
在同一电场中,电势能为正值表示电势能大于零势能点的电势能,电势能为负值表示电势能小于零势能点的电势能。
5.静电力做功与电势能变化的关系(1)W AB=E p A-E p B.静电力做正功,电势能减少;静电力做负功,电势能增加.(2)在同一电场中,正电荷在电势高的地方电势能大,而负电荷在电势高的地方电势能小.三、电势1.定义:电荷在电场中某一点的电势能与它的电荷量之比.2.公式:φ=E p q。
(1)φ取决于电场本身;(2)公式中的E p 、q 均需代入正负号。
3.单位:国际单位制中,电势的单位是伏特,符号是V ,1 V =1 J/C.4.电势高低的判断:(1)电场线法:沿电场线方向,电势越来越低.(2)电势能判断法:由φ=E p q知,对于正电荷,电势能越大,所在位置的电势越高;对于负电荷,电势能越小,所在位置的电势越高.5.电势的相对性:只有规定了零电势点才能确定某点的电势,一般选大地或离场源电荷无限远处的电势为0.6.电势是标量,只有大小,没有方向,但有正、负之分,同一电场中电势为正表示比零电势高,电势为负表示比零电势低.7.电场中某点的电势是相对的,它的大小和零电势点的选取有关.在物理学中,常取离场源电荷无限远处的电势为零,在实际应用中常取大地的电势为零.8.电势虽然有正负,但电势是标量.在同一电场中,电势为正值表示该点电势高于零电势,电势为负值表示该点电势低于零电势,正负号不表示方向.2 电势差一、电势差1.定义:电场中两点之间电势的差值,也叫作电压.U AB =φA -φB ,U BA =φB -φA ,U AB =-U BA .2.电势差是标量,有正负,电势差的正负表示电势的高低.U AB >0,表示A 点电势比B 点电势高.3.单位:在国际单位制中,电势差与电势的单位相同,均为伏特,符号是V .4.静电力做功与电势差的关系(1)公式:W AB =qU AB 或U AB =W AB q. (2)U AB 在数值上等于单位正电荷由A 点移到B 点时静电力所做的功.二、电势差的理解1.电势差反映了电场的能的性质,决定于电场本身,与试探电荷无关.2.电势差可以是正值也可以是负值,电势差的正负表示两点电势的高低,且U AB =-U BA ,与零电势点的选取无关.3.电场中某点的电势在数值上等于该点与零电势点之间的电势差.三、静电力做功与电势差的关系1.公式U AB=W ABq或W AB=qU AB中符号的处理方法:把电荷q的电性和电势差U的正负代入进行运算,功为正,说明静电力做正功,电荷的电势能减小;功为负,说明静电力做负功,电荷的电势能增大.2.公式W AB=qU AB适用于任何电场,其中W AB仅是电场力做的功,不包括从A到B移动电荷时其他力所做的功.3.电势和电势差的比较1.定义:电场中电势相同的各点构成的面.2.等势面的特点(1)在同一等势面上移动电荷时静电力不做功.(2)等势面一定跟电场线垂直,即跟电场强度的方向垂直.(3)电场线总是由电势高的等势面指向电势低的等势面.3.等势面的特点及应用(1)在等势面上移动电荷时静电力不做功,电荷的电势能不变.(2)电场线跟等势面垂直,并且由电势高的等势面指向电势低的等势面,由此可以绘制电场线,从而可以确定电场的大致分布.(3)等差等势面密的地方,电场强度较强;等差等势面疏的地方,电场强度较弱,由等差等势面的疏密可以定性确定场强大小.(4)任意两个等势面都不相交.4.几种常见电场的等势面(如图1所示)图1(1)点电荷的等势面是以点电荷为球心的一簇球面.(2)等量异种点电荷的等势面:点电荷的连线上,从正电荷到负电荷电势越来越低,两点电荷连线的中垂线是一条等势线.(3)等量同种点电荷的等势面①等量正点电荷连线的中点电势最低,两点电荷连线的中垂线上该点的电势最高,从中点沿中垂线向两侧,电势越来越低.②等量负点电荷连线的中点电势最高,两点电荷连线的中垂线上该点的电势最低.从中点沿中垂线向两侧,电势越来越高.(4)匀强电场的等势面是垂直于电场线的一簇平行等间距的平面.3 电势差与电场强度的关系一、匀强电场中电势差与电场强度的关系1.在匀强电场中,两点间的电势差等于电场强度与这两点沿电场方向的距离的乘积.2.公式:U AB =Ed .二、公式E =U AB d的意义 1.意义:在匀强电场中,电场强度的大小等于两点间的电势差与这两点沿电场强度方向距离之比.2.电场强度的另一种表述:电场强度在数值上等于沿电场方向单位距离上降低的电势.3.电场强度的另一个单位:由E =U AB d可导出电场强度的另一个单位,即伏每米,符号为V /m.1 V/m =1 N/C.三、匀强电场中电势差与电场强度的关系1.公式E =U AB d及U AB =Ed 的适用条件都是匀强电场. 2.由E =U d可知,电场强度在数值上等于沿电场方向单位距离上降低的电势. 式中d 不是两点间的距离,而是两点所在的等势面间的距离,只有当此两点在匀强电场中的同一条电场线上时,才是两点间的距离.3.电场中电场强度的方向就是电势降低最快的方向.4.电势差的三种求解方法(1)应用定义式UAB =φA -φB 来求解.(2)应用关系式UAB =WAB q来求解. (3)应用关系式UAB =Ed(匀强电场)来求解.5.在应用关系式UAB =Ed 时可简化为U =Ed ,即只把电势差大小、场强大小通过公式联系起来,电势差的正负、电场强度的方向可根据题意另作判断.四、利用E =U d定性分析非匀强电场 U AB =Ed 只适用于匀强电场的定量计算,在非匀强电场中,不能进行定量计算,但可以定性地分析有关问题.(1)在非匀强电场中,公式U =Ed 中的E 可理解为距离为d 的两点间的平均电场强度.(2)当电势差U 一定时,场强E 越大,则沿场强方向的距离d 越小,即场强越大,等差等势面越密.(3)距离相等的两点间的电势差:E 越大,U 越大;E 越小,U 越小.五、用等分法确定等势线和电场线1.在匀强电场中电势差与电场强度的关系式为U =Ed ,其中d 为两点沿电场方向的距离. 由公式U =Ed 可以得到下面两个结论:结论1:匀强电场中的任一线段AB 的中点C 的电势φC =φA +φB 2,如图1甲所示. 图1结论2:匀强电场中若两线段AB ∥CD ,且AB =CD ,则U AB =U CD (或φA -φB =φC -φD ),同理有U AC =U BD ,如图乙所示。
静电场的能量

【解】带电球形电容器的电场分布是对称的,由有介质中 的高斯定理可求其电场强度的大小为
E
Q
40 rr 2
则电场能量密度为
we
1 2
0
r
E
2
Q2
322 0 r r 4
现取半径为r、厚为dr的球壳为一体积元,则该体积元的体积为
dV 4r2dr
因此,球壳中储存的电场能量为
于是总能量为
dWe
wedV
Q2
8 0 r r 2
U Ed
将平行板电容器的电容公式(7-38)带入式(7-43),可得
We
=
1 2
CU
21 20r Sd(Ed )21 2
0r E2Sd
1 2
E 2V
上式说明了电场能量的携带者是电场本身。
由上式可得单位体积电场内所具有的电场能量为
we
We V
=
1 E2
2
上式表明,电场的强度越大,电场的能量密度也越大。上 式虽然是从平行板电容器中求得的,但可以证明,对于任意电 场,这个结论也成立。
对于非均匀电场,我们可以任取一体积元dV,可以认为dV 内是均匀电场,则在dV内电场所储存的能量为
dWe
wedV
1 E2dV
2
因此,整个电场的能量为
We
V dWe =
V wedV
1 E2dV
V2
【例7-11】一球形电容器,内、外半径分别为R1和R2,所 带电量分别为+Q和-Q,两球间充满相对电容率为εr的电介 质,如下图所示。求此电容器储存的电场能量是多少?
物理学
静电场的能量
1.1 电容器的静电能
电容器充电时,电源必须做功,才能克服电容器极板上
高中物理精品课件:静电场中的能量

构建知识网络
归纳专题小结
典练素养提升
物理 必修 第三册 配人教版
第十章 静电场中的能量
例2 如图所示,水平地面上方分布着水平向右的匀强电场.一L形的绝缘硬质管竖直固定在 匀强电场中,管的水平部分长为l1=0.2 m,离水平地面的距离为h=5.0 m,竖直部分长为l2=0.1 m.一带正电的小球从管的上端口A由静止释放,小球与管间摩擦不计且小球通过管的弯曲部分(长 度极短,可不计)时没有能量损失,小球在电场中受的静电力大小为重力的一半.求:
(3)判断电场强度的大小(定性)——电场线密处电场强度大,电场线疏处电场强 度小,进而可判断电荷受静电力大小和加速度的大小.
(4)判断电势的高低与电势降低的快慢——沿电场线的方向电势逐渐降低,电
场强度的方向是电势降低最快的方向.
构建知识网络
归纳专题小结
典练素养提升
物理 必修 第三册 配人教版
第十章 静电场中的能量
构建知识网络
归纳专题小结
典练素养提升
物理 必修 第三册 配人教版
第十章 静电场中的能量
专题2 带电体(粒子)在静电力作用下的运动
1.力和运动的角度 带电体的运动情况取决于它的受力情况及初始状态,准确分析带电体的受力情 况是解题的关键,通过受力分析可判断带电体的运动性质及运动轨迹.从力和运动 的角度进行分析是解决带电体在电场中运动问题的最基本方法. 2.运动分解的角度 带电体在电场和重力场的复合场中,若做类平抛或其他曲线运动,都可以考虑 运动分解的思想,把它分解为两个分运动,可使问题很快得到解决.
物理 必修 第三册 配人教版
第十章 静电场中的能量
例1 (多选)如图所示,实线为不知方向的三条电场线,从电场中M 点以相同速度中虚线所示.则( CD )
静电场的能量(精)

静电场的能量静电场的能量一个物体带了电是否就具有了静电能?为了回答这个问题,让我们把带电体的带电过程作下述理解:物体所带电量是由众多电荷元聚集而成的,原先这些电荷元处于彼此无限离散的状态,即它们处于彼此相距无限远的地方,使物体带电的过程就是外界把它们从无限远聚集到现在这个物体上来。
在外界把众多电荷元由无限远离的状态聚集成一个带电体系的过程中,必须作功。
根据功能原理,外界所作的总功必定等于带电体系电势能的增加。
因为电势能本身的数值是相对的,是相对于电势能为零的某状态而言的。
按照通常的规定,取众多电荷元处于彼此无限远离的状态的电势能为零,所以带电体系电势能的增加就是它所具有的电势能。
于是我们就得到这样的结论:一个带电体系所具有的静电能就是该体系所具有的电势能,它等于把各电荷元从无限远离的状态聚集成该带电体系的过程中,外界所作的功。
那么带电体系所具有的静电能是由电荷所携带呢,还是由电荷激发的电场所携带?也就是,能量定域于电荷还是定域于电场?在静电学范围内我们无法回答这个问题,因为在一切静电现象中,静电场与静电荷是相互依存,无法分离的。
随时间变化的电场和磁场形成电磁波,电磁波则可以脱离激发它的电荷和电流而独立传播并携带了能量。
太阳光就是一种电磁波,它给大地带来了巨大的能量。
这就是说,能量是定域于场的,静电能是定域于静电场的。
既然静电能是定域于电场的,那么我们就可以用场量来量度或表示它所具有的能量。
,式中C是电容器的电容。
电容器所带电量从零增大到Q的整个过程中,外力所作的总功为.外力所作的功A等于电容器这个带电体系的电势能的增加,所增加的这部分能量,储存在电容器极板之间的电场中,因为原先极板上无电荷,极板间无电场,所以极板间电场的能量,在数值上等于外力所作的功A,即. (9-77)若电容器带电量为Q时两极板间的电势差为U AB ,则平行板电容器极板间电场的能量还可以表示为,(9-78)和(9-79)设电容器极板上所带自由电荷的面密度为s,极板间充有电容率为e的电介质,电场强度可以表示为,极板上的电量可以表示为Q = s S = e E S , (9-80)式中S是电容器极板的面积。
静电场的能量5

W球面 <W球体 e e
课堂讨论
13.5 静电场的能量 (electrostatic energy)
定义: 定义: 把系统从当前状态无限分裂到彼此相距无 限远的状态中静电场力作的功, 限远的状态中静电场力作的功,叫作系统 在当前状态时的静电势能。简称静电能。 在当前状态时的静电势能。简称静电能。 或: 把这些带电体从无限远离的状态聚合到当 前状态过程中,外力克服静电力作的功。 前状态过程中,外力克服静电力作的功。
r
比较均匀带电球面和均匀带电球体所储存的能量。 比较均匀带电球面和均匀带电球体所储存的能量。
q
0 E = q 4 r2 πε0
R
R
r <R r >R
q
R
r q 4 ε R π0 3 E = q 4 ε0r2 π
∞
r <R r >R
1 1 2 2 2 2 W = ∫ ε0E ⋅ 4 r dr +∫ ε0E ⋅ 4 r dr π π e 2 2 0 R
3.电容器储存的能量 电容器储存的能量
K
a
b
开关倒向a,电容器充电。 开关倒向 ,电容器充电。 开关倒向b,电容器放电。 开关倒向 ,电容器放电。
灯泡发光
←电容器释放能量
←电源提供
计算电容器带有电量Q,相应电势差为U 计算电容器带有电量 ,相应电势差为 时所 具有的能量。 具有的能量。
电容器中的能量是在充电过 程中建立起来的。 程中建立起来的。 充电过程, 充电过程,使电容器的两极 板分别带上等量的正负电荷, 板分别带上等量的正负电荷,这 相当于将某一极板上的电荷拉到 另一极板上。 另一极板上。这是电荷在两极板 间的搬迁过程。 间的搬迁过程。 搬迁过程中, 搬迁过程中,随着极板上电 荷的累积,要做的功越来越大, 荷的累积,要做的功越来越大, 这就像粮仓中粮食的囤积过程, 这就像粮仓中粮食的囤积过程, 粮越来越高,再往上倒, 粮越来越高,再往上倒,就越来 越困难。 越困难。
大学物理8-5 静电场的能量
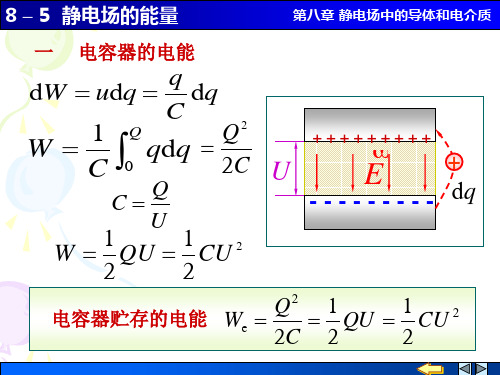
E ( R1 r R2 ) 2π 0 r
r R1
max Eb 2π 0 R1
l
max 2 0 R1 Eb
-+ - + R1 - + R2 -+
8 – 5
静电场的能量
第八章 静电场中的导体和电介 质
(2)电场的能量
E ( R1 r R2 ) 2π 0 r
( R1 r R2 )
1 1 R12 Eb2 2 wm 0 Em 0 2 2 2 r
R2
沿轴线单位长度的最大电场能量
Wm wm dV
2 1 2 b
R1
1 R E 0 2 1 2rdr 2 r
2 1
2 b
R2 4 1 0R E ln 5.76 10 J m R1
8 – 5
静电场的能量
第八章 静电场中的导体和电介 质
作业:
Q2 6 8 0 R
2
R
0
Q 2 dr 4 r dr R r 2 8 0
2 2
Q Q 3Q 40 0 R 8 0 R 20 0 R
8 – 5
静电场的能量
例8-6 如图所示,球形电容器的内、外半径分别为 R1和 所带电荷为 Q.若在两球壳间充以相对介电常数为 的电介质,求此电容器贮存的电场能量.
8 – 5 一
静电场的能量 电容器的电能
第八章 静电场中的导体和电介 质
q d W udq d q C
1 W C
Q
0
1 1 W QU CU 2 2 2
Q2 1 1 电容器贮存的电能 We QU CU 2 2C 2 2
静电场的能量

ϕa =
Q 4πε 0 a
因此静电场总能量为
W=
Q2 8πε 0 a
方法之二:
1 v v W = ∫ E ⋅ Dd V 2 ∞
因为球内电场为零, 故只须对球外积分
2 Q 2 drdQ = W= ∫ r 2 2 2 (4πε 0 r ) 8πε 0
ε0
Q2r = . 2 8πε 0 a r
式中右边第二项散度体积分化为面积分
v v v r →∞ → 0 ∫ ∇ ⋅ (ϕD)dV = ∫ ϕD ⋅ dS
所以
1 W = ∫ ρϕdV 2
例3 求带电量Q、半径为a的导体球的静电场总能量。 解 整个导体为等势体, 导体球的电荷分布于球 面上,方法之一:
1 1 W = ∫ ρϕdV = Qϕ a 2 2
第一项是设想体系的电 荷集中于原点上时在外 场中的能量 第二项是体系的电 偶极矩在外电场中 的能量 第三项是四极 子在外电场中 的能量
W (0 ) = Qϕ e (0 )
W
(2 )
(1)
v v = p ⋅ Ee (0 )
只有在非均匀场 中四极子的能量 才不为零
W
v 1 t = − D : ∇Ee 6
六、静电场的能量 电荷体系与 外电场的相互作用
1、静电场能量
1 v v W = ∫ E ⋅ DdV 2 ∞
由E=-∇ϕ和∇⋅D=ρ得 v v v v v E ⋅ D = −∇ϕ ⋅ D = −∇ ⋅ (ϕD) + ϕ ∇ ⋅ D v = −∇ ⋅ (ϕD) + ρϕ 因此
v 1 1 W = ∫ ρϕdV − ∫ ∇ ⋅ (ϕD )dV 2 2
代入得
3 1 3 ∂ ∂2 W = ∫ ρ ϕ e (0 ) + ∑ xi ϕ e (0) + ∑ xi x j ϕ e (0) + L dV 2! i , j =1 ∂xi ∂xi ∂x j i =1 1 ∂ ∂2 ϕ e (0 ) + ∑ Dij ϕ e (0) + L = Qϕ e (0 ) + ∑ pi 6 i, j ∂xi ∂xi ∂x j i 1 t v = Qϕ e (0 ) + p ⋅ ∇ϕ e (0 ) + D : ∇∇ϕ e (0 ) + L 6
静电场的能量公式

静电场的能量公式好的,以下是为您生成的关于“静电场的能量公式”的文章:咱们在学习物理的时候,静电场可是个挺有意思的家伙。
说到静电场,就不得不提到它的能量公式,这玩意儿可是藏着不少奥秘呢!先来说说静电场能量公式到底是个啥。
简单来讲,静电场的能量可以用公式 $W = \frac{1}{2} \int \varepsilon E^2 dV$ 来表示。
这里头的$\varepsilon$ 是介电常数,$E$ 是电场强度,$dV$ 是体积元。
这公式看起来可能有点复杂,但别慌,咱们慢慢捋捋。
就拿我曾经观察过的一个小实验来说吧。
有一次,我在教室里给同学们演示静电实验。
我拿了一块塑料板和一些碎纸屑,把塑料板在头发上摩擦了几下,然后靠近碎纸屑。
嘿,那些碎纸屑就像被施了魔法一样,纷纷跳起来粘在了塑料板上。
这其实就是静电场在起作用。
那这个和静电场的能量公式有啥关系呢?其实,当塑料板摩擦产生静电的时候,就形成了一个小小的静电场。
这个静电场具有一定的能量,而这个能量的大小就可以用咱们刚才提到的公式来计算。
只不过这个实验中的静电场比较简单,真正复杂的静电场,比如在电容器中,那能量的计算可就没这么轻松啦。
咱们再回到这个公式,为啥会有这样的形式呢?想象一下,电场就像是一个大力士,它在空间中“使劲”,而这个“使劲”的程度就由电场强度 $E$ 来表示。
介电常数 $\varepsilon$ 呢,则反映了介质对电场的影响。
就好像在不同的环境中,大力士发挥的效果不一样。
比如说在空气里和在水里,同样的电场强度,产生的效果可能就不同。
而积分 $\int dV$ 则是把空间中每一个小部分的能量都加起来,这样才能得到整个静电场的总能量。
在实际应用中,静电场的能量公式可重要了。
比如说在电子电路中,电容器储存电能就是依靠静电场。
我们要设计一个高效的电路,就得搞清楚电容器中静电场的能量有多少,这时候这个公式就派上用场啦。
还有在研究电磁辐射的时候,也离不开对静电场能量的理解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
WAq1
r
q2E1 dl
q2
E1 dl
r
V1q2
q1q 2
4 0 r
q1在q2处产生的电势
.
W q2q1
4 0r
1 2q14q20 r1 2q2
q1
40 r
状态a
q1 r q2
1
1
2q1V1 2q2V2
q1在q2处产生的电势
q2在q1处产生的电势
.
W12q1V1 12q2V2
状态a
W0的__________r__倍.
.
平行板电容器充电后与电源断开 Q 不变
0 ++++++++++
E0
-0 - - - - - - - - - -
W0
Q2 2C 0
0 +++++++++++
r
E
-0 - - - - - - - - - - -
W
Q2 2C
Q2 2 rC 0
W0 r
.
平行板电容器充电后未与电源断开 U 不变
E
1
4π
Q r2
we 1 2E2
Q2
32π2r4
.
R1 dr
r
R2
we
1
2
E2
Q2
32π2
r4
变量
dW e wedV8π Q 2r2dr
R1 dr
r
R2
W ed W e8 Q π 2 R R 1 2d rr 28 Q π 2(R 1 1R 1 2)
.
Q2 1 1 1 Q2
We8π(R1R2)24π R2R1
(A) E↑,C↑,U↑,W↑. (B) E↓,C↑,U↓,W↓. (C) E↓,C↑,U↑,W↓. (D) E↑,C↓,U↓,W↑.
.
0 ++++++++++
E0
-0 - - - - - - - - - -
0 +++++++++++
r E -0 - - - - - - - - - - -
C C0 Q 不变
匀电介质中,这时它的静电能量
W =________W__0___r___.
.
2. 如图所示, 一球形导体,带有电荷q,置于一任
意形状的空腔导体中.当用导线将两者连接后,
则与未连接前相比系统静电场能量将
(A) 增大.
(B) 减小.
(C) 不变.
q
(D) 如何变化无法确定.
答案B
.
3. 一空气平行板电容器充电后与电源断开,然后 在两极板间充满某种各向同性、均匀电介质,则 电场强度的大小E、电容C、电压U、电场能量W 四个量各自与充入介质前相比较,增大(↑)或减小 (↓)的情形为
We
1 CU2
2
1 E 2V
2
电场能量密度 we W V1 2E21 2ED
电场空间所存储的能量
W eVwedVV1 2E2dV
.
例1 如图所示,球形电容器的内、外半径分别为
和 R 1 ,所R带2 电荷为 .若 Q在两球壳间充以电容率
为 的电介质,问此电容器贮存的电场能量为多少?
解:两球壳间的电场强度为
1 U r U0
E E0 r
We Q 2C2 12QU12CU 2
(B) E↓,C↑,U↓,W↓.
.
答案B
3. 一空气电容器充电后切断电源,电容器储能W0,
若此时在极板间灌入相对介电常量为 的煤r 油,
则电容器储能变为W0的________1___r 倍.如果灌煤
油时电容器一直与电源相连接,则电容器储能将是
吸引力所作的功为 两极板的相互吸引力为
Q 2d 2 0S
Q2 2 0S
0 ++++++++++
E0
-0 - - - - - - - - - -
0 +++++++++&# - - - - -
W0
1 2
C0U2
W
1 CU2 2
1 2
r
C0U
2
rW0
.
4.一个平行板电容器的极板面积为S, 间距为d,用 电源充电后两极板上带电分别为 Q ,断开电源后 将电容器两极板间距离拉到2d,外力克服两极板的
.
二、静电场的能量
1、讨论:充电电容器所储存的能量谁是其携带者?
We
1 CU2 2
设此电容器是一个平行平板电容器则有:
W e 1 2 C U 2 1 2d S (E d ) 2 1 2E 2 (S d ) 1 2E 2 V
上述分析表明:电场具有能量。它是静电场本身 所具有的能量。
.
2. 能量密度
q1 r q2
1
W 2
i
qiVi
点电荷系
Vi
除 q i 以外的电荷在 q i 处的电势
.
若带电体连续分布
W 1 dqV 2 Q
dq
V: 所有电荷在dq 处的电势
如均匀 带电球面 带电量 Q半径 R
静电能
W 1 dq Q
2Q 40R
Q2
80 R
.
如均匀 带电球体 带电量 Q半径 R
静电能
W
§6-4 静电场的能量
§6-4-1 点电荷系的静电势能
状态a
以两个点电荷系统为例 想象q1 q2 初始时相距无限远
q1 r q2
第一步 先把q1摆在某处 外力不作功
第二步 再把q2从无限远移过来 使系统处于状态a
.
使系统处于状态a,
状态a
外力克服q1的场作功等于该 q1 r q2
带电系统静电能的增加
1 dqV 2 Q
3Q 2
20 0 R
真空中均匀带电的球面和球体,如果两者的半 径和总电量都相等,则带电球面的电场能量W1与 带电球体的电场能量W2相比,W1 ________W2
(填< 、=、>)。
.
§6-4 -2 电容器的能量 一 充电电容器的储能 1 充电电容器储存有能量的实验验证
K 。a
R2R1
讨论
(1)W e
Q2
2 C C4π
R2R1 (球形电容器电容) R2 R1
(2)以上为求电容器电容的第二种方法,即先求 能量,再求电容
.
例2. 一绝缘金属物体,在真空中充电达某一电势值, 其电场总能量为W0.若断开电源,使其上所带电荷
保持不变,并把它浸没在相对介电常量为 的无r
限大的各向同性均匀液态电介质中,问这时电场总 能量有多大?
解:因为所 带电荷保持不变,故电场中各点的电 位移矢量 D 保持不变,
又 w 1 2D E 2 1 0rD 21 r2 10D 0 2w r 0
因为介质均匀,∴电场总能量 WW0/r
.
1. 一个带电的金属球,当其周围是真空时, 储存的静电能量为W0,使其电荷保持不变,
它浸没在相对介电常量为 r 的无限大各向同性
εC
K 。b
K打到a电容器充电
R K打到b,电容器放电, 灯泡R发出强闪光
.
根据功能原理充电后电容
器所储存的能量应等于外力
搬运电荷过程中所做的功。
dWUdqqdq C
U
+++++++++
E +
- - - - - - - - - dq
W
1 C
Q
0 qdq
Q2 2C
WW e2 Q C 2 1 2QU 1 2C2 U
