高等桥梁结构理论课程讲义2014-05
合集下载
高等桥梁结构理论课程讲义2014-04概要
v( z , s ) ( s ) ( z )
式中， ( z ) 为截面 z 的扭转角。
11/26/2018
（4-7）
4
将式（4-7）及（4-5）代入到式（4-6）中，有
M u (s) ' ( z ) K s G 在选定曲线坐标 s 的起算点后（ s 0 ），对上式积分，即 s M K s ds u ( z, s) u0 ( z ) ' ( z ) ( s)ds 0 G 0
q MK
（4-5）
1.1.1 截面自由扭转的翘曲位移
为了求得纵向翘曲 u ( s) ，从杆件中面上任意一点 M ( z, s) 处取一微元 dz ds ，其剪切变形的几何物理 方程为
u v s z G
（4-6）
其中， —— 剪应变； G —— 剪切模量； u —— 沿轴向 z 的位移； v —— 沿曲线坐标 s 的位移。 由于假定截面外形轮廓线保持不变，则在截面 z const上，可以将 v( z, s) 写成
i 1 i
n
i
M K GJ d '
（4-2）
M K ( s) ( s) ( s)ds
式中， ( s) 为扭转中心 O1 点到轮廓线上某点 M (s) 的切线垂直距离。
11/26/2018
（4-3）
3
将式（4-2）代入（4-3），则
M K q ( s )ds q Nhomakorabea式中，
（4-4）
(s)ds 为外形轮廓线所围面积的两倍，即截面剪力流强度为
u ( z, s) u0 ( z )
即
M K s ds M K G 0 GJ d
高等桥梁结构理论课程讲义2014-01
1874年，美国工程师J. Eads建造了世界上第一座3跨钢桁拱桥(155.1+158.5 +153.1m）。1890年建成了Forth桥（主跨519m，B. Baker和J.Fowler设计）。
Eads Bridge（ Over the Mississippi at St. Louis, Missouri，1867-1874 ）
Britannia Bridge
Britannia Bridge（改建后）
（三）桁架分析理论（钢材出现，1856年开始）
1847年美国工程师S. Whipple撰写了《桥梁建筑研究》，把桁架设计从经验 时代推进到科学时代，建议用铸铁做压杆，用锻铁做拉杆，形成金属桁架桥；
1857年德国工程师H.Gerber受木桁架的启发，建造了多腹杆格子桁架桥，后 来这种结构被推广到带挂孔的桁架体系；
尽管有限元软件功能强大，但近代桥梁工程师所创立的各种古典解析理论和 近似方法仍具有定性分析的意义，对于工程师在桥梁结构概念设计阶段进行估计 和把握体系力学性能、理解规范和分析病害等具有重要的意义。
（二）预应力混凝土技术
预应力概念在古代最初的应用是以绳索或铁箍缠绕桶板做水桶。直到1886年， 这一概念才应用到混凝土中。美国工程师P.H.Jackson独立地获得了在混凝土拱 内张紧钢拉杆做专用楼板的专利。1888年德国人C. E. W.Doehring获得了在楼板 受荷载前用施加预应力钢筋来加强的专利。
且牢固，申请专利。（混凝土结构的创始人！）1875年建造了世界上第一座跨 度为13.8m的钢筋混凝土人行桥（Chazelet Bridge）。The important point of Monier‘s idea was that it combined steel and concrete in such a way that the best qualities of each material were brought into play.
Eads Bridge（ Over the Mississippi at St. Louis, Missouri，1867-1874 ）
Britannia Bridge
Britannia Bridge（改建后）
（三）桁架分析理论（钢材出现，1856年开始）
1847年美国工程师S. Whipple撰写了《桥梁建筑研究》，把桁架设计从经验 时代推进到科学时代，建议用铸铁做压杆，用锻铁做拉杆，形成金属桁架桥；
1857年德国工程师H.Gerber受木桁架的启发，建造了多腹杆格子桁架桥，后 来这种结构被推广到带挂孔的桁架体系；
尽管有限元软件功能强大，但近代桥梁工程师所创立的各种古典解析理论和 近似方法仍具有定性分析的意义，对于工程师在桥梁结构概念设计阶段进行估计 和把握体系力学性能、理解规范和分析病害等具有重要的意义。
（二）预应力混凝土技术
预应力概念在古代最初的应用是以绳索或铁箍缠绕桶板做水桶。直到1886年， 这一概念才应用到混凝土中。美国工程师P.H.Jackson独立地获得了在混凝土拱 内张紧钢拉杆做专用楼板的专利。1888年德国人C. E. W.Doehring获得了在楼板 受荷载前用施加预应力钢筋来加强的专利。
且牢固，申请专利。（混凝土结构的创始人！）1875年建造了世界上第一座跨 度为13.8m的钢筋混凝土人行桥（Chazelet Bridge）。The important point of Monier‘s idea was that it combined steel and concrete in such a way that the best qualities of each material were brought into play.
高等桥梁结构理论课程讲义
严格控制混凝土的施工过程和养护条 件，确保混凝土质量符合设计要求。
混凝土的配合比设计
根据桥梁结构的要求和原材料情况， 进行科学的配合比设计，优化混凝土 性能。
预应力技术应用与效果评估
预应力技术的原理与应用
01
通过预先对桥梁结构施加压力，提高结构的承载能力和抗裂性。
预应力筋的选材与张拉
02
选择适合的预应力筋材料，并进行科学的张拉工艺设计，确保
拱桥结构形式及优势分析
上承式拱桥
桥面在拱肋上方，构造简单，施工方便；
下承式拱桥
桥面在拱肋下方，景观效果好，适用于城市 桥梁。
中承式拱桥
桥面在拱肋中部，适用于较大跨径，但施工 复杂；
拱桥优势
跨越能力大，承载能力高，造型美观。
悬索桥和斜拉桥结构形式简介
悬索桥
由主缆、加劲梁、主塔和锚碇组成， 适用于大跨径海洋桥梁；
斜拉桥
由主梁、斜拉索和塔柱组成，造型优 美，适用于城市桥梁和景观桥梁。
构造设计注意事项和优化建议
注意事项
确保结构安全性、适用性和耐久性；考虑施工方法和顺序；重视细部构造设计。
优化建议
采用新型材料和结构形式；进行结构分析和优化；加强施工监控和质量控制。
05 高等桥梁结构施工方法探 讨
施工方法分类及适用条件
预应力效果。
预应力效果的评估与监测
03
对预应力桥梁进行定期检测和评估，及时发现并处理潜在问题。
新型复合材料在桥梁中应用
01
新型复合材料的种类与特点
介绍新型复合材料的种类、性能特点及其在桥梁结构中的应用优势。
02
新型复合材料在桥梁中的应用实例
通过具体案例，展示新型复合材料在桥梁结构中的应用效果。
高等桥梁结构理论(第五章)
第五章 斜桥计算理论本章介绍斜交桥的参数及斜交板的受力特征、各项同性斜交板的微分方程、斜梁桥的计算、超静定简支斜梁的内力。
最后做一小结。
5.1 斜交桥的参数及受力特征1．斜梁排当斜交板或斜交梁排的斜交角θ（见图5-1图示定义）小于20°时，一般可忽略斜交作用，按斜交跨径的正交桥进行分析计算，这样计算出的纵向弯矩与剪力均偏于安全方面。
如果用半连续体方法（见参考文献[3]）分析斜交梁桥的荷载横向分布，则可以根据下面介绍的两个无量纲参数来确定。
⎪⎪⎭⎪⎪⎬⎫=⎪⎭⎫ ⎝⎛=L a EI LD a L m y θεπηtan 2)(1234 （5-1）式中：m ——和谐数；y D ——横向单位长度的挠曲刚度；EI ——一片主梁的挠曲刚度； η、ε——两个无量纲参数。
图5-1 斜交桥参数与斜交角定义L -斜交跨径；a -主梁间距；θ-斜交角；α-桥台或桥梁支承处的倾角式（5-1）可以确定三片主梁的荷载横向分布系数（参考文献[1]的论述）。
对于斜交多主梁，设跨径为16m ，跨中弯矩与支点反力如图5-2所示。
θtan a (m) θtan a (m)图5-2 五片斜主梁，M 与R 变化曲线a -主梁间距；θ-斜交角在斜梁排中，如图5-3所示，如果A、B、C和D代表车轮，轴距为'l，A与B、C 与D的横向间距为a，我们可将斜梁排转成正交桥，A、B、C、D位置不变，如图5-3b）。
如将AB与CD也转一个斜交角，则按图5-3c）算出的正交桥的结果与原斜交桥图5-3a）的结果是等价的。
a）b）c）图5-3 斜梁排的转换2.斜交板斜交板与直交板不同，它有许多特殊之处，其受力特征比斜梁排更为突出。
斜交板随宽跨比、抗弯刚度、抗扭刚度，斜交角、支承条件、荷载形式的不同而变化，现扼要说明如下：错误！未找到引用源。
图5-4 斜交板纵向弯矩变化线（1）斜交板在均布荷载作用下，沿桥跨方向的最大弯矩随 角的增大从跨中向钝角部位移动，如图5-4所示，实线表示︒=50α时纵向最大弯矩的位置，虚线表示︒=70α，点虚线表示︒=30α时的相应位置。
桥梁高等钢结构理论
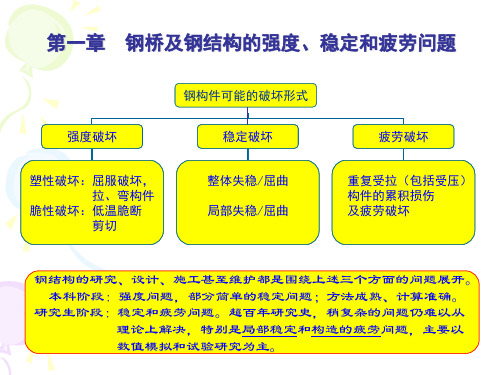
钢结构的研究、设计、施工甚至维护都是围绕上述三个方面的问题展开。 本科阶段：强度问题，部分简单的稳定问题；方法成熟、计算准确。
研究生阶段：稳定和疲劳问题。超百年研究史，稍复杂的问题仍难以从 理论上解决，特别是局部稳定和构造的疲劳问题，主要以 数值模拟和试验研究为主。
1.1 钢结构的强度问题
1.1.1 强度问题破坏形式
（1-12）
微分方程（1-12）的通解： y Acoskx B sin kx Q x 2k 2 EI
（1-13）
当Q=0时，图1-5为理想的轴心受压杆件，式（1-13）变为：
y Acoskx Bsin kx
（1-14）
位移边界条件：x=0,y=0; x=L, y=0; 解得：
（3）强度破坏（除个别受剪脆断及低温脆断外）大都为塑性破坏，即 破坏之前会出现明显的变形，容易被觉察并采取措施防止破坏。
钢结构设计的目的：
在于使结构的可靠与经济之间选择一种合理的平衡，力求以最经济 的途径与适当的可靠度满足各种预定的功能（安全性、耐久性）的要求。 就是说，结构设计的准则应为：由各种作用所产生的作用效应（内力和 变形）不大于结构和连接的抗力或限值（由几何参数、材料性能甚至荷 载性质决定）。
如果采用容许应力来描述式（1-4），设
R f
K
y
f 为钢材的屈服强度，a为构件截面几何特征 y
则式（1-4）可写成：
f
f
S y y [ ]
K KKK
K
123
（1-5）
对于原A3钢： K 1.231.143 1.41 对于原16Mn钢： K 1.231.175 1.45
[ ] 2400 1700 1.41
1.1.2 基于强度的钢结构设计方法发展概述
桥梁高等钢结构理论(ch1)PPT课件
如果采用数学表达式描述结构设计准则，为：
S R
（1-1）
如果结构设计准则中的内力和变形以及抗力或限值都是确定性的，则所进行的计算
和验算将是比较简单的。
然而，影响结构功能的因素如结构上的作用、材料性能、构件几何参数、连接（构 造细部）类型、施工质量、计算模型、试验方法及设备等，很多都是具有随机性的 非确定值。因此，在设计中如何合理地考虑S这 些R 因素，使设计方法更接近于实际情 况，是长期以来钢结构设计方法发展演变所要达到的目的。
然而，无论是极限荷载法还是容许应力法，所采用的安全系数实际上是凭借 工程经验笼统地确定一个定值，这样各种构件的可靠度将不能保证具有比较一致 的水平，这是因为，结构的可靠性（安全性、适用性、耐久性）受各种随机因素 的影响，不能事先确定，只能用概率方S法 来R描述。
（2）半概率极限状态法
半概率极限状态法特点是明确了两种极限状态的概念：承载能力极限状态和变形极 限状态。我国的《钢结构设计规范》（TJ17-74）就是采用这样的设计方法编制的。 尽管该设计方法仍采用了容许应力法的表达方式，但其安全系数则分成了荷载系数 K1，材料系数K2和调整系数K3。是按承载力极限状态经多系数分析得到的。
1.1.2 基于强度的钢结构设计方法发展概述
基于强度的钢结构设计方法大致分为： 容许应力法和极限荷载法、半概率极限状态法、概率极限状态法。
（1）容许应力法和极限荷载法（最大荷载法）
容许应力法
S R
设计原则：结构构件的实际应力小于或等于所给定的容许应力，即：
f
[] y
K
（1-2）
优点：简单、明确，有大量工程数据S，R特 别是应力均匀的构件； 缺点：单一安全系数，保守（受弯构件）；
不能合理反映结构设计的目的（经济性+适当的可靠度）。
第1章 桥梁结构稳定理论ppt课件
在相邻位置 平衡，满足：
sin 0
sin cos cos sin 0
由于 1 ，则 sin co，s 1
cos 1 0
薄壁杆件的弯扭屈曲
中心受压开口薄壁杆件的弯扭屈曲 压弯开口薄壁杆件的弯扭屈曲 纯弯梁的侧向屈曲
3
教学计划
框架及桁梁的屈曲
压杆的柔度方程及刚度方程 框架的平面屈曲 桁架桥弦杆的屈曲 框架相关问题的屈曲
拱的稳定
拱的面内屈曲 拱的面外失稳
板的屈曲
板的弹性屈曲 受压板的屈曲分析 承剪腹板的屈曲及其屈曲后承载力 板件的设计
7
•① 杆、柱、梁、轴、环、拱； •② 薄板、薄壳；
•③ 开口截面薄壁梁.
•q •P •P
•受横向载荷的狭长梁 •横向均布压力作用下的扁拱
8
•轴向压力作用下的薄板
Nx
•一阶屈曲模态 •二阶屈曲模态
•三阶屈曲模态
9
•横向均布压力作用下的薄壳 •受均匀压力作用的拱形薄板1—0 —由拱形平衡变成翘曲平衡
力；
3）桥梁恒载计算错误，低估了桥梁恒载； 4） 迷信“桥梁专家”的权威，桥梁设计、施工过程中缺
乏必要的监督。
——摘自《Royal Commission Report》
25
结构 简支跨（半跨）
悬臂跨 锚固跨
恒载估计值 (kN) 21538
58740
59240
恒载实际值 (kN) 25328
0.6
0.4 -1.5 -1.2 -0.9 -0.6 -0.3 0.0 0.3 0.6 0.9 1.2 1.5
稳定判别准则： λ<1时，稳定平衡 λ=1时，随遇平衡 λ>1时，两个解
sin 0
sin cos cos sin 0
由于 1 ，则 sin co，s 1
cos 1 0
薄壁杆件的弯扭屈曲
中心受压开口薄壁杆件的弯扭屈曲 压弯开口薄壁杆件的弯扭屈曲 纯弯梁的侧向屈曲
3
教学计划
框架及桁梁的屈曲
压杆的柔度方程及刚度方程 框架的平面屈曲 桁架桥弦杆的屈曲 框架相关问题的屈曲
拱的稳定
拱的面内屈曲 拱的面外失稳
板的屈曲
板的弹性屈曲 受压板的屈曲分析 承剪腹板的屈曲及其屈曲后承载力 板件的设计
7
•① 杆、柱、梁、轴、环、拱； •② 薄板、薄壳；
•③ 开口截面薄壁梁.
•q •P •P
•受横向载荷的狭长梁 •横向均布压力作用下的扁拱
8
•轴向压力作用下的薄板
Nx
•一阶屈曲模态 •二阶屈曲模态
•三阶屈曲模态
9
•横向均布压力作用下的薄壳 •受均匀压力作用的拱形薄板1—0 —由拱形平衡变成翘曲平衡
力；
3）桥梁恒载计算错误，低估了桥梁恒载； 4） 迷信“桥梁专家”的权威，桥梁设计、施工过程中缺
乏必要的监督。
——摘自《Royal Commission Report》
25
结构 简支跨（半跨）
悬臂跨 锚固跨
恒载估计值 (kN) 21538
58740
59240
恒载实际值 (kN) 25328
0.6
0.4 -1.5 -1.2 -0.9 -0.6 -0.3 0.0 0.3 0.6 0.9 1.2 1.5
稳定判别准则： λ<1时，稳定平衡 λ=1时，随遇平衡 λ>1时，两个解
《高等桥梁结构理论》教学大纲
《高等桥梁结构理论》教学大纲
课程编号：1321007
英文名称：Advanced Structural Theory in the Bridge
课程类别：学位课学时：60 学分：3 适用专业：土木工程
预修课程：有限元理论与程序设计、桥梁工程
课程内容：
《高等桥梁结构理论》主要介绍桥梁结构的力学理论和分析方法。
介绍桥梁设计计算公式的由来和规范条文的理论依据，从原理上和问题的本质上去认识桥梁结构的受力性能。
课程的主要内容包括：长悬臂行车道板计算理论；薄壁箱梁计算理论；曲线桥计算理论；斜桥计算理论；混凝土的收缩、徐变及温度效应理论；混凝土的强度、裂缝及刚度理论；钢桥的计算理论；桥梁结构几何非线性计算理论；大跨度桥梁的稳定理论。
目的是使学生运用已经掌握的数学力学知识，在解决桥梁结构的基本力学问题时，能够获得比较满意的结果。
学习的重点在于掌握桥梁结构基本分析理论、掌握大跨径桥梁用高性能材料的性能、掌握大跨径桥梁结构模拟分析方法等。
教材：
项海帆. 高等桥梁结构理论. 北京:人民交通出版社，2001
参考书目：
1. 杜国华. 桥梁结构分析. 上海:同济大学出版社，1997
2. 张士铎. 桥梁设计理论. 北京:人民交通出版社，1984
3. 范立础. 桥梁工程. 北京:人民交通出版社，1987
4. 李国豪. 桥梁结构稳定与振动. 北京:中国铁道出版社，1992
考核方式与要求：
课程论文。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
4/14/2015
s
0
ds 0 ( z ) z
（5-53）
其中， 0 ( z ) 是任意积分函数，其物理意义表示曲线坐标 s 0 点的剪应力。
8
将式（5-47）代入到（5-53），则
( z, s) E ' ' ' ( z) (s)ds 0 ( z)
将式（5-45）、（5-46）代入式（5-39）中，有
（5-46）
( z, s) E ' ' ( z) (s)
（5-47）
从上式中可以看出，截面上约束扭转正应力的分布是和广义扇性坐标成正比的。对应扇性零点的物理意义 是：该点上广义扇性坐标为零，或者说正应力为零，因而在该点上的积分起始值也是零。
0
，则
s s ds u ( z , s ) u 0 ( z ) ' ( z ) ( s )ds 0 ds 0 J s ds s u 0 ( z ) ' ( z ) ( s )ds d 0 0
u ( z, s) u0 ( z )
s M K s ds ' ( z ) 0 (s)ds G 0
（5-31）
对于闭口薄壁杆件，由截面 s 0 处的位移连续条件可得，即
u ( z, s) u 0 ( z )
化简，得
M K ds ' ( z ) ( s)ds u 0 ( z ) G
0
s
（5-54）
令
S (s)ds
0
s
（5-55）
则
( z, s) E ' ' ' ( z)S 0 ( z)
（5-56）
图 5-12 薄壁箱梁在扭转力矩 M（注：图中 Mk 应修改为 M）
4/14/2015
9
初始剪力流 0 ( z ) ，如图 5-12，由薄壁箱梁内、外力平衡条件可得
（5-37）
z u0 ' ( z,0) ' ' ( z) (s)
（5-38）
5.2.1 约束扭转正应力
闭口薄壁截面约束扭转正应力为
E[u0 ' ( z,0) ' ' ( z) (s)]
（5-39）
由于杆件截面仅有扭转力矩 M ，故截面上的轴力 N 、绕两个轴的弯矩 M x , M y 均为零，即翘曲应力 （或约束扭转正应力）是自相平衡的，根据力的平衡，可列出如下方程：
4/14/2015
7
5.2.2 约束扭转剪应力
在闭口薄壁截面杆件中面上任取一 M ( z, s) 点附近微元体，如图 5-11 所示。
图 5-11 闭口薄壁截面杆件中面上任取一点 M ( z, s)
由力的平衡条件可知，
0 z s
对上式积分，即
（5-52）
( z, s)
当截面周边不变形时，切线位移为
（5-63）
v ( s) ( z )
式中： ( z ) 为截面的扭转角。 将式（ 5-64）微分一次，并代入式（ 5-63），则
（5-64）
u (s) ' ( z ) s G
将式（5-60）代入上式，即
（5-65）
u M E ' ' ' ( z ) S ( s) ' ( z ) s G G
（5-61）
由公式（5-28）可知，上式还可以写成如下表达式
( z, s)
4/14/2015
（5-62）
10
5.2.3 ( z ) 函数的确定
对于闭口截面而言 ，为确定约束扭转 正应力和 剪应力， 必须先确定函数 ( z ) 。故必须先列出薄壁杆 件约束扭转微分方程 式：
u v s z G
4/14/2015 4
N 0, ds 0 M 0, yds 0 M 0, xds 0
x y
（5-40）
将（5-39）代入到（5-40）中，则有
u ' ( z,0) ds "( z ) ( s)ds 0 u ' ( z,0) yds "( z ) ( s) yds 0 u ' ( z,0) xds "( z ) ( s) xds 0
第五讲 薄壁箱梁约束扭转
1
5.2 闭口截面的约束扭转
乌曼斯基闭口薄壁杆件约束扭转理论基本假定： 横截面周边不变形； 横截面上的法向应力和剪切应力沿壁厚是均匀分布的；
横截面上轴向位移沿本截面的分布规律与自由扭转时是相同的。
图5-10 薄壁杆件约束扭转
2015-4-14
2
令轴向位移为 u ( s, z ) ， z 为纵向坐标， s 表示沿横截面周边。当闭口截面发生自由扭转时，由式（4-9） 可知，薄壁截面轴向位移为：
对式（ 5-66）积分，有
（5-66）
u ( z, s)
4/14/2015
s M s ds E ' ' ' ( z ) s ds S ' ( z ) 0 0 (s)ds u0 ( z) G 0 G
（5-67）
11
为了满足周期条件（或变形协调条件），沿周边积分一周后 u( z, s) u0 ( z) ，即
4/14/2015
6
与开口截面薄壁杆件类似，闭口截面薄壁杆件的广义内力——双力矩定义如下：
B( z ) ( z , s ) ( s ) dF
将式（5-47）代入上式，即
（5-48）
B( z ) E ' ' ( z ) ( s) 2 dF EJ ' ' ( z )
5
将式（5-42）、（5-43）代入到式（5-41）中，有
u ' ( z,0) ds 0 u ' ( z,0) yds 0 u ' ( z,0) xds 0
当截面对称，且扇性零点为对称轴与周边的交点时，有 （5-44）
u ' ( z,0) 0
则
（5-45）
u ( z,0) const
（5-76）
对式（5-76）化简，则
J M ' ( z ) ' ( z ) 1 d GJ J
令
（5-77）
1
则式（5-77）记为
Jd J
（5-78）
M ' ( z) ' ( z) GJ
2 2 式中： J ds dF 为截面的极惯性矩；
M ds E ' ' ' ( z ) S 0 ( z ) ds 0 ( z ) ds E ' ' ' ( z ) S ds
故
（5-57）
0 ( z )
将式（5-58）带入到（5-56）中，有
M E ' ' ' ( z ) S ds
对于闭口截面的扭转中心而言，广义扇性惯性矩应该为零，即 （5-41）
Jx ( s) xds 0 Jy ( s) yds 0
S ( s )ds 0
4/14/2015
（5-42）
当选择适当的积分起点（扇性坐标零点，即 S 坐标的起点）时，使广义扇性静矩也等于零，则 （5-43）
EJ ' ' ' ' ( z) GJ d ' ' ( z) mt
由式（5-37）可知，
（5-71）
u( z, s) u0 ( z) ' ( z) (s)
4/14/2015
（5-72）
12
由于 ( s )
s
0
( s )ds
ds
s
ds
将（5-69）对 z 微分一次，并将各项除以
（5-69）
，且将 ( s ) ds 代入，即
dM K ds 2 E ' ' ' ' ( z ) S G ' ' ( z ) 0 ds ds dz
（5-70）
ds dM 2 S 令 mt ，Jd （自由扭转惯性矩）， J （扇性惯性矩），则式（5-70）可记为 ds ds dz
2 式中， J 为闭口薄壁截面广义主扇性惯性矩，即 J ( s ) dF 。
（5-49）
' ' ( z)
将式（5-50）代入到（5-47）中，有
B( z ) EJ
（5-50）
( z, s)
B( z ) ( s) J
（5-51）
上式即为闭口薄壁杆件截面约束扭转正应力与双力矩的关系。
（5-32）
G 2 MK '( z) ds
（5-33）
将（5-33）代入到（5-31）中，则有
令
s s ds u ( z, s) u0 ( z ) ' ( z ) ( s)ds 0 0 ds s s ds (s) (s)ds 0 ds 0
J 1 G ' ( z ) d ( s ) ' ( z )
s
0
ds 0 ( z ) z
（5-53）
其中， 0 ( z ) 是任意积分函数，其物理意义表示曲线坐标 s 0 点的剪应力。
8
将式（5-47）代入到（5-53），则
( z, s) E ' ' ' ( z) (s)ds 0 ( z)
将式（5-45）、（5-46）代入式（5-39）中，有
（5-46）
( z, s) E ' ' ( z) (s)
（5-47）
从上式中可以看出，截面上约束扭转正应力的分布是和广义扇性坐标成正比的。对应扇性零点的物理意义 是：该点上广义扇性坐标为零，或者说正应力为零，因而在该点上的积分起始值也是零。
0
，则
s s ds u ( z , s ) u 0 ( z ) ' ( z ) ( s )ds 0 ds 0 J s ds s u 0 ( z ) ' ( z ) ( s )ds d 0 0
u ( z, s) u0 ( z )
s M K s ds ' ( z ) 0 (s)ds G 0
（5-31）
对于闭口薄壁杆件，由截面 s 0 处的位移连续条件可得，即
u ( z, s) u 0 ( z )
化简，得
M K ds ' ( z ) ( s)ds u 0 ( z ) G
0
s
（5-54）
令
S (s)ds
0
s
（5-55）
则
( z, s) E ' ' ' ( z)S 0 ( z)
（5-56）
图 5-12 薄壁箱梁在扭转力矩 M（注：图中 Mk 应修改为 M）
4/14/2015
9
初始剪力流 0 ( z ) ，如图 5-12，由薄壁箱梁内、外力平衡条件可得
（5-37）
z u0 ' ( z,0) ' ' ( z) (s)
（5-38）
5.2.1 约束扭转正应力
闭口薄壁截面约束扭转正应力为
E[u0 ' ( z,0) ' ' ( z) (s)]
（5-39）
由于杆件截面仅有扭转力矩 M ，故截面上的轴力 N 、绕两个轴的弯矩 M x , M y 均为零，即翘曲应力 （或约束扭转正应力）是自相平衡的，根据力的平衡，可列出如下方程：
4/14/2015
7
5.2.2 约束扭转剪应力
在闭口薄壁截面杆件中面上任取一 M ( z, s) 点附近微元体，如图 5-11 所示。
图 5-11 闭口薄壁截面杆件中面上任取一点 M ( z, s)
由力的平衡条件可知，
0 z s
对上式积分，即
（5-52）
( z, s)
当截面周边不变形时，切线位移为
（5-63）
v ( s) ( z )
式中： ( z ) 为截面的扭转角。 将式（ 5-64）微分一次，并代入式（ 5-63），则
（5-64）
u (s) ' ( z ) s G
将式（5-60）代入上式，即
（5-65）
u M E ' ' ' ( z ) S ( s) ' ( z ) s G G
（5-61）
由公式（5-28）可知，上式还可以写成如下表达式
( z, s)
4/14/2015
（5-62）
10
5.2.3 ( z ) 函数的确定
对于闭口截面而言 ，为确定约束扭转 正应力和 剪应力， 必须先确定函数 ( z ) 。故必须先列出薄壁杆 件约束扭转微分方程 式：
u v s z G
4/14/2015 4
N 0, ds 0 M 0, yds 0 M 0, xds 0
x y
（5-40）
将（5-39）代入到（5-40）中，则有
u ' ( z,0) ds "( z ) ( s)ds 0 u ' ( z,0) yds "( z ) ( s) yds 0 u ' ( z,0) xds "( z ) ( s) xds 0
第五讲 薄壁箱梁约束扭转
1
5.2 闭口截面的约束扭转
乌曼斯基闭口薄壁杆件约束扭转理论基本假定： 横截面周边不变形； 横截面上的法向应力和剪切应力沿壁厚是均匀分布的；
横截面上轴向位移沿本截面的分布规律与自由扭转时是相同的。
图5-10 薄壁杆件约束扭转
2015-4-14
2
令轴向位移为 u ( s, z ) ， z 为纵向坐标， s 表示沿横截面周边。当闭口截面发生自由扭转时，由式（4-9） 可知，薄壁截面轴向位移为：
对式（ 5-66）积分，有
（5-66）
u ( z, s)
4/14/2015
s M s ds E ' ' ' ( z ) s ds S ' ( z ) 0 0 (s)ds u0 ( z) G 0 G
（5-67）
11
为了满足周期条件（或变形协调条件），沿周边积分一周后 u( z, s) u0 ( z) ，即
4/14/2015
6
与开口截面薄壁杆件类似，闭口截面薄壁杆件的广义内力——双力矩定义如下：
B( z ) ( z , s ) ( s ) dF
将式（5-47）代入上式，即
（5-48）
B( z ) E ' ' ( z ) ( s) 2 dF EJ ' ' ( z )
5
将式（5-42）、（5-43）代入到式（5-41）中，有
u ' ( z,0) ds 0 u ' ( z,0) yds 0 u ' ( z,0) xds 0
当截面对称，且扇性零点为对称轴与周边的交点时，有 （5-44）
u ' ( z,0) 0
则
（5-45）
u ( z,0) const
（5-76）
对式（5-76）化简，则
J M ' ( z ) ' ( z ) 1 d GJ J
令
（5-77）
1
则式（5-77）记为
Jd J
（5-78）
M ' ( z) ' ( z) GJ
2 2 式中： J ds dF 为截面的极惯性矩；
M ds E ' ' ' ( z ) S 0 ( z ) ds 0 ( z ) ds E ' ' ' ( z ) S ds
故
（5-57）
0 ( z )
将式（5-58）带入到（5-56）中，有
M E ' ' ' ( z ) S ds
对于闭口截面的扭转中心而言，广义扇性惯性矩应该为零，即 （5-41）
Jx ( s) xds 0 Jy ( s) yds 0
S ( s )ds 0
4/14/2015
（5-42）
当选择适当的积分起点（扇性坐标零点，即 S 坐标的起点）时，使广义扇性静矩也等于零，则 （5-43）
EJ ' ' ' ' ( z) GJ d ' ' ( z) mt
由式（5-37）可知，
（5-71）
u( z, s) u0 ( z) ' ( z) (s)
4/14/2015
（5-72）
12
由于 ( s )
s
0
( s )ds
ds
s
ds
将（5-69）对 z 微分一次，并将各项除以
（5-69）
，且将 ( s ) ds 代入，即
dM K ds 2 E ' ' ' ' ( z ) S G ' ' ( z ) 0 ds ds dz
（5-70）
ds dM 2 S 令 mt ，Jd （自由扭转惯性矩）， J （扇性惯性矩），则式（5-70）可记为 ds ds dz
2 式中， J 为闭口薄壁截面广义主扇性惯性矩，即 J ( s ) dF 。
（5-49）
' ' ( z)
将式（5-50）代入到（5-47）中，有
B( z ) EJ
（5-50）
( z, s)
B( z ) ( s) J
（5-51）
上式即为闭口薄壁杆件截面约束扭转正应力与双力矩的关系。
（5-32）
G 2 MK '( z) ds
（5-33）
将（5-33）代入到（5-31）中，则有
令
s s ds u ( z, s) u0 ( z ) ' ( z ) ( s)ds 0 0 ds s s ds (s) (s)ds 0 ds 0
J 1 G ' ( z ) d ( s ) ' ( z )