19感生电动势涡旋电场解读
涡旋电场.

无散场(无源场),电力线是闭 合的; (3)
E dl 0
库
dl 0
dB d dS E 感 d l dt dt S
保守力场,可以引入电 位的概念.
非保守场,不能引入电位的概念
dB d dS E 感 dl dt dt S
第四节 涡旋电场
§14.4
感应电动势
涡旋(感生)电场
动生电动势: 洛仑兹力
{
v B d l
i E
涡
感生电动势: 涡旋电场或感生电场
14.4.1 涡旋电场 感生电场(麦克斯韦)
dl
1. 涡旋电场 即使不存在导体回路,变化的磁场在其周围空间也激发 一种电场,它提供一种非静电力能产生 ,这种电场叫做涡 旋电场。 2.涡旋电场与静电场比较
E感
在管内:
在管外:
B E 涡 2 r r2 t
E涡 2 r
B R2 t
r dB E涡 内 2 dt
R 2 dB E涡 外 2r dt
R
r
例2. 圆筒内均匀磁场,以
dB 速率减小,a、b、c离轴 dt
线距离均为r,问电子在各点的加速度的大小和方向如何 ?若电子在轴线上,加速度又如何?
d E 涡 d l dt
d E 涡 2 R dt
1 d E涡 2R dt
0 v0
e d mv d 2R
设加速开始时, 0 v 0
e eR B 2 mv R B 2R 2
mv eRBR
1 BR B 2
轨道环内的磁场等于它围绕面积内磁场平均值的 一半时,电子能在稳定的圆形轨道上被加速。
第二十六讲:§感生电动势和感生电场

第二十六讲: §7.3感生电动势和感生电场一、感生电动势 涡旋电场1、感生电动势:由于dtm φd 所产生的感应电动势。
2、感生电场(涡旋电场):变化的磁场所激发的电场为感生电场。
其特点:①感生电场是非保守场;②电场线是闭合的。
3、感生电场与静电场的比较①相同点:都是电场(物理场,物质性,具有能量,即对电荷有电场力的作用)。
②不同点:⑴激发方式不同,感生电场是由变化的磁场激发的;静电场是由相对观察者静止的带电体激发的。
⑵感生电场电场线是闭合的,静电场电场线是非闭合的。
⑶感生电场是非保守场,静电场是保守场。
因为静电力是保守力,故而静电场力沿闭合路径的积分等于零, 由0W =⋅=⋅=⎰⎰ d q d 静静 ⑴看出, ∵ 0≠q ∴ 0=⋅⇒⎰d 静 静电场为保守场。
由0≠-=⋅=⎰dt d d m i φε 涡看出, 当 0dtd ≠m φ为变化的磁场, 则 0≠⋅⇒⎰ d 涡 也可推出0≠⋅=⇒⎰ d q W 涡⑵比较⑴、⑵式可推出感生电场是非保守场。
4、感生电场与磁场的关系式d m ⋅=⎰φ ; d dtd dt d m ⋅=⎰φ ; d t d S i ⋅∂∂-=⋅=⎰⎰ 涡ε ☆ 5、与涡E 、()i i I ε方向的确定注意:与绕行方向满足右手螺旋法则 当0d dt B 时,0 dS dtdB S i ⎰-=⇒ε i ε与绕行方向相反; 当0d dt B 时,0 dS dtdB S i ⎰-=⇒ε i ε与绕行方向相同。
P264例题7-5已知:如图所示,R,=dt B d 正常数 求:⑴1涡;⑵2E 涡解: ⑴∵d td S i ⋅∂∂-=⋅=⎰⎰ 涡ε R r 21r 2r t B E ππ∂∂-=⋅⇒涡 tB E ∂∂=⇒2r -1涡 R r 22r 2R t B E ππ∂∂-=⋅⇒涡 tB r E ∂∂=⇒2R -22涡 涡电场线绕行方向相反,如上图所示。
P264例题7-6 已知:0d dtB ,L ab = ,h 求:ab ε解:解法一:利用法拉第电磁感应定律S d t dt d S m ⋅∂∂-=-=⎰B i φεtB hL S t B t B i ∂∂=⋅∂∂=⋅∂∂=⎰2ε∵Oa 和Ob 沿径向,而涡E 与径向垂直。
第19讲动生电动势与感生电动势
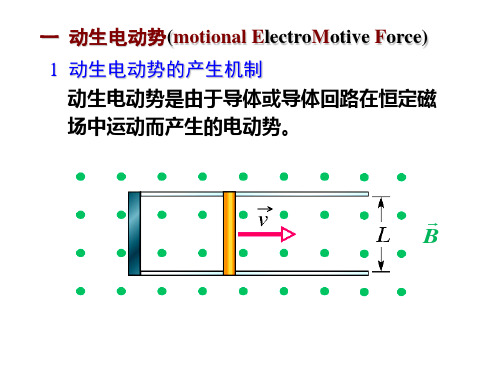
解:由 B 0, 与B同向 感生电场沿逆时针。 t
取逆时针回路, r < R 时
l Ei dl
B dS S t
l
Ei
dl
cos
0
B t
dS
cos
Ei
2
r
dB dt
r2
r dB Ei 2 dt
××××× ×××××××
r × × × × × × ×
×××××××
×R× × × × B
r > R时,
3. 动生电动势的计算
作为电源的这段运动导体杆,其中的洛仑兹力 是非静电力。
非静电力 对应的非静电场强 由电动势定义
Fk e(v B)
Ek
Fk e
v
B
i Ek dl
运动导线ab产生的动生电动势为
i
(v B) dl
l
例题1 有一半圆形金属导线在匀强磁场中作切 割磁力线运动。已知 v, B, R. 求动生电动势.
解:
d (v B)dl
dl Rd v B
vB sin900 dl cos
2
vBR cos d 2 vB2R 有效段!
b dl
d
v
0:与假定的方向相同
R
B
方向:a b
a
例题2 如图,长为L 的铜棒在匀强磁场中以角速度 ω绕 o 轴转动。求:棒中感应电动势的大小 和方向。
解:取如图所示微元(此微元暗示了假定的正方向)
C × × ×O× ×
B t
Ei Dx
L
d Ei dx cos
r dB dx cos
2 dt
r dB Ei 2 dt
逆时针
r cos h
03感生电动势涡旋电场-PPT精品文档

由变化的磁场激发
电 力 线 形 状
电 场 的 性 质
电力线为非闭合曲线
电力线为闭合曲线 dB 0 E感 dt
感生电场为有旋场 为非保守场作功与路径有关
静电场为无旋场 为保守场作功与路径无关
d l 0 E
静电场为有源场
B d l d S E S t
t
电磁场的基本方程之一
B 0 在稳恒条件下,一切物理量不随时间变化, t l 0 Ed
L
静电场的环路定理
5
dB 增加 k ,求空间的感生电场的分布情况。 dt 解: 由于磁场均匀增加,圆形磁场区 R 域内、外E感线为一系列同心圆; 1. r < R 区域: 作半径为 r 的环形路径; o r 设涡旋电场的绕向也为逆时针方向。 B dB B E d l d S d S 感 S t S dt dB 2 dB 2 r r, E dS , E 感 感 dl dt S dt
感生电动势 感应电场
(第六章第4节)
1
一、感生电动势
这种电磁感应现象是 由于穿过导体回路的磁场 发生变化而引起的。在回 路中产生的感应电动势称 为感生电动势. 此感生电动势产生的原因是什么呢?
K
二、感应电场
麦克斯韦提出:即使不存在导体回路,在变化的磁场周 围也存在一个变化的电场,这个电场称为感生电场。
dB k ,在磁场中放置一长为 L 的导体棒,求 dt
d E dl cos i 感
R oh B r dl L
r dB 由上题结果,圆形区域内部的感生电场: E感 2 dt
第五节感生电动势涡旋电场

B t
πr
2
××
×L × n×
× ×× ×
B × ×t
× ××
××R
E感 =
rB 2t
×××××
× E感
B
式中负号表示 E感 的方向
×× ×× ×× ××
和所设的 E 感方向相反
在圆域外 ( r >R )
× × × ×
2-3-5
B
t
× n×
× ××
L ×× × × ×
×××× r
RB
在圆域外 ( r >R )
××
×L × n×
× ×× ×
B × ×t
× ××
××R
× × × ×
×××××
× E感
B
×× ×× ×× ××
l E 感.d l =
s
B t
.
dS
设E感与dl 方向一致。
. . l ES cos 0o
× × × ×
E感
l
dl
=
E感 2π r =
B t
s dS
B t
ε . i = l E 感 d l
l
E 感.d l
=
s
B t
.
dS
由法拉第电磁感应定律:
2-3-5
εi =
dΦ dt
=
d dt
s
B
.dS
=
s
B t
.
dS
由电动势的定义:
ε . i = l E 感 d l
l
E 感.d l
=
s
B t
.
dS
讨论: 1. 此式反映变化磁场和感生电场的相互
涡旋电场的概念

涡旋电场是有变化的磁场所产生,既变化的磁场在其周围也会激发一种电场,叫做感应电场或涡旋电场.这种电场与静电场(由静止电荷所产生的电场)的共同点就是对点电荷有作用力(库伦力);而不同之处就在于这种电场不是由电荷所激发,而是有变化的电场所激发;并且描述该电场线是闭合的,所以它不是保守场(所谓保守场,举个例子,譬如重力场,静电力场,该类场的性质是有心力场,对受力物体所做的功与路径无关,只于起点和终点有关).有个例子是这样的,在某一区域内磁场随时间均匀改变,dB/dt =C(constant 常数)这种磁场所产生的也是涡旋电场,具体方法可由选择一圆形回路,再由麦克斯韦方程组中的rotE=-dB/dt(该式是微分形式),再由对称性分析可得涡旋电场的方向和大小:E=-(R/2)(dB/dt )符号表示方向,为一圆形闭合回路。
感生电动势与涡旋电场
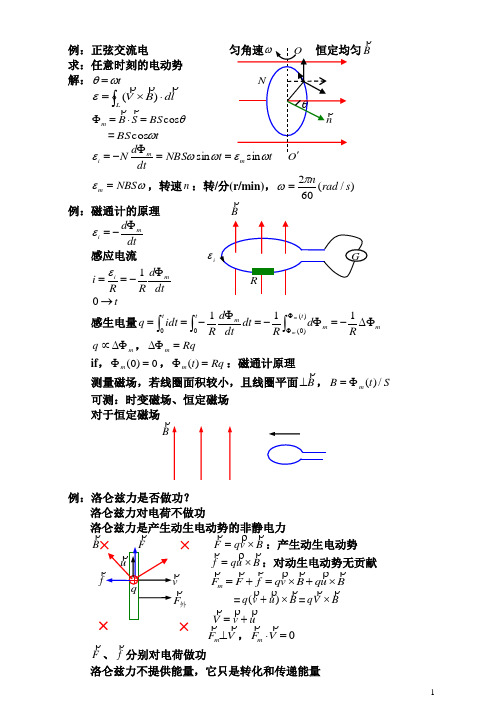
例:正弦交流电B求:任意时刻的电动势解:t ωθ= ⎰⋅⨯=L l d B V)(ε θcos BS S B m =⋅=Φ =t BS ωcost NBS dtd N m mi ωωεsin ==Φ-=ωεNBS m =,转速n :转/分(r/min),)/(602s rad nπω=例:磁通计的原理 Bdtd m i Φ-=ε感应电流 i εdt d R R i mi Φ-==1ε t →0感生电量m t m m t t Rd R dt dt d R idt q m m ∆Φ-=Φ-=Φ-==⎰⎰⎰ΦΦ111)()0(00m q ∆Φ∝,Rq m =∆Φif ,0)0(=Φm ,Rq t m =Φ)(:磁通计原理测量磁场,若线圈面积较小,且线圈平面B⊥,S t B m /)(Φ=可测:时变磁场、恒定磁场 对于恒定磁场B例:洛仑兹力是否做功?洛仑兹力对电荷不做功洛仑兹力是产生动生电动势的非静电力B v q F⨯=:产生动生电动势B u q f ⨯=:对动生电动势无贡献 B u q B v q f F F m ⨯+⨯=+=外 =B u v q⨯+)(=B V q ⨯u v V+=V F m ⊥,0=⋅V F mF、f 分别对电荷做功洛仑兹力不提供能量,它只是转化和传递能量第3节感生电动势与涡旋电场一、涡旋电场假说例:求矩形回路中的感生电动势解:⎰⎰=⋅=ΦSSmdSBS dBtθcos)(=dxlxt Ilrr122)(⎰+πμ,I t Iωs i n)(==rlrtl I210lnsin2+ωπμ,rlrtl Idtdmi210lncos2+-=Φ-=ωωπμε产生电动势的非静电力是什么力?从哪里来的?涡旋电场假说:变化的磁场⇒具有闭合力线的电场:涡旋电场(感应电场),场强VE,非静电场一段导线:⎰⋅=L Vil dEε,闭合回路:⎰Φ-=⋅=LmVi dtdl dEε静电场涡旋电场产生原因静电荷变化的磁场电力线不闭合闭合环路定理0=⋅⎰L l dE⎰Φ-=⋅=LmVi dtdl dEε保守场、电势非保守场,电势高斯定理∑⎰=⋅内iSqS dE1ε=⋅⎰S V S dE对q的作用力EqF=VEqF=⎰Φ-=⋅LmV dtdl dE=0S Sd BB dS dSdt t∂-⋅-⋅<∂⎰⎰固定回路,LVEV tB∂∂t∂二、 涡旋电场的计算⎰Φ-=⋅L mV dt d l d E L H d l I ⋅=∑⎰ 传内 例:半径为R 的无限长 直螺线管内有均匀磁场B设磁场以恒定速率增加,0>∂∂t B求:V E解:tB ∂∂ (1)R r <,沿电力线积分,n向外2)(2cos r tB BS dt d dt d r E dl E l d E L m V LV V ππθ∂∂=--=Φ-===⋅⎰⎰ r tB E V ∂∂=21(2)R r > ⎰Φ-==⋅L m V Vdt d r E l d E π2 22)(R t B R B dt d ππ∂∂=--=rR t B E V 1212∂∂=例:无限长直螺线管(R 、B 0>∂∂tB)求:直导线ab 解:⎰⎰⎰∂∂==⋅=b a L b L a V b L a V ab dl rhr t B dl E l d E 21cos )()()(θε =0)2/(212122>-∂∂=∂∂l R l t B hl t B ,方向b a →,b 端电势高讨论:(1)对于涡旋电场不能引入电势概念,为什么说b 端 电势高?答:b 端积累正电荷,a 端积累负电荷电势概念是针对积累电荷的静电场引入的(2)直导线ab 向上平移ab ε如何变化?答:hl tBab ∂∂=21ε,ab 向上平移,↓h ,↓ab ε直导线通过O 点,0=h ,ab ε=0⎰⋅=baV L ab l d E )(ε,V E l d ⊥,ab ε=0(3)BO a b l ab bO ab Oa OabO εεεεε=++=hl t B hl B dtd dtd m OabO ab 21)21(∂∂=--=Φ-==εε(4)I 、 MN 中有无电动势?II 、 G 中有无电流? B0/≠∂∂t B III 、N M ''中有无电动势? M NIV 、G '中有无电流?M ' N 'G '计算电动势的小结:(1)磁场恒定,回路或其一部分运动:动生电动势一段导线:l d B V bL a ab ⋅⨯=⎰)()(ε闭合回路:⎰⋅⨯=L l d B V )(ε,dtd mi Φ-=ε(2)磁场变化,回路不动:感生电动势一段导线:⎰⋅=LV i l d Eε闭合回路:⎰⋅=L V i l d E ε,dtd mi Φ-=ε(3)磁场变化,且回路或其一部分又运动:既有感生电动势,又有动生电动势,最好使用:dtd mi Φ-=εGh第4节 自感一、 自感现象及其规律I B ∝,I m ∝Φ,LI m =Φ(无铁磁) L :L :自感(系数),SI :亨利(H ) dt d m L Φ-=ε=dtdI L I dt dL LI dt d --=-)(如果L 恒定,=L εdtdIL - L ε L εL ε:自感电动势 自感电动势总是阻碍电流变化 I I。
涡旋电场_精品文档

涡旋电场介绍涡旋电场是一种特殊的电场配置,它由一个或多个电荷以涡旋状排列而成。
涡旋电场在电场理论和实际应用中具有重要的意义,尤其在电磁感应和电动势的产生中起着重要作用。
本文将介绍涡旋电场的基本概念、产生原理以及其在科学研究和技术应用中的重要性。
涡旋电场的基本概念涡旋电场是指一组电荷按照某种特定的方式排列在空间中,使得电场沿着某个轴线形成一个类似于旋涡的结构。
在涡旋电场中,电荷的位置和数量决定了电场的形态和强度分布。
通常情况下,涡旋电场是由电流通过线圈或螺线管所产生的。
涡旋电场的主要特点是其强度和方向随着距离和角度的变化而变化。
在涡旋电场中,电场强度随着距离的增加而减小,而方向则沿着轴线旋转。
涡旋电场的强度和方向分布可用数学表示来描述,其中最常用的是使用矢量场的方法。
涡旋电场的产生原理涡旋电场的产生主要有以下几种方式:1.通过电流在螺线管中产生:当电流通过一个线圈或螺线管时,会产生一个弯曲的磁场,进而产生涡旋电场。
这种方式下,涡旋电场的形状和大小取决于线圈或螺线管的几何形状和电流的强度。
2.通过正负电荷组合:当正负电荷按照一定的规律排列在空间中时,也可以形成涡旋电场。
这种方式下,电场的涡旋结构取决于电荷的位置、数量以及电荷之间的相对位置。
3.通过变化的磁场:当磁场的方向或强度发生变化时,也会产生涡旋电场。
这种方式下,涡旋电场的形态和强度分布取决于磁场的变化规律。
涡旋电场的重要性涡旋电场在科学研究和技术应用中具有广泛的应用价值和重要性:1.电磁感应:涡旋电场是电磁感应现象的重要原因之一。
当磁场的强度或方向发生变化时,会产生涡旋电场,从而产生感应电流和电动势。
2.电动势测量:涡旋电场广泛应用于电动势的测量。
通过将导线放置在涡旋电场中,当导线在电场中运动时,涡旋电场可以通过导线的运动产生电动势。
3.电场分析:涡旋电场可以用于电场的分析和计算。
通过研究涡旋电场的形态和分布规律,可以更好地理解电场的性质和行为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
静电场为无旋场 为保守场作功与路径无关
E dl 0
d m i E感 dl dt
感生电场为无源场
静电场为有源场
S
q E dS
0
S
中的电场既有静电场也有 感生电场,即总场强为:
E感
R dB 2 dt
dB 2 E 感 2r R dt R 2 dB 1 所以 E 感 2r dt r
o
R
r
7
E感分布曲线
例2:圆形均匀分布的磁场半径为 R,磁场随时间均匀
dB k ,在磁场中放置一长为 L 的导体棒,求 dt 棒中的感生电动势。 解: R E感作用在导体棒上,使导体
EK dl ,
在限定导体回路不运动的情况及回路面积不变的情况下, 有: B d d i E感 dl m B dS dS S t dt s dt
E感 •感生电场的电力线类似于磁力线,是无头无尾的闭合 曲线,呈涡旋状,所以 称之为涡旋电场。 •涡旋电场永远和磁感应强度矢量的变化连在一起。
讨论
9
d L dB L 2 i R dt 2 dt 2
2
三、涡电流
1.涡电流 将导体放入变化的磁场中时, 由于在变化的磁场周围存在着涡 旋的感生电场,感生电场作用在 导体内的自由电荷上,使电荷运 动,形成涡电流。 2.涡电流的应用 (1)工频感应炉的应用 在冶金工业中,某些熔化活泼 的稀有金属在高温下容易氧化,将 其放在真空环境中的坩埚中,坩埚 外绕着通有交流电的线圈,对金属 加热,防止氧化。
dB 0 dt
I涡
抽真空
10
抽真空 (2)用涡电流加热金属电极 在制造电子管、显像管或激光管时, 在做好后要抽气封口,但管子里金属电 极上吸附的气体不易很快放出,必须加 热到高温才能放出而被抽走,利用涡电 显像管 流加热的方法,一边加热,一边抽气, 然后封口。 接高频发生器 (3)电磁炉 在市面上出售的一种加热炊具----电磁炉。这种电 磁炉加热时炉体本身并不发热,在炉内有一线圈, 当接通交流电时,在炉体周围产生交变的磁场,
B dS , 把它代入 E感 dl S t B E dl ( E感 E静 ) dl E感 dl dS S t B 电磁场的基本方程之一 E dl dS S t
由上题结果,圆形区域内部的感生电场: E感
r dB 2 dt
8
h r dB i dl cos 其中 cos 则: r 0 2 dt 2 L hL dB r dB h L 2 其中 h R i dl 2 dt 2 0 2 dt r
12
增加 棒上产生一个向右的感生电动势, 沿 E感 线作半径为 r的环路,分割 导体元 dl, 在 dl 上产生的感生电动势为:
oh r B dl L
d i E 感dl cos
i d i E 感dl cos
感生电场也会对电荷有作用力。 感生电动势的非静电力:感生电场施于导体中电荷的力。
2
回路中的感生电动势为: i E感 dl d m 由法拉第电磁感应定律: , dt d m 回路中的感生电动势为: i E感 dl dt
根据电动势的定义
感生电动势 感应电场
(第十章第3节 )
1
一、感生电动势
在这电磁感应现象的实 验中,当电键 K 闭合时,线 圈1中要产生感生电流, 这种电磁感应现象是由于穿过导体回路的磁场发 生变化而引起的。在回路中产生的感应电动势称为感 生电动势. 此感生电动势产生的原因是什么呢?
K
二、感应电场
麦克斯韦提出:即使不存在导体回路,在变化的磁场周 围也存在一个变化的电场,这个电场称为感生电场。
环路上各点的 E 大小相等,方向与路径方向相同,且磁 感 场均匀增加, dB
例1: 圆形均匀分布的磁场半径为R,磁场随时间均匀
dt r dB dB dB 2 E感 dl dS , E感 2r E r , 感 dt S 2 dt dt
// dS, cos 1
L
E静 dl 0
E E静 E感
B 在稳恒条件下,一切物理量不随时间变化, 0 t 静电场的环路定理 E dl 0
L
5
dB 增加 k ,求空间的感生电场的分布情况。 dt 解: 由于磁场均匀增加,圆形磁场区 R 域内、外 E感 线为一系列同心圆; 1. r < R 区域: 作半径为 r 的环形路径; o r 设涡旋电场的绕向也为逆时针方向。 B dB B E感 dl S t dS S dt dS
B 由此得到方程: E感 dl d S S
t
dB 0 dt
3
感生电场与静电场的区别 感生电场 E感 静电场 E
起源 由静止电荷激发 由变化的磁场激发
电 力 线 形 状
电 场 的 性 质
电力线为非闭合曲线
电力线为闭合曲线 dB 0 E感 dt
当金属容器放在炉上时,在容器 上产生涡电流,使容器发热,达到加 热食物的目的。
11
(4)电度表记录电量 电度表记录用电量,就是利用通有 交流电的铁心产生交变的磁场,在 缝隙处铝盘上产生涡电流,涡电流 的磁场与电磁铁的磁场作用,表盘 受到一转动力矩,使表盘转动。
o
o’
3.涡电流的危害 由于涡电流在导体中产生热效应, 在制造变压器时,就不能把铁心制成实 心的,这样在变压器工作时在铁心中产 生较大的涡电流,使铁心发热,造成漆 包线绝缘性能下降,引发事故。 因此在制作变压器铁心时,用多片硅钢片叠合而 成,使导体横截面减小,涡电流也较小。
r
6
r < R 区域:E 感
2. r > R 区域
r dB r 2 dt
E感
R o r r B
作半径为 r 的环形路径;
dB 同理 E感 dl dS dt S
∵积分面积为回路中有磁 场存在的面积,
L
L dB L 方向向右。 2 i R R 2 dt 2 o
法2:用法拉第电磁感应定律求解, 如图构造逆时针方向闭合回路,
2 L L 2 B dS B R S 2 2
2
E感 h r h dl
