7电路的化简方法
精选数字电路逻辑函数的化简方法讲解讲义

000 001 010 011 100 101 110 111
0
1
2
3
4
5
6
7
m0
m1
m2
m3 m4
m5
m6
m7
第四页,共28页。
4. 最小项是组成逻辑函数的基本单元
任何逻辑函数都是由其变量的若干个最小项构成,都 可以表示成为最小项之和的形式。
[例] 写出下列函数的标准与或式:
Y F ( A ,B ,C ) AB AC [解] Y AB(C C ) AC(B B)
核心
Y AB AC BC 最简与或式
最简
与非-与非式
AB AC
AB AC
最简或与非式 ( A B)( A C )
最简与或非式
AB AC BC
最简或与式 ( A B) ( A C )
A B AC
最简或非-或式
最简或非-或非式
AB AC
第七页,共28页。
1. 2. 2 逻辑函数的公式化简法
Y F ( A ,B ,C ,D ) ( 4 变量共有 16 个最小项) ABC D ABCD ABC D … … ABC D ABCD
( n 变量共有 2n 个最小项)
第二页,共28页。
2. 最小项的性质:
ABC
000 001 010 011 100 101 110 111
ABC ABC ABC ABC ABC ABC ABC ABC
(1) 两个相邻最小项合并可以消去一个因子
BC
A 00 01 11 10
00
32
CD AB 00 01 11 10
00
1
01 4
6
14
数字电路化简

数字电路化简
数字电路化简是一种复杂的技术,用于设计数字逻辑电路和数字系统。
它有助于减少电路的复杂性,提高工作效率,降低系统成本。
数字电路化简的主要步骤包括:识别可以合并和简化的信号路径,替换大型逻辑门为小型数字电路模块,处理多个输入和输出端口,将多层信号生成简单的逻辑图形,并使用SIMD,MIMD补偿延迟,更改信号路径,并使用复杂的电路设计来提高系统的效率。
此外,数字电路化简还可以使用多种低功耗电路设计和高效分析工具,提高系统的功率利用率和性能等。
通过使用数字电路化简技术和电路设计工具,可以减少设计时间和研发成本,并可以更快更准确地完成电路设计,使系统可靠性更高,维护更容易,竞争优势更强。
高中物理电路的简化的方法[整理版]
![高中物理电路的简化的方法[整理版]](https://img.taocdn.com/s3/m/b47bb4280812a21614791711cc7931b765ce7b64.png)
高中物理电路的简化的方法?[ 标签:高中物理,电路 ]解决时间:2009-09-26 00:33满意答案好评率:66%1、节点法就是标出所有的连接点(电路元件左右两端),用导线直接连在一起的算一个连接点,用同一个字符来标示,然后画出串、并联关系非常明确的等效电路图,再进行简化。
2、局部化简法从局部入手,找出其中的串联、并联部分。
例,某段电路有R1、R2两个电阻串联,又与R3并联。
则把R1、R2这两个电阻去掉,换成一个电阻,记为R12,连入原图中。
然后把R12和R3都去掉,换成一个电阻,记为R(12)/3连入原图中。
你会发现这样下去,电路图越来越简单,并且看你自己标记的电阻符号,你就知道其关系了。
如果1、2两电阻串联,3、4两电阻串联,然后再并上。
记为R(12)/(34)如2、3并联,前串1、后串4,记为R1(2/3)4求高中物理电路图简化方法2009-1-23 13:52浏览次数:1426次2009-1-23 13:55最佳答案:1、元件的等效处理,理想电压表--开路、理想电流表--短路;2、电流流向分析法:从电源一极出法,依次画出电流的分合情况。
注意:○1有分的情况,要画完一路再开始第二路,不要遗漏。
○2一般先画干路,再画支路。
3、等势点分析法:先分析电路中各点电势的高低关系,再依各点电势高低关系依次排列,等电势的点画在一起,再将各元件依次接入相应各点,就能看出电路结构了。
4、弄清结构后,再分析各电表测量的是什么元件的电流或电压。
说明:2、3两点往往是结合起来用的。
这是我复制来的,多做些题目仔细体会一下高中物理串联、并联电路的简化来源:4221学习网整理| 作者:未知| 本文已影响683 人在我们平常所遇到的串联、并联电路问题中,最头痛的莫过于碰到一个复杂的电路而不知如何下手。
其实,对于物理中的复杂电路计算,可采取简化电路的方法,化为几个简单的问题进行解决。
简化电路的原则是根据题目提出的要求,取消被短路与开路的器件,保留通路的器件,从而简化出其等效电路。
(word完整版)电路化简
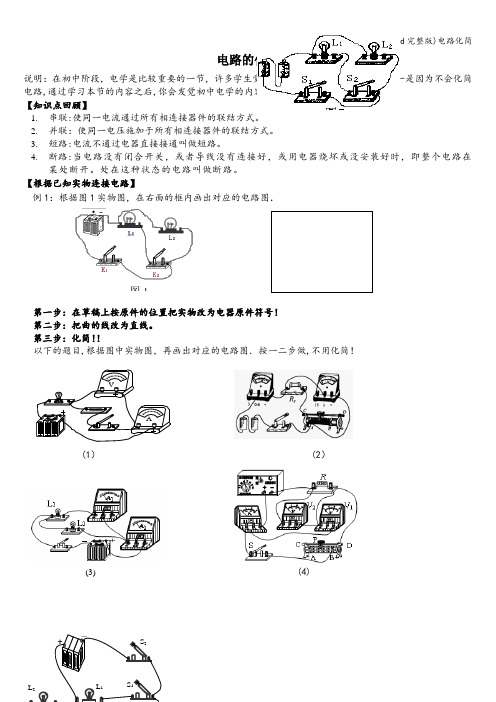
电路的化简说明:在初中阶段,电学是比较重要的一节,许多学生觉得电学内容比较难懂,其原因之一是因为不会化简电路,通过学习本节的内容之后,你会发觉初中电学的内容其实是非常简单的! 【知识点回顾】1. 串联:使同一电流通过所有相连接器件的联结方式。
2. 并联:使同一电压施加于所有相连接器件的联结方式。
3. 短路:电流不通过电器直接接通叫做短路。
4. 断路:当电路没有闭合开关,或者导线没有连接好,或用电器烧坏或没安装好时,即整个电路在某处断开。
处在这种状态的电路叫做断路。
【根据已知实物连接电路】例1:根据图1实物图,在右面的框内画出对应的电路图.第一步:在草稿上按原件的位置把实物改为电器原件符号! 第二步:把曲的线改为直线。
第三步:化简!!以下的题目,根据图中实物图,再画出对应的电路图.按一二步做,不用化简!(1) (2)(3)(4)图1V__ _A(5)(6)(7)(8)(9)(10)【化简电路】从上述化简的结果可以得知,某些复杂的电路图是由于实物连接所得,通过化简将有利于我们计算.例2:化简以下电路图:通过化简。
.。
.。
例3:化简以下电路图:(11)通常的学生会认为上述中有其中一个灯泡被短路了,事实上三者都是并联的!!电路化简的方法:一,电路化简的原则:1)电流表在电路中相当于短路,电压表相当于断路!!2)电流优先流过没有电阻的地方!3) 只要有电流流经用电器就不是短路,哪怕两者的电阻相距很大! 二,电路化简的步骤: 以下图为例:(12) 第一步:去电表!第二步:先别着急判断短路,从电源正极出发,经R1为一回路,再从电源正极出发经R2为一回路,再从正极出发,经R3又一回路!。
.。
第三步:判断电表测那里的电流电压! 【课堂检测】1.把前面实物连接所得的电路进行化简2.对以下的电路图进行化简并判断对应电表测哪里的电流电压!(13) (14)(15) (16)L 1L 2A 1A 2(17)(18)(20)(19)(word完整版)电路化简(21)(22)(23)(24)(26)(25)(28)(27)。
电路的化简

R5
R1 R2
R3 R4
A
R5
B
2.画下图的等效电路。
R1
A
R2
B
R3
R3
A
R1
R2
B
3.已知每个电阻的电流I1I2I3,求 两表的读数。
A1
R2
结点电流原理:流 入某个结点的电流 强度等于流出该点 电流大小。 R3
A
R1
B
A2
A1电流表示数为I2+I3 A2电流表示数为I1+I2
4.若已知UAB=U,R=R1=R2=R3,求
A
R2
R3
A
R1
V
电流表读数:U/R 电压表读数:U
B
A
R2
R3
A
R1
B
V
R2
R5
A R1
R4
R3 R6
B
R7
断开时:
R2 R5 R4
R1 R7
R3 R6
R2
R5
A R1
R4
R3 R6
B
R7Βιβλιοθήκη 闭合时:R2R5A R1
R4
R3 R6
B
R7
求:φA, φB的大小关系
R A 2R
2R B 4R 结论:相等 若在间连一根导线呢? 或接一个电阻呢? 结论:无电流
如何理解电流经过电阻后降压 U=IR
R1
R2
R3
A
B
U1=IR1 U2=IR2
U3=IR3
一、化简方法
1.电流分支法
二、化简原则
2.等电势排列法
1.理想导线可任意长短 2.无电流支路可去掉 3.等电势点可合并 4.两等势点间的电阻可以省去或视为短路
数字电路公式化简

4.取消法:AB+AC+BC=AB+AC 例:Y=ABC+AD+CD+BD =ABC+ACD+BD =ABC+ACD =ABC+AD+CD 作业:P46 10,14,16(3小题除外) 第四版:P33 8,15 自考:P35 6,7 P93 4,5
常用英语:
Minterm 最小项 Maxterm 最大项 Standard sum of product 最小项之和(标准积之和)
0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1
§4.2 逻辑函数化简的含义
Y=ABC+ABC+ABC+ABC 3;B)(A+C) 最简或与式 =ACAB =A+B+A+C =AB+AC =(A+C)(A+B) 与非-- 与非式
常用公式
公式1: AB+AB=A 公式2: A+AB=A 公式3: A+AB=A+B 证明: 左=A+(AB+AB)=A+B 如果一个变量的反变量是另一式的因子, 则这个反变量是多余的。
公式4: AB+AC+BC=AB+AC AB+AC+(A+A)BC=AB+AC 互反变量的因子构成的第三项与式是多余的 推论:AB+AC+BCD=AB+AC 对偶:如果将一个函数式中的 与换成或,或换成与,0换成1,1换成0, 保持优先级和长反号 则得到原函数的对偶式。 对偶定理:一个等式的对偶式也相等。
或非--或非式 与或非式 或与非式
数电公式法化简

数电公式法化简
在数字电路中,使用布尔代数的基本法则可以对逻辑表达式进行化简。
下面介绍几个常见的数电公式化简的方法:
1.代数法:利用布尔代数的基本规则(如分配律、结合律、德摩根定律等)对逻辑表达式中的项进行展开和合并,以简化逻辑电路。
2.卡诺图法:卡诺图是一种将逻辑表达式可视化的方法。
通过将逻辑函数的真值表转化为卡诺图,可以直观地找出逻辑表达式中的最简形式。
3.真值表法:列出逻辑函数的真值表,并找出其中的规律,通过观察真值表中的1的分布情况,判断哪些项可以合并,从而得到最简形式。
4.极小项与极大项法:将逻辑函数表示为与或表达式后,利用极小项(逻辑函数为1的最小项)和极大项(逻辑函数为0的最大项)来化简逻辑函数。
将重复出现的项进行合并和消去。
需要注意的是,在化简过程中,应注意遵循布尔代数的基本规则,并要合理利用化简后的逻辑表达式的特点,例如选择合适的公式展开
顺序、尽量合并重复的项等。
除了以上方法外,还可以使用电路分解、电路索引和逻辑运算性
质等技巧来帮助化简逻辑表达式。
需要根据具体题目的要求和逻辑表
达式的复杂程度选择适合的方法进行化简。
第三章:布尔代数分析与数字电路逻辑化简表示(不同的展开方式)
第二章:布尔代数及其分析数字电路基于排列组合与数字集合论,和数理逻辑有一定距离。
在逻辑函数的计算方面,使用数理逻辑的非计算,能够化简布尔表达式。
布尔逻辑代数引进数字电路,与命题的真假判断有区别,因此逻辑函数用数字函数描述更有广泛的内涵:既包括逻辑计算也包括组合功能.英国数学家布尔的研究导致逻辑代数的出现,并被命名为布尔代数。
逻辑代数给数字电路建立二值逻辑模型,可进行具体数字系统的分析和设计,并在此基础上化简运算,得到数字系统的最优实现方法.使用布尔代数还可以揭示不同逻辑函数之间的相互关系,很清楚的发现这些逻辑函数所对应的具体数字电路之间的转换关系,根据实际需要灵活选择,实现不同数字电路的互换.§1.布尔代数系统的基本内容布尔代数系统建立在集合{0,1}上的运算和规则。
布尔代数的基本定律用恒等式的形式表示,包括代入,反演,对偶,展开四个基本运用规则,主要用来解决逻辑函数的变换与化简. 1布尔代数系统简介数字函数表达式:12(,,...,)n Y F A A A =,其中:12,,...,n A A A 称为输入变量,Y 叫做输出变量,F 称为逻辑函数,表示基本逻辑运算或复合逻辑运算。
def1在二值集{0,1}E =中,逻辑变量取值为0或1,称为布尔变元或变量。
注:布尔变元可用大写字母,也可用小写字母表示,但是一定要保持一致性。
def2从n E 到E 的函数被称为n 度布尔函数,其中n E =011{,,...,,,01}n i x x x x E i n -<>∈≤≤- 说明:n 度布尔函数与n 元组逻辑函数是一个概念,定义域是()n In E 。
2布尔代数的基本运算和复合运算表1:布尔代数与,或,非运算真值表说明:①与运算表示只有全部输入变量都为1时,输出变量为1;其它输入变量组合,得到得输出都为0。
②或运算表示只有全部输入变量都为0时,输出变量为0;其它输入变量组合,得到得输出都为1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
*选学内容:电路的化简方法
★知识要点
1. 稍复杂的混联电路的等效化简方法: (1) 电路化简时的原则:
① 无电流的支路化简时可去除,为什么? ② 等电势的点化简时可合并,为什么? ③ 理想..
导线可任意长短; ④ 理想..电流表可认为短路,理想..电压表可认为断路; ⑤ 电压稳定..
的电容器可认为断路. (2) 常用等效化简方法: ① 电流分支法:
a. 先将各结点用字母标上;
b. 判定各支路元件的电流方向(若电路原无电压电流,可假设在总电路两端加上电压后判定);
c. 按电流流向,自左到右将各元件、结点、分支逐一画出;
d. 将画出的等效电路图加工整理. ② 等势点排列法:
a. 将各结点用字母标上;
b. 判定各结点电势的高低(若原电路未加电压,可先假设加上电压);
c. 将各结点按电势高低自左到右排列,再将各结点间的支路画出;
d. 将画出的等效电路图加工整理.
注意:若能将以上两种方法结合使用,效果更好. 2. 含有电容器的直流电路的分析方法: (1) 电路稳定时,电容器是断路的,其两端电压等于所并联的电路两端的电压. (2) 电路的电流、电压变化时,将会引起电容器的充(放)电. 如果电容器两端电压升高,电容器将充电;如果电压降低,电容器将通过与并联的电路放电.
★应用演练
【例1】如右图所示,R 1=R 2=R 3= R 4=R ,求:电键S 闭合和开启时,A 、B 两端电阻之比. 解析:化简时可假设电键S 开启,而无电流的支路化简时可去除,等化简结束后再补上.
方法(一):用电流分支法化简电路.设A 点电势高于B 点电势,判断各支路上的电流情况:
甲
乙
电流由A 经R 1到B 为第一支路;电流由A 经R 2到C ,再到B 为第二支路;电流由A 经R 3到D ,再经R 4到B 为第三支路. 沿电流方向画出电路图,然后在C 、D 间补上电键S (如图乙).
S 闭合:R 4短路,相当于R 1、R 2、R 3并联,故R AB =R/3.
S 开启:相当于R 3、R 4串联后再和R 1、R 2并联,故
1234
1111
AB R R R R R =++'+,R AB ′=2R/5.
∴R AB :R AB ′=5:6. 方法(二):用等电势排列法化简电路. 设A 点电势高于B 点电势,判断电路上各点的电势情况:φA >φD >φC =φB .
在A 、B 之间有三条支路并联:第一条为R 1;第二条为R 2;第三条为R 3和R 4的串联电路.
由等电势的点化简时可合并可得:S 与R 4并联. 答案:5:6
〖点评〗对于复杂的电路化简时应交替使用分支法和等势法 【例2】如右图所示,R 1=R 2=R 3=R 4=R ,则:A 、B 两端总电阻是多大?
解析:方法(一):用电流分支法化简电路.设A 点电势高于B 点电势,判断各支路上的电流情况(如A 图所示). 沿电流方向画出电路图(如B 图所示),经整理得到C 图.故R AB =R 1+R 并=R +R/3=4R/3.
方法(二):用等电势排列法化简电路. 设A 点电势高于B 点电势,判断电路上各点的电势情况(电势相同的点标相同的字母):φA >φC >φB . 在A 、C 之间有R 1;在C 、B 之间有R 2、
R 3、R 4三个电阻并联.
★同步练习
1. 如右图所示,AB 之间的总电阻为:甲图R AB = Ω;乙图R AB = Ω;丙图S 断开时R AB = Ω,S 闭合时R AB ′= Ω;丁图S 断开时R AB = Ω,S 闭合时R AB ′= Ω. 0、12/13、4、2、3、
D 图
乙
甲
丙
丁
A 图
B 图
C 图
2. 用三个完全相同的金属环,将其相互垂直放置,并把相交点焊接起来成为如右图所示的球形骨架,如每个圆环的周长导线电阻阻值为4Ω,则A 、C 间的总电阻阻值R AC = Ω. 0.5 解析:设A 点接高电势,B 点接低电势. 由题目的对称性可推断出B 、D 、E 、F 各点的电势相等,因此B 、D 、E 、F 各点可合并为一点. 电路可简化为右图所示电路. 则A 、C 间的总电阻阻值R AC =(R/4)/4×2=R/8=0.5Ω.
3. 如下图所示的电路,R 1=R 2=4Ω,R 3=R 4=2Ω,U AB =6V ,求:
A. 安培表A 1和A 2的示数(不计安培表的内阻); I A1=1.5A ;I A2=1.0A
B. R 1与R 4两端电压之比. U 1:U 4=1:2
解析:⑴ R 1、R 2与R 3相并联,再跟R 4相串联,其等效电路如右图所示. 根据并联电路的性质,可知R 1、R 2、R 3三个电阻并联的总电阻R 并,即:
123
1111R R R R =++并. ∴R 并=1Ω.
根据欧姆定律,干路中电流为4
AB
U I R R =
+并=2A.
并联部分的电压为:U 并=I·R 并=2V . 则通过R 1、R 2、R 3的电流分别为:1U I R =
并1
=0.5A ,22
U I R =
并=0.5A ,33
U I R =
并=1.0A.
由图可知,安培表A 1的示数是通过R 2与R 3的电流之和,则有:I A1=I 2+I 3=1.5A. 安培表A 2的示数是通过R 1与R 2的电流之和,则有:I A2=I 1+I 2=1.0A. ⑵ 根据串联电路电压分配关系可知:
14
44R U 1U U U R =
=并并=2
.
-
A2。
