机器人学第七章(机器人动力学的凯恩方法)
基于Kane法的五杆式人机合作机器人动力学分析及仿真

引言
是牛顿的矢量力学和拉格朗日的分析力学[7-9]。矢量力学需
人机合作机器人(collaborative robot 简称 Cobot)的出 现使机器人和操作者在同一工作空间内协同作业成为可能。 Cobot 以 被 动 和 约 束 方 式 工 作 , 利 用 不 完 全 约 束 机 构 (Nonholonomic Constrant Tansmission ,简称 NCT)使动力 源的运动只改变关节之间的速度比,对机器人末端的运动轨 迹只能进行约束而不是驱动。操作者和 Cobot 合作时,承载 重力、轨迹约束控制等功能由 Cobot 完成,操作者只需提供
第 21 卷第 6 期 2009 年 3 月
系 统 仿 真 学 报© Journal of System Simulation
Vol. 21 No. 6 Mar., 2009
基于 Kane 法的五杆式人机合作机器人动力学分析及仿真
路敦民 1, 张立勋 2, 杨向东 3, 陈 恳 3
(1.北京林业大学工学院, 北京 100083;2.哈尔滨工程大学机电工程学院, 哈尔滨 150001;3.清华大学精仪系, 北京 100084)
要将机构的每一个构件都进行隔离,对每个构件都建立相应 的牛顿方程和欧拉方程,方程中包含了不做功的内力(矩) 和外力(矩),求解时常采用递推算法,十分繁琐,工作量 大。拉格朗日基于功能原理把整个系统描述成一个封闭的数 学表达式,方程中包含有大量的积分和求导,给求解带来困 难。美国学者Kane在20世纪60年代发明了Kane方法,Kane 方法综合了分析力学与矢量力学的优点,采用广义速率作为 广义坐标的独立变量,引入偏速度(偏角速度)的概念,建
3. Department of Precision Instruments and Mechanology, Tsinghua University, Beijing 100084, China)
机器人学ppt完整版

视觉传感器
通过图像采集和处理获取 环境信息。
听觉传感器
通过声音采集和处理获取 环境信息。
触觉传感器
通过接触力、压力等检测 获取环境信息。
信息融合与处理技术
数据级融合
直接对原始数据进行融合处理。
特征级融合
提取各传感器数据的特征后进行融合。
信息融合与处理技术
决策级融合
在各传感器做出决策后进行融合。
信号处理
机器人结构组成
机器人本体
包括基座、腰部、臂部 、腕部等部分,构成机
器人的主体结构。
驱动系统
驱动机器人各关节进行 运动,通常由电机、减
速器等组成。
控制系统
实现对机器人运动的控 制,包括控制器、传感
器等部分。
感知系统
获取机器人内部和外部 环境的信息,如位置、
姿态、力等。
关节与连杆描述
关节描述
机器人的关节可分为转动关节和移动 关节,分别用旋转角度和平移距离来 描述。
稳定性分析与优化
李雅普诺夫稳定性分析
轨迹优化
通过构造李雅普诺夫函数,判断机器人系 统的稳定性,为控制器设计提供依据。
基于最优控制理论,对机器人运动轨迹进 行优化,提高机器人的运动性能和效率。
鲁棒性优化
控制分配与优化
针对机器人系统中存在的不确定性和干扰 ,设计鲁棒控制器,提高系统的稳定性和 抗干扰能力。
控制策略与方法
PID控制
通过比例、积分和微分环节对机器人 关节误差进行调节,实现关节位置、 速度和加速度的精确控制。
滑模控制
设计滑模面,使系统状态在滑模面上 滑动,从而实现对机器人关节的鲁棒 控制。
自适应控制
根据机器人动态特性的变化,实时调 整控制器参数,以保证系统性能的最 优。
第七讲机器人动力学

然后求微分,则其速度就为:
l cos( ) 2 l1 cos 1 1 2 )( x 1 2 1 2 ) 1 2 )( 1 2 y2 l1 sin 1 l 2 sin(
2 2 2 2 2 2 2 2 2 2 2 v2 x y l1 1 l 2 (1 2 1 2 2 ) 2l1l 2 cos 2 (1 1 2 )
d L 2 m l 2 m l l sin ( m l m l l cos ) 2 2 2 1 2 2 1 2 2 2 2 1 2 2 1 2 dt 2
L m2 gl 2 sin( 1 2 ) 2
势能为: U 2 m2 gl1 cos1 m2 gl 2 cos( 1 2 )
则可构造出拉格朗日函数为:
L 1 2 1 m l 2 ( 2 2 2 ) m l l cos ( 2 ( m1 m2 )l12 1 2 2 1 1 2 2 2 1 2 2 1 1 2) 2 2
当机器人有n个关节时,上式可推广为普遍形式:
j H ijkq jq k Gi Fi Dij q
j 1 j 1 k 1
n
n
n
(i 1,2,, n)
2019年1月15日星期二
4.1
动力学模型
3、动力学模型
将上式进一步简化为如下所示的矩阵形式:
H (q , q ) G (q ) F D(q)q
第四章
数学模型:
机器人动力学
i , q i 关节运动→位移、速度、加速度变化→ qi , q
关节驱动力(矩)→驱动力或驱动力矩→τi
机器人学第七章(机器人动力学的凯恩方法)

第七章 机器人动力学的凯恩方法7.1 引言机器人动力学凯恩方程方法是建立在凯恩动力学方程基础上的,因而本章首先介绍凯恩动力学方程。
7.1.1 质点系的凯恩动力学方程设一质点系具有n 个质点,该质点系的动力学普遍方程为()[]01=⋅-∑=ni i i i ir a m fδ (7-1)式中 i f ——作用于第i 质点主动力矢量;i m ——质点i 的质量;i a ——质点i 的加速度矢量;i r ——质点i 在参考坐标系中的位置矢量;i r δ——质点i 的微分位移;“·”——数量积符号。
设质点系为完全系,即它具有l 个自由度和l 个广义坐标,则()t q q q r r li i (21)= (7-2)式中 i q ――广义坐标;t ——时间变量; 质点i 的线速度为j lj q i j l j j i i i q v q q r dt r v j ∑∑===⎪⎪⎭⎫ ⎝⎛∂∂=∂=1.1 式中j i j i q i qvq r v j ∂∂=∂∂=. (7-3)凯恩(kane )定义,j i q i j v v q =∂∂为质点I 相对于广义速度的偏速度。
微分i r δ可表示为j lj q i j lj j ii q v q q r r j δδδ∑∑===∂∂=1.1 (7-4)将(7-4)代入(7-1)式,得(), 110j ll i i i i q j i j f m a v q δ==⎡⎤-⋅=⎢⎥⎣⎦∑∑ 交换求和符号,得(), 110j ln i i i i q j i j f m a v q δ==⎡⎤-⋅=⎢⎥⎣⎦∑∑因为j q 是独立变量,故(), 10j nii i i q j fm a v =-⋅=∑ j=1,2,...,l (7-5) 或, , 110j j nnii q i i i q j i fv m a v ==⋅-⋅=∑∑这就是质点系的凯恩动力学方程(Kane Dynamics Equation ),可以改写为', 1', 101,2,,_______j j j j nj i i q i n j i i i q i F j l F f v F m a v F ==⎫⎪+==⋅⋅⋅⎪⎪=⎬⎪⎪=⎪⎭⋅⋅∑∑广义主动力广义惯性力 (7-6)7.1.2 刚体的凯恩动力学方程如图7-1所示将刚体看成是由n 个质点组成的。
机器人 (7)
机器人动力学的研究有
牛顿-欧拉(Newton-Euler) 法
拉格朗日(Langrange)法
高斯(Gauss)法
凯恩(Kane)法
罗伯逊-魏登堡(Roberon-Wittenburg) 法等。
角度设定法
“角度设定法”就是 采用相对参考坐标系或相对运动坐标系作三次连续转动来规
定姿态的方法,。
手部位姿可用一个6维列矢量来表示
X [ px py pz x y z ]T
φx、 φy、 φz表 示绕x、y、z轴的
转角。
4
设q为广义关节变量 q [q1 q2 ... qn ]T
x x(q1,q2,..., qn ) x(q)
τ
τ
2
M
τ n
假定关节无摩擦,并忽略各杆件的重力,利用虚功原理则可得广 义关节力矩τ与机器人手部端点力F的关系可用下式描述:
τ=JTF 式中: JT为n*6阶机器人力雅可比矩阵。 机器人力雅克比是机器人速度雅可比J的转置矩阵。是机 器人静力计算的基础。
23
• 机器人静力计算的两类问题
– (1) 已知外界环境对机器人手部的作用力F,求相应的满足 静力平衡条件的关节驱动力矩τ。
–运动学方程x=x(q)可以看成是由关节空间向操作空 间的映射;
–而运动学反解则是由其映像求其关节空间的原像。
6
二.机器人的雅可比矩阵
机器人的雅可比矩阵揭示了操作空间与关节空间的映射关系。 雅可比矩阵不仅表示操作空间与关节空间的速度映射关系, 也表示两者之间力的传递关系,为确定机器人的静态关节力 矩及不同坐标系间速度、加速度和静力的变换提供了便捷的 方法。
机器人工程基础知识单选题100道及答案解析

机器人工程基础知识单选题100道及答案解析1. 机器人的定义是()A. 一种能够自动执行任务的机械装置B. 一种能够模仿人类行为的电子设备C. 一种能够进行复杂计算的计算机系统D. 一种能够感知环境并作出反应的智能系统答案:A解析:机器人通常被定义为一种能够自动执行任务的机械装置。
2. 工业机器人最常见的驱动方式是()A. 液压驱动B. 气压驱动C. 电动驱动D. 以上都是答案:D解析:液压驱动、气压驱动和电动驱动在工业机器人中都较为常见。
3. 机器人的运动学主要研究()A. 机器人的运动轨迹B. 机器人的速度和加速度C. 机器人的受力情况D. 机器人的能量消耗答案:A解析:运动学主要关注机器人的运动轨迹,不考虑力等因素。
4. 以下哪种传感器常用于机器人的位置测量()A. 温度传感器B. 压力传感器C. 光电编码器D. 湿度传感器答案:C解析:光电编码器能精确测量机器人的位置。
5. 机器人的控制系统中,负责计算关节运动轨迹的是()A. 传感器B. 控制器C. 驱动器D. 执行器答案:B解析:控制器承担计算关节运动轨迹的任务。
6. 机器人的精度主要取决于()A. 机械结构B. 控制系统C. 传感器精度D. 以上都是答案:D解析:机器人的精度受机械结构、控制系统和传感器精度等多方面因素影响。
7. 以下哪种机器人常用于医疗领域()A. 工业机器人B. 服务机器人C. 特种机器人D. 教育机器人答案:B解析:服务机器人在医疗领域有较多应用,如辅助手术等。
8. 机器人的编程语言中,应用最广泛的是()A. C 语言B. PythonC. JavaD. 汇编语言答案:B解析:Python 在机器人编程中应用广泛,具有丰富的库和易用性。
9. 机器人的自由度是指()A. 机器人能够到达的空间位置数量B. 机器人关节的数量C. 机器人能够执行的任务种类数量D. 机器人的运动速度答案:B解析:自由度通常指机器人关节的数量。
机器人学导论
机器人的动力学模型
牛顿-欧拉方程
拉格朗日方程
凯恩方法
雅可比矩阵
机器人的运动规划与控制
运动学:研究机器人末端执行器的位置和姿态信息 动力学:研究机器人末端执行器的力和力矩信息 运动规划:根据任务要求,规划机器人的运动轨迹 控制:通过控制器对机器人进行实时控制,实现运动规划
机器人的感知与感
05
知融合
01
添加章节标题
02
机器人学概述
机器人的定义与分类
机器人的定义: 机器人是一种能 够自动执行任务 的机器系统,具 有感知、决策、
执行等能力
机器人的分类: 根据应用领域、 结构形式、智能 化程度等不同, 机器人可分为多 种类型,如工业 机器人、服务机 器人、特种机器
人等
机器人学的研究领域
机器人设计:研究机器人的结构、 运动学和动力学
机器人的感知技术
添加项标题
视觉感知技术:通 过摄像头获取环境 信息,识别物体、 场景等,实现机器 人视觉导航、物体 识别等功能。
添加项标题
听觉感知技术:通 过麦克风获取声音 信息,识别语音、 音乐等,实现机器 人语音交互、音乐 识别等功能。
添加项标题
触觉感知技术:通过 触觉传感器获取接触 信息,识别物体的形 状、大小、硬度等, 实现机器人触觉导航、 物体抓取等功能。
执行器作用:根据控制信号执行相应的动作,如移动、转动等
机器人的感知系统
传感器类型:视觉、听觉、触觉等 传感器工作原理:图像处理、语音识别、触觉反馈等 传感器在机器人中的应用:导航、目标识别、物体抓取等 感知系统对机器人性能的影响:精度、稳定性、安全性等
机器人的运动学与
04
动力学
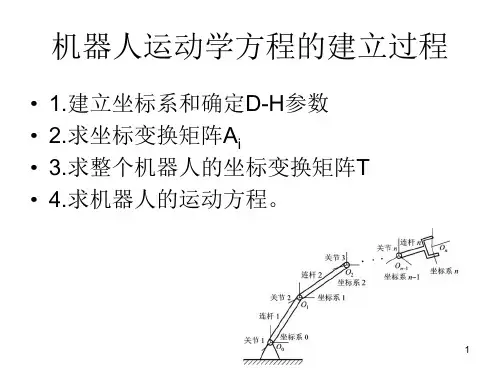
机器人的运动学方程
3.2 机器人动力学
x3h θ3 x2
2018年5月18日星期五
3.2
运动学方程的建立
解:(4)建立方程
将相邻杆件位姿矩阵依次相乘,则有:
c 123 s 123 0 0 s 123 c 123 0 0 0 l1c 1 l 2 c 12 l 3 c 123 0 l1 s 1 l 2 s 12 l 3 s 123 1 0 0 1
{i-1}
{0}
M0n M01 M12 Mi 1i Mn1n
3.2
运动学方程的建立
1、运动学方程建立步骤 (1)建立坐标系 (2)确定参数 (3)相邻杆件的位姿矩阵 (4)建立方程 2、运动学方程的解
2018年5月18日星期五
3.2
运动学方程的建立
1、运动学方程建立步骤
运动学方程的模型: M=f(qi), i=1,…,n M——机器人手在空间的位姿 qi——机器人各个关节变量
机器人运动学
姿态可以用坐标系 三个坐标轴两两夹角的
z
zh
余弦值组成3×3的姿态
矩阵来描述。
xh o p(x,y,z) h o x
yh y
cos(x, xh ) cos(x, yh ) cos(x, z h ) R cos( y, xh ) cos( y, yh ) cos( y, z h ) cos(z , xh ) cos(z , yh ) cos(z , z h )
3.2
运动学方程的建立
解:(4பைடு நூலகம்建立方程
若用矩阵形式表示,则为:
nx n y nz 0 ox oy oz 0 ax ay az 0 p x c 123 s py 123 pz 0 1 0 s 123 c 123 0 0 0 l1c 1 l 2 c 12 l 3 c 123 0 l1 s 1 l 2 s 12 l 3 s 123 1 0 0 1
工业机器人技术课程总结
工业机器人技术课程总结任课:班级:学号:姓名:之前在工厂实习见识和操作过很多工业机器人,有焊接机器人,涂装机器人,总装机器人等,但是学习了盖老师教授的工业机器人课程,才真正算是进入了工业机器人的理论世界学习机器人的相关知识。
以下是课程总结。
一、第一章主要是对机器人的概述,从机器人的功能和应用、机器人的机构以及机器人的规格全面呈现学习机器人的框架。
研制机器人的最初目的是为了帮助人们摆脱繁重劳动或简单的重复劳动,以及替代人到有辐射等危险环境中进行作业,因此机器人最早在汽车制造业和核工业领域得以应用。
随着机器人技术的不断发展,工业领域的焊接、喷漆、搬运、装配、铸造等场合,己经开始大量使用机器人。
另外在军事、海洋探测、航天、医疗、农业、林业甚到服务娱乐行业,也都开始使用机器人。
本书主要介绍工业机器人,对譬如军用机器人等涉及不多。
机器人的机构方面,主要介绍了操作臂的工作空间形式、手腕、手爪、和闭链结构操作臂。
工作空间形式常见的有直角坐标式机器人、圆柱坐标式机器人、球(极)坐标式机器人、SCARA机器人以及关节式机器人。
手腕的形式也可分为二自由度球形手腕、三轴垂直相交的手腕以及连续转动手腕。
同时手爪也可分为夹持式手爪、多关节多指手爪、顺应手爪。
机器人的其他规格主要介绍驱动方式、自动插补放大、坐标轴数、工作空间、承载能力、速度和循环时间、定位基准和重复性以及机器人的运行环境。
第一章的内容主要是对机器人各个方面有个简单的介绍使机器人更形象化和具体化。
工业机器人定义为一种拟人手臂、手腕和手功能的机电一体化装置,能将对象或工具按照空间位置姿态的要求移动,从而完成某一生产的作业要求。
工业机械应用:主要代替人从事危险、有害、有毒、低温和高热等恶劣环境中的工作;代替人完成繁重、单调重复劳动。
它带来的好处:减少劳动力费用提高生产率改进产品质量增加制造过程柔性减少材料浪费控制和加快库存的周转消除了危险和恶劣的劳动岗位。
机器人的直角坐标型:结构简单;定位精度高;空间利用率低;操作范围小;实际应用较少。
《机器人动力学》课件
机器人动力学有助于优化机器人的设 计和性能,提高机器人的运动性能和 作业能力。
安全性和稳定性
通过机器人动力学的研究,可以预测 机器人在不同环境和操作条件下的行 为,从而避免潜在的危险和保证机器 人的安全稳定运行。
机器人动力学的发展历程
初始阶段
早期的机器人动力学研究主要关注于简单的机械臂模型,采用经典力学理论进行分析。
刚体动力学是研究刚体在力作用下的运动规律的科学。刚体动力学建模
是研究刚体运动过程中力和运动状态之间的关系。
02
牛顿-欧拉法
牛顿-欧拉法是一种基于牛顿运动定律和欧拉方程的刚体动力学建模方
法。通过这种方法,可以建立刚体的运动方程,描述刚体的运动状态。
03
拉格朗日法
拉格朗日法是一种基于拉格朗日方程的刚体动力学建模方法。这种方法
《机器人动力学》ppt 课件
目录
Contents
• 机器人动力学概述 • 机器人动力学的基本原理 • 机器人动力学建模 • 机器人控制中的动力学应用 • 机器人动力学研究的挑战与展望 • 机器人动力学实验与案例分析
01 机器人动力学概述
定义与特点
定义
机器人动力学是研究机器人运动过程中力和运动状态之间关系的学科。它主要关注机器人在操作物体 、环境交互以及自身运动过程中产生的力和扭矩,以及这些力和扭矩如何影响机器人的运动状态。
在实际应用中的表现。
06 机器人动力学实验与案例分析
实验一:刚体动力学实验
总结词
理解刚体动力学基本原理
详细描述
通过实验一,学生将学习刚体动力学 的基本原理,包括刚体的运动学和动 力学特性。实验将通过演示刚体在不 同条件下的运动,帮助学生理解刚体 动力学的概念和应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章 机器人动力学的凯恩方法7.1 引言机器人动力学凯恩方程方法是建立在凯恩动力学方程基础上的,因而本章首先介绍凯恩动力学方程。
7.1.1 质点系的凯恩动力学方程设一质点系具有n 个质点,该质点系的动力学普遍方程为()[]01=⋅-∑=ni i i i ir a m fδ (7-1)式中 i f ——作用于第i 质点主动力矢量;i m ——质点i 的质量;i a ——质点i 的加速度矢量;i r ——质点i 在参考坐标系中的位置矢量;i r δ——质点i 的微分位移;“·”——数量积符号。
设质点系为完全系,即它具有l 个自由度和l 个广义坐标,则()t q q q r r li i (21)= (7-2)式中 i q ――广义坐标;t ——时间变量; 质点i 的线速度为j lj q i j l j j i i i q v q q r dt r v j ∑∑===⎪⎪⎭⎫ ⎝⎛∂∂=∂=1.1 式中j i j i q i qvq r v j ∂∂=∂∂=. (7-3)凯恩(kane )定义,j i q i j v v q =∂∂为质点I 相对于广义速度的偏速度。
微分i r δ可表示为j lj q i j lj j ii q v q q r r j δδδ∑∑===∂∂=1.1 (7-4)将(7-4)代入(7-1)式,得(), 110j ll i i i i q j i j f m a v q δ==⎡⎤-⋅=⎢⎥⎣⎦∑∑ 交换求和符号,得(), 110j ln i i i i q j i j f m a v q δ==⎡⎤-⋅=⎢⎥⎣⎦∑∑因为j q 是独立变量,故(), 10j nii i i q j fm a v =-⋅=∑ j=1,2,...,l (7-5) 或, , 110j j nnii q i i i q j i fv m a v ==⋅-⋅=∑∑这就是质点系的凯恩动力学方程(Kane Dynamics Equation ),可以改写为', 1', 101,2,,_______j j j j nj i i q i n j i i i q i F j l F f v F m a v F ==⎫⎪+==⋅⋅⋅⎪⎪=⎬⎪⎪=⎪⎭⋅⋅∑∑广义主动力广义惯性力 (7-6)7.1.2 刚体的凯恩动力学方程如图7-1所示将刚体看成是由n 个质点组成的。
设刚体的质心为C ,以C 为力的简化中心并设作用于刚体的主动力的合力为C Q ,合力矩为C N :∑==ni i c f Q 1(7-7)()∑=⨯=ni i i c R f N 1(7-8)当刚体以角速度ω旋转时,其中点i 的速度为c i i v v R ω=+⨯其中 i R ——点到质心C 的位置矢量;i v ——质心C 的线速度。
Z 点对广义速度的偏速度为(), ωj i i c i q j j jR v v v q q q ∂⨯∂∂==+∂∂∂ 或, , j j j q i q C q i v v R ω=+⨯ (7-9)式中, j C q v ——质心C 相对于j q的偏速度: , j cC q jv v q ∂=∂ (7-10) jqω——刚体相对于j q的偏角速度: ωωj q jq ∂=∂ (7-11) 于是作用在刚体上相对于j q的广义力为 ()(),,111,11ωωj j jj jn n nj i i q i C q i i q i i i nni C q i i q i i F f v f v f R f v f R ======⋅=⋅+⋅⨯=⋅+⨯⋅∑∑∑∑∑或(),11 ωj j j C C q C q nc i i n c i i i F Q v N Q f N f R ==⎫⎪=⋅+⋅⎪⎪=⎬⎪⎪=⨯⎪⎭∑∑ (7-12)相对于j q的广义惯性力为 ()111',,j j j n n nji i i q i i C q i i i q i i i F m a v m a v m a R ω====-⋅=-⋅-⨯∑∑∑而 ()()dt dH R v m dt d R a m cn i i i i ni i i i =⎪⎭⎫ ⎝⎛⨯=⨯∑∑==11式中动量矩c H 用刚体的惯性张量表示为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡z y x zz zyzxyz yy yx xz xyxxz y x I I I I I I I I I H H H ωωω (7-13)因此()1nCi i i i dH m a R I I dt ωωω==⨯=+⨯∑ (7-14) 得广义惯性力表示为()112',,,,j jnji i C q q i F m a v I I j l ωωωω==-⋅-+⨯⋅=⋅⋅⋅∑ (7-15)将(7-12)和(7-15)式合并,从而得到刚体的凯恩动力学方程为112,, ,,, j j j j nC C q C q i i C q C q i C Q v N m a v N N I I j l ωωωωω=⎫⋅+⋅=⋅+⋅⎪⎬⎪=+⨯=⋅⋅⋅⎭∑ (7-16) 式中 I ——刚体相对于质心C 的惯性张量。
7.2 机器人杆件速度、加速度及偏速度的递推计算公式如图9-2所示,杆件坐标系均设置在各杆件上编号关节处,n 个自由度的机器人有n 个关节。
图中i e ~——指定杆件坐标系各iz 轴方向的单位矢量,共有i =0,1,2,...,n 个,它们均是以杆件坐标系描述的常矢量,[]T ie e100~0==; i p ~——以杆件坐标系{i -1}的原点为始点到以{i }系原点为终点的矢量,但它是以{i }系描述的矢量;i R ~——以杆件坐标系{i }描述的第i 号杆件质心i C 的位置矢量;两相邻坐标系{i -1}及{i }中速度、加速度等的关系可用变换矩阵i A 中的旋转子矩阵C i i1-及R i i 1-相联系。
仿照第六章处理杆件坐标系及杆件质心的速度及加速度的方法,并考虑到坐标系设置方法上的区别,不难得到如下所述的速度及加速度递推计算公式:2qx 1n qa 22 2R()()()110111100111011 ii i i i i i i i i i i i i i i i i i i i i i i i i i c i i i i ii i R s q e R s R q e q e v Rv p s Rq e v v s R v R ωωωωωωω----------=+=+⨯+=+⨯+-=+⨯=()()()()110012 i i i i i i i ii i i i c i i i i i i v p p s R qe q e v v R R ωωωωωωω--⎫⎪⎪⎪⎪⎪⎬⎪+⨯+⨯⨯⎪⎪+-⨯+⎪=+⨯+⨯⨯⎪⎭(7-17)式中 i q——广义坐标对时间的1阶导数,即关节轴的数量速度; i q——广义坐标对时间的2阶导数,即关节轴的数量加速度; i s ——关节类型识别符号;⎩⎨⎧为移动关节为转动关节i i s i 01 (7-18) 与第六章相同,令000Tv g ⎡⎤⎣⎦= (7-19)式中 g ——重力加速度。
上式是假定绝对参考系的0Z 轴垂直于地面且指向向上的。
若0Y 轴垂直于地面,则[]Tg v000-= 其中负号表示0Y 轴指向地心(0Y 于重力场同方向)。
偏速度的递推公式为:()11101110010, , , , , .Re Re j j j j j j i i i q i i q i i i i q i i i q ii q i i q i i i R j i s j i j i p Rv v s p s ωωωω------⎧<⎪⎪==⎨⎪>⎪⎩⨯+=⨯+-()()101010, , , ,Re Re j j i j j i q i q i i ic q i i q i i i i i j i j i j i v R v s p R s ωω--⎧<⎪⎪=⎨⎪>⎪⎩+⨯=⨯+⨯+- j i j i j i ⎫⎪⎪⎪⎪⎪⎪⎪⎪⎬⎪⎪⎪⎧⎪<⎪⎪⎪=⎪⎨⎪⎪>⎪⎪⎩⎭(7-20)例7-1 如图7-3所示的平面包2自由度机器人,1θ 、2θ 为已知,试用(7-17)及(7-20)式计算各杆的速度、加速度及偏速度。
杆件的质心均在杆件的末端。
解:11101100001C S R S C ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦=-, 22212200001C S R S C ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦=-, 120R R ==[]1100TP l =,[]2200TP l =,00ω=,00ω=,00v =,[]000Tv g =。
式中 g ——重力加速度。
0Y 轴与重力场反向,故g 取正。
i =1时:()110010100TR e ωωθθ⎡⎤=+=⎣⎦11001, Tθω⎡⎤⎣⎦=1111100111000000l v p Rv l ωθθ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦=⨯+=⨯=1111100, C v v l θθ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦∂==∂ ()111100010101111000000001C S R e e S C ωωωθθθθ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=+⨯+=-⨯=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦()111100111111211111111111000001000000000000 C S v Rv p p S C g l l l S g l C g ωωωθθθθθ⎡⎤⎡⎤⎢⎥⎢⎥=+⨯+⨯⨯=-⨯⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤⎛⎫-+⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥ ⎪⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥+⨯+⨯⨯=+⎢⎥⎪⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥ ⎪⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎝⎭⎣⎦()1211111*********C l S g v v R R v l C g θωωωθ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦-+=+⨯+⨯⨯==+i =2时:()2222112022211200000000011C S R e S C ωωθθθθθ⎛⎫⎡⎤⎡⎤⎡⎤⎡⎤ ⎪⎢⎥⎢⎥⎢⎥⎢⎥=+=-+= ⎪⎢⎥⎢⎥⎢⎥⎢⎥ ⎪⎢⎥⎢⎥⎢⎥⎢⎥+⎣⎦⎣⎦⎣⎦⎣⎦⎝⎭ 12001, θω⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦=, 22001, θω⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦= 1x2θ1θ1lX 平面2自由度机器人()22222112222111212121212100000000100 0C S l v Rv p S C l l S l l C ωθθθθθθθ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦=+⨯=-+⨯+=++()212122222121210C l S v v R v l l C θωθθθ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦=+⨯==++2112212, 0Cl S v l l C θ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦=+, 222, 00C v l θ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦= ()2211120202222112212000000 000000001R e e C S S C ωωωθθθθθθθθ⎛⎫⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤ ⎪⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥ ⎪⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥ ⎪⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥ ⎪⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎝⎭=+⨯+=-+⨯+=+()2222222112212121221112222111000 00000000 00010v p p Rv l l l S g C S S C l C g ωωωθθθθθθθθ⎛⎫⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤ ⎪⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥ ⎪⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥ ⎪⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥ ⎪⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎝⎭⎡⎡⎤⎢⎢⎥⎢⎢⎥⎢⎥⎣⎦⎣=⨯+⨯+=⨯+⨯⨯+++-++-+⎤⎥⎥⎢⎥⎢⎥⎦()22222222C v p p v v ωωω=⨯+⨯+= (同上式)此例所得各质心的速度及加速度的计算结果与上一章的计算方法得到的结果是完全相同(例7-2将用此例的偏速度)。
