现代控制理论第五章
合集下载
现代控制理论第5章
第五章 Lyapunov稳定性分析和二次型最优控制5.1 概述本章首先讨论Lyapunov稳定性分析，然后介绍线性二次型最优控制问题。
我们将使用Lyapunov稳定性方法作为线性二次型最优控制系统设计的基础。
应用于线性定常系统的稳定性分析方法很多。
然而，对于非线性系统和线性时变系统，这些稳定性分析方法实现起来可能非常困难，甚至是不可能的。
Lyapunov稳定性分析是解决非线性系统稳定性问题的一般方法。
虽然在非线性系统的稳定性问题中，Lyapunov稳定性分析方法具有基础性的地位，但在具体确定许多非线性系统的稳定性时，却并不是直截了当的。
技巧和经验在解决非线性问题时显得非常重要。
在本章中，对于实际非线性系统的稳定性分析仅限于几种简单的情况。
本章5.1节为概述。
5.2节介绍Lyapunov意义下的稳定性定义。
5.3节给出Lyapunov稳定性定理，并将其应用于非线性系统的稳定性分析。
5.4节讨论线性定常系统的Lyapunov稳定性分析。
5.5节给出模型参考控制系统，首先用公式表示Lyapunov稳定性条件，然后在这些条件的限制下设计系统。
5.6节讨论线性二次型最优控制系统，将采用Lyapunov稳定性方程导出线性二次型最优控制的条件。
5.7节给出线性二次型最优控制问题的MATLAB解法。
5.2 Lyapunov意义下的稳定性问题对于一个给定的控制系统，稳定性分析通常是最重要的。
如果系统是线性定常的，那么有许多稳定性判据，如Routh-Hurwitz稳定性判据和Nyquist稳定性判据等可资利用。
然而，如果系统是非线性的，或是线性时变的，则上述稳定性判据就将不再适用。
本节所要介绍的Lyapunov第二法（也称Lyapunov直接法）是确定非线性系统和线性时变系统的最一般的方法。
当然，这种方法也可适用于线性定常系统的稳定性分析。
此外，它还可应用于线性二次型最优控制问题。
5.2.1 平衡状态、给定运动与扰动方程之原点考虑如下非线性系统),(t x f x = (5.1)式中x 为n 维状态向量，),(t x f 是变量x 1,x 2,…,x n 和t 的n 维向量函数。
现代控制理论---状态反馈和状态观测器
第五章 系统的状态反馈及观测器
现代控制理论基础
主讲人: 主讲人:荣军 mail:rj1219 163. 1219@ E-mail:rj1219@
第五章 系统的状态反馈及观测器
在第二章， 在第二章，研究的是在己知系统的结构和参数情况下系统的 运动，从而了解系统的运动形态。 运动，从而了解系统的运动形态。第三章介绍了系统的能控性和 能观测性。第四章是系统稳定性问题。 能观测性。第四章是系统稳定性问题。如果将上述研究的内容概 括起来说，就是在已知系统的结构和参数情况下， 括起来说，就是在已知系统的结构和参数情况下，研究系统的性 能或特性，即所谓系统分析问题。 能或特性，即所谓系统分析问题。 本章将研究线性定常系统的综合。 本章将研究线性定常系统的综合。这是一个与系统分析相反 的命题，是在给定被控对象的情况下， 的命题，是在给定被控对象的情况下，通过设计控制器的结构和 参数，使系统满足预先规定的性能指标要求。 参数，使系统满足预先规定的性能指标要求。采用的方法是先测 量系统的状态，再用状态来确定被控对象上所加的控制输人， 量系统的状态，再用状态来确定被控对象上所加的控制输人，从 而构成状态反馈系统。 而构成状态反馈系统。
第五章 系统的状态反馈及观测器
采用状态反馈， 采用状态反馈，对系统能控性和能观测性有 无影响呢?这是本章讨论的重要内容之一 这是本章讨论的重要内容之一。 无影响呢 这是本章讨论的重要内容之一。同时 研究一个能控的系统， 研究一个能控的系统，引入状态反馈可以任意配 置状态反馈系统的极点， 置状态反馈系统的极点，保证系统具有所希望的 瞬态性能和稳态性； 瞬态性能和稳态性；对于系统的状态变量无法测 量但又要用它来实现反馈的情况， 量但又要用它来实现反馈的情况，通过状态重构 方法。设计状态观测器。 方法。设计状态观测器。
现代控制理论基础
主讲人: 主讲人:荣军 mail:rj1219 163. 1219@ E-mail:rj1219@
第五章 系统的状态反馈及观测器
在第二章， 在第二章，研究的是在己知系统的结构和参数情况下系统的 运动，从而了解系统的运动形态。 运动，从而了解系统的运动形态。第三章介绍了系统的能控性和 能观测性。第四章是系统稳定性问题。 能观测性。第四章是系统稳定性问题。如果将上述研究的内容概 括起来说，就是在已知系统的结构和参数情况下， 括起来说，就是在已知系统的结构和参数情况下，研究系统的性 能或特性，即所谓系统分析问题。 能或特性，即所谓系统分析问题。 本章将研究线性定常系统的综合。 本章将研究线性定常系统的综合。这是一个与系统分析相反 的命题，是在给定被控对象的情况下， 的命题，是在给定被控对象的情况下，通过设计控制器的结构和 参数，使系统满足预先规定的性能指标要求。 参数，使系统满足预先规定的性能指标要求。采用的方法是先测 量系统的状态，再用状态来确定被控对象上所加的控制输人， 量系统的状态，再用状态来确定被控对象上所加的控制输人，从 而构成状态反馈系统。 而构成状态反馈系统。
第五章 系统的状态反馈及观测器
采用状态反馈， 采用状态反馈，对系统能控性和能观测性有 无影响呢?这是本章讨论的重要内容之一 这是本章讨论的重要内容之一。 无影响呢 这是本章讨论的重要内容之一。同时 研究一个能控的系统， 研究一个能控的系统，引入状态反馈可以任意配 置状态反馈系统的极点， 置状态反馈系统的极点，保证系统具有所希望的 瞬态性能和稳态性； 瞬态性能和稳态性；对于系统的状态变量无法测 量但又要用它来实现反馈的情况， 量但又要用它来实现反馈的情况，通过状态重构 方法。设计状态观测器。 方法。设计状态观测器。
现代控制理论第五章-01
（Book 214 )
0
X AX Bu : Y CX
R
0
x
y
F
x
仅讨论标量系统∑0 ,它的经典频域描述是：
G0 s G s y( s) M 0 (s) i.e. m n u ( s ) D0 ( s)
k 0
假定原系统是状态完全能控的，即 X
u
R
框图结
构如右：
考虑实际 D=0
uf
B
x
x
C
y
A
F
or
x
R
uf
u
0
x
y
F
x
10
Thursday, August 17, 2017
Modern Control Theory
于是，可利用框图代数推出状态反馈系统的状态空 间模型：
有, X AX BR BFX Y CX
G F s C SI A BF B
1
2
当然，也可以求得 GF s 和 G0 s 的关系：
G F s G 0 s [I F SI A B] 即：
1 1
(3)
显然，这个关系同经典理论中的结果相类似。
Thursday, August 17, 2017 Modern Control Theory 12
我们可以推导出如下状态空间模型：
H
X A BHC X BR Y CX
(1)
和传递函数矩阵：
GH s
y ( s )R ( s ) C SI A BHC B
《现代控制理论》第三版 第五章.习题答案
由于状态分量 x3 可由 y 直接提供,故只需 设计二维状态观测器。 g1 (3) 引入 G 得观测器特征多项式: g2
f ( ) det I ( A11 GA21 ) = 0 0 0 g1 0 1 det 0 1 0 g 2 g1 2 det g 2 g1 = 1 g 2
f * ( ) ( 10)( 1 j 3)( 1 j 3)
3 12 2 24 40 解之： K 4 1.2 0.1 解法 2：（1）
0 10 0 2 0 ， M b , Ab , A b 10 110 10 100 990 rankM 3满秩 可以任意极点配置
1
（2）化为能控标准 I 型
I A 3 11 2 11
0 0
2 TcI A b
1 11
1 0 Ab b 2 1 1 2
2 11
0 10 0 0 1 0 0 0 110 10 0 11 1 0 1 990 100 10 11 11 1
第五章 作业
参考答案
5-2．解法 1： （1） 0 10 0 2 0 ， M b , Ab , A b 10 110 10 100 990
rankM 3满秩 可以任意极点配置
（2）设 K k0
k1
k2
f ( ) det I ( A bk ) 3 (11 10k2 ) 2 (11 10k1 10k 2 ) 10k0
法二： (1) 检验能观性 由于系统属于能观I型， 显然能观，
课件-现代控制理论-刘豹第三版-第5章
能控性与能观性的判别方法
能观性判别方法
能控性判别方法
表示系统是否可以通过输入控制实现任意状态转移。若系统完全能控，则可以通过设计合适的控制器实现任意状态轨迹的跟踪或镇定；若部分能控或不能控，则存在状态无法被有效控制的风险。
能控性的物理意义
表示系统状态是否可以通过输出完全反映出来。若系统完全能观，则可以通过观测输出信号来准确估计系统状态；若部分能观或不能观，则存在状态无法被准确观测的风险，进而影响控制性能的实现。
控制系统稳定性分析是控制理论的核心内容之一，对于确保控制系统的正常运行具有重要意义。
章节内容结构
稳定性概念及定义
介绍稳定性的基本概念和定义，包括Lyapunov稳定性和BIBO稳定性等。
线性系统稳定性判据
详细阐述线性系统稳定性的判据，如Routh-Hurwitz判据、Nyquist判据和Bode图等。
图解法
状态转移矩阵的计算方法
1
2
3
状态转移矩阵反映了系统在时间间隔内从初始状态到最终状态的动态变化过程。
描述系统状态的动态变化过程
若系统稳定，则状态转移矩阵将逐渐趋于零，表示系统状态将逐渐趋于稳定。
反映系统稳定性
状态转移矩阵是进行系统分析和设计的重要工具，可用于研究系统的稳定性、能控性、能观性等性质。
非线性系统稳定性分析
介绍非线性系统稳定性分析方法，如相平面法、Lyapunov直接法等。
熟练掌握线性系统稳定性的判据和分析方法，能够应用所学知识分析和设计线性控制系统。
了解非线性系统稳定性分析方法的基本原理和应用范围，能够运用所学知识分析和设计简单的非线性控制系统。
掌握稳定性的基本概念和定义，理解不同稳定性定义之间的联系与区别。
现代控制理论基础_周军_第五章状态反馈与状态观测器
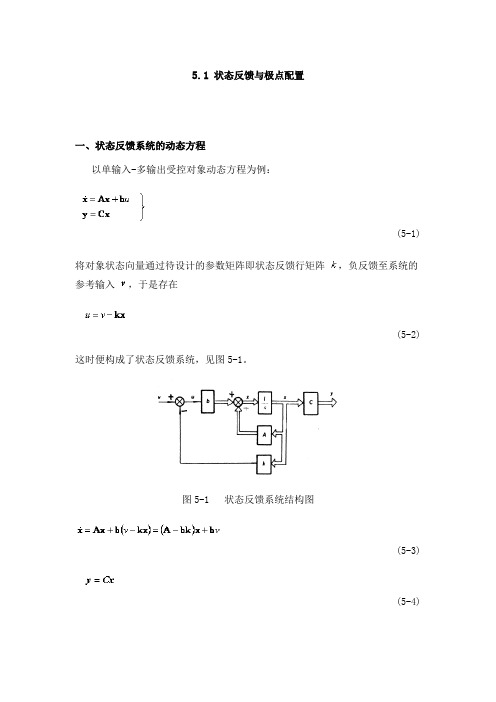
5.1状态反馈与极点配置一、状态反馈系统的动态方程以单输入-多输出受控对象动态方程为例：(5-1)将对象状态向量通过待设计的参数矩阵即状态反馈行矩阵，负反馈至系统的参考输入，于是存在(5-2)这时便构成了状态反馈系统，见图5-1。
图5-1 状态反馈系统结构图(5-3)(5-4)式中v为纯量，为维向量，为维矩阵，为维向量，为维行矩阵，为维向量，为维矩阵。
为闭环状态阵，为闭环特征多项式。
二、用状态反馈使闭环极点配置在任意位置上的充要条件是：受控对象能控证明若式(5-1)所示对象可控，定可通过变换化为能控标准形，有若在变换后的状态空间内引维状态反馈矩阵：(5-5)其中分别为由状态变量引出的反馈系数，则变换后的状态反馈系统动态方程为：(5-6)(5-7)式中(5-8)该式与仍为能控标准形，故引入状态反馈后，系统能控性不变。
特征方程为：(5-9)显见，任意选择阵的个元素，可使特征方程的个系数满足规定要求，能保证特征值（即闭环极点）任意配置。
将逆变换代入式(5-6)，可求出原状态空间内的状态反馈系统状态方程：(5-10)与式(5-3)相比，式(5-10)所示对象应引入状态反馈阵为：(5-11)需指出，当受控对象可控时，若不具有能控标准形形式，并不必象如上证明那样去化为能控标准形，只要直接计算状态反馈系统闭环特征多项式，这时，其系数为的函数，与给定极点的特征多项式系数相比较，便可确定。
能控的多输入-多输出系统，经如上类似分析可知，实现闭环极点任意配置的状态反馈阵K为维。
若受控对象不稳定，只要有能控性，完全可由状态反馈配置极点使系统稳定。
状态变量受控情况下，引入状态反馈表示增加一条反馈通路，它能改变反馈所包围环节的传递特性，即通过改变局部回路的极点来改变闭环极点配置。
不能控状态变量与控制量无关，即使引入状态反馈，对闭环极点位置也不会产生任何影响，这是因为传递函数只与系统能控、能观测部分有关的缘故。
若不能控状态变量是稳定的状态变量，那么系统还是能稳定的，否则，系统不稳定。
现代控制理论第五章2012_3
0 A I GC I A GC BK I BK 0 x I ~ I x I 0 B v, I B
I y C 0 I
0 x ~ I x
~ K
闭环特征值
引入状态反馈
~ ~~ ~ ~~ ~ det(sI A BK ) det(sI1 ( Ac B1Kl ) det(sI 2 Ac )
5.5 状态观测器(1)
本节主要解决的问题 • 什么是状态观测器?它的作用是什么?
• 状态观测器在什么条件下是存在的?
• 如何构造状态观测器?
0 xo Bo u Ao xo Bo
xo 0 x o
G [G1
G2 ]
5.5 状态观测器（6）
A11 0 G1 A GC C1 0 A21 A22 G2 A11 0 G1C1 0 A11 G1C1 A21 A22 G2C1 0 A21 G2C1
5.5 状态观测器(13)
例题：设计全维观测器，将极点配 置在-10，-10。 0 2 2 x x u 解 步骤 1 3 0 （1）状态空间表达式 y 0 1x （2）能观性判别
（3）计算反馈阵 G
2 w( s) ( s 1)(s 2)
BK
x 0 ˆ x
A2
闭环系统的基本特性
1 闭环极点的分离性: •闭环系统的极点由直接状态反馈系统(A-BK,B,C)的极点和观测 器系统(A-GC,B,C)的极点组成,两者独立,相互分离.
det(sI A2) det[sI ( A BK )]det[sI ( A GC)]
I y C 0 I
0 x ~ I x
~ K
闭环特征值
引入状态反馈
~ ~~ ~ ~~ ~ det(sI A BK ) det(sI1 ( Ac B1Kl ) det(sI 2 Ac )
5.5 状态观测器(1)
本节主要解决的问题 • 什么是状态观测器?它的作用是什么?
• 状态观测器在什么条件下是存在的?
• 如何构造状态观测器?
0 xo Bo u Ao xo Bo
xo 0 x o
G [G1
G2 ]
5.5 状态观测器（6）
A11 0 G1 A GC C1 0 A21 A22 G2 A11 0 G1C1 0 A11 G1C1 A21 A22 G2C1 0 A21 G2C1
5.5 状态观测器(13)
例题：设计全维观测器，将极点配 置在-10，-10。 0 2 2 x x u 解 步骤 1 3 0 （1）状态空间表达式 y 0 1x （2）能观性判别
（3）计算反馈阵 G
2 w( s) ( s 1)(s 2)
BK
x 0 ˆ x
A2
闭环系统的基本特性
1 闭环极点的分离性: •闭环系统的极点由直接状态反馈系统(A-BK,B,C)的极点和观测 器系统(A-GC,B,C)的极点组成,两者独立,相互分离.
det(sI A2) det[sI ( A BK )]det[sI ( A GC)]
现代控制理论第五章线性系统的设计与综合
第五章 线性系统的设计与综合
熟练掌握状态反馈与输出反馈，极点配置 熟练掌握状态观测器设计方法 掌握分离原理
教学要求：
状态反馈与输出反馈的基本结构、性质和有关定理 单输入、多输出系统的极点配置 全维观测器的设计 状态反馈与观测器的工程应用
重点内容：
5.1 状态反馈与输出反馈
CONTENTS
则：
令： 式中 标量 这说明 的列 是 列的线性组合。
01
列的线性组合。
同理： 的列 是
列的线性组合。
的列 是
输出反馈实现极点配置
01
输出反馈 状态微分 设多输入／单输出系统：
02
B
A
I/s
C
h
u
y
-
+
x
定理：由输出至 的反馈任意配置极点的充要条件是被控系统能观。
证明：运用对偶原理：
若(A,B,C)能观，则
能控，可由状态反馈实现极点配置：
可求出h 。
03
04
05
设
令
闭环系统状态空间表达式:
1/s
01
1/s
02
1/s
03
2
04
3
05
3
06
+
07
+
08
y
09
v
10
11
状态反馈
12
闭环系统的传递函数：
A
设单输入-单输出系统：
B
已知(A,b,c,d)能控，则经过 将(A,b,c,d)化为能控型
5.4 状态反馈对系统零极点的影响
引入状态反馈：
设：
01
02
Ｂ
Ｖ
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 0 0 a1
β1 βn1 x
0 0 1 0 x u 0 0 1 1 an 1 0
5.2
极点配置
系统传递函数：g ( s ) C [ sI A]1 b C [ sI A ]1 b
0 1 0 0 P 1 12 1 18 144
5.2
极点配置
1 0 0 4 66 140 1 12 k kP 1 18 144 14 186 1220
5.2
方法二：
极点配置
a* ( s ) ( s 1 )( s 2 ) ( s n )
* * * s n an 1s n 1 a1 s a0
5.2
极点配置
（4）计算 G
G a a0
* 0
a a1 a
* 1
* n1
an1
（5）计算变换矩阵
0 0 0 1 x 0 u 1 6 x 0 0 1 12 0
求状态反馈向量k，使系统的闭环特征值为
1 2 2 1 j 3 1 j
5.2
极点配置
解：系统的可控性判别矩阵为：
Qc b
*
s a s
n
* n 1 n 1
a s a
* 1
* 0
5.2
（3）计算
极点配置
* k a0 a0
k
* * a1 a1 an1 an1
（4）计算变换矩阵
（5）计算状态反馈增益向量
1 a 1 n 1 n 1 1 P A b Ab b a1 an 1 1
k kP
5.2
方法二：
极点配置
引入状态反馈k后，系统的状态空间表达式为
x ( A bk) x Bv
y Cx
系统的特征多项式为 det[ sI ( A bk )] ， 令其各项的系数与希望特征多项式中对应项的系
数相等，便可确定反馈增益向量k。
5.2
极点配置
例：已知单输入线性定常系统的状态方程为
* * * Δ ( s) ( s si ) s n an 1s n 1 a1 s a0 * K i 1 n
选择 k i 使同次幂系数相同。有
* K a0 a0
* * a1 a1 an1 an1
而状态反馈矩阵
K KP k0
5.2
1
极点配置
变换矩阵为：
P Ab
2
Ab
0 0 1 1 6 1 0 18 1 0 0 72
1 0 0 a b 2 1 0 a1 a2 1 0 0 72 18 1 12 1 0 1 0 18 1 1 0 0
状态反馈系统特征多项式为
Δ K ( s ) det[sI ( A b K )] s n (an 1 k n 1 ) s n 1 (a1 k1 ) s (a0 k0 )
5.2
极点配置
设状态反馈系统希望的极点为 s1 , s2 , , sn 其特征多项式为
系统不稳定
（3）引人输出反馈
5.3 镇定问题
此时，特征多项式为：
无论怎样选择H，也不能使系统镇定。
注：利用输出反馈未必能使能控且能观的系统得到镇定。
5.3 镇定问题
定理3： 线性定常系统方程为
x Ax bu y Cx
引入从输出到
x 反馈实现镇定的充要条件为：结构分
解中不能观测子系统是渐近稳定的。
5.4 解耦问题
一、 问题的提出 考虑MIMO系统
x Ax Bu y Cx
在 x(0) 0 的条件下，输出与输入之间的关系， 可用传递函数 G ( s) 描述：
y(s) G(s)u (s) C (sI A) 1 Bu (s)
5.4 解耦问题
y1 ( s) g11 ( s)u1 ( s) g12 ( s)u2 ( s) g1 p ( s)u p ( s) y2 ( s) g 21 ( s)u1 ( s) g 22 ( s)u2 ( s) g 2 p ( s)u p ( s) yq ( s) g q1 ( s)u1 ( s) g q 2 ( s)u2 ( s) g qp ( s)u p ( s)
性能。
(2) 线性定常系统引入状态反馈后，不改变系统的能控
性，但不能保证系统的能观性不变。
5.1 引言
二、输出反馈
线性定常系统方程为：
x Ax Bu y Cx Du
输出线性反馈控制律为：
u V Hy
H 为 r m 常数矩阵
5.1 引言
x Ax B(V Hy) [A BH(I DH)1 C]x [B BH(I DH)1 D]V
x Ax Gy Bu y Cx Du
x (A+GC)x (B+GD)u y Cx Du
5.1 引言
注： 矩阵G的引入能改变系统特征值，进而改 变系统获得所要求性能。
5.2
极点配置
一、极点配置问题
通过对反馈增益矩阵的选择，使闭环系统的极点 配置在所希望的位置上，从而获得所希望的性能指 标要求。
耦合：每一个输入控制着多个输出，而每一个输出 被多个输入所控制。 解耦控制：每个输出受且只受一个输入的控制。
状态线性反馈控制律为：
u V Kx
其中，K 为反馈增益矩阵，V 为输入向量。
5.1 引言
则有
x Ax B(V Kx) ( A BK ) x BV y (C DK ) x DV
5.1 引言
注：
(1) 状态反馈阵K的引入，并不增加系统维数， 但可通 过K的选取改变系统特征值，进而改变系统获得所要求
k k1
k2
k3
k3 s k1 k2 a* ( s) det sI ( A bk ) 1 s 6 0 0 1 s 12 s 3 (k1 18) s 2 (18k1 k2 72) s (72k1 12k2 k3 )
βn-1s n 1 βn-2 s n 2 β1s β0 ( s ) n n 1 s an-1s a1s a0 (s)
引入状态反馈
u V Kx V KP 1 x V Kx
令
K KP 1 k0
k1 kn1
希望的特征多项式为：
a* ( s) ( s 1 )( s 2 )( s 3 ) ( s 2)( s 1 j )( s 1 j ) s 4s 6s 4
3 2
* k a0 a0
* a1 a1
* a2 a2 4 66 14
G T G
x (A+GC)x (B+GD)u y Cx Du
5.2
方法二：
极点配置
引入反馈后，系统的状态空间表达式为
x (A+GC)x (B+GD)u y Cx Du
系统的特征多项式为 det[ sI ( A GC )] ,令其各项的 系数与希望特征多项式中对应项的系数相等，便可确
定反馈增益向量k。
5.2
例：
极点配置
5.2
解：（1）
极点配置
（2）
5.3 镇定问题 一、镇定问题
非渐近稳定系统通过引入反馈，使其极点
均具有负实部，保证系统渐近稳定。
5.3 镇定问题 二、镇定条件
定理1： 线性定常系统方程为
x Ax bu y Cx
引入状态反馈能镇定的充要条件为：不能控的状态分 量是渐近稳定的。
其中 k0 , k1 , , kn1 为待定常数
5.2
极点配置
1 0 0 0 k k k A bK 0 1 n 1 0 1 0 a0 a1 an 1 1 0 1 0 0 1 (a0 k0 ) (a1 k1 ) (an 1 k n 1 )
第五章 线性定常系统的综合
引言
极点配置
镇定问题
解耦问题
状态观测器 状态观测器实现状态反馈
5.1 引言
线性定常系统综合：给定被控对象，通过 设计控制器的结构和参数，使系统满足性能指 标要求。
5.1 引言
一、 状态反馈
线性定常系统方程为：
x Ax Bu y Cx Du
5.3 镇定问题
定理2： 线性定常系统方程为
x Ax bu y Cx
引入输出反馈能镇定的充要条件为：结构分解中能控 且能观测子系统是输出反馈能镇定的，其余子系统是渐近 稳定的。
5.3 镇定问题 例：证明下列系统不能通过输出反馈使之镇定。
5.3 镇定问题
证明：（1）系统能控且能观测 （2）系统特征多项式：
输出反馈只能将闭环系统的极点配置在系
统根轨迹上，而不能做到任意配置。
5.2
极点配置
四、采用从输出到 x 反馈极点配置 线性定常系统可以采用输出到 x 的线性反 馈实
现闭环极点任意配置的充分必要条件是系统状态完全 能观测。
5.2
极点配置