数学建模投入产出模型
投入产出数学模型
投入产出的基本平衡关系
从左到右： 中间需求＋最终需求＝总产出 (1)
从上到下： 中间消耗＋净产值＝总投入
(2)
由此得产出平衡方程组(也称分配平衡方程组)：
x11 x12 x1n y1 x1
x21
x22
x2n
表1：投入产出表（一般格式）
流量 产出 消耗部门
最终需求
投入
1 2 n 消费 累计 出口
生
1
x11 x12 x1n
产
2
x21 x22 x2n
部
门
n
xn1 xn2
xnn
新 创 价 值
工资 纯收入 合计
v1 v2 m1 m2 z1 z2
vn mn zn
总投入
x1 x2 xn
合计
y1 y2 yn
数学建模讲座
（二）投入产出数学模型
李媛
1
在经济活动中分析投入多少财力、物力、
人力，产出多少社会财富是衡量经济效益高
低的主要标志。
投入产出技术正是研究一个经济系统各部 门间的“投入”与“产出”关系的数学模型， 该方法最早由美国著名的经济学家瓦.列昂捷 夫（W.Leontief）提出，是目前比较成熟的 经济分析方法。
i1
由直接消耗系数的定义 xij aij x j，代入(3)，得
a11x1 a12x2 a1n xn y1 x1
a21x1
a22x2
a2n xn
y2
x2
an1x1 an2 x2 ann xn yn xn
令 X x1 x2 xn ,Y y1 y2
(10)
投入产出-CGE模型及其应用
n 1
~ V j avibij
n i 1
n
j vj bij
i 1
n
*
j vj bij
i 1
就业乘数
Ej
*
a ei ~ zij
i 1
n 1
~ E j aei bij
n i 1
产出乘数
产出乘数=初始值+直接消耗系数+间接消耗系数+诱导系数 初始值=1（ 一个单位的最终产品） 直接消耗：直接消耗系数按列相加的值。
前提
在进行经济影响分析时，需要确定以下方面： • • • • 经济影响分析的对象是什么（基础设施建设、旅游消费、体育赛事）？ 经济影响分析的区域范围（市、省国家）？ 经济影响分析的时间范围（哪一年）？ 经济影响分析的结果表现（总产出、GDP、居民收入、就业）？
经济影响的三个方面
• 产出：某一部门增加一个单位最终产品对国民经济各个部门所产生 的生产需求量（产出乘数） • 居民收入：增加最终产品→扩大生产规模→增加居民收入（居民收 入乘数） • 就业：增加最终产品→扩大生产规模→增加劳动力需求（就业乘数）
投入产出、CGE模型及其应用
张伟 博士 环境保护部环境规划院 环境规划与政策模拟重点实验室
目录页
CONTENTS PAGE
1.投入产出模型 介绍
2.相关研究 介绍
3.CGE模型现有 工作基础
4.未来设想
投入产出模型介绍
Part
1
Part 1
Part 2
Part 3
Part 4
什么是投入产出法
投入产出法：在一定经济理论指导下，通过编制投入产出表，建立相应的投入产出数学模型， 综合系统地分析国民经济各部门、再生产各环节之间数量依存关系的一种经济数量分析方法。 是经济学、统计学、数学、计算机技术相结合的产物。属于宏观经济的范畴。 （一）投入：指一项经济活动中的各种消耗。 包括：物质和非物质产品消耗；有形和无形产品消耗 有形:原材料、辅助材料、燃料、动力、固定资产折旧、 无形：劳动力、金融、保险、技术专利、服务等。
投入产出数学模型练习题 数学建模
投入产出数学模型经济应用案例投入产出数学模型的应用领域很广，常用于分析经济系统的部门结构和比例关系、进行经济预测、调整经济计划等各个方面。
由投入产出模型的理论知道，只要经济系统各个部门的生产技术条件没有变化，就可将报告期的投入产出数学模型直接应用于计划期的经济工作。
下面将以实例说明其在经济中的应。
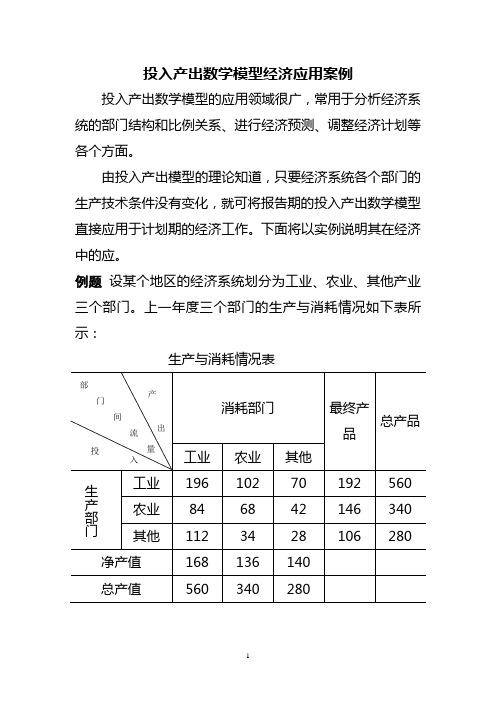
例题设某个地区的经济系统划分为工业、农业、其他产业三个部门。
上一年度三个部门的生产与消耗情况如下表所示：生产与消耗情况表假定该系统三个部门的生产技术条件都没有变化，从而该系统的直接消耗系数矩阵不变，由此建立的产品分配方程组和产值构成方程组也不变。
在此基础上，分别分析该系统的报告期投入产出数学模型在计划期经济计划工作方面的下列应用。
（1）在经济预测中的应用假定根据上例所示经济系统的生产发展情况，预计该系统工业、农业、其他产业三个部门的计划期总产品将在报告期总产品的基础上分别增长9%、7%、6%。
由于在生产过程中系统内部存在着复杂的产品消耗关系，故一般说来，各个部门最终产品的增长幅度与总产品的增长幅度并不一致。
试预测该系统最终产品的增长情况。
（2）在制订计划中的应用投入产出数学模型为合理制订经济系统的生产计划提供了一个科学的方法。
根据社会需要确定社会产品的原则，先通过对计划期需要量的预测，确定系统各个部门的最终产品，再利用投入产出数学模型推算出各个部门的总产品，在此基础上编制经济系统计划期的投入产出表，作为安排各个部门计划期生产活动的依据。
现假定通过预测，引例所示经济系统三个部门的计划期最终产品需要量分别为工业部门：1216y=亿元，农业部门：2716y=亿元，其他产业部门：3120y=亿元。
试确定计划期总产品、部门间流量及计划期各部门净产值。
（3）在调整计划中的应用以上介绍了如何根据对最终产品的需求，制订经济系统的生产计划。
但是在执行计划时，可能由于不可预测的原因，导致系统某些部门的最终产品出现缺口(计划产量小于需要量)，或者某些部门的最终产品出现余量(计划产量大于需求量)，从而破坏了经济系统原计划的平衡性。
线性代数方法建模4投入产出分析--数学建模案例分析
§4 投入产出分析在一个国家或区域的经济系统中，各部门（或企业）既有消耗又有生产，或说既有投入又有产出，生产的产品供给系统内部各部门和系统以外的需求，同时也消耗系统内各部门所提供的产品。
消耗的目的是为了生产，生产的结果又必然要创造新价值，以支付工资和获取利润。
对每一部门，物质消耗和新创造的价值等于它生产的总产值，这就是投入和产出之间的平衡关系。
美国经济学家、哈佛大学教授W.Leontief 于20世纪30年代首先提出并成功建立了国民经济的投入产出数学模型，并数次制定主持美国的国民经济投入产出表，这一方法即投入产出法以其重要的应用价值迅速为世界各国经济学界和决策部门所采纳，因此他获得1973年的Nobel 经济学奖。
设有n 个经济部门组成的经济系统，假设1、部门i 仅生产一种产品i ，称为部门i 的产出，不同部门的产品不能相互替代；2、部门i 在生产过程中至少需要消耗另一部门 j 的产品，称为部门 j 对部门i 的投入，并且消耗的各部门产品的投入量与该部门的总产出量成正比。
记i x —部门i 的总产出 ),,2,1(n i =ij x —部门i 分配给部门j 的产品量),,2,1,(n j i =ij a —部门 j 的单位产品对部门i 产品的消耗),,2,1,(n j i =，显然j ij ij x a x =i y —外部对部门i 的需求),,2,1(n i =j z —部门j 新创造的价值),,2,1(n j =利用统计资料，可以编制下面的投入产出表。
投入产出模型按计量单位的不同，分为价值型和实物型，在价值型模型中，各部门的投入、产出均以货币单位表示；在实物型模型中，则按各产品的实物单位（如吨、米等）为单位。
我们在这里仅讨论价值型模型，至于实物型模型，可以证明相应的直接消耗系数矩阵与货币型模型的直接消耗系数矩阵相似，因此模型的结论是一致的。
一、平衡方程组对每一部门，作为系统内部各部门的消耗＋外部需求＝总产品即 ),,2,1(1n i x y x a i i j ij nj ==+∑= （1）(1) 称为分配平衡方程组。
《投入产出模型》课件
目录
CONTENTS
• 投入产出模型概述 • 投入产出模型的构建 • 投入产出模型的分析方法 • 投入产出模型的应用案例 • 投入产出模型的未来发展
01
CHAPTER
投入产出模型概述
定义与特点
定义
投入产出模型是一种经济数量分析方法，通过建立数学模型来描述和分析各部 门之间的经济技术联系和投入产出关系。
02
Excel是一款常用的办公软件， 可以通过添加插件或使用自定 义函数来处理投入产出模型的 数据。
03
SAS和Stata则是专业的统计分 析软件，具有强大的数据处理 和模型分析功能，适用于复杂 的投入产出模型分析。
04
CHAPTER
投入产出模型的应用案例
地区经济分析
总结词
投入产出模型在地区经济分析中，能够全面反映各产业间的经济联系，为地区经济发展战略制定提供决策依据。
数据来源
通过调查、统计和会计资料等途径获取各部门之间的 经济联系数据。
编制方法
采用会计和经济统计方法，按照生产活动的流程和特 点，将各部门之间的经济联系进行分类和整理。
直接消耗系数的计算
直接消耗系数
表示某部门生产单位产品所需直接消耗的另一 部门产品的数量。
计算方法
通过投入产出表中的投入数据计算，反映部门 之间的直接经济联系。
特点
投入产出模型具有系统性、动态性、预测性和政策模拟性，能够全面反映经济 系统的结构、功能和运行机制，为政策制定和经济发展提供科学依据。
投入产出模型的应用领域
产业结构分析
投入产出模型可以用于分析产业 间的关联关系和依存度，揭示产 业发展的内在规律和趋势，为产 业结构调整和优化提供决策支持 。
投入产出数学模型
x12 x22
. . .
... ...
...
x1 n x2 n
x nn
y1 y2
. . . yn
x1 x2
. . .
社会纯收入 m1 , … ,mn 合计
z1 , … , zn
x1 , … , xn
服务业
n
xn 2
xn
总产值
xij ：第i个部门的产品流入 (投入 到第 个部门的数量 (价值量 投入) 价值量) 第 个部门的产品流入 投入 到第j个部门的数量 价值量
因为 A
1
i)
= max
j 1
∑
∞
n
i =1
a ij = max
j k
∑
n
i =1
a ij < 1 i, j
所以 ( I A )
=
∑
k =1
A = ( b ij ) n × n b ij ≥ 0
所以 y ≥ 0 有 又因为
x = ( I A ) 1 y ≥ 0 I O 为可行的
T
V ≥ 0由 V
∑a P
i =1
n
ij i
(V = P AT P )
四 模型的可行和有利问题
定义： 1 定义：
①若在I-O模型中 y ≥ 0 x ≥ 0 则称模型为可行的 ( 价值型 ) 若在 模型中 ②若对 V ≥ 0 P ≥ 0 则称模型为有利的 ( 实物型 )
判别准则： 2 判别准则：
①矩阵范数： 矩阵范数：
1.3459 0.2504 0.3443 ( I A) 1 = 0.5634 1.2676 0.4930 0.4382 0.4304 1.2167
x = ( I A) 1 y y = ( I A) x
【数学建模】投入产出模型
推论 . 若 A ≥ 0 且存在一个非负 p ≥ 0 , 使得 pT(I-A) > 0, 则 (I - A)-1 存在且非负 .
投入产出
• •
2. 消耗分析 10. 直接消耗系数 aij : 生产单位产品 j 对产品 i 的直接需求量 .
⎡0.059 ⎢0.002 A= ⎢ ⎢0.026 ⎢ ⎣0.026
0.254 0.192 0.208⎤ 0.456 0.069 0.150⎥ ⎥ 0.493 0.888 0.495⎥ ⎥ 0.362 0.315 0.295⎦ -1
投入产出
Байду номын сангаас直接需求
a33>a22>a34>a42>a44>a32>a43. 完全需求 b33>b34>b32>b22>b42>b43>b44. 直接: 轻需轻 > 轻需他 > 轻需重 完全需求 : 轻需重 > 轻需轻> 轻需他
I. 中间产品的投入和产出, II. 总产品中可供社会最终使 用的部分, III. 外购资源和劳力, 社会投入, IV. 国民收入 的再分配
• 3. 例. 全国农、轻、重投入产出表
产出 投 入
农业 农业 98.3
中
244.2 631.4 304.9 351.7 1532.2
间
209.0 36.8
产
11 12 11 21 22
1− a11 − a12 1− a11 > 0 , > 0, − a21 1− a22
, | D |> 0
Hawkins-Simon 条件.
投入产出
定理 2 . 若 A ≥ 0 且存在一个非负x ≥ 0 , 使得 (I-A) x > 0, 则 (I - A)-1 存在且非负 .
线性代数数学建模案例
【问题描述】： 某城市单行线如下图所示, 其中的数字表示该路段每小时按 箭头方向行驶的车流量(单位: 辆).
400
500 1
x1
2 300
x2 100
3
200
x3 X4 4 300
图3 某城市单行线车流量示意图
现在需要解决的问题如下：
（1） 建立确定每条道路流量的线性方程组. （2） 为了唯一确定未知流量, 还需要增添哪几条道路的流量统计? （3） 当x4 = 350时, 确定x1, x2, x3的值.
【模型分析】
• 若令1 = (2, 3, 1, 1)T, 2 = (1, 2, 1, 1)T, = (4, 7, 5, 3)T, 则原问题等价于“线性方程组Ax = b是否有 解”, 也等价于“能否由1, 2线性表示”。
• 若四种原料的比例是按体积计算的, 则还要考虑混合前后体 积的关系(未必是简单的叠加), 因而最好还是先根据具体情 况将体积比转换为重量比, 然后再按上述方法处理.
图5 日常膳食搭配
图6 几种常见的作料
【模型准备】：
一种佐料由四种原料A、B、C、D混合而成. 这种佐料现有两种规格, 这 两种规格的佐料中, 四种原料的比例分别为2:3:1:1和1:2:1:2. 现在需要四种 原料的比例为4:7:3:5的第三种规格的佐料. 问: 第三种规格的佐料能否由前两 种规格的佐料按一定比例配制而成?
一个网络由一个点集以及连接部分或全部点的直线或弧线构成。 网络中的 点称作联结点(或节点)，网络中的连接线称作分支. 每一分支中的流量方向已经指
定，并且流量(或流速)已知或者已标为变量。
x3
x1
60
x4
80
x2
(a)
x5 (b)
《投入产出模型》课件
投入产出模型的发展趋势与展望
智能化与自动化
跨学科融合
定制化与个性化
随着大数据和人工智能技术的 发展，未来投入产出模型将更 加智能化和自动化。通过数据 挖掘和分析，能够更准确地评 估经济系统的结构和效率，为 政策制定提供科学依据。
未来投入产出模型将进一步融 合其他学科的理论和方法，如 地理信息系统、复杂网络等， 以更全面地揭示经济系统的内 在规律和动态变化。
特点
投入产出模型能够全面反映经济系统 的结构和运行规律，揭示各部门之间 的经济联系，为政策制定者提供决策 依据。
投入产出模型的基本假设
假设一
生产过程中消耗的中间产品与 最终产品之间存在固定的比例
关系。
假设二
生产技术系数在一定时期内保 持稳定。
假设三
生产过程中不存在外部经济和 内部经济的影响。
假设四
投入产出模型的起源
投入产出模型的起源可以追溯到 20世纪30年代，当时美国经济学 家瓦西里·列昂惕夫提出了投入产 出分析方法，用于研究经济系统 中各部门之间的投入与产出关系 。
投入产出模型的发展
随着时间的推移，投入产出模型 的应用范围不断扩大，逐渐成为 宏观经济分析和政策制定的有力 工具。在实践中，投入产出模型 不断得到完善和改进，以适应不 同国家和行业的需要。
动态投入产出模型考虑了时间因素对 经济系统的影响，能够更好地模拟经 济系统的动态变化和趋势。该模型在 政策制定和预测方面具有广阔的应用 前景。
03
全球投入产出模型
随着全球经济一体化的加速，全球投 入产出模型逐渐成为研究前沿之一。 该模型能够全面地反映全球范围内各 国家、各行业之间的经济联系和相互 影响。
02
投入产出模型的建立
投入产出数学模型练习题解答 数学建模
投入产出数学模型练习题解答（1）在经济预测中的应用该系统的计划期总产品和最终产品分别记为()123,,x x x x '= 和()123,,y y y y '= 。
根据表中报告期的总产品数据以及预计的计划期总产品增长幅度，该系统三个部门的计划期总产品应分别为工业部门： ()156019%610.4x =+=亿元农业部门： ()234017%363.8x =+=亿元 其他产业部门：()328016%296.8x =+=亿元将这些数据代入产品分配平衡方程组，可求得 ()y I A x =-即 1230.650.30.25610.4213.420.150.80.15363.8154.960.20.10.9296.8108.66y y y --⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪⎪ ⎪=--= ⎪ ⎪⎪ ⎪ ⎪⎪ ⎪⎪--⎝⎭⎝⎭⎝⎭⎝⎭ 由此可对该系统三个部门的计划期最终产品及其相对于报告期最终产品的增长幅度作出预测工业部门：1213.42y =亿元，增长213.4219211.2%192-= 农业部门：2153.96y =亿元，增长153.961466.1%146-= 其他产业部门：2108.66y = ，增长108.661062.5%106-= 根据预测结果，可对该系统的计划期最终产品与实际需要是否相符作出判断，避免出现大的偏差。
（2）在制订计划中的应用将数据代入产品分配方程组，可求得()1x I A y -=-即 1230.7050.2950.24521664010.1650.5350.1351764000.3650.1750.1250.475120320x x x ⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪⎪ ⎪== ⎪ ⎪⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭由此可知，该系统三个部门的计划期总产品分别为工业部门：1640x = 亿元 农业部门：2400x = 亿元其他产业部门：3320x = 亿元用上述三个部门的总产品分别乘该系统的直接消耗系数矩阵中对应列的元素，可得到该系统计划期部门间流量的矩阵6400.354000.33200.256400.154000.23200.156400.24000.13200.1⨯⨯⨯⎛⎫ ⎪⨯⨯⨯ ⎪ ⎪⨯⨯⨯⎝⎭224120809680481284032=⎛⎫ ⎪ ⎪ ⎪⎝⎭工业农业其他工业农业其他再将上述三个部门的总产品(总产值)代入产值构成平衡方程组，可求得该系统三个部门的计划期净产值分别为11(1,2,,)nj ij j i z a x j n =⎛⎫=-= ⎪⎝⎭∑工业部门：110.30.3640192z x ==⨯=亿元农业部门：220.40.4400160z x ==⨯=亿元 其他产业部门：330.50.5320160z x ==⨯=亿元 根据以上所求得的各项数据即可编制出该系统的计划期投入产出表（3）在调整计划中的应用将该系统计划期的总产品调整量和最终产品调整量分别记作()123,,x x x x '∆=∆∆∆ 和()123,,y y y y '∆=∆∆∆。
投入产出系数及其模型
○ 根据它与直接消耗系数的关系计算。 ● 完全消耗系数的矩阵幂级数解法。 1. 在此介绍第一种方法
完全消耗系数 的计算
n
b ik a kj
k 1
K表示j部门对k部门产品的直接消耗； akj是j部门生产单位产品直接消耗k中间产品的数量； bik是k单位产品在生产中直接、间接消耗第i产品的量； bikakj表明通过中间产品k实现的j部门单位产品对i部门产品的间接消耗量； A. 表示j部门通过k中间产品对i部门产品的全部间接消耗量。也称作全部间接消耗系数。
增加值Nj 根据其构成要素可分解为：
dVSMd V S M j j j j j j j
j
a 单 击 此 处 添 加 正 文 ， 文 字 是 您 思 想 的 提 炼 ， 请 尽 量 言 简 意 赅 地 阐
述观点。
N j
X X X X X j
jjj j
dj
固定资产折旧
单击此处添加正文，文字是您思想的提炼，请尽量言简意赅地阐 述观点。
整理：
X=(I+B)Y （1）
或： Y=(I+B)-1X （2）
应用：
由（1）式可知 最终产品求总产 出。
由（2）式可知总 产出求最终产品。
第三节 列 昂惕夫逆矩 阵 和完全需要 系数
主要内容
1. 列昂惕夫逆矩阵 2. 完全需要系数 3. 完全消耗系数与完全需要系数的比较
列昂惕夫 逆矩阵和 完全需要 系数
Y120140140 T y1, y2 , y3
0.2 0.1 0 0.3077 0.2308 0.0769
A
0.2 0
0.4 0.1
0.3 0.1
B00..40651153
数学建模、层次分析法、投入产出模型
2013第十届五一数学建模联赛承诺书我们仔细阅读了五一数学建模联赛的竞赛规则。
我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与本队以外的任何人（包括指导教师）研究、讨论与赛题有关的问题。
我们知道，抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其它公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺，严格遵守竞赛规则，以保证竞赛的公正、公平性。
如有违反竞赛规则的行为，我们愿意承担由此引起的一切后果。
我们授权五一数学建模联赛赛组委会，可将我们的论文以任何形式进行公开展示（包括进行网上公示，在书籍、期刊和其他媒体进行正式或非正式发表等）。
我们参赛选择的题号为（从A/B/C中选择一项填写）：我们的参赛报名号为：参赛组别（研究生或本科或专科）：所属学校（请填写完整的全名）参赛队员(打印并签名) ：1.2.3.日期：年月日获奖证书邮寄地址：邮政编码2013第十届五一数学建模联赛编号专用页竞赛评阅编号（由竞赛评委会评阅前进行编号）：裁剪线裁剪线裁剪线竞赛评阅编号（由竞赛评委会评阅前进行编号）：参赛队伍的参赛号码：（请各参赛队提前填写好）：2013第十届五一数学建模联赛题目关键词摘要随着经济的发展，公路运输业逐渐成为一个城市经济发展的命脉，是社会经济发展中的重要基础设施和支柱产业。
对国内生产总值产生巨大影响。
本文通过层次分析以及投入产出法对公路运输业对GDP的影响进行定量分析，把影响量化并考虑公路运输业前期所产生的对资源的占用问题进一步优化模型问题一：通过对GDP的经济分析，得出影响GDP的因素主要在交通建设阶段以及之后的交通运输和随之带动的相关产业的发展具体表现为交通建设时对道路建设的原材料需求以及人力资源需求，还表现为交通运输业客货运输的发展对经济的拉动以及旅游业的发展。
然后利用投入产出法对这些影响因素进行求解得出各因素对经济的贡献率，从而进一步阐述对GDP的影响。
投入产出表的数学模型
178.54 = 1549.98 (亿元) 445.26
例：若把农业、工业、“其他”三个部门的最终使用由现在 的175亿元、1410亿元、395亿元分别增长4%、8%和10%，直接消 耗系数同上，试测算各部门的总产出。
175 × 104% = 182 Y 解：由题意知 = 1410 × 108% = 1522.8 395 × 110% = 434.5
(a11 a 21 a n1 ) X 1G1 X 1 (a a a ) X G X 12 22 n2 2 2 2 ...... (a1n a 2 n a nn ) X n Gn X n
第二列各直接消耗系 数之和，用C2表示； 第n列各直接消耗系 数之和，用Cn表示。 把该式变 形可得投 入产出表 的列模型 (见下页)
…
…
合
计
∑xi ∑xi … ∑xi d1 v1 T1 r1 G1 X1 d2 v2 T2 r2 G2 X2 dn vn Tn rn Gn Xn
… ∑Ei
∑Y ’i
∑Mi ∑X
最 初 投 入
固定资产折 旧 劳动者报酬 生产税净额 营业盈余 合 计
…
∑dj ∑vj ∑Tj ∑rj ∑Gj ∑Xj
… …
总
0.8947 -0.1404 -0.0526
-0.0111 0.8889 -0.0333
-0.1053 -0.2632 0.8254
3.1 投入产出模型
3.1.2 投入产出模型的产品分配方程
投入产出模型建立在两个基本假设之上：(1)同质 性假设。假定每个部门只生产一种产品，任何一 种产品只属于一个部门，不同部门之间的产品无 相互替代现象；(2)比例性假设。假定每个部门的 投入与每个部门的产品产量或产值成正比关系， 因此投入和产出之间的关系是线性函数关系。 投入产出表如下表3.1.1所示：
表3.1.1 投入产出表
yi 设 xij 表示第 i 部门为第 j部门提供的产品的使用量， 表示第 i部门提供给居民、政府、出口和社会储备等 xi 表示第i部 i 1, 2,, n, j 1, 2,, n ， 最终需求， 门提供的产品产量（或产值），因此投入产出表的 第 i行表示第 i部门的产出，它反映了n个部门对第 i 部门的中间需求与最终需求之和应等于第 i部门的总 产出，则有如下产品分配的平衡关系方程式：
T
预测各部门提供的中间产品价值
T ˆ X AX 80.03 62.56 131.31 0.94 14.02 19.04
若在本年度的基础上，计划下一年度最终产品产值
农业增长3%，轻工业增长8%，重工业增长5%，建
筑业增长8%，运邮业增长12%，商业增长10%，则
计划目标最终产品产值向量为：
n i 1 ij
n
cj
i 1
ij
为中间消耗比率矩阵。令固定资产折旧向量 T T D d1 , d 2 , , d n ,活劳动的报酬向量 V v1 , v2 , , v ， n T M m , m , , m 1 2 纯收入向量 n ，则（3.1.4）可写为 Ac X D V M X ： （3.1.5） 式（3.1.5）称为投入产出产值构成模型。 令 N V M ，则称 N 为n个部门的国民收入向量或 创新价值向量，则有： ( I Ac ) X D N （3.1.6） 式（3.1.6）表明第 j 部门的总产值中扣除中间消耗部 分是固定资产折旧与新创价值之和。
投入产出模型的基本假设和求解条件
§ 1・5投入产出模型的基本假设和求解条件任何经济数学模型都是都实际经济活动的抽象，都是在若干基本假设下建立的，或者只有在若干基本假设下才能成立。
关键在于所舍弃的是事物的本质方面还是非本质方面。
一、投入产出模型的基本假设投入产出模型是在如下重要假设下建立的。
1.不可替代假设投入产出模型假设一个部门只生产一种产品，而且只采用一种技术生产；同时，一种产品只由一个部门生产。
为什么要作出该假设？实际经济活动是否满足这一假设？2.线性假设投入产出模型假设投入量与产出量是成正比的，比例系数就是直接消耗系数。
为什么要作出该假设？实际经济活动是否满足这一假设？3.系数不变假设投入产出模型假设直接消耗系数在一个周期内是不变的。
为什么要作出该假设？实际经济活动是否满足这一假设？4.关于生产周期的假设投入产出模型假设每个部门的生产经营活动，从生产要素的投入到产出的分配与使用，都在一个周期内完成。
为什么要作出该假设？实际经济活动是否满足这一假设？如何处理？二、投入产出模型的求解条件所谓“投入产出模型的求解条件”，是指投入产出模型能够求解的条件。
1.投入产出模型能够求解的条件投入产出模型X (I A) 1Y能够求解的条件是矩阵(I A )有逆，且逆矩阵的元素不为负。
是从数学和经济意义两方面提出的。
2.价值型投入产出模型求解条件的证明对于价值型投入产出模型，其直接消耗系数满足：n aij 1 j 1,2, ,ni 1即满足：n a 1 a j 1,2, ,ni 1而在矩阵(I A)中，主对角线元素为1 a jj,其它元素为a ij0所以该矩阵是主对角线元素占优势的矩阵。
由线性代数知识可知，I A 0。
所以矩阵(I A)有逆。
又因为对于矩阵(I A),不仅存在ai 1, 而且存在nai 1. 所以有|I A|。
对于矩阵(I A )的逆矩阵：E 由 其分子为矩阵(I A )对应元素的代数余子式作为元素构成的伴随矩阵，而这些代数余子式 都是大于0,所以(I A )的逆矩阵的元素的都大于0。
投入产出分析投入产出经济数学模型
§1.4 投入产出经济数学模型本节介绍两个最基本的投入产出经济数学模型。
第三章将要介绍的各种复杂的投入产出应用模型，都是这两个最基本的投入产出经济数学模型的扩展。
一、分配方程组和按行建立的模型⒈ 分配方程组对于投入产出表的每一行，不管是价值型还是实物型，都存在如下平衡方程：n i X Y xi i n j ij ,,2,11==+∑= （1.4.1） 可以写成：n i X Y X ai i n j j ij ,,2,11 ==+∑= （1.4.2）这就是分配方程组。
它反映每个部门的总产出是如何分配与使用的。
用矩阵表示该方程组，有X Y AX =+ （1.4.3） 其中⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=nn n n n n a a a a a a a a a 212222111211A ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n Y Y Y 21Y ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n X X X 21X 分别为直接消耗系数矩阵、最终使用量矩阵和总产出量矩阵。
⒉ 按行建立的经济数学模型⑴ 模型形式由（1.4.3），容易得到：Y A I X 1)(--= （1.4.4） 这就是按行建立的投入产出基本经济数学模型。
⑵ 模型的经济意义该模型揭示了最终使用量和总产出量之间的关系。
换句话说，如果知道最终使用量，通过模型就可以求出既满足最终使用的需求、又保证经济系统各部分之间综合平衡的总产出量。
这里的最终使用量就是支出法计算的国内生产总值。
⑶ 模型的应用价值该模型虽然简单，但具有很大的应用价值。
因为在投入产出分析出现以前，还没有什么方法能够揭示最终使用量和总产出量之间的关系。
而这个关系对于经济预测、经济计划、结构分析等无疑是不可缺少的。
⑷ 模型与完全消耗系数的联系所谓最终使用量和总产出量之间的关系，实际上就是完全消耗关系。
将（1.4.4）中Y 前的系数矩阵1)(--A I 与完全消耗系数矩阵I A I B --=-1)(比较，二者仅相差一个单位阵。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
x ( I A) 1 y y ( I A) x
若 ①最终产品
y (100,200,300)T x ( 287.96,457.76,494.91) y (300,200,300)T x (557.14,570.44,582.55)
企 业 I-O 模 型
例：某企业 I-O表
企业内部消耗
产品Ⅰ 产品 Ⅱ 产品Ⅲ 1 2 3
合计
平衡 因子
最终 产品 20 10 1210
总产品
自 产 产 品 外 购 材 料
产品Ⅰ 吨 产品 Ⅱ 吨 产品Ⅲ 吨
480
140 750
620 750
10 10 5
650 770 1215
原料Ⅰ 吨
原料Ⅱ 水 电 煤 吨 吨 吨 吨
因为 A 1 max aij max aij 1
j i 1 j i 1
n
n
所以 ( I A)
1
Ak (bij ) nn bij 0
k 1
i, j
所以 y 0有 x ( I A) 1 y 0 I O为可行的 又因为 V 0 由V T P T ( I A) P T V T ( I A) 1 0 所以 I O为有利。 证毕
投入产出数学模型
三 数学模型 ：
1 投入产出表：实物型、价值型
投入—产出表
作为消耗部门 生产部门 农 工 业 业 . . . 1 2
*
最终 产品 总产出 新 创 造 价 值
农业 工业 … 服务业 1 2 … n
* 附：
劳动报酬
v1 , … , vn
x11 x21
xn1
x12 x22
xn 2
. . .
n
A (aij ) nn
ij
(列的绝对值和)
A
2
max
i
a
ij
(行的绝对值和)
1 ②矩阵性质： 2 3
A B A B (用定义证明 ) 若 A 1 lim
k
Ak 0 ( T k T
n k 1
k
)
A 1 I A可逆.注意： ( I - A )( Ak ) I Ak )
n
最终产品 总产品 y1 y2 yn
x x x
11 11
x … x x … x
12 12
1n 1n
x1 x2 xn
n1
x … x
n2
1n
1 2 n
l11
l
l
21
k1
l12 … l22 … lk2 …
l1n l2n lkn
企 业 I-O 模 型
三 数学模型: 1. x y x 或 x
lk 或
l
j 1
n
kj
Tk lk , 这里Tk 是第k种外购物料的损耗平衡 因子。 D (d kj ) k n , d kj lkj xj
Dx L 或 Dx T L
d kj : 生产单位j中产品消耗第k种外购物料的数量— 外购物料的直接消耗系 数 x ( I A) 1 y y ( I A) x L Dx
150 180 520 800 200 2200 420 8000 12000 15000 28000 140 100 440
850 1000 10620 55000 680
①建立该企业的I-O模型
②若下 个月的最终产品为
0 y 0 总产出 x ? 外购物料 L ? 1 40 0
... x1n y1 ... x2n y2
. . .
x1 x2
xn
. . .
社会纯收入 m1 , … ,mn
合计
z1 , … , zn
x1 , … , xn
服务业
n
... xnn yn
总产值
xij ：第i个部门的产品流入 (投入) 到第j个部门的数量 (价值量)
投入产出数学模型
2 基本平衡方程：
产品分配平衡方程： xi
n
x
j 1
n
ij yi
(i 1,...,n)
产值平衡方程： x j
x
i 1
ij z j
aij xij x j ：生产单位第 j种产品消耗第 i种产品的数量 (直接消耗系数 ) x Ax y 1 x ( I A ) y —— 投入产出数学模型 ( I A) x y
y ( B I ) 1 x x (B I ) y
消耗部门
农业
制造业
服务业
最终产品
总产量
例： 生产部门
农 业 制造业 服务业
15 30 20
20 10 60
30 45 /
35 115 70
100 200 150
0.15 0.10 0.20 0.85 0.10 0.20 直接消耗系数矩阵 A 0.30 0.05 0.30 I A 0.3 0.95 0.3 0.20 0.30 0.00 0 . 2 0 . 3 1. 0
企 业 I-O 模 型
分析：
640 x x T 760 视为模型中的 x 1210 1 0.632 0.208 y1 1 x ( I A) y 0 0 0.920 y2 0 0 1 y3 0.234 0.237 0.430 0 x1 1.250 0.263 L D x 3.438 0.553 6.612 x2 18 . 750 19 . 737 23 . 140 x3 0.219 0.132 0.364 974.1 1117 . 3 0 711.2 当 y 0 时, x 868.2 L 12182 .0 1400 1400 .0 62863 780.0 650 x 770 1215 20 T 10 5
2 价格—价值系统
Pj 产品j的价格 V j 单位产品j增值 显然有 : V j Pj V T PT PT A V T PT ( I A) V T x PT ( I A) x PT y 即V T x PT y 揭示了I O模型与伴随价格 价值系统之间的联系 V T x 可解释为国民经济产生 的价值 PT y 可解释为国民经济产生 的收入 V1 P 1 V 增值向量 P _ 价格向量 V P n n
n n j 1 ij i i j 1 ij
yi Ti xi
Ti 第i种物 (产) 品的损耗平衡因子
x Ax y x ( I A) 1 y y ( I A) x
2.
A (aij ) nn
aij
xij xj
x : x T
l
j 1
n
kj
投入产出数学模型
一 问题 ：
国民经济各个部门之间存在着关系，一个经济部门的生产依赖于其他 部门的产品或者半成品，如何在确定的经济环境下确定各经济部门的投入 产出水平以满足整个社会的经济需要。
U.S.A经济学家Leontief（列昂第夫）最早提出，
在 1936 发表《美国经济系统中的投入和产出的数量关系》
我国于70年代开始应用该模型编制国民经济预算 ， 1974 目的：①编制国民经济预算 ②经济结构分析等
二 模型假设:
H1: 国民经济划分为n个部门，每个部门生产一种或
一类产品
H2 : 每个生产部门的生产意味着将本部门和其它部门
的产品经过加工变成本部门的产品。在这个过程中
消耗的产品称“投入”，生产所得的最终产品 称为“产出”。对于每个部门而言，投入产出的关 系是不变的。
③ 判别定理：
若投入系数矩阵 A (aij ) (直接消耗系数矩阵) 满足
i, j aij 0 n n a 1 j (or a 1 ij ij j 1 i 1
则 I-O模型为可行的 ( 价值型 ) I-O模型为有利的 ( 实物型 ) 证明：
i )
y ( I A) x
x1 其中：x x n y1 y y n A (aij ) nn
补充： 完全消耗系数 bij 直接消耗系数 间接消耗系数 aij bik akj
k 1 n
B A BA 所以 B A( I A) 1 ( I ( I A))(I A) 1 ( I A) 1 I B ( I A) 1 这样，投入产出模型的 另一种表达形式
②若给出投入x，则可计算出最终产品y
企 业 I-O 模 型
一 问题：一个大型企业由若干个部门组成，企业与外部及企业内部
各个部门之间存在着关系，如何在确定的经济环境下确定企业与外部 的关系及企业内部各部门的投入产出水平以满足整个企业的生产需要。
二 企业I-O表:
企业内部消耗 1 2 … n
企 业 自 产 产 品 外 购 物 料 1 2
三 开放的I-O模型
1 实物型I-O模型
xi 部门i的总产量 xij 部门i提供给部门j的产品数 yi 对部门i的产品社会需求量 aij 生产一件产品 j需要消耗产品 i的件数 aij 投入系数or直接消耗系数 aij xij xj (i, j 1,...,n)