投入产出表数学模型共19页文档
投入产出模型

投入产出模型投入产出模型是指对于经济系统(这一经济系统可以是一个国家,一个地区,一个行业或一个企业的经济活动)的多部门的投入与产出进行研究,编制投入产出表,并建立其数学模型,称作投入产出模型。
这种将经济系统的投入产出关系编制成投入产出表,建立投入产出模型进行研究的方法叫做投入产出法。
投入产出法是由美国著名经济学家瓦西里·列昂节夫20世纪30年代首先提出的。
最初是由研究一国的国民经济各个产业部门间的联系发展起来的,因此被人们称作部门联系平衡法,又叫产业关联法。
利用投入产出模型对经济活动进行分析和进行经济预测,这是一种重要的经济数量分析,叫做投入产出分析。
投入产出分析的理论基础是第七章我们所介绍的一般均衡理论,主要是对一个国家或一个地区宏观经济的研究。
但随着这一方法的广泛应用,它也可以研究一个部门(行业)的经济活动,一个公司或企业的生产经营活动。
本章将在介绍投入产出模型的基础上,着重介绍投入产出模型在国民经济预测和企业经济预测方面的应用。
第一节投入产出模型的基本形式一、投入产出表所谓投入,是指产品生产所需原材料、辅助材料、燃料、动力、固定资产折旧和劳动力的投入;所谓产出,是指产品生产的总量及其分配使用的方向和数量,包括生产消费(中间产品)、生活消费、积累和净出口等。
生产过程就是投入与产出关系的客观反映,一定时期内产品的产出受投入的影响。
投入与产出的数量关系可以编制成一种矩形的表格表示,即投入产出表。
投入产出表可以按实物形态编制,也可以按价值形态编制。
按实物形态编制的投入产出表叫实物表,按价值形态编制的投入产出表叫价值表,两者基本结构形式是相同的,它们之间只差一个价格因素。
投入产出表按编制的范围不同,可以分作世界投入产出表、国家投入产出表、地区投入产出表、部门投入产出表和企业投入产出表。
这里仅以价值形态的全国表为例介绍投入产出表的结构。
假设把国民经济划分为n 个部分,用1,2,…,n 等号码表示。
4-4投入产出模型(I0)

产出 投入 农业 制造业 服务业 劳动 总投入
中间产品 农业 40 40 0 120 200 制造业 80 40 80 200 400 服务业 0 20 20 160 200
最终产品 总产品 80 300 100 20 500 200 400 200 500 1300
投入产出模型(I/O)
农业 0.2 0.1 0.0 0.15
最终产品 160 300 50 10
总产品 400 400 100 250
80
制造业 0.4 0.1 0.1 0.25
表3 直接消耗系数 服务业 0.0 0.2 0.1 0.8
投入产出模型(I/O)
2、投入产出表中的基本关系
完全消耗系数
完全消耗矩阵包含了直接消耗与全部间接消耗。
投入产出模型(I/O)
2、投入产出表中的基本关系
产出分配方程:
在投入分配表中,每一行满足以下关系:
xi xij yi
j 1
n
i 1,2,, n
(式1)
每一部门的总产出,等于该部门流向各部门作为中间消 耗用的产品(包括自身消耗)与提供给社会的最终产品之和。
投入产出模型(I/O)
等式两边消去相同项xij,则得
x
j 1 j i
n
ij
yi x ji zi
j 1 j i
n
i 1,2,, n
投入产出模型(I/O)
2、投入产出表中的基本关系
直接消耗系数 由表1可知,生产400单位的农业产品需要投入80单位农产品、 40单位制造业产品以及60单位的劳动。现在要问,如果要生产 500单位的农产品,需要各种投入量将是多少?在投入产出法中 采用了线性假设:当产出的水平变动幅度不大时,所需要的各种 投入量按比例变动。这种假设是我们能够根据一个给定的投入产 出表来计算各种产出水平时需要的投入量。 Eg:要生产500单位农产品,其投入需要量就可以将表中第1列数据 乘以1.25得到,即需要投入100单位农产品,50单位制造业产品 以及75单位的劳动。 表示第j部门生 为了计算与分析的方便,我们引入直接消耗系数aij: 产单位产品所需
投入产出模型

投入产出模型投入产出模型是指对于经济系统(这一经济系统可以是一个国家,一个地区,一个行业或一个企业的经济活动)的多部门的投入与产出进行研究,编制投入产出表,并建立其数学模型,称作投入产出模型。
这种将经济系统的投入产出关系编制成投入产出表,建立投入产出模型进行研究的方法叫做投入产出法。
投入产出法是由美国著名经济学家瓦西里·列昂节夫20 世纪30年代首先提出的。
最初是由研究一国的国民经济各个产业部门间的联系发展起来的,因此被人们称作部门联系平衡法,又叫产业关联法。
利用投入产出模型对经济活动进行分析和进行经济预测,这是一种重要的经济数量分析,叫做投入产出分析。
投入产出分析的理论基础是第七章我们所介绍的一般均衡理论,主要是对一个国家或一个地区宏观经济的研究。
但随着这一方法的广泛应用,它也可以研究一个部门(行业)的经济活动,一个公司或企业的生产经营活动。
本章将在介绍投入产出模型的基础上,着重介绍投入产出模型在国民经济预测和企业经济预测方面的应用。
第一节投入产出模型的基本形式一、投入产出表所谓投入,是指产品生产所需原材料、辅助材料、燃料、动力、固定资产折旧和劳动力的投入;所谓产出,是指产品生产的总量及其分配使用的方向和数量,包括生产消费(中间产品)、生活消费、积累和净出口等。
生产过程就是投入与产出关系的客观反映,一定时期内产品的产出受投入的影响。
投入与产出的数量关系可以编制成一种矩形的表格表示,即投入产出表。
投入产出表可以按实物形态编制,也可以按价值形态编制。
按实物形态编制的投入产出表叫实物表,按价值形态编制的投入产出表叫价值表,两者基本结构形式是相同的,它们之间只差一个价格因素。
投入产出表按编制的范围不同,可以分作世界投入产出表、国家投入产出表、地区投入产出表、部门投入产出表和企业投入产出表这里仅以价值形态的全国表为例介绍投入产出表的结构。
假设把国民经济划分为n个部分,用1,2,⋯,n 等号码表示。
4-4 投入产出数学模型

xj
zj 1 aij
i 1 n
( j 1,2,..., n)
18 上一页 下一页 返 回
第四节 投入产出数学模型
1、投入产出模型
2、直接消耗系数 3、投入产出分析
1 上一页 下一页 返 回
一、投入产出模型
设一个经济系统可以分为n个生产部门,各部门 分别用1,2,…,n 表示,部门 i 只生产一种产品 i,
并且没有联合生产,即产品 i 仅由部门 i 生产.
每一生产部门的活动可以分为两个方面:一方面, 作为消耗部门,为了完成其经济活动,需要供给它 所需要的物质,叫做投入;
y z
i 1 i j 1
n
n
j
即整个经济系统的最终产品价值等于该系统新创 造的价值,但
x
j 1
n
kj
xik (k 1,2,..., n)
i 1
n
即
yk zk (k 1,2,..., n).
10 上一页 下一页 返 回
二、直接消耗系数
为了确定经济系统各部门间在生产消耗上的数量 依存关系,我们引入直接消耗系数的概念. 定义4.1 第 j 部门生产单位价值产品直接消耗第 i
j 1
上一页 下一页
7 返 回
称为分配平衡方程组. 表4-1中左上角、左下角部分的每一列也有一个等 式,即每一个消耗部门对各部门的生产消耗加上该 部门新创造的价值等于它的总产品价值,可用方程
组
x1 x11 x21 xn1 z1 , x x x x z , 2 12 22 n2 2 xn x1n x2 n xnn zn
x1 x11 x12 x1n y1 , x x x x y , 2 21 22 2n 2 xn xn1 xn 2 xnn yn
投入产出表表式
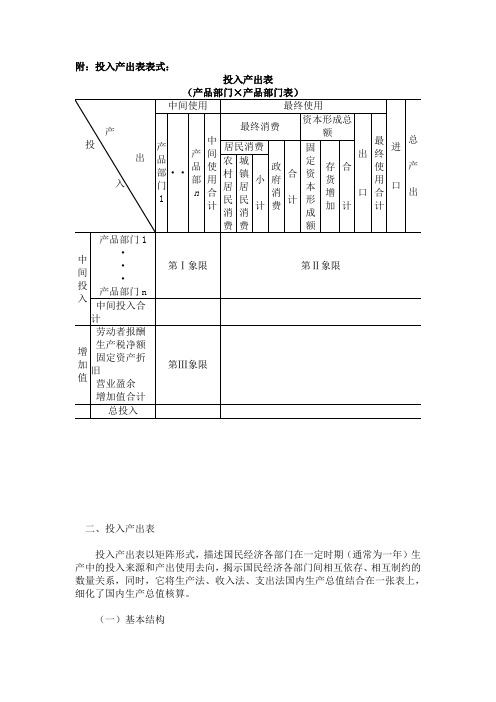
附:投入产出表表式:投入产出表二、投入产出表投入产出表以矩阵形式,描述国民经济各部门在一定时期(通常为一年)生产中的投入来源和产出使用去向,揭示国民经济各部门间相互依存、相互制约的数量关系,同时,它将生产法、收入法、支出法国内生产总值结合在一张表上,细化了国内生产总值核算。
(一)基本结构投入产出表由供给表、使用表和产品部门×产品部门表组成。
供给表又称产出表,主栏为n个产品部门,宾栏为m个产业部门,沿行方向看,反映属于某一产品部门的货物或服务是由哪些产业部门生产的,合计为属于该产品部门的货物或服务的总产出;沿列方向看,反映某一产业部门生产各产品部门货物或服务的价值量,合计为该产业部门总产出。
全部产业部门总产出等于全部产品部门总产出。
通常产品部门个数多于产业部门个数。
按生产者价格计算的总供给等于按生产者价格计算的总产出与进口之和;按购买者价格计算的总供给等于按生产者价格计算的总供给与商业和运输费用之和。
使用表又称投入表,通常由三部分组成,第一部分的主栏包括n个产品部门,宾栏包括m个产业部门。
沿行方向看,表明各产品部门生产的货物或服务提供给各产业部门使用的价值量,沿列方向看,表明各产业部门从事生产活动所消耗各产品部门生产的货物或服务的价值量;第二部分是第一部分在水平方向上的延伸,其主栏与第一部分相同,也是n个产品部门,其宾栏由最终消费、资本形成总额、出口等最终使用项组成,它反映各产品部门生产的货物或服务用于最终使用的价值量及其构成;第三部分是第一部分在垂直方向上的延伸,其主栏由劳动者报酬、生产税净额、固定资产折旧和营业盈余等增加值项组成,宾栏与第一部分的宾栏一致,也是m个产业部门,它反映各产业部门增加值的构成情况。
产品部门×产品部门表,形式上与使用表相似,也是由三部分组成,第一部分是由名称相同、排列次序相同、数目一致的n个产品部门纵横交叉而成的,其主栏为中间投入、宾栏为中间使用,它充分揭示了国民经济各产品部门之间相互依存、相互制约的技术经济联系,反映了国民经济各部门之间相互依赖、相互提供劳动对象供生产和消耗的过程。
投入产出模型

证明 由定理3知,
n
bij aij bik akj
k 1
将 n2个等式用矩阵表示为
i, j 1,2,,n
B A BA或BE A A
由定理1知(E-A)可逆,故
B AE A1
E E AE A1 E A1 E 16
例3 假设某公司三个生产部门间的报告价值型投入产出表如表4,
投入产出数学模型
1
一、投入产出数学模型(基础) 二、区域间投入产出模型基础知识
2
一、投入产出数学模型(基础)
在经济活动中分析投入多少财力、物力、人力,产出多 少社会财富是衡量经济效益高低的主要标志。
投入产出技术正是研究一个经济系统各部门间的“投入” 与“产出”关系的数学模型.
该方法最早由美国著名的经济学家瓦.列昂捷夫 (W.Leontief)提出,是目前比较成熟的经济分析方法。
4
表1:投入产出表
流量 产出 消耗部门
最终需求
投入
生1
产2
部
门
n
新 工资
创 纯收入
价 值
合计
总投入
1 2 n 消费 累计 出口
x11 x12 x1n x21 x22 x2n
xn1 xn2
xnn
v1 v2 vn m1 m2 mn z1 z2 zn
x1 x2 xn
合计
y1 y2 yn
3
(一)投入产出数学模型的概念
投入:从事一项经济活动的消耗; 产出:从事经济活动的结果; 投入产出数学模型:通过编制投入产出表,运用线性代数工具
建立数学模型,从而揭示国民经济各部门、再生产各环节之 间的内在联系,并据此进行经济分析、预测和安排预算计划。
按计量单位不同,该模型可分为价值型和实物型。 首先,必须清楚投入产出表。见下:
投入产出模型

99 . 56
2
0.00 0.00 72.09 0.00 0.00 11.06 83 . 15
3
33.07 21.66 11.39 11.06 16.67 11.06 193 . 91
4
11.11 10.09 27.77 5.57 5.59 5.49
66 . 46
5
11.11 16.29 27.77 5.57 5.59 5.49
求各部门间的完全消耗系数矩阵。
解 依次用各部门的总产值去除中间消耗栏中 各列,得到直接消耗系数矩阵为
0.6 0 0.1 6 0 1 A0 0.2 0.11100 2 1
0.1 0.5 0.6 1 5 6 4 0 1
EA110 0 8 1 1 5 4
27 5 8
EA1 1101 15 4
8 20 32
EA10.4145 0.517 0.59 0.095
0.1 0.0850.58
XEA1Y
0.63 0.09 0.09235 400 0.414505.17 0.59 0.095125300
0.1 0.0850.58210 350
即三个车间的总产值分别为400,300,350。
三、完全消耗系数
直接消耗系数只反映各部门间的直接消耗, 不能反映各部门间的间接消耗,为此我们给出 如下定义。 定义7.2.2 第j部门生产单位价值量直接和间
例1 已知某经济系统在一个生产周期内投入
产出情况如表7.2,试求直接消耗系数矩阵。
表7.2
产出 中间消耗
投入
123
中 1 100 25 30
间 投
2
80 50 30
入 3 40 25 60
净产值
投入产出数学模型

x12 x22
. . .
... ...
...
x1 n x2 n
x nn
y1 y2
. . . yn
x1 x2
. . .
社会纯收入 m1 , … ,mn 合计
z1 , … , zn
x1 , … , xn
服务业
n
xn 2
xn
总产值
xij :第i个部门的产品流入 (投入 到第 个部门的数量 (价值量 投入) 价值量) 第 个部门的产品流入 投入 到第j个部门的数量 价值量
因为 A
1
i)
= max
j 1
∑
∞
n
i =1
a ij = max
j k
∑
n
i =1
a ij < 1 i, j
所以 ( I A )
=
∑
k =1
A = ( b ij ) n × n b ij ≥ 0
所以 y ≥ 0 有 又因为
x = ( I A ) 1 y ≥ 0 I O 为可行的
T
V ≥ 0由 V
∑a P
i =1
n
ij i
(V = P AT P )
四 模型的可行和有利问题
定义: 1 定义:
①若在I-O模型中 y ≥ 0 x ≥ 0 则称模型为可行的 ( 价值型 ) 若在 模型中 ②若对 V ≥ 0 P ≥ 0 则称模型为有利的 ( 实物型 )
判别准则: 2 判别准则:
①矩阵范数: 矩阵范数:
1.3459 0.2504 0.3443 ( I A) 1 = 0.5634 1.2676 0.4930 0.4382 0.4304 1.2167
x = ( I A) 1 y y = ( I A) x
