恒成立和有解
恒成立与有解问题

学员编号: 年 级: 课 时 数:学员: 辅导科目: 数学 学科教师:授课类型恒成立与有解问题授课日期及时段 教学内容恒成立问题【知识梳理】函数的内容作为高中数学知识体系的核心,也是历年高考的一个热点.函数类问题的解决最终归结为对函数性质、函数思想的应用.恒成立问题,在高中数学中较为常见.这类问题的解决涉及到一次函数、二次函数、三角函数、指数与对数函数等函数的性质、图象,渗透着换元、化归、数形结合、函数与方程等思想方法,有利于考查学生的综合解题能力,在培养思维的灵活性、创造性等方面起到了积极的作用.〔一〕恒成立问题基本类型1:先别离参数,再求函数的最值〔或值域〕假设不等式()A x f >在区间D 上恒成立,则等价于:在区间D 上, 函数()A x f >min假设不等式()A x f <在区间D 上恒成立,则等价于:在区间D 上, 函数()A x f <max例1:〔1〕设实数,x y 满足22(1)1x y +-=,假设0x y c ++≥恒成立,则c 的取值范围是______〔2〕不等式a x x >-+-34对一切实数x 恒成立,求实数a 的取值范围_____〔3〕a a x x x 恒成立,求实数,不等式对任意实数>--+21的取值范围______方程、不等式有解问题〔存在性问题〕(一)关于方程的实数解的问题方程0)(=x f 有解的问题实际上是求函数)(x f y =零点的问题,判断方程0)(=x f 有几个解的问题实际上就是判断函数)(x f y =有几个零点的问题,这类问题通常有以下处理方法:一、直接法通过因式分解或求根公式直接求方程0)(=x f 的根,此法一般适合于含有一元二次〔三次〕的整式函数,或由此组合的分式函数。
例1函数⎩⎨⎧>+-≤-+=)0(ln 2)0(32)(2x xx x x x f 的零点个数为〔 〕 A. 0 B. 1 C. 2 D. 3二、图象法对于不能用因式分解或求根公式直接求解的方程0)()(=-x g x f ,可以先转化为方程)()(x g x f =,再在同一坐标系中分别画出函数)(x f y =和)(x g y =的图象,两个图象交点的横坐标就是原函数的零点,有几个交点原函数就有几个零点。
恒成立与有解问题

高三“恒成立与有解”问题一.关于一个函数的“恒成立与有解”问题问题1.已知函数1)(2--=mx mx x f , 若对于,R x ∈0)(<x f 恒成立,求实数m 的取值范围.变式1:已知函数1)(2--=mx mx x f ,若对于任意[]3,1∈x ,m x f -<5)(恒成立,求实数m 的取值范围.变式2:已知函数1)(2--=mx mx x f ,若存在[]3,1∈x ,m x f -<5)(成立,求实数m 的取值范围.变式3:已知函数1)(2--=mx mx x f ,若存在[]3,1∈x ,m x f -=5)(成立,求实数m 的取值范围.变式4:已知函数1)(2--=mx mx x f ,若对于任意的[]3,1∈m ,5)(<x f 恒成立,求实数x 的取值范围.变式5:若存在[]3,1∈m ,使得5)(<x f 成立,求实数x 的取值范围.二.关于两个函数的“恒成立与有解”问题问题2.已知函数=)(x f m x x +-22()R m ∈,x x x g ln 2)(+=.若对于任意的]2,1[∈x ,都有)(x f ≤)(x g ,求实数m 的取值范围.变式1:已知函数=)(x f m x x +-22()R m ∈,x x x g ln 2)(+=.若存在]2,1[∈x ,使得)(x f ≤)(x g ,求实数m 的取值范围.变式2: 已知函数=)(x f m x x +-22()R m ∈,x x x g ln 2)(+=.若对于任意的 1x ,2x ∈[1,2],都有)(1x f ≤)(2x g ,求实数m 的取值范围.变式3:已知函数=)(x f m x x +-22()R m ∈,x x x g ln 2)(+=.若对于任意的1x ∈[1,2], 存在2x ∈[1,2],使得)(1x f =)(2x g ,求实数m 的取值范围.变式4: 已知函数=)(x f m x x +-22()R m ∈,x x x g ln 2)(+=.若对于任意的1x ∈[1,2], 存在2x ∈[1,2],使得)(1x f ≤)(2x g ,求实数m 的取值范围.变式5:已知函数=)(x f m x x +-22()R m ∈,x x x g ln 2)(+=.若存在1x ,2x ∈[1,2],使得)(1x f ≤)(2x g ,求实数m 的取值范围.。
高中数学不等式恒成立与有解问题

高中数学不等式恒成立与有解问题不等式恒成立与有解问题一直是中学数学的重要内容. 它是函数、数列、不等式等内容交汇处的一个较为活跃的知识点,随着中学数学引进导数,它为我们更广泛、更深入地研究函数、不等式提供了强有力的工具. 在近几年的高考试题中,涉及不等式恒成立与有解的问题,有时在同一套试题中甚至有几道这方面的题目。
其中,特别是一些含自然对数和指数函数的不等式恒成立与有解问题,将新增内容与传统知识有机融合,用初等方法难以处理,而利用导数来解,思路明确,过程简捷流畅,淡化繁难的技巧,它不仅考查函数、不等式等有关的传统知识和方法,而且还考查极限、导数等新增内容的掌握和灵活运用. 它常与思想方法紧密结合,体现能力立意的原则,带有时代特征,突出了高考试题与时俱进的改革方向. 因此,越来越受到高考命题者的青睐. 下面通过一些典型实例作一剖析.1.不等式恒成立与有解的区别不等式恒成立和有解是有明显区别的,以下充要条件应细心思考,甄别差异,恰当使用,等价转化,切不可混为一团.(1)不等式f(x)<k 在x ∈I 时恒成立•k•x f ,)(max <⇔x ∈I. 或f(x)的上界小于或等于k ;(2)不等式f(x)<k 在x ∈I 时有解•k•x f ,)(min <⇔x ∈I. 或f(x)的下界小于k ;(3)不等式f(x)>k 在x ∈I 时恒成立•k•x f ,)(min >⇔x ∈I. 或f(x)的下界大于或等于k ;(4)不等式f(x)>k 在x ∈I 时有解•k•x f ,)(max >⇔x ∈I. 或f(x)的上界大于k ;解决不等式恒成立和有解解问题的基本策略常常是构作辅助函数,利用函数的单调性、最值(或上、下界)、图象求解;基本方法包括:分类讨论,数形结合,参数分离,变换主元等等.例1 已知两函数f(x)=8x 2+16x-k ,g(x)=2x 3+5x 2+4x ,其中k 为实数.(1)对任意x ∈[-3,3],都有f (x)≤g(x)成立,求k 的取值范围;(2)存在x ∈[-3,3],使f (x)≤g(x)成立,求k 的取值范围;(3)对任意x 1x 2∈[-3,3],都有f (x 1)≤g(x 2),求k 的取值范围.解析 (1)设h(x)=g(x)-f(x)=2x 2-3x 2-12x+k ,问题转化为x ∈[-3,3]时,h(x)≥0恒成立,故h m in (x)≥0.令h′ (x)=6x 2-6x-12=0,得x= -1或2.由h(-1)=7+k ,h(2)=-20+k ,h(-3)=k-45,h(3)=k-9,故h m in (x)=-45+k ,由k-45≥0,得k≥45.(2)据题意:存在x ∈[-3,3],使f (x)≤g(x)成立,即为:h(x)=g(x)-f(x)≥0在x ∈[-3,3]有解,故h m ax (x)≥0,由(1)知h m ax (x )=k+7,于是得k≥-7.(3)它与(1)问虽然都是不等式恒成立问题,但却有很大的区别,对任意x 1x 2∈[-3,3],都有f (x 1)≤g(x 2)成立,不等式的左右两端函数的自变量不同,x 1,x 2的取值在[-3,3]上具有任意性,因而要使原不等式恒成立的充要条件是:]3,3[,)()(min max ••x •x g x f -∈≤,由g′(x)=6x 2+10x+4=0,得x=-32或-1,易得21)3()(min -=-=g x g ,又f(x)=8(x+1)2-8-k ,]3,3[•x -∈. 故.120)3()(max k f x f -==令120-k≤-21,得k≥141.点评 本题的三个小题,表面形式非常相似,究其本质却大相径庭,应认真审题,深入思考,多加训练,准确使用其成立的充要条件2.不等式有解问题例3 设x=3是函数f(x)=(x 2+ax+b)e x -3,x ∈R 的一个极值点.(1)求a 与b 的关系(用a 表示b ),并求f(x)的的单调区间;(2)设a>0,g(x)=x e a ⎪⎭⎫ ⎝⎛+4252,若存在S 1,S 2∈[0,4],使得|f(S 1)-g(S 2)|<1成立,求a 的取值范围.解析 (1)x e a b x a x x f --+-+-='32])2([)(,由)3(f '=0得b=-2a-3. 故f(x)=(x 2+ax-2a-3)x e -3. 因为)(x f '=-[x 2+(a-2)x-3a-3] x e -3=-(x-3)(x+a+1) x e -3. 由)(x f '=0得:x 1=3,x 2==-a-1. 由于x=3是f(x)的极值点,故x 1≠x 2,即a≠-4.当a<-4时,x 1<x 2,故f(x)在(]3,•∞-上为减函数,在[3,-a-1]上为增函数,在[)+∞--,1•a 上为减函数.当a>-4时,x 1>x 2,故f(x)在(]1,--∞-a •上为减函数,在[-a-1,3]上为增函数,在[)+∞,3•上为减函数.(2)由题意,存在S 1,S 2∈[0,4],使得|f(S 1)-g(S 2)|<1成立,即不等式|f(S 1)-g(S 2)|<1在S 1,S 2∈[0,4]上有解.于是问题转化为|f(S 1)-g(S 2)|m in <1,由于两个不同自变量取值的任意性,因此首先要求出f(S 1)和g(S 2)在[0,4]上值域.因为a>0,则-a-1<0,由(1)知:f(x)在[0,3]递增;在[3,4]递减. 故f(x)在[0,4]上的值域为[min{f(0),f(4)},f(3)]=[-(2a+3)e 3,a+6],而g(x)=x e a ⎪⎭⎫ ⎝⎛+4252在[0,4]上显然为增函数,其值域⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++422425,425e a •a . 因为4252+a -(a+6)=⎪⎭⎫ ⎝⎛-21a 2≥0, 故4252+a ≥(a+6).|f(S 1)-g(S 2)|m in =4252+a -(a+6)从而解230,01)6(4252<<⎪⎩⎪⎨⎧><+-+a ••••a a a 得. 故a 的取值范围为⎪⎭⎫ ⎝⎛23,0••. 假若问题变成:“对任意的S 1,S 2∈[0,4],使得|f(S 1)-g(S 2)|<1都成立,求a 的取值范围.”则可将其转化为|f(S 1)-g(S 2)|m ax <1点评 函数、不等式、导数既是研究的对象,又是决问题的工具. 本题从函数的极值概念入手,借助导数求函数的单调区间,进而求出函数 闭区间上的值域,再处理不等式有解问题. 这里传统知识与现代方法交互作用,交相辉映,对考生灵活运用知识解决问题的能力是一个极好的考查.3.不等式恒成立问题例2 设函数f(x)=(x+1)ln(x+1),若对所有x≥0,都有f(x)≥ax 成立,求实数a 的取值范围.解析 构作辅助函数g(x)=f(x)-ax=(x+1)ln(x+1)-ax ,原问题变为g(x)≥0对所有的 x≥0恒成立,注意到g(0)=0,故问题转化为g(x)≥g(0)在x≥0时恒成立,即函数g(x)在[)∞+••,0为增函数.于是可通过求导判断g(x)的单调性,再求出使g(x)≥g(0)成立的条件.g′(x)=l n(x+1)+1-a ,由g′(x)=0,得x=e1-a -1. 当x>e 1-a -1时,g′(x)>0,g(x)为增函数.当-1<x<e 1-a -1时,g′(x)<0,g(x)为减函数.那么对所有的x≥0,都有g(x)≥g(0),其充要条件是e 1-a -1≤0,故得a 的取值范围是(]1,••∞-.假若我们没有注意到g(0)=0,那么在解g(x)≥0对所有的x≥0恒成立时,也可转化为)0(0)(min ≥≥x x g ,再以导数为工具,稍作讨论即可得解.值得一提的是,本题还有考生采用参数分离法求解:由f(x)=(x+1)ln(x+1)≥ax 对所有的x≥0恒成立可得:(1)当x=0时,a ∈R . (2)当x>0时,.)1ln()1(x x x a ++≤设g(x)=xx x )1ln()1(++,问题转化为求g(x)在开区间(0,+∞)上最小值或下界,2)1ln()(x x x x g +-=',试图通过g′(x)=0直接解得稳定点,困难重重!退一步令h(x)=x-ln(x+1),因为0,111)(>+-='•x •x x h ,故)(x h '>0,则h(x)在(0,+∞)单调递增,即h(x)>h(0)=0,从而)(x g '>0,于是g(x)在(0,+∞)单调递增,故g(x)无最小值,此时,由于g(0)无意义,g(x)的下界一时也确定不了,但运用极限知识可得:)(lim )(0x g x g x →>,然而求此极限却又超出所学知识范围,于是大部分考生被此难关扫落下马,无果而终. 事实上采用洛比达法则可得:1]1)1[ln(lim )1ln()1(lim )(lim 000=++=++=→→→x xx x x g x x x ,故x>0时,g(x)>1,因而a≤1.综合(1)(2),得a 的取值范围是:(]1,••∞-. 点评 采用参数分离法求解本题,最大的难点在于求分离后所得函数的下界.它需要考生拥有扎实的综合素质和过硬的极限、导数知识,并能灵活地运用这些工具来研究函数的性态,包括函数的单调性,极值(最值)或上下界.突出考查了函数与方程思想、有限与无限的思想.。
数学中恒成立与有解问题

数学中的恒成立与有解问题一、恒成立问题若不等式 f x A 在区间 D 上恒成立 , 则等价于在区间 D 上 f x若不等式 f xB 在区间 D 上恒成立 , 则等价于在区间D 上 f x minmaxAB常用方法1、分别变量法;2、数形结合法;3、利用函数的性质;4、改正主元等;1、由二次函数的性质求参数的取值范围例题 1. 若关于 x 的不等式 ax 22x2 0 在 R 上恒成立 , 求实数 a 的取值范围 .解题思路 :结合二次函数的图象求解解析:当 a0 时 , 不等式 2x2 0 解集不为 R , 故 a 0 不满足题意 ;当 a0 时 , 要使原不等式解集为a 0, 解得a1R , 只要4 2a 0 222综上 , 所求实数 a 的取值范围为 ( 1,)22、转变成二次函数的最值求参数的取值范围例题 2:已知二次函数满足 f (0) 1,而且 f ( x 1) f ( x) 2x ,请解决以下问题( 1) 求二次函数的解析式。
,求 m 的取值范围。
( 2) 若 f (x) 2x m 在区间 [ 1,1] 上恒成立解题思路 :先分别系数 , 再由二次函数最值确定取值范围.解析: (1)设 f ( x)ax 2 bx c(a 0) .由 f (0)1 得 c 1,故 f ( x) ax2 bx 1.∵ f ( x 1) f ( x)2x ∴ a( x1)2 b( x 1)1 (ax2 bx 1) 2x即 2axa b 2x ,因此 2a 2, a b 0 ,解得 a 1,b1 ∴ f ( x)x 2x 1(2)由 (1) 知 x 2x 12x m 在 [ 1,1]恒成立 ,即 m x 2 3x 1 在 [ 1,1] 恒成立 .令 g( x)x 23x 1 (x 3)2 5 , 则 g(x) 在 [ 1,1] 上单调递减 . 因此 g(x) 在 [ 1,1] 上的最小值为g(1)1 .2 ( 4 , 1) .m 的取值范围是因此 规律总结 :m f (x) 对所有 x R 恒成立 , 则 m [ f (x)]min ; m f ( x) 对所有 x R 恒成立 , 则 m [ f (x)]max ;注意参数的端点值能否取到需检验。
不等式有解与恒成立问题

不等式恒成立与能成立问题学号 姓名不等式恒成立指不等式对指定其间上的任意值都成立;不等式能成立指不等式在指定其间上至少有一个解(或称有解)。
下面从三个例子针对这两类问题的解决策略作比较说明。
例1.(1)若不等式()350x a -+<在[]1,1x ∈-内恒成立,求实数a 的取值范围。
(2).若不等式()350x a -+<在[]1,1x ∈-内能成立,求实数a 的取值范围。
例2.(1)若不等式22310x x m ++-≥在[]0,1x ∈内恒成立,求实数m的取值范围. (2)若不等式22310x x m ++-≥在[]0,1x ∈有解,求实数m的取值范围.例3.(1)若不等式245462x x a x -+≤+-在[]3,5x ∈内恒成立,求实数a的取值范围. (2)若不等式245462x x a x -+≤+-在[]3,5x ∈内有解,求实数a的取值范围。
总结:1.不等式恒成立与能成立(有解)解法策略比较:2.恒成立的参数范围是有解的参数范围的子集。
3. 不等式恒成立与能成立(有解)问题都是转化为最值解决。
作业:1.已知关于x 的不等式2350x a +-<。
(1)若此不等式对[]1,5x ∈上恒成立,求实数a的取值范围。
(2)若此不等式对[]1,5x ∈上能成立,求实数a的取值范围。
2.已知关于x 的不等式20x a +>。
(1)若此不等式对[]1,2x ∈上恒成立,求实数a的取值范围。
(2)若此不等式对[]1,2x ∈上能成立,求实数a的取值范围。
3. 已知关于x 的不等式2+2310x x a -+>。
(1)若此不等式对[]0,1x ∈上恒成立,求实数a的取值范围。
(2)若此不等式在[]0,1x ∈上有解,求实数a的取值范围。
4. 若不等式4213a x x +≤+-在[]0,1x ∈内有解,求实数a的取值范围。
数学中的恒成立与有解问题

数学中的恒成立与有解问题求二次函数的解析式。
若f(x) 2x m 在区间[1,1]上恒成立,求m 的取值范围解题思路:先分离系数,再由二次函数最值确定取值范围.2解析:⑴设f (x) axbx c(a 0) .由 f (0) 1得c21,故 f(x) ax bx 1••• f (x 1) f (x) 2xa(x1)2 b(x 1) 1 (ax 2 bx 1) 2x即2ax a b 2x ,所以2a 2,a b 0,解得a1,b1 二 f(x) x x 15,则g(x)在[1,1]上单调递减.所以g(x)在[1,1]上的最小值为g(1)4所以m 的取值范围是(,1).规律总结:m f(x)对一切x R 恒成立,则m [f(x)]min ;m f (x)对一切x R 恒成立,则m [f (x)]max ;注意参数的端点值能否取到需检验。
二、有解问题3、方程的有解问题例题3:题干与例题 2相同 同例题2.(2)若f(x) 2x m 在区间[1,1]上恒成立,求m 的取值范围、恒成立问题若不等式 f xA 在区间 D 上恒成立 ,则等价于在区间 D 上 f x minA 若不等式 f xB 在区间 D 上恒成立 ,则等价于在区间 D 上 f x max B 常用方法1、分离变量法;2、数形结合法;3、 利用函数的性质;4、变更主元等;1、由二次函数的性质求参数的取值范围 2例题1.若关于X 的不等式ax 2x 2 0在R 上恒成立,求实数a 的取值范围. 解题思路:结合二次函数的图象求解 解析:当a 0时,不等式2x 2 0解集不为0不满足题意;a 当a 0时,要使原不等式解集为 R ,只需…222a,解得a -0 21综上,所求实数a 的取值范围为(一,)2 2、转化为二次函数的最值求参数的取值范围 例题2 :已知二次函数满足f (0) 1,而且f (x1) f(x) 2x ,请解决下列问题2⑵由⑴知x x 12x m 在[1,1]恒成立,即m 2x 3x 1在[1,1]恒成立.令 g(x) x 2 3x 1 (x 3)22解题思路:先分离系数,再由二次函数值域确定取值范围.解析:⑴解法同例题22 2⑵由⑴知x x 1 2x m在[1,1]恒成立,即m x 3x 1在[1,1]恒成立.3 252令g(x) x2 3x 1 (x -)2-,则g(x)在[1,1]上单调递减.所以g(x)在[1,1]上的最大值为2 4g( 1) 5,最小值为g(1) 1,所以m的取值范围是1,5。
04高三一轮复习-恒成立有解问题-教师版
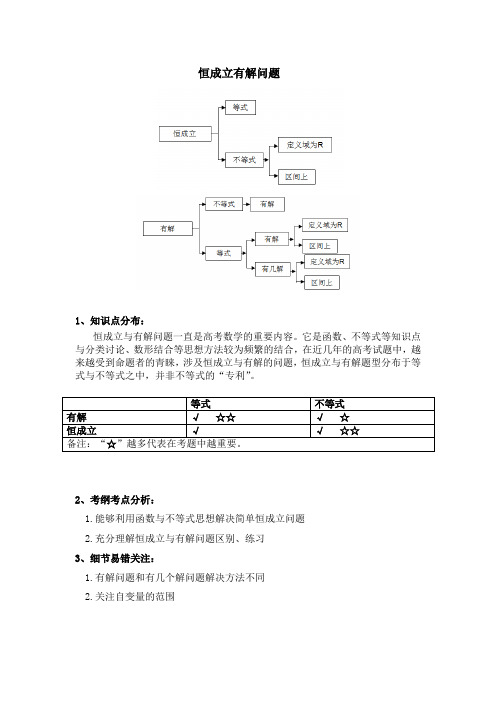
恒成立有解问题1、知识点分布:恒成立与有解问题一直是高考数学的重要内容。
它是函数、不等式等知识点与分类讨论、数形结合等思想方法较为频繁的结合,在近几年的高考试题中,越来越受到命题者的青睐,涉及恒成立与有解的问题,恒成立与有解题型分布于等式与不等式之中,并非不等式的“专利”。
等式不等式有解√☆☆√☆恒成立√√☆☆备注:“☆”越多代表在考题中越重要。
2、考纲考点分析:1.能够利用函数与不等式思想解决简单恒成立问题2.充分理解恒成立与有解问题区别、练习3、细节易错关注:1.有解问题和有几个解问题解决方法不同2.关注自变量的范围例1: 有解题型 1. 等式中“有解”题型1.等式中有解题型: 例题:① 已知方程220x x a -+=在x R ∈有解。
求实数a 的取值范围。
答案:a ≤1② 已知方程220x x a -+=在[]2,3x ∈有解。
求实数a 的取值范围。
答案:[-3,0]③ 已知不等式220x x a -+=在x R ∈有1个解。
求实数a 的取值范围。
答案:a=1④ 已知不等式220x x a -+=在[]2,3x ∈-有1个解。
求实数a 的取值范围。
答案:[-8,-3 )∪{1}⑤(2017延安中学周考)若关于x 的方程1936(5)0xx k k k +⋅-⋅+-=在[0,2]x ∈内总有两个不同的实数解,那么k 的取值范围是____________.答案:1582⎡⎫⎪⎢⎣⎭,2.不等式中有解题型:“有x ∈(a,b )型:解题方法:分离变量→数形x ∈R 型:解题方法:△与0的关系x ∈R 型:解题方法:考虑△x ∈(a,b )型:解题方法:分离变量→求最值例题:① 已知不等式220x x a -+≤在x R ∈有解。
求实数a 的取值范围。
答案:结合图像,换言之,图像在x 轴下面有,所以△≥0,a ≤1. ② 已知不等式220x x a -+≥在[]2,3x ∈有解。
求实数a 的取值范围。
浅析“有解”与“恒成立”问题

B
2
f A= 0 f A=0 ̄ f A=1
i B : 0 或l B : 1 i ‘ 】 3 : 0 ‘
因此 满 足条 件 的 数 列 有 三 个 ,它们 的 前 n 项 和分别为S =
O, S = n, S = n 。 故 其对
,
=
所以, 当a ≥4 时, 方 程x 。 一 a l x l + 4 = O 在x ∈E - 2 , 2 3 上 有解 . 点评 : 本题通过 “ 分离变量a ” 求值 域 , 方法 简单易行 , 在 以
后 的学 习 中经 常 遇 到 这 一 方 法 . 例2 : ( 2 0 1 3 重庆. 理. 1 6 ) 若 关于X 的不 等式I x 一 5 I + l x + 3 I < a 无 解。 则实数a 的 取 值 范 围 是 . 分析 : 要 使I x 一 5 1 + l x + 3 1 < a 无解 , 只要求I x 一 5 1 + l x + 3 1 < a 有 解 时 实数a 的范围 , 然 后 求a 的补集 即可. 要使 I x 一 5 1 + l x + 3 1 < a 有解, 则 至 少 有 一 个 或 一 个 以上 的X 值使 要I x 一 5 1 + l x + 3 1 < a 成 立 , 因此 只 要求 a 大 于代 数 式 I x 一 5 1 + 1 x + 3 1 的 最小 值.
a = I x l + I ≥2 、 / ・ 二= 4 ( 当且仅当I x l = 2 时取到“ = ” ) , 此时
x l V I x l
= A
厂—
x = ± 2 ∈[ 一 2 , 2 ] .
上式对一切正整数k 恒成立的充要条件是{ 2 A B = 0 , 解之得
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
恒成立和有解
一 复习上次课内容:
1. 有界二次函数的最值的求解:
2.函数x a
x x f +=)(的性质。
二 梳理知识
恒成立和有解是有明显区别的,以下充要条件应细心思考,甄别差异,恰当使用,等价转化,切不可混为一团。
(1)不等式f(x)<k 在x ∈I 时恒成立•
k •x f ,)(max <⇔x ∈I. 或f(x)的上界小于或等于k ; (2)不等式f(x)<k 在x ∈I 时有解•
k •x f ,)(min <⇔x ∈I. 或f(x)的下界小于k ; (3)不等式f(x)>k 在x ∈I 时恒成立•
k •x f ,)(min >⇔x ∈I. 或f(x)的下界大于或等于k ; (4)不等式f(x)>k 在x ∈I 时有解•
k •x f ,)(max >⇔x ∈I. 或f(x)的上界大于k ; 三 典型例题
例1. 已知对于任意的a ∈[-1,1],函数f (x )=ax 2
+(2a -4)x +3-a >0 恒成立,求x 的取值范围.
例2.已知函数])1(lg[22a x a x y +-+=的定义域为R ,求实数a 的取值范围。
例3.已知偶函数)(x f 在),0[+∞上是增函数,若)3()1(->+x f ax f 在]2,1[∈x 上恒成立,则实数a 的取值范围是 .
例4.当x ∈(1,2)时,不等式(x-1)2<log a x 恒成立,求a 的取值范围。
例5.不等式220kx k +-<有解,求k 的取值范围.
例6.已知二次函数满足1)0(=f ,而且x x f x f 2)()1(=-+。
(1)求二次函数的解析式。
(2)若m x x f +2)(>在区间[]11,-上恒成立,求m 的取值范围。
(3)若m x x f +2)(>在区间[]11,-上有解,求m 的取值范围。
四 课堂练习
1.对于满足|p|≤2的所有实数p,求使不等式x 2+px+1>2p+x 恒成立的x 的取值范围。
2.若不等式)1(122->-x m x 对满足22≤≤-m 的所有m 都成立,求x 的范围。
3.对任意]1,1[-∈a ,不等式024)4(2
>-+-+a x a x 恒成立,求x 的取值范围。
4.若不等式02)1()1(2>+-+-x m x m 的解集是R ,求m 的范围。
5.设22)(2+-=mx x x f ,当),1[+∞-∈x 时,m x f ≥)(恒成立,求实数m 的取值范围。
6.已知
a ax x x f -++=3)(2,若0)(],2,2[≥-∈x f x 恒成立,求a 的取值范围.
7.已知f (x )是定义在[-1,1]上的奇函数,且f (1)=1,若0)()(0],1,1[,>++≠+-∈n m n f m f n m n m 时
,若12)(2+-≤at t x f 对于所有的]1,1[],1,1[-∈-∈a x 恒成立,求实数t 的取值范围.
8.已知函数a x f x x 421)(++=在(]1,
∞-上有意义,求a 的取值范围。
9.设函数是定义在(,)-∞+∞上的增函数,如果不等式2(1)(2)f ax x f a --<-对于任意[0,1]x ∈恒成立,求实数a 的取值范围。
10.若不等式0log 32<-x x a 在⎪⎭⎫ ⎝⎛∈31,0x 内恒成立,求实数a 的取值范围。
11.已知关于x 的方程lg(x 2+20x)-lg(8x-6a-3)=0有唯一解,求实数a 的取值范围。
12.对于不等式21x x a -++<,存在实数x ,使此不等式成立的实数a 的集合是M ;对
于任意[05]x ∈,
,使此不等式恒成立的实数a 的集合为N ,求集合M N ,.
五 课堂小结
解决恒成立和有解解问题的基本策略常常是构作辅助函数,利用函数的单调性、最值(或上、下界)、图象求解;基本方法包括:分类讨论,数形结合,参数分离,变换主元等等。
