(完整word版)人工智能习题答案搜索推理技术.docx
人工智能课后习题答案(清华大学出版社)

3
1
8
4
7
6
5
仙1(5)
K(5)
J(7)
2
3
1
8
4
7
6
5
1
2
3
8
4
7
6
5
1
2
3
8
4
7
6
5
F
L(5)
1
2
3
7
8
4
6
5
1
2
3
8
4
7
6
5
2
3
1
8
4
7
6
5
1
2
3
8
4
7
6
5
J(5)
A
I(5)
G(5)此
2
3
1
8
4
7
6
5
1
3
7
8
4
6
5
〔2)(0(釘肯i
九•上A•一
、丄:丿
上d
0丿11丿
第3章
3.18
(1)证明:待归结的命题公式为
(此文档为Word格式,下载后可以任意编辑修改!)
试卷装订封面
学年第学期
课程名称:
课程代码
学生系别
专业
班级
任课教师
阅卷教师
考试方式
开卷□闭卷V
考试日期
考试时间
阅卷日期
装订教师
装订日期
缺卷学生姓名及原因:
无
附:课程考试试卷分析表、期末考核成绩登记表
1.1解图如下:
规则顺序定义如下:
(1) 1->2
(完整word版)人工智能课后练习题

上海大学《人工智能》网络课课后习题答案1。
1育才新工科-人工智能简介1【判断题】《人工智能》课程为理工类通选课,本课程给予学生的主要是思想而不是知识。
对1.2图灵是谁?1【单选题】图灵曾协助军方破解()的著名密码系统Enigma。
A、英国B、美国C、德国D、日本2【判断题】电影《模仿游戏》是纪念图灵诞生90周年而拍摄的电影。
X3【判断题】图灵使用博弈论的方法破解了Enigma。
对1.3为什么图灵很灵?1【单选题】1937年,图灵在发表的论文()中,首次提出图灵机的概念。
A、《左右周期性的等价》B、《论可计算数及其在判定问题中的应用》C、《可计算性与λ可定义性》D、《论高斯误差函数》2【单选题】1950年,图灵在他的论文()中,提出了关于机器思维的问题.A、《论数字计算在决断难题中的应用》B、《论可计算数及其在判定问题中的应用》C、《可计算性与λ可定义性》D、《计算和智能》3【判断题】存在一种人类认为的可计算系统与图灵计算不等价。
X4【判断题】图灵测试是指测试者与被测试者(一个人和一台机器)隔开的情况下,通过一些装置(如键盘)向被测试者随意提问。
如果测试者不能确定出被测试者是人还是机器,那么这台机器就通过了测试,并被认为具有人类智能。
对1.4为什么图灵不灵?1【单选题】以下叙述不正确的是()。
A、图灵测试混淆了智能和人类的关系B、机器智能的机制必须与人类智能相同C、机器智能可以完全在特定的领域中超越人类智能D、机器智能可以有人类智能的创造力2【单选题】在政府报告中,()的报告使用“机器智能”这个词汇。
A、中国B、英国C、德国D、美国3【多选题】机器智能可以有自己的“人格"体现主要表现在().A、模型间的对抗—智能进化的方式B、机器智能的协作-机器智能的社会组织C、机器智能是社会的实际生产者D、机器智能可以有人类智能的创造力4【判断题】图灵测试存在的潜台词是机器智能的极限可以超越人的智能,机器智能可以不与人的智能可比拟.X1.5人类智能与机器智能如何共融及未来1【单选题】以下关于未来人类智能与机器智能共融的二元世界叙述不正确的是()。
人工智能确定性推理部分参考答案

人工智能确定性推理部分参考答案(共8页)-本页仅作为预览文档封面,使用时请删除本页-确定性推理部分参考答案1 判断下列公式是否为可合一,若可合一,则求出其最一般合一。
(1) P(a, b), P(x, y)(2) P(f(x), b), P(y, z)(3) P(f(x), y), P(y, f(b))(4) P(f(y), y, x), P(x, f(a), f(b))(5) P(x, y), P(y, x)解:(1) 可合一,其最一般和一为:σ={a/x, b/y}。
(2) 可合一,其最一般和一为:σ={y/f(x), b/z}。
(3) 可合一,其最一般和一为:σ={ f(b)/y, b/x}。
(4) 不可合一。
(5) 可合一,其最一般和一为:σ={ y/x}。
2 把下列谓词公式化成子句集:(1)(∀x)(∀y)(P(x, y)∧Q(x, y))(2)(∀x)(∀y)(P(x, y)→Q(x, y))(3)(∀x)(∃y)(P(x, y)∨(Q(x, y)→R(x, y)))(4)(∀x) (∀y) (∃z)(P(x, y)→Q(x, y)∨R(x, z))解:(1) 由于(∀x)(∀y)(P(x, y)∧Q(x, y))已经是Skolem标准型,且P(x, y)∧Q(x, y)已经是合取范式,所以可直接消去全称量词、合取词,得{ P(x, y), Q(x, y)}再进行变元换名得子句集:S={ P(x, y), Q(u, v)}(2) 对谓词公式(∀x)(∀y)(P(x, y)→Q(x, y)),先消去连接词“→”得:(∀x)(∀y)(¬P(x, y)∨Q(x, y))此公式已为Skolem标准型。
再消去全称量词得子句集:S={¬P(x, y)∨Q(x, y)}(3) 对谓词公式(∀x)(∃y)(P(x, y)∨(Q(x, y)→R(x, y))),先消去连接词“→”得:(∀x)(∃y)(P(x, y)∨(¬Q(x, y)∨R(x, y)))此公式已为前束范式。
人工智能复习参考(带答案).doc

复习参考题一、填空I•构成产生式系统的基本元素有综合数据库、规则库、控制系统,控制策略按执行规则的方式分类,分为止向、逆向、双向三类。
2•归结过程中控制策略的作用是给出控制策略,以使仅对选择合适的子句间方可做归结,避免多余的、不必要的归结式出现或者说,少做些归结仍能导出空子句。
常见的控制策略有线性归结策略、支持集策略、单元归结、输入归结。
3.公式G和公式的子句集并不等值,但它们在不可满足的意义下是一致的。
4.与或图的启发式搜索算法(A0*算法)的两个过程分别是图生成过程即扩展节点和计算耗散值的过程。
5.人工智能的研究途径主要有两种不同的观点,一种观点称为符号主义,认为人类智能基木单元是符号。
另一种观点称为连接主义(仿牛主义),认为职能的基本单元是神经元。
6.集合{P(a, x, f (g(y))? P(z, f (z) ,f(u)))的mgu (最一般合一置换)为{z/a, f(x)/x, u/g(y)}o7•语义网络是对知识的有向图表示方法,一个最简单的语义网络是一个形如节点1、弧、节点2的三元组,语义网络可以描述事物间多种复杂的语义关系、常用ISA、AKO弧表示节点间具有类屈的分类关系。
语义网络下的推理是通过继承和匹配实现的。
8.当前人工智能研究的热点之一就是机器学习。
常见的机器学习方法可分为连接学习、归纳学习、分析学习和遗传算法与分类器系统等。
一个机器学习系统应有环境、知识库、学习环节和执行环节四个基本部分组成。
9•常用的知识表示法有逻辑表示法、产牛式规则表示法、语义网络表示法、框架理论表示法、过程表示法等。
10.有两个A*算法A1和A2,若A1比A2有较多的启发信息,贝9hl(n)>h2(n)oII.关于A算法与A*算法,若规定h(n)M0,并J1定义启发函数:P|c(n)=g*(n)+h*(n) 表示初始状态S。
经点n到Fl标状态Sg最优路径的费用。
其屮g*(n)为So到n的最小费用,h*(n)为到Sg的实际最小费用。
人工智能技术导论(第三版)习题.docx

三大块: 一、搜索1.什么是搜索?有哪两大类搜索方法?两者的区别是什么?2.什么是状态空间?用状态空间表示问题时,什么是问题的解?什么是最优解,最优解唯一吗?3.在状态空间的搜索过程中,Open表和Closed表的作用与区别是什么?4.广度优先搜索与深度优先搜索有何区别?什么时候使用广度?什么时候使用深度?5. 下列问题应使用什么优先策略?1.国际象棋程序2.医疗诊断程序3.寻找使机器人从A点到B点的路径规划程序4.一个决定从原料到最终产品的生产步骤地最优次序的程序5.用于判断两个命题演算表达式是否等同的程序6.分析深度和广度的优缺点。
7.什么是与树?什么是或树?什么是与/或树?什么是可解节点?什么是解树?8.何为估价函数?在估价函数中,g(n)和h(n)各起什么作用?9.移动将牌游戏:B B W W EB表示黑色将牌,W表示白色将牌,E表示空格,走法为:(1)任意一个将牌可移入邻近的空格,其代价规定为1(2)任何一个将牌可相隔…个其他的将牌跳入空格,其代价为跳过奖牌的数H加1。
游戏要达到的目标是把所有的W移到B的左边,请定义一个启发式函数h(n),并给出用这个启发式函数产生的搜索树。
10.与或树如下图所示,请分别用与或树的广度和深度搜索求出解树。
二、确定性推理(一阶谓词)1.什么是置换?什么是合一?什么是二元归结式?2.什么是子句集?如何将谓词公式转化为子句集?3.把下列谓词公式转化为子句集。
1.(Vx)(Vy)(P(x,y)A2U,y))2.(Vx)(3y)(P(x, y) v (g(x, y) T R(x, y)))4.对下列各题分别证明G是否为Fl, F2,……Fn 的逻辑结论1.F1: (Vx)(P(x) t (Vy)(Q(y) t 7(九刃))F2: (3x)(P(x) A (Vy)(/?(y) L(x, y)))G:(色)(R(x) t2.F:(V X)(P(X)A((2(«)V2O)G: (%)(P(x)人Q(x))5.设有如下一段知识张、王、李都属于高山协会,该协会的每个成员不是滑雪运动员就是登山运动员,登山运动员不喜欢雨, 而且任一个不喜欢雪的运动员不是滑雪运动员,王讨厌李所喜欢的一切东西,而喜欢张所讨厌的一切东西, 张喜欢雨和雪。
(完整word版)人工智能课后习题答案(清华大学出版社)
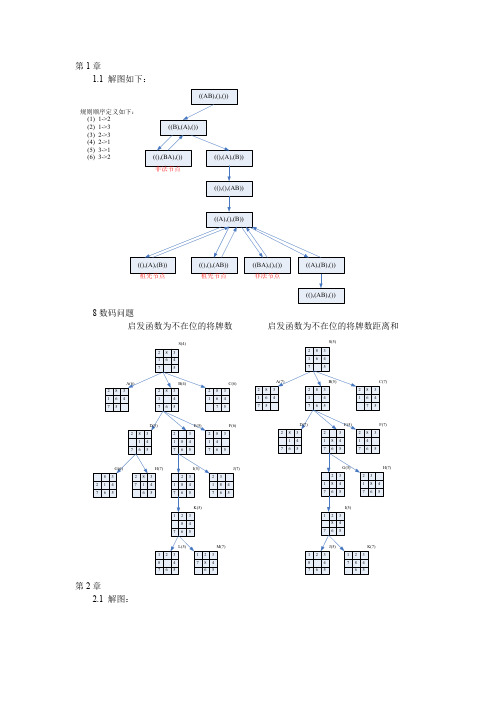
第1章 1.1 解图如下:(1) 1->2(2) 1->3(3) 2->3(6) 3->2(5) 3->1(4) 2->1 8数码问题 启发函数为不在位的将牌数启发函数为不在位的将牌数距离和S(4)S(5)第2章 2.1 解图:第3章 3.18(1)证明:待归结的命题公式为()P Q P ∧→,合取范式为:P Q P ∧∧,求取子句集为{,,}S P Q P =,对子句集中的子句进行归结可得:① P ② Q③P ④ ①③归结 由上可得原公式成立。
(2)证明:待归结的命题公式为())(()())P Q R P Q P R →→∧→→→(,合取范式为:()()P Q R P Q P R ∨∨∧∨∧∧,求取子句集为{,,,}S P Q R P Q P R =∨∨∨,对子句集中的子句进行归结可得:① P Q R ∨∨ ② P Q ∨③ P ④R ⑤ Q②③归结⑥ P R ∨ ①④归结⑦ R ③⑥归结 ⑧ ④⑦归结 由上可得原公式成立。
(3)证明:待归结的命题公式为()(())Q P Q P Q →∧→→,合取范式为:()()Q P Q P Q ∨∧∨∧,求取子句集为{,,}S Q P Q P Q =∨∨,对子句集中的子句进行归结可得:① Q P ∨ ② Q③ Q P ∨④ P ①②归结 ⑤ P ②③归结 ⑥ ④⑤归结 由上可得原公式成立。
3.19 答案(1) {/,/,/}mgu a x b y b z = (2) {(())/,()/}mgu g f v x f v u = (3) 不可合一(4) {/,/,/}=mgu b x b y b z3.23 证明R1:所有不贫穷且聪明的人都快乐:(()()())∀∧→x Poor x Smart x Happy x R2:那些看书的人是聪明的:(()())∀→x read x Smart xR3:李明能看书且不贫穷:()()∧read Li Poor LiR4:快乐的人过着激动人心的生活:(()())∀→x Happy x Exciting x 结论李明过着激动人心的生活的否定:()Exciting Li将上述谓词公式转化为子句集并进行归结如下:由R1可得子句:①()()()Poor x Smart x Happy x∨∨由R2可得子句:②()()read y Smart y∨由R3可得子句:③()read Li④()Poor Li由R4可得子句:⑤()()∨Happy z Exciting z有结论的否定可得子句:⑥()Exciting Li根据以上6条子句,归结如下:⑦()Happy Li⑤⑥Li/z⑧()()∨⑦①Li/xPoor Li Smart Li⑨()Smart Li⑧④⑩()read Li⑨②Li/y⑩③⑪第4章4.9 答案4.11 答案第5章 5.9 答案 解:把该网络看成两个部分,首先求取(1|12)P T S S ∧。
(完整word版)人工智能 第7章 参考答案

第7章机器学习参考答案7-6 设训练例子集如下表所示:序号属性分类x1x21 T T +2 T T +3 T F -4 F F +5 F T _6 F T _请用ID3算法完成其学习过程。
解:设根节点为S,尽管它包含了所有的训练例子,但却没有包含任何分类信息,因此具有最大的信息熵。
即:H(S)= - (P(+)log2 P(+) + P(-)log2 P(-))式中P(+)=3/6,P(-)=3/6分别是决策方案为“+”或“-”时的概率。
因此有H(S)= - ((3/6)log2(3/6) + (3/6)log2(3/6))=1按照ID3算法,需要选择一个能使S的期望熵为最小的一个属性对根节点进行扩展,因此我们需要先计算S关于每个属性的条件熵:H(S|x i)= ( |S T| / |S|)* H(S T) + ( |S F| / |S|)* H(S F)其中,T和F为属性x i的属性值,S T和S F分别为x i=T或x i=F时的例子集,|S|、| S T|和|S F|分别为例子集S、S T和S F的大小。
下面先计算S关于属性x1的条件熵:在本题中,当x1=T时,有:S T={1,2,3}当x1=F时,有:S F={4,5,6}其中,S T和S F中的数字均为例子集S中的各个例子的序号,且有|S|=6,| S T |=| S F |=3。
由S T可知,其决策方案为“+”或“-”的概率分别是:P ST(+)=2/3P ST (-)=1/3因此有:H(S T)= - (P ST (+)log2 P ST (+) + P ST (-)log2 P ST (- ))= - ((2/3)log2(2/3) + (1/3)log2(1/3))=0.9183再由S F可知,其决策方案为“+”或“-”的概率分别是:P SF (+)=1/3P SF (-)=2/3则有:H (S F)= - (P SF (+)log2 P SF (+) + P SF (-)log2 P SF (- ))= - ((1/3)log2(1/3)+ (2/3)log2(2/3))=0.9183将H(S T)和H (S F)代入条件熵公式,有:H(S|x1)=(|S T|/|S|)H(S T)+ (|S F|/|S|)H(S F)=(3/6)﹡0.9183 + (3/6)﹡0.9183=0.9183下面再计算S关于属性x2的条件熵:在本题中,当x2=T时,有:S T={1,2,5,6}当x2=F时,有:S F={3,4}其中,S T和S F中的数字均为例子集S中的各个例子的序号,且有|S|=6,| S T |=4,| S F |=2。
人工智能习题作业推理I习题答案

5. 非单调推理的特点是:
(D)
A 在整个推理过程中,只采用正向推理,而不用反向推理
B 在整个推理过程中,只采用反向推理,而不用正向推理
C 在整个推理过程中,已知为真的命题数目随时间而严格减少
D 在整个推理过程中,已知为真的命题数目并不一定随时间而严格增加
6. 已知规则“如果张三是 25 岁,则李四很可能是 20 岁”,请选出下列表达式
D 启用规则不一定是触发规则
16. 假设有四条规则:
R1: IF 他在家 THEN 他做饭
R2: IF 他在家且他妻子也在家 THEN 他妻子做饭
R3: IF 他在家且他儿子也在家 THEN 他做饭
R4: IF 他在家且他儿子和妻子也在家 THEN 他妻子做饭
请问:当数据库为{他在家, 他妻子在家}时,哪些规则有冲突? ( A )
论 启动方法 从一个事件启动
解答 由询问关于目标状态的一个问题而
透明程序 推理方向 优点 缺点
不能解释其推理过程 由底向上推理 算法简单,容易实现 盲目搜索,可能会求解许多
启动 可解释其推理过程 由顶向下推理 搜索目的性强,推理效率高 目标的选择具有盲目性,可能会求
与总目标无关的子目标,每 解许多假的目标;当可能的结论数
D. (AGE HIS-FARTHER 25)
8. 公式(▽x){[(彐 y)(▽z)P(x,y,z)]=>(▽u)Q(x,u)},在消去蕴涵符号后,得到:
(C)
A ~(▽x){[(彐 y)(▽z)P(x,y,z)] ∧(▽u)Q(x,u)}
B (▽x){~[(彐 y)(▽z)P(x,y,z)] ∧(▽u)Q(x,u)}
C (▽x){~[(彐 y)(▽z)P(x,y,z)] ∨(▽u)Q(x,u)}
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3-2试举例比较各种搜索方法的效率。
宽度优先搜索
(1)把起始节点放到OPEN表中(如果该起始节点为一目标节点,则求得一个解答)。
(2)如果OPEN是个空表,则没有解,失败退出;否则继续。
(3)
把第一个节点(节点n)从OPEN表移出,并把它放入
CLOSED扩展节点表中。
更换变量符号的名称,使一个变量符号不出现在一个以上的子句中
3-4如何通过消解反演求取问题的答案?
给出一个公式集S和目标公式L,通过反证或反演来求证目标公式L,其证明步骤如下:
(1)否定L,得~L;
(2)把~L添加到S中去;
(3)把新产生的集合{~L,S}化成子句集;
(4)应用消解原理,力图推导出一个表示矛盾的空子句NIL。
择一个目标节点作为节点i(要是有目标节点的话);否则,就从中选一个作为节点i。
把节点i从OPEN表移至扩展节点表CLOSED中。
(4)如果节点i为目标节点,则求得一个解。
(5)
扩展节点i。如果没有后继节点,则转向第
(2)步。
(6)
对于节点i的每个后继节点j,计算g(j)
=g(i)+c(i,j),并把所有后继节点
(2)。
等代价搜索方法以g(i)的递增顺序扩展其节点,其算法如下:
(1)把起始节点S放到未扩展节点表OPEN中。如果此起始节点为一目标节点,则求得一个解;否则令g(S) =0。
(2)如果OPEN是个空表,则没有解而失败退出。
(3)从OPEN表中选择一个节点i,使其g(i)为最小。如果有几个节点都合格,那么就要选
(4)选择OPEN表上的第一个节点,把它从OPEN表移出并放进CLOSED表中。称此节点为节点n,它是CLOSED表中节点的编号
(5)若n为一目标节点, 则有解并成功退出。 此解是追踪图G中沿着指针从n到S这条路径而得到的(指针将在第7步中设置)
(6)扩展节点n,生成不是n的祖先的那些后继节点的集合M。将M添入图G中。
3-7用有界深度优先搜索方法求解图3.34所示八数码难题。
2
8
1
2
3
1
6
3
8
4
7
5
4
7
6
5
So
Sg
图3-34八数码难题
按顺时针方向(上、右、下、左)试探,尝试移动空格,将最大深度定为5
S0(So)
2
8
1
6
3
7
5
4
S1
2
8
3
1
6
7
5
4
S2
2
8
3
1
6
4
7
(4)
扩展节点n。如果没有后继节点,则转向上述第(2)
步。
(5)
把n的所有后继节点放到OPEN表的末端 ,并提供从这些后继节点回到
n的指针。
(6)
如果n的任一个后继节点是个目标节点,则找到一个解答,成功退出;否则转向第
(2)
步。
有界深度优先搜索
(1)把起始节点S放到未扩展节点OPEN表中。如果此节点为一目标节点,则得到一个解。
j放进OPEN
表。提供回到节点i的指针。
(7)
转向第(2)步。
3-3化为子句形有哪些步骤?请结合例子说明之。
任一谓词演算公式可以化成一个子句集。其变换过程由下列九个步骤组成:
(1)消去蕴涵符号
将蕴涵符号化为析取和否定符号
(2)减少否定符号的辖域
每个否定符号最多只用到一个谓词符号上,并反复应用狄·摩根定律
(8)按某一任意方式或按某个探试值,重排OPEN表。
(9) GO LOOP。
重排OPEN表意味着,在第(6)步中,将优先扩展哪个节点,不同的排序标准对应着不同的
搜索策。
重排的原则当视具体需求而定,不同的原则对应着不同的搜索策略,如果想尽快地找到一个
解,则应当将最有可能达到目标节点的那些节点排在OPEN表的前面部分,如果想找到代
(5)只有按规则(1)~(4)求得的公式,才是合式公式等价关系有:
否定之否定
蕴含与与或形式的等价
狄.摩根定律分配律
交换律
结合律
逆否律
否定跨越量词
全称量词同与或连词
量词中的哑元
3-6用宽度优先搜索求图3.33所示迷宫的出路。
图3.33迷宫一例
第一步
SAB
第二步
BH B C
第三步
HG C F
最终路径为SABCF
前缀=全称量词串
母式=无量词公式
(6)把母式化为合取范式
反复应用分配律, 将母式写成许多合取项的合取的形式,而每一个合取项是一些谓词公式和
(或)谓词公式的否定的析取
(7)消去全称量词
消去前缀,即消去明显出现的全称量词
(8)消去连词符号(合取)
用{合取项1,合取项2}替换明显出现的合取符号
(9)更换变量名称
(2)如果OPEN为一空表,则失败退出。
(3)把第一个节点(节点n)从OPEN表移到CLOSED表。
(4)
如果节点n的深度等于最大深度,则转向(2)。
(5)
扩展节点n,产生其全部后裔,并把它们放入
OPEN表的 前头。如果没有后裔,则转向
(2)。
(6)
如果后继节点中有任一个为目标节点,则求得一个解,成功退出;否则,转向
第三章搜索推理技术
3-1什么是图搜索过程?其中,重排OPEN表意味着什么,重排的原则是什么?
图搜索的一般过程如下:
(1)建立一个搜索图G(初始只含有起始节点S),把S放到未扩展节点表中(OPEN表)中。
(2)建立一个已扩展节点表(CLOSED表),其初始为空表。
(3)LOOP:若OPEN表是空表,则失败退出。
3-5什么叫合适公式?合适公式有哪些等价关系?
合式公式的递归定义为:
(1)原子谓词公式是合式公式
(2)若A为合式公式,则A的否定也是合式公式
(3)
若A、B都是合式公式,则
A AND B, AOR B, AB, A
>B也都是合式公式
(4)
若A是合式公式,x为A
中的自由变元,则(ANY x)A
和(EXT x)A都是合式公式
(3)对变量标准化
对哑元改名以保证每个量词有其自己唯一的哑元
(4)消去存在量词
引入Skolem函数,消去存在量词
如果要消去的存在量词不在任何一个全称量词的辖域内,那么我们就用不含变量的Skolem
函数即常量。
(5)化为前束形
把所有全称量词移到公式的左边,并使每个量词的辖域包括这个量词后面公式的整个部分。前束形= (前缀) (母式)
(7)对那些未曾在G中出现过的(既未曾在OPEN表上或CLOSED表上出现过的)M成员设置一
个通向n的指针,并将它们加进OPEN表。
对已经在OPEN或CLOSED表上的每个M成员,确定是否需要更改通到n的指针方向。
对已在CLOSED表上的每个M成员,确定是否需要更改图G中通向它的每个后裔节点的
指针方向。
