建模实例(多元线性回归模型)
多元线性回归分析范例

多元线性回归分析范例多元线性回归是一种用于预测因变量和多个自变量之间关系的统计分析方法。
它假设因变量与自变量之间存在线性关系,并通过拟合一个多元线性模型来估计因变量的值。
在本文中,我们将使用一个实际的数据集来进行多元线性回归分析的范例。
数据集介绍:我们选取的数据集是一份汽车销售数据,包括了汽车的价格(因变量)和多个与汽车相关的特征(自变量),如车龄、行驶里程、汽车品牌等。
我们的目标是通过这些特征来预测汽车的价格。
数据集包括了100个样本。
数据集的构成如下:车龄(年),行驶里程(万公里),品牌,价格(万元)----------------------------------------5,10,A,153,5,B,207,12,C,10...,...,...,...建立多元线性回归模型:我们首先需要将数据集划分为自变量矩阵X和因变量向量y。
其中,自变量矩阵X包括了车龄、行驶里程和品牌等特征,因变量向量y包括了价格。
在Python中,我们可以使用NumPy和Pandas库来处理和分析数据。
我们可以使用Pandas的DataFrame来存储数据集,并使用NumPy的polyfit函数来拟合多元线性模型。
首先,我们导入所需的库并读取数据集:```pythonimport pandas as pdimport numpy as np#读取数据集data = pd.read_csv('car_sales.csv')```然后,我们将数据集划分为自变量矩阵X和因变量向量y:```python#划分自变量矩阵X和因变量向量yX = data[['车龄', '行驶里程', '品牌']]y = data['价格']```接下来,我们使用polyfit函数来拟合多元线性模型。
我们将自变量矩阵X和因变量向量y作为输入,并指定多项式的次数(线性模型的次数为1):```python#拟合多元线性模型coefficients = np.polyfit(X, y, deg=1)```最后,我们可以使用拟合得到的模型参数来预测新的样本。
建模实例(多元线性回归模型)
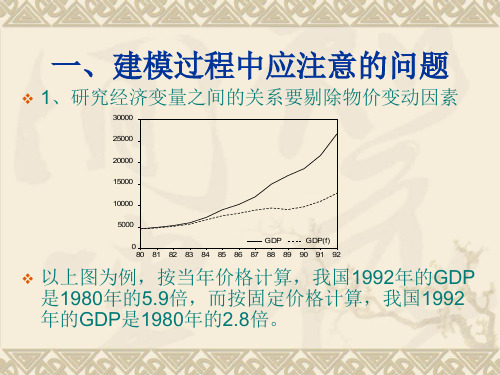
以上图为例,按当年价格计算,我国1992年的GDP 是1980年的5.9倍,而按固定价格计算,我国1992 年的GDP是80年的2.8倍。
2、依照经济理论以及对具体经济问题的深入
分析初步确定解释变量。例:关于某市的食 用油消费量,文革前常驻人口肯定是重要解 释变量。现在则不同,消费水平是重要解释 变量,因为食用油供应方式已改变。 3、当引用现成数据时,要注意数据的定义是 否与所选定的变量定义相符。例:“农业人 口”要区别是“从事农业劳动的人口”还是 相对于城市人口的“农业人口”。
t
案例2:《全国味精需求量的计量经济模型》
1.依据经济理论选择影响味精需求量变化的因素 依据经济理论初设为: 商品需求量 = f (商品价格,代用品价格,收入水 平,消费者偏好) 根据分析,针对味精需求量只考虑两个重要解释变 量,商品价格和消费者收入水平。 味精需求量 = f (商品价格,收入水平)
一建模过程中应注意的问题?1研究经济变量之间的关系要剔除物价变动因素?以上图为例按当年价格计算我国1992年的gdp是1980年的59倍而按固定价格计算我国1992年的gdp是1980年的28倍
一、建模过程中应注意的问题
1、研究经济变量之间的关系要剔除物价变动因素
30000 25000 20000 15000 10000 5000 GD P GD P(f) 0 80 81 82 83 84 85 86 87 88 89 90 91 92
4、通过散点图,相关系数,确定解释变量与
被解释变量的具体函数关系。(线性、非线 性、无关系)
5、谨慎对待离群值(outlier)。离群值可能是正常
值也可能是异常值。不能把建立模型简单化为一个纯 数学过程,目的是寻找经济规律。(欧盟对华投资和 中国从欧盟进口)
多元线性回归模型的案例讲解

多元线性回归模型的案例讲解以下是一个关于房价的案例,用多元线性回归模型来分析房价与其他变量的关系。
假设我们想研究一些城市的房价与以下变量之间的关系:房屋面积、卧室数量、厨房数量和所在区域。
我们从不同的房屋中收集了这些变量的数据,以及对应的房价。
我们希望通过构建多元线性回归模型来预测房价。
首先,我们需要收集数据。
我们找到100个不同房屋的信息,包括房屋的面积、卧室数量、厨房数量和所在区域,以及对应的房价。
接下来,我们需要进行数据处理和探索性分析。
我们可以使用统计软件,如Python的pandas库,对数据进行清洗和处理。
我们可以检查数据的缺失值、异常值和离群点,并对其进行处理。
完成数据处理后,我们可以继续进行变量的选择和模型构建。
在多元线性回归中,我们需要选择合适的自变量,并建立模型。
可以使用统计软件,如Python的statsmodels库,来进行模型的构建。
在本例中,我们使用房屋面积、卧室数量、厨房数量和所在区域作为自变量,房价作为因变量。
我们可以构建如下的多元线性回归模型:房价=β0+β1*面积+β2*卧室数量+β3*厨房数量+β4*所在区域其中,β0、β1、β2、β3和β4是回归模型的系数,表示因变量与自变量之间的关系。
我们需要对模型进行拟合和检验。
使用统计软件,在模型拟合之后,我们可以得到回归模型的系数和统计指标。
常见的指标包括回归系数的显著性、解释方差、调整R方和残差分析等。
根据回归模型的系数,我们可以解释不同自变量对因变量的影响。
例如,如果回归系数β1大于0且显著,说明房屋面积对房价有正向影响。
同理,其他自变量的系数也可以解释其对因变量的影响。
最后,我们可以使用建立的多元线性回归模型进行房价的预测。
通过输入房屋的面积、卧室数量、厨房数量和所在区域等自变量的数值,我们可以预测其对应的房价。
需要注意的是,多元线性回归模型的效果不仅取决于数据的质量,还取决于模型的选择和拟合程度。
因此,在模型选择和拟合过程中,我们需要进行多次实验和优化,以得到较好的模型。
多元线性回归--数学建模

2
ˆ ˆ Se( 1 ) Var( 1 ) ˆ ˆ Se( 2 ) Var( 2 )
i 1 i 1
i 1
• 根据最小二乘原理, 参数估计值应该是右列 方程组的解
ˆ 0 ˆ 1 ˆ 2 ˆ k
Q 0 Q 0 Q 0 Q 0
• 于是得到关于待估参数的正规方程组:
ˆ ˆ ˆ ˆ ( 0 1 X 1i 2 X 2i k X ki ) Yi ˆ ˆ ˆ ˆ ( 0 1 X 1i 2 X 2 i k X ki ) X 1i Yi X 1i ˆ ˆ ˆ ˆ ( 0 1 X 1i 2 i X 2i k X ki ) X 2i Yi X 2 i ˆ ˆ ˆ ˆ ( 0 1 X 1i 2 X 2i k X ki ) X ki Yi X ki
Yi 0 1 X 1i 2 X 2 i k X ki i
也被称为总体回归函数的随机表达形式。它 的 非随机表达式为:
E (Yi | X 1i , X 2i , X ki ) 0 1 X 1i 2 X 2i k X ki
表示:各变量X值给定时Y的平均响应。
j被称为偏回归系数,表示在其他解释变量
保持不变的情况下,X j每变化1个单位时,Y的 均值E(Y)的变化; 或者说j给出了X j的单位变化对Y均值的 “直接”或“净”(不含其他变量)影响。
多元线性回归模型案例

多元线性回归模型案例多元线性回归是统计学中常用的一种回归分析方法,它可以用来研究多个自变量与因变量之间的关系。
在实际应用中,多元线性回归模型可以帮助我们理解不同自变量对因变量的影响程度,从而进行预测和决策。
下面,我们将通过一个实际案例来介绍多元线性回归模型的应用。
案例背景:某电商公司希望了解其产品销售额与广告投入、季节因素和竞争对手销售额之间的关系,以便更好地制定营销策略和预测销售额。
数据收集:为了分析这一问题,我们收集了一段时间内的产品销售额、广告投入、季节因素和竞争对手销售额的数据。
这些数据将作为我们多元线性回归模型的输入变量。
模型建立:我们将建立一个多元线性回归模型,以产品销售额作为因变量,广告投入、季节因素和竞争对手销售额作为自变量。
通过对数据进行拟合和参数估计,我们可以得到一个多元线性回归方程,从而揭示不同自变量对产品销售额的影响。
模型分析:通过对模型的分析,我们可以得出以下结论:1. 广告投入对产品销售额有显著影响,广告投入越大,产品销售额越高。
2. 季节因素也对产品销售额有一定影响,不同季节的销售额存在差异。
3. 竞争对手销售额对产品销售额也有一定影响,竞争对手销售额越大,产品销售额越低。
模型预测:基于建立的多元线性回归模型,我们可以进行产品销售额的预测。
通过输入不同的广告投入、季节因素和竞争对手销售额,我们可以预测出相应的产品销售额,从而为公司的营销决策提供参考。
结论:通过以上分析,我们可以得出多元线性回归模型在分析产品销售额与广告投入、季节因素和竞争对手销售额之间关系时的应用。
这种模型不仅可以帮助我们理解不同因素对产品销售额的影响,还可以进行销售额的预测,为公司的决策提供支持。
总结:多元线性回归模型在实际应用中具有重要意义,它可以帮助我们理解复杂的变量关系,并进行有效的预测和决策。
在使用多元线性回归模型时,我们需要注意数据的选择和模型的建立,以确保模型的准确性和可靠性。
通过以上案例,我们对多元线性回归模型的应用有了更深入的理解,希望这对您有所帮助。
多元线性回归数学建模经典案例

多元线性回归黄冈职业技术学院数学建模协会胡敏作业:在农作物害虫发生趋势的预报研究中,所涉及的5个自变量及因变量的10组观测数据如下,试建立y对x1-x5的回归模型,指出那些变量对y有显著的线性贡献,贡献大小顺序。
x1 x2 x3 x4 x5 y9.200 2.732 1.471 0.332 1.138 1.1559.100 3.732 1.820 0.112 0.828 1.1468.600 4.882 1.872 0.383 2.131 1.84110.233 3.968 1.587 0.181 1.349 1.3565.600 3.732 1.841 0.297 1.815 0.8635.367 4.236 1.873 0.063 1.352 0.9036.133 3.146 1.987 0.280 1.647 0.1148.200 4.646 1.615 0.379 4.565 0.8988.800 4.378 1.543 0.744 2.073 1.9307.600 3.864 1.599 0.342 2.423 1.104编写程序如下:data ex;input x1-x5 y@@;cards;9.200 2.732 1.471 0.332 1.138 1.155 9.100 3.732 1.820 0.112 0.828 1.146 8.600 4.882 1.872 0.383 2.131 1.841 10.233 3.968 1.587 0.181 1.349 1.356 5.600 3.732 1.841 0.297 1.815 0.8635.367 4.236 1.873 0.063 1.352 0.9036.133 3.146 1.987 0.280 1.647 0.114 8.200 4.646 1.615 0.379 4.565 0.898 8.800 4.378 1.543 0.744 2.073 1.9307.600 3.864 1.599 0.342 2.423 1.104 ;proc reg;model y=x1 x2 x3 x4 x5/cli;run;运行结果如下:(1)回归方程显著性检验.Analysis of VarianceSum of MeanSource DF Squares S quare F Value Pr > FModel 5 2.252070.45041 11.63 0.0170Error 4 0.154970.03874Corrected Total 9 2.40704Root MSE 0.19683 R-Square 0.9356Dependent Mean 1.13100 Adj R-Sq 0.8551Coeff Var 17.40333由Analysis of Variance表可知,其F Value=11.63,Pr > F的值0.0170小于0.05,故拒绝原假设,接受备择假设,认为y与x1 x2 x3 x4 x5之间具有显著性相关系;由R-Square的值为0.9356可知该方程的拟合度高,样本观察值有93.6%的信息可以用回归方程进行解释,故拟合效果较好,认为y与x1 x2 x3 x4 x5之间具有显著性的相关关系。
多元线性回归模型案例
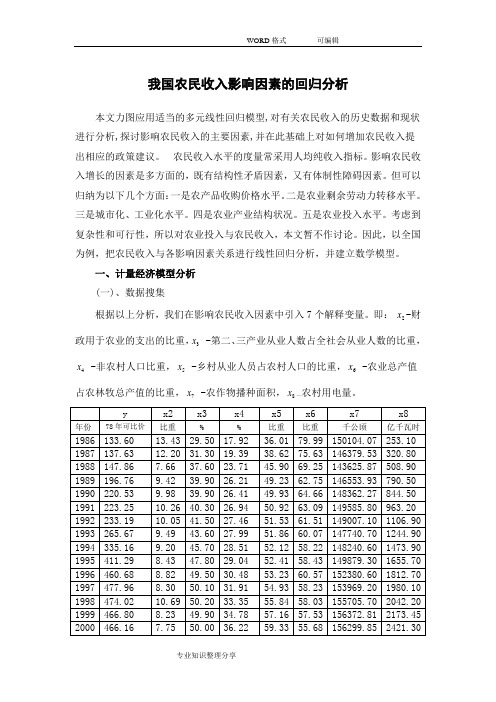
我国农民收入影响因素的回归分析本文力图应用适当的多元线性回归模型,对有关农民收入的历史数据和现状进行分析,探讨影响农民收入的主要因素,并在此基础上对如何增加农民收入提出相应的政策建议。
农民收入水平的度量常采用人均纯收入指标。
影响农民收入增长的因素是多方面的,既有结构性矛盾因素,又有体制性障碍因素。
但可以归纳为以下几个方面:一是农产品收购价格水平。
二是农业剩余劳动力转移水平。
三是城市化、工业化水平。
四是农业产业结构状况。
五是农业投入水平。
考虑到复杂性和可行性,所以对农业投入与农民收入,本文暂不作讨论。
因此,以全国为例,把农民收入与各影响因素关系进行线性回归分析,并建立数学模型。
一、计量经济模型分析 (一)、数据搜集根据以上分析,我们在影响农民收入因素中引入7个解释变量。
即: 2x -财政用于农业的支出的比重,3x -第二、三产业从业人数占全社会从业人数的比重,4x -非农村人口比重,5x -乡村从业人员占农村人口的比重,6x -农业总产值占农林牧总产值的比重,7x -农作物播种面积,8x —农村用电量。
资料来源《中国统计年鉴2006》。
(二)、计量经济学模型建立 我们设定模型为下面所示的形式:122334455667788t t Y X X X X X X X u ββββββββ=++++++++ 利用Eviews 软件进行最小二乘估计,估计结果如下表所示:Dependent Variable: Y Method: Least Squares Sample: 1986 2004 C -1102.373 375.8283 -2.933184 0.0136 X1 -6.635393 3.781349 -1.754769 0.1071 X3 18.22942 2.066617 8.820899 0.0000 X4 2.430039 8.370337 0.290316 0.7770 X5 -16.23737 5.894109 -2.754847 0.0187 X6 -2.155208 2.770834 -0.777819 0.4531 X7 0.009962 0.002328 4.278810 0.0013 R-squared0.995823 Mean dependent var 345.5232 Adjusted R-squared 0.993165 S.D. dependent var 139.7117 S.E. of regression 11.55028 Akaike info criterion 8.026857 Sum squared resid 1467.498 Schwarz criterion 8.424516 Log likelihood -68.25514 F-statistic 374.6600 表1 最小二乘估计结果回归分析报告为:()()()()()()()()()()()()()()()()23456782ˆ -1102.373-6.6354X +18.2294X +2.4300X -16.2374X -2.1552X +0.0100X +0.0634X 375.83 3.7813 2.066618.37034 5.8941 2.77080.002330.02128 -2.933 1.7558.820900.20316 2.7550.778 4.27881 2.97930.99582i Y SE t R ===---=230.99316519 1.99327374.66R Df DW F ====二、计量经济学检验(一)、多重共线性的检验及修正①、检验多重共线性(a)、直观法从“表1 最小二乘估计结果”中可以看出,虽然模型的整体拟合的很好,但是x4 x6的t统计量并不显著,所以可能存在多重共线性。
《2024年多元线性回归建模以及SPSS软件求解》范文

《多元线性回归建模以及SPSS软件求解》篇一多元线性回归建模及SPSS软件求解一、引言多元线性回归是一种常用的统计分析方法,用于探讨多个自变量与因变量之间的线性关系。
它可以帮助我们理解自变量对因变量的影响程度,预测因变量的变化趋势,以及分析自变量之间的相互作用。
本文将介绍多元线性回归建模的基本原理,并使用SPSS软件进行求解。
二、多元线性回归建模1. 模型基本形式多元线性回归模型的基本形式为:Y = β0 + β1X1 + β2X2 + … + βkXk + ε,其中Y为因变量,X1、X2、…、Xk为自变量,β0为常数项,β1、β2、…、βk为回归系数,ε为随机误差项。
2. 模型假设多元线性回归模型需要满足以下假设:自变量与因变量之间存在线性关系;自变量之间不存在多重共线性;随机误差项服从正态分布;随机误差项的方差保持不变等。
3. 模型应用多元线性回归模型广泛应用于各个领域,如经济学、医学、社会学等。
它可以帮助我们了解多个因素对某一结果的影响程度,以及因素之间的相互作用关系。
三、SPSS软件求解多元线性回归模型1. 数据准备首先,需要准备好自变量和因变量的数据。
将数据输入SPSS 软件中,并进行必要的清洗和整理。
2. 建立模型在SPSS软件中,选择“回归”菜单,然后选择“线性”选项,将自变量和因变量分别放入相应的框中。
在模型设置中,可以选择进入法、逐步回归法等方法建立模型。
3. 模型求解SPSS软件将根据设定的模型进行求解,并输出相应的统计结果。
包括回归系数、标准误、t值、P值等。
4. 结果解释根据SPSS软件输出的统计结果,可以解释自变量对因变量的影响程度以及因素之间的相互作用关系。
同时,还需要对模型进行假设检验和诊断,以确保模型的可靠性和有效性。
四、实例分析以某地区房价为例,探讨多元线性回归模型的应用。
选取该地区房价作为因变量,自变量包括该地区的房屋面积、房龄、地理位置等。
使用SPSS软件建立多元线性回归模型,并求解出各因素对房价的影响程度以及因素之间的相互作用关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、建模案例 例1中国国债发行额模型(多元回归)
首先分析中国国债发行额序列的特征。1980年国债发行 额是43.01亿元(占GDP的1%),2001年国债发行额 是4604亿元(占GDP的4.8%)。以当年价格计算,21 年间(1980-2001)增长了106倍。平均年增长率是 24.9%。
5000 DEBT 4000
若F检验结果能拒绝原假设,应进一步作t检验(检验k次。
H 0 : b1 = b 2 = ...... = b k - 1 = 0 H 1 : b j 不全为零
t检验是对单个解释变量的回归显著性的检验。若回归系 数估计值未通过t检验,则相应解释变量应从模型中剔除。 剔除该解释变量后应重新回归。按经济理论选择的变量 剔出时要慎重。
12、 残差项应非自相关(用DW检验,亦可判 断虚假回归)。否则说明了: ①仍有重要解释变量被遗漏在模型之外。 ②选用的模型形式不妥。 13、 通过对变量取对数消除异方差。 14、 避免多重共线性。 15、 解释变量应具有外生性,与误差项不相关。
16、 应具有高度概括性。若模型的各种检验及 预测能力大致相同,应选择解释变量较少的 一个。 17、 模型的结构稳定性要强,超样本特性要好。 18、 世界是变化的,应该随时间的推移及时修 改模型。
4、通过散点图,相关系数,确定解释变量与
被解释变量的具体函数关系。(线性、非线 性、无关系)
5、谨慎对待离群值(outlier)。离群值可能是正常
值也可能是异常值。不能把建立模型简单化为一个纯 数学过程,目的是寻找经济规律。(欧盟对华投资和 中国从欧盟进口)
年 INV(投资) IMPORT(进口)
9、在作F与t检验时,不要把自由度和检验水平 用错(正确查临界值表)。回归系数的t检 验是双端检验,但t检验表的定义有P(t > t) = , P(t < t) =
10、
对于多元回归模型,当解释变量的量纲 不相同时,不能在估计的回归系数之间比较 大小。若要在多元回归模型中比较解释变量 的相对重要性,应该对回归系数作变换。 11、 回归模型的估计结果应与经济理论或常 识相一致。如边际消费倾向估计结果为1.5, 则模型很难被接受。(产出对劳动力的弹性 为负值!)
6、 过原点回归模型与非过原点回归模型相比有如 下不同点。以一元线性过原点模型
Y t = b1X t +ut
7、改变变量的测量单位可能会引起回归系数值的改 变,但不会影响t值。即不会影响统计检验结果。
8、 回归模型给出估计结果后,首先应进行F检验。F检 验是对模型整体回归显著性的检验。
H 0 : b1 = b 2 = ...... = b k - 1 = 0 H 1 : b j 不全为零
其中GDPt表示年国内生产总值(百亿元),DEFt表示年财政赤字额(亿 元),REPAYt表示年还本付息额 。
DEBTt = 4.38 + 0.34GDPt +1.00DEFt + 0.88REPAY t
(0.2) (2.1) (26.6 ) (17.2) R 2 = 0.9986, DW=2.12, T =21, (1980-2000) 预测2001年的国债发行额( DEB 亿元): 2001 = 4608.71 预测误差是 DEBt = = 0.001
2.选择恰当的变量(既要考虑代表性,也要考虑可能性) 用销售量代替需求量。 用人均消费水平代替收入水平。 味精销售量 = f (销售价格,人均消费水平) 用平均价格作为销售价格的代表变量。 取不变价格的人均消费水平:消费水平都是用当年价格计 算的,应用物价指数进行修正。
味精销售量 = f (平均销售价格,不变价格的消费水平)
2、依照经济理论以及对具体经济问题的深入
分析初步确定解释变量。例:关于某市的食 用油消费量,文革前常驻人口肯定是重要解 释变量。现在则不同,消费水平是重要解释 变量,因为食用油供应方式已改变。 3、当引用现成数据时,要注意数据的定义是 否与所选定的变量定义相符。例:“农业人 口”要区别是“从事农业劳动的人口”还是 相对于城市人口的“农业人口”。
3000
84 86 88 90 92 94 96 98 00
选择3个解释变量,国内生产总值(百亿元),财政赤字额(亿元), 年还本付息额(亿元),根据散点图建立中国国债发行额(DEBTt,亿 元)模型如下:
DEBTt = b0 +b1GDPt +b2DEFt +b3REPAY t +ut
ˆ 1
yt= -65373.6 + 642.4 x2t (-10.32) (13.8) R2 = 0.95, DW = 1.5, t0.05 (9) = 2.26 问题: 1 = 6313.4,为什么检验结果是 1 b = 0? 量纲的变化对回归结果会造成影响吗?
1
3. 收集样本数据(抽样调查,引用数据) 从中国统计年鉴和有关部门收集样本数据 。 (1972-1982, T = 11。 算相关系数:
ˆt y
4. 确定模型形式并估计参数 yt=-144680.9 + 6313.4 x1t + 690.4 x2t (-3.92) (2.17) (15.32) R2 = 0.97, DW = 1.8, t0.05 (8) = 2.3 回归系数6313.4无显著性(x1t与x2t应该是负相 关,回归系数估计值却为正,可见该估计值不可 信)。剔除不显著变量x1t,再次回归,
一、建模过程中应注意的问题
1、研究经济变量之间的关系要剔除物价变动因素
30000 25000 20000 15000 10000 5000 GD P GD P(f) 0 80 81 82 83 84 85 86 87 88 89 90 91 92
以上图为例,按当年价格计算,我国1992年的GDP 是1980年的5.9倍,而按固定价格计算,我国1992 年的GDP是1980年的2.8倍。
1991 1992 1993 1994 1995 1996 1997 1998
2.562000 2.429700 6.712400 15.37600 21.31000 27.37000 41.71000 39.78000
23.47000 32.29000 63.99000 78.75000 149.1300 113.8100 106.1500 112.2000
t
案例2:《全国味精需求量的计量经济模型》
1.依据经济理论选择影响味精需求量变化的因素 依据经济理论初设为: 商品需求量 = f (商品价格,代用品价格,收入水 平,消费者偏好) 根据分析,针对味精需求量只考虑两个重要解释变 量,商品价格和消费者收入水平。 味精需求量 = f (商品价格,收入水平)
