§1二重积分概念
高等数学第九章课件.ppt

z
用若干个小平
顶柱体体积之
和近似表示曲
o
顶柱体的体积,
x
曲顶柱体的体积
n
i
V
lim 0 i1
f (i ,i ) i .
y
(i ,i )
(二) 平面薄片的质量
设有一平面薄片,占有 xoy 面上的闭区域
D ,在点( x, y)处的面密度为 ( x, y) ,假定 ( x, y)在D 上连续,平面薄片的质量为多少?
o 12 x
立体在第一卦限部分可以看 成是一个曲顶柱体,它的曲 顶为
它的底为
于是,
y
1 y 1 4x2
D
o 12 x
所求立体的体积
例2 求两个圆柱面 的立体在第一卦限部分的体积。
解 所求立体 可以看成 是一个曲 顶柱体, 它的曲顶为
它的底为
所围
它的曲顶为
它的底为 于是,立体体积为
例3 求球体 x2 y2 z2 4a2 被圆柱面 x2 y2 2ax 所截得的(含在圆柱面内的部分)立体的体积。(a 0)
第一节 二重积分的概念及其性质
一、二重积分的概念 二、二重积分的性质
一、二重积分的概念
(一) 曲顶柱体的体积
z f (x, y) D
柱体体积=底面积*高 特点:平顶. 柱体体积=? 特点:曲顶.
求曲顶柱体的体积采用 “分割、求和、取极限”的方 法,如下动画演示.
步骤如下:
先分割曲顶柱体的底,并 取典型小区域,
间的关系:
x=rcos , y=rsin ,
(1)若极点O在区域D*之外,且D*由射线=,=和两 条连续曲线r=r1(),r=r2()围成.
(2)若r1()=0,即极点O在区域D*的边界上,且D*由射 线=,=和连续曲线r=r ()围成.
二重积分的概念及性质

积分对变量的可加性
定义
如果f(x,y)在平面上是可积的,那么对于任 意的a和b,有 ∫∫Df(x,y)dσ=∫a→bf(x,y)dσ+∫∫Df(x,y)dσ, 其中D是包含在区间[a,b]内的可积区域。
应用
该性质可以用于计算二重积分,特别是当被 积函数与某个变量的关系较为简单时。
04 二重积分的物理应用
个小弧段进行积分,然后将结果相加得到总长度。
平面曲线的曲率与挠率
曲率
曲率是描述曲线弯曲程度的量,可以 通过二重积分计算出曲线的曲率。
挠率
挠率是描述曲线在垂直方向上的弯曲 程度的量,也可以通过二重积分计算 出曲线的挠率。
THANKS FOR WATCHING
感谢您的观看
积分区域的可加性
定义
如果D1和D2是平面上互不相交的可积区域,则它们分别上的二重积分之和等于它们并集上的二重积分。 即,如果D=D1∪D2,则∫∫Df(x,y)dσ=∫∫D1f(x,y)dσ+∫∫D2f(x,y)dσ。
应用
该性质可以用于简化复杂的积分区域,将复杂区域分解为简单区域进行计算。
积分对区域的可加性
转换坐标
将被积函数从直角坐标转换为极坐标形式,即$x = rhocostheta$,$y = rhosintheta$。
分层积分
将极坐标下的二重积分拆分成两个累次积分,即先对角度积分再对极径积分。
逐个计算
对每个角度范围,计算其在极径上的积分值,并求和。
得出结果
将所有角度范围的积分结果相加,得到整个极坐标区域上的二重积分值。
二重积分的概念及性质
目录
• 二重积分的定义 • 二重积分的计算方法 • 二重积分的性质和定理 • 二重积分的物理应用 • 二重积分的数学应用
二重积分概念

?
o
x
z z R2 x 2 y 2
R
y
例1. 设由锥面 解: 所求体积可以看成 是两个曲顶柱体的 体积之差.
和球面
所围成 , 请用二重积分表示的体积.
z 2
V 4 x y d
2 2 D
D
x y d
2 2
D
o x
y
直角坐标系下的面积元素 如果 f ( x , y ) 在D上可积, 可用平行坐标轴的直线来划 分区域D , 这时 记作: d xd y 则面积元素为: d 二重积分记作:
的点集是平ห้องสมุดไป่ตู้上的有界点集,即存在一矩形R ,使得P R .
设 P 是一平面有界图形, 用平行于坐标轴的某一
组直线网 T 分割这个图形 (图21-1) , 这时直线网 T
的网眼 (小闭矩形) i 可分为三类: (i) i 上的点都是 P 的内点;
y
P
(ii) i 上的点都是 P 的外点, 即
所以也有 S K (T ) . 由上述推论, P 的边界K 的面积 为零.
定理21.3 若曲线 K 为定义在 [a , b] 上的连续函数
f ( x ) 的图象, 则曲线 K 的面积为零.
推论1 参量方程 x ( t ), y ( t ) ( t ) 所表 示的光滑曲线或按段光滑曲线,其面积一定为零. 推论2 由平面光滑曲线或按段光滑曲线所围的平面 图形都是可求面积的.
曲顶柱体的体积
( i ,i )
i
f ( i , i ) i . V lim 0
i 1
为各小闭区域的直径的最大者.
2.求平面薄片的质量 有一个平面薄片, 在 xoy 平面上占有区域 D , 其面密 度为 计算该薄片的质量 M . (常数) 设D 的面积为 , 则M 若 非常数 , 仍可用 “大化小,常代变,近似和, o 求极限” 解决.
211二重积分概念-5页精选文档

第二十一章 二重积分§1 二重积分概念教学目的与要求:1.掌握二重积分的定义和性质, 二重积分的可积条件.2.了解有界闭区域上的连续函数的可积性.3.了解平面点集可求面积的充要条件.教学重点:二重积分的定义和性质.教学难点:二元函数可积条件.教学过程一、平面图形的面积(一)、内、外面积(约当,黎曼外内测度)的概念直线网T 分割平面图形P ,T 的网眼中小闭矩形i ∆的分类:(ⅰ)i ∆含的全是P 的内点,(ⅱ)i ∆含的全是P 的外点(不含P 的点),(ⅲ)i ∆内含有P 的边界点,记()T s P 为T 的第ⅰ类i ∆的面积的和.记()T S P 为T 的第ⅰ和第三类i ∆的面积的和.记P I =(){}T s P T sup ,称为P 的内面积. 记P I =(){}T S P T inf ,称为P 的外面积.定义1 若平面图形P 的内面积P I 等于它的外面积P I ,则称P 为可求面积,并称其共同值P I =P I =P I 为P 的面积(约当,黎曼测度)定理21.1 平面有界图形P 可求面积的充要条件是:对任给的0>ε,总存在直线网T ,使得()()ε<-T s T S P P . (2)证明 [必要性]设平面有界图形P 的面积为P I .由定义1,有P I =P I =P I .对任给的ε,由P I 及P I 的定义知道,分别存在直线网1T 与2T ,使得记T 为由1T 与2T 这两个直线网合并的直线网,可证得()()T s T s P P ≤1,()()T S T S P P ≥2, (3)于是由(3)可得从而得到对直线网T 有 ()()ε<-T s T S P P ,[充分性]对任给的0>ε,存在直线网T ,使得(2)式成立.但所以 ()()ε<-≤-T s T S I I P P P P ,由ε的任意性,因此P I =P I ,因而平面图形P 可求面积.推论 平面有界图形P 的面积为零的充要条件是它的外面积0=P I ,即对任给的0>ε,存在直线网T ,使得,或对任给的0>ε,平面图形P 能被有限个其面积总和小于ε的小矩形所覆盖. 定理21.2 平面有界图形P 可求面积的充要条件是:P 的边界K 的面积为零.证明 由定理21.1,P 可求面积的充要条件是:对任给的0>ε,存在直线网T ,使得()()ε<-T s T S P P .由于所以也有()ε<T S K .由上述推论,P 的边界K 的面积为零.定理21.3 若曲线K 为由定义在[]b a ,上的连续函数()x f 的图象,则曲线K 的面积为零证明 由于()x f 在闭区间[]b a ,上连续函数,从而一致连续.因而对任给的0>ε,总存在0>δ,当把区间[]b a ,分成n 个小区间[]i i x x ,1-()n i ,,1 =并且满足{}n i x x x i i i ,,1max 1 =-=∆-δ<时,可使在每个小区间[]i i x x ,1-上的振幅都成立a b i -<εω.现把曲线K 按自变量n x x x x ,,,10 =分成n 个小段,这时每一个小段都能被以i x ∆为宽,i ω为高的小矩形甩覆盖.由于这个小矩形面积的总和为 所以由定理21.1的推论即得曲线K 的面积为零.还可证明得到:由参量方程()()()βαψϕ≤≤==t t Y t x ,所表示的光滑曲线或按段光滑曲线,其面积为零.二、 二重积分的定义及其存在性背景:求某曲顶柱体的体积时,通过“分割、近似,求和、取极限”的步骤,利用求柱体的体积的方法来得到结果.一类大量的“非均匀”问题都采用类似的方法,从而归结出下面一类积分的定义.定义 设()y x f ,是定义在可求面积的有界闭区域D 上的函数,用任意曲线把D 分成n 个可求面积的小区域:,,,,21n σσσ∆∆∆ 以i σ∆表示i σ∆的面积,这些小区域构成D 的一个分割T ,以i d 表示i σ的直径,称{}i n i d T ≤≤=1max 为分割T 的细度,在每一个i σ上任取一点(i i ηξ,),作和式: ∑=∆n i i i i f 1),(σηξ,称之为函数在上属于分割的一个积分和. 定义2 设()y x f ,是定义在可求面积的有界闭区域D 上的函数,J 是一个确定的数,若对任给的正数ε,总存在某个正数δ,使对于D 的任何分割T ,当它的细度δ<T 时,属于T 的所有积分和都有则称()y x f ,在D 上可积,数J 称为函数()y x f ,在D 上的二重积分,记作其中()y x f ,称为二重积分的被积函数,y x ,称为积分变量,D 称为积分区域.几何意义:当()y x f ,0≥时,二重积分()⎰⎰D d y x f σ,在几何上表示以=z ()y x f ,为曲顶,D 为底的曲顶柱体的体积.在直角坐标系下用平行于坐标轴的直线网来划分区域D ,则面积元素为dxdy d =σ直角坐标系下可表示为: ()⎰⎰D d y x f σ,=()⎰⎰D dxdy y x f ,.可积的必要条件:()y x f ,在可求面积的区域D 上有界函数()y x f ,在可求面积的区域D 上有界时,T 是D 的一个分割,把D 分成个可求面积的小区域n σσ,,1 ,令()y x f , 关于分割T 的上和与下和:定理21.4 ()y x f ,在D 上可积的充要条件是:定理21.5 ()y x f ,在D 上可积的充要条件是:对于任给的正数ε,存在D 的某个分割T ,使得()()ε<-T s T S .定理21.6 有界闭区域D 上的连续函数必可积.定理21.7 设()y x f ,是定义在有界闭区域D 上的有界函数.若()y x f ,的不连续点都落在有限条光滑曲线上,则()y x f ,在D 上可积.证明 不失一般性,可设()y x f ,的不连续点全部落在某一条光滑曲线L上.记L 的长度为l ,于是对任给的ε>0,把L 等分成1+⎥⎦⎤⎢⎣⎡=εl n 段: 在每段i L 上取—点i P ,使段与其一端点的弧长为n l2,以i P 为中心作边长为ε的正方形i ∆,则i L ⊂i ∆,从而有n i i L 1=∆⊂记 n i i 1=∆⊂∆,则∆为一多边形.设∆的面积为W ,那么 现在把区域D 分成两部分.第一部分∆= D D 1.第二部分121D D D -=.由于()y x f ,在2D 上连续,根据定理21.6与定理21.5,存在2D 的分割2T ,使得()()ε<-22T s T S .又记()()y x f M y x ,sup ,∆∈∆=,()()y x f m y x ,inf ,∆∈∆=,以T 表示由2T 与多边形∆的边界所组成的区域D 的分割,则有其中ω是()y x f ,在D 上的振幅.由于()y x f ,在D 上有界,故ω是有限值.于是由定理21,5就证明了()y x f ,在上可积.三、二重积分的性质二重积分具有一系列与定积分完全相类似的性质,现列举如下:1. 若()y x f ,在区域D 上可积,k 为常数,则k ()y x f ,在D 上也可积,且2.若()y x f ,,()y x g ,在D 上都可积,则()y x f ,±()y x g ,在D 上也可积,且()()[]⎰⎰±D d y x g y x f σ,,=()⎰⎰D d y x f σ,±()⎰⎰D d y x g σ,.3. 若()y x f ,在1D 和2D 上都可积,且1D 与2D 无公共内点,则()y x f ,在1D 2D 也可积,且()⎰⎰21,D D d y x f σ=()⎰⎰1,D d y x f σ+()⎰⎰2,D d y x f σ.4.若()y x f ,与()y x g ,在D 上可积,且()y x f ,≤()y x g ,,()∈y x ,D ,则5.若()y x f ,在D 上可积,则函数()y x f ,在D 上也可积,且6. 若()y x f ,在D 上可积.且 m ≤()y x f ,≤M , ()∈y x , D则这里D S 是积分区域D 的面积.7.(中值定理) 若()y x f ,在有界闭区域D 上连续,则存在()∈ηξ,D ,使得 这里D S 是积分区域D 的面积.中值定理的几何意义:以D 为底,()())0,(,,≥=y x f y x f z 为曲顶的曲顶柱体体积等于一个同底的平顶柱体的体积,这个平顶柱体的高等于在()y x f ,区域D 中某点()ηξ,的函数值()ηξ,f .作业2,4,5.。
数学分析课本-习题及答案第二十一章

第十一章 重积分§1 二重积分的概念1.把重积分⎰⎰D xydxdy 作为积分和的极限,计算这个积分值,其中D=[][]1,01,0⨯,并用直线网x=n i ,y=nj (i,j=1,2,…,n-1)分割这个正方形为许多小正方形,每一小正方形取其右上顶点为其界点.2.证明:若函数f 在矩形式域上D 可积,则f 在D 上有界.3.证明定理:若f 在矩形区域D 上连续,则f 在D 上可积.4.设D 为矩形区域,试证明二重积分性质2、4和7.性质2 若f 、g 都在D 上可积,则f+g 在D 上也可积,且()⎰+D g f =⎰⎰+D D g f . 性质4 若f 、g 在D 上可积,且g f ≤,则 ⎰⎰≤D Dg f , 性质7(中值定理) 若f 为闭域D 上连续函数,则存在()D ,∈ηξ,使得()D ,f f D∆ηξ=⎰. 5.设D 0、D 1和D 2均为矩形区域,且210D D D =,∅=11D int D int , 试证二重积分性质3.性质3(区域可加性) 若210D D D =且11D int D int ∅=,则f 在D 0上可积的充要条件是f 在D 1、D 2上都可积,且⎰0D f =⎰⎰+21D D f f , 6.设f 在可求面积的区域D 上连续,证明:(1)若在D 上()0y ,x f ≥,()0y ,x f ≠则0f D>⎰; (2)若在D 内任一子区域D D ⊂'上都有⎰'=D 0f ,则在D 上()0y ,x f ≡。
.7.证明:若f 在可求面积的有界闭域D 上连续,,g 在D 上可积且不变号,则存在一点()D ,∈ηξ,使得()()⎰⎰D dxdy y ,x g y ,x f =()ηξ,f ()⎰⎰Ddxdy y ,x g .8.应用中值定理估计积分⎰⎰≤-++10y x 22ycos x cos 100dxdy 的值§2 二重积分的计算1.计算下列二重积分:(1)()⎰⎰-Ddxdy x 2y ,其中D=[][]2,15,3⨯;(2)⎰⎰D2dxdy xy ,其中(ⅰ)D=[][]3,02,0⨯,(ⅱ)D=[]3,0 []2,0⨯; (3)()⎰⎰+Ddxdy y x cos ,其中D=[]π⨯⎥⎦⎤⎢⎣⎡π,02,0; (4)⎰⎰+D dx dy x y 1x ,其中D=[][]1,01,0⨯. 2. 设f(x,y)=()()y f x f 21⋅为定义在D=[]⨯11b ,a []22b ,a 上的函数,若1f 在[]11b ,a 上可积,2f 在[]22b ,a 上可积,则f 在D 上可积,且⎰D f =⎰⎰⋅1122b a b a 21f f . 3.设f 在区域D 上连续,试将二重积分()⎰⎰Ddxdy y ,x f 化为不同顺序的累次积分:(1)D 由不等式x y ≤,a y ≤,b x ≤()b a 0≤≤所确的区域:(2)D 由不等式222a y x ≤+与a y x ≤+(a>0)所确定的区域;(3)D=(){}1,≤+y x y x .4.在下列积分中改变累次积分的顺序:(1) ()⎰⎰20x 2x dy y ,x f dx ; (2) ()⎰⎰----11x 1x 122dy y ,x f dx ; (3)()⎰⎰10x 02dy y ,x f dy +()()⎰⎰-31x 3210dy y ,x f dx .5.计算下列二重积分:(1)⎰⎰D2dxdy xy ,其中D 由抛物线y=2px 与直线x=2p (p>0)所围的区域; (2)()⎰⎰+D 22dxdy y x,其中D=(){1x 0y ,x ≤≤, y x ≤ }x 2≤; (3)⎰⎰-D x a 2dx dy (a>0),其中D 为图(20—7)中的阴影部分; (4)⎰⎰Ddxdy x ,其中D=(){}x y x y ,x 22≤+; (5)⎰⎰D dxdy xy ,其中为圆域222a y x ≤+.6.写出积分()⎰⎰ddxdy y ,x f 在极坐标变换后不同顺序的累次积分:(1)D 由不等式1y x 22≤+,x y ≤,0y ≥所确定的区域;(2)D 由不等式2222b y x a ≤+≤所确定的区域;(3)D=(){}0x ,y y x y ,x 22≥≤+.7.用极坐标计算二重积分: (1) ⎰⎰+D22dxdy y x sin ,其中D=(){222y x y ,x +≤π }24π≤; (2)()⎰⎰+Ddxdy y x ,其中D=(){}y x y x y ,x 22+≤+; (3)()⎰⎰+'D22dxdy y x f ,其中D 为圆域222R y x ≤+.8.在下列符号分中引入新变量后,试将它化为累次积分:(1) ()⎰⎰--20x 2x 1dy y ,x f dx ,其中u=x+y,v=x-y;(2) ()dxdy y ,x f D⎰⎰,其中D=(){a y x y ,x ≤+,0x ≥, }0y ≥,若x=v cos U 4, v sin U y 4=.(3)()⎰⎰dxdy y ,x f ,其中D=(){a y x y ,x ≤+,0x ≥, }0y ≥,若x+y=u,y=uv.9.求由下列曲面所围立体V 的体积:(1) v 由坐标平面及x=2,y=3,x+y+Z=4所围的角柱体;(2) v 由z=22y x +和z=x+y 围的立体; (3) v 由曲面9y 4x Z 222+=和2Z=9y 4x 22+所围的立体.11.试作适当变换,计算下列积分:(1)()()⎰⎰-+Ddxdy y x sin y x ,D=(){π≤+≤y x 0y .x }π≤-≤y x 0;(2)⎰⎰+D y x y dxdy e,D=(){1y x y ,x ≤+,0x ≥,}0y ≥.12.设f:[a,b]→R 为连续函数,应用二重积分性质证明:()≤⎥⎦⎤⎢⎣⎡⎰2b a dx x f ()()⎰-b a 2dx x f a b , 其中等号仅在f 为常量函数时成立。
第十章重积分
f (x, y)
与
xoy 面所围的
曲顶柱体的体积的代数和.
当 f ( x, y) 1,( x, y) D 时,得二重积分
问:1d =? D (D的面积)
3.可积条件
若函数 f ( x, y) 在有界闭区域 D 上连续,
则二重积分 f ( x, y) d 一定存在.
D
(不证)
二、二重积分的性质
z z f (x, y)
xO
y
DLeabharlann ( i )(i ,i )
3. 求和
n
n
V Vi f (i ,i ) . i
i 1
i 1
z z f (x, y) 4. 将 D 分得越细,
近似值
n
f (i ,i ). i
i 1
xO
y
( i ) D
就越接近于精确值 V
记 ( i )的直径为 di ,最大直径 max di
1 i n
n
lim
0i1
f (i ,i ) i
存在 ,且该极限值与
D 的分法以及点 (i ,i ) 的取法无关,
则称该极限值为函数 f (x, y) 在闭区域 D
上的二重积分,记为 f ( x, y)d ,即
D
n
f (x, y)d
D
=
lim
0
i 1
f
( i
,i
)
i
说明 按定义
n
f ( x, y) d =
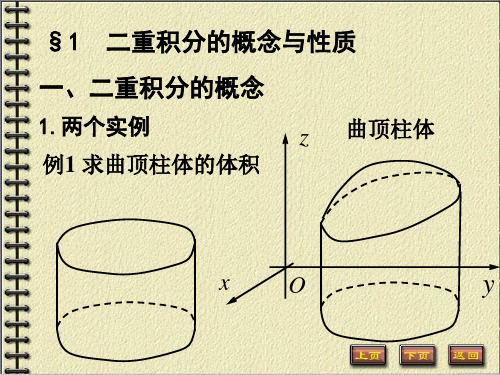
§1 二重积分的概念与性质
一、二重积分的概念
1.两个实例
z 曲顶柱体
例1 求曲顶柱体的体积
xO
y
z
z f (x, y)
二重积分的概念和计算方法

二重积分的概念和计算方法在数学中,我们经常遇到需要对二维区域上的函数进行求和或求平均的情况。
为了解决这类问题,人们引入了二重积分的概念。
本文将探讨二重积分的概念以及常见的计算方法。
一、二重积分的概念二重积分是对二维平面上的函数进行求和的操作。
它可以看作是将一个二维区域分割成无穷多个小的矩形,然后对每个小矩形内的函数值进行求和的过程。
一般来说,我们通过累次积分的方法来计算二重积分。
对于函数f(x, y)在区域D上的二重积分,可以表示为:∬f(x, y)dA其中,D表示二维区域,dA表示微元面积。
二重积分的结果是一个数值,代表了函数f(x, y)在区域D上的总体特征。
二、二重积分的计算方法1. 直角坐标系下的二重积分在直角坐标系下,计算二重积分需要先确定积分范围。
一般情况下,我们将区域D分割成一个个小矩形或小三角形,根据积分的性质进行求和。
对于给定的函数f(x, y),其在区域D上的二重积分可以表示为:∬f(x, y)dA = ∫∫f(x, y)dxdy其中,积分区域D的边界可以表示为[a, b]和[c(x), d(x)],其中c(x)和d(x)是关于x的函数。
通过确定积分的次序和边界,我们可以将二重积分转化为一重积分的形式,然后按照一重积分的计算方法进行求解。
2. 极坐标系下的二重积分在某些情况下,使用极坐标系进行二重积分的计算更为方便。
特别是当积分区域具有简单的几何形状,如圆形、扇形或圆环等情况下,使用极坐标系可以简化计算过程。
对于给定的函数f(x, y),在极坐标系下的二重积分可以表示为:∬f(x, y)dA = ∫∫f(r, θ)rdrdθ其中,积分区域D的边界可以表示为[r1(θ), r2(θ)]和[a, b],其中r1(θ)和r2(θ)是关于θ的函数。
通过确定积分的次序和边界,我们可以将二重积分转化为一重积分的形式,然后按照一重积分的计算方法进行求解。
3. 格林公式的应用在某些情况下,利用格林公式可以简化二重积分的计算。
高数课件27二重积分

二重积分的物理应用
重力场中的质点位移
重力场:地球 表面或天体表
面的重力场
质点:质量集 中于一点的物
体
位移:质点在 重力场中的位
置变化
二重积分:计 算质点在重力 场中的位移所 需的数学工具
电场中的电势计算
电势的定义:电场 中单位电荷所具有 的电势能
电势的计算公式: U=∫Edx
电势的应用:计算 电场中的电势分布 ,分析电场特性
电势的物理意义: 描述电场中电荷所 具有的能量状态
磁场中的磁通量计算
磁通量:磁场穿 过一个平面的磁 力线数量
计算公式:Φ=B·S, 其中B为磁感应强 度,S为平面面积
应用:计算磁场 中的磁通量,了 解磁场分布情况
实例:计算一个圆 形线圈中的磁通量, 了解线圈磁场的分 布情况
感谢您的耐心观看
汇报人:
极坐标系下的计算方法
极坐标系下的二重积分定义 极坐标系下的二重积分计算公式 极坐标系下的二重积分计算步骤 极坐标系下的二重积分应用实例
参数方程下的计算方法
确定参数方程的形 式
计算参数方程的偏 导数
计算参数方程的雅 可比矩阵
计算二重积分的值
二重积分的几何应用
计算平面图形的面积 计算旋转体的体积 计算曲面的面积 计算曲线的长度
二重积分的性质
积分区域的可加性
积分区域的可加性是指,如果两个积分区域的可加性是二重积分的一个重要性质,它使得我们可以将复杂的积分区域分解为若干个 简单的积分区域,从而简化计算
积分区域的可加性还可以用于证明一些积分公式,如格林公式、高斯公式等
积分区域的可加性还可以用于求解一些复杂的积分问题,如曲面积分、曲线积分等
二重积分是计算曲面面积 的一种方法
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
示的光滑曲线或按段光滑曲线,其面积一定为零.
证 由光滑曲线的定义,, 均存在且不同时为零.
由隐函数存在性定理, t0 [ , ], x(t0 ) 0 (或 y(t0 ) 0 ), 因此 U (t0; ), x x(t ) (或 y y(t) ) 在 U (t0; )上有反函数. 再由有限覆盖定理, 可把区间
前页 后页 返回
二、二重积分的定义及其存在性
二重积分的几何背景是 求曲顶柱体的体积.设
z
z f (x, y)
f ( x , y) 为定义在可求
SP (T ) sP (T ) .
但 sP (T ) I P I P SP (T ), 所以
前页 后页 返回
I P I P SP (T ) sP (T ) . 由 的任意性, 得 I P I P , 因而平面图形 P 可求面
积. 推论 平面有界图形 P 的面积为零的充要条件是它
(3)
记 T 为由 T1 与 T2 这两个直线网合并所成的直线网, 可证得
前页 后页 返回
sP (T1 ) sP (T ) , SP (T2 ) SP (T ) .
于是由(3)可得
sP (T ) IP 2 ,
SP (T ) IP 2 .
从而对直线网 T 有 SP (T ) sP (T ) . 充分性 设对任给的 0, 存在某直线网 T, 使得
前页 后页 返回
对任给的 0, 总存在直线网 T, 使得
SP (T ) sP (T ) .
(2)
证 必要性 设有界图形 P 的面积为 I P . 由定义1, 有
IP I P I P . 0 , 由 I P 及 I P 的定义知道, 分别
存在直线网 T1 与 T2 , 使得
sP (T1 ) IP 2 , SP (T2 ) IP 2 .
P ;
前页 后页 返回
(iii) i 上含有 P 的边界点. 将所有属于第(i) 类小矩形 y
(图 21-1 中紫色部分)的面
P
积加起来,记这个和数为
sP
(T
),
则有
sP
(T
)
(这
R
O
x
里 R 表示包含P 的那个矩
图 21 1
形 R 的面积); 将所有第 (i) 类与第 (ii) 类小矩形的
的 0, 存在直线网T, 使得SP (T ) sP (T ) . 由于
SK (T ) SP (T ) sP (T ),
所以也有SK (T ) .由上述推论, P 的边界K 的面积
为零. 定理21.3 若曲线 K 为定义在 [a , b] 上的连续函数 f ( x) 的图象, 则曲线 K 的面积为零.
[ti1 , ti ] 上的曲线面积为零, 从而整个曲线面积为零. 推论2 由平面光滑曲线或按段光滑曲线所围的平面 图形都是可求面积的.
前页 后页 返回
注 平面中并非所有的点集都是可求面积的. 例如
D ( x, y) x, y Q [0,1].
易知 0 I D I D 1, 因此 D 是不可求面积的.
前页 后页 返回
证 由于 f ( x) 在闭区间 [a , b]上连续, 所以它在
[a , b]上一致连续. 因而, 0, 0,当
a x0 x1 xn b ,
max{xi xi xi1 | i 1, 2, , n}
时, 可使 f ( x) 在每个小区间 [ xi1 , xi ]上的振幅都成
面积加起来(图 21-1中着色部分),记这个和数为
SP (T ), 则有 sP (T ) SP (T ).
前页 后页 返回
由确界存在定理可以推得,对于平面上所有直线网,
数集 { sP (T )}有上确界, { SP (T )} 有下确界. 记
I P sup{ sP (T )},
T
IP
inf T
{
的外面积 I P 0, 即对任给的 0, 存在直线网 T,
使得
SP (T ) , 或对任给的 0,平面图形 P 能被有限个面积总和 小于 的小矩形所覆盖.
前页 后页 返回
定理 21.2 平面有界图形 P 可求面积的充要条件是: P 的边界 K 的面积为零.
证 由定理21.1,P 可求面积的充要条件是: 对任给
P 是有界的, 是指构成这个平面图形的点集是平面
上的有界点集, 即存在一矩形 R , 使得 P R.
设 P 是一平面有界图形, 用平行于二坐标轴的某一
组直线网 T 分割这个图形 (图21-1) , 这时直线网 T
的网眼 (小闭矩形) i 可分为三类: (i) i 上的点都是 P 的内点; (ii) i 上的点都是 P 的外点, 即 i
§1 二重积分概念
二重积分是定积分在平面上的推广, 不 同之处在于: 定积分定义在区间上, 区间的 长度容易计算, 而二重积分定义在平面区 域上, 其面积的计算要复杂得多.
一、平面图形的面积 二、二重积分的定义及其存在性 三、二重积分的性质
前页 后页 返回
一、平面图形的面积
我们首先定义平面图形的面积. 所谓一个平面图形
SP
(T
)
},
显然有
0 IP IP .
(1)
通常称 I P 为 P 的内面积, I P 为 P 的外面积.
定义1 若平面图形 P 满足 I P = I P , 则称 P 为可求面
积的图形,并把共同值 IP I P I P 作为 P 的面积.
定理21.1 平面有界图形 P 可求面积的充要条件是:
立
i
b
a
.
即若把曲线
K
按
x
x0 ,
x1 ,
, xn 分
成 n 个小段, 则每一小段都能被以 xi 为宽,i 为
高的小矩形所覆盖. 由于这 n 个小矩形面积的总和
前页 后页 返回
n
i xi
i1
ba
n
xi
i1
,
因此由定理21.1 的推, y (t) ( t ) 所表
前页 后页 返回
[ , ] 分成 n 段: t0 t1 tn ,
使得在每一段 [ti1 , ti ] 上,x (t) (或 y (t)) 存在 反函数 t 1( x) (或 t 1( x) ) ,于是在 [ti1 , ti ] 上 有连续的 y ( 1( x)) (或 x ( 1( y)) ). 所以在
