六自由度运动平台正解(几何法)
并联六自由度运动平台

并联六自由度运动平台1.概述并联六自由度运动平台通过六个驱动缸(伺服缸或电动缸)的协调伸缩来实现平台在空间六个自由度的运动,即平台沿x、y、z向的平移和绕x、y、z轴的旋转运动(包括垂直、水平、横向、俯仰、侧倾和旋转六个自由度的运动),以及这些自由度的复合运动。
并联六自由度运动平台可用于机器人、飞行模拟器、车辆驾驶模拟器、新型加工机床、及卫星、导弹等飞行器、娱乐业的运动模拟(动感电影摇摆台)、多自由度振动摇摆台的精确运动仿真等。
图0-1:六自由度及其坐标系定义图我公司通过自行设计、安装调试,并开发控制软件,同时采用进口关键件对并联六自由度运动平台进行研究开发,目前已完成多套六自由度运动平台应用,典型应用有列车风档液压仿真试验台、F1国际赛车运动仿真台、汽车驾驶模拟器、飞机和飞碟运动模拟器、振动谱试验、海浪模拟试验等。
六自由度运动平台的研制,涉及机械、液压、电气、控制、计算机、传感器,空间运动数学模型、实时信号传输处理、图形显示、动态仿真等一系列高科技领域,是液压及控制技术领域的顶级产品。
2.系统组成2.1液压伺服类典型的液压式并联六自由度运动平台主要由机械系统、液压系统、控制系统硬件和控制系统软件四部分组成。
机械系统主要包括:承载平台、上下连接铰链、固定座。
液压系统主要包括:泵站系统、伺服阀、驱动器、伺服油缸和阀块管路。
控制系统硬件主要包括:实时处理器、伺服控制单元、信号调理单元、监控单元和泵站控制单元。
控制系统软件包括:实时信号处理单元、实时运算单元、伺服控制和特殊要求处理单元。
2.2 电动伺服类电动式并联六自由度运动平台则将伺服油缸用电动缸代替,而伺服阀、泵站系统及阀块管路等则相应取消,增加运动控制单元。
具有系统简洁、响应速度快等优点,是多自由度平台今后重点发展的方向。
3.主要技术参数以下参数为液压类平台典型值,具体可按用户要求设计制造。
3.1平台主要参数平台最大负载:静态≥2000KG,动态≥3000KG。
6-UCU并联六自由度平台运动及其控制系统的研究

6-UCU并联六自由度平台运动及其控制系统的研究侯骏飞;曾亿山;鲁军【摘要】以6-UCU并联六自由度平台为研究对象,介绍了六自由度平台的结构及工作原理.利用Solidworks和Ad-ams对六自由度平台进行运动学仿真和分析,得出伺服液压缸的运动特性曲线,验证6-UCU型并联六自由度平台的设计是否合理、准确,对整个六自由度平台的液压系统的安全性及可靠性具有指导作用.通过PID控制器的设计和Simulink仿真,研究了参数变化对系统性能的影响,找出了影响系统性能的关键参数,从而为改进和优化系统方案提供了合理的参考.%As the research object, the structure and the working principle of 6- UCU six degreeoffreedom parallel platform are introduced in this paper. Using Solidworks and Adams for kinematics simulation and analysis of 6-DOF platform, the motion curves of the servo cylinders are gotten to validate the accuracy of the 6-DOF aircraft platform. It plays an important role for the security and reliability of the hydraulic six degrees of freedom system. PID control-ler and simulink simulation are done to study the effect of the change of parameters on system performance. The key parameters are found out, which will affect the system performance. Thus it will provide reasonable references when the system is optimized.【期刊名称】《流体传动与控制》【年(卷),期】2015(000)005【总页数】5页(P11-15)【关键词】6-UCU;并联;六自由度;运动学仿真【作者】侯骏飞;曾亿山;鲁军【作者单位】合肥工业大学机械与汽车工程学院安徽合肥 230009;合肥工业大学机械与汽车工程学院安徽合肥 230009;合肥工业大学机械与汽车工程学院安徽合肥 230009【正文语种】中文【中图分类】TH137.9目前多数的六自由度运动平台都是双端球铰型六自由度平台,而球铰存在着承载能力差,运动间隙大等缺点。
六自由度运动方程计算
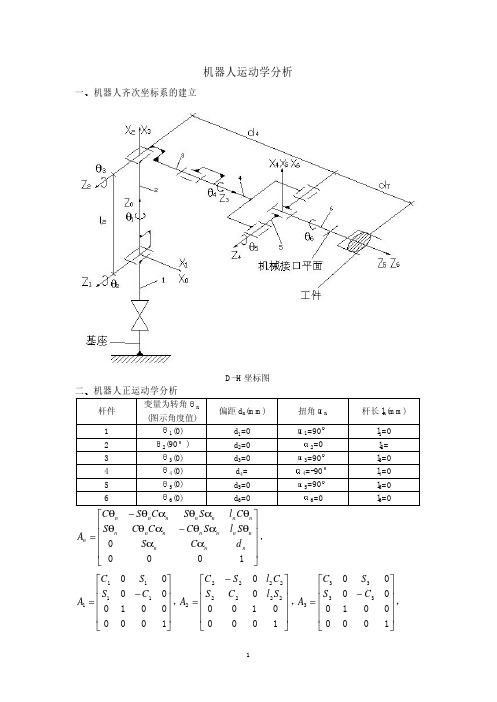
n x n 0 由正运动学方程 T6 = T6 = A1 A2 A3 A4 A5 A6 = y nz 0
2
ox oy oz 0
ax ay az 0
px py 可得 pz 1
n x = C1 [C23 (C4 C5 C 6 − S 4 S 6 ) − S 23 S 5 C 6 ] + S1 (C 4 S 6 + S 4 C5 C6 ) n y = − C1 (C4 S 6 + S 4 C5 C 6 ) + S1 [C 23 (C 4 C5 C6 − S 4 S 6 ) − S 23 S 5 C6 ] n z = C23 S 5 C 6 + S 23 (C4 C5 C 6 − S 4 S 6 ) o x = C1 [−C 23 (C 4 C5 S 6 + S 4 C6 ) + S 23 S 5 S 6 ] + S1 ( C4 C6 − S 4 C5 S 6 ) o y = − C1 (C4 C6 − S 4 C5 S 6 ) + S1 [−C 23 (C 4 C5 S 6 + S 4 C6 ) + S 23 S 5 S 6 ] o z = − C23 S 5 S 6 − S 23 (C 4 C 5 S 6 + S 4 C6 ) a x = C1 (C23 C 4 S 5 + S 23 C5 ) + S1 S 4 S 5 a y = − C1 S 4 S 5 + S1 (C 23 C4 S 5 + S 23 C5 ) a z = − C23 C5 + S 23 C4 S 5 p x = C1 (l 2 C2 + d 4 S 23 ) p y = S1 (l 2 C 2 + d 4 S 23 ) p z = l 2 S 2 − d 4 C23 三 机器人逆运动学分析 S1 0 − C1 0 S3 0 − C3 0 0 1 0 0 0 0 0 1 0 1 0 0 C2 − S −1 A2 = 2 0 0 0 0 0 1 S2 C2 0 0 0 0 1 0 S4 0 C4 0 − l2 0 0 1 0 −1 0 0 C1 0 A1−1 = S1 0 C 3 0 −1 A3 = S3 0 1 求 θ1 ox oy oz 0 ax ay az 0 px py pz 1
六自由度混联机构运动学分析

六自由度混联机构运动学分析周辉;周睿;朱景原;丁泽华;曹浩峰;曹毅【摘要】混联机构结合了并联机构和串联机构两者的优点,有效地扩大了机器人的应用范围.提出了一种由两个不同的三自由度并联机构串接而成的混联机构,对其进行运动学分析,分别求取上下两个并联模块的运动学正解方程,从而得到整个混联机构的运动学正解.通过给定机构结构参数和驱动输入参数,用一组算例求得运动学动平台位姿,并画出三维机构位姿状态图模型,更加直观地了解机构的位姿状态.然后求解其运动学逆解,按照运动学正解结果,给定机构的两组位姿,求得此时机构的驱动输入参数及各转动副的状态,对比正反解的结果,进而验证了双并联型混联机构运动学正反解模型的正确性.最后,在运动学分析的基础上,利用极限坐标搜索法,结合混联机构的运动学反解,给出机构工作空间求解的算法.给定机构的结构参数,考虑杆长约束、关节转动副约束及杆件干涉等影响条件下,利用数值搜索法在圆柱坐标系中搜索工作空间的边界.在Matlab软件中仿真得到混联机构在给定不同姿态下的位置工作空间和给定位置下的姿态工作空间.%Hybrid mechanisms combine the advantages of parallel mechanisms and series mechanisms,which can effectively expand the application field of robot.A hybrid mechanism is presented,which is combined by two different 3-DoF parallel mechanisms connected in series.Through the analysis of the kinematics of the upper and lower parallel modules,the forward kinematics solution of the whole hybrid mechanism is obtained.A set of numerical examples of position and posture of the moving platform is obtained by given the structural parameters and driving parameters,meanwhile,the 3D models of the mechanism are obtained in order to more intuitive understanding of themechanism.Then the inverse kinematics solution is solved.According to the forward kinematic results,a group of position and posture is given to obtain the driving input parameters of the mechanism and the state of each rotation pair,by compared with the result of the forward and inverse solutions,the correctness of the forward and inverse solution is verified.Finally,on the basis of kinematics analysis,using limit coordinate searching method,algorithm of working space is put out.Considering the length constraints,joint constraint and the interference of the member,the boundary of workspace is obtained in cylindrical coordinates by given the structural parameters.Position workspace respect to a variety of postures posture and orientationworkspace respect to a variety of positions are simulated in Matlab.【期刊名称】《东华大学学报(自然科学版)》【年(卷),期】2017(043)005【总页数】11页(P709-719)【关键词】混联机构;运动学;极限坐标搜索法;工作空间【作者】周辉;周睿;朱景原;丁泽华;曹浩峰;曹毅【作者单位】江南大学机械工程学院,无锡江苏214122;江苏省食品先进制造装备技术重点实验室,无锡江苏214122;江南大学机械工程学院,无锡江苏214122;江苏省食品先进制造装备技术重点实验室,无锡江苏214122;江南大学机械工程学院,无锡江苏214122;江苏省食品先进制造装备技术重点实验室,无锡江苏214122;江南大学机械工程学院,无锡江苏214122;江苏省食品先进制造装备技术重点实验室,无锡江苏214122;江南大学机械工程学院,无锡江苏214122;江苏省食品先进制造装备技术重点实验室,无锡江苏214122;江南大学机械工程学院,无锡江苏214122;上海交通大学系统控制与信息处理教育部重点实验室,上海200240;江苏省食品先进制造装备技术重点实验室,无锡江苏214122【正文语种】中文【中图分类】TH112混联机构结合了传统的串联机构和并联机构的优点,具有承载能力强、刚度大、精度高、工作空间大等优点,有效地扩大了机器人的应用领域[1-2].混联位置分析是机构分析中的基础问题,并联机构的位置分析具有反解简单、正解复杂的特点,而串联机构正好相反.两者综合起来,混联机构的位置正解和反解都变得极为复杂[3]. 目前对于混联机构整体位置正反解的研究较少.Pisla等[4]研究了一种由PARAMIS 机器人和一个新型串联定位模块组成的混联机构,并给出了数值解.Zeng等[5]研究了空间多回路运动支链的串并联型混联机构,提出了一种分析输出位移子集和空间多支链机构的自由度的方法.文献[6]提出了一种适用于重载操作的串并联锻造机械臂,根据机构的几何约束求得了封闭形式的运动学正反解.刘海涛等[7]研究了一类由二自由度球面并联机构和一条通过移动副与之串接的两转动一移动串联运动链组成的五自由度可重构混联机械手的设计和尺度综合问题.Lu等[8]提出了一种上端由3-RPS并联机构,下端由3-SPR并联机构串接起来的混联机构,分析了机构的位置正反解、速度、加速度、位置工作空间和姿态工作空间.本文提出的混联机构由两个并联机构模块串接而成,每个并联模块由两条SPS六自由度的支链,由于其具有6个自由度,故只需对另外一条支链进行运动学分析即可.然后分析了机构的位置工作空间和姿态工作空间,对该混联机构的推广应用提供一定的理论基础.混联机构由两个并联机构串联起来,每个并联机构都有3个自由度.如图1所示,位于混联机构下端部分的并联机构具有两条SPS支链和一条RPR支链,其中RPR 支链3个运动副呈R1⊥P⊥R2.上面的并联机构具有两条SPS支链和一条RRR支链,其中RR支链的3个转动副相互垂直,呈R3⊥R4⊥R5. R2和R3的转动轴线相互垂直.下面并联机构模块的驱动是位于3条分支上的3个移动副,上面并联机构模块的驱动是两个位于分支上的移动副和另一条支链上中间的R4转动副.上下两个并联机构的动平台和静平台都是正三角形.正确分析计算机构自由度是机构结构分析的基础,是机构运动学分析的重要内容.机构自由度分析为确定机构驱动数目及进行运动学分析提供了依据.位于底部的并联机构2SPS+RPR称为并联模块1,位于上端的并联机构2SPS+RRR称为并联模块2.整个混联机构总的构件数目n=15,包括一个静平台,一个动平台,一个中间平台.运动副有g= 18,包括8个球副S,5个移动副P,5个转动副R.由于SPS支链都可以绕着自身两端的球副旋转,所以每条SPS支链存在一个局部自由度[9],因此ζ=4.运用计算空间机构自由度的Grübler-Kutzbach公式得到此混联机构的自由度[10]为式中:fi为第i个运动副的自由度数;ν为并联冗余约速,这里不存在.由式(1)可知,此双并联型混联机构具有6个自由度.混联机构附坐标系的机构简图如图2所示.R2和R5转动副的轴线分别垂直于支链A3B3和B3D3,它们分别与B3B2和D3D2重合.参考坐标系OXYZ以A3为原点置于静平台上,OX轴与A3A2共线,坐标原点O与A3点重合.坐标系O1X1Y1Z1的Z1轴附于支链A3B3上,坐标原点O1与A3点重合.O2X2Y2Z2附于中间平台上,O2X2轴与B3B2共线,坐标原点O2与B3点重合.R2和R3的转动轴线相互垂直.坐标系O3X3Y3Z3和坐标系O4X4Y4Z4分别固定在支链B3D3的两端,Z3轴和Z4轴与B3D3重合,坐标原点O3和O4分别与B3和D3点重合.O5X5Y5Z5位于上部并联机构的动平台上,O5X5的轴线即转动副的R5的轴线沿着D3D2方向,坐标原点O5与D3点重合.由机构的坐标关系可得相应的变换矩阵为式中:si和ci(i=1, 2, 3, 4, 5)分别表示sin θi和cos θi,θi表示i个转动副的角度;L3=‖A3B3‖;L6=‖B3D3‖;Ai表示坐标系OiXiYiZi相对于坐标系Oi-1Xi-1Yi-1Zi-1的变化(i=1, 2, 3, 4, 5).混联机构的变换矩阵可以写为首先,给定驱动支链坐标系及驱动支链的长度为L1, L2, L3, L4, L5和驱动角度θ4,分别求取两个并联机构的运动学正解,然后再求整个混联机构的运动学正解.末端操作器的位置相对于参考坐标系可以写为式中: AM1=A1A2, AM2=A3A4A5分别为上下两个并联机构的齐次变换矩阵.AM1是描述中间动平台相对于参考坐标系的位置和姿态的齐次变换矩阵,AM2是描述上面并联机构动平台相对于坐标系O2X2Y2Z2的位置和姿态的齐次变换矩阵.5rp是动平台相对于坐标系O5X5Y5Z5的向量.本文中左上标表示向量相对的坐标系,相对于参考坐标系OXYZ则没有上标.首先定义静平台和动平台上各端点关于各自坐标原点的向量,得到下面4个向量如式(4)~(7)所示.位置向量OBi(i=1, 2)相对于参考坐标系可以写为支链长度L1和L2(L1=A1B1, L2=A2B2)可以写为式中:‖·‖表示欧式范数.将其展开得到支链一和支链二的表达式为化简式(10)和(11)可以得到下列带有未知角θ1和θ2的方程:式中: p1、 p2、 q1、 f1、 f2、 f3、 f4、 f5、 f6、 L3的表达式为由式(12)可以得到θ1的表达式.化简式(12)并用三角函数万能公式进行代换,得到θ1的解为得到θ1解之后,整理式(13)就可以写为式中: p3=f3+f5s1; p4=f4; q2=-f1s1-f2c1-f6.这样,式(15)就和式(12)保持相同的形式,使用相同的三角函数万能公式代换可求出θ2的解为由于θ1的解有两个,所以p3, q2的解有两个,所以代入求θ2的解就有4种情况.得到θ1和θ2的解,把它们代入A1和A2中,就可以得到下端并联机构变换矩阵AM1的形式.这样就得到了下端并联机构的位置正解.下端并联模块正解有4组解.上端并联机构的位置正解可以通过和下部并联机构类似的求解方法得到.首先,得到以下向量:位置向量O2Di(i=1, 2)相对于坐标系O2X2Y2Z2可以写成:支链长度L4和L5(L4=B1D1, L5=B2D2)可以写为将式(17)、(18)和式(21)所得的2O2D1、 2O2D2代入式(22)就可以得到:将式(23)和(24)展开,并化简可以得到下列两个有关于未知角θ3和θ5的方程为式中:式(25)是一个关于θ3的表达式.化简式(25)并用三角函数万能公式进行代换,得到θ3的解为得到θ3的解之后,就可以将式(26)写为式中:v3=w3+w5s3; v4=w4+w6c3; q4=-w1s3-w2c3-w7.运用三角函数万能公式,同理就可以求出θ5的解为由θ3和θ5的表达式可知,θ3和θ5都有两种表达形式,故θ3有两组解,而θ5表达式中的v3、 v4和q4都是关于θ3的表达式,将不同的θ3值代入v3、 v4和q4中,会得到两组不同的解,所以θ5也就有4组解.因此上部并联机构模块也有4种情形.此六自由度混联机构的两个并联模块都有4种位置正解,这样每个并联模块都可以通过4种方式达到指定的位置.通过上述推导得到θ1,θ2,θ3和θ5的表达式,就可以求出整个六自由度混联机构的位置正解变化矩阵A.式中:nx=c4(c1c3-c2s1s3)+s1s2s4;ny=c2s4+c4s2s3;nz=c1s2s4-c4(c3s1+c1c2s3);ox=s5(c1s3+c2c3s1)-c5[s4(c1c3-c2s1s3)-c4s1s2];oy=c5(c2c4-s2s3s4)-c3s2s5;oz=c5[s4(c3s1+c1c2s3)+c1c4s2)-s5(s1s3-c1c2c3);ax=s5[s4(c1c3-c2s1s3)-c4s1s2]+c5(c1s3+c2c3s1);ay=-s5(c2c4-s2s3s4)-c3c5s2;az=-s5[s4(c3s1+c1c2s3)+c1c4s2]-c5(s1s3-c1c2c3);px=L3s1+L6(c1s3+c2c3s1);py=-L6c3s2;pz=L3c1-L6(s1s3-c1c2c3).对于矩阵A前三行三列表示混联机构末端执行器的姿态方程,式(31)为混联机构的位置方程.根据六自由度混联机构的运动学位置正解,通过具体算例来验证此混联机构的位置正解.定义整个混联机构的结构尺寸参数并给定一组驱动构件的输入参数L1、 L2、L3、 L4、 L5、θ4,根据运动学正解求解公式,采用数值法分别求出上下两个并联机构模块的位置正解的解析解.分别得到上端和下端并联机构模块静平台和动平台正三角形三个端点相对于世界坐标系的位置坐标,给出位姿的三维位姿图,更加直观地了解机构的位置和姿态.给定整个混联机构的尺寸参数如下:上下两个并联机构模块的动平台和静平台都是正三角形,假定下面并联机构模块的静平台边长为0.5 m,动平台的边长为0.4 m.下端并联机构模块结构参数如表1所示.由于上端并联机构模块的静平台和下面并联机构模块的动平台重合,所以上面并联机构模块的静平台边长也为0.4 m,假定上面并联机构模块的动平台边长为0.3 m.上端并联机构模块的结构参数如表2所示.同时,上端并联机构模块的第三条支链长度给定L6=0.5 m.给定六自由度混联机构运动输入如表3所示.根据上述输入,就可以得到下端并联机构模块的各端点相对于参考坐标系的位置坐标数值,如表4所示.上端并联机构模块各端点相对于参考坐标系的位置坐标数值,如表5所示.上述分析得到了上下两个并联机构模块动平台和静平台各端点相对于各自静平台的位置坐标.由于上端并联机构模块的静平台与下端并联机构模块的动平台重合,故将上端并联机构模块的静平台位置与下端并联机构模块的动平台位置保持一致.只需将上端并联机构模块静平台的3个点B1、 B2、 B3的坐标值乘以变换矩阵AM1,就可以得到B1、 B2、 B3在坐标系OXYZ下的值.同理,将上述求得的D1、 D2、 D3点的坐标值也需要相应地乘以变换矩阵AM1,就可以得到如表6所示的D1、 D2、 D3点在坐标系OXYZ下的值.对于整个六自由度混联机构,可以得到机构在此输入状态下的4种位姿情况,如图3所示.这4种不同解析解情况下的位姿与表6给出的解析解对应.由图4可以直观地看出,第四组数值解支链之间不会发生干涉,符合要求.在给定双并联型混联机构上平台的位姿参数,求整个机构输入关节的运动状态是运动学位姿反解问题.求此混联机构的位置反解,就是给定上端并联机构模块动平台上末端的位姿,求解6个驱动,即5个移动副Li(i=1, 2,…, 5)和1个转动副θ4.假定给定混联机构末端执行器的位姿用变换矩阵表示为式中:px, py, pz表示固连在上端并联机构模块末端执行器上的坐标系O5X5Y5Z5原点O5的位置坐标.由式(30)可以得到混联机构的位置向量可以写成p=(px, py, pz, 1)T,式中px, py, pz的值如式(31)所示.将式(2)左右两边同时右乘可以得到:代入展开可得:令方程(34)左右两边的(1, 3),(2, 3),(3, 3)元素相等,可得:观察发现式(31)中py的表达式与式(36)表达式右边都有s2c3,所以把式(31)中py 的表达式代入式(36)可以得到:式中:q5=py/L6.同理,将式(35)代入式(31)中px,式(37)代入式(31)中pz,可以得到:将式(39)和(40)左右两边同时取平方然后相加就可以得到驱动L3的表达式为由于θ5有两组解,故L3也就有两组解.将L3的值代入式(39)和(40)中,从而可以得到θ1的表达式为式中:s1=;c1=.将式(2)两边同时左乘可以得到:由式(43)第二行第四列左右两边的元素相等可得:从而可以得到θ2的表达式为由θ2的表达式可知,θ2有两组解.将式(31)中px的表达式写成:式中:f1=c1; f2=s1c2; f3=.由式(46),并用三角函数万能公式就可以得到θ3的表达式为由θ3的表达式可知,θ3有两组解.由式(43)所得的左右两个矩阵,令第一行第一列左右两边的元素与第二行第一列左右两边的元素分别相等可得:从而就可以得到θ4的表达式为由式(38)、(42)、(45)、(47)、(50)就得到了θi(i=1, 2,…, 5) 的值,由此可以写出所有的变换矩阵Ai(i=1, 2,…, 5)的表达式.从而可以写出移动副驱动的表达式为式中:OBi=A1A22O2Bi;ODi=A5O5Di.至此,推导得到了六自由度双并联型混联机构的运动学逆解.已知运动学输出位姿,就可以求解得到机构5个移动副输入L1、 L2、 L3、 L4、 L5和1个转动副输入θ4的解.由于θ5、θ2、θ3都有两组解,所以此混联机构具有8组解.根据双并联型混联机构的位姿逆解的分析,给定混联机构结构参数,然后给定动平台的位置与姿态参数.选取与之前正解算例相同的结构参数,并且以混联机构位置正解算例中得到的数值解作为反解的输入,从而实现双并联型混联机构位置正反解模型的相互验证.给定混联机构的结构参数如表1和表2所示.由位置正解分析的三维模型位姿图3可知,位置正解的第四组数值解支链之间不会发生干涉,符合要求.所以取i=4时的结果,此双并联型混联机构的位姿变换矩阵为将此时的位姿状态作为输入,代入双并联型混联机构运动学逆解求解公式中,利用Matlab软件求得各运动副的状态如表7所示.对逆解所得的8组数据进行分析可以发现,第八组输入参数与位置正解算例中的第四组输入参数相同.在此将两组数据单独提炼出来进行比较分析,如表8所示.经过比较之后发现,双并联型混联机构的两者之间存在微小误差,且误差可以忽略不计.经过两组解的对比,发现用正解得到的双并联型混联机构末端位姿作为输入,求得的机构驱动输入参数与一开始求正解的输入参数相同,两者之间的误差微乎其微.验证了运动学正反解的正确性.工作空间分析在混联机构的分析中占有非常重要的地位[11].混联机构工作空间会受到很多因素的影响,机构整体尺寸的大小,移动副P行程的约束,转动副R转角(包括虎克铰U、球铰S)角度值的限制,机构中各杆件之间的干涉现象都会对其产生影响[12].机构在不同的限定条件下,其工作空间的形状和体积都会不一样[13].不同的机构根据不同的用途和应用场合会提出不一样的限制因素,每种因素的限制条件也不尽相同.在实际应用中,也会考虑成本因素提出不同的限制条件[14].对本文混联机构的位置可达工作空间进行分析,运用运动学反解分析结果,结合极限边界数值搜索算法,求出其位置工作空间的形状.求解位置工作空间内所有点的算法如图4所示.给定合适的机构尺寸,通过圆柱坐标系逐个搜索,将Z坐标等分成n份,然后在每个Z坐标截面下,搜索边界轮廓,直到在整个Z坐标下都搜索完成后,所有的边界轮廓组合起来就是整个混联机构的工作空间边界图[15].运用Matlab数学软件采用上述的算法,结合混联机构的运动学反解和约束条件对工作空间的算法进行编程,求解了给定算例的工作空间.给定机构参数与运动学算例保持一致.针对此双并联型六自由度混联机构,为了得到其位置工作空间,可以先将其末端固定在给定的姿态下,从而得到在此姿态下机构所能到达的所有满足约束条件的位置空间.由于混联机构上下两个并联模块的机构尺寸不一样,给定双并联混联机构的移动副的运动范围为0.5 m≤Li≤0.8 m (i=1, 2, 3),0.3 m≤Li≤0.5 m (i=4, 5),转动副的运动范围为-≤θi≤ (i=1, 2, 3, 4, 5).首先由蒙特卡洛法根据输入参数的变化范围得到机构的大致位置点云图,判断机构的大致位置.限定Z坐标的变化范围为[0.75, 1.7],r≤2.利用上面给定的约束条件,用Matlab软件编程,给出机构在给定不同姿态情况下的定姿态位置工作空间,结果如图5所示,其中用YXZ欧拉角表示机构动平台的姿态.由图5可知,改变机构的姿态角,就可以得到不同定姿态的位置工作空间.这4种姿态条件下得到的位置工作空间边界图大致是一个从上到下边界逐渐增大的近似拉长的连续锥形体.当姿态角达到(20°,20°,20°)时,机构的位置可达工作空间有一个凹洞,说明机构在此位置范围内存在奇异位形.根据定姿态位置工作空间图可以看出该混联机构位置在(0, 0, 1.3)时,具有较为规则的位置工作空间边界,所以选择在此位置进行机构的姿态工作空间搜索,其得到的姿态工作空间是指与末端执行器固结在一起的坐标系在该位置所能实现的所有的姿态坐标的集合,如图6所示.(1) 本文介绍了双并联型六自由度混联机构的结构,求解了机构的自由度数目.指定机构驱动构件,通过分别对下端并联机构模块和上端并联机构模块的运动学正解分析,得到整个混联机构的运动学正解.通过给定机构结构参数和驱动输入参数,用一组算例求得运动学动平台位姿,并画出三维机构位姿模型.然后求解运动学逆解,按照运动学正解结果,给定机构的两组位姿,求得此时机构的驱动输入参数及各转动副的状态,对比正反解结果,进而验证了双并联型混联机构运动学正反解模型的正确性.(2) 根据混联机构的运动学反解,利用极限边界搜索法给出机构工作空间的算法.给定机构的结构参数,考虑工作空间影响因素,利用数值搜索法在圆柱坐标系中搜索工作空间的边界.在Matlab软件中仿真得到了混联机构在给定不同姿态下的位置工作空间和给定位置下的姿态工作空间.【相关文献】[1] 姜铭,孙钊,秦康生,等.混联机器人的分析与研究[J].制造业自动化,2009,31(1):61-65.[2] 伞红军.新型五轴并串联机床的运动学分析与结构参数设计[D].哈尔滨:哈尔滨工业大学机电工程学院,2009.[3] 高建设,李明祥,侯伯杰,等.新型四足步行机器人串并混联腿的运动学分析[J].光学精密工程,2015,23(11):3147-3160.[4] PISLA D, SZILAGHYI A, VAIDA C, et al. Kinematics and workspace modeling of a new hybrid robot used in minimally invasive surgery[J]. Robotics and Computer-Integrated Manufacturing, 2013, 29(2):463-474.[5] ZENG Q, FANG Y. Structural synthesis and analysis of serial-parallel hybrid mechanisms with spatial multi-loop kinematic chains[J]. Mechanism & Machine Theory,2012, 49(3):198-215.[6] CHANGYA YAN, FENG GAO, YONG ZHANG. Kinematic modeling of a serial-parallel forging manipulator with application to heavy-duty manipulations#[J]. Mechanics Based Design of Structures & Machines, 2010, 38(1):105-129.[7] 刘海涛,黄田,CHETWYND D G,等.5自由度大工作空间/支链行程比混联机械手的概念设计与尺度综合[J].机械工程学报,2007,43(6):14-20.[8] LU Y, DAI Z, YE N, et al. Kinematics/statics analysis of a novel serial-parallel robotic arm with hand[J]. Journal of Mechanical Science & Technology, 2015, 29(10):4407-4416.[9] 石岩,路懿.一种2SPS+RPRR并联机构的运动学与工作空间分析[J].燕山大学学报,2010,34(1):18-23.[10] 黄真,刘婧芳,李艳文.论机构自由度[M].科学出版社,2011.[11] CAMMARATA A. Optimized design of a large-workspace 2-DOF parallel robot for solar tracking systems[J]. Mechanism & Machine Theory, 2015, 83:175-186.[12] 韩方元.并联机器人运动学正解新算法及工作空间本体研究[D].长春:吉林大学机械科学与工程学院,2011.[13] HAY A M, SNYMAN J A. A multi-level optimization methodology for determiningthe dextrous workspaces of planar parallel manipulators[J]. Structural & Multidisciplinary Optimization, 2005, 30(30):422-427.[14] 黄秀琴,辛秀梅,沈惠平,等.一种新型3自由度并联机构的设计和运动学分析[J].机械设计,2010,27(7):4-6.[15] 陈伟海,徐颖俊,王建华,等.并联式下肢康复外骨骼运动学及工作空间分析[J].机械工程学报,2015,51(13):158-166.。
基于ADAMS的六自由度运动平台运动学分析

: a11 a 12 a 22 a 32 a 13 a 23 a 33 a21 a31
RPY ( C , B , A) = Ro t( z, C ) Ro t( y, B) R ot(x, A) =
式中: a 11 = cos( C) cos( B); a12 = cos( C ) sin ( B) sin ( A) - sin ( C ) cos( A); a13 = cos( C) sin ( B) cos ( A) + sin (C ) sin ( A); a 21 = sin( C) cos( B); a 22 = sin ( C) sin ( B) sin ( A) + cos( C ) cos( A); a23 = sin ( C ) sin ( B) cos( A) - cos( C) sin ( A); a 31 = - sin ( B); a 32 = cos( B) sin( A); a33 = cos( B) cos( A). 可以求出 a 1, a 2, a3 三点在定系中的坐标分别为 A 1 ( x 1, y 1, z1 ), A 2 ( x 2, y 2, z2 ), A 3 ( x 3, y 3, z 3 ). 进而得出液压缸的长度分别为 : Li = 式中: n 11 = a 12 r + p x + py + ni 1 + n i2 + n i3
+ px + r; n62 = -
① 液压缸位移 ( 伸长量 ):
# 72# vi = si = ③ 液压缸加速度:
福州大学学报 ( 自然科学版 ) 1 ( ni 1 n i1 + n i2 n i2 + n i3 n i3 ) Li ai = & si = vi (i= 1 , 2 , 3 , 4 , 5 , 6)
六自由度运动平台设计方案
六自由度运动平台设计方案1概述YYPT原理样机用原库房留存的345厂的直流电机作为动力源,直流驱动器及工控机作为控制系统元件,采用VB软件进行控制软件的编制,因设计及器件选型的原因,导致YYPT原理样机,在速度、精度、运动规律上等几个技术指标无法满足原规定的指标要求,现在此基础上进行优化方案的设计。
2原理样机技术状态2.1原理样机方案2.1.1组成原理样机采用工控机作为系统的控制单元,工控机内配有研华PCI1716和PCI1723作为A/D和D/A模拟量卡,驱动器采用AMC公司的型号为12A8的伺服驱动器,并配有直流可调电源其输出电流可达到150A,采用KH08XX(3)电动缸作为运动平台的六条支腿,电动缸上安装有电阻尺作为位置反馈器件,上平台与电动缸连接采用球笼联轴器,下平台与电动缸连接采用虎克铰链方式。
具体产品组成表见表2.1。
2.1.2结构方案六自由度运动平台是由六条电动缸通过虎克铰链和球笼万向节联轴器将上、下两个平台连接而成,下平台固定在基础上,借助六条电动缸的伸缩运动,完成上平台在三维空间六个自由度(X,丫,Z,a,B, 丫)的运动,从而可以模拟出各种空间运动姿态。
图1六自由度平台外形图a)球笼联轴器(如图2所示)采用球笼铰链与上平面连接。
球笼铰链结构简单、体积小、运转灵活、易于维护。
初选球笼铰链型号BJB (JB/T6139-1992),公称转矩Tn=2000N/m,工作角度40度,外径D=68mm,轴孔选用圆柱孔d=24mm,总长度L1=148mm ,转动惯量为0.00008kg.m2,重量5kg。
图2球笼联轴器b)虎克铰链(如图3所示)采用虎克铰链与下平面连接。
万向节铰链传动效率高,允许两轴间的角位移大,适用于有大角位移的两轴之间的连接,一般两轴的轴间角最大可达35o~45o,噪音小,对润滑要求不高,传递转矩大,而且使用可靠,因此获得广泛的应用。
图3虎克铰链F固定板的连接(如图4所示)F 固定板与电动缸用法兰连接初选深沟球轴承型号61808 (GB/T276-1994),额定载荷 Cr=5.1kN ,外径D=52mm ,轴承孔选用 d=40mm ,宽 B=7mm ,重量 0.26kg 。
六自由度模型

42212312222212''22'212[()()][][()()][()()()()()()()]()sin ()[r r c c qq rr pr u vrc wq c uu c vv c ww c uw c c uvc c c rm u v v r w w q L X q X r X pr L X u X v v r X w w q L X u u X v v X w w X u u w w X u u v v W B L u u X X δδδρρρθρδ'''--+-=++'''++-+-'''+-+-+-+--+----+-+'2]s s spropT δδ+(1)○2 横向运动方程4'1||2312||2212[()()][][()()()()||][()()()c c r p pqqr r r p p v ur c vq c wp cwr c v r uu c uv c c v m v u u r w w p L Y r Y p Y p p Y pq Y qr Y r r L Y v Y u u r Y v v q Y w w p Y w w r Y r L Y u u Y u u v v Y ρρρ+---='''''+++++'''''++-+-+-+-'+'''+-+--+()||2212()()(cos sin ()w c c v v c r c r v v w w Y v v W B L Y u u δθϕρδ--'+-'+-+-(2)4221||2312||2221[()()][][()()()||][()()()()()c c q pp rr rp q q w uq c vr c vp c w q uu c vv c uv c c uwc m w u u q v v p L Z q Z p Z r Z rp Z q q L Z w Z u u q Z v v r Z v v p Z q L Z u u Z v v Z u u v v Z u u ρρρ'''''--+-=++++''''++-+-+-'+'''+-+-+--'+-()||2212()()()(()cos cos ()c c c u w ww c wwc s c s w w Z u u w w Z w w Z w w W B L Z u u δθϕρδ'-+--'+-'+-'+-+-(3)○4 横倾运动方程 51||||24123321||()[][()()()()()()][()()()(x z y p r p p qrpq r r v up c ur c vq c wpc wr c vvv c uu c uv c c v v I p I I qr L K p K r K p p K qr K pq K r r L K v K u u p K u u r K v v q K w w p K w w r K v v L K u u K u u v v K v v ρρρ+-=''''''+++++''''++-+-+-'''+-+-+-''+-+--'+-3212()()]()cos cos ()cos sin ()c vwc c G B G B r c r K v v w w y W y B z W z B L K u u δθϕθϕρδ'+--'+---+-(4)5221||2412||32212()[][()()()][()()()()()()Y X Z q pp q q rr pr w uq c vr c vp c w uu c vv c uv c c uwc c u w I q I I pr L M q M p M q q M r M pr L M w M u u q M v v r M v v p M L M u u M v v M u u v v M u u w w M ρρρ'''''+-=++++''''++-+-+-'+'''+-+-+--''+--+||321()()()(()cos cos ()sin ()c c wwc ww c G B G B s c s u u w w M w w M w w x W x B z W z B L M u u δθϕθρδ--'+-'+-'----+-(5)○6 偏航运动方程 51||||2412||3212()[][()()()()()][()()()z y X r p p p r r pq qrv upc ur c wr c wpc vq c v r uuc uv c c I r I I pq L N r N p N p p N r r N pq N qr L N v N u u p N u u r N w w r N w w p N v v q N L N u u N u u v v ρρρ''''''+-=+++++''''++-+-+-''+-+-'+''+-+--+||3212()()(()cos sin ()sin ()vw c c v v c G B G B r c rN v v w w N v v x W x B y W y B L N u u δθϕθρδ'--'+-'+-+-+-(6)○7 姿态方程: sin tan cos tan cos sin sin /cos cos /cos p q r q r q r ϕϕθϕθθϕϕψϕθϕθ=++=-=+○8 运动关系式:cos cos (cos sin sin sin cos )(cos sin cos sin sin )sin cos (sin sin sin cos cos )(sin sin cos cos sin )sin cos sin cos cos u v w u v w u v w ξψθψθϕψϕψθϕψϕηψθψθϕψϕψθϕψϕςθθϕθϕ=+-++=+++-=-++ 式中:下标为prop 的项为推进器产生的推力;)('∙X 、)('∙Y 、)('∙Z -----无因次水动力导数; )('∙K 、)('∙M 、)('∙N -----无因次水动力矩导数;u-----航速(m/s); v-----横荡速度(m/s); w-----垂荡速度(m/s); p-----横摇角速度(rad/s); q-----纵摇角速度(rad/s); r-----艏摇角速度(rad/s);r δ-----方向舵舵角(rad); s δ-----水平舵舵角(rad);m-----质量(Kg);x I -----绕x 轴的转动惯量(N.m2); y I -----绕y 轴的转动惯量(N.m2); z I -----绕z 轴的转动惯量(N.m2);,,c c c u v w 分别表示海流在,,u v w 方向的分量;,,G G G x y z :表示平台重心位置(m ); ,,B B B x y z :表示平台重心位置(m ); W 、B-----重力和浮力(N)。
六自由度汽车驾驶运动模拟器设计

摘要汽车驾驶模拟器是一种用于汽车产品开发、“人—车—环境”交通特性研究或驾驶培训的重要工具。
近年来,由于具有安全性高、再现性好、可开发性强、成本低等显著特点,研究开发驾驶模拟器已经成为国内外一个重要发展方向。
本文在查阅国内外大量资料的基础上,结合老师的研究课题主要对六自由度汽车驾驶模拟器液压系统部分进行设计。
六自由度汽车运动模拟器采用液压伺服阀控制液压缸来驱动模拟平台的运动,以实现汽车驾驶模拟器运动姿态模拟。
本文主要进行机械机构的设计、液压伺服系统设计、液压泵站设计和液压缸的设计等。
通过模拟器的机构设计和驱动液压伺服系统设计,结合电气系统能够实现汽车在不同运行状态的模拟,当驾驶员坐在驾驶舱系统的座椅上进行模拟驾驶时,完全能够感受到实际汽车驾驶的各种体感,为实车训练驾驶提供了可替代的模拟平台;本设计也为今后的进一步研究及其在娱乐模拟器、动感电影等产业的实际推广和应用方面奠定了基础。
关键词:汽车驾驶模拟器六自由度运动平台液压伺服系统运动姿态控制AbstractThe Automobile-driving i an important tool which used for the development of auto mobile product and the study of the transportation characteristics of “man-car-environment”or the driver training .In recent years, the study of the automobile-driving simulator used for development has become an important development direction in the world because of the notable characteristics of high safety, well reappearance of scene, easy to develop and low cost.This article is based on searching the large quantity of information about at home and abroad, and combines with the tea cher’s research task which mainly designs the part of 6-dof driving Simulator of hydraulic system .The 6-dof motion simulator adopts valves of hydraulic servo to control actuator to drive the movement of driving simulation platform, and to achieve the movement posture simulation of the automobile driving simulator. This article is mainly about the designing of machine, the system of hydraulic servo, hydraulic pump station, and actuator and so on.According to the designing of agencies of simulator and hydraulic servo system, it can combines the electrical system which can bring out the imitation of cars in different movement conditions, when the driver simulating drive on the seat of cockpit system, you can feel the feeling of driving a true car, and it also offer the simulator platform which can be replaced for true driving training. At the same time, this designing is also establishes for the further researches and the practice extension and use.Keywords:Driving-automobile simulator, 6-dof of motion platform, the system of hydraulic servo, the control of campaign attitude目录1绪论 (1)引言 (1)国内外发展现状 (2)1.2.1国内外研究和发展概述 (2)1.2.2驾驶模拟器的应用和发展 (3)课题任务 (5)论文的主要研究内容 (5)2 运动学及力学分析 (6)六自由度运动模拟器机构位置反解 (6)2.1.1坐标系的建立 (6)2.1.2广义坐标定义 (6)2.1.3坐标变换矩阵 (7)2.1.4液压缸铰支点坐标的确定 (8)2.1.5位置反解 (10)六自由度运动模拟器机构位置正解 (11)静力学分析 (11)3 机械及液压部分设计 (12)运动模拟平台的设计 (12)3.1.1液压缸内壁D活塞杆直径d的计算 (12)3.1.2液压缸壁厚和外径的计算 (14)3.1.3缸盖壁厚的确定 (14)3.1.3液压缸工作行程的确定 (15)3.1.4缸体长度的确定 (15)3.1.5液压系统的计算 (15)液压泵站 (17)铰链的设计 (18)执行机构单元组成 (21)电液伺服控制单元与液压系统 (22)反馈单元 (23)4 电气部分设计 (24)电气原理及接口设计 (24)4.1.1MCS-51系列单片机的引脚及其功能 (24)4.1.2单个电液伺服液压缸位置控制电路设计 (26)4.1.3扩展电路 (26)电气原理图 (27)5 结论 (28)本文结论 (28)本文研究工作的不足 (28)参考文献 (29)致谢 (30)1绪论引言驾驶模拟器是一种用于汽车产品开发、“人-车-环境”交通特性研究或驾驶培训的重要工具。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六自由度运动平台正解(几何法)
1. 对上平台(运动平台)进行扩展,示意如下:
Pic 1 上平台示意图
由于确定一个平面状态只需要三个点,因此获得C1,C2,C3坐标,即可确定平面状态。
如图,h1,h2均为已知量,设L h k /1=,212*h h L +=,),,(i i i i z y x C =。
设下平台各点坐标为),,(i i i i s n m B =,设各轴长为i i i l B A =。
于是问题简化为:已知:L k l B i i ,,,,求解i C 。
2. 建立方程组 2.1 i l 相关
对于1l ,分析如下:
Pic 2 单轴示意图
由图可知:向量3111111111*C C k C B A C C B A B +=+=,
即,1111111131313),,(),,(l s z n y m x z z y y x x k
=---+---
所以:
)1......(0])1([])1([])1([21211321132113=---++--++--+l s z k kz n y k ky m x k kx
同理有:
)6......(0])1([])1([])1([)5......(0])1([])1([])1([)4......(0])1([])1([])1([)
3......(0])1([])1([])1([)
2......(0])1([])1([])1([262631263126312525322532253224242324232423232321232123212
2221222122212=---++--++--+=---++--++--+=---++--++--+=---++--++--+=---++--++--+l s z k kz n y k ky m x k kx l s z k kz n y k ky m x k kx l s z k kz n y k ky m x k kx l s z k kz n y k ky m x k kx l s z k kz n y k ky m x k kx
2.2 L 相关
)
9......(0)()()()8......(0)()()()7......(0)()()(222322322322312312312221221221=--+-+-=--+-+-=--+-+-L z z y y x x L z z y y x x L z z y y x x 3. 求解
3.1 联立方程组(1)-(9),牛顿迭代法解方程组,即可求的i C ,
取0>i z ,可得唯一解。
3.2 由i C 求出平台姿态
根据实际情况,建立坐标系如下
Pic 3
取中心向C1方向为X 正方向,逆时针90度为Y 正方向,则XY 方向在静坐标系中的方向向量为:
),,()5.05.0,5.05.0,5.05.0(131313321321321z z y y x x VectorY z z z y y y x x x VectorX ---=------=
显然平台中心点为3/)(321C C C O ++=
)/arctan()/arctan()/arctan(3
/)(3/)(3/)(321032103210VectorXx VectorXy VectorXx VectorXz VectorYy VectorYz z z z z y y y y x x x x -=-==++=++=++=γβα。
