垂径定理及其推论
专题24.3 垂径定理【十大题型】(人教版)(原卷版)

专题24.3 垂径定理【十大题型】【人教版】【题型1 利用垂径定理求线段长度】 (1)【题型2 利用垂径定理求角度】 (2)【题型3 利用垂径定理求最值】 (3)【题型4 利用垂径定理求取值范围】 (4)【题型5 利用垂径定理求整点】 (6)【题型6 利用垂径定理求面积】 (7)【题型7 垂径定理在格点中的运用】 (8)【题型9 垂径定理与分类讨论中的综合运用】 (10)【题型10 垂径定理的应用】 (11)【题型1 利用垂径定理求线段长度】【例1】(2022•雨花区校级开学)如图,⊙O的半径OD⊥弦AB交AB于点C,连接AO并延长交⊙O于点E,连接EC.若AB=8,EC=2√13,则CD的长为()A.1B.3C.2D.4【变式1-1】(2022•宁津县二模)如图,已知圆O的半径为10,AB⊥CD,垂足为P,且AB=CD=16,则OP的长为()A.6B.6√2C.8D.8√2【变式1-2】(2022•建华区二模)如图,⊙O的直径AB与弦CD相交于点E,若AE=5,EB=1,∠AEC =30°,则CD的长为()A.5B.2√3C.4√2D.2√2+√3+1【变式1-3】(2022春•徐汇区校级期中)如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,且CE=CB,若BE=2AE,CD=5,那么⊙O的半径为.【题型2 利用垂径定理求角度】【例2】(2022•泰安模拟)如图,⊙O的半径OA,OB,且OA⊥OB,连接AB.现在⊙O上找一点C,使OA2+AB2=BC2,则∠OAC的度数为()A.15°或75°B.20°或70°C.20°D.30°̂上的【变式2-1】(2022秋•天心区期中)如图,已知⊙O半径OA=4,点B为圆上的一点,点C为劣弧AB一动点,CD⊥OA,CE⊥OB,连接DE,要使DE取得最大值,则∠AOB等于()A.60°B.90°C.120°D.135°【变式2-2】(2022秋•青田县期末)如图,在⊙O中,半径OC过弦AB的中点E,OC=2,OE=√2.(1)求弦AB的长;(2)求∠CAB的度数.【变式2-3】(2022秋•开州区期末)如图,在⊙O中,弦BC与半径OA垂直于点D,连接AB、AC.点E 为AC的中点,连接DE.(1)若AB=6,求DE的长;(2)若∠BAC=100°,求∠CDE的度数.【题型3 利用垂径定理求最值】【例3】(2022•威海模拟)⊙O中,点C为弦AB上一点,AB=1,CD⊥OC交⊙O于点D,则线段CD的最大值是()A.12B.1C.32D.2【变式3-1】(2022•河北模拟)如图所示,在⊙O中,AB为弦,OC⊥AB交AB于点D.且OD=DC.P为⊙O上任意一点,连接P A,PB,若⊙O的半径为1,则S△P AB的最大值为()A.1B.2√33C.3√34D.3√32【变式3-2】(2022秋•龙凤区校级期末)如图,矩形ABCD中,AB=20,AD=15,P,Q分别是AB,AD 边上的动点,PQ=16,以PQ为直径的⊙O与BD交于点M,N,则MN的最大值为.【变式3-3】(2022秋•延平区校级期末)在Rt△ABC中,∠C=90°,BC=3,AC=4,D、E分别是AC、BC上的一点,且DE=3,若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为()A.910B.65C.85D.125【题型4 利用垂径定理求取值范围】【例4】(2022•包河区校级二模)如图,在⊙O中,直径AB=10,CD⊥AB于点E,CD=8.点F是弧BC 上动点,且与点B、C不重合,P是直径AB上的动点,设m=PC+PF,则m的取值范围是()A.8<m≤4√5B.4√5<m≤10C.8<m≤10D.6<m<10【变式4-1】(2022•佛山)如图,⊙O的直径为10cm,弦AB=8cm,P是弦AB上的一个动点,求OP的长度范围.【变式4-2】(2022秋•盐都区校级月考)如图,点P是⊙O内一定点.(1)过点P作弦AB,使点P是AB的中点(不写作法,保留作图痕迹);(2)若⊙O的半径为13,OP=5,①求过点P的弦的长度m范围;②过点P的弦中,长度为整数的弦有条.【变式4-3】(2022秋•天河区校级期中)已知⊙O的半径为5,点O到弦AB的距离OH=3,点P是圆上一动点,设过点P且与AB平行的直线为l,记直线AB到直线l的距离为d.(1)求AB的长;(2)如果点P只有两个时,求d的取值范围;(3)如果点P有且只有三个时,求连接这三个点所得到的三角形的面积.【题型5 利用垂径定理求整点】【例5】(2022•山海关区一模)已知⊙O的直径CD=10,CD与⊙O的弦AB垂直,垂足为M,且AM=4.8,则直径CD上的点(包含端点)与A点的距离为整数的点有()A.1个B.3个C.6个D.7个【变式5-1】(2022秋•新昌县期末)如图,AB是⊙O的弦,OC⊥AB于点C,连接OB,点P是半径OB上任意一点,连接AP,若OB=5,OC=3,则AP的长不可能是()A.6B.7C.8D.9【变式5-2】(2022•桥西区校级模拟)如图,AB是⊙C的弦,直径MN⊥AB于点O,MN=10,AB=8,如图以O为原点建立坐标系.我们把横纵坐标都是整数的点叫做整数点,则线段OC长是3,⊙C上的整数点有个.【变式5-3】(2022秋•肇东市期末)已知⊙O的半径为5,点O到弦AB的距离为3,则⊙O上到弦AB所在直线的距离为2的点有()A.4个B.3个C.2个D.1个【题型6 利用垂径定理求面积】【例6】(2022•武汉模拟)如图,在半径为1的⊙O中有三条弦,它们所对的圆心角分别为60°,90°,120°,那么以这三条弦长为边长的三角形的面积是()A.√2B.1C.√32D.√22【变式6-1】(2022秋•黄州区校级月考)如图,矩形MNGH的四个顶点都在⊙O上,顺次连接矩形各边的中点,得到菱形ABCD,若BD=12,DF=4,则菱形ABCD的面积为.【变式6-2】(2022秋•西城区校级期中)如图,AB为⊙O直径,过点O作OD⊥BC于点E,交⊙O于点D,CD∥AB.(1)求证:E为OD的中点;(2)若CB=6,求四边形CAOD的面积.【变式6-3】(2022•新洲区模拟)如图,点A,C,D均在⊙O上,点B在⊙O内,且AB⊥BC于点B,BC ⊥CD于点C,若AB=4,BC=8,CD=2,则⊙O的面积为()A.125π4B.275π4C.125π9D.275π9【题型7 垂径定理在格点中的运用】【例7】(2022秋•襄都区校级期末)如图所示,一圆弧过方格的格点AB,试在方格中建立平面直角坐标系,使点A的坐标为(0,4),则该圆弧所在圆的圆心坐标是()A.(﹣1,2)B.(1,﹣1)C.(﹣1,1)D.(2,1)【变式7-1】(2022春•海门市期中)如图所示,⊙P过B、C两点,写出⊙P上的格点坐标.【变式7-2】(2022•商城县三模)如图所示的网格中,每个小正方形的边长均为1,点A、B、C均在小正方形的顶点上,点C同时也在AB̂上,若点P是BĈ的一个动点,则△ABP面积的最大值是.【变式7-3】(2017秋•靖江市校级月考)如图,在单位长度为1的正方形网格中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格图中进行下列操作(以下结果保留根号):(1)利用网格作出该圆弧所在圆的圆心D点的位置,并写出D点的坐标为;(2)连接AD、CD,则⊙D的半径为,∠ADC的度数.【题型8 垂径定理在坐标系中的运用】【例8】(2022•博山区一模)如图,在平面直角坐标系中,半径为5的⊙E与y轴交于点A(0,﹣2),B (0,4),与x轴交于C,D,则点D的坐标为()A.(4−2√6,0)B.(−4+2√6,0)C.(−4+√26,0)D.(4−√26,0)【变式8-1】(2022秋•西林县期末)如图,⊙P与y轴交于点M(0,﹣4),N(0,﹣10),圆心P的横坐标为﹣4.则⊙P的半径为()A.3B.4C.5D.6【变式8-2】(2022•印江县三模)如图,直线l为y=x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画圆弧交x轴于点A3;…,按此作法进行下去,则点A2022的坐标为.【变式8-3】(2015•宜春模拟)如图,半径为5的⊙P与y轴交于点M(0,﹣4),N(0,﹣10),函数y =﹣2x+m图象过点P,则m=.【题型9 垂径定理与分类讨论中的综合运用】【例9】(2022秋•化德县校级期末)⊙O的半径为10cm,弦AB∥CD,且AB=12cm,CD=16cm,则AB 和CD的距离为()A.2cm B.14cm C.2cm或14cm D.10cm或20cm【变式9-1】(2022•包河区二模)已知圆O的半径为5,弦AB=8,D为弦AB上一点,且AD=1,过点D 作CD⊥AB,交圆O于C,则CD长为()A.1B.7C.8或1D.7或1【变式9-2】(2022秋•方正县期末)如图,⊙O的弦AB与半径OC垂直,点D为垂足,OD=DC,AB=2√3,点E在⊙O上,∠EOA=30°,则△EOC的面积为.【变式9-3】(2022秋•淮南月考)如图,已知⊙O的半径为2.弦AB的长度为2,点C是⊙O上一动点,若△ABC为等腰三角形,则BC2的长为.【题型10 垂径定理的应用】【例10】(2022秋•武昌区校级期末)某地有一座圆弧形拱桥,它的跨度(弧所对的弦的长)24m,拱高(弧的中点到弦的距离)4米,则求拱桥的半径为()A.16m B.20m C.24m D.28m【变式10-1】(2022•望城区模拟)《九章算术》是我国古代著名数学经典,其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深1寸,锯道长1尺.如图,已知弦AB=1尺,弓形高CD=1寸,(注:1尺=10寸)问这块圆柱形木材的直径是()A.13寸B.6.5寸C.26寸D.20寸【变式10-2】(2022秋•西城区校级期中)京西某游乐园的摩天轮采用了国内首创的横梁结构,风格更加简约.如图,摩天轮直径88米,最高点A距离地面100米,匀速运行一圈的时间是18分钟.由于受到周边建筑物的影响,乘客与地面的距离超过34米时,可视为最佳观赏位置,在运行的一圈里最佳观赏时长为分钟.【变式10-3】(2022•浙江)如图,公园内有一个半径为20米的圆形草坪,A,B是圆上的点,O为圆心,̂,一部分市民为走“捷径”,踩坏了花草,走出了一条小路AB.通∠AOB=120°,从A到B只有路AB过计算可知,这些市民其实仅仅少走了步(假设1步为0.5米,结果保留整数).(参考数据:√3≈1.732,π取3.142)。
公开垂径定理及其推论讲义PPT课件
M
证明:作直径MN垂直于弦AB
D ∵ AB∥CD
B ∴ 直径MN也垂直于弦CD
∴A⌒M=B⌒M,
O
C⌒M=D⌒M
∴A⌒M-C⌒M =B⌒M-D⌒M
即 A⌒C=B⌒D
N
两条弦在圆心的同侧
垂径定理的推论2 有这两种情况:
O
A
B 两条弦在圆心的两侧
C
D
A
B
O
C
D
SUCCESS
THANK YOU
2019/8/21
∵AB=16cm
∴AE=8cm
在Rt△AOE中,根据勾股定理有OA=
10cm
∴⊙O的半径为10cm.
4、如图,CD是⊙O的直径,弦AB⊥CD于E,
CE=1,AB=10,求直径CD的长。
解:连接OA,
A
∵ CD是直径,OE⊥AB
C E O·
D
∴ AE=1/2 AB=5 B
设OA=x,则OE=x-1,由勾股定理得
SUCCESS
THANK YOU
2019/8/21
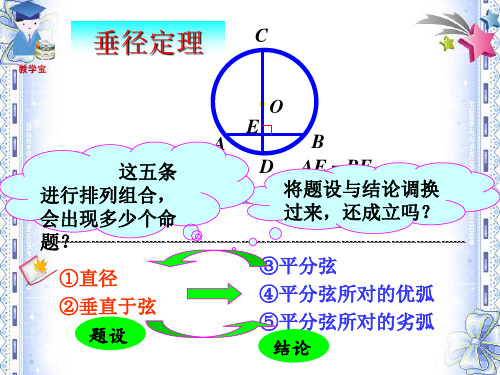
③④ ①②⑤ 平分弦并且平分弦所对的一条弧的直线经过圆心,垂直于弦
③⑤ ①②④ ,并且平分弦所对的另一条弧.
④⑤ ①②③ 平分弦所对的两条弧的直线经过圆心,并且垂直平分弦.
4. 解决有关弦的问题
经常是过圆心作弦的垂线,或作垂直 于弦的直径,连结半径等辅助线,为应用垂径 定理创造条件.
随堂练习
1. 判断:
x2=52+(x-1)2 解得:x=13
∴ OA=13 ∴ CD=2OA=26 即直径CD的长为26.
9. 在以O为圆心的
两个同心圆中,大圆的弦AB交
O.
三垂径定理

三垂径定理一、垂径定理的内容1. 定理表述- 垂直于弦的直径平分弦且平分这条弦所对的两条弧。
- 用几何语言表示:- 已知圆O,直径CD⊥弦AB于点E,则AE = BE,widehat{AD}=widehat{BD},widehat{AC}=widehat{BC}。
2. 定理的证明(以人教版教材思路为例)- 连接OA,OB。
- 因为OA = OB(同圆半径相等),OE⊥ AB,根据等腰三角形三线合一的性质,可得AE=BE。
- 再根据圆的对称性,可得widehat{AD}=widehat{BD},widehat{AC}=widehat{BC}。
3. 相关概念理解- 弦:连接圆上任意两点的线段。
如在圆O中,AB就是一条弦。
- 直径:经过圆心的弦。
例如CD是圆O的直径。
- 弧:圆上任意两点间的部分。
圆O中的widehat{AD}、widehat{BD}、widehat{AC}、widehat{BC}等都是弧。
二、垂径定理的推论1. 推论内容- 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
- 用几何语言表示:- 已知圆O,直径CD平分弦AB(AB不是直径)于点E,则CD⊥ AB,widehat{AD}=widehat{BD},widehat{AC}=widehat{BC}。
2. 推论的证明- 连接OA,OB。
- 因为OA = OB,AE = BE,所以 OAB是等腰三角形,根据等腰三角形三线合一的性质,可得OE⊥ AB,即CD⊥ AB。
- 再根据圆的对称性,可得widehat{AD}=widehat{BD},widehat{AC}=widehat{BC}。
- 这里要注意弦不能是直径,因为任意一条直径都可以平分另一条直径,但不一定垂直。
三、垂径定理及其推论的应用1. 计算类应用- 例1:已知圆O的半径为5,弦AB = 8,求圆心O到弦AB的距离。
- 解:设圆心O到弦AB的距离为d。
- 连接OA,因为OA = 5,AB = 8,根据垂径定理,OE⊥ AB时AE=(1)/(2)AB = 4。
垂径定理及其10个推论

垂径定理是指,在一个曲线上,任意一点到曲线的切线的距离都是一样的。
它的10个推论是:1)曲线的切线方程是垂径定理的特例;2)曲线的切线方程可以由垂径定理推导出来;3)曲线的切线方程的斜率是曲线的切线的斜率;4)曲线的切线方程的斜率是曲线的曲率的平方根;5)曲线的切线方程的斜率是曲线的曲率的平方根;6)曲线的切线方程的斜率是曲线的曲率的平方根;7)曲线的切线方程的斜率是曲线的曲率的平方根;8)曲线的切线方程的斜率是曲线的曲率的平方根;9)曲线的切线方程的斜率是曲线的曲率的平方根;10)曲线的切线方程的斜率是曲线的曲率的平方根。
3.3 垂径定理 课件 2023-2024学年 北师大版数学九年级下册

*3.3 垂径定理
续表
(1)定理中的“垂径”可以是直径、半径或过圆心的直线(线段),其 本质是“过圆心”; 特别提醒 (2)“平分弦所对的两条弧”是指既平分弦所对的优弧(如图中的
),又平分弦所对的劣弧(如图中的 )
-2-
*3.3 垂径定理
2. 垂径定理的推论
文字描述 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧 如图,直径 CD 与非直径的弦 AB
的是 ( )
A. CM=DM B.
C. ∠ACD=∠ADC D. OM=MB
(第 1 题图)
(第 2 题图)
2. 如图所示,⊙O 的半径为 13,弦 AB 的长度是 24,ON⊥AB,垂足为 N,
则 ON= ( )
A. 5
B. 7
C. 9
D. 11
-1-
*3.3 垂径定理
3.(教材 P76,习题 T2 变式)如图,AE 是⊙O 的直径,半径 OD 垂直于 弦 AB,垂足为 C,AB=8 cm,CD=2 cm,求 BE 的长.
∴AN= AB=12, 在 Rt△AON 中, ∵AO=13,∴ON=
=5.
3. 解:∵ 半径 OD 垂直于弦 AB,垂足为 C, AB=8 cm,∴AC= AB=4 cm,
设 CO=x cm,则 AO=DO=(x+2)cm,在 Rt△AOC 中,AO2=CO2+AC2, ∴(x+2)2=x2+42,解得 x=3,即 CO=3 cm. ∵AO=EO,AC=CB,OC 为△ABE 的中位线,∴BE=2CO=6 cm. 4. D 提示:一条直线经过圆心,平分弦所对的劣弧,根据垂径定理及其推论可 知,它垂直平分这条弦,并且平分弦所对的优弧. 5. 120 提示:∵ 弦 AC 与半径 OB 互相平分,∴OA=AB,∵OA=OB,∴△OAB 是 等边三角形,∴∠AOB=60°,∴∠AOC=2∠AOB=120°.
垂径定理

(1) 垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.(2) 垂径定理的推论:平分弦(不是直径)的直径垂直弦,并且平分弦所对的两条弧. (3) 圆中最长弦和最短弦问题(4)弧、弦、弦心距、圆心角关系定理:在等圆或同圆中,相等圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.(5) 弧、弦、弦心角、圆心角关系定理推论: 在等圆或同圆中 ,如果两个圆心角,两条弧,两条弦或两条弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等.(6) 圆周角定理: 在等圆或同圆中 ,同弧或等弧所对的圆周角相等,都等于这条弧所对圆心角的一半.(7) 切线的判定定理:经过半径的外端点且垂直于这条半径的直线是圆的切线. (8) 切线的性质定理:圆的切线垂直于过切点的半径. (9) 在等圆或同圆中 ,同弦所对的圆周角相等或者互补.(10) 切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.∙习题练习∙1. 过o 内一点M 的最长的弦为10cm,最短的弦长为8cm,求OM 的长?2. 若两圆的半径分别为3cm 和 4 cm ,则这两个圆相切时圆心距为3. 如图,已知A 、B 、C 是⊙O 上的三点,若∠ACB=44°,则∠AOB 的度数为4.如图,一宽为2cm 的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm ),则该圆的半径为 cm 。
5. 如图,矩形ABCD 中,BC= 2 , DC = 4.以AB 为直径的半圆O 与DC 相切于点E ,则阴影部分的面积为 (结果保留л)6. 林业工人为调查树木的生长情况,常用一种角卡为工具,可以很快测出大树的直径,其工作原理如图所示.现已知∠BAC =60°,AB=0.5米,则这棵大树的直径为 _________米.7.在o 中,90的圆心角所对的弧长是2πcm,则o 的半径是________cm.确定圆的条件不共线的三点确定一个圆三角形的外接圆 圆与圆有关的位置关系圆的定义,弧、弦等概念点和圆的位置关系点在圆上d r ⇔=点在圆外d r ⇔>点在圆内d r ⇔<判定性质 切线长定理三角形的内切圆相交d r ⇔<相切d r ⇔= 相离d r ⇔>直线与圆的位置关系基本性质垂径定理及其推论圆的对称性弧、弦、弦心距、圆心角关系定理及其推论 圆周角定理及其推论相交R r d R r ⇔-<<+ 相切的两圆的连心线过切点 相交的两圆的连心线垂直平分相交弦外离d R r ⇔>+ 内含d R r ⇔<+ 外切d R r ⇔=+ 内切d R r ⇔=-相交 相切相离圆与圆的位置关系圆内接正多边形正多边形与圆正多边形的有关计算圆内接正多边形作法----等份圆扇形的弧长、面积正多边形的半径、边心距、正多边形的内角、中心角、外角、正多边形的正三、六、十二边形 正四、八边形180n Rl π=213602n R S lR π==扇形 正多边形和圆。
垂径定理及其推论
28.1.2垂径定理及推论的教学设计活动一:画一个圆,并把一个圆沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得到什么结论?结论:活动二:在刚才的⊙O内画一条弦AB和一条直径CD,使CD⊥AB,垂足为E,你能发现图中有那些相等的线段和弧?为什么?相等的线段:相等的弧:垂径定理:1、图形语言2、文字语言:垂直于弦的直径平分弦,并且平分弦所对的两条弧。
3、几何语言:∵ABCD于E ,AB是⊙O的直径CE=DE,AC=AB,BC=BD练习1、判断下列图是否是表示垂径定理的图形。
()()()※垂径定理的几个基本图形定理中垂直于弦的直径,可以是直径、半径、也可以是过圆心的直线或线段。
2、请画图说明垂径定理的条件和结论。
条件结论AB为直径 AB平分弦CD点A平分弧CAD点B平分弧CD①过圆心③平分弦②垂直于弦④平分弦所对的优弧⑤平分弦所对的优弧推论:知其二可推其三①②③④⑤注意:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.活动三:例题与练习例1:如图,圆的直径为10,圆心O到弦AB的距离OM的长为3,那么弦AB的长是()A.4 B.6 C.7 D.8变式1:在⊙O中,已知AB等于8,圆心O到弦AB的距离OM的长为3,求圆的直径。
变式2:在⊙O中,已知直径为10,弦AB等于8,求圆心O到弦AB的距离OM的长。
例1图例2图例2:如图,已知:⊙O 中, AB为弦,D为 AB 中点, OC交AB 于D ,AB = 6cm ,CD = 1cm. 求⊙O 的半径OA.变式1:已知:⊙O中,AB为弦,C为弧AB中点,OC交AB 于D ,AB = 6cm ,CD = 1cm. 求⊙O的半径OA.变式2:已知:⊙O中,AB为弦,D为AB中点,OC交AB于D ,AB=6cm ,⊙O的半径OA为5,求CD的长。
变式3:已知:⊙O中,AB为弦,D为AB中点,OC交AB 于D ,CD =1cm ,⊙O的半径OA为5,求AB的长。
人教版初三数学上册垂径定理及其推论
垂径定理及其推论
【垂径定理】
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
【注】
(1)定理中的直径过圆心即可,可以是直径、半径、过圆心的直线或线段;
(2)此定理是证明等线段、等角、垂直的主要依据,同时也为圆的有关计算提供了方法和依据。
【垂径定理的推论】
推论一:平分弦(不是直径)的直径垂直于这条弦,并且平分这条弦所对的两段弧;
推论二:弦的垂直平分线经过圆心,并且平分这条弦所对的弧;
推论三:平分弦所对的一条弧的直径垂直平分这条弦,并且平分这条弦所对的另一条弧;
推论四:在同圆或者等圆中,两条平行弦所夹的弧相等一条直线,在下列5条中只要具备其中任意两条作为条件,就可以推出其他三条结论:
1.平分弦所对的优弧
2.平分弦所对的劣弧
(前两条合起来就是:平分弦所对的两条弧)
3.平分弦 (不是直径)
4.垂直于弦
5.经过圆心。
垂径定理及其推论课件
B
于点C.
3. 作AC、BC的
垂直平分线.
4. 三条垂直平分线
交于一点O.
O
点O就是A⌒B的圆心.
第十六页,共30页。
第十七页,共30页。
你 能 破 镜
重A
圆
吗?
m
n
C
B
O
作法:
作弦AB、AC及它们的垂直平分线m、n,交 于O点;以O为圆心,OA为半径作圆. 依据:
弦的垂直平分线经过圆心,并且平分弦所 对的两条弧.
长为16cm,圆心O到AB的距离为 6cm,求⊙O的半径.
E
B
.
O
解:连结OA.过O作OE⊥AB,垂足为E, 则OE=3cm,AE=BE. ∵AB=16cm ∴AE=8cm 在Rt△AOE中,根据勾股定理有OA=10cm ∴⊙O的半径为10cm.
第二十六页,共30页。
4、如图,CD是⊙O的直径,弦AB⊥CD于E,
① 直径过圆心 ③ 平分弦
⑤ 平分弦所对的劣弧
② 垂直于弦
⑤ 平分弦所对的劣弧
① 直径过圆心
③ 平分弦 ④ 平分弦所对优弧
(4)垂直于弦并且平分弦所对的一条弧的 直径过圆心,并且平分弦和所对的另一条弧.
第八页,共30页。
③ 平分弦 ④ 平分弦所对优弧
① 直径过圆心
② 垂直于弦 ⑤ 平分弦所对的劣弧
第十八页,共30页。
垂径定理三角形
有哪些等量关系?
d+h=r
rd h a
第十九页,共30页。
在a,d,r,h
中,已知其中任意 两个量,可以求出
其它两个量.
课堂小结
1. 圆是轴对称图形
任何一条直径所在的直线都是它的对称轴.
垂径定理及其推论
证明: OE AC OD AB AB AC
OEA 90 EAD 90 ODA 90
∴四边形ADOE为矩形,
AE
1 2
AC,AD
1 2
AB
又 ∵AC=AB
C
∴ AE=AD
E
·O
∴ 四边形ADOE为正方形.
A
D
B
课堂讨论
① 根据已知条件进行推导: ②
③ ④ ⑤
①过圆心 ②垂直于弦 ③平分弦
D
A
B
E
O
A
DB
1.过⊙o内一点M的最长的弦长为10㎝,最短弦长为8 ㎝,那么⊙o的半径是 5㎝ 2.已知⊙o的弦AB=6㎝,直径CD=10㎝,且AB⊥CD, 那么C到AB的距离等1于㎝或9㎝
3.已知⊙O的弦AB=4㎝,圆心O到AB的中点C的距离为1 ㎝,那么⊙O的半径为 5 Cm
4.如图,在⊙O中弦AB⊥AC,
垂径定理及其推论
赵州桥主桥拱的半径是多少?
问题 :你知道赵州桥吗?它是1300多年前我国隋代建造的石 拱桥, 是我国古代人民勤劳与智慧的结晶.它的主桥是圆弧 形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦 的距离)为7.2m,你能求出赵洲桥主桥拱的半径吗?
实践探究
把一个圆沿着它的任意一条直径对折, 重复几次,你发现了什么?由此你能得到 什么结论?
短的弦等于 2 5cm .
2.过⊙O内一点M的最长弦长为4厘米,最短 弦长为2厘米,则OM的长是多少?
B
O
D
P E
C
A
A OM
2、如图,点P是半径为5cm的⊙O内一点, 且OP=3cm, 则过P点的弦中, (1)最长的弦= cm (2)最短的弦= cm (3)弦的长度为整数的共有( )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆部分知识点总结
垂径定理及其推论
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧。
推论1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
(3)平分弦所对的一条弧的直径垂直平分弦,并且平分弦所对的另一条弧。
推论2:圆的两条平行弦所夹的弧相等。
垂径定理及其推论可概括为: 过圆心 垂直于弦
直径平分弦知二推三 平分弦所对的优弧 平分弦所对的劣弧
弧、弦、弦心距、圆心角之间的关系定理
1:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等。
2:在同圆或等圆中,如果两个圆的圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等。
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半。
推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等。
推论2:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径。
推论3:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
点和圆的位置关系
设⊙O 的半径是r ,点P 到圆心O 的距离为d ,则有:d<r ⇔点P 在⊙O 内;
d=r ⇔点P 在⊙O 上; d>r ⇔点P 在⊙O 外。
过三点的圆
1、不在同一直线上的三个点确定一个圆。
2、经过三角形的三个顶点的圆叫做三角形的外接圆。
3、三角形的外接圆的圆心是三角形三条边的垂直平分线的交点,它叫做这个三角形的外心。
直线与圆的位置关系
直线和圆有三种位置关系,具体如下:
(1)相交:直线和圆有两个公共点时,叫做直线和圆相交,这时直线叫做圆的割线,公共点叫做交点; (2)相切:直线和圆有唯一公共点时,叫做直线和圆相切,这时直线叫做圆的切线, (3)相离:直线和圆没有公共点时,叫做直线和圆相离。
如果⊙O 的半径为r ,圆心O 到直线L 的距离为d,那么:直线L 与⊙O 相交⇔d<r ;
直线L 与⊙O 相切⇔d=r ; 直线L 与⊙O 相离⇔d>r ;
圆的内接四边形定理:圆的内接四边形的对角互补,外角等于它的内对角。
切线的性质与判定定理
1、切线的判定定理:过半径外端且垂直于半径的直线是切线;
两个条件:过半径外端且垂直半径,二者缺一不可
2、性质定理:切线垂直于过切点的半径 推论1:过圆心垂直于切线的直线必过切点。
推论2:过切点垂直于切线的直线必过圆心。
以上三个定理及推论也称二推一定理:
即:①过圆心;②过切点;③垂直切线,三个条件中知道其中两个条件就能推出最后一个。
切线长定理
切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,这点和圆心的连线平分两条切线的夹角。
即:∵PA 、PB 是两条切线
P B A
O
∴PA PB =;PO 平分BPA ∠ 圆幂定理
1、相交弦定理:圆内两弦相交,交点分得的两条线段的乘积相等。
即:在⊙O 中,∵弦AB 、CD 相交于点P ,
∴PA PB PC PD ⋅=⋅
推论:如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项。
即:在⊙O 中,∵直径AB CD ⊥, ∴2
CE AE BE =⋅
切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
即:在⊙O 中,∵PA 是切线,PB 是割线 ∴2
PA PC PB =⋅
割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等(如右图)。
即:在⊙O 中,∵PB 、PE 是割线
∴PC PB PD PE ⋅=⋅
两圆公共弦定理 圆公共弦定理:两圆圆心的连线垂直并且平分这两个圆的的公共弦。
如图:12O O 垂直平分AB 。
即:∵⊙1O 、⊙2O 相交于A 、B 两点
∴12O O 垂直平分AB 圆的公切线
(1)公切线的长:12Rt O O C ∆中,22221122AB CO O O CO ==-; (2)外公切线的长:2CO 是半径之差;2CO 是半径之和
三角形的内切圆和外接圆
1、三角形的内切圆与三角形的各边都相切的圆叫做三角形的内切圆。
2、三角形的内心三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心。
圆和圆的位置关系 1、圆和圆的位置关系
如果两个圆没有公共点,那么就说这两个圆相离,相离分为外离和内含两种。
如果两个圆只有一个公共点,那么就说这两个圆相切,相切分为外切和内切两种。
如果两个圆有两个公共点,那么就说这两个圆相交。
2、圆心距
两圆圆心的距离叫做两圆的圆心距。
3、圆和圆位置关系的性质与判定
设两圆的半径分别为R 和r ,圆心距为d ,那么
两圆外离⇔d>R+r 两圆外切⇔d=R+r 两圆相交⇔R-r<d<R+r (R ≥r ) 两圆内切⇔d=R-r (R>r )两圆内含⇔d<R-r (R>r ) 4、两圆相切、相交的重要性质
如果两圆相切,那么切点一定在连心线上,它们是轴对称图形,对称轴是两圆的连心线;相交的两个圆的连心线垂直平分两圆的公共弦。
D
E C
B
P
A O B
A O1
O2
C O2
O1
B A
圆内正多边形的计算
1.正三角形在⊙O 中△ABC 是正三角形,有关计算在Rt BOD ∆中进行:::1:3:2OD BD OB =;
2.正四边形
同理,四边形的有关计算在Rt OAE ∆中进行,::1:1:2OE AE OA =: 3.正六边形
同理,六边形的有关计算在Rt OAB ∆中进行,::1:3:2AB OB OA =. 弧长和扇形面积
1、弧长公式n °的圆心角所对的弧长l 的计算公式为180
r
n l π= 2、扇形面积公式lR R n S 2
13602==
π扇 其中n 是扇形的圆心角度数,R 是扇形的半径,L 是扇形的弧长。
3、圆锥的侧面积rl r l S ππ=∙=
22
1
其中L 是圆锥的母线长,r 是圆锥的底面半径。
内切圆及有关计算。
(1)三角形内切圆的圆心是三个内角平分线的交点,它到三边的距离相等。
(2)△ABC 中,∠C=90°,AC=b ,BC=a ,AB=c ,则内切圆的半径r=2
c
b a -+。
(3)S △ABC =
)(2
1
c b a r ++,其中a ,b ,c 是边长,r 是内切圆的半径。
拱高问题
1.如图,圆弧形桥拱的跨度AB =12米,拱高CD =4米,则拱桥的半径为()
A .6.5米
B .9米
C .13米
D .15米 2.如图,用表示主桥拱,设所在圆的圆心为O ,半径为R .经过圆心O 作弦AB 的垂线OC ,D 为垂足,
OC 与AB 相交于点D ,根据前面的结论,D 是AB 的中点,
C 是的中点,C
D 就是拱高.
S
l
B
A
O
A B。
