力矩分配法解对称结构
结构力学练习题及答案
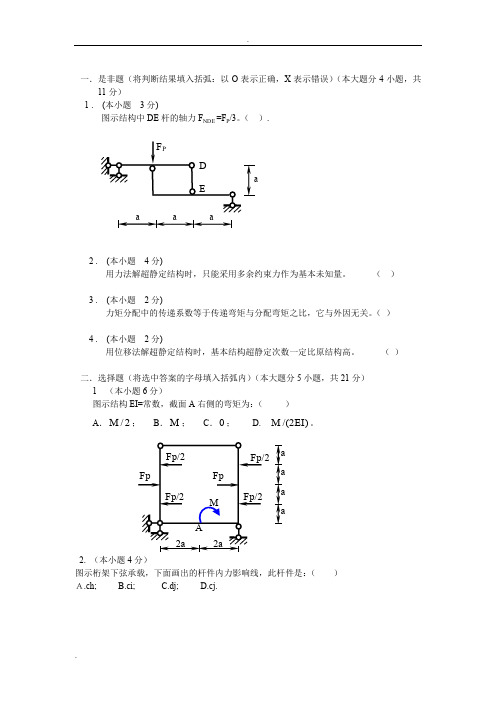
一.是非题(将判断结果填入括弧:以O 表示正确,X 表示错误)(本大题分4小题,共11分)1 . (本小题 3分)图示结构中DE 杆的轴力F NDE =F P /3。
( ).2 . (本小题 4分)用力法解超静定结构时,只能采用多余约束力作为基本未知量。
( )3 . (本小题 2分)力矩分配中的传递系数等于传递弯矩与分配弯矩之比,它与外因无关。
( )4 . (本小题 2分)用位移法解超静定结构时,基本结构超静定次数一定比原结构高。
( )二.选择题(将选中答案的字母填入括弧内)(本大题分5小题,共21分) 1 (本小题6分)图示结构EI=常数,截面A 右侧的弯矩为:( )A .2/M ;B .M ;C .0; D. )2/(EI M 。
2. (本小题4分)图示桁架下弦承载,下面画出的杆件内力影响线,此杆件是:( ) A.ch; B.ci; C.dj; D.cj.F p /2M2a2a a aa aA F p /2F p /2 F p /2F p F pa a aa F PED3. (本小题 4分)图a 结构的最后弯矩图为:A. 图b;B. 图c;C. 图d;D.都不对。
( )( a) (b) (c) (d)4. (本小题 4分)用图乘法求位移的必要条件之一是: A.单位荷载下的弯矩图为一直线; B.结构可分为等截面直杆段; C.所有杆件EI 为常数且相同; D.结构必须是静定的。
( ) 5. (本小题3分)图示梁A 点的竖向位移为(向下为正):( ) A.F P l 3/(24EI); B. F P l 3/(!6EI); C. 5F P l 3/(96EI); D. 5F P l 3/(48EI).三(本大题 5分)对图示体系进行几何组成分析。
A l /2l /2EI 2EIF Pa d c eb fgh iklF P =11j llM /4 3M /4M /43M /43M /4M /4M /8 M /2EIEIM四(本大题 9分)图示结构B 支座下沉4 mm ,各杆EI=2.0×105 kN ·m 2,用力法计算并作M 图。
【doc】用对称性简化力矩分配法计算刚架实例

用对称性简化力矩分配法计算刚架实例用对称性简化力矩分配法计算刚架实例解超静定结构的方法很多,以位移法为基础的力矩分配法,是其中一种比较实用的渐近法,它可以避免建立和解算联立方程.本文则又运用对称性进一步简化力矩分配法,尽量减少节点角位移的未知数,使计算很快收敛.现举--I程实俪说明如下.已知-由2根截面惯性矩为I,的主粱和2根截面惯性矩为I的端粱剐性连接组成的双粱式起重机桥架,当大车纵向运行机构起动和翩动时,P和c1分别代表在水平面内由带载小车质量和桥梁质量引起的惯性力.试用力矩分配法怍出此桥架由水平面内荷载引起的夸矩图.结构的计算简图见图1.解t为保证桥架正常运行发生偏斜时不被楔住,桥架滔常取B》L/6.现假设B=L/6,lL/9,C=L/36,I.=4I,PqLo为运用对称性,现将图1(a)变动一下,调整成图1(b).即在粱两端的A,S点,各增加1根沿Y轴方向的支座连杆'这样荷载对Y轴是对称的,对z轴是反对称的.根据对称性原理,Y向支杆反力都相等,图1(a)中Ry=p十q=2p,圈l<b)中,R;=(p+qL)/2=p|图l(a),(b)只表现为浦端粱轴力不周,其他内力分置都相同.由于轴向力对位移的影响,对以弯曲变形为主的剐架来说.通常极其赦小,可以忽略.因此.我们完全可以用图l(b)代图1(a)来分析剐架的内力,这样我们可以设想沿Y轴Z轴将剐架切取出嗪结构的1/4加以研究(见图2).根据结构,荷载均对称于Y轴所知,图2中K截面的内力分量中剪力QK=0,而位移分量中转角:0.对Z轴因结构对称,荷载反对称,故端粱中间截面0的内力分量轴力和弯矩均等予零(No=0,M.=O),而位移分量vo=0.与fa,-RPR(b1.图1桥辈水平面受力图(a)一正常运行的受力图l(b)一调整为对#性求解对的受力图Y图2四分之一挢架受力分析简图此内力,位移等效的约束条侔,应是在0点娃加一水平支杆,而在K截面处则设置一个定向支座.由图2简化的1/4剐架,是一个无侧移的简单目架,用力矩分配法求解时,只辩对节点J进行力矩分配和传递.与节点J刚接的杆件有JK杆,J0 杆,JD秆三杆,线刖度备为-TiIK=II/詈:BI/L,:18I/Li】D=I/L136:36I/L根据文献[1]中表10-1,可查得节点J各l_端劲度系数的总和为:璐JJ=j』I十3i,o十31】D=IV0L/L'p寰1杆端弯矩计算(圈2)点:…0JKD杆端0JJojDJKxJDJ分配雨魏0.817050.6290.0{706固端_鸯炬O—PL/3—7PL/24分配弯矩与抟递弯矩o.10j88PL8.2116PL0.0150BPL一0.015087PL 最终弯矩00.10588PL0.81I6PL一001764PL一0.80735PL则各杆端分配系数为:JK=SK,磷【j=i/n=0.(~470BI=S~o/XSn=3iI./】{0.31765D=Sm/ES~l=3ilD/=S;=0.63529各杆传递系数为{ClK=一l,C】.=Cm=0各耔厣端弯矩为(颧时针为正):M}K:一等一导=一孚Ml】=二鲁一半=一Jo杆,JD杆:因两杆无荷载,故固端弯矩均为零,即M=M=0.这样节点J的不平衡力矩是三Mf:M+Mfo+M=-PL/3将此不平橱力矩反号乘以各耔端分配系数,即得出各杆端的分配弯矩,再将分配弯矩乘吼传递系数,即相应得出各杆远端弯矩.最届把固端弯与分配弯矩.传递弯矩相加,即可得出结构稆应的各杆端最终弯矩(见表1).超静定结构计算结果,通常应满足静力平撕条件和变形协调关系关于静力平衡可根据每一节点处EM=0进行校核,由于在上避力矩分配法中,每次分配已使节点平衡,因此,无需再作碴棱.到}变形协调问题,可根据各节点处汇交各枵的秆端角位移币是否相同来进行验证.即可在力矩分配浩计算完成岳,将任一端i的最终弯矩与定弯矩相减得出Ⅵik,然后减去它端的△M之半后,捡盎每一节点所得AM,一昙M是否与相立各杆的线刚度l成比倒,见公式(1)|(M一{砒.):({△M)-..…iI;i¨: (1)现以节点J校核之.这里应注意的是,此时对正对称轩JK应取顾杆弹JT的线尉度表示,见表2. 寰2节点J变形协啊的技赣t根据公式(1),将表2中!文值代一得(△M.一dM.,):(厶M—M(M一)珊=7m!——氟凰3最终弯矩乓挠受图示(左半为弯矩圈,右半为瓷度到)=0.10588PL:0.21176PL:0.02353PL=4.5:0:1(下转第l8页)+28mc.一60m.hc一72m.hc:+36m.ch一24mhc.+12mhca+24mhc一9mc一12hc+c1 (22)在m≤x≤h区域内V=Vq+V+v一茜(X26h乙4hx)+酱(3x叫十(3x刊(23)当x:h时的挠虚最大,将x=h和式(18)中的H-H2代入式(23)中,整理后得.一~24EJ(m-c)(4m-c)xf--12h'Ⅱ1+15h'mc-3h'c.+1812].ch.+5m'hc--36hmc+l4mh+36m.h.--36mh+18121ch一3me3h一16m.c=h十mc+3n,.c.--2m一2mc,(24)c,m值求解为使整根烟囱的弯曲应力和弯曲挠度最小,应使V一AxVI"Vm一为此可建立方程组求解…~~(25)LVc…IV—n…x将式(20),(22),(24)代入式(25) 中,可列出如下方程组16m一27mc一48m'h一3mc ÷24m.h+120mhc+28mc.一60mhc~96m!ch+48mch+24hc.一l6mc'一12h.c.+2c=048m+5mc一272mh一25mc. +600mh40m'hc一20m.c--348m.h.C+184m.hc一576mh.一252mchJ'24mhc.J'192hIll+576hm.c+12mhc.+24mhc一9mc一240h'mc一12hc'+48hc!+c.=0解得c:0.420h,m=0.835h将c,m值代人式(18),可得H=0.42qh,H2=0..949qh点,结论根据上述理论分析计算,为使钢板烟囱内力较小,缆风绳处支点挠度较小,在~道缆风绳时,缆风绳的支点高度应设在烟晦l高度0:715h处;在二遗缆风绳时,下道缆风绳的支点高度,应设在烟囱高度的0.42h处,上道缆风绳的支点高度,应设在烟囱高度的0.835h处,较为合适.当然,实际工程设计中,尚应根据气候和周围环境进行调整和媾正,以及按此原理另行计算本文不妥处尚冀专家指正.(上接第60页)而,.:T18L:丁36I.:T41o=18:38:4:4.5:g:1这表明变形调条件也是满足的.最后,根据备杆端最终弯矩,利用对称性就不难画出原超静定刚架的弯矩图了(见图3).丽由弯矩图即可进而大致绘出挠曲线,弯矩为零处亦即是18挠曲线拐点.参考文献t11湖南大学结构力学教研室编,结构力学(下册),高等教育出版社,1983年【21程重机设计手册,机械二业出版{±.188D年I3】徐光晋主犏,金属结构,机械工业出版社. 1982年(生桐簋厂职工丈学藏洪锥)。
结构力学试卷(计算)

题目部分,(卷面共有100题,1232.0分,各大题标有题量和总分)一、非客观(100小题,共1232.0分)(12分)[1]求作图示结构的弯矩图。
EI =常数,二力杆EA =∞.q =3kN/m(12分)[2]图示体系各柱EI =常数,柱高均为l ,θ=(/())183EI ml 。
求最大动力弯矩。
(12分)[3]求图示体系的自振频率及绘主振型图。
l l /2/2/2(12分)[4]求图示结构中BE 杆的伸缩变形。
已知:EA EI ==⋅10310552kN kN m ,。
4m 2m(12分)[5]求作图示结构的M 图及结点B 的转角ϕB 。
EI =常数。
10kN/m3m(12分)[6]求图示结构D 截面的转角ϕD 。
EI =常数。
l/l ll/2l/2(12分)[7]作图示结构的M 图。
除注明者外,其余各杆EI =常数。
l(12分)[8]求图示梁结构刚度矩阵的各元素K K K K 11122122,,,。
C (12分)[9]图示结构,已知EI 及B支座的弹簧系数k EI l =33/,试用位移法计算,并作M 图。
(10分)[10]求作图示刚架的M 图。
EI =常数。
l /2l l /3l /3(12分)[11]求图示结构杆C 轴力及B 支座反力。
a /2a /2a /2(12分)[12]图示梁端支承抗转弹簧刚度k 12700=⋅kN m /rad ,梁的弹性模量E =⨯200106kN /m ,2 m 4I =⨯-160106。
求作梁的弯矩图。
B k 1q(12分)[13]图示刚架,EI =常数,P =1在AB 间移动。
求反力矩M C 的影响线。
l(12分)[14]求作图示结构的弯矩图。
各杆相对线刚度如图所示。
(12分)[15]利用结构的对称性,选择恰当的方法计算,并作出图示结构的M 图。
EA =∞。
EA EA(11分)[16]绘图示梁的M C 、Q C 的影响线。
(12分)[17]用力法计算图示结构,并绘出M 图。
力矩分配法计算超静定结构典型例题(附详细解题过程)

力矩分配法计算超静定结构——典型例题
【例1】用力矩分配法作如图1(a)所示连续梁的弯矩图。
已知EI 为常数。
【解】该连续梁为对称结构承受对称荷载作用,可取如图1(b)所示左半结构来分析。
此时,只有一个结点转角,可以采用力矩分配法进行分析,这里记线刚度。
计算结点B 处的分配系数:
,
, 在结点B 加入附加刚臂,计算由荷载单独作用时产生的各杆端固端弯矩值
, 附加刚臂中产生的约束力矩为:
放松结点B ,力矩分配和传递的过程如图1(c)所示。
根据最后的杆端弯矩可先绘制半结构的M 图,再根据对称性可绘出整个结构的M 图,如图1(d)所示。
/i EI l =3BA S i =4BC S i =BA 3
7μ=BC 47
μ=12F AB M Fl =-14
F BA M Fl =-14
B M Fl =
-
图1
【例2】用力矩分配法作如图2(a)所示刚架的弯矩图。
已知EI 为常数。
【解】该对称刚架承受对称荷载作用,可取如图2(b)所示半结构来分析,可采用力矩分配法分析,记线刚度。
计算结点A 处的分配系数:
,
在结点A 加入附加刚臂,各杆均无固端弯矩,附加刚臂中产生的约束力矩为:
放松结点B ,将约束力矩反号后进行分配和传递,可得各杆端的分配、传递弯矩分别为:
根据各杆端弯矩值可绘制结构构的M 图,如图2(c)所示,为对称的图形。
/i EI l =3AB S i =A 3C S i =AB AC 0.5μμ==A M Fl =-12
AC AB M M Fl μμ==0C C CA BA M M ==。
§8-2_多结点的力矩分配法
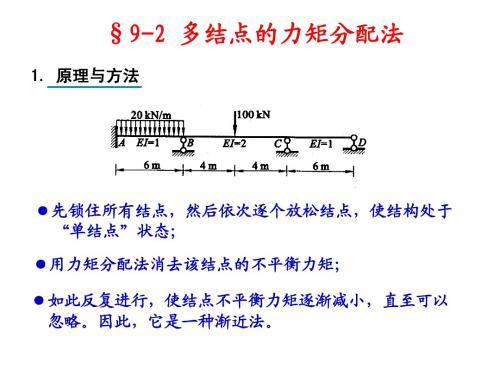
1. 原理与方法
●先锁住所有结点,然后依次逐个放松结点,使结构处于 “单结点”状态; ●用力矩分配法消去该结点的不平衡力矩; ●如此反复进行,使结点不平衡力矩逐渐减小,直至可以 忽略。因此,它是一种渐近法。
下面做一个薄钢片连续梁的试验:
FP
原结构在荷载作用下, 发Hale Waihona Puke 如图所示的变形。(刚架的荷载)
M图
▲ 悬臂端的处理
[例3] 解图示带悬臂的等截面连续梁。 ⑴ 锁住结点B、C 固端弯矩: F M CD 50kN m ⑵ 放松结点C EI SCB=4iCB 4 5 SCD=0 CB=1 CD=0
先 处 理 悬 臂
⑶ 放松结点B(C铰支不再锁固) EI EI S BC=3 S BA 3 5 1 5 1 BA= BC= 6 6
3. 例题 [例1] 试求作图示连续梁的弯矩图。
解: ⑴ 求结点的分配系数 1 0.667 结点B: S BA=4i BA 4 0.667 BA= 0.4 6 1 0.667 2 1 S BC=4i BC 4 1 BC= 0.6 8 1 0.667 结点C: SCB=4i BC 4
FP 1 2
把1、2结点锁固,使其 变成3个独立的单跨梁。
把1号刚臂放松,相当于 释放了支座处的不平衡 力矩。
FP 1
FP 1 2
2
把1号结点锁住,放松2 号刚臂。如此反复进行, 结构的变形越来越接近 原结构。
把刚才的实验过程体现在解题上:
FP 1 2
原结构
把结点固定起来,求 固端弯矩。 用单结点的力矩分配 法,对1结点的不平衡 力矩进行分配。 锁住1结点,用单结点 的力矩分配法,对2结 点的不平衡力矩进行分 配。
结构力学复习题
B.对计算和计算结果有影响;
C.对计算无影响;
D.对计算有影响,而对计算结果无影响。
07.在力矩分配法计算中,传递系数 为:()
A.B端弯矩与A端弯矩的比值;
B.A端弯矩与B端弯矩的比值;
C.A端转动时,所产生A端弯矩与B端弯矩的比值;
D.A端转动时,所产生B端弯矩与A端弯矩的比值。
B.只有 时,由于 在附加约束i处产生的约束力;
C. 在附加j处产生的约束力;
D.只有 时,由于 在附加约束j处产生的约束力。
06.杆件杆端转动刚度的大小取决于______________与______________。
07.位移法可解超静定结构,解静定结构,位移法的典型方程体现了___________条件。
20.用力法作图示结构的M图。
21.用力法作M图。各杆EI相同,q=40kN/m,l=3m。
22.用力法作M图。各杆EI相同。
23.用力法作M图。各杆EI相同,杆长均为3m, 28kN/m。
24.用力法求图示桁架支座B的反力。各杆EA相同。
25.用力法求图示桁架支座B的反力。 ,各杆A相同。
26.已知图示结构的 图(仅 杆承受向下均布荷载),求 点竖向位移 。各杆 相同,杆长均为 m。
15.对图示体系进行几何组成分析。
16.对图示体系进行几何组成分析。
17.对图示体系进行几何组成分析。
18.对图示体系进行几何组成分析。
19.对图示体系进行几何组成分析。
二.静定结构内力计算
01.静定结构的全部内力及反力,只根据平衡条件求得,且解答是唯一的。()
02.静定结构受外界因素影响均产生内力。大小与杆件截面尺寸无关。()
结构力学——力矩分配法分解课件
THANK YOU
复杂结构的力矩分配法分析
总结词
需要对复杂结构进行精细的力矩分配
详细描述
对于复杂结构,如桥梁、高层建筑等,力矩分配法需要更加精细的分析。这需要对结构的各种参数进 行详细的计算和调整,包括转动刚度、分配系数、传递系数等。通过合理的简化模型和精细的计算, 可以获得结构的整体性能和局部细节,满足工程设计的需要。
应用范围
适用于具有刚性转动 部分的连续梁和框架
适用于具有弹性支撑 的连续梁和框架
适用于具有弹性转动 部分的连续梁和框架
适用条件
结构体系为连续梁或框架 结构具有刚性转动部分,且转动部分在分配力矩后不会出现弹性变形
结构具有弹性支撑,且弹性支撑在分配力矩后不会出现弹性变形
计算复杂度与精度要求
力矩分配法的计算复杂度取决于梁和框 架的自由度数量,自由度越多,计算越
。
误差传递
由于传递系数和分配系数的近似 计算,可能会引入一定的误差,
影响分析结果的准确性。
计算复杂度
对于大型复杂结构,力矩分配法 的计算量可能会变得很大,需要
借助计算机辅助分析。
改进与发展方向
01
02
03
04
数值优化
通过改进算法和优化计算方法 ,提高力矩分配法的计算效率
和精度。
考虑非线性因素
将非线性因素纳入力矩分配法 中,以适应更广泛的结构类型
在力矩分配法中,将结构中的结点分为两类:基本结点和附属结点。基本结点是承 受力矩的结点,附属结点则是传递力矩的结点。
力矩分配法的原理是将所有结点的力矩自由度进行分配,通过调整传递系数来使各 结点的力矩平衡,从而求解出各个结点的位移。
刚度系数与传递系数
刚度系数是指单位力矩作用下结 点的位移,它反映了结点的刚度
第8章力矩分配法
1 4
传递系数
远端固定,CAB=0.5
远端简支,CAD=0
远端滑动,CAC=-1
D i
分配系数
AB
2 3
AC
1 12
AD
1 4
120kNm
A
2i
i
C
传递系数
CAB=0.5
CAD=0
CAC=-1
B
D
80kNm A 30kNm
B 40kNm
10kNm C
M图
杆端弯矩
M AB
AB M
2 *120
3
固端弯矩
分配和传 递弯矩 杆端弯矩
A -150 -17.2
-167.2
分配系数
4 7
150
3 7
B
-90
-34.3 -25.7
115.7 -115.7
167.2 A
115.7
300
90
B 32.1
158.5
M图(单位kNm)
C 0 0 0 单位kNm
C
单结点力矩分配法计算举例
3)非结点荷载作用刚架
渐近法概述
1、线性代数方程组的解法: 直接法,渐进法
2、结构力学的渐近法:
力学建立方程,数学渐近解 不建立方程式,直接逼近真实受力状态。其 突出的优点是每一步都有明确的物理意义。
3、位移法方程的两个特点:
(1)每个方程一般不超过五项式; (2)主系数大于副系数的总和,即 kii > kij,
适于渐近解法。
80kNm
M AC AC M 10kNm
M AD AD M 30kNm
M BA CAB M AB 40kNm
M CA CAC M AC 10kNm
结构力学 课件 力矩分配法
SAB
1
2 传递系数C
传递系数: 一单跨超静定梁的一端(A端)单位转角时,发生于远 端(B端)的弯矩与近端(A端)的弯矩之比。
如: 当远端(B端)固定,C AB
M
BA
SAB
1 2 S AB
MBA
A B
图(a)
1
C 当远端(B端)铰支 , AB
M
SAB
A
B
BA
0
SAB
A
1
图(b)
S AB
(1)设想在结点B增加一个附加刚臂,得到位 移法基本结构。阻止其转动如图(g)所示。 查表容易得到各单跨超静定梁的杆 端弯矩。则附加刚臂的约束力矩由 结点B的平衡条件得
M
B
Fp
A
q
B C
图(f)
MB
A
Fp
B
q
C
图(g)
M
F BA
M
F BC
MB MBAF -MB
A B C
附加刚臂的约束力矩MB 是原结构 上所没有的,它反映了基本结构汇 交于B结点的各杆B端弯矩所不能平 衡的差额。我们称之为B结点的不 平衡力矩。
MBCF
图(h)
(2)原结构在结点B本来没有转动约束,即不存在不平衡力矩MB ,因 此,为了与实际情况相符,必须消除人为引入的附加刚臂,即使MB 0,这就相当于在 MB的基础上再施加上一个(- MB )如图(h)所示。
此时梁将产生新的杆端弯矩M´BA 、 M´BC (分配弯矩),在远端将产生新 的杆端弯矩M´AB 、 M´CB 、(传递弯 矩)。 (3)原结构在荷载的作用下的实际杆端弯 矩应为图(g) 和图(h)两种情况的叠加。 下面举例说明力矩分配法的解题过 程。
(完整版)结构力学2期末考试复习题(2)
一、判断题:1、力矩分配法中的分配系数、传递系数与外来因素(荷载、温度变化等)有关。
( )2、若图示各杆件线刚度i 相同,则各杆A 端的转动刚度S 分别为:4i ,3i ,i 。
(√)AAA3、图示结构EI =常数,用力矩分配法计算时分配系数4 A μ=4/11。
()1234Allll4、图示结构用力矩分配法计算时分配系数μAB =12/,μAD =18/。
(√)BCADE=1i =1i =1i =1i 5、用力矩分配法计算图示结构,各杆l 相同,EI =常数。
其分配系数μBA =0.8,μBC =0.2,μBD =0。
(√)ABCD6、单元刚度矩阵反映了该单元杆端位移与杆端力之间的关系。
(√)7、单元刚度矩阵均具有对称性和奇异性。
(X )8、局部坐标系与整体坐标系之间的坐标变换矩阵T 是正交矩阵。
(√)9、结构刚度方程矩阵形式为:[]{}{}K P ∆=,它是整个结构所应满足的变形条件。
(X )10、矩阵位移法中,等效结点荷载的“等效原则”是指与非结点荷载的结点位移相等。
(√)二.选择题(1)欲使图2-1所示体系的自振频率增大,在下述办法中可采用:(D)A.增大质量m;B.将质量m移至梁的跨中位置;C.减小梁的EI;D.将铰支座改为固定支座。
图2-1k,就其(2)平面杆件结构一般情况下的单元刚度矩阵[]66⨯性质而言,是:(B)A.非对称、奇异矩阵;B.对称、奇异矩阵;C.对称、非奇异矩阵;D.非对称、非奇异矩阵。
(3)已知图2-3所示刚架各杆EI=常数,当只考虑弯曲变形,且各杆单元类型相同时,采用先处理法进行结点位移编号,其正确编号是:(A)图2-3二、用力矩分配法计算图2所示结构M 图。
EI =常数。
6图2解:1、固端弯矩3分m kN M AB ⋅=9(上侧受拉)(2分),0=BAM (1分)2、分配系数6分(各2分)ABμ=0.5,31=AC μ,61=AD μ3、弯矩图画对6分(各1分)m kN M AB ⋅=5.4(上侧受拉),m kN M AD ⋅=5.1(上侧受拉)m kN M AC ⋅=3(右侧受拉),m kN M DA ⋅=5.1(上侧受拉)m kN M CA ⋅=5.1(右侧受拉),0=BA M三、用力矩分配法计算图3所示结构,并绘M 图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
力矩分配法解对称结构
对称结构的力矩分配法是一种结构力学设计分析的有效方法,它的定义是指将结构的力矩由支撑点分配到结构支撑点上的一种方法。
力矩分配法是一个结构力学分析的关键步骤,它将结构力学分析结果转化为实际的结构力学设计。
对称结构的力矩分配法利用坐标轴对齐方法来进行分配,将结构整体化为两个相等的部分,然后将所有工作荷载分配到支撑点上,并计算出结构力学所需的变形量。
需要考虑到力矩分配法计算中可能存在的以下情况:工作的参数是一个完整的参数方程,包括支撑节和载荷单元;变形在计算中也必须考虑;整体考虑将更有效地恢复力学力;用户可以根据需要选择坐标轴对齐来完成支撑点的计算;同时,有必要考虑结构性能和消耗性能的要求。
力矩分配法可以帮助结构工程师更加精确地将荷载透过支撑点传导给结构,使结构能够更加稳定。
力矩分配法还具有预期风险和安全性考虑的优势,包括:力矩分配法可以帮助分析者更加精确地识别结构中所受荷载的支撑点;并且,如果荷载变化,可以快速地找到结构中最具有风险的点,可以更有效地确定力学变形量;最后,可以根据实际需要,选择合适的坐标轴来进行力矩分配法。
总之,力矩分配法是一种有效的分析和设计方法,可以帮助结构工程师精确地将荷载分配到支撑点上,提高结构的安全性和稳定性。
力矩分配法的使用需要考虑到结构的力学参数和变形能力以及工作环境的要求,才能有效地进行力矩分配计算。
