大学数学(高数微积分)专题七第1讲(课堂讲解)
合集下载
《微积分》(上下册) 教学课件 01.第1章 函数、极限、连续 高等数学第一章第9-10节
12
定义 2 设函数 f ( x)在U(x0, )内有定义,如果
y
lim f (x) f (x ),
x x0
0
y f (x)
称函数 f ( x)在点 x 连续. 0
如 f ( x) x2,
0
x0
x
lim f ( x) lim x2 4 f (2),
x2
x2
f ( x) x2在x 2点连续.
说明 y f (x)在x x0点连续 下列三条同时成立 (1) f (x0)有定义;
(2) lim f (x)存在; xx0
(3)lim x x0
f
(x)
f (x0 ).
13
例1
试证函数
f
ห้องสมุดไป่ตู้
(
x)
x
sin1 x
,
0,
处连续.
证 lim x sin 1 0,
x0
x
又 f (0) 0, lim f ( x) f (0), x0
3、反函数函数的连续性
严格单调的连续函数必有严格单调的连续反函数. 例如, y sin x在[ , ]上单调增加且连续,
22 故 y arcsinx 在[1,1]上也是单调增加且连续.
同理 y arccosx 在[1,1]上单调减少且连续;
y arctanx, y arccot x 在(,)上单调且连续.
§1.9 无穷小量的比较与等价代换
例如, 当x 0时, x, x2,sin x, x2 sin 1 都是无穷小.
x2
lim 0,
观
x0 x
x x2比x要快得多;
察 各 极 限
lim sin x x0 x
定义 2 设函数 f ( x)在U(x0, )内有定义,如果
y
lim f (x) f (x ),
x x0
0
y f (x)
称函数 f ( x)在点 x 连续. 0
如 f ( x) x2,
0
x0
x
lim f ( x) lim x2 4 f (2),
x2
x2
f ( x) x2在x 2点连续.
说明 y f (x)在x x0点连续 下列三条同时成立 (1) f (x0)有定义;
(2) lim f (x)存在; xx0
(3)lim x x0
f
(x)
f (x0 ).
13
例1
试证函数
f
ห้องสมุดไป่ตู้
(
x)
x
sin1 x
,
0,
处连续.
证 lim x sin 1 0,
x0
x
又 f (0) 0, lim f ( x) f (0), x0
3、反函数函数的连续性
严格单调的连续函数必有严格单调的连续反函数. 例如, y sin x在[ , ]上单调增加且连续,
22 故 y arcsinx 在[1,1]上也是单调增加且连续.
同理 y arccosx 在[1,1]上单调减少且连续;
y arctanx, y arccot x 在(,)上单调且连续.
§1.9 无穷小量的比较与等价代换
例如, 当x 0时, x, x2,sin x, x2 sin 1 都是无穷小.
x2
lim 0,
观
x0 x
x x2比x要快得多;
察 各 极 限
lim sin x x0 x
大学课程《微积分》PPT课件:微积分7章1节

1
正确答案选(C)。
例 3 判别级数
1
n1 (2n 1)(2n 1)
= 1+
1+
1 +…+
13 35 57
1
+…的敛散性,
(2n 1)(2n 1)
若收敛则求其和。
解 由于
un
(2n
1 1)(2n
1)
1 2
(1 2n 1
1) 2n 1
所以级数的部分和
Sn
=1 13
+1 35
+1 57
+…+
1 (2n 1)(2n 1)
例3(讲义例3)讨论等比级数(又称为几何级数)
aqn a aq aq2 aqn
n0
(a 0) 的收敛性.
注:几何级数是收敛级数中最著名的一个级数.阿贝尔曾经指出“除了几何级数 之外,数学中不存在任何一种它的和已被严格确定的无穷级数”.几何级数在判断 无穷级数的收敛性、求无穷级数的求和以及将一个函数展开为无穷级数等方面都有 广泛而重要的应用.
(4)级数收敛的必要条件:若级数
un
n1
收敛,则
lim
n
un
0
例 1 讨论几何级数(也叫等比级数)
aq n1 = a+ aq+ aq2 +…+aq n1 +… (a≠0,q≠0)
n 1
的敛散性,若收敛则求其和。
解 级数的部分和
Sn
a(1 qn ) ; q 1q
1
na; q 1
(1)当
q
1
1
11
解 由于 n1 3n 与 n1 7 n 都是几何级数,公比分别为 3, 7,
大学数学(高数微积分)专题五第1讲解析几何(课堂讲义)

x,y的系数应对应相等.
主干知识梳理
4.圆的方程的两种形式
(1)圆的标准方程:(x-a)2+(y-b)2=r2.
(2)圆的一般方程:x2+y2+Dx+Ey+F=0(D2+E2-4F>0).
本 讲
5.直线与圆、圆与圆的位置关系
栏 目
(1)直线与圆的位置关系:相交、相切、相离,代数判断法与
开 关
几何判断法.
本
讲 栏 目
=12sin∠AOB≤12.
开 关
当∠AOB=2π时,S△AOB面积最大.
此时O到AB的距离d=
2 2.
设AB方程为y=k(x- 2)(k<0),
即kx-y- 2k=0.
热点分类突破
由d=
|k22+k|1=
22得k=-
3 3.
(也可k=-tan∠OPH=- 33).
(2)设P(x,0),设C1(2,3)关于x轴的对称点为C1′(2,-3),
即x2+(y+1)2=4,
所以点M在以D(0,-1)为圆心,2为半径的圆上.
由题意,点M(x,y)在圆C上,所以圆C与圆D有公共点, 则2-1≤|CD|≤2+1,
热点分类突破
即1≤ a2+2a-32≤3.
由5a2-12a+8≥0,得a∈R;
本
讲 栏 目
由5a2-12a≤0,得0≤a≤152.
开 关
k 2
,0)位于直线x-y-1
=0上,于是有-2k-1=0,即k=-2,
因此圆心坐标是(1,0),半径是1.
由题意可得|AB|=2 2,直线AB的方程是-x2+2y=1,
热点分类突破
即x-y+2=0,圆心(1,0)到直线AB的距离等于
|1-0+2| 2
高等数学第七章第一节微分方程的基本概念课件.ppt

解: 如图所示, 点 P(x, y) 处的法线方程为
令 Y = 0 , 得 Q 点的横坐标
即 yy 2x 0
y P
Qo xx
引例1 通解:
dy dx
2x
y x1 2
引例2
y x2 C
d2y dx2
0.4
s t0 0 ,
ds dt
t0 20
s 0.2t 2 C1t C2
特解: y x2 1
s 0.2t 2 20t
例1. 验证函数 是微分方程
(C1 , C2为常数 )
的解, 并求满足初始条件
x
t0
A, dx
dt
t00
的特解 .
解:
k 2 (C1 sin kt C2 cos kt ) 这说明 x C1 cos kt C2 sin kt 是方程的解 .
是两个独立的任意常数, 故它是方程的通解.
利用初始条件易得:
故所求特解为
x Acos k t
例2. 已知曲线上点 P(x, y) 处的法线与 x 轴交点为 Q 且线段 PQ 被 y 轴平分, 求所满足的微分方程 .
微分方程的基本概念
含未内容)
分类 偏微分方程
方程中所含未知函数导数的最高阶数叫做微分方程 的阶.
一般地 , n 阶常微分方程的形式是
F (x, y, y,, y(n) ) 0
或 y(n) f (x, y, y,, y(n1) ) ( n 阶显式微分方程)
微分方程的解 — 使方程成为恒等式的函数.
通解 — 解中所含独立的任意常数的个数与方程 的阶数相同.
特解 — 不含任意常数的解, 其图形称为积分曲线.
定解条件 — 确定通解中任意常数的条件.
令 Y = 0 , 得 Q 点的横坐标
即 yy 2x 0
y P
Qo xx
引例1 通解:
dy dx
2x
y x1 2
引例2
y x2 C
d2y dx2
0.4
s t0 0 ,
ds dt
t0 20
s 0.2t 2 C1t C2
特解: y x2 1
s 0.2t 2 20t
例1. 验证函数 是微分方程
(C1 , C2为常数 )
的解, 并求满足初始条件
x
t0
A, dx
dt
t00
的特解 .
解:
k 2 (C1 sin kt C2 cos kt ) 这说明 x C1 cos kt C2 sin kt 是方程的解 .
是两个独立的任意常数, 故它是方程的通解.
利用初始条件易得:
故所求特解为
x Acos k t
例2. 已知曲线上点 P(x, y) 处的法线与 x 轴交点为 Q 且线段 PQ 被 y 轴平分, 求所满足的微分方程 .
微分方程的基本概念
含未内容)
分类 偏微分方程
方程中所含未知函数导数的最高阶数叫做微分方程 的阶.
一般地 , n 阶常微分方程的形式是
F (x, y, y,, y(n) ) 0
或 y(n) f (x, y, y,, y(n1) ) ( n 阶显式微分方程)
微分方程的解 — 使方程成为恒等式的函数.
通解 — 解中所含独立的任意常数的个数与方程 的阶数相同.
特解 — 不含任意常数的解, 其图形称为积分曲线.
定解条件 — 确定通解中任意常数的条件.
高等数学 同济大学第七版第1章第1节课件C1S1

那么称函数f (x)在X上有上界
y
K1 称为函数f (x)在X上的一个上界
类似可以定义函数f (x)在X上有下界
o
x
函数的几种特性
1.函数的有界性
设函数f (x) 的定义域为D,数集 X D
如果存在数 K1, 使得 f ( x) K1 对任一 x X 都成立
那么称函数f (x)在X上有上界
o
x
注 函数f (x)在X上有界
函数f (x)在X上既有上界,又有下界
例:f ( x) sin x 在(, )内有界,f ( x) 1 在(0, 1)内无界 x
函数的几种特性
2.函数的单调性
设函数f (x) 的定义域为D,区间 I D
y
如果对于区间I上的任意两点x1及x2,
积 f g ( f g)( x) f ( x) g( x), x D
商 f g
f ( x) f ( x) , x D \ x | g( x) 0
g g(x)
概念
概念
集映 合射
逆映射
区邻 间域
构造 复合映射
初等函数 函
反函数
数
复合函数 构造
四则运算
第一讲 映射与函数
映
特例
函
射
数
概念
映
函
射
数
映射的概念
定义 设X、Y是两个非空集合,如果存在一个法则f,使得 对X中每个元素x,按法则f,在Y中有唯一确定的元素 y与之对应,那么称f为从X到Y的映射,记作:y=f (x)
f Xx
原像
像
定义域
Y y
值域
注
(1) 映射的三要素:定义域、值域的范围、对应法则; (2) 映射的像唯一,但原像不一定唯一; (3) 映射又称为算子,在不同数学分支中有不同的名称
微积分讲解ppt课件

多元函数的表示 方法
多元函数可用记号 f(x1,x2,…,xn)或z=f(x,y) 表示。
多元函数的定义 域
使多元函数有意义的自 变量组合(x1,x2,…,xn) 的集合。
多元函数的值域
多元函数所有值的集合 。
偏导数与全微分
偏导数的定义
设函数z=f(x,y)在点(x0,y0)的某一邻域内有定义,当y固定在y0而x在x0处有增量Δx时,相应地函数有增量 f(x0+Δx,y0)-f(x0,y0)。如果Δz与Δx之比当Δx→0时的极限存在,那么此极限值称为函数z=f(x,y)在点(x0,y0)处对 x的偏导数。
齐次方程法
通过变量替换,将齐次方程转化为可分离变 量的形式
一阶线性微分方程法
利用积分因子,将方程转化为可积分的形式
二阶常微分方程解法
可降阶的二阶微分方程
通过变量替换或分组,将方程降为一阶微分方 程求解
二阶线性微分方程法
利用特征根的性质,求解二阶线性常系数齐次 和非齐次微分方程
常系数线性微分方程组法
在经济学中的应用
边际分析
通过求导计算边际成本、边际收益等,为企业的决策 提供依据。
弹性分析
研究价格、需求等经济变量之间的相对变化关系,微 积分可用于计算弹性系数。
最优化问题
在资源有限的情况下,通过微积分求解最大化或最小 化某一经济指标的问题。
在工程学中的应用
结构力学
分析建筑、桥梁等结构的受力情况和稳定性,微积分可用 于求解复杂的力学方程。
通过消元法或特征根法,求解常系数线性微分方程组
05
多元函数微积分
多元函数的基本概念
多元函数的定义
设D为一个非空的n元有 序数组的集合,f为某一 确定的对应规则。若对 于每一个有序数组 (x1,x2,…,xn)∈D,通过 对应规则f,都有唯一确 定的实数y与之对应, 则称对应规则f为定义在 D上的n元函数。
高等数学上册第七章课件.ppt
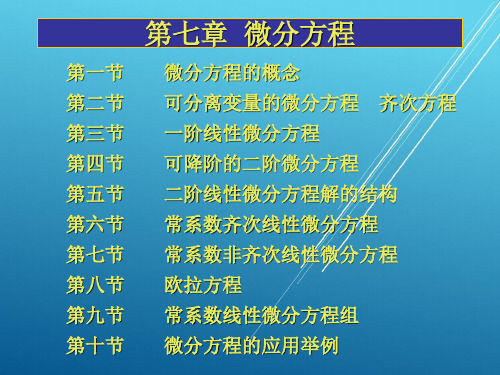
y C2 ex ,再利用 y (0) = 1 得 C2 1, 故所求曲线方程为
第四节 可降阶的二阶微分方程
小结 可降阶微分方程的解法 —— 降阶法
逐次积分
令 y p(x) ,
令 y p(y) ,
第五节 二阶线性微分方程解的结构
•n 阶线性微分方程的一般形式为
y(n) a1(x) y(n1) an1(x) y an (x) y f (x) f (x) 0 时, 称为非齐次方程 ; f (x) 0 时, 称为齐次方程.
第四节 可降阶的二阶微分方程
例 求解 解
代入方程得
则 y d p d p dy p d p dx dy dx dy
两端积分得 ln p ln y ln C1 , 即 p C1y,
(一阶线性齐次方程)
故所求通解为
第四节 可降阶的二阶微分方程
例
解初值问题
y e2y 0 y x 0 0 ,
y p(x) y q(x) y f (x), 为二阶线性微分方程.
复习: 一阶线性方程 y P(x) y Q(x)
通解:
y
C
e
P(x)d
x
eP(x)d x
Q(x) eP(x)d x dx
齐次方程通解Y 非齐次方程特解 y
第五节 二阶线性微分方程解的结构
•线性齐次方程解的结构
定理 若函数 y1(x), y2 (x) 是二阶线性齐次方程 y P(x) y Q(x) y 0
的两个解, 则 y C1y1(x) C2 y2 (x)
也是该方程的解. (叠加原理)
证 将 y C1y1(x) C2 y2 (x) 代入方程左边, 得 [C1y1 C2 y2 ] P(x)[C1y1 C2 y2 ]
高数(第七版)第7章讲稿

说明 1的通解为:
y Q(x)e P(x)dxdx C1 e P(x)dx e P(x)dx Q(x)e P(x)dxdx C1e P(x)dx
这表明:一阶非齐次线性方程的通解等于对应于它 的齐次方程的通解加上该非齐次方程的一个特解.
例1.(P316,例1)求方程 dy 2 y (x 1)5/2的通解. dx x 1
从而 dy u x du ,方程 1变为u x du (u)
dx
dx
dx
即 du (u) u ,这是可分离变量方程,求出它的
dx
x
通解,再将u y 代入得1的通解.
x
例1P310?解方程 y2 x2 dy xy dy .
dx dx
解:先化为标准形式
(xy x2 ) dy y2 dx
解法 : 作换元,令 y p, y dp dx
原方程变为 dp f (x, p) 一阶方程 dx
设其通解为: p (x,C1),C1是任意常数 即 y (x,C1)
y (x,C1)dx C2 , (C1, C2是任意常数)
只表示一个原函数
例2.(P323,例3)求(1 x2) y 2xy的通解,并求满足初始
y C(x)(x 1)2 2C(x)(x 1)
代入原方程,得
C(x)(x 1)2 2C(x)(x 1) 2 C(x)(x 1)2 x 1
(x 1)5/2
C(x)(x 1)2 (x 1)5/2
C(x) (x 1)1/2
C(x)
(x
1)1/2 dx
2 3
(x
1)3/ 2
C1
y C(x)(x 1)2
过点(x0 , y0 )的那条积分曲线.
初值问题 3的几何意义:求微分方程 y f (x, y, y)
y Q(x)e P(x)dxdx C1 e P(x)dx e P(x)dx Q(x)e P(x)dxdx C1e P(x)dx
这表明:一阶非齐次线性方程的通解等于对应于它 的齐次方程的通解加上该非齐次方程的一个特解.
例1.(P316,例1)求方程 dy 2 y (x 1)5/2的通解. dx x 1
从而 dy u x du ,方程 1变为u x du (u)
dx
dx
dx
即 du (u) u ,这是可分离变量方程,求出它的
dx
x
通解,再将u y 代入得1的通解.
x
例1P310?解方程 y2 x2 dy xy dy .
dx dx
解:先化为标准形式
(xy x2 ) dy y2 dx
解法 : 作换元,令 y p, y dp dx
原方程变为 dp f (x, p) 一阶方程 dx
设其通解为: p (x,C1),C1是任意常数 即 y (x,C1)
y (x,C1)dx C2 , (C1, C2是任意常数)
只表示一个原函数
例2.(P323,例3)求(1 x2) y 2xy的通解,并求满足初始
y C(x)(x 1)2 2C(x)(x 1)
代入原方程,得
C(x)(x 1)2 2C(x)(x 1) 2 C(x)(x 1)2 x 1
(x 1)5/2
C(x)(x 1)2 (x 1)5/2
C(x) (x 1)1/2
C(x)
(x
1)1/2 dx
2 3
(x
1)3/ 2
C1
y C(x)(x 1)2
过点(x0 , y0 )的那条积分曲线.
初值问题 3的几何意义:求微分方程 y f (x, y, y)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目 开 关
bn=Sn1+1+Sn1+2+…+S12n
=n+11n+2+n+21n+3+…+2n21n+1
=n+1 1-n+1 2+n+1 2-n+1 3+…+21n-2n1+1
热点分类突破
=令nf(+x1)=1-2x2+n1+1x(1x=≥21n),2+n3n+1=2n+1n1+3,
本 讲 栏 目 开 关
【高考考情解读】
数学家华罗庚先生说过:数学是一个原则,无数内容,一种
本 讲
方法,到处可用.数学思想是中学数学的灵魂,在二轮复习
栏 目
过程中,我们要在把握知识主干这条复习主线的同时,活用
开 关
数学思想,加强数学应用意识,方能跳出题海,轻松应对高
考.
思想方法概述
第1讲 函数与方程思想
热点分类突破
(1)等差(比)数列中各有5个基本量,建立方程组可
“知三求二”;
本 讲
(2)数列的本质是定义域为正整数集或其有限子集的函数,数
栏 目
列的通项公式即为相应的解析式,因此在解决数列问题时,
开 关
应注意用函数的思想求解.
热点分类突破
已知数列{an}是等差数列,a1=1,a2+a3+…+
a10=144.
热点分类突破
类型一 函数与方程思想在数列中的应用
例1 已知数列{an}是各项均为正数的等差数列.
本 讲
(1)若a1=2,且a2,a3,a4+1成等比数列,求数列{an}的通
栏 目
项公式an;
开 关
(2)在(1)的条件下,数列{an}的前n项和为Sn,设bn=
1 Sn+1
+
1 Sn+2
+…+
1 S2n
1.函数与方程思想的含义
本 讲
(1)函数的思想,是用运动和变化的观点,分析和研究数
栏 目
学中的数量关系,是对函数概念的本质认识,建立函数关
开 关
系或构造函数,运用函数的图象和性质去分析问题、转化
问题,从而使问题获得解决.经常利用的性质是单调性、
奇偶性、周期性、最大值和最小值、图象变换等.
思想方法概述
本 过三角函数关系化为未知量的表达式,那么问题就能化为未
讲 栏
知量的方程来解.
目 开
(4)解析几何中的许多问题,例如直线与二次曲线的位置关系
关 问题,需要通过解二元方程组才能解决.这都涉及二次方程
与二次函数的有关理论.
(5)立体几何中有关线段的长、面积、体积的计算,经常需要
运用列方程或建立函数表达式的方法加以解决.
关 2.和函数与方程思想密切关联的知识点
(1)函数与不等式的相互转化.对函数y=f(x),当y>0时,
就化为不等式f(x)>0,借助于函数的图象和性质可解决有
关问题,而研究函数的性质也离不开不等式.
思想方法概述
(2)数列的通项与前n项和是自变量为正整数的函数,用函数
的观点去处理数列问题十分重要.
(3)在三角函数求值中,把所求的量看作未知量,其余的量通
(1)求数列{an}的通项an;
本
(2)设数列{bn}的通项bn=
1 anan+1
,记Sn是数列{bn}的前n项和,
讲 栏
若n≥3时,有Sn≥m恒成立,求m的最大值.
目
开 关
解
(1)∵{an}是等差数列,a1=1,a2+a3+…+a10=144,
∴S10=145,∴S10=10a12+a10,
∴a10=28,∴公差d=3.
本 则f′(x)=2-x12,当x≥1时,f′(x)>0恒成立,
讲 所以f(x)在[1,+∞)上是增函数,
栏
目 开
故当 x=1 时,[f(x)]min=f(1)=3,
关 即当n=1时,(bn)max=16,
要使对任意的正整数n,不等式bn≤k恒成立,
则须使k≥(bn)max=16,
所以实数k的最小值为16.
(2)方程的思想,就是分析数学问题中变量间的等量关系,
建立方程或方程组,或者构造方程,通过解方程或方程
组,或者运用方程的性质去分析、转化问题,使问题获得
本
解决.方程的思想是对方程概念的本质认识,用于指导解
讲 栏
题就是善于利用方程或方程组的观点观察处理问题.方程
目 开
思想是动中求静,研究运动中的等量关系.
∴an=3n-2(n∈N*).
热点分类突破
(2)由(1)知bn=ana1n+1=3n-213n+1
=+…+bn=131-3n1+1, ∴Sn=3nn+1.
开 关
∵Sn+1-Sn=3nn++14-3nn+1=3n+413n+1>0,
讲
栏 目
显然当且仅当a属于f(x)的值域时,a=f(x)有解.
开 关
∵f(x)=-(1-sin2x)+sin x=(sin x+12)2-54,
且由x∈(0,π2]知sin x∈(0,1].
易求得f(x)的值域为(-1,1].
故a的取值范围是(-1,1].
热点分类突破
方法二 令t=sin x,由x∈(0,π2],可得t∈(0,1]. 将方程变为t2+t-1-a=0.
依题意,该方程在(0,1]上有解.
设f(t)=t2+t-1-a.
本
讲 栏
其图象是开口向上的抛物线,对称轴t=-12,
目
开 如图所示.
关
因此f(t)=0在(0,1]上有解等价于ff01<≥00 ,
即-1-1-a≥a<00 ,∴-1<a≤1.故 a 的取值范围是(-1,1].
∴数列{Sn}是递增数列. 当n≥3时,(Sn)min=S3=130, 依题意,得m≤130,∴m的最大值为130.
热点分类突破
类型二 函数与方程思想在方程问题中的应用
例2
如果方程cos2x-sin
x+a=0在(0,
π 2
]上有解,求a的取
值范围.
本
解 方法一 设f(x)=-cos2x+sin x(x∈(0,π2]).
,若对任意的n∈N*,不等式bn≤k恒成立,
求实数k的最小值.
热点分类突破
解 (1)因为a1=2,a32=a2·(a4+1),
又因为{an}是正项等差数列,故d≥0,
所以(2+2d)2=(2+d)(3+3d),得d=2或d=-1(舍去),
所以数列{an}的通项公式an=2n.
本
讲 栏
(2)因为Sn=n(n+1),
热点分类突破
研究此类含参数的三角、指数、对数函数等复杂方 程解的问题,通常有两种处理思路:一是分离参数构建函
本
讲 数,将方程有解转化为求函数的值域;二是换元,将复杂方
栏
目 程问题转化为熟悉的二次方程,进而利用二次方程解的分布
