工科数学分析基础课件:5-4-2第四节 多元函数的泰勒公式与极值问题
合集下载
多元函数的Taylor公式与极值问题课件

实际应用中的考虑因素
实际问题的背景
在应用极值理论时,需要考虑实际问题的背景和限制条件,如物 理定律、约束条件等。
数据的不确定性
在实际问题中,数据往往存在不确定性,需要考虑这些不确定性 对极值分析的影响。
模型的适用性
在应用极值理论时,需要考虑模型的适用性,确保模型能够准确 地反映实际情况。
07
与望
05
利用Taylor公式求解极
方法概述
定义
Taylor公式是用于近似表达一 个多元函数在某点附近的行 为
的公式。
形式
Taylor公式的一般形式为 f(x)≈f(a)+f'(a)(x−a)+12f''(a) (x−a)2+…+1n!f(n)(a)(x−a)n
+…。
应用
利用Taylor公式,我们可以找 到函数在某点的极值。
06
极求解的注事与 技巧
常见错误分析
忽视函数的定义域
在求解极值问题时,必须先确定函数的定义域,否 则可能导致错误的结论。
对导数的理解不足
导数描述了函数在某一点的切线斜率,若对导数的 理解不准确,可能导致错误的极值点判断。
未考虑多极值点的情况
在某些情况下,函数可能有多个极值点,需要全面 考虑,避免遗漏。
定义
一元函数在某点的Taylor公式是 该函数在该点附近的一个多项式 近似表示。
形式
一元函数的Taylor公式的一般形 式为 f(x) = f(a) + f'(a)(x-a) + f''(a)(x-a)^2/2! + ... + f^(n)(a)(x -a)^n/n! + Rn(x)
数学分析-Taylor公式与科学计算PPT课件

03 Taylor公式在科学计算中 的应用
多项式逼近
多项式逼近
利用Taylor公式,可以将复杂的函数展开 为多项式形式,从而实现对复杂函数的 近似计算。这种多项式逼近方法在数值 分析和科学计算中具有广泛的应用。
VS
逼近精度
通过选择合适的阶数和节点,可以控制多 项式逼近的精度。高阶多项式逼近能够更 好地逼近函数,但同时也需要更多的计算 资源和时间。
总结词
通过Taylor展开,可以将微分方程转化为差分方程,从 而简化求解过程。
详细描述
在求解微分方程时,有时可以利用Taylor展开将微分方 程转化为差分方程,从而简化求解过程。这种方法在数 值分析中有着广泛的应用,尤其在处理偏微分方程时非 常有效。
05 结论
Taylor公式的意义与价值
1 2
精确近似
数学分析-Taylor公式与科学计算 PPT课件
目录
• 引言 • Taylor公式简介 • Taylor公式在科学计算中的应用 • 实例演示 • 结论
01 引言
主题简介
数学分析
数学分析是研究函数的极限、连 续性、可微性、可积性和实数完 备性的学科,是数学专业的重要
基础课程之一。
Taylor公式
算过程。
求解微分方程
要点一
初值问题
在求解微分方程时,可以利用Taylor公式对微分方程进行 离散化,从而转化为数值求解问题。通过选择合适的步长 和阶数,可以控制数值解的精度和稳定性。
要点二
边值问题
对于微分方程的边值问题,可以利用Taylor公式将问题转 化为有限元方法或边界元方法等数值方法进行求解。这种 方法在科学计算和工程领域中具有广泛的应用。
02 Taylor公式简介
4 多元函数的taylor公式与极值问题2 工科数学分析基础

3 + 3 = 9−5 3 + 3 = 9+ 5
3, 3.
故原点至已知曲线上点的最小距离与最大距离分
别为
dmin = 9 − 5 3 , dmax = 9 + 5 3 . 例3 已知圆柱面
x2 + y2 + z2 − x y − yz − zx − 1 = 0 , (4)
2007年8月
南京航空航天大学 理学院 数学系
南京航空航天大学 理学院 数学系
10
三、应 用 举 例
定理 1 指出的方法称为拉格朗日乘数法. 下面
用这种方法先来求解本节开头给出的两个例题.
例1 解 此例以往的解法是从条件式解出显函数,
例如
z
=
V xy
,
代入目标函数后,
转而求解
S = 2V ( x + y) + x y xy
的普通极值问题. 可是这样做并不总是方便的, 而
Ω = { P | P ∈ D, ϕk (P) = 0, k = 1, 2, , m }. 若存在 P0 ∈ Ω , δ > 0, 使得
f (P0 ) ≤ f (P) , ∀ P ∈ Ω ∩ U (P0;δ ) ( 或 ∀ P ∈ Ω ),
则称 f (P0 ) 是 f (P) 在约束条件 Φ 之下的极小值 (或最小值) , 称 P0是相应的极小值点 (或最小值 点). 类似地又可定义条件极大 (或最大) 值.
目标函数: S = 2z( x + y) + x y; 约束条件: x yz = V .
2007年8月
南京航空航天大学 理学院 数学系
2
例2 设曲线 z = x2 + y2, x + y + z = 1. 求此曲线上 的点到原点距离之最大、最小值. 对此问题有
泰勒公式与极值问题

⎧ x2 − y2 2 2 , x + y ≠0 ⎪ xy 2 2 f ( x, y ) = ⎨ x + y . ⎪0, 2 2 + =0 x y ⎩
4. 混合偏导
f xyx ( x , y ), f xxy ( x , y ), f yxx ( x , y ).
是否一定相等?何时相等?
若Z=f(x,y)的两个偏导函数 fx(x,y)与fy(x,y)关于x和y存在偏导数,则称 f(x,y)具有二阶偏导数。 z=f(x,y)的二阶偏导数有四种情形:
分析:
f ( x + Δx , y ) − f ( x , y ) f x ( x , y ) = lim , Δx →0 Δx
Δy →0
f xy ( x , y ) = lim
Δy →0
f x ( x , y + Δy ) − f x ( x , y ) Δy
f y ( x + Δx , y ) − f y ( x , y ) Δx
§4 泰勒公式与极值问题 一、高阶偏导数 问题:
1. 以下符号的含义:
∂2 z ∂2 z ∂2 z ∂2 z , f xy ( x , y ), , f yx ( x , y ), , f yy ( x , y ). , f xx ( x , y ), 2 2 ∂x∂y ∂y∂x ∂y ∂x
2. 二阶偏导数的定义(极限形式). 3. 典型例子:求二元函数f(x,y)在的二阶偏导数:
ϕ ( x ),ψ ( y )
问题答:
5. 若记 则
ϕ ( x ) = f ( x , y + Δy ) − f ( x , y ), ψ ( y ) = f ( x + Δx , y ) − f ( x , y ),
数学分析课件5.2泰勒公式1.48MB
0 . 03 12 . 03
100 % 0 . 25 %,
称这样的百分比为相对误差. 显然,轴长精度比键销 长的精度高得多. 一般地,有定义:
7
【数学分析课件】
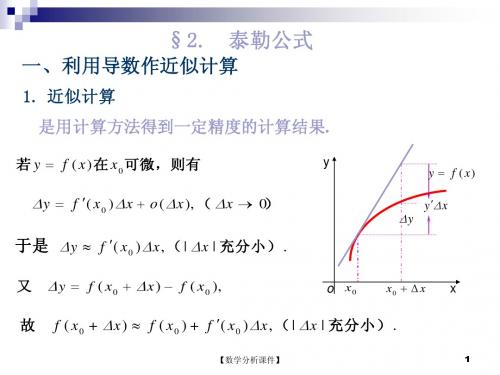
Def : 若一个量 A 的近似值是 a ,则
叫做绝对误差,而
| A a |
.
a
100 % 叫做相对误差
对于函数 y f ( x ),若由 x 计算 y 时, x 有误差 x ,则
f ( x ) f ( 0 ) f ( 0 ) x o ( x ),
从而
即一次多项式
一阶近似 .
f ( x ) f ( 0 ) f ( 0 ) x .
P1 ( x ) f ( 0 ) f ( 0 ) x 是 f ( x ) 在 x 0 点的
P1 ( 0 ) f ( 0 ), P1 ' ( 0 ) f ( 0 ).
3
) 5 . 08
【数学分析课件】 5
2.误差估计
——是估计近似值与精确值的差 例如:设计一根轴长度120毫米,加工后量得120.03毫米, 误差为 | 120 120 . 03 | 0 . 03 毫米. 设计一个键销长度12毫米,加工后量得12.03毫米, 误差为 | 12 12 . 03 | 0 . 03 毫米. 称这种误差为绝对误差,表明了一个量与它的近似值之间 的差值,反映了某种近似程度.
f ( x ) f ( x 0 ) f ( x 0 )( x x 0 )
f
(n)
f ( x 0 ) 2!
n
( x x0 )
2
( x0 )
n!
( x x0 )
多元函数泰勒公式

的一阶偏导数为仍存在偏导数则称它们为函数的二阶偏导数连续都在点例如对三元函数u说明
4 泰勒公式与极值
高阶导数 中值定理和泰勒公式
问题
一、高阶偏导数
函数z f ( x, y)的一阶偏导数为 fx ( x, y) , f y ( x, y) 仍存在偏导数,则称它们为函数 z f ( x, y) 的二阶
其中记号
h
x
k
y
f
(
x0
,
y0
)
表示 hf x ( x0 , y0 ) kf y ( x0 , y0 ),
2
h k x y
f ( x0 , y0 )
表示 h2 f x x ( x0 , y0 ) 2hkfxy ( x0 , y0 ) k 2 f yy ( x0 , y0 ),
f xy ( x0 1x, y0 2y)xy, 0 1,2 1
F(x, y) f ( x0 x, y0 y) f ( x0, y0 y) f ( x0 x, y0 ) f ( x0 , y0 ) ( x0 ) (x0 x)
( y0 x) ( y0 ) ( y0 3y)y
内为一常数.
在泰勒公式(1) 中, 如果取 x0 0, y0 0 , 则(1)式成为n阶麦克劳林公式.
f ( x, y) f (0,0) x y f (0,0) x y
1 x
y
2
f (0,0)
1 x
y
n
f (0,0)
2! x y
n! x y
n1
1 x y f (x,y),
(n 1)! x y
(0 1) (5)
例 6 求函数 f ( x, y) ln(1 x y) 的三阶麦
泰勒公式ppt课件精选全文完整版

令n=2m,于是有
sin x
x
x3 3!
x5 5!
(1)m1 x2m1 (2m 1)
!
R2m
(
x)
其中 R2m (x)
s(in1()mxcos2(m2x1) ) x2m1 (0 1)
(2m 1) !
精选编辑ppt
18
机动 目录 上页 下页 返回 结束
类似地,可得
cos x
1 x2 2!
x4 4!
f (k)( x0 )
n!an f (n) ( x0 ). (k 0,1,2,, n)
代入 Pn ( x)中得
Pn ( x)
f ( x0 )
f ( x0 )( x x0 )
f
( x0 2!
)
(
x
x0
)2f(n)( x n!)(x
x0
)n
精选编辑ppt
10
机动 目录 上页 下页 返回 结束
三、泰勒(Taylor)中值定理
泰勒(Taylor)中值定理 如果函数 f ( x) 在含有 x0 的某个开区间(a, b) 内具有直到(n 1) 阶的导数,则
当 x在(a,b)内时, f ( x)可以表示为( x x0 )的一个 n次多项式与一个余项Rn ( x)之和:
f (x)
f ( x0 )
精选编辑ppt
16
机动 目录 上页 下页 返回 结束
例1:求函数 f (x) ex 的n阶麦克劳林展开式.
解:因为 f'x f''x fn x e x ,
所以 f0 f'0 f''0 fn 0 1 .
故
ex
1 x x2
sin x
x
x3 3!
x5 5!
(1)m1 x2m1 (2m 1)
!
R2m
(
x)
其中 R2m (x)
s(in1()mxcos2(m2x1) ) x2m1 (0 1)
(2m 1) !
精选编辑ppt
18
机动 目录 上页 下页 返回 结束
类似地,可得
cos x
1 x2 2!
x4 4!
f (k)( x0 )
n!an f (n) ( x0 ). (k 0,1,2,, n)
代入 Pn ( x)中得
Pn ( x)
f ( x0 )
f ( x0 )( x x0 )
f
( x0 2!
)
(
x
x0
)2f(n)( x n!)(x
x0
)n
精选编辑ppt
10
机动 目录 上页 下页 返回 结束
三、泰勒(Taylor)中值定理
泰勒(Taylor)中值定理 如果函数 f ( x) 在含有 x0 的某个开区间(a, b) 内具有直到(n 1) 阶的导数,则
当 x在(a,b)内时, f ( x)可以表示为( x x0 )的一个 n次多项式与一个余项Rn ( x)之和:
f (x)
f ( x0 )
精选编辑ppt
16
机动 目录 上页 下页 返回 结束
例1:求函数 f (x) ex 的n阶麦克劳林展开式.
解:因为 f'x f''x fn x e x ,
所以 f0 f'0 f''0 fn 0 1 .
故
ex
1 x x2
多元函数的Taylor公式与极值

矩阵为: H f ( x0 )
f11 f21
f12
f
22
f1n
f
2n
设u f (P)在点
f
n1
f
n
2
f
nn
x0
P0 ( x01 , x02 , , x0n ) 的所有二阶偏导数
f11
f12
f1n
f 在点P0的 Hessian
H
f
(P0 )
f21
f
22
f
2n
矩阵为:
f
n1
f
x
, y)2
3 f
2! ,
x py3 p (1 x y)3
( p 0,1,2,3),
4 f 3! , ( p 0,1,2,3,4), x py4 p (1 x y)4
20
x x
y y
f
(0,0)
xfx (0,0)
yf y (0,0)
x
y,
x
y
2
f
(0,0)
x y
由假设, (t) 在 [0,1] 上满足一元函数泰勒公式的条件
于是有 (1) (0) (0) (0)
1!
2!
(n) (0) (n1) ( )
(0
1) .
n!
(n 1)!
(0) f ( x0 , y0 ) , (1) f ( x0 h , y0 k)
利用多元复合函数求导法则可得:
11
(4)在泰勒公式中,如果取 x0 0, y0 0,则 成为n阶麦克劳林(Maclaurin)公式.
f (x, y)
f
(0,0)
x
x
y
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
令 L x, y, x2 y x2 y2 1 ,
Lx
2 xy
2 x
0,
Ly x2 2 y 0,
L
x2
y2
1
0,
x
y
2, 3 1,
பைடு நூலகம்
3
2
2
z2 3
3 , z3 3
. 3
与D内驻点处的函数值 z1 0,a 0 比较知
z的最大值为
z2
2, 33
最小值为
2
z3 3
最大与最小距离。
解 设( x, y, z)为椭圆上的任一点,它到原点的
距离为
r x2 y2 z2 下求 r 2 在条件
x2
y2
z2
1
3 2
x y z 0
下的极值。
作函数
L x2 y2 z2 ( x2 y2 z2 1) ( x y z)
32
Lx
2x
2 3
在条件( x, y) 0下, 求函数z f ( x, y)的极值 . 如方法 1 所述 设 ( x, y) 0 可确定隐函数 y y( x),
则, 问题等价于一元函数 z f ( x, y( x)) 的极值问题,
故极值点必满足
dz
dy
d x fx fy d x 0
因 d y x ,故有 dx y
x
S xy 且 x2 y2 4R2 .
问题的实质:求 函数 S xy ( x 0, y 0)
在约束条件 x2 y2 4R2 0 下的极值.
有约束极值:对自变量有附加条件的极值.
求函数 f (x, y) 在条件(x, y) = 0下的极值问题, f (x, y) 称为目标函数;(x, y) = 0 称为约束条件。
x
0
(1)
令
Ly 2 y y 0
Lz
2z
2 z
0
(2) (3)
L
x2 3
y2 2
z2
1
0
(4)
L
x
y
z
0
(5)
(1)x (2) y (3)z ,并将(4) 、(5)两式代入得
2( x2 y2 z2 ) 2 0
即有 ( x2 y2 z2 ) r 2
将上式分别代入(1) ,(2),(3)得
第四节 多元函数的泰勒公式 与极值问题
多元函数的Taylor公式 无约束极值,最大值与最小值 有约束极值,拉格朗日(Lagrange)乘数法 小结
4.3有约束极值, 拉格朗日(Lagrange)乘数法
问题的提出
一矩形内接于半径为 R 的圆,
求该矩形最大的面积. 设矩形的长与宽分别为x, y
2R
y
面积为 S, 则有
例9 确定函数 z x2 y 在区域D : x2 y2 1上的 最大值与最小值.
解 (1)求函数 z x2 y在区域 D 内的驻点
z x
2 xy
0,
z
x2
0,
y
x 0,
y
a,
| a | 1.
z1 z1 0,a 0.
(2)求 z x2 y 在边界 x2 y2 1上的最值
x
3
2(r 2
3)
,
y
r2
2
,
z
2(r 2 1)
,
代入(5)得
3
2(r 2 3) r 2 2 2(r 2 1) 0
3
1
1
2(r 2 3) r 2 2 2(r 2 1) 0
解此方程得 r 2 11 13 6
r 0,
r1,2
11 13 6
因为r 一定存在最大与最小值,所以
r1
11 13 , 6
r2
11 13 6
分别为所求椭圆的长短半轴。
小结
有约束极值问题,Lagrange乘数法。 步骤: (1)由题意确定目标函数与约束条件; (2)作Lagrange 函数; (3)求偏导数得方程组; (4)解方程组得Lagrange 函数在讨论范围内 的驻点,并根据题意确定极值.
. 3
例10* 求椭球面 x2 y2 z2 1 被平面 32
x y z 0 截得的椭圆的长半轴与短半轴
之长。
分析:椭球面的中心在原点,平面 x y z 0
也过原点,所以椭圆的中心在原点。从而问题 即求椭圆
x2
y2
z2
1
3 2
x y z 0
上的点( x, y, z)到原点的
叫Lagrange乘数. 利用拉格朗日函数求极值的方法
称为拉格朗日乘数法.
推广 拉格朗日乘数法可推广到多个自变量和多 个约束条件的情形.
例如, 求函数 u f ( x, y, z) 在条件 ( x, y, z) 0,
( x, y, z) 0 下的极值.
作拉格朗日函数
L f ( x, y, z) 1 ( x, y, z) 2 ( x, y, z)
有时约束条件不止一个,可能由几个方程联合给出。
条件极值的求法: 方法1 代入法. 例如 ,
在条件( x, y) 0 下 , 求函数z f ( x, y)的极值
转
化 从条件( x, y) 0中解出y y( x)
求一元函数 z f ( x, y( x)) 的无条件极值问题.
方法2 拉格朗日乘数法. 例如,
解方程组
即 L 0. 可得到条件极值的可疑点 . 再由具体问题确定最值.
例8. 要设计一个容量为 V0 的长方体开口水箱, 试问
水箱长、宽、高等于多少时所用材料最省?
解 设 x , y , z 分别表示长、宽、高, 则问题为求x , y , z 使在条件 xyz V0 下水箱表面积
S 2( xz yz) xy 最小.
令 F 2( xz yz) xy ( xyz V0 )
2z y yz 0
解方程组
2z x xz 0 2( x y) x y 0
z y x
x y z V0 0
得唯一驻点
x
y 2z
3 2V0 ,
4 3 2V0
由题意可知合理的设计是存在的,
因此
,
当高为
3
V0 4
,
长、宽为高的 2 倍时,所用材料最省.
z
思考:
y
1) 当水箱封闭时, 长、宽、高的尺寸如何? x
提示: 利用对称性可知, x y z 3 V0 2) 当开口水箱底部的造价为侧面的二倍时, 欲使造价
最省, 应如何设拉格朗日函数? 长、宽、高尺寸如何?
提示: F 2( xz yz) 2 xy ( xyz V0 )
长、宽、高尺寸相等 .
fx
f
y
x y
0
记
fx
x
fy
y
极值点必满足
fx x 0 fy y 0 (x, y) 0
引入辅助函数 L( x, y, ) f ( x, y) ( x, y)
L( x, y, ) f ( x, y) ( x, y)
则极值点满足:
即 L 0
辅助函数L 称为拉格朗日( Lagrange )函数. 数
