社会保险基金精算(第一章)寿险精算基础(2)
寿险精算习题及答案
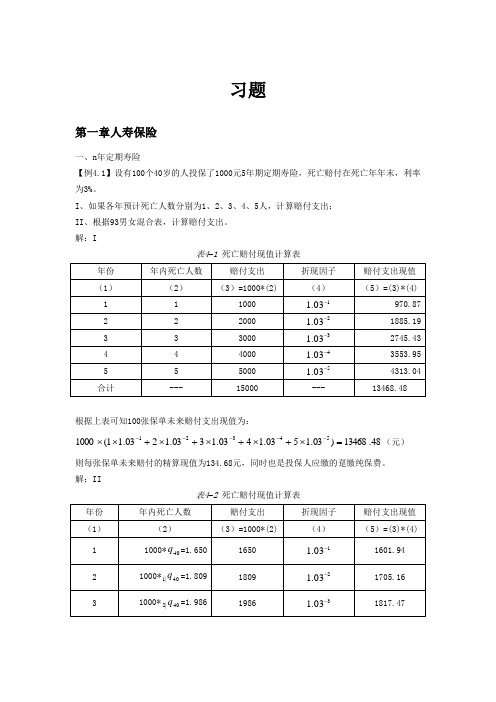
习题第一章人寿保险一、n 年定期寿险【例4.1】设有100个40岁的人投保了1000元5年期定期寿险,死亡赔付在死亡年年末,利率为3%。
I 、如果各年预计死亡人数分别为1、2、3、4、5人,计算赔付支出; II 、根据93男女混合表,计算赔付支出。
解:I表4–1 死亡赔付现值计算表根据上表可知100张保单未来赔付支出现值为:48.13468)03.1503.1403.1303.1203.11(100054321=⨯+⨯+⨯+⨯+⨯⨯-----(元)则每张保单未来赔付的精算现值为134.68元,同时也是投保人应缴的趸缴纯保费。
解:II表4–2 死亡赔付现值计算表根据上表可知100张保单未来赔付支出现值为:86.9124)03.103.103.103.103.1(1000540|4440|3340|2240|11402=⨯+⨯+⨯+⨯+⨯⨯-----q q q q q (元)则每张保单未来赔付的精算现值为91.25元,同时也是投保人应缴的趸缴纯保费。
【例4.2】某人在40岁时投保了10000元3年期定期寿险,死亡赔付在死亡年年末,利率为5%。
根据93男女混合表计算:I 、单位趸缴纯保费;II 、单位赔付现值期望的方差;III 、(总)趸缴纯保费; 解:I 、单位趸缴纯保费为,)()(424023414024040|2340|1240240|11|3:40q p v q p v vq q v q v vq q v Ak k k ++=++=⨯=∑=+]05.1001993.0)001812.01()00165.01(05.1001812.0)00165.01(05.100165.0[32⨯-⨯-+⨯-+=00492793.0=(元)。
II 、单位赔付现值期望的方差为,00444265.0)()()()(21|3:4040|2640|1440221|3:40240|)1(221|3:401|3:402=-++=-⨯=-∑=+A q v q v q v A q v AAk k k III 、趸缴纯保费为,28.49100001|3:40=⨯A (元) 【例4.3】某人在50岁时投保了100000元30年期定期寿险,利率为8%。
保险精算学课件(第二部分内容)-

又由条件概率公式和定理1.3.2,有
u|t qx P(T (x) t u,T (x) u)
P(T (x) u) P(T (x) t u | T (x) u)
§1.3.2 一些国际通用精算表示法
P(T (x) u) P(T (x u) t) u px t qxu ; u|t qx P(T (x) t u,T (x) u)
§1.3.2 一些国际通用精算表示法
□定理1.3.3 (1)生存概率
t
px
s(x t) s(x)
(2)对t 0,u 0, 生存概率与死亡概率有如下
的关系:
t qx 1t px , u|t qx u px t qxu , u|t qx u px ut px
(3)对 0 h t ,有 t px h px th pxh
(x
t)
fT (x) (t)
d dt
[FT (x) (t)]
d dt
[sT (x) (t)]
t
fT (x) (t)
( xu )du
e 0
(x
t)
t
px
(x
t)
§1.3.2 一些国际通用精算表示法
其次,对关系式(1.3.6)两边对t求导数,有
d dt
(
fT (x) (t)
fX (x t) , s(t)
t 0;
生存分布为
t
sT
(x)
(t)
e
0
( xs)ds
;
(1.3.3) (1.3.4)
寿险基本原理及精算基础

华夏“英才一期”培训班·北京
保险基本原理
投连型终身寿险(变额终身寿险)
保费固定,保额可变(通常要保证一个最低限额); 有专项账户,与公司的一般账户是分开的; 投保人通常可以选择账户投向; 保额随着投资组合和投资业绩的情况而变动。
华夏“英才一期”培训班·北京
保险基本原理
万能寿险 保费灵活 保额可调 万能寿险由于其特有的灵活性而提供了一种可能,即一个人一 生需要的惟一的寿险保单就是万能寿险。
寿险基本原理及精算基础
华夏“英才一期”培训班·北京
1 2 3 4 5
寿险基本原理及盈利模式
寿险产品定价和利润测试
准备金、现金价值与偿付能力 内含价值 再保险
华夏“英才一期”培训班·北京
保险基本原理
保险的雏形
古罗马:“丧葬互助会” 古巴比伦:征收赋金以备救济火灾及其他天灾损失 中国夏周时期:“积谷防饥” 中国古代:镖局组织
华夏“英才一期”培训班·北京
保险基本原理
年金保险
被保险人,张先生,今年28周岁,为自己投保某养老年金保险 (分红型),年交保费1万元,交费期间10年,选择60岁开始领取20 年。可获得如下收益: 客户从60岁年生效对应日开始每年领取10260元直至79周岁年生 效对应日,20年共计领取205200元,是所交保费的2.05倍;若在本 合同约定的养老年金领取期间身故,按约定领取期限内尚未领取的 各期养老年金之和一次性给付身故保险金,本合同终止。
短期险:一次性缴费,保障高,无返还,费用率低(20%)。
华夏“英才一期”培训班·北京
保险基本原理
人身保险的缴费方式
每年可更新的定期寿险方法 一次缴清(趸交)保险费方法 均衡保险费方法
1、社会保障精算(第一章)寿险精算基础(3)

死亡率
0.003500 0.003000 0.002500 0.002000 0.001500 0.001000 0.000500 0.000000
12
16
20
24
28
32
36
40
44
48
0
4
8
年龄
1.2.1 基本函数(生命表的基本内容) 基本函数(生命表的基本内容)
已知: 已知: 求: 解:
1|
l20 = 1000
1|
l21 = 998
l22 = 992
q 20
d 20 +1 d 21 l 21 − l 22 = = = l 20 l 20 l 20
998 − 992 = = 0 . 006 1000
q 20
q 20
1|
已知40岁的死亡率为0.04,41岁的死亡率 已知40岁的死亡率为0.04,41岁的死亡率 40岁的死亡率为0.04 0.06,42岁的人生存到43岁的概率为0.92。 岁的人生存到43岁的概率为0.92 为0.06,42岁的人生存到43岁的概率为0.92。如果 40岁生存人数为100人 岁生存人数为100 43岁时的生存人数 岁时的生存人数。 40岁生存人数为100人,求43岁时的生存人数。
0
x
定义式
死亡 时点
ω −1
105
时间
s( x) = Pr( X > x)
s ( 0) = 1
s (105) = 0
lx s( x) = l0
s ( x ) = x p0
s( x) = 1 − F ( x)
岁的人在0~ 之间存活的概率 之间存活的概率) (表示0岁的人在 ~x之间存活的概率) 表示 岁的人在
寿险精算学(第3版)习题答案2

【解2.1】(1)可以被写成=(90−p(r200)18000,又由于达到极限寿命时=0,故=90。
(2)证明:因为,0=1;其次,达到极限寿命=90时,有90=0;且,的导数−110−218000<0,>0。
由此,生存函数的三个条件都被满足。
(3)93333.0)0()10(00010==S S p (4)(030−050)020(5)=−0'(p/0==110+218000−110−2因此,40=0.015833。
【解2.2】作为生存函数的基本属性有:(0)1,S =函数是单调递减的,同时lim ()0x S x →∞=。
(1)由于()exp[0.7(21)](10.72ln 2)xxS x x '=---⨯⨯,(0)0.51480S '=>,说明该函数不满足单调递减的性质。
所以,它不能作为生存函数。
(2)由于(0)1S =,3()2(1)0S x x -'=-+<,21lim ()lim0(1)x x S x x →∞→∞==+。
该函数可以作为生存函数。
(3)由于(0)1S =,()2()(2)0x S x ex -'=-<,lim ()0x S x →∞=。
该函数可以作为生存函数。
【解2.3】(1)4320751001)75(1)75(=--=-=S F (2)20017510040175)()75(=-==-=x x S dx d f (3)501412001)75()75()75(===S f μ【解2.4】(40)40(40)(40)40(40)(40)60(),060(40)60(40)1(),060(40)601()(),06060T t T T t T S t tS t p t S S t t t S t tf x p t t μμ+-===<≤'+=-=<≤+-==<≤【解2.5】()18)100(9)100(6)100(3100)100()100(2)]([2)]([3100)100()100()]([)100()100(222210002221000100022100022x x x x dt x t x t x T E dt p t x T Var xdt x t x dt p x T E x t x l l p xxx t xxx tx t x x t -=---=⎪⎭⎫⎝⎛------=-=-=---==---==⎰⎰⎰⎰----+【解2.6】所有表达式均为非负,因此需要验证是否满足0∞B =∞,使得0)(=∞S (1)∞==∞∞⎰0ln C BC dx BC xx,可以(2)∞=+=+∞∞-⎰001)ln()(x b a dx x b a ,可以(3)21)1(21)1(023=+-=+∞∞-⎰x dx x ,不可以【解2.7】把30.250x q +=代入120.170x q +=式中,得11232120.1700.680x x x x x x q p p q p p ++++++=⋅⋅=⇒=上式与已知条件11210.090x x x q p q+++=⋅=联立求解,解出10.770x p +=,20.117x q +=最后得1212(1)0.230.1170.347x x x x q q p q +++++=-+=+=【解2.8】由()1xS x ω=-,可知~(0,)X U ω,且有(20)~(0,20)T U ω-则[()]2x E T x ω-=,2()[()]12x Var T x ω-=已知020e 40=,即20401002ωω-=⇒=所以2(20)Var[T(20)]533.312ω-==【解2.9】首先计算K 的生存函数k012197k p +1015415则210414()09715151502210422()(21)13509715151513422()()[()]225E K p k k E K k p k k Var K E K E K ==++=∑==+⋅=⋅+⋅+⋅=∑==-=【解2.10】证明:(1)x t x x x t q t T t T p -=<-=≥=1)Pr(1)Pr((2)xu t x t x x x x ut p p u t T t T u t T t q +-=+≥-≥=+≤≤=)Pr()Pr()Pr((3)()()()tx u x t t x x x ut p p u T t T p ++⋅=≥⋂≥=Pr 【解2.11】(1)证明:110111111111+∞+∞+-∞∞+=+≤⋅+=+==⎰⎰⎰⎰⎰⎰x x x t x x t x t x t x t x e dt p dtp p dt p dt p dt p dt p e (2)证明:由于是关于的递减函数,因此有K1B≥所以xk x k k k kx tx t x e p dtp dt p e =≥==∑∑⎰⎰∞=+∞=+∞101【解2.12】证明:()()()()()()()t x t x x t S x t f x t S x t x t p p t t S x S x S x μμ+∂∂++-++====∂∂【解2.13】318.02005exp 20025exp 20015exp )5()25()15(200exp 100exp )(2225101020=⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛-=-=⎪⎪⎭⎫⎝⎛-=⎭⎬⎫⎩⎨⎧-=⎰S S S q x dt t x S x 【解2.14】[][]8684284p =其中86l 已知,而[][][][][]2848484184841(1)(1)p p p q q ++==--由已知条件推导出[][][]85841848483144508030360.3225550803343640050800.20644556400q q q q q ++-=⋅=⋅=-==⋅⋅=⋅=【解2.15】(1)7[76]=83[76]=1192816608=0.718208(2)6|275+1=82−8475+1=0.084631【解2.16】40+1=40(1−40),40+2=402p [40],43=40+2−40∗2|40,46=43−40+1∗2|340+1.因此343=46/43=1−(1−40)2|340+1/(2p [40]−2|40)=1−(1−0.01608)×0.08964/(0.95977-0.02383)=0.905765【解2.17】151025:2525152540015100.040.04150.06015.40667t t tte p dt p p dtedt eedt--⨯-=+=+=⎰⎰⎰⎰【解2.18】(1)0.752.5=1−53.252.5=1−0.853+0.2540.552+0.553=0.0068381.7|1.252.5=54.2−55.452.5=0.854+0.255−0.655−0.4560.552+0.553=0.022690(2)0.752.5=1−0.5p 52.50.2p 53=1−520.5530.2=0.0068351.7|1.252.5=1.7p 52.51−1.2p 54.2=0.5p 52.5530.2p 541−0.8p 54.20.4p 55=520.553540.21−540.8550.4=0.022668【解2.19】因为{}10102102221exp ()=1exp 2()1exp ()1()1(1)2x x x x x q x t dt x t dt x t dt p q q q μμμ⎡⎤''=--+⎢⎥⎣⎦⎡⎤--+⎢⎥⎣⎦⎡⎤=--+⎢⎥⎣⎦=-=--=-⎰⎰⎰由此推出2x xq q '<。
保险精算基础 (2)

复利计算公式:
• 复利积累值
• 积累值 = A (1+i)计息期间 = A (1+i)t
•
(1+i)t
复利计算公式:
• 复利现值
• 现值= 积累值/(1+i)t
名义利率与实际利率
• 名义利率
当在一个度量期中利息支付不止一次 或多个度量期支付一次利息时,我们称相 应的一个度量期的利率为名义利率。名义 利率又叫合同利率或挂牌利率。 实际利率
• 现值和终值是以时间点区分的, 是相对概念。
单利计算公式:
• 本金 A • 利率 i • 计息期间 t
• 单利积累值 • 利息 = 本金×利率×计息期间 • 积累值 = 本金+利息 • 积累值 = A+ A×i×t = A×(1 + i×t)
单利计算公式:
• 单利现值 • 现值 =积累值/(1+i×t)
以前产生的利息也加入到原始的本金,所以本金 在增加,俗称“利滚利”。
• 现值 • 未来的货币价值按照一定的利率换算成现在时
刻的价值,现在这个价值叫现值。
• 终值 • 终值又叫积累值 • 把以前的或者现在的货币价值按照一定利率积
累到将来某个时候的价值,将来的那个值叫终值, 所以积累值是本金与利息之和。
• 利率在实际当中有各种各样的情况 • 基准利率 • 市场利率
• 利率是金融领域的基础,也就是经济关系
运行的基础就是利率。
第二节 利率的度量
• 利率的度量就是计算利息的方式,常分为两种: • 单利 • 计算利息时,在计息期间仅对本金进行计算。 • 复利 • 计算利息时,在计息期间不仅对本金进行计算,
相对名义利率来说,利息支付只在度量 期初或期末支付。
file社会保险基金

《社会保险基金精算》课程教学大纲一、课程基本信息1. 课程代码: 0306152. 课程名称:社会保险基金精算 / Actuarial Principle of Social Insurance3. 课程性质:专业特色课4. 适用专业:劳动与社会保障专业5. 总学时: 326. 总学分: 27. 预修课程:社会保障概论、概率论、高等数学8. 推荐教材:王晓军.社会保险精算原理与实务[M].北京:中国人民大学出版社,2009.9. 参考书目:•宋世斌、申曙光《社会保险精算,中国劳动社会保障出版社,2007.8;•李秀芳等《保险精算》(第二版), 中国人民大学出版社,2008.2;•张思锋《社会保障精算理论与应用》,人民出版社,2006.8;•Bowers etal. Actuarial Mathematics。
二、课程简介《社会保险基金精算》是劳动与社会保障专业的特色课程。
社会保险精算是一门以概率论、保险学、人口学和金融学等学科为基础、运用数学、统计学等工具,对社会保障领域涉及的风险问题进行评价和数量化处理的综合学科。
目前我国已建立起适合本国国情的社会保障制度与体系,保险精算在社会保障制度的运行过程中发挥着重要作用。
通过对年老、疾病、工伤、失业和生育等使经济收入失去保障的风险事件进行评价,对社会保险的成本与债务、社会保险基金的长期精算平衡状况等进行估计与预警,以保证社会保障制度的稳定性。
本课程注重保险精算原理和基本方法在社会保障领域的具体应用,尽量避免烦琐的数学推导;尤其将重点置于养老保险和医疗保险精算原理与实务的阐述和案例分析上。
本课程以Excel、Matlab作为教学支持软件。
三、课程设置目标通过本课程学习,使学生理解和掌握社会保险精算的基本原理与方法;学会灵活使用Excel、Matlab软件进行保险精算;能够运用所学理论和方法处理社会保障领域的精算问题;能够计算社会保障的成本与债务;能够估计社会保障基金的长期精算平衡和财务稳定性;使学生具有进一步学习和应用保险精算理论与方法的基础,形成一定的分析问题与解决问题的能力,并使这种能力在其专业领域中得到充分发挥。
社会保障精算--人寿与年金保险精算PPT课件

1、早期皮肌炎患者,还往往 伴有全身不适症状,如-全身肌肉 酸痛,软弱无力,上楼梯时感觉 两腿费力;举手梳理头发时,举 高手臂很吃力;抬头转头缓慢而 费力。
2 定期寿险
实用公式
3 两全保险
A1 x:n
Mx
M xn Dx
两全保险 = n 年定期寿险 + n 年纯生存保险
纯生存保险: n年期满后,如果被保险人仍存活, 赔付保险金。赔付现值的随机变量 Z 为:
vn
(k n, n 1,, )
Z
0
(k 0,1,2,, n 1)
11
纯生存保险的精算现值为
A 1 x:n
k0 v xlx
Ax
Mx Dx
8
2 定期寿险
A1x:n
投保时点
v k 1
1
k
死亡
赔付时点
0
x
x k x k 1 xn
时间
理论公式
n1
A1 x:n
E(Z )
v k 1 k| q x
k 0
vK1 (k 0,1,2,, n 1)
Z 0
(k n, n 1,, )
9
皮肌炎图片——皮肌炎的症状表现
理论公式
Ax E(Z )
v t
0
t
px
xt dt
15
对于1单位元的终身寿险,赔付现值随机变量为
Z vT (t 0)
实用公式
Ax
i
Ax
i ln(1
i)
Ax
其中, 称为利息力,是衡量确切时点上年利率水平的指标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n −1
− nv
n
= a n − nv n
a n − nv ( Ia ) n = i
n
对于期首付等差递增年金来说, 对于期首付等差递增年金来说, 期首付等差递增年金来说
a n − nv ( Ia ) n = d
n
期末付等差递增年金的终值 期末付等差递增年金的终值 (FV) 等差递增年金的
(1 + i) n
(1 + i) n
(1 + i ) 2
(1 + i )
1 0
1 1
1 2
1 3
L
1 n-2
1 n-1 n
付款额 时间
L
思路1 思路
sn
= (1 + i ) + (1 + i ) 2 + L + (1 + i ) n
1 − (1 + i) n 1 + i (1 + i) n − 1 (1 + i) n − 1 s n = (1 + i) ⋅ = ⋅ = 1 − (1 + i) i 1 d
1000
0 1
1100 1200
2 3
L
1700
8
1800
9
1900
10
付款额
L
时间
900 100
0 1
900 200
2
900 300
3
L
900 800
8
900 900
9
900 1000
10
付款额
L
时间
900
900 200
2
900 300
3
100
0 1
L
900 800
8
900 900
9
900 1000
10
付款额
L
+
时间
FV
=
900 ⋅ S 10
100 ⋅ ( Is ) 10
+
=
(1 + i ) 10 − 1 900 ⋅ i
S 10 − 10 100 ⋅ i
年金的现值 (2) 期首付等比递增年金的现值 (PV) ) 期首付等比递增年金的
(1 + j ) n −1 ⋅ v n −1
(1 + j ) 2 ⋅ v 2
n
n
=
1− vn i
年金的终值 (4) 期末付年金的终值 (FV) ) 期末付年金的
• n年内每年 元的期末付年金终值的计算 年内每年1元的期末付年金终值的计算 年内每年 元的期末付年金终值
(1 + i) n
sn
a
1 - v = n i
n
1 0 1
1
1
L
1
1
1
付款额 时间
2
3
L
n-2
n-1
n
思路
(1)计算年金的现值 )
• n 年内每年收付 m 次,每次 1/m 元的期首付年金现值 元的期首付年金现值 期首付年金
1 m v m 1 m v m
1
2
− 1 ( n −1) + mm 1 1 v = v m m
mn −1 m
1/m 0
1/m
1/m
1/m
1/m 1
1 m
L
1/m n
付款额 时间
L
2 m
an
(2)计算该现值在 年后 )计算该现值在n年后 的累积额 年金终值) (=年金终值) 年金终值
sn
=
=
a n ⋅ (1 + i)n
1 − vn (1+ i)n −1 ⋅ (1+ i)n = i i
万元购房, 【例1.3】某人贷款 万元购房,还款期 年,假定贷款 】某人贷款20万元购房 还款期30年 利率5%,如果从贷款第二年开始每年等额还款,求每年的 利率 ,如果从贷款第二年开始每年等额还款, 还款额。 还款额。
寿险精算基础( 第一章 寿险精算基础(2)
§1.1 利息理论
累积函数、实际利率与实际贴现率、名 累积函数、实际利率与实际贴现率、 义利率与名义贴现率、 义利率与名义贴现率、年金
§1.2 生命表
生命函数、生命表、多减因表(自学) 生命函数、生命表、多减因表(自学)
1.1.2 年金
1 年金现值与终值
何谓年金? 何谓年金? 按相等间隔收付款(方式或款项) 相等间隔收付款(方式或款项) 收付款
如购物分期付款、住房按揭、养老金给付等。 如购物分期付款、住房按揭、养老金给付等。 (1) 期首付年金 期首付年金
1 1 1 1
L
1
1
付款额
n
0
1
2
3
L
L
n-2
n-1
时间
(2) 期末付年金 期末付年金
1 1 1 1 1 1
付款额 时间
0
1
2
3
L
n-2
n-1
n
年金的现值 (1) 期首付年金的现值 (PV) ) 期首付年金的
n-2
n-1
n
付款额 时间
0
1
2
3
L
n-2
n-1
n
PV = ( Ia) n = v + 2v 2 + L + nv n (1 + i )( Ia) n = 1 + 2v + 3v L + nv
2 n −1
(1)
(2)
(2)-(1)得 ) ( )
i ⋅ ( Ia) n = 1 + v + v L + v
PV =20
x
0 1
x
2
x
3
L
x
28
x
29
x
付款额
30
L
a 30
时间
PV = x ⋅ a 30
PV ⋅ i x = 1 − v 30
1 − v 30 = i
=
2 00000 × 0 .05 1 30 1− ( ) 1 + 0 .05
=
13010.29
2 永续年金
收付时期无限( 的年金,如一些奖励基金等。 收付时期无限( n = ∞)的年金,如一些奖励基金等。
【例1.5】我国城镇职工基本养老金保险采取社会统筹与个人 】
账户相结合的方法,个人账户以工资的 计入。 账户相结合的方法,个人账户以工资的8%计入。如果某职工 计入 岁参加个人账户保险, 从20岁参加个人账户保险,当年工资 岁参加个人账户保险 当年工资6000元,工资年增长 元 2%,个人账户的年利率 岁退休时, ,个人账户的年利率4%,求他 岁退休时,其个人账户 ,求他60岁退休时 的累积额。 的累积额。
付款额 时间
L
(2) 等比递增年金(期首付) 等比递增年金(期首付) 年金
1 1+j (1+j)2 (1+j)3
L
(1+j)n-2
(1+j)n-1
付款额
n
0
1
2
3
L
n-2
n-1
时间
等差递增年金的 (1)期末付等差递增年金的现值 (PV) )期末付等差递增年金的现值
n ⋅ vn
2 ⋅ v2
v
1
2
3
L
(1 + j ) ⋅ v
1
1+j
(1+j)2 (1+j)3
L
(1+j)n-2
(1+j)n-1
付款额
n
0
1
2
3
L
n-2
n-1
时间
PV = 1 + (1 + j ) ⋅ v + (1 + j ) 2 ⋅ v 2 + L + (1 + j ) n −1 v n −1
1 − [(1 + j ) ⋅ v]n PV = 1 − (1 + j ) ⋅ v
n 期 1 单位期首付年金的现值,用符号 单位期首付年金的现值,
an
表示,所以, 表示,所以,
a n = 1 + v + v 2 + L + v n −1
a
1-v 1-v = = n 1-v d
n
n
小课题: 小课题: (1) 等比级数求和; ) 等比级数求和; 的推导。 (2) d=1-v 的推导。 )
年金的现值 (3) 期末付年金的现值 (PV) ) 期末付年金的
• n 年内每年 1 元的期末付年金现值的计算 元的期末付年金现值 期末付年金现值的计算
v2
vn
v
1 0 1
1
1
L
1
1
1
付款额 时间
2
3
L
2
n-2
n-1
n
PV = v + v + L + v
an
1− v = v ⋅ 1− v
an
a∞ a∞
=
1− v i
n → ∞
n
=
lim a n
1 i
=
lim∞ 1 − v n → i
n
=
3 变额年金
定义:每次收付额不等的年金。 定义:每次收付额不等的年金。 收付额不等的年金
(1) 等差递增年金(期末付) 等差递增年金(期末付) 年金
n n
1 0 1
2 2
3 3
L
n-2 n-2
n-1 n-1
