八年级全等三角形单元测试题(供参考)
八年级数学上册《第十二章 三角形全等的判定》单元测试题及答案(人教版)

八年级数学上册《第十二章三角形全等的判定》单元测试题及答案(人教版)学校:___________班级:___________姓名:___________考号:___________知识点回顾1.三角形全等的判定:(1)边边边(SSS):三边分别相等的两个三角形全等。
(2)边角边(SAS):两边和它们的夹角分别相等的两个三角形全等。
(3)角边角(ASA):两角和它们的夹边分别相等的两个三角形全等。
(4)角角边(AAS):两角和其中一个角的对边分别相等的两个三角形全等。
(5)斜边、直角边(HL):斜边和一条直角边分别相等的两个直角三角形全等。
一、选择题1.如图,已知AB=AD,∠BAD=∠CAE,则添加下列条件之一,仍不一定能判定△ABC≌△ADE的是()A.AC=AE B.∠C=∠E C.BC=DE D.∠B=∠D 2.用三角尺可按下面方法画角的平分线.如图,在∠AOB两边上,分别取OM=ON,再分别过点M,N作OA,OB的垂线,交点为P,画射线OP,可得△POM≌△PON则判定三角形全等的依据是()A.SSS B.SAS C.ASA D.HL3.下列命题中,真命题的是()A.有一直角边和一锐角对应相等的两个直角三角形全等B.周长相等的两个三角形全等C.两边及其中一边的对角分别相等的两个三角形全等D.全等三角形的面积相等,面积相等的两个三角形全等4.如图,若OP平分∠AOB,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论中错误的是()A.PC=PD B.OP、PC不一定相等C.∠CPO=∠DPO D.OC=OD5.如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,AB=5,BD=1,则CF的长度为()A.2 B.2.5 C.4 D.56.如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的度数和为()A.60°B.75°C.90°D.120°7.如图所示,AB∥CD,AD∥BC,BE=DF,则图中全等三角形共有( )对.A.2 B.3 C.4 D.18.如图,在△ABC中∠B=∠C,BF=CD,BD=CE,∠A=50°,则∠FDE的度数为()A.75°B.70°C.65°D.60°二、填空题9.如图,已知BF=CE,AC=DF请添加一个条件,使得△ABC≌△DEF则添加的条件可以是:.(不添加其他字母及辅助线)10.已知,如图AD=AE,BD=CE那么图中△ADC≌.11.如图,在△ABC中AD⊥BC,CE⊥AB垂足分别是D,E.AD,CE交点H,已知EH=EB=3,AE=5则CH的长是.12.如图,△ABC的面积为6cm2,AP垂直∠ABC的平分线BP于点P,则△PBC的面积是cm2.13.如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=28°,∠2=30°,则∠3=.三、解答题14.如图,已知点C,F在直线AD上,且有BC= EF,AB=DE,CD=AF。
八年级数学上册《第十二章 全等三角形》单元测试卷及答案(人教版)

八年级数学上册《第十二章 全等三角形》单元测试卷及答案(人教版)学校:___________班级:___________姓名:___________考号:___________一、选择题:(本题共8小题,每小题5分,共40分.)1.下列可以判定两个直角三角形全等的条件是( )A .斜边相等B .面积相等C .两对锐角对应相等D .两对直角边对应相等2.到三角形三边的距离相等的点是( )A .三角形三内角平分线的交点;B .三角形三边中线的交点;C .三角形三边高的交点;D .三角形三边中垂线的交点。
3.如图,ABC ≌△DEC ,B 、C 、D 在同一直线上,且CE=5,AC=7,则BD 长( )A .12B .7C .2D .144.如图,在ABC 中,AD 平分BAC ∠,DE AB ⊥于点E ,再添加一个条件仍然不能证明△ADC ≌△ADE 的是( )A .90ACB ∠=︒ B .∠ADC =∠ADE C .AC AE =D .DC DE =5.如图,在△ABC 中,∠A=90°,AB=AC=6,点D 是BC 中点,点E 、F 分别在AB 、AC 上,且BE=AF ,则四边形AEDF 的面积为( )A .6B .7C .D .96.如图,在ABC 中90A ∠=︒,AB =2,BC =5,BD 是ABC ∠的平分线,设ABD 和BDC 的面积分别是1S 和2S ,则S 1:S 2的值为( )A .5:2B .2:5C .12:D .1:5 7.如图,∠A=∠B ,AE=BE ,点D 在AC 边上,∠1=∠2,AE 和BD 相交于点O ,若∠1=38°,则∠BDE 的度数为( )A .71°B .76°C .78°D .80°8.如图所示,点 ,A B 分别是 ,NOF MOF ∠∠ 平分线上的点, AB OF ⊥ 于点 E , BC ⊥MN 于点 C , AD ⊥MN 于点 D ,下列结论错误的是( )A .90AOB ∠= B .AD +BC =ABC .点 O 是 CD 的中点 D .图中与 ∠CBO 互余的角有两个二、填空题:(本题共5小题,每小题3分,共15分.)9.如图,在△ABC 和△DEF 中,已知CB =DF ,∠C =∠D ,要使△ABC ≌△EFD ,还需添加一个条件,那么这个条件可以是 .10.在Rt △ABC 中,∠ACB=90°,BC=2cm ,CD ⊥AB ,在AC 上取一点E ,使EC=BC ,过点E 作EF ⊥AC 交CD 的延长线于点F ,若EF=5cm ,则AE= cm.11.如图,AC 平分∠DCB ,CB =CD ,DA 的延长线交BC 于点E ,若∠BAE =80°,则∠EAC 的度数为 .12.如图,有一个直角三角形ABC ∠C =90° , AC=10 , BC=5 ,一条线段PQ=AB ,P 、Q 两点分别在线段AC 和过点A 且垂直于AC 的射线AX 上运动,动点P 从C 点以2个单位秒的速度出发,问P 点运动 秒时(不包括点C ),才能使△ABC ≌△QPA .13.如图,已知ABC ∆的周长是 21 ,OB ,OC 分别平分ABC ∠和ACB ∠,OD BC ⊥于D ,且OD =4,ABC ∆ 面积是 .三、解答题:(本题共5题,共45分)14.如图,△ABO ≌△CDO ,点B 在CD 上,AO ∥CD ,∠BOD=30°,求∠A 的度数.15.如图,在ABC 中,∠ACB =90°,AC =BC ,BE ⊥CE 于E ,AD CE ⊥于D ,AD =2.5cm ,DE =1.7cm ,求BE 的长.16.如图,DE AC ⊥于点E ,BFAC ⊥于点F .AB =CD ,AE =CF ,BD 交AC 于点M ,求证:MB =MD .17.如图所示,已知 AD//BC , 点 E 为 CD 上一点,AE 、BE 分别平分∠DAB 、∠CBA ,BE 交 AD 的延长线于点 F.求证:(1)△ABE ≌△AEF ;(2) AD+BC=AB18.如图,在△ABC 中,∠B =60°,AD 平分∠BAC ,CE 平分∠BCA ,AD 、CE 交于点F ,CD =CG ,连结FG.(1)求证:FD =FG ;(2)线段FG 与FE 之间有怎样的数量关系,请说明理由;(3)若∠B ≠60°,其他条件不变,则(1)和(2)中的结论是否仍然成立?请直接写出判断结果,不必说明理由参考答案:1.D 2.A 3.A 4.D 5.D 6.B 7.A 8.D9.AC =ED 或∠A =∠FED 或∠ABC =∠F .10.311.50°12.2.513.4214.解:∵△ABO ≌△CDO∴OB=OD ,∠ABO=∠D∴∠OBD=∠D=12(180°﹣∠BOD )=12×(180°﹣30)=75° ∴∠ABC=180°﹣75°×2=30°∴∠A=∠ABC=30°.15.解:∵90ACB ∠=︒∴90BCE ACD ∠+∠=︒∵AD CE BE CE ⊥⊥,∴9090ADC CEB CAD ACD ∠=∠=︒∠+∠=︒, ∴CAD BCE ∠∠=在ACD 与CBE 中{∠ADC =∠CEB∠BCE =∠CAD AC =BC∴()AAS ACD CBE ≌∴BE CD CE AD ==,∴ 2.5 1.70.8cm BE CD CE DE AD DE ==-=-=-=. 答:BE 的长为0.8cm .16.证明:∵AE =CF∴AE +EF =CF +EF ,即AF =CE∵DE ⊥AC 于点E ,BF AC ⊥于点F∴ABF 和CDE 是直角三角形在Rt ABF 和Rt CDE 中{AB =CD AF =CE∴Rt △ABF ≌Rt △CDE(HL),∴BF =DE ;在DEM 和△BFM 中{∠DEM =∠BFM =90°∠DME =∠BMF DE =BF∴△DEM ≌△BFM(AAS),∴MB =MD .17.(1)证明:如图,∵AE 、BE 分别平分∠DAB 、∠CBA∴∠1=∠2,∠3=∠4∵AD∥BC∴∠2=∠F,∠1=∠F在△ABE和△AFE中∴△ABE≌△AFE(AAS)(2)证明:∵△ABE≌△AFE∴BE=EF在△BCE和△FDE中∴△BCE≌△FDE(ASA)∴BC=DF∴AD+BC=AD+DF=AF=AB即AD+BC=AB.18.(1)证明:∵EC平分∠ACB ∴∠FCD=∠FCG∵CG=CD,CF=CF∴△CFD≌△CFG(SAS)∴FD=FG.(2)解:结论:FG=FE.理由:∵∠B=60°∴∠BAC+∠BCA=120°∵AD平分∠BAC,CE平分∠BCA∴∠ACF+∠FAC=12(∠BCA+∠BAC)=60°∴∠AFC=120°,∠CFD=∠AFE=60°∵△CFD≌△CFG∴∠CFD=∠CFG=60°∴∠AFG=∠AFE=60°∵AF=AF,∠FAG=∠FAE∴△AFG≌△AFE(ASA)∴FG=FE.(3)解:结论:(1)中结论成立.(2)中结论不成立. 理由:①同法可证△CFD≌△CFG(SAS)∴FD=FG.②∵∠B≠60°∴无法证明∠AFG=∠AFE∴不能判断△AFG≌△AFE∴(2)中结论不成立。
第13章 全等三角形 华东师大版八年级数学上册单元测试(含答案)

第13章 全等三角形(90分钟 100分)一、选择题(每小题3分,共24分)1.△ABC中,AB=AC=2,∠B=60°,则BC=( )A.2B.3C.4D.52.(2024·泉州期末)下列命题的逆命题是真命题的是( )A.全等三角形的对应角相等B.对顶角相等C.若x>y,则x-y>0D.若C是线段AB的中点,则AC=BC3.(2024·南通质检)如图,已知△ABC≌△DEC,∠ACB=100°,∠D=35°,则∠E=( )A.35°B.45°C.55°D.无法计算4.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,要求用圆规和直尺作图,把它分成两个三角形,其中一个三角形是等腰三角形.其作法错误的是( )5.(2023·台州中考)如图,锐角三角形ABC中,AB=AC,点D,E分别在边AB,AC上,连结BE,CD.下列命题中,假命题是( )A.若CD=BE,则∠DCB=∠EBCB.若∠DCB=∠EBC,则CD=BEC.若BD=CE,则∠DCB=∠EBCD.若∠DCB=∠EBC,则BD=CE6.如图,在Rt△ABC中,∠C=90°,AC=12 cm,BC=6 cm,线段PQ=AB,P,Q两点分别在线段AC和AC的垂线AX上移动,若以A,B,C为顶点的三角形与以A,P,Q为顶点的三角形全等,则AP的值为( )A.8 cmB.12 cmC.12 cm或6 cmD.12 cm或8 cm7.如图,OE是∠AOB的平分线,BD⊥OA,AC⊥OB,垂足分别为D,C,BD,AC都经过点E,则图中全等的三角形共有对( )A.3B.4C.5D.68.(2024·天津期中)如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④连结OC,OC平分∠AOE;⑤∠AOB=60°.恒成立的结论有( )A.①⑤B.①②⑤C.①②③⑤D.①②③④⑤二、填空题(每小题4分,共24分)9.定理“直角三角形的两个锐角互余”的逆定理是.10.检测房梁是否水平,可以采用下面的方法:在等腰直角三角尺斜边中点拴一条线绳,线绳的另一端拴一个铅锤,把这块三角尺的斜边贴在房梁上,结果线绳经过三角尺的顶点,则可以判断房梁是水平的.这样做的根据是:.11.如图,D在BC边上,△ABC≌△ADE,∠EAC=44°,则∠B的度数为.12.如图,在△ABC中,∠B=30°,∠C=50°,通过观察尺规作图的痕迹,∠DEA的度数是.13.(2023·重庆中考A卷)如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D为BC上一点,连结AD.过点B作BE⊥AD于点E,过点C作CF⊥AD交AD的延长线于点F.若BE=4,CF=1,则EF的长度为.14.如图,∠BOC=60°,A是BO的延长线上一点,OA=10 cm,动点P从点A出发,沿AB 以3 cm/s的速度移动,动点Q从点O出发沿OC以2 cm/s的速度移动,若点P,Q 同时出发,当△OPQ是等腰三角形时,移动的时间是.三、解答题(共52分)15.(6分)(2023·云南中考)如图,C是BD的中点,AB=ED,AC=EC.求证:△ABC≌△EDC.16.(8分)(2024·北京期中)下面是“过直线上一点作已知直线的垂线”的尺规作图过程:已知:如图,点P在直线l上.求作:直线PQ,使PQ⊥l.作法:①以点P为圆心,任意长为半径画弧,交直线l于A,B两点,AB长为半径画弧,两弧在直线l上方交于点Q,②分别以A,B为圆心,大于12③作直线PQ.直线PQ即为所求的垂线.(1)使用直尺和圆规,补全图形(保留作图痕迹);(2)完成下面的证明.证明:连结AQ,BQ,∵根据作法,有AQ=BQ,AP=BP,∴PQ⊥AB,即PQ⊥l.()(填推理的依据)17.(8分)如图,在长方形纸片ABCD中,点P在BC边上,将△CDP沿DP折叠,点C 落在点E处,PE,DE分别交AB于点G,F,且GF=GP.(1)求证:△GEF≌△GBP;(2)若PC=2,求BF的长.18.(8分)(2023·苏州中考)如图,在△ABC中,AB=AC,AD为△ABC的角平分线.以点A 为圆心,AD长为半径画弧,与AB,AC分别交于点E,F,连结DE,DF.(1)求证:△ADE≌△ADF;(2)若∠BAC=80°,求∠BDE的度数.19.(10分)已知,如图,AD为△ABC的角平分线,且AD=AC,E为AD延长线上的一点,AE=AB.(1)求证:△ABD≌△AEC;(2)求证:BE=EC.20.(12分)如图,△ABC是等边三角形,点D在AC上,点E在BC的延长线上,且BD=DE.(1)若点D是AC的中点,如图1,则线段AD与CE的数量关系是;(2)若点D不是AC的中点,如图2,试判断AD与CE的数量关系,并证明你的结论;(提示:过点D作DF∥BC,交AB于点F)(3)若点D在线段AC的延长线上,(2)中的结论是否仍成立?如果成立,请给予证明;如果不成立,请说明理由.【附加题】(10分)(1)已知△ABC中,∠BAC=60°,以AB和BC为边向外作等边△ABD和△BCE.①连结AE,CD,如图1,求证:∠BCD=∠AEB;②若AB⊥BC,延长AB交DE于点M,求证:点M为DE的中点;(2)如图3,HE⊥CE于点E,∠BEH=30°,点G在EH上运动,以BG为边作等边△BGF,当BF的长最小时,求∠FBE的度数.第13章 全等三角形(90分钟 100分)一、选择题(每小题3分,共24分)1.△ABC中,AB=AC=2,∠B=60°,则BC=(A)A.2B.3C.4D.52.(2024·泉州期末)下列命题的逆命题是真命题的是(C)A.全等三角形的对应角相等B.对顶角相等C.若x>y,则x-y>0D.若C是线段AB的中点,则AC=BC3.(2024·南通质检)如图,已知△ABC≌△DEC,∠ACB=100°,∠D=35°,则∠E=(B)A.35°B.45°C.55°D.无法计算4.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,要求用圆规和直尺作图,把它分成两个三角形,其中一个三角形是等腰三角形.其作法错误的是(B)5.(2023·台州中考)如图,锐角三角形ABC中,AB=AC,点D,E分别在边AB,AC上,连结BE,CD.下列命题中,假命题是(A)A.若CD=BE,则∠DCB=∠EBCB.若∠DCB=∠EBC,则CD=BEC.若BD=CE,则∠DCB=∠EBCD.若∠DCB=∠EBC,则BD=CE6.如图,在Rt△ABC中,∠C=90°,AC=12 cm,BC=6 cm,线段PQ=AB,P,Q两点分别在线段AC和AC的垂线AX上移动,若以A,B,C为顶点的三角形与以A,P,Q为顶点的三角形全等,则AP的值为(C)A.8 cmB.12 cmC.12 cm或6 cmD.12 cm或8 cm7.如图,OE是∠AOB的平分线,BD⊥OA,AC⊥OB,垂足分别为D,C,BD,AC都经过点E,则图中全等的三角形共有 对(B)A.3B.4C.5D.68.(2024·天津期中)如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④连结OC,OC平分∠AOE;⑤∠AOB=60°.恒成立的结论有(D)A.①⑤B.①②⑤C.①②③⑤D.①②③④⑤二、填空题(每小题4分,共24分)9.定理“直角三角形的两个锐角互余”的逆定理是 有两个角互余的三角形是直角三角形 .10.检测房梁是否水平,可以采用下面的方法:在等腰直角三角尺斜边中点拴一条线绳,线绳的另一端拴一个铅锤,把这块三角尺的斜边贴在房梁上,结果线绳经过三角尺的顶点,则可以判断房梁是水平的.这样做的根据是: 等腰三角形的底边上的中线、底边上的高重合 .11.如图,D在BC边上,△ABC≌△ADE,∠EAC=44°,则∠B的度数为 68° .12.如图,在△ABC中,∠B=30°,∠C=50°,通过观察尺规作图的痕迹,∠DEA的度数是 85° .13.(2023·重庆中考A卷)如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D为BC上一点,连结AD.过点B作BE⊥AD于点E,过点C作CF⊥AD交AD的延长线于点F.若BE =4,CF =1,则EF 的长度为 3 .14.如图,∠BOC =60°,A 是BO 的延长线上一点,OA =10 cm,动点P 从点A 出发,沿AB 以3 cm/s 的速度移动,动点Q 从点O 出发沿OC 以2 cm/s 的速度移动,若点P ,Q 同时出发,当△OPQ 是等腰三角形时,移动的时间是 2 s 或10 s .三、解答题(共52分)15.(6分)(2023·云南中考)如图,C 是BD 的中点,AB =ED ,AC =EC.求证:△ABC ≌△EDC.【解析】∵C 是BD 的中点,∴BC =DC ,在△ABC 和△EDC 中,AB =ED AC =EC BC =DC,∴△ABC ≌△EDC (S.S.S.).16.(8分)(2024·北京期中)下面是“过直线上一点作已知直线的垂线”的尺规作图过程:已知:如图,点P 在直线l 上.求作:直线PQ ,使PQ ⊥l.作法:①以点P 为圆心,任意长为半径画弧,交直线l 于A ,B 两点,②分别以A ,B 为圆心,大于12AB 长为半径画弧,两弧在直线l 上方交于点Q ,③作直线PQ.直线PQ即为所求的垂线.(1)使用直尺和圆规,补全图形(保留作图痕迹);(2)完成下面的证明.证明:连结AQ,BQ,∵根据作法,有AQ=BQ,AP=BP,∴PQ⊥AB,即PQ⊥l.(等腰三角形底边上的中线与底边上的高重合)(填推理的依据)【解析】(1)补全的图形如图所示:【解析】(2)连结AQ,BQ,∵根据作法,有AQ=BQ,AP=BP,∴PQ⊥AB,即PQ⊥l.(等腰三角形底边上的中线与底边上的高重合)17.(8分)如图,在长方形纸片ABCD中,点P在BC边上,将△CDP沿DP折叠,点C 落在点E处,PE,DE分别交AB于点G,F,且GF=GP.(1)求证:△GEF≌△GBP;【解析】(1)∵纸片ABCD为长方形,∴∠B=∠C=90°,由折叠的性质得,∠E=∠C,∴∠E=∠B,在△GEF 和△GBP 中,∠E =∠B ∠EGF =∠BGP GF =GP,∴△GEF ≌△GBP (A.A.S.);(2)若PC =2,求BF 的长.【解析】(2)由△GEF ≌△GBP 得GE =GB ,∵GF =GP ,∴BF =GB +GF =GE +GP =PE ,由折叠的性质得,PE =PC =2,∴BF =2.18.(8分)(2023·苏州中考)如图,在△ABC 中,AB =AC ,AD 为△ABC 的角平分线.以点A 为圆心,AD 长为半径画弧,与AB ,AC 分别交于点E ,F ,连结DE ,DF.(1)求证:△ADE ≌△ADF ;【解析】(1)∵AD 是△ABC 的角平分线,∴∠BAD =∠CAD.由作图知:AE =AF.在△ADE 和△ADF 中,AE =AF ∠BAD =∠CAD AD =AD,∴△ADE ≌△ADF (S.A.S.);(2)若∠BAC =80°,求∠BDE 的度数.【解析】(2)∵∠BAC =80°,AD 为△ABC 的角平分线,∴∠EAD =12∠BAC =40°,由作图知:AE =AD ,∴∠AED =∠ADE ,∴∠ADE =12×(180°-40°)=70°,∵AB =AC ,AD 为△ABC 的角平分线,∴AD ⊥BC ,∴∠BDE =90°-∠ADE =20°.19.(10分)已知,如图,AD 为△ABC 的角平分线,且AD =AC ,E 为AD 延长线上的一点,AE =AB.(1)求证:△ABD≌△AEC;【证明】(1)∵AD平分∠BAC,∴∠BAD=∠DAC,在△ABD与△AEC中,AB=AE∠BAD=∠EAC AD=AC,∴△ABD≌△AEC(S.A.S.); (2)求证:BE=EC.【证明】(2)∵AD=AC,AE=AB,∴∠ACD=∠ADC=180°-∠DAC2,∠ABE=∠AEB=180°-∠BAD2,∴∠ACD=∠ADC=∠ABE=∠AEB,∵∠BDE=∠ADC,∴∠BDE=∠BED,∴BD=BE,∵△ABD≌△AEC,∴BD=EC,∴BE=EC.20.(12分)如图,△ABC是等边三角形,点D在AC上,点E在BC的延长线上,且BD=DE.(1)若点D是AC的中点,如图1,则线段AD与CE的数量关系是AD=CE;【解析】(1)AD=CE,理由如下:∵△ABC是等边三角形,∴∠ABC=∠ACB=60°,AB=AC=BC.∵点D为AC的中点,∴∠DBC=30°,AD=DC,∵BD=DE,∴∠E=∠DBC=30°,∵∠ACB=∠E+∠CDE,∴∠CDE=∠E=30°,∴CD=CE,又∵AD=DC,∴AD=CE.(2)若点D不是AC的中点,如图2,试判断AD与CE的数量关系,并证明你的结论;(提示:过点D作DF∥BC,交AB于点F)【解析】(2)AD=CE,理由如下:如图,过点D作DF∥BC,交AB于点F,则∠ADF=∠ACB=60°,∵∠A=60°,∴△AFD是等边三角形,∴AD=DF=AF,∠AFD=60°,∴∠BFD=∠DCE=180°-60°=120°,∵DF∥BC,∴∠FDB=∠DBE=∠E,在△BFD和△DCE中,∠FDB=∠E∠BFD=∠DCE BD=DE,∴△BFD≌△DCE(A.A.S.),∴DF=EC,又∵AD=DF,∴AD=CE;(3)若点D在线段AC的延长线上,(2)中的结论是否仍成立?如果成立,请给予证明;如果不成立,请说明理由.【解析】(3)结论仍成立,理由如下:如图,过点D作DP∥BC,交AB的延长线于点P,则∠ABC=∠APD=60°,∠ACB=∠ADP=60°,∵∠A=60°,∴△APD是等边三角形,∴AP=PD=AD,∴∠DCE=∠ACB=∠P,∵DP∥BC,∴∠PDB=∠CBD,∵DB=DE,∴∠DBC=∠DEC,∴∠PDB=∠DEC,在△BPD和△DCE中,∠PDB=∠CED ∠P=∠DCE BD=DE,∴△BPD≌△DCE(A.A.S.),∴PD=CE,又∵AD=PD,∴AD=CE.【附加题】(10分)(1)已知△ABC中,∠BAC=60°,以AB和BC为边向外作等边△ABD和△BCE.①连结AE,CD,如图1,求证:∠BCD=∠AEB;②若AB⊥BC,延长AB交DE于点M,求证:点M为DE的中点;【解析】(1)①∵△ABD和△BCE是等边三角形,∴BD=BA,BC=BE,∠DBA=∠EBC=60°,∴∠DBA+∠ABC=∠EBC+∠ABC,即∠DBC=∠ABE,在△DBC和△ABE中,BD=BA∠DBC=∠ABE BC=BE,∴△DBC≌△ABE(S.A.S.),∴∠BCD=∠AEB;②如图,过点E作AD的平行线,交AM的延长线于点F,∵AD∥EF,∴∠DAM=∠AFE=60°,∵AB⊥BC,∴∠EBF=180°-∠ABC-∠CBE=30°,∴∠BEF=90°,在△ABC与△FEB中,∠BAC=∠EFB ∠ABC=∠FEB BC=EB,∴△ABC≌△FEB(A.A.S.),∴AB=EF=AD,在△MAD与△MFE中,∠AMD=∠FME ∠DAM=∠EFM AD=FE,∴△MAD≌△MFE(A.A.S.),∴DM=EM,即点M为DE的中点;(2)如图3,HE⊥CE于点E,∠BEH=30°,点G在EH上运动,以BG为边作等边△BGF,当BF的长最小时,求∠FBE的度数.【解析】(2)当BF的长最小时,即BG最小,则BG⊥HE,当以BG为边在BG左侧作等边△BGF时,如图所示:可得∠GBE=180°-∠BEH-∠BGE=60°,∵△FBG为等边三角形,∴∠FBG=60°,∴∠FBE=∠FBG+∠GBE=120°;当以BG为边在BG右侧作等边△BGF时,如图所示:此时点F在BE上,∴∠FBE=0°,综上所述,∠FBE=0°或120°.。
苏科版八年级数学上册试题 第1章 全等三角形 单元测试卷(含详解)

第1章《 全等三角形》单元测试卷一、单选题(本大题共10小题,每小题3分,共30分)1.下列说法正确的是( )A .两个等边三角形一定全等B .腰对应相等的两个等腰三角形全等C .形状相同的两个三角形全等D .全等三角形的面积一定相等2.已知与全等,A 、B 、C 的对应点分别为D 、E 、F ,且E 点在AE 上,B 、F 、C 、D 四点共线,如图所示若,,则下列叙述何者正确?( )A .,B .,C .,D .,3.如图,在△ABC 中,AB =BC ,点D 为AC 上的点,连接BD ,点E 在△ABC 外,连接AE ,BE ,使得CD =BE ,∠ABE =∠C ,过点B 作BF ⊥AC 交AC 点F ,若∠BAE =21°,∠C =28°,则∠FBD =( )A .49°B .59°C .41°D .51°4.如图,有一块边长为4的正方形塑料模板,将一块足够大的直角三角板的直角顶点落在点,两条直角边分别与交于点F ,与延长线交于点E .则四边形的面积是( )ABC V DEF V .=40A ∠︒=35CED ∠︒=EF EC =AE FC=EF EC AE FC ≠EF EC ≠=AE FC EF EC ≠AE FC≠ABCD A CD CB AECFA .4B .6C .10D .165.如图,在的网格中,每一个小正方形的边长都是1,点,,,都在格点上,连接,相交于,那么的大小是( )A .B .C .D .6.△ABC 中,AB =AC ,∠ABC =72°,以B 为圆心,以任意长为半径画弧,分别交BA 、BC 于M 、N ,再分别以M 、N为圆心,以大于MN 为半径画弧,两弧交于点P ,射线BP 交AC 于点D ,则图中与BC 相等的线段有( )A .BD B .CD C .BD 和AD D .CD 和AD7.如图,在Rt △ABC 中,∠C=90°,以顶点A 为圆心,适当长为半径画弧,分别交AB 、AC 于点M 、N ,再分别以点M 、N 为圆心,大于MN 的长为半径画弧,两弧交于点P ,射线AP 交边BC 于点D .下列说法错误的是( )33⨯A B C D AC BD P APB ∠80︒60︒45︒30︒1212A .B .若,则点D 到AB 的距离为2C .若,则D .8.如图,长方形中,点为上一点,连接,将长方形沿着直线折叠,点恰好落在的中点上,点为的中点,点为线段上的动点,连接、,若、、,则的最小值是( )A .B .C .D .9.如图,点在线段上,于,于.,且,,点以的速度沿向终点运动,同时点以的速度从开始,在线段上往返运动(即沿运动),当点到达终点时,,同时停止运动.过,分别作的垂线,垂足为,.设运动时间为,当以,,为顶点的三角形与全等时,的值为( )A .1或3B .1或C .1或或 D .1或或510.如图,在中,,和的平分线、相交于点,交于点,交于点,若已知周长为,,,则长为( )CAD BAD ∠=∠2CD =30B ∠=CDA CAB ∠=∠2ABD ACDS S =V V ABCD E AD CE ABCD CE D AB F G CF P CE PF PG AE a =ED b =AF c =PF PG +a c b +-2b c +2a b c ++a b+C BD AB BD ⊥B ED BD ⊥D 90ACE ∠=︒5cm AC =6cm CE =P 2cm/s A C E →→E Q 3cm/s E EC E C E C →→→→⋅⋅⋅P P Q P Q BD M N s t P C M QCN △t 115115235115ABC V 60A ∠=︒ABC ∠ACB ∠BD CE O BD AC D CE AB E ABC V 207BC =:4:3AE AD =AEA. B . C . D .4二、填空题(本大题共8小题,每小题4分,共32分)11.如图,已知正方形中阴影部分的面积为3,则正方形的面积为 .12.数学课上,老师出示如下题目:“已知:.求作:.”如图是小宇用直尺和圆规的作法,其中的道理是作出△,根据全等三角形的性质,得到.△的依据是 .13.如图,已知,,,直线与,分别交于点,,且,,则的度数为 .14.如图,在△ABC 中,点D 是AC 的中点,分别以AB ,BC 为直角边向△ABC 外作等腰直角三角形ABM 和等腰直角三角形BCN ,其中∠ABM =NBC =∠90°,连接MN ,已知MN =4,则BD = .187247267AOB ∠A O B AOB '''∠=∠ΔC O D COD ''≅'A O B AOB '''∠=∠ΔC O D COD ''≅'AB AD =AC AE =BC DE =BC AD DE F G 65DGB ∠=︒120EAB ∠=︒CAD ∠15.如图,为的平分线,为上一点,且于点,,给出下列结论:①;②;③;④;⑤四边形的面积是面积的2倍,其中结论正确的个数有 .16.如图,把两块大小相同的含45°的三角板ACF 和三角板CFB 如图所示摆放,点D 在边AC 上,点E 在边BC 上,且∠CFE =13°,∠CFD =32°,则∠DEC 的度数为 .17.如图,在中,,,,有下列结论:①;②;③连接,;④过点作交于点,连接,则.其中正确的结论有 .18.如图,在Rt △ABC 中,∠C =90°,两锐角的角平分线交于点P ,点E 、F 分别在边BC 、AC 上,且都不与点C 重合,若∠EPF =45°,连接EF ,当AC =6,BC =8,AB =10时,则△CEF的BN MBC ∠P BN PD BC ⊥D 180APC ABC ∠+∠=︒MAP ACB ∠=∠PA PC =2BC AB CD -=BP AC =BAPC PBD △ABC V AD BC ⊥AD BD =BF AC =ADC BDF △≌△BE AC ⊥DE 135AED ∠=︒D DM AB ∥AC M FM BF AM MD =+周长为 .三、解答题(本大题共6小题,共58分)19.(8分)如图,,点E 在BC 上,且,.(1) 求证:;(2) 判断AC 和BD的位置关系,并说明理由.BD BC =BE AC =DE AB =ABC EDB V V ≌20.(8分)如图,在五边形中,,.(1) 请你添加一个条件,使得,并说明理由;(2) 在(1)的条件下,若,,求的度数.21.(10分)在复习课上,老师布置了一道思考题:如图所示,点M ,N 分别在等边的边上,且,,交于点Q .求证:.同学们利用有关知识完成了解答后,老师又提出了下列问题:(1) 若将题中“”与“”的位置交换,得到的是否仍是真命题?请你给出答案并说明理由.ABCDE AB DE =AC AD =ABC DEA △△≌66CAD ∠=︒110B ∠=︒BAE ∠ABC V ,BC CA BM CN =AM BN 60BQM ∠=︒BM CN =60BQM ∠=︒(2) 若将题中的点M ,N 分别移动到的延长线上,是否仍能得到?请你画出图形,给出答案并说明理由.22.(10分)如图1,点P 、Q 分别是边长为4cm 的等边三角形ABC 的边AB 、BC 上的动点,点P 从顶点A ,点Q 从顶点B 同时出发,且它们的速度都为1cm/s .(1)连接AQ 、CP 交于点M ,则在P ,Q 运动的过程中,证明≌;(2)会发生变化吗?若变化,则说明理由,若不变,则求出它的度数;(3)P 、Q 运动几秒时,是直角三角形?,BC CA 60BQM ∠=︒ABQ ∆CAP ∆CMQ ∠PBQ ∆(4)如图2,若点P 、Q 在运动到终点后继续在射线AB 、BC 上运动,直线AQ 、CP 交点为M ,则变化吗?若变化说明理由,若不变,则求出它的度数。
八年级数学上册《第十二章 全等三角形》单元测试卷及答案(人教版)
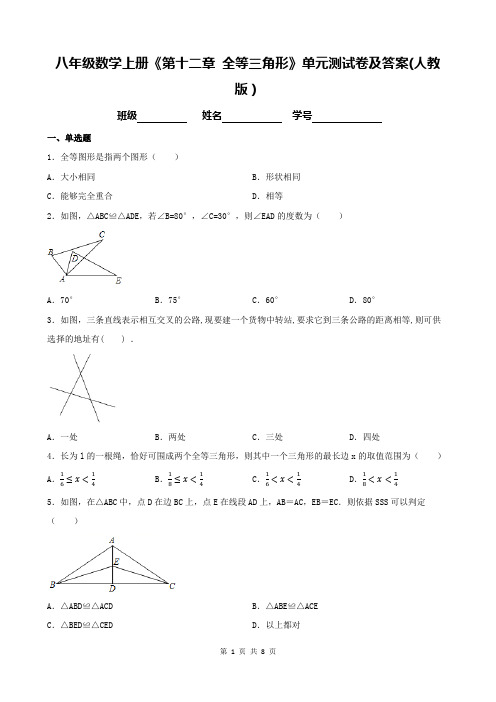
八年级数学上册《第十二章全等三角形》单元测试卷及答案(人教版)班级姓名学号一、单选题1.全等图形是指两个图形()A.大小相同B.形状相同C.能够完全重合D.相等2.如图,△ABC≌△ADE,若∠B=80°,∠C=30°,则∠EAD的度数为()A.70°B.75°C.60°D.80°3.如图,三条直线表示相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( ) .A.一处B.两处C.三处D.四处4.长为l的一根绳,恰好可围成两个全等三角形,则其中一个三角形的最长边x的取值范围为()A.16≤x<14B.18≤x<14C.16<x<14D.18<x<145.如图,在△ABC中,点D在边BC上,点E在线段AD上,AB=AC,EB=EC.则依据SSS可以判定()A.△ABD≌△ACD B.△ABE≌△ACEC.△BED≌△CED D.以上都对6.如图,在△ABC中,∠B=∠C,BF=CD,BD=CE,∠FDE=α,则下列结论正确的是()A.2α+∠A=180°B.α+∠A=90°C.2α+∠A=90°D.α+∠A=180°7.如图,点O在△ABC内,且到三边的距离相等,∠A=64°,则∠BOC的度数为()A.58°B.64°C.122°D.124°8.如图,在△ABC中,P是BC上的点,作PQ∥AC交AB于点Q,分别作PR⊥AB,PS⊥AC,垂足分别是R,S,若PR=PS,则下面三个结论:①AS=AR;②AQ=PQ;③△PQR≌△CPS;④AC﹣AQ=2SC,其中正确的是()A.②③④B.①②C.①④D.①②③④二、填空题9.已知△ABC≌△DEF,若∠B=40°,∠D=30°,则∠F=10.如图,已知B、E、F、C在同一直线上,BE=CF,AF=DE,则添加条件,可以判断△ABF≌△DCE.11.如图,△ABD≌△ACE,点B和点C是对应顶点,AB=9cm,BD=7cm,AD=4cm,则DC= cm.12.如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中:①∠ABC=∠ADC;②AC与BD相互平分;③AC,BD分别平分四边形ABCD的两组对角;④四边形ABCD的面AC•BD.正确的是(填写所有正确结论的序号)积S= 1213.如图,在△ABC中AC=BC,∠ACB=50°,AD⊥BC于点D,MC⊥BC于点C,MC=BC点E,点F分别在线段AD,AC上CF=AE,连接MF,BF,CE.(1)图中与MF相等的线段是;(2)当BF+CE取最小值时∠AFB=°三、解答题14.将Rt△ABC的直角顶点C置于直线l上AC=BC,分别过点A、B作直线l的垂线,垂足分别为点D、E连接AE若BE=3,DE=5求△ACE的面积.15.如图,点A,B,C,D在同一条直线上,CE∥DF,EC=BD,AC=FD.求证:AE=FB.16.如图,已知AC∥BD、EA、EB分别平分∠CAB和△DBA,CD过点E,则线段AB与AC、BD有什么数量关系?请说明理由.17.如图,已知B,C,E三点在同一条直线上AC//DE,AC=CE,∠ACD=∠B .求证:△ABC≌△EDC .18.如图,点D为锐角∠ABC的平分线上一点,点M在边BA上,点N在边BC上,∠BMD+∠BND=180°.试说明:DM=DN.19.已知:AD=BC,AC=BD.(1)如图1,求证:AE=BE;(2)如图2,若AB=AC,∠D=2∠BAC,在不添加任何辅助线的情况下,请直接写出图2中四个度数为36°的角.参考答案 1.C 2.A 3.D 4.A 5.D 6.A 7.C 8.B 9.110° 10.AB=DC 11.5 12.①④ 13.(1)EC (2)9514.解:∵AD ⊥CE ,BE ⊥CE ∴∠ADC =∠CEB =90° ∵∠ACB =90°∴∠ACD =∠CBE =90°−∠ECB 在 △ACD 与 △CBE 中{∠ADC =∠CEB∠ACD =∠CBE AC =BC∴△ACD ≌△CBE (AAS) ∴CD =BE =3 AD =CE ∵CE =CD +DE =3+5=8 ∴AD =8 .S △ACE =12CE ·AD =12×8×8=32 . 15.证明:∵CE ∥DF ∴∠ACE=∠D 在△ACE 和△FDB 中{AC=FD ∠ACE=∠D EC=BD∴△ACE≌△FDB(SAS)∴AE=FB.16.解:AB=AC+BD理由是:在AB上截取AC=AF,连接EF∵AE平分∠CAB∴∠CAE=∠BAE在△CAE和△FAE中{AC=AF∠CAE=∠BAE AE=AE∴△CAE≌△FAE(SAS)∴∠C=∠AFE∵AC∥BD∴∠C+∠D=180°∴∠AFE+∠D=180°∵∠EFB+∠AFE=180°∴∠D=∠EFB∵BE平分∠ABD∴∠DBE=∠FBE在△BEF和△BED中{∠D=∠EFB∠FBE=∠DBEBE=BE∴△BEF≌△BED(AAS)∴BF=BD∵AB=AF+BF,AC=AF,BF=BD ∴AB=AC+BD.17.证明:∵AC//DE∴∠BCA =∠E ∠ACD =∠D . 又∵∠ACD =∠B ∴∠B =∠D .在 △ABC 和 △EDC 中{∠B =∠D∠BCA =∠E AC =EC∴△ABC ≌△EDC .18.解:过点D 作DE ⊥AB 于点E ,DF ⊥BC 于点F . ∴∠DEB =∠DFB =90°. 又∵BD 平分∠ABC ∴DE =DF .∵∠BMD+∠DME =180°,∠BMD+∠BND =180° ∴∠DME =∠BND . 在△EMD 和△FND 中{∠DEM =∠DFN∠EMD =∠FND DE =DF∴△EMD ≌△FND (AAS ). ∴DM =DN .19.(1)证明:在△ABD 和△BAC 中:{AB =BAAD =BC BD =AC∴△ABD ≌△BAC (SSS ) ∴∠ABD=∠BAC ∴AE=BE ;(2)∠BAC ,∠ABD ,∠DAC ,∠DBC。
八年级数学上册《全等三角形》单元测试题(含答案解析)

八年级数学上册《全等三角形》单元测试题(含答案解析)一、选择题(每题4分,共40分)1. 在三角形ABC中,AB=AC,点D是边BC上的一个点,且BD=DC。
以下结论正确的是()A. AD平分∠BACB. AD垂直平分BCC. AD平分∠BD. AD平分∠C【答案】B【解析】因为AB=AC,所以三角形ABC是等腰三角形,∠B=∠C。
又因为BD=DC,所以AD垂直平分BC。
2. 如果两个三角形的两边和它们夹角分别相等,那么这两个三角形()A. 相似B. 全等C. 不一定全等D. 以上都对【答案】B【解析】根据SAS全等定理,如果两个三角形的两边和它们夹角分别相等,那么这两个三角形全等。
3. 在全等三角形ABC和DEF中,如果∠A=40°,∠B=50°,那么∠E的度数是()A. 40°B. 50°C. 60°D. 90°【答案】C【解析】因为三角形ABC和DEF全等,所以∠A=∠D,∠B=∠E。
所以∠E=∠B=50°。
又因为三角形内角和为180°,所以∠E=180°-∠A-∠D=60°。
4. 如果两个三角形的两边及其中一边的对角分别相等,那么这两个三角形()A. 相似B. 全等C. 不一定全等D. 以上都对【答案】C【解析】这种情况不能确定两个三角形全等,因为可能存在两种情况:一种是两个三角形全等,另一种是两个三角形不全等但相似。
5. 在全等三角形ABC和DEF中,如果AB=5cm,BC=8cm,AC=10cm,那么DE的长度是()A. 5cmB. 8cmC. 10cmD. 13cm【答案】C【解析】因为三角形ABC和DEF全等,所以对应边相等,即AB=DE,所以DE=5cm。
6. 如果两个三角形的三个角分别相等,那么这两个三角形()A. 相似B. 全等C. 不一定全等D. 以上都对【答案】C【解析】如果两个三角形的三个角分别相等,那么这两个三角形不一定全等,但一定相似。
八年级数学人教版(上册)单元测试(二)全等三角形

单元测试(二) 全等三角形
一、选择题(每小题 5 分,共 25 分)
1.如图,△ABC≌△CDA,AB=5,BC=6,AC=7,则 AD 的
长是( B )
A.5
B.6
C.7 D.不能确定
第 1 题图
2.如图,已知 AB=AC,点 D,E 分别在线段 AB,AC 上,BE 与 CD 相交于点 O,添加以下哪个条件仍不能判定△ABE≌△ACD( D )
A.∠B=∠C B.AE=AD C.BD=CE D.BE=CD
第 2 题图
3.如图,AB∥CD,以点 A 为圆心,小于 AC 的长为半径画弧, 分别交 AB,AC 于 E,F 两点;再分别以点 E,F 为圆心,大于12EF 的长为半径画弧,两弧相交于点 P,作射线 AP,交 CD 于点 M.若 ∠CMA=25°,则∠C 的度数为( D )
∵ED⊥FD,∴∠EDF=∠EDG=90°. ∴△EDF≌△EDG(SAS).∴EF=EG. ∵在△BEG 中,BE+BG>EG, ∴BE+CF>EF.
(1)求证:△ABC≌△CDE. 证明:∵∠ACB+∠ACE+∠ECD=180°,∠B+∠A+∠ACB
=180°, ∠ACE=∠B, ∴∠A=∠ECD. ∴△ABC≌△CDE(AAS).
(2)若 BC=2,AB=3,则 BD= 5 .
13.(15 分)如图,在△ABC 中,D 是 BC 的中点,DE⊥AB,DF ⊥AC,垂足分别是 E,F.
(2)问题解决: 如图 2,在△ABC 中,D 是 BC 边的中点,DE⊥DF 于点 D, DE 交 AB 于点 E,DF 交 AC 于点 F,连接 EF.求证:BE+CF>EF. 证明:延长 FD 至点 G,使 DG=DF,连接 BG,EG. ∵点 D 是 BC 的中点,∴DB=DC. 又∵∠BDG=∠CDF,∴△BDG≌△CDF(SAS). ∴BG=CF.
八年级全等三角形单元综合测试(Word版 含答案)

八年级全等三角形单元综合测试(Word版含答案)一、八年级数学轴对称三角形填空题(难)1.△ABC与△DEF是两个全等的等腰直角三角形,∠BAC=∠D=90°,AB=AC=6.现将△DEF与△ABC按如图所示的方式叠放在一起,使△ABC保持不动,△DEF运动,且满足点E在边BC上运动(不与B,C重合),边DE始终经过点A,EF与AC交于点M.在△DEF 运动过程中,若△AEM能构成等腰三角形,则BE的长为______.【答案】363【解析】【分析】分若AE=AM 则∠AME=∠AEM=45°;若AE=EM;若MA=ME 则∠MAE=∠AEM=45°三种情况讨论解答即可;【详解】解:①若AE=AM 则∠AME=∠AEM=45°∵∠C=45°∴∠AME=∠C又∵∠AME>∠C∴这种情况不成立;②若AE=EM∵∠B=∠AEM=45°∴∠BAE+∠AEB=135°,∠MEC+∠AEB=135°∴∠BAE=∠MEC在△ABE和△ECM中,BBAE CENAE EIIC∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ABE≌△ECM(AAS),∴CE=AB6,∵AC=BC2AB=3∴BE=23﹣6;③若MA=ME 则∠MAE=∠AEM=45°∵∠BAC=90°,∴∠BAE=45°∴AE平分∠BAC∵AB=AC,∴BE=1BC=3.2故答案为23﹣6或3.【点睛】本题考查了等腰三角形的判定,掌握分类讨论的数学思想是解答本题的关键.2.在平面直角坐标系xOy中,已知点A(2,3),在x轴上找一点P,使得△AOP是等腰三角形,则这样的点P共有_____个.【答案】4【解析】【分析】以O为圆心,OA为半径画弧交x轴于点P1、P3,以A为圆心,AO为半径画弧交x轴于点P4,作OA的垂直平分线交x轴于P2.【详解】解:如图,使△AOP是等腰三角形的点P有4个.故答案为4.【点睛】本题考查了在平面直角坐标系中寻找等腰三角形,掌握两圆一线找等腰三角形是解题的关键.3.在ABC ∆中,边AB 、AC 的垂直平分线分别交边BC 于点D 、点E ,20DAE ∠=︒,则BAC ∠=______°.【答案】80或100【解析】【分析】根据题意,点D 和点E 的位置不确定,需分析谁靠近B 点,则有如下图(图见解析)两种情况:(1)图1中,点E 距离点B 近,根据垂直平分线性质可知,,BD AD AE CE ==,从而有1,2B DAE C DAE ∠=∠+∠∠=∠+∠,再根据三角形的内角和定理可得180B C BAC ∠+∠+∠=︒,联立即可求得;(2)图2中,点D 距离点B 近,根据垂直平分线性质可知,,BD AD AE CE ==,从而有3,4B C ∠=∠∠=∠,由三角形的内角和定理得180B C BAC ∠+∠+∠=︒,联立即可求得.【详解】由题意可分如下两种情况:(1)图1中,根据垂直平分线性质可知,,BD AD AE CE ==,1,2B DAE C DAE ∴∠=∠+∠∠=∠+∠(等边对等角),两式相加得12B C DAE DAE ∠+∠=∠+∠+∠+∠,又12DAE BAC ∠+∠+∠=∠20B C BAC DAE BAC ∴∠+∠=∠+∠=∠+︒,由三角形内角和定理得180B C BAC ∠+∠+∠=︒,20180BAC BAC ∴∠+︒+∠=︒,80BAC ∴∠=︒;(2)图2中,根据垂直平分线性质可知,,BD AD AE CE ==,3,4B C ∴∠=∠∠=∠(等边对等角),两式相加得34B C ∠+∠=∠+∠,又34DAE BAC ∠+∠+∠=∠,3420BAC DAE BAC ∴∠+∠=∠-∠=∠-︒,20B C BAC ∴∠+∠=∠-︒由三角形内角和定理得180B C BAC ∠+∠+∠=︒,20180BAC BAC ∴∠-︒+∠=︒,100BAC ∴∠=︒.故答案为80或100.【点睛】本题考查了垂直平分线的性质(垂直平分线上的点到线段两端点的距离相等)、等腰三角形的定义和性质(等边对等角)、以及三角形内角和定理,本题的难点在于容易漏掉第二种情况,出现漏解.4.如图,在01A BA △中,20B ∠=︒,01A B A B =,在1A B 上取点C ,延长01A A 到2A ,使得121A A AC =;在2A C 上取一点D ,延长12A A 到3A ,使得232A A A D =;…,按此做法进行下去,第n 个等腰三角形的底角n A ∠的度数为__________.【答案】11()802n -︒⋅.【解析】【分析】先根据等腰三角形的性质求出∠BA 1 A 0的度数,再根据三角形外角的性质及等腰三角形的性质分别求出∠CA 2A 1,∠DA 3A 2及∠EA 4A 3的度数,找出规律即可得出第n 个等腰三角形的底角∠A n 的度数.【详解】解:∵在△A 0BA 1中,∠B=20°,A 0B=A 1B , ∴∠BA 1 A 0= 1801802022B ︒︒︒-∠-= =80°, ∵A 1A 2=A 1C ,∠BA 1 A 0是△A 1A 2C 的外角,∴∠CA 2A 1= 108022BA A ︒∠= =40°; 同理可得,∠DA 3A 2=20°,∠EA 4A 3=10°,∴第n个等腰三角形的底角∠A n= 11()802n-︒⋅.【点睛】本题考查的是等腰三角形的性质及三角形外角的性质,根据题意得出∠CA2A1,∠DA3A2及∠EA4A3的度数,找出规律是解答此题的关键.5.如图,线段AB,DE的垂直平分线交于点C,且72ABC EDC∠=∠=︒,92AEB∠=︒,则EBD∠的度数为 ________ .【答案】128︒【解析】【分析】连接CE,由线段AB,DE的垂直平分线交于点C,得CA=CB,CE=CD,ACB=∠ECD=36°,进而得∠ACE=∠BCD,易证∆ACE≅∆BCD,设∠AEC=∠BDC=x,得则∠BDE=72°-x,∠CEB=92°-x,BDE中,∠EBD=128°,根据三角形内角和定理,即可得到答案.【详解】连接CE,∵线段AB,DE的垂直平分线交于点C,∴CA=CB,CE=CD,∵72ABC EDC∠=∠=︒=∠DEC,∴∠ACB=∠ECD=36°,∴∠ACE=∠BCD,在∆ACE与∆BCD中,∵CA CBACE BCDCE CD=⎧⎪∠=∠⎨⎪=⎩,∴∆ACE≅∆BCD(SAS),∴∠AEC=∠BDC,设∠AEC=∠BDC=x,则∠BDE=72°-x,∠CEB=92°-x,∴∠BED=∠DEC-∠CEB=72°-(92°-x)=x-20°,∴在∆BDE中,∠EBD=180°-(72°-x)-(x-20°)=128°.故答案是:128︒.【点睛】本题主要考查中垂线的性质,三角形全等的判定和性质定理以及三角形内角和定理,添加辅助线,构造全等三角形,是解题的关键.6.如图,在ABC ∆中,AB AC =,点D 和点A 在直线BC 的同侧,,82,38BD BC BAC DBC =∠=︒∠=︒,连接,AD CD ,则ADB ∠的度数为__________.【答案】30°【解析】【分析】先根据等腰三角形的性质和三角形的内角和定理以及角的和差求出ABD ∠的度数,然后作点D 关于直线AB 的对称点E ,连接BE 、CE 、AE ,如图,则BE=BD ,∠EBA=∠DB ,∠BEA =∠BDA ,进而可得∠EBC=60°,由于BD=BC ,从而可证△EBC 是等边三角形,可得∠BEC =60°,EB=EC ,进一步即可根据SSS 证明△AEB ≌△AEC ,可得∠BEA 的度数,问题即得解决.【详解】解:∵AB AC =,82BAC ∠=︒,∴180492BAC ABC ︒-∠∠==︒, ∵38DBC ∠=︒,∴493811ABD ∠=︒-︒=︒,作点D 关于直线AB 的对称点E ,连接BE 、CE 、AE ,如图,则BE=BD ,∠EBA=∠DBA =11°,∴∠EBC=11°+11°+38°=60°,∵BD=BC,∴BE=BC,∴△EBC是等边三角形,∴∠BEC=60°,EB=EC,又∵AB=AC,EA=EA,∴△AEB≌△AEC(SSS),∴∠BEA=∠CEA=1302BEC∠=︒,∴∠ADB=30°.【点睛】本题考查了等腰三角形的性质、三角形的内角和定理、等边三角形的判定和性质、全等三角形的判定和性质以及轴对称的性质等知识,涉及的知识点多、综合性强,难度较大,作点D关于直线AB的对称点E,构造等边三角形和全等三角形的模型是解题的关键.7.如图,在△ABC中,AB=AC,∠BAC=120°,D为BC上一点,DA⊥AC,AD=24 cm,则BC 的长________cm.【答案】72【解析】【分析】按照等腰三角形的性质、角的和差以及含30°直角三角形的性质进行解答即可.【详解】解:∵AB=AC,∠BAC=120°∴∠B=∠C=30°∵DA⊥AC,AD=24 cm∴DC=2AD=48cm,∵∠BAC=120°,DA⊥AC∴∠BAD=∠BAC-90°=30°∴BD=AD=24cm∴BC=BD+DC=72cm故答案为72.【点睛】本题考查了腰三角形的性质、角的和差以及含30°直角三角形的性质,其中灵活运用含30°直角三角形的性质是解答本题的关键.8.如图,在△ABC中,AB=AC,D、E是△ABC内的两点,AE平分∠BAC,∠D=∠DBC=60°,若BD=5cm,DE=3cm,则BC的长是 ______cm.【答案】8.【解析】【分析】作出辅助线后根据等边三角形的判定得出△BDM为等边三角形,△EFD为等边三角形,从而得出BN的长,进而求出答案.【详解】解:延长DE交BC于M,延长AE交BC于N,作EF∥BC于F,∵AB=AC,AE平分∠BAC,∴AN⊥BC,BN=CN,∵∠DBC=∠D=60°,∴△BDM为等边三角形,∴△EFD为等边三角形,∵BD=5,DE=3,∴EM=2,∵△BDM为等边三角形,∴∠DMB=60°,∵AN⊥BC,∴∠ENM=90°,∴∠NEM=30°,∴NM=1,∴BN=4,∴BC=2BN=8(cm),故答案为8.【点睛】本题考查等边三角形的判定与性质;等腰三角形的性质.9.如图,ABC ∆中,AB AC =,点D 是ABC ∆内部一点,DB DC =,点E 是边AB 上一点,若CD 平分ACE ∠,100AEC =∠,则BDC ∠=______°【答案】80【解析】【分析】根据角平分线得到∠ACE=2∠ACD ,再根据角的和差关系得到∠ECB =∠ACB -2∠ACD ,然后利用外角定理得到∠ABC+∠ECB=100°,代换化简得出∠ACB -∠ACD=50°,即∠DCB=50°,从而求出∠BDC 即可.【详解】∵CD 平分∠ACE ,∴∠ACE=2∠ACD=2∠ECD ,∴∠ECB=∠ACB -∠ACE=∠ACB -2∠ACD ,∵∠AEC=100°,∴∠ABC+∠ECB=100°,∴∠ABC+∠ACB -2∠ACD=100°,∵AB=AC ,∴∠ABC=∠ACB,∴2∠ACB -2∠ACD=100°,∴∠ACB-∠ACD=50°,即∠DCB=50°,∵DB=DC,∴∠DBC=∠DCB,∴∠BDC=180°-2∠DCB=180°-2×50°=80°.【点睛】本题考查了角平分线,三角形内角和,外角定理,及等边对等角的性质等知识,熟练掌握基本知识,找出角与角之间的关系是解题的关键.10.如图,∠BOC=60°,点A是BO延长线上的一点,OA=10cm,动点P从点A出发沿AB 以2cm/s的速度移动,动点Q从点O出发沿OC以1cm/s的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间,当t=_____s时,△POQ是等腰三角形.【答案】103或10【解析】【分析】根据△POQ是等腰三角形,分两种情况进行讨论:点P在AO上,点P在BO上,分别计算,即可得解.【详解】当PO=QO时,△POQ是等腰三角形,如图1所示当点P在AO上时,∵PO=AO-AP=10-2t,OQ=t当PO=QO时,102t t-=解得103 t=当PO=QO时,△POQ是等腰三角形,如图2所示当点P在BO上时∵PO=AP-AO=2t-10,OQ=t当PO=QO时,210t t-=解得10t=故答案为:103或10【点睛】本题考查等腰三角形的性质及动点问题,熟练掌握等腰三角形的性质以及分类讨论思想是解题关键.二、八年级数学轴对称三角形选择题(难)11.如图,平面直角坐标系中存在点A(3,2),点B(1,0),以线段AB为边作等腰三角形ABP,使得点P在坐标轴上.则这样的P点有()A.4个B.5个C.6个D.7个【答案】D【解析】【分析】本题是开放性试题,由题意知A、B是定点,P是动点,所以要分情况讨论:以AP、AB为腰、以AP 、BP 为腰或以BP 、AB 为腰.则满足条件的点P 可求.【详解】由题意可知:以AP 、AB 为腰的三角形有3个;以AP 、BP 为腰的三角形有2个;以BP 、AB 为腰的三角形有2个.所以,这样的点P 共有7个.故选D .【点睛】本题考查了等腰三角形的判定及坐标与图形的性质;分类别寻找是正确解答本题的关键.12.如图,AOB α∠=,点P 是AOB ∠内的一定点,点,M N 分别在OA OB 、上移动,当PMN ∆的周长最小时,MPN ∠的值为( )A .90α+B .1902α+C .180α-D .1802α-【答案】D【解析】【分析】 过P 点作角的两边的对称点,在连接两个对称点,此时线段与角两边的交点,构成的三角形周长最小.再根据角的关系求解.【详解】解:过P 点作OB 的对称点1P ,过P 作OA 的对称点2P ,连接12PP ,交点为M,N ,则此时PMN 的周长最小,且△1P NP 和△2PMP 为等腰三角形.此时∠12P PP =180°-α;设∠NPM=x°,则180°-x°=2(∠12P PP -x°)所以 x°=180°-2α【点睛】求出M,N在什么位子△PMN周长最小是解此题的关键.13.如图,在锐角△ABC中,AC=10,S△ABC=25,∠BAC的平分线交BC于点D,点M,N分别是AD和AB上的动点,则BM+MN的最小值是()A.4 B.245C.5 D.6【答案】C【解析】试题解析:如图,∵AD是∠BAC的平分线,∴点B关于AD的对称点B′在AC上,过点B′作B′N⊥AB于N交AD于M,由轴对称确定最短路线问题,点M即为使BM+MN最小的点,B′N=BM+MN,过点B作BE⊥AC于E,∵AC=10,S△ABC=25,∴12×10•BE=25,解得BE=5,∵AD是∠BAC的平分线,B′与B关于AD对称,∴AB=AB′,∴△ABB′是等腰三角形,∴B′N=BE=5,即BM+MN的最小值是5.故选C.14.如图,点D,E是等边三角形ABC的边BC,AC上的点,且CD=AE,AD交BE于点P,BQ⊥AD于点Q,已知PE=2,PQ=6,则AD等于( )A.10 B.12 C.14 D.16【答案】C【解析】【分析】由题中条件可得△ABE≌△CAD,得出AD=BE,∠ABE=∠CAD,进而得出∠BPD=60°.在Rt△BPQ中,根据30度角所对直角边等于斜边的一半,求出BP的长,进而可得结论.【详解】∵△ABC是等边三角形,∴AB=AC,∠BAC=∠C=60°.又∵AE=CD,∴△ABE≌△CAD(SAS),∴∠ABE=∠CAD,AD=BE,∴∠BPD=∠ABE+∠BAP=∠CAD+∠BAP=∠BAC=60°.∵BQ⊥AD,∴∠PBQ=30°,∴BP=2PQ=2×6=12,∴AD=BE=BP+PE=12+2=14.故选C.【点睛】本题考查了含30度角的直角三角形的性质、等边三角形的性质以及全等三角形的判定和性质,证明∠BPD=60°是解答本题的关键.15.如果一个三角形能被一条线段分割成两个等腰三角形,那么称这个三角形为特异三角形.若△ABC是特异三角形,∠A=30°,∠B为钝角,则符合条件的∠B有()个.A.1 B.2 C.3 D.4【答案】B【解析】【分析】【详解】如下图,当30°角为等腰三角形的底角时有两种情况:∠B=135°或90°,当30°角为等腰三角形的顶角时有一种情况:∠B=112.5°,所以符合条件的∠B有三个.又因为∠B为钝角,则符合答案的有两个,故本题应选B.点睛:因为不确定这个等腰三角形的底边,所以应当以点A为一个确定点进行分类讨论:①当以B为顶点时,即以B为圆心,AB长为半径画弧交AC于点D,构成等腰△BAD;②当以点A为顶点时,即以点A为圆心,AB长为半径画弧,交AC于点D,构成等腰△ABD;或作线段AB的垂直平分线交AC于点D构成等腰△DAB.16.如图,在△ABC中,BI,CI分别平分∠ABC,∠ACB,过I点作DE∥BC,交AB于D,交AC于E,给出下列结论:①△DBI是等腰三角形;②△A CI是等腰三角形;③AI平分∠BAC;④△ADE周长等于AB+AC.其中正确的是( )A.①②③B.②③④C.①③④D.①②④【答案】C【解析】【分析】根据角平分线的性质、平行线的性质、等腰三角形的判定与性质分别对各选项分析判断后利用排除法求解.【详解】①∵IB平分∠ABC,∴∠DBI=∠CBI.∵DE∥BC,∴∠DIB=∠CBI,∴∠DBI=∠DIB,∴BD=DI,∴△DBI是等腰三角形.故本选项正确;②∵∠BAC不一定等于∠ACB,∴∠IAC不一定等于∠ICA,∴△ACI不一定是等腰三角形.故本选项错误;③∵三角形角平分线相交于一点,BI,CI分别是∠ABC和∠ACB的平分线,∴AI平分∠BAC.故本选项正确;④∵BD=DI,同理可得EI=EC,∴△ADE的周长=AD+DI+EI+AE=AD+BD+EC+AE=AB+AC.故本选项正确;其中正确的是①③④.故选C.【点睛】本题考查了等腰三角形的判定与性质,熟记三角形的角平分线相交于一点是解题的关键.17.如图,等腰三角形ABC的底边BC长为4,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,若△CDM周长的最小值为8,则△ABC的面积为()A.12 B.16 C.24 D.32【答案】A【解析】【分析】连接AD,由于△ABC是等腰三角形,点D是BC边的中点,故AD⊥BC,再根据EF是线段AC的垂直平分线可知,点C关于直线EF的对称点为点A,故AD的长为CM+MD的最小值,再根据三角形的周长求出AD的长,由此即可得出结论.【详解】连接AD,∵△ABC是等腰三角形,点D是BC边的中点,∴AD⊥BC,∵EF是线段AC的垂直平分线,∴点C关于直线EF的对称点为点A,∴AD的长为CM+MD的最小值,∵△CDM周长的最小值为8,∴AD=8-12BC=8-2=6∴S△ABC=12BC•AD=12×4×6=12,【点睛】本题考查的是轴对称-最短路线问题,熟知等腰三角形三线合一的性质是解答此题的关键.18.如图,已知长方形ABCD,AB=1,BC=2,点M为矩形内一点,点E为BC边上任意一点,则MA+MD+ME的最小值为( )A.1 B.1+3C.2+3D.3【答案】B【解析】【分析】将△AMD绕点A逆时针旋转60°得到△AM’D’,MD=M’D’,易得到△ADD’和△AMM’均为等边三角形,推出AM=MM’可得MA+MD+ME=D’M+MM’+ME,共线时最短;由于点E 也为动点,可得当D’E⊥BC时最短,此时易求得D’E=DG+GE的值.【详解】将△AMD绕点A逆时针旋转60°得到△AM’D’,MD=M’D’,易得到△ADD’和△AMM’均为等边三角形,∴AM=MM’,∴MA+MD+ME=D’M+MM’+ME,∴D′M、MM′、ME共线时最短,由于点E也为动点,∴当D’E⊥BC时最短,此时易求得D’E=DG+GE=4+33,∴MA+MD+ME的最小值为4+33.故选B.本题考查轴对称、旋转变换、矩形的性质等知识,解题的关键是学会添加常用辅助线,构造等边三角形解决问题,学会用转化的思想思考问题.19.如图,在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,点A、C的坐标分别为A(10,0 ),C(0,4),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为()A.(3,4),(2,4)B.(3,4),(2,4),(8,4)C.(2,4),(8,4)D.(3,4),(2,4),(8,4),(2.5,4)【答案】B【解析】试题解析:有两种情况:①以O为圆心,以5为半径画弧交BC于P点,此时OP=OD=5,在Rt△OPC中,OC=4,OP=5,由勾股定理得PC=3,则P的坐标是(3,4);②以D为圆心,以5为半径画弧交BC于P′和P″点,此时DP′=DP″=OD=5,过P′作P′N⊥OA于N,在Rt△OP′N中,设CP′=x,则DN=5-x,P′N=4,OP=5,由勾股定理得:42+(5-x)2=52,x=2,则P′的坐标是(2,4);过P″作P″M⊥OA于M,设BP″=a,则DM=5-a,P″M=4,DP″=5,在Rt△DP″M中,由勾股定理得:(5-a)2+42=52,解得:a=2,∴BP″=2,CP″=10-2=8,即P ″的坐标是(8,4);假设0P=PD ,则由P 点向0D 边作垂线,交点为Q 则有PQ 2十QD 2=PD 2,∵0P=PD=5=0D ,∴此时的△0PD 为正三角形,于是PQ=4,QD=120D=2.5,PD=5,代入①式,等式不成立.所以排除此种可能.故选B .20.如图,在平面直角坐标系中,A(1,2),B(3,2),连接AB ,点P 是x 轴上的一个动点,连接AP 、BP ,当△ABP 的周长最小时,对应的点P 的坐标和△ABP 的最小周长分别为( )A .(1,0),224+B .(3,0),224+C .(2,0), 25D .(2,0),252+【答案】D【解析】 作A 关于x 轴的对称点N (1,-2),连接BN 与x 轴的交点即为点P 的位置,此时△ABP 的周长最小.设直线BN 的解析式为y kx b =+,∵N (1,-2),B (3,2),∴232k b k b +=-⎧⎨+=⎩, 解得24k b =⎧⎨=-⎩, ∴24y x =-,当0y =时,240x -=,解得,2x=,∴点P的坐标为(2,0);∵A(1,2),B(3,2),∴AB//x轴,∵AN⊥x轴,∴AB⊥x轴,在Rt△ABC中,AB=2,AN=4,由勾股定理得,BN==∵AP=NP,∴△ABP的周长最小值为:AB+BP+AP=AB+BP+PN=AB+BN故选D.点睛:本题考查最短路径问题.利用轴对称作出点P的位置是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
任中八年级全等三角形 单元测试题(5、6、7班)
姓名_________分数____________
一、选择题(30分)
1.下列说法:①全等图形的形状相同大小相等;②全等三角形的对应边相等;③全等三角形的对应角相等;④全等三角形的周长、面积分别相等,其中正确的说法为( )
A.①②③④ B.①③④ C.①②④ D.②③④
2.一定是全等三角形的是( )
A. 面积相等的三角形
B.周长相等的三角形
C.形状相同的三角形
D.能够完全重合的两个三角形.
3.如图在RT △ABC 沿直角边BC 所在的直线向右平移得到△DEF ,下列结论错误的是( )
A.△ABC ≌△DEF
B.∠DEF =90°
C.AC =DF
D.EC =CF
4.已知E 是AC 上一点,AB =AD ,BE =DE ,应用“SSS ”可直接证明全等的三角形是( )
A.△ABC ≌△ADC
B.△ABE ≌△ADE
C.△CBE ≌△CDE
D.没有全等的三角形.
5.如图∠CAB=∠DBA ,AC=BD ,得到△CAB ≌△DBA ,所依据的理由是( )
A.SAS
B. SSS
C. SAS 或SSS
D.以上说法都不对
6.如图,在ABC △和DEF △中,已知AB DE =,BC EF =,根据“SAS ”判定 ABC DEF △≌△,还需的条件是( )
A.A D ∠=∠ B.B E ∠=∠ C.C F ∠=∠ D .以上三个均可以
7.如图,△ACB ≌△A ′CB ′,∠BCB ′=30°,则∠ACA ′的度数为( )
A .20°
B .30°
C .35°
D .40°
8.如图所示的4×4正方形网格中,∠1+∠2+∠3+∠4+∠5+∠6+∠7=( )
A .330°
B .315°
C .310°
D .320°
9.如图所示,在Rt △ABC 中,AD 是斜边上的高,∠ABC 的平分线分别交AD 、AC 于点F 、E ,EG ⊥BC 于G ,下列结论正确的是( )
A .∠C=∠ABC
B .BA=BG
C .AE=CE
D .AF=FD
10.附图为八个全等的正六边形紧密排列在同一平面上的情形.根据图
中标示的各点位置,判断△ACD 与下列哪一个三角形全等?( )
A .△ACF
B .△ADE
C .△ABC
D .△BCF
二、填空(18分)
11.如图,△ABC ≌△DEF ,请根据图中提供的信息,写出x= . 12.△ABC 中,∠C =90°,AC =BC ,AD 是∠BAC 的平分线,DE ⊥
AB ,垂足为E ,若AB =12cm ,则△DBE 的周长为 .
13.如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻
璃店去配一块完全一样的玻璃,那么最省事的办法是带 去玻璃店.
14.如图,AB =AC ,AD =AE ,∠BAC =∠DAE,∠1=25°,∠2=30°,
则∠3=____.
,第13题图) 第14题
15.如图,B ,C ,D 在同一直线上,∠B =∠D=90°,AB =CD ,
BC =DE ,则△ACE 的形状为_________________________.
16.如图,已知△ABC 中,∠ABC ,∠ACB 的角平分线交于点O ,连接AO 并延长交BC 于D ,OH ⊥BC 于H ,若∠BAC=60°,OH =5 cm ,则∠BAD=____,点O 到AB 的距离为____ cm.
三、解答题(72分)
17.已知:如图AC ,BD 相交于点O ,∠A=∠D ,AB=CD ,求证:△AOB ≌△
DOC .
18.(6分)(2016·武汉)如图,点B ,E ,C ,F 在同一条直线上,AB
=DE ,AC =DF ,BE =CF ,求证:AB∥DE. 19.已知:AD 是△ABC 的角平分线,DE ⊥AB ,DF ⊥AC ,垂足分 别是E 、F ,BE =CF , 求证:∠B =∠C.
20.如图所示,CE ⊥AB 于点E ,BD ⊥AC 于点D ,BD ,CE 交于点O ,且AO 平分∠BAC.
(1)图中有多少对全等三角形?请一一列举出来(不必说明理由);
(2)求证:BE =CD ;
21.如图,在△ABC 中,∠C=90°,AD 平分∠CAB ,交CB 于点D ,过点D 作DE ⊥AB 于点E .
(1)求证:△ACD ≌△AED ;
(2)若∠B=30°,CD=1,求BD 的长.
22.(9分)如图,在△ABC,△ADE 中,∠BAC =∠DAE=90°,AB =AC ,AD =AE ,点C ,D ,E 三点在同一直线上,连接BD 交AC 于点F.
(1)求证:△BAD≌△CAE;
(2)猜想BD ,CE 有何特殊位置关系,并说明理由.
23.已知:在△ABC 中,∠BAC=90°,AB=AC,AE 是过点A 的一条直线,且BD ⊥AE 于D,
CE ⊥AE 于E.
(1)当直线AE 处于如图①的位置时,有
BD=DE+CE,请说明理由;
(2)当直线AE 处于如图②的位置时,则BD 、
DE 、CE 的关系如何?请说明理由;
(3)归纳(1)、(2),请用简洁的语言表达BD 、
DE 、CE 之间的关系.
1.如图,平面内有一等腰直角三角形ABC (∠
ACB=90°)和一直线MN .过点C 作CE ⊥MN 于点E ,过点B 作BF ⊥MN 于点F ,小明同学过点C 作BF 的垂线,如图1,请说明AF+BF 与CE 的数量关系.
(1)若三角板绕点A 顺时针旋转至图2的位置,其他条件不变,试猜想线段AF 、BF 、CE 之间的数量关系,并证明你的猜想.
(2)若三角板绕点A 顺时针旋转至图3的位置,其他条件不变,则线段AF 、BF 、CE 之间的数量关系为 .
A
F C E。
