直言命题与对当关系推理(精选)
公务员考试判断推理之直言命题
直言命题及其推理• 1、全称肯定命题。
• [例1] 所有法院都是审判机关。
• [例2] 所有法人都是具有民事行为能力的。
• 全称肯定命题形式为：所有S 都是P 。
用符号表示为：SAP 。
简记为：A 。
因此，全称肯定命题陈述了S 和P 之间是全同关系或直包含于关系2、全称否定命题[例3] 所有抢罪都不是过失犯罪。
• [例4] 正当防卫不是违法行为。
• 全称否定命题形式为：所有S 都不是P 。
用符号表示：SEP 。
简记为：E 。
因此，全称否定命题陈述了S 和P 之间是全异关系。
图9• 3、特称肯定命题[例5] 有的民事诉讼证据是能够证明民事案件真实情况的事实。
S PPSSP• [例6] 有的民事诉讼证据是证据。
• [例7] 有的证据是民事诉讼证据。
• [例8] 有的民事诉讼证据是物证。
• 特称肯定命题的形式为：有S 是P 。
用符号表示为：SIP 。
简记为：I 。
图10因此，特称肯定命题陈述了S 和P 之间是全同关系或真包含于关系或真包含关系或交叉关系，但并未陈述S 与P 究竟是其中的哪一种关系。
4、特称否定命题• [例9] 有的遗嘱不是书面遗嘱。
• [例10] 有的一审判决不是生效判决。
• [例11] 有的人民法院不是法律的监督机关。
• 特称否定命题的形式是：有S 不是P 。
用符号表示为：SOP 。
简记为：O 。
S pspspspspsp图11•因此，特称否定命题陈述了S和P之间是真包含关系或交叉关系或全异关系，但并未陈述S与P究竟是其中的哪一种关系。
•5、单称肯定命题•当直言命题的主项是单独词项时，其指称的对象是独一无二的，因此它不需要量词来刻画主项的数量。
这种主项是单独词项的命题叫单称命题。
•单称命题的主项可以是专有名词，如“兰州市人民法院是中级人民法院”中的“兰州市人民法院”；也可以是摹状词（通过对某一种对象某方面特征的描述而指称该对象的词组），如“《古代法》的作者是梅因”中的“《古代法》的作者”或“这个合同不是有效合同”中的“这个合同”。
关于a、e、i、o对当关系推理的规则
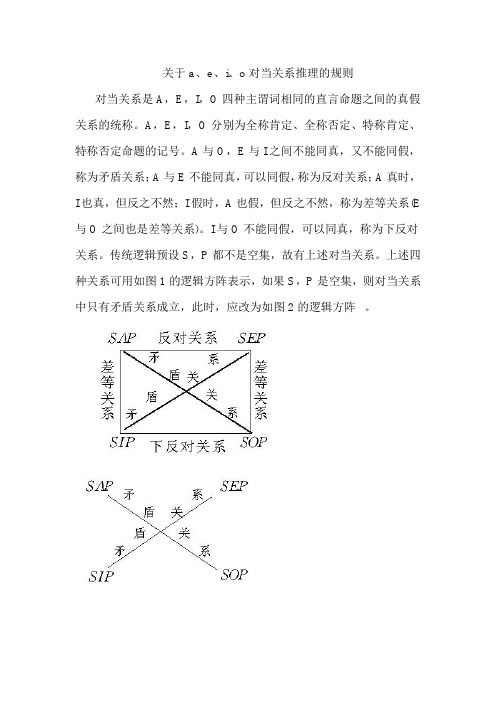
关于a、e、i、o对当关系推理的规则
对当关系是A，E，I，O四种主谓词相同的直言命题之间的真假关系的统称。
A，E，I，O分别为全称肯定、全称否定、特称肯定、特称否定命题的记号。
A与O，E与I之间不能同真，又不能同假，称为矛盾关系；A与E不能同真，可以同假，称为反对关系；A真时，I也真，但反之不然；I假时，A也假，但反之不然，称为差等关系(E 与O之间也是差等关系)。
I与O不能同假，可以同真，称为下反对关系。
传统逻辑预设S，P都不是空集，故有上述对当关系。
上述四种关系可用如图1的逻辑方阵表示，如果S，P是空集，则对当关系中只有矛盾关系成立，此时，应改为如图2的逻辑方阵。
可能性的对当关系直言直接推理
我们 将前提断 定 了
推理归 为 ; 类
∋∀
、
;
与 & 非 包 含 于关 系 的上述 类包 括前 面所 说 的 推 理 形 式 ! ∀
、
5
,
#
,
#
,
#
,
− + ∀ 面沪 , 可 能 ∃
# #
&
,
. ∀
,
#
/ 甲 一 可能 亏 0百
, ,
#
1 ∀ 瓦护一 可 能 )2& 3 ∀
4∀
#
百币一 可 能 5 6 (
#
,
而 凡 类
∀
推理的 前提对此毫无作 用 它 断 定 至少 有一 个
’ 子 是 # 因 此 我 们要 想 确定
,
,
分
法确 定 , 的可靠 性 + 5 在思 维实 际 中 当我 们 知 道 ∀ 部 分分 子 不 具 有 性质 # 时 自然会想 到是否所 有 类分子 都 不 是 # ∀ ∋ 类其 他分子 中有 无 一 个 是 # 前 一 个 问 题 是 . , 类 ∋
。 、
, ,
,
进行 . 或 氏 那样 的 推理 最后 运 用 归纳 办法考 察 & 结 论 的 可 靠 性 就 会 做很 多 无谓 的劳 动 总之 如 果 可 能性 的 对 当关 系 直 言直 接 推 理对 思维 实 际 有 意 义 就应 有办 法对 其 结 论 的 可 靠性 进 行 考 察 就得运 用 归纳或 具体考察 某 类 分 子 的办 法 而 运 用 上 述 办法 又可 以 独立 地 得 出可 能 性对 当 关 系 直言直 接 推理所 要 推 出 的东 西 而 且 还能 得 出这 种 推理所 推不 出 的东 西 因 此 我 们 得 出 了 这样 的结 论 可 能性对 当关系直言 直 接 推 理虽 然 形 式 上 成 立 但 无 实 际 意 义 也 许 有 人 会 问 必然 性 的 对当关 系 直 言 直 接推 理 如 一 − 其结论 运 用 归 纳 或 具 体考 察某 类分 子 的办法 也 可 得 出 为 何 不 用后 者代替 前 者 ∋ 请不 要 忘 记前者 可 以 得 出对实 际 有 用的 实然 性
逻辑学：第六章 直接推理
【例】
某公请客，尚有人未到。于是他说：“该来的不来。” 有些客人听了此话便起身走了。某公又说：“不该走 的走了。”于是剩下的客人全都走光了。请分析某公 为何请客不成。
【例】 以下三句话一真两假，试确定S与P的外延关系。 （1）有S是P （2）有S不是P。 （3）有P不是S。
【例】 以下三句话一真两假，试确定S与P的外延关系。 （1）有S不是非P。 （2）有S不是P。 （3）有非S是P。
该文档是极速PDF编辑器生成，
如果想去掉该提示,请访问并下载： /
第一节 对当关系直接推理 第二节 命题变形直接推理
第一节 对当关系直接推理 第二节 命题变形直接推理
直接推理是以一个命题为前提推出结论的演绎推理。
直言命题的直接推理，是以一个直言命题为前提，推 出一个直言命题结论的推理，包括： 对当关系直接推理和命题变形直接推理。
换位，没有推出预期的结论。
再连续换位质： SEP =>PES=>PAS =>S IP =>S OP 。
推出了预期的结论。所以，该推理成立。
四种直言命题连续变形推理的有效式如下：
(1)SAP => SEP =>P ES => P A S =>S IP => S OP
(2)SAP =>PIS =>PO S
4. SOP => 并非SAP 并非SAP => SOP
【例】 有三角形不是等腰三角形，所以，并非所有三角形是 等腰三角形。 并非所有金属是固体，所以，有金属不是固体。
（四）从属关系直接推理 依据从属关系，可由A真推得I真，由I假推得A假。可 由E真推得O真，由O假推得E假。于是有下列推理形 式： 1. SAP => SIP 【例】所有金属是导体，所以，有金属是导体。
【精品】直言命题与对当关系
0 0 1 1
0 1 0 1
一、直言命题及其直接推理
A、E、I、O之间的真假关系，也叫命题间的对当关系， 主要包括以下四种关系： ①矛盾关系：是指A与O、E与I之间的真假关系。矛 盾关系的内容：一个命题真，另一个命题必假；一个命题 假，另一个命题必真。即逻辑上矛盾关系的两个命题既不 同真，也不同假，总是一真一假的。
一、直言命题及其直接推理
1.直言命题的类型
命题名称 结构式 ⑴全称肯定命题 所有S是P ⑵全称否定命题 所有S不是P ⑶特称肯定命题 有的S是P ⑷特称否定命题 有的S不是P ⑸单称肯定命题 某个S是P ⑹单称否定命题 某个S不是P 简写 SAP SEP SIP SOP SaP SeP 命题简称 A E I O a e
从 属 关 系 I
矛 矛盾 盾盾 关 关 系 系 矛 关系
a
从 属 关 系 O
e
下反对关系
一、直言命题及其直接推理
没有人爱每一个人；牛郎爱织女；织女爱每一个爱牛郎的人。 如果以上陈述为真，则下列哪项不可能为真？ Ⅰ. 每一个人都爱牛郎。 Ⅱ. 每一个人都爱一些人。 Ⅲ. 织女不爱牛郎。 A．仅Ⅰ。 B．仅Ⅱ 。 C．仅Ⅰ和Ⅱ 。 D．仅Ⅰ和Ⅲ 。 E． Ⅰ、Ⅱ和Ⅲ 。 解析：若Ⅰ为真，加上“织女爱每一个爱牛郎的人”，则可推出 “织女爱每一个人”，这与题干断定“没有人爱每一个人”矛盾，故 Ⅰ不能为真，Ⅱ、Ⅲ的断定真假不定。选择答案A。
一、直言命题及其直接推理
2.同素材性质命题的真假对当关系
同素材性质命题是指主项相同、谓项也相同的性质命 题，它们间有真假对当制约关系。如： ①所有电视机都是液晶彩色电视机。 （A） ②所有电视机都不是液晶彩色电视机。（E） ③有些电视机是液晶彩色电视机。 （I） ④有些电视机不是液晶彩色电视机。 （O） 设：A为真，则E假、I真、O假。 不是同素材的性质命题，它们之间不能推导真假。
难道就真假难辨吗？——直言命题间的对当关系.pptx
㈢ 课后练习（ 见“蓝墨云班课”）
⒈ 在某次税务检查后，四个工商管理人员的结论
分别是：甲：所有个体户都没纳税。乙：服装个体户陈
老板纳了税。丙：个体户不都没纳税。丁：有的个体户
没纳税。已知四人中只有一人断定为假，请问：谁的断Biblioteka 定为假？陈老板是否纳了税？
⒉ 某律师事务所共有12名工作人员。⑴有人会使用
计算机。⑵有人不会使用计算机。⑶所长不会使用计算
二、直言命题间对当关系的种类
㈠反对关系 ㈡下反对关系 ㈢差等关系
㈣矛盾关系
⒈含义 ⒉特点
⒈含义 ⒉特点
⒈含义 ⒉特点
⒈含义 ⒉特点
二、直言命题间对当关系的种类
㈠ 反对关系
⒈ 含义
反对关系是指 同一素材的SAP与 SEP 间 的 对 当 关 系 。
⒉ 特点
不同真、 可同假、 必有一假。
二、直言命题间对当关系的种类
㈡ 情境任务文字解析
其次，根据假设条件“四个犯罪
嫌疑人中有两个人的口供是真话，有 两个人的口供是假话”，可知，丙和 丁的口供也必有一真一假。
㈡ 情境任务文字解析
最后，运用假设法找到答案。假设丙的口供“乙和丁至少 有人没作案”是假话，那么意味着乙和丁都作了案，由此可知， 丁的口供“我没作案”是假话，这与丙和丁的口供必有一真一 假相矛盾，所以，假设不成立，则丙说的是真话。因为丙和丁 的口供也必有一真一假，当丙说的是真话时，则丁说的是假话， 而丁的口供为“我没作案”，所以，丁作了案，既然丁作了案， 则甲的口供“我们四人都没作案”就是假话，那么，乙的口供 就是真话，因此，说真话的是乙和丙。
难道就真假难辨吗？
—直言命题间的对当关系
难道就真假难辨吗？ ——直言命题间的对当关系
逻辑学简单命题及其推理直言命题的直接推理
（二）换位法
1.含义：换位法是通过改变命题主谓项的位置而推 出一个新命题的推理。
例如：“所有的法律都是有强制性的，所以，有 些有强制性的是法律。”
2.换位法的规则
（1）命题的质不变，肯定命题仍为肯定命题， 否定命题仍为否定命题。
（2）在原命题中不周延的项，在新命题中也不 得变为周延。
注意：
• O命题不可以进行换位，而A、E、I则可以进行换 位。
（2）SEP（换质） → SAP（换位） → PIS 。 “所有的故意犯罪不是过失犯罪。”
→“所有的故意犯罪都是非过失犯罪。” →“有的非过失犯罪是故意犯罪。” →“有的非过失犯罪不是非故意犯罪。”
因病而死的都不是非正常死亡。” “所有的犯罪行为都是不合法行为。所以，所
有的犯罪行为都不是合法行为。”
（2）SEP → SAP 。
“所有的故意犯罪不是过失犯罪。所以，所有 的故意犯罪是非过失犯罪。”
“所有的犯罪行为都不是不具有社会危害性， 所以，所有的犯罪行为都是具有社会危害性的。”
（3）SIP → SOP 。
（1）SAP →SEP→PES （2）SEP →SAP→PIS （3）SIP 不能换质位。 （4）SOP →SIP→PIS
（1）SAP（换质） → SEP（换位） → PES
“所有的犯罪行为都是具有社会危害性的行为”
→“所有的犯罪行为都不是不具有社会危害性的行 为”
→“所有的不具有社会危害性的行为都不是犯罪行 为”
（1）换质法推理从肯定方面和否定方面考虑同 一对象，使人们从正和反、反和正两个维度加深了 对事物的了解，便于人们明确对象有那些性质和没 有哪些性质，或者对象“是什么”和“不是什么”。
例如：
孟德斯鸠从两个维度界定自由，指出“自由是 做法律所许可的一切事物的权利”，“自由的主要 意义就是，一个人不被强迫做法律所没有规定要做 的事情”。前者是对自由的肯定意义的表达，或者 是对自由的否定意义的表达，从“自由是什么”和 “自由不是什么”两个维度界定了自由。
第三节 直言命题直接推理
德军当机立断，刻不容缓，集中了6个炮兵营的火 力向法军阵地发起了猛烈的进攻，法军因抵挡不 了如此猛烈的炮火，整个坟地被夷为平地。
事后证实，那个坟地的确是法军一个旅的指挥部， 其内部的人员深居简出，但是他们做梦也没有想 到，一只小小的波斯猫泄漏了机密，致使法军损
失相当严重。
德军的指挥官们根据在坟地上晒太阳的一只猫， 推断出坟地下面是一个法军的高级指挥所，运用 了如下的推理：
2、矛盾关系命题构成的对当关系推理
A与O、E与I之间是构成不能同真，不能同假的矛盾 关系，即其中一个为真时，另一个必定为假；且其 中一个为假时，另一个必定为真。
这样，依据矛盾关系的有效推理形式有以下8种：
（3） SAP — ﹁S0P （4） SOP —﹁SAP （5） ﹁SAP —SOP （6） ﹁S0P —SAP （7）SEP —﹁SIP （8）SIP —﹁SEP
例如：（1）真金是不怕火炼的，
所以，怕火炼的不是真金。
这是一个推理。它包含两个命题，前一个 是已知命题，后一个是根据前一个命题得 出的新命题。
再如：
（2）一班所有的同学都是广东人，
刘宁是一班的同学，
所以，刘宁是广东人。
这也是一个推理。这个推理包括三个命题前两个是已 知命题，后一个是根据前两个命题推出的新命题。
（16） ﹁ SOP — SIP
四、直言命题变形直接推理
定义：指通过（1）改变原命题联项性质的方法； 或者（2）将原命题的主谓项位置相互置换的方法， 从而推出新结论的一种推理形式。
种类：命题变形直接推理细分为：换质法、换位 法、换质位法三种形式。
1、换质法
（1）定义：换质法是通过改变原命题的质，从而推出 一个新命题的直接推理。
狼这两天也饿得前心贴了后背，一听乳酪就忘乎 所以了，急忙坐入桶中，狼下到井底，它的分量 正好把坐在另一只桶中的狐狸拉上井口。这回轮 到狼在井底熬日月了。 狐狸出了水桶，边走边想：别看乳酪是又圆又白 的东西，可又圆又白的东西不一定是乳酪。 它恍然大悟：“乳酪是又圆又白的东西”， 但不能说：“凡又圆又白的东西都是乳酪”， 只能说：“有些又圆又白的东西是乳酪。” 狐狸心中这一来一往，就用到了逻辑上的换位法。 换位法是直接推理中的一种方法，这种方法就是 将一个直言命题的主项与谓项的位置对调，而得 出一个新的直言命题。在新命题中，原命题的谓 项成了主项，原命题的主项成了谓项，来了一个 大掉个儿。
直言命题及其推理练习题答案
一、填空1.任何命题都有两个特征，即___都有所断定__和__都有真假__。
2.直言命题由__主项___、__谓项___、__联项___、__量项__四个部分组成。
3.在直言命题中，主、谓项周延的是___E__命题；主、谓项都不周延的是___I__命题。
4.已知SAP真，根据对当关系，可推知SEP___假___，SOP___假____，SIP____真_。
5.根据直言命题对当关系，____反对___关系可以由真推假，但不能由假推真。
6.“有的大学生是党员”这一命题的种类是___特称肯定命题__，其逻辑形式是_ __SIP___。
7.“有些刑事被告人是有罪的”这一命题的逻辑常项是__有些；是_，逻辑变项是__刑事被告人；有罪的。
8.根据换位法规则，__O___命题不能换位；SAP换位后得__PIS___。
9.违反“前提中不周延的项在结论中不得变为周延”这一三段论的规则所犯的逻辑错误叫__大项不当周延___或__小项不当周延____。
10.在三段论前提中，__中项__至少要周延一次，否则就要犯__中项两次不周延_的逻辑错误。
11.在三段论中，两个前提中有一特称的，结论必____特称__；两个前提有一否定的，结论必____否定____。
12.三段论第一格，中项分别是大前提的___主项____和小前提的___谓项___。
13.如果第二格三段论的大前提为PEM，结论为SOP。
那么小前提应为___SIM___。
14．一个正确的三段论，若中项周延两次，则它不可能是第一格，也不可能是第二格。
15．AEE可能是三段论第二格和第四格中的式。
二、单项选择题1.根据对当关系，由SAP假，可推出（ C ）真。
A.SEPB.SIPC.SOPD. PIS2.如果A、B两个命题不能同假，但却可以同真，则它们之间的关系是（ C ）。
A.差等关系B.矛盾关系C.下反对关系D.上反对关系3.“所有的商品都是有使用价值的”为前提进行换位法直接推理，推出的结论是（ C ）。
直言命题的对当关系和推理
直言命题的对当关系和推理在相同素材(谓语部分有相同内容或对象)的A、E、I,O直言命题之间的推理简称直言推理，也称直接推理，是以一个直言命题为前提，直接推出一个结论的推理，得到的结论也是直言命题。
相同素材的A、E、I、O直言命题之间的关系，称作对当关系。
有如下对当关系：矛盾关系：指A与O、E与I的关系，它们之间既不能同真，也不能同假，因而必有一真，也必有一假。
差等关系：指A与I、E与O之间的关系，如果全称命题真，则相应的特称命题真；如果特称命题假，则相应的全称命题假；如果特称命题假，则相应的全称命题假；如果全称命题假，则相应的特称命题真假不定；如果特称命题真，则相应的全称命题真假不定。
反对关系：指A与E的关系，它们之间不能同真，但可以同假。
于是，若一个为真，则另一个必为假；若一个为假，则另一个真假不定。
下反对关系：指I与O之间的关系，它们之间可以同真，但不能同假。
于是由一个为假，可以逻辑地推出另一个为真；但从一个为真，不能确切的知道另一个的真假。
1．(广东2006—83)：在毕业考试结束后，班长想从老师那里打听成绩9班长说：“老师，这次考试不太难，估计我们班同学的成绩都在70分以上吧。
”老师说：“你的前半句话不错，后半句不对。
”根据老师的意思，下列哪项必为真实?( )A．少数同学的成绩在70分以上，多数同学的成绩在70分以下B．多数同学的成绩在70分以上，少数同学的成绩在70分以下C．有的同学的成绩在70分以上，有的同学的成绩在70分以下D．如果以70分为及格，肯定有的同学成绩不及格[答案]D[解析](1)“你的前半句话不错，后半句不对。
”，即“一所有人都70分以上”，推出O命题“有些人不是70分以上”；(2)根据有人不是70分以上可推知D：如果以 70分为及格，肯定有的同学成绩不及格。
[误区]：从断定O命题“有些人不是70分以上”，推不出I命题“有人70分以上”。
C是错误选项。
(3)B项是对I命题的否定；C项是O命题；D项是I命题，均不能由对A命题的肯定推出。
四种直言命题的关系
四种直言命题的关系
一、直言命题的概念
直言命题亦称“定言命题”。
即性质命题。
由于在性质命题中，对对象具有或不具有某种性质的断定是直接的、无条件的，因而，逻辑史上就把这种命题称为直言命题，以别于假言命题(对对象的某种断定是有条件的)和选言命题(对对象的某种断定是有选择的)。
二、直言命题的对当关系
直言命题的对当关系也即直言命题之间的真假制约关系，四种常见的直言命题之间的对当关系。
例子“所有明星是东北人”和“有的明星不是东北人”是矛盾关系
当“所有明星是东北人”为真时，“有的明星不是东北人”必然为假;当“所有明星是东北人”为假时，“有的明星不是东北人”必然为真。
即两者之间必有一真一假。
一个命题前面加“并非”，等值于这个命题的矛盾命题，即
并非“所有A是B”=有的A不是B;并非“有的A不是B”=所有A是B 并非“所有A不是B”=有的A是B;并非“有的A是B”=所有A不是B 可简记为:“所有”与“有的”互换，有“不”的去掉，没“不”的加上。
在考试中，当题干给出几个直言命题并且告知这几个命题中为真或为假的个数，却不知道具体哪个命题为真或为假时，解题关键在于找到具有对当关系的一对命题，然后绕开这对命题的真假，判断其他命题的真假从而得出答案。
直言命题与对当关系推理-PPT文档资料共38页
直言命题与对当关系推理-PPT文档资 料
16、云无心以出岫，鸟倦飞而知还。 17、童孺纵行歌，斑白欢游诣。 18、福不虚至，祸不易来。 19、久在樊笼里，复得返自然。 20、羁鸟恋旧林，池鱼思故渊。
谢谢你的阅读
❖ 知
直言命题与对当关系-精品文档
命题是对思维对象有所断定的思维形式。其基 本逻辑特征为：有断定、有真假。 命题可分为：简单命题和复合命题。 直言命题是断定对象具有或不具有某种性质的 简单判断。直言命题也叫性质命题或性质判断， 它由主项、谓项、联项和量项四种词项组成。
一、直言命题及其直接推理
例如：
①所有网上信息都是有价值的信息。 ②有些IT技术是二十年前难以想象的。 ③这辆汽车不是2019年设计制造的。 ①主项是反映被断定对象的概念，通常用“S”来表示。 ②谓项是反映被断定对象具有或不具有的性质的概念， 通常用“P”来表示。 ③联项是表明主项与谓项联系情况的概念。联项分两 种：肯定联项（用“是”表示）和否定联项（用“不是” 表示）。联项表明判断的质。
一、直言命题及其直接推理
④量项是反映被断定对象数量的概念。量项分为三种： 全称量项：通常用“所有”、“一切”等表示，指明对 主项的全部外延作了断定。全称量项在表达命题时可以省略。 特称量项：通常用“有”、“有的”、“有些”等表示， 指明对主项的部分外延作了断定。特称量项的逻辑含义与日 常用法有重要区别，简单地说就是，断定“有些是”，并不 意味“另一些不是”。 单称量项：通常用“这个”、“那个”等表示，指明所 断定的主项是某一个别对象。 此外，在日常语言中，有些直言命题的表达并不规范， 做题和考试时应先将其整理为标准形式。如“没有一种金属 不导电”，“工商户不都没纳税”，等等。
一、直言命题及其直接推理
在某次税务检查后，四个工商管理人员有如下结论： 甲：所有个体户都没纳税。 乙：服装个体户陈老板没纳税。 丙：个体户不都没纳税。 丁：有的个体户没纳税。 如果四人中只有一人断定属实，则以下哪项是真的？ A．甲的断定属实，陈老板没纳税。 B．丙的断定属实，但陈老板没纳税。 C．丙的断定属实，陈老板纳税了。 D．丁的断定属实，陈老板没纳税。