三角形中线性质及拓展补充
三角形五心及其性质延伸

三角形五心及其性质延伸1.内心:三角形三条内角平分线的交点,也是三角形内切圆的圆心。
角平分线性质:到角两边距离相等. 内心性质:到三角形三边距离相等。
延伸:①内角平分线定理如图,AD 为△ABC 中BAC ∠的平分线,则有(=)AB BD AC DC =上左下左上右下右证明过程如下:作BE E DAC ∠=∠∵BAD DAC ∠=∠,∴E BAD ∠=∠,AB BE ==c.又∵BEBD =DC AB EB AC AC =()AB BDAC DC=同上AEC EAF ∠=∠EAF EAC ∠=∠, ∴AEC EAC ∠=∠,AC AE =.ABDCEc b cABCDEF又∵CEBD=DCAB AB AC CE =BAC ∠2bccos2cos2211b+c +b c A AAD =(或)⊥b c ADAC DE BE ==又+DE=AE AD ,即b b+cAD AE =.而△ABE 为等腰三角形, BF ⊥AE, ∴22sin =2csin 2AAE AF AB BAF ==∠,∴2bccos 2cos 2211b+c +b cA AAD =(或). ④内心到三边距离r(三角形内切圆半径) 设三角形面积为S ,则有2r=a+b+cS(即面积的2倍除以周长)证明过程如下:连接OA,OB,OC. ∵相切,∴OF AB ⊥,即S △AOB = 11cr 22AB OF •=,同理S △AOC = 1br 2,S △BOC = 1ar 2.又∵S=S △AOB + S △AOC + S △BOC ,即S=1(a+b+c)r 2, ∴2r=a+b+cS.2.重心:三角形三条中线交点c b cAF B DC EBDC中线性质:将三角形面积等分成两部分.重心性质:分三角形的中线两段长比例为2:1(长:短)如图:AD,BE,CF 为△ABC 三条中线,G 为其重心,则有 :::2:1AG GC BG GE CG GF ===证明过程如下:作BH ,2GD DH GH GD ==2AG GH GD ==:2:1AG GC = 延伸:三角形中线长公式 如图,AD 为△ABC 的中线,则有AD =证明过程如下: 作BE 1,=2AD DE AD AE =即ABF A ∠=∠⊥cos ABF ∠cos c A sin c A cos c A b+12AD AE ==三角形三边垂直平分线的交点,三角形外接圆圆心。
三角形的中线与垂线性质总结

三角形的中线与垂线性质总结在数学的广袤世界中,三角形是一个基础而又极为重要的图形。
其中,三角形的中线和垂线具有独特而关键的性质,这些性质不仅在理论研究中有着重要地位,更在解决实际问题时发挥着巨大作用。
首先,咱们来聊聊三角形的中线。
中线,简单来说,就是连接三角形一个顶点和它对边中点的线段。
三角形的中线有一个非常重要的性质,那就是三条中线相交于一点,这个点被称为三角形的重心。
而且重心将每条中线都分成了长度比为2 : 1 的两段。
比如说,在三角形 ABC 中,AD 是 BC 边上的中线。
那么 BD =DC。
如果连接其他两条中线 BE 和 CF,它们也会相交于一点 G,并且AG : GD = 2 : 1,BG : GE = 2 : 1,CG : GF = 2 : 1。
中线还有一个实用的性质,就是它将三角形分成了面积相等的两个部分。
还是以三角形 ABC 和中线 AD 为例,三角形 ABD 和三角形ACD 的面积是相等的。
这是因为这两个三角形等底等高,底都是 BD或者 DC,高都是从 A 点向 BC 边作的垂线的长度。
接下来,咱们再看看三角形的垂线。
垂线,也被称为高,是从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段。
三角形的三条垂线也有一个重要的性质,那就是它们相交于一点,这个点被称为三角形的垂心。
在直角三角形中,两条直角边就是两条垂线,而斜边的垂线则在三角形内部。
对于锐角三角形,三条垂线都在三角形内部;而对于钝角三角形,两条短边的垂线在三角形外部,长边的垂线在三角形内部。
三角形的垂线长度与三角形的面积有着密切的关系。
三角形的面积可以用底乘以高除以 2 来计算。
假设三角形 ABC 中,BC 边上的高是AD,那么三角形 ABC 的面积就等于 BC×AD÷2。
此外,垂线还有一些有趣的定理。
比如,在直角三角形中,斜边的平方等于两条直角边的平方和,这就是著名的勾股定理。
三角形的中线和垂线的性质在实际生活中也有很多应用。
“直角三角形斜边上的中线”的性质及其应用
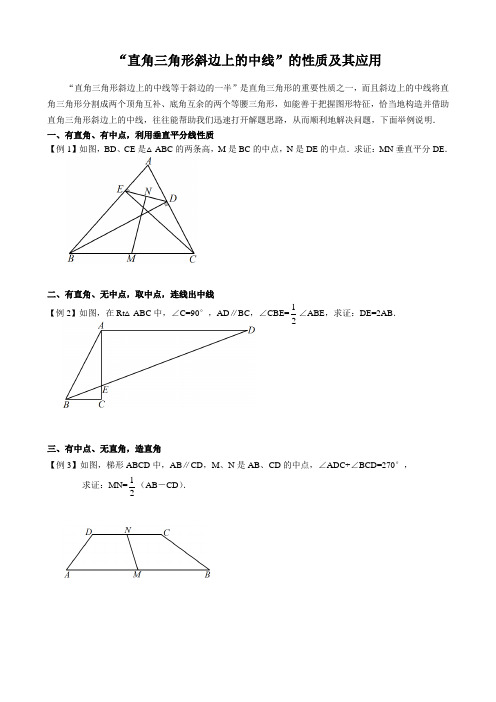
“直角三角形斜边上的中线”的性质及其应用“直角三角形斜边上的中线等于斜边的一半”是直角三角形的重要性质之一,而且斜边上的中线将直角三角形分割成两个顶角互补、底角互余的两个等腰三角形,如能善于把握图形特征,恰当地构造并借助直角三角形斜边上的中线,往往能帮助我们迅速打开解题思路,从而顺利地解决问题,下面举例说明.一、有直角、有中点,利用垂直平分线性质【例1】如图,BD 、CE 是△ABC 的两条高,M 是BC 的中点,N 是DE 的中点.求证:MN 垂直平分DE .二、有直角、无中点,取中点,连线出中线【例2】如图,在Rt △ABC 中,∠C=90°,AD ∥BC ,∠CBE=21∠ABE ,求证:DE=2AB .三、有中点、无直角,造直角【例3】如图,梯形ABCD 中,AB ∥CD ,M 、N 是AB 、CD 的中点,∠ADC+∠BCD=270°,求证:MN=21(AB -CD ).四、逆用性质解题【例4】如图,延长矩形ABCD 的边CB 至E ,使CE=CA ,P 是AE 的中点.求证:BP ⊥DP .【习题练习】1、如图,△ABC 中,AB=AC ,∠ABD=∠CBD ,BD ⊥DE 于D ,DE 交BC 于E ,求证:CD=21BE .2、如图,△ABC 中,∠B=2∠C ,AD ⊥BC 于D ,M 是BC 的中点,求证:AB=2DM .3、如图,在四边形ABCD 中,∠DAB=∠DCB=90°,点M 、N 分别是BD 、AC 的中点.确定MN 、AC 的位置关系.直角三角形斜边上中线性质的应用一、直角三角形斜边上中线的性质1、性质:直角三角形斜边上的中线等于斜边的一半.如图,在Rt △BAC 中,∠BAC=90°,D 为BC 的中点,则BC 21AD =.2、性质的拓展:如图:因为D 为BC 中点,所以BC 21DC BD ==, 所以AD=BD=DC=BC 21, 所以∠1=∠2,∠3=∠4,因此∠ADB=2∠1=2∠2,∠ADC=2∠3=2∠4.因而可得如下几个结论:①直角三角形斜边上的中线将直角三角形分成两个等腰三角形;②分成的两个等腰三角形的腰相等,两个顶角互补、底角互余,并且其中一个等腰三角形的顶角等于另一个等腰三角形底角的2倍.二、性质的应用1、21倍关系求值 例1、如图,CD 是Rt △ABC 斜边AB 上的中线,若CD=4,则AB= .2、证明线段相等例2、如图,在△ABC 中,∠BAC=90°,延长BA 到D 点,使AB 21AD =,点E 、F 分别为边BC 、AC 的中点.(1)求证:DF=BE ;(2)过点A 作AG ∥BC ,交DF 于G .求证:AG=DG .3、证明角相等及角的倍分关系例3、已知,如图,在△ABC中,∠BAC 90°,BD、CE分别为AC、AB上的高,F为BC的中点,求证:∠FED=∠FDE.例4、已知:如图,在△ABC中,AD是高,CE是中线。
直角三角形斜边上的中线性质练习
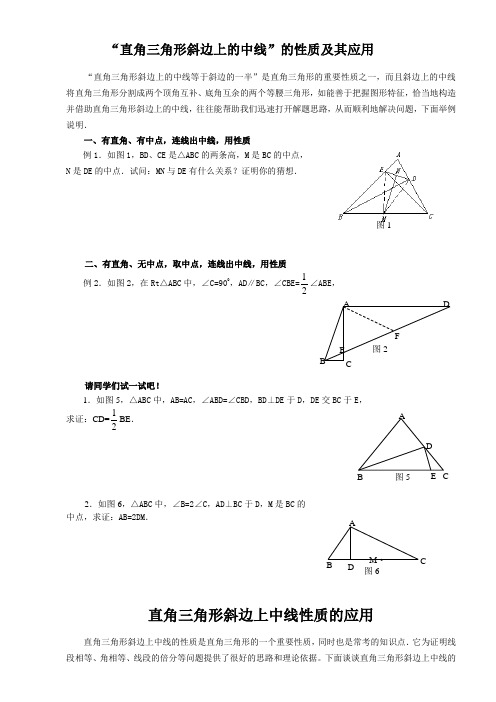
“直角三角形斜边上的中线”的性质及其应用“直角三角形斜边上的中线等于斜边的一半”是直角三角形的重要性质之一,而且斜边上的中线将直角三角形分割成两个顶角互补、底角互余的两个等腰三角形,如能善于把握图形特征,恰当地构造并借助直角三角形斜边上的中线,往往能帮助我们迅速打开解题思路,从而顺利地解决问题,下面举例说明.一、有直角、有中点,连线出中线,用性质例1.如图1,BD 、CE 是△ABC 的两条高,M 是BC 的中点, N 是DE 的中点.试问:MN 与DE 有什么关系?证明你的猜想.二、有直角、无中点,取中点,连线出中线,用性质 例2.如图2,在Rt △ABC 中,∠C=900,AD ∥BC ,∠CBE=12∠ABE ,请同学们试一试吧!1.如图5,△ABC 中,AB=AC ,∠ABD=∠CBD ,BD ⊥DE 于D ,DE 交BC 于E , 求证:CD=12BE .2.如图6,△ABC 中,∠B=2∠C ,AD ⊥BC 于D ,M 是BC 的 中点,求证:AB=2DM .直角三角形斜边上中线性质的应用直角三角形斜边上中线的性质是直角三角形的一个重要性质,同时也是常考的知识点.它为证明线段相等、角相等、线段的倍分等问题提供了很好的思路和理论依据。
下面谈谈直角三角形斜边上中线的图1BADCEF图2B图5ACBD M · 图6性质及应用。
一、直角三角形斜边上中线的性质1、性质:直角三角形斜边上的中线等于斜边的一半.如图1,在Rt △BAC 中,∠BAC=︒90,D 为BC 的中点,则BC 21AD =。
2、性质的拓展:如图1:因为D 为BC 中点,所以BC 21DC BD ==,所以AD=BD=DC=BC21,所以∠1=∠2,∠3=∠4, 因此∠ADB=2∠3=2∠4, ∠ADC=2∠1=2∠2。
因而可得如下几个结论:①直角三角形斜边上的中线将直角三角形分成两个等腰三角形;②分成的两个等腰三角形的腰相等,两个顶角互补、底角互余,并且其中一个等腰三角形的顶角等于另一个等腰三角形底角的2倍. 二、性质的应用 1、求值例1、(2004年江苏省苏州市中考)如图2,CD 是Rt △ABC 斜边AB 上的中线,若CD=4,则AB= .2、证明线段相等例2、(2004年上海市中考)如图4,在△ABC 中,∠BAC=90°,延长BA 到D 点,使AB 21AD =,点E 、F 分别为边BC 、AC 的中点。
三角形的高度和中线

三角形的高度和中线三角形是几何中最基本的形状之一,具有许多独特的性质和特点。
其中,三角形的高度和中线是我们常常研究和关注的重要内容。
本文将深入探讨三角形的高度和中线的概念、性质以及它们在几何学中的应用。
一、三角形的高度三角形的高度是指从一个顶点到与对边垂直相交的线段。
根据三角形的形状和特点,我们可以得到以下几种常见的三角形高度:1. 等腰三角形高度:在等腰三角形中,高度也是对称轴,将底边一分为二。
由于等腰三角形的两边等长,所以高度也是等长。
2. 直角三角形高度:在直角三角形中,高度对应直角边的垂直线段。
根据勾股定理,直角三角形的两条直角边平方和等于斜边平方,所以利用高度和底边构成的直角三角形也是相似的。
3. 普通三角形高度:对于普通三角形,高度可以通过作垂线来求得。
可以利用垂直相交线段长度的性质,或者应用三角形面积公式来计算高度。
二、三角形的中线三角形的中线是指连接一个顶点与对边中点的线段。
根据三角形的不同类型,我们可以得到下面三种常见的中线:1. 等腰三角形中线:在等腰三角形中,中线和高度是重合的。
由于等腰三角形的底边中点与对边中点重合,所以中线和高度重合。
2. 直角三角形中线:在直角三角形中,中线可以将斜边一分为二,连接直角顶点与斜边中点。
根据性质,直角三角形的中线与斜边垂直,并且长度等于斜边的一半。
3. 一般三角形中线:普通三角形的中线不同于高度可以通过作垂线来构造。
一般情况下,三角形中线的长度与对边的长有着一定的关系。
比如,如果一个三角形的两个中线交于一点,并且这个点距离第三个顶点的距离为a,那么这个点到对边两边的距离为2a。
三、高度和中线的性质高度和中线作为三角形的重要性质,具有以下几个重要的性质和应用:1. 高度与底边的关系:三角形的高度将底边分成两部分,根据性质可以得到两个三角形的相似关系。
如等腰三角形中,底边中点、高度起始点和顶点构成的三角形与底边中点、高度终止点和底边起点构成的三角形是相似的。
中线的性质

三角形中线以及性质
一、中线的概念:
三角形中,连接一个顶点和它所对边的中点的线段叫做三角形的中线。
二、中线的性质
1. 三角形的三条中线都在三角形内。
2.三角形的三条中线交于一点,该点叫做三角形的重心
3.三角形重心将中线分为长度比为1:2的两条线段。
4.直角三角形斜边上的中线等于斜边的1/2。
三、区别中线与中位线
中线指的是三角形定的一个顶点与对边中点连线的线段
中位线指的是三角形两边中点连线的线段
四、与“重心”有关的四心
内心:三角形的内心是三角形三条内角平分线的交点。
外心:三角形三条边的中垂线的交点叫作三角形的外心,即外
接圆圆心。
重心:三角形三条中线的交点叫作三角形的重心。
垂心:三角形三条垂线的交点叫作三角形的垂心。
注意:“中心”与“重心”容易混淆,“中心”只存在于正三角形,在等边三角形中,其内心,外心,重心,垂心都在一个点上,称之为中心。
高中几何知识解析中线与三角形的性质

高中几何知识解析中线与三角形的性质几何学是数学的一个重要分支,而在高中几何学中,中线是一个重要的概念。
本文将对中线与三角形的性质进行解析,并探讨其相关应用。
一、中线的定义在三角形ABC中,从顶点A到边BC的中点D引一条直线,称为三角形ABC的中线。
同理,从顶点B和C也可以引出中线DE和FG。
二、中线的性质1. 三角形的三条中线交于一点中线的一个重要性质是它们三条始终交于一点,该交点称为三角形的重心,通常用G表示。
重心划分中线的长度成比例的规律是AG:GD=BG:GE=CG:GF=2:1。
2. 重心到顶点的距离连接重心G和三角形的各个顶点A、B、C,我们可以发现重心G到任意顶点的距离都等于中线的长度的两倍,即GA=2GD,GB=2GE,GC=2GF。
3. 中点连线平行于第三边三角形的任意两条中线连线,不仅与一条中线垂直相交于其中点,而且还与另一条中线平行。
例如,中线GF与中线DE平行。
4. 中线长度之比三角形的中线有一个有趣的性质,即三条中线的长度之比为1:1,即AD=BD=CD。
5. 中线与面积的关系三角形的中线与三角形面积之间有一定的关系。
根据公式,三角形的面积可由底边长度和对应的高得出。
因此,对于三条中线,它们可以将三角形分成六个小三角形,而这六个小三角形的面积之和等于整个三角形面积的三分之一。
三、中线的应用中线作为几何学中的基本概念之一,具有重要的应用价值。
1. 利用中线求三角形的重心通过求三角形的中线,我们可以轻松地求得三角形的重心G。
只需要连接中线的交点即可得到三角形的重心。
2. 研究三角形的形状特性通过研究中线,我们可以更深入地了解三角形的形状特性。
例如,通过研究什么样的条件下,三角形的中线与边相等或平行等,我们可以得到一些三角形的性质。
3. 解决实际问题中线作为几何学的一个概念,在解决实际问题时也有广泛的应用。
例如,在建筑设计中,通过中线我们可以更准确地确定建筑物的重心,从而保证建筑物的稳定性。
直角三角形斜边上的中线的性质及其应用

“直角三角形斜边上的中线”的性质及其应用而且斜边上的中线将“直角三角形斜边上的中线等于斜边的一半”是直角三角形的重要性质之一,恰当地构造并直角三角形分割成两个顶角互补、底角互余的两个等腰三角形,如能善于把握图形特征,下面举例说借助直角三角形斜边上的中线,往往能帮助我们迅速打开解题思路,从而顺利地解决问题,明.一、有直角、有中点,连线出中线,用性质 BC的中点,CE是△ABC的两条高,M是例1.如图1,BD、有什么关系?证明你的猜想.DE的中点.试问:MN与DEN是DE.垂直平分猜想:MN1图1,∴NDBC,又NE=、MD,在Rt△BEC中,∵点M是斜边BC的中点,∴ME=证明:如图:连接ME2DE.垂直平分的垂直平分线,∴NM⊥DE.即直线MN是线段DEMN,“直角三角形斜边上的中线等于斜边的一半”评析:题目中给出了三角形的两条高与两个中点,联想问题便迎刃而解.二、有直角、无中点,取中点,连线出中线,用性质1A DADBC,∠CBE=,∠ABE例2.如图2,在Rt△ABC中,∠C=902DE=2AB0∥,求证:FAB相等,分析:欲证DE=2AB,则可寻DE的一半,再让其与2图E 1B取DE的中点F,连AF,则AF=FD=DE,可证得△AFD, C2△ABF均为等腰三角形,由此结论得证.1DE,所以∠DAF=∠ADF,又因为AD∥BCAFF,连,则AF=FD=,所以∠CBE=∠ADF,证明:DE的中点21∠ABE,所以∠ABF=又因为∠CBE=∠AFB,所以AF=AB,即DE=2AB.2评析:本题是有直角、无中点的情况,这时要取直角三角形的斜边上的中点,再连结该点与直角顶点,然后用性质来解决问题.P 三、有中点、无直角,造直角,用性质CD CD的中点,N是AB、,梯形ABCD中,AB∥CD,M、.如图例33N K 0 BCD=270,∠ADC+∠1M A B.MN=(AB-CD)求证:3图20证明:延长AD、BC交于P,∵∠ADC+∠BCD=270,、MK重合,则P、N于APB=90,连结PN,连结PM交DCK,下证N和∴∠11CD,PM=BM=DM=AB,0三点共线,PM分别是直角三角形△PDC、△PAB斜边上的中线,∴PN=CN=DN= 、∵PN22∵∠PNC=2∠PDN=2∠A,∠PMB=∠PKC=2∠A,∴∠PNC=∠PKC,∴N、K重合,1(AB-CD).∴MN=PM-PN=2评析:本题只有中点,而没有直角,这时要想方设法构造直角,应用性质,而条件中正好有角的关系“∠0,这样问题就易以解决了”BCD=270∠ADC+DA 四、逆用性质解题E,使CE=CA,至例4.如图4,延长矩形ABCD的边CP的中点.是AEODP.求证:BPEBC4图,于点O,连结PO证明:如图3,连结BD交AC AO=OC=OB=OD∵四边形ABCD是矩形,∴,11,EC=AC∵PA=PE,∴PO=,∴PO=BDEC,∵22.BP⊥DPOP=OB=OD即,∴“直角三角形斜边上的中线等于斜边的一半”这个性质是众所周知的,而它的逆定理往往被评析:的一半.BD边的中线等于BD大家所忽视,本题就是利用这个性质构造△PBD,证请同学们试一试吧!于E,于D,DE交BCDE1.如图5,△ABC中,AB=AC,∠ABD=∠CBD,BD⊥A 1CD=BE.求证:2 BC的于BCD,M是2.如图6,△ABC中,∠B=2∠C,AD⊥D.中点,求证:AB=2DM ACE B5图M·C B D6 图1应想到“直角三角形斜边上的中线等于斜边的一BEBE是直角三角形的斜边,由1.提示:结论中的2DFC.,即证∠C=∠DF,故应取BE的中点F,连结,只需证明DC=DF半”即可.、,连结DNMN2.提示:取AB的中点N直角三角形斜边上中线性质的应用它为证明线同时也是常考的知识点.直角三角形斜边上中线的性质是直角三角形的一个重要性质,下面谈谈直角三角形斜边上中线的线段的倍分等问题提供了很好的思路和理论依据。
