中点四边形好 ppt课件
合集下载
中点四边形-文档资料

D
E
H
A
O
C
F
G
B
17
对角线相等且垂直的四 边形的中点四边形为正 方形
18
结合刚才的证明过程,小组讨论并思考:
❖ (1)中点四边形的形状与原四边形的什么有着密
切的关系? 对角线
❖ (2)要使中点四边形是菱形,原四边形一定要是 矩形吗?
❖ (3)要使中点四边形是矩形,原四边形一定要是
菱形吗?
B
A
G
E
E
H
AB
C
FG
D
G
C
F
19
D
“我”的命运由对角线主宰
原四边形的对角线
既不相等又不垂直 相等 垂直
相等且垂直
中点四边形
平行四边形 菱形 矩形
正方形
20
小组合作交流:
❖ 任意四边形的中点四边形都是平__行__四_边__形_; ❖ 平行四边形的中点四边形是_平__行__四_边__形__; ❖ 矩形的中点四边形是______菱_形_________; ❖ 菱形的中点四边形是________________; ❖ 正方形的中点四边形是______________; ❖ 梯形的中点四边形是________________; ❖ 直角梯形的中点四边形是____________; ❖ 等腰梯形的中点四边形是____________。
任意四边形的中点四 边形都为平行四边形
6
我思考,我进步2
顺次连接矩形各边中点所成的四边 形是什么四边形?
连结两条对角线
7
H
A
B
E
G
C
D
F
矩形的中点四边形是菱形。
8
我思考,我进步3
E
H
A
O
C
F
G
B
17
对角线相等且垂直的四 边形的中点四边形为正 方形
18
结合刚才的证明过程,小组讨论并思考:
❖ (1)中点四边形的形状与原四边形的什么有着密
切的关系? 对角线
❖ (2)要使中点四边形是菱形,原四边形一定要是 矩形吗?
❖ (3)要使中点四边形是矩形,原四边形一定要是
菱形吗?
B
A
G
E
E
H
AB
C
FG
D
G
C
F
19
D
“我”的命运由对角线主宰
原四边形的对角线
既不相等又不垂直 相等 垂直
相等且垂直
中点四边形
平行四边形 菱形 矩形
正方形
20
小组合作交流:
❖ 任意四边形的中点四边形都是平__行__四_边__形_; ❖ 平行四边形的中点四边形是_平__行__四_边__形__; ❖ 矩形的中点四边形是______菱_形_________; ❖ 菱形的中点四边形是________________; ❖ 正方形的中点四边形是______________; ❖ 梯形的中点四边形是________________; ❖ 直角梯形的中点四边形是____________; ❖ 等腰梯形的中点四边形是____________。
任意四边形的中点四 边形都为平行四边形
6
我思考,我进步2
顺次连接矩形各边中点所成的四边 形是什么四边形?
连结两条对角线
7
H
A
B
E
G
C
D
F
矩形的中点四边形是菱形。
8
我思考,我进步3
中点四边形ppt

快速练习:
(1)中点四边形是菱形,原四边形是( D ) A 矩形 B 菱形 C 正方形 D 对角线相等的四边形 (2)中点四边形是矩形,原四边形是( D ) A 矩形 B 菱形 C 正方形 D 对角线互相垂直的四边形 (3)中点四边形是正方形,原四边形是( D ) A 矩形 B 正方形 C 对角线互相垂直且平分的四边形 D 对角线互相垂直且相等的四边形 (4)一个梯形的中点四边形是菱形,这个梯形是 (等腰梯形 )
什么情况是矩形呢? 若四边形EFGH是矩形,则FH⊥BC B 连接AO ∵FH//AO ∴AO⊥BC E G O A F H C
小结1: 从一般到特殊的研究方法
我们从原四边形两条对角线的位置关系 和数量关系探索了中点四边形的形状变化, 从中我们可以体会到当原四边形从一般到特 殊的变化中(也就是对角线关系从一般到特 殊),常常伴随着中点四边形从一般到特殊 的变化。
H A
D G
证明:连接AC、BD.
E
∵AE=EB,BF=FC, B F ∴EF∥ AC EF=1/2AC. 同理GH ∥ AC GH=1/2AC. ∴EF ∥ GH EF=GH=1/2AC, ∴四边形EFGH是平行四边形. 注:同理 HE=FG=1/2BD ∴EF+FG+GH+HE=AC+BD
C
分析:根据上题我们有“任意四边形 的中点四边形都是平行四边形” ,再结 合四边形对角线的关系我们可以得出 结论:(课堂点睛P55第4题)
B
D
F
E
C
中点四边形: 定义:顺次连接一个四边形四边中点所 得四边形称为这个四边形的中点四边形。 思考:依次连接任意四边形各边中点 所成的中点四边形是什么图形呢?
已知:如图,点E、
中点四边形课件(共31张PPT)全文

中点四边形是菱形;
• 〔3〕只要原四边形的两条对角线 互相垂直,就 能使中点四边形是矩形;
• 〔4〕要使中点四边形是正方形,原四边形要符合 的条件是 对角线相等且互相垂直。
巩固练习
1.如图,在四边形ABCD中,E,F,G,H分别是 AB,BC,CD,DA的中点,请添加一个条件,使 四边形EFGH为菱形,并说明理由。 解:添加的条件_______
已知:任意四边形ABCD,E、F、G、H分别是AB、BC、CD、DA的中点,顺次连接E、F、G、H,则四边形EFGH称为中点四边形。
对角线相等的四边形的中点四边形为菱形
什么四边形?并证明你的结论?
解:添加的条件_______
B
四边形A3B3C3D3的周长是_____。
形EFGH是什么四边形?并证明你的
如图,中点四边形EFGH的周长与原四边
形ABCD的什么量有关系?是什么关系?能证 明你的猜想吗?
HD A
温馨提示:△DHG 的HG与 △ADC的哪一边有关系?
E
G
结论:中点四边形
B F C 的周长等于原四边
形对角线的和
挑战自我
四边形ABCD中,AC=6,
BD=8,且AC⊥BD,
顺次连接四边ABCD的中 点得到四边形A1B1C1D1, 依次类推,得到四边形 AnBnCnDn;
四边形的什么有着密切的联系?要使中点四边
形EFGH是下列图形,原四边形ABCD需具有什么
特征? (1)是矩形; (2)是菱形; (3)是正方形。
HD A
E
G
B
F
C
把你的想法与同伴交流。
填空:
• 〔1〕中点四边形的形状与原四边形的 对角线有 密切关系;
• 〔3〕只要原四边形的两条对角线 互相垂直,就 能使中点四边形是矩形;
• 〔4〕要使中点四边形是正方形,原四边形要符合 的条件是 对角线相等且互相垂直。
巩固练习
1.如图,在四边形ABCD中,E,F,G,H分别是 AB,BC,CD,DA的中点,请添加一个条件,使 四边形EFGH为菱形,并说明理由。 解:添加的条件_______
已知:任意四边形ABCD,E、F、G、H分别是AB、BC、CD、DA的中点,顺次连接E、F、G、H,则四边形EFGH称为中点四边形。
对角线相等的四边形的中点四边形为菱形
什么四边形?并证明你的结论?
解:添加的条件_______
B
四边形A3B3C3D3的周长是_____。
形EFGH是什么四边形?并证明你的
如图,中点四边形EFGH的周长与原四边
形ABCD的什么量有关系?是什么关系?能证 明你的猜想吗?
HD A
温馨提示:△DHG 的HG与 △ADC的哪一边有关系?
E
G
结论:中点四边形
B F C 的周长等于原四边
形对角线的和
挑战自我
四边形ABCD中,AC=6,
BD=8,且AC⊥BD,
顺次连接四边ABCD的中 点得到四边形A1B1C1D1, 依次类推,得到四边形 AnBnCnDn;
四边形的什么有着密切的联系?要使中点四边
形EFGH是下列图形,原四边形ABCD需具有什么
特征? (1)是矩形; (2)是菱形; (3)是正方形。
HD A
E
G
B
F
C
把你的想法与同伴交流。
填空:
• 〔1〕中点四边形的形状与原四边形的 对角线有 密切关系;
苏科版八年级数学下册第九章《中点四边形课件》公开课课件(共14张PPT)

(3)写出四边形AnBnCnDn的面积;
A
(4)求四边形A5B5C5D5的周长.
A1
D2
D1
D3
C3
A2
…
C2
B
D
A3
B3
B1
B2
C1
C
图13
D
G
H
C
F
A
E
B
问题2:已知: 平行四边形ABCD中,E、F、G、H分别是
四边中点,试说明四边形EFGH的形状并说明理由
H
A
D
E
G
B
C
F
问题3:如果四边形ABCD是矩形,则四边形 EFGH是什么特殊四边形呢?
A
H
D
答案:菱形 E
B
G C F
问题4:如果四边形 ABCD是菱形,则四边形
EFGH是什么特殊的四边形呢?
•
问题5:如果四边形 ABCD是正方形,则四边
形EFGH又是什么特殊四边形?
A
H
D
答案:正方形 E
G
B
C
F
已知:在四边形ABCD中, E、F、G、H分别是
四边中点; (1)如果AC=BD,则
四边形EFGH是 菱形。
(2)如果AC⊥BD,则
D G
H
C
四边形EFGH是 矩形 。
F
A
(3)如果AC=BD、 AC⊥BD,
• 11、一个好的教师,是一个懂得心理学和教育学的人。2021/7/242021/7/242021/7/24Jul-2124-Jul-21
• 12、要记住,你不仅是教课的教师,也是学生的教育者,生活的导师和道德的引路人。2021/7/242021/7/242021/7/24Saturday, July 24, 2021
中考数学全程复习方略 微专题四 中点四边形课件

【题组过关】 1.(2019·株洲模拟)如图,点E,F,G,H分别为四边形 ABCD的四边AB,BC,CD,DA的中点,则关于四边形EFGH,下 列说法正确的为 ( C )
A.一定不是平行四边形 B.一定不是中心对称图形 C.可能是轴对称图形 D.当AC=BD时它是矩形
2.(2019·呼和浩特模拟)如图,在四边形ABCD中,对角 线AC⊥BD,垂足为点O,点E,F,G,H分别为边AD,AB,BC,CD 的中点.若AC=8,BD=6,则四边形EFGH的面积为___1_2___.
谢谢观赏
You made my day!
图
形 关
若原四边形正对方角形线互相垂直且相等,则中点四
系 边形为___________
【微点警示】 1.中点四边形的证明:中点四边形只与原四边形的对角 线有关,其证明运用了三角形的中位线定理.
2.特殊的中点四边形:
原图形 平行四边形
矩形 菱形 正方形 梯形 等腰梯形
对应的中点四边形 平行四边形 菱形 矩形 正方形 平行四边形 菱形
∴EF∥AC,且EF= 1 AC,同理:HG∥AC,且HG=1 AC,
2
2
∴EF∥HG,且EF=HG,∴四边形EFGH是平行四边形.
(2)略
•1、书籍是朋友,虽然没有热情,但是非常忠实。2022年3月21日星期一2022/3/212022/3/212022/3/21 •2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那些善于独 立思考的人,给那些具有锲而不舍的人。2022年3月2022/3/212022/3/212022/3/213/21/2022 •3、做老师的只要有一次向学生撒谎撒漏了底,就可能使他的全部教育成果从此为之失败。 2022/3/212022/3/21March 21, 2022
中点四边形课件

学习目标:
1.理解中点四边形的概念; 2.掌握中点四边形的判定、证明及 应用; 学习重难点: 中点四边形的判定、证明及应用;
复习旧知:
三角形中位线:
如图,在△ABC中,D、E分别是AB、AC的
中点. DE就是△ABC的中位线.
几何语言: ∵ D、E分别是AB、AC的中点 D ∴DE为△ABC的中位线, ∴DE∥BC,DE=
G
∵ E、F是AB、BC边中点
∴EF是△ABC中位线 1 ∴EF∥AC且EF= 2 AC ∴EF ∥ HG且EF = HG ∴四边形EFGH为平行四边形。
B
F
C
1 同理:HG ∥ AC且HG = AC 2
结论:任意四边形的中点四边形都为平行 四边形。 (对角线既不相等又不垂直)
平行四边形的中点四边形是什么形 状?
探究三:
已知:如图,点E、F、G、H分别是四边形ABCD各 边的中点,且AC⊥BD,则四边形EFGH是什么形 状呢?为什么?
D
H
A
G
O E
Bቤተ መጻሕፍቲ ባይዱ
C
F
结论:对角线互相垂直 的四边形的中点四边形 为矩形。
想一想:
菱形的中点四边形是什么形状?
A E B F C G H
D
结论:菱形的中点四边形是矩形。
探究四:
“任中平”
“平中平” • 矩形的中点四边形是________________; 菱形 “矩中菱” ________________; • 菱形的中点四边形是 矩形
• 正方形的中点四边形是 ______________; “菱中矩”
正方形
“正中正”
“我”的命运由 对角线 主宰
原四边形的对角线
1.理解中点四边形的概念; 2.掌握中点四边形的判定、证明及 应用; 学习重难点: 中点四边形的判定、证明及应用;
复习旧知:
三角形中位线:
如图,在△ABC中,D、E分别是AB、AC的
中点. DE就是△ABC的中位线.
几何语言: ∵ D、E分别是AB、AC的中点 D ∴DE为△ABC的中位线, ∴DE∥BC,DE=
G
∵ E、F是AB、BC边中点
∴EF是△ABC中位线 1 ∴EF∥AC且EF= 2 AC ∴EF ∥ HG且EF = HG ∴四边形EFGH为平行四边形。
B
F
C
1 同理:HG ∥ AC且HG = AC 2
结论:任意四边形的中点四边形都为平行 四边形。 (对角线既不相等又不垂直)
平行四边形的中点四边形是什么形 状?
探究三:
已知:如图,点E、F、G、H分别是四边形ABCD各 边的中点,且AC⊥BD,则四边形EFGH是什么形 状呢?为什么?
D
H
A
G
O E
Bቤተ መጻሕፍቲ ባይዱ
C
F
结论:对角线互相垂直 的四边形的中点四边形 为矩形。
想一想:
菱形的中点四边形是什么形状?
A E B F C G H
D
结论:菱形的中点四边形是矩形。
探究四:
“任中平”
“平中平” • 矩形的中点四边形是________________; 菱形 “矩中菱” ________________; • 菱形的中点四边形是 矩形
• 正方形的中点四边形是 ______________; “菱中矩”
正方形
“正中正”
“我”的命运由 对角线 主宰
原四边形的对角线
中点四边形优秀课件ppt
一、 知识预备
2、中位线: 中位线定义: 连接三角形两边 中点 的线段叫做三角形的中位线 中位线定理: 三角形的中位线 平行 于第三边并且等于它的 一半 ;
7/10/2024
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
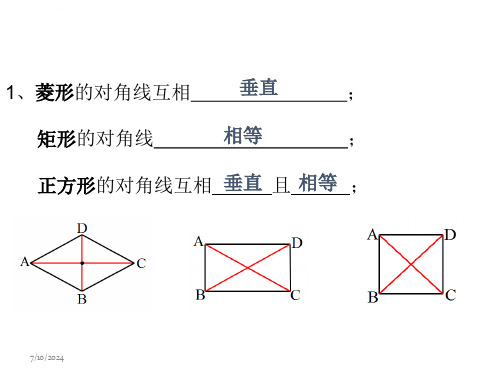
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确一Βιβλιοθήκη 知识预备1、菱形的对角线互相
垂直
;
矩形的对角线
相等
;
正方形的对角线互相 垂直 且 相等 ;
7/10/2024
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
AC⊥BD
AC=BD
当四边形对角线互相垂直时,中点四边形为矩形; 当四边形对角线相等时,中点四边形为菱形; 当四边形对角线互相垂直且相等时,中点四边形为正方形。
7/10/2024
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
一、 知识运用
3、中点四边形:依次连接任意四边形各边 中点 所得的 四边形称为中点四边形. 活动1: (1)任意作一个四边形,并作出 它的中点四边形; (2)观察:你作出的中点四边形是 什么四边形?
任意四边形的中点四边形为平行四边形
7/10/2024
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
2、中位线: 中位线定义: 连接三角形两边 中点 的线段叫做三角形的中位线 中位线定理: 三角形的中位线 平行 于第三边并且等于它的 一半 ;
7/10/2024
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确一Βιβλιοθήκη 知识预备1、菱形的对角线互相
垂直
;
矩形的对角线
相等
;
正方形的对角线互相 垂直 且 相等 ;
7/10/2024
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
AC⊥BD
AC=BD
当四边形对角线互相垂直时,中点四边形为矩形; 当四边形对角线相等时,中点四边形为菱形; 当四边形对角线互相垂直且相等时,中点四边形为正方形。
7/10/2024
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
一、 知识运用
3、中点四边形:依次连接任意四边形各边 中点 所得的 四边形称为中点四边形. 活动1: (1)任意作一个四边形,并作出 它的中点四边形; (2)观察:你作出的中点四边形是 什么四边形?
任意四边形的中点四边形为平行四边形
7/10/2024
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
中考专题复习中点四边形(实用资料)ppt

边形是菱形 求证:四边形EFGH是矩形。
3、依次连接菱形ABCD各边中点得四边形EFGH,再依次连接四边形EFGH各边中点得四边形MNPQ,则四边形EFGH,四边形MNPQ
的形状是(
)
3、如图,在正方形ABCD中,点E,F分别是BC,CD的中点,AF,DE相交于点G,则可得结论:
依次连接矩形四边中点得到的四边形是什么四边形?
H A
E
D G C
F B
问题6:
依次连接怎样一个四边形四边中点的图形是矩形?
连接对角线互相垂直的四边形四条边中点得到 的四边形是矩形
问题7:
依次连接怎样一个四边形四边中点的图形是正方形?
问题8:
依次连接普通平行四边形四边中点得到的四边形是什么四边形?
求证:四边形EFGH是菱形。
连接对角线相等的四边形四条边中点得到的四边形是菱形
平行四边形
问题2:
依次连接矩形四边中点得到的四边形是什么四边形?
已知:如图,E、F、G 、H分别是矩形ABCD四条边AB、 BC、CD、DA的中点, 求证:四边形EFGH是菱形。
A
H
D
E
G
B
F
C
问题3:
依次连接等腰梯形四边中点的四边形是什么四边形?
已知:如图,E、F、G 、H分别是等腰梯形ABCD四 条边AB、BC、CD、DA的中点, 求证:四边形EFGH是菱形。
连接对角线互相垂直的四边形四条边中点得到的四边形是矩形
连接对角线互相垂直的四边形四条边中点得到的四边形是矩形
H 依次连接矩形四边中点得到的四边形是什么四边形? A D 3、如图,在正方形ABCD中,点E,F分别是BC,CD的中点,AF,DE相交于点G,则可得结论:
3、依次连接菱形ABCD各边中点得四边形EFGH,再依次连接四边形EFGH各边中点得四边形MNPQ,则四边形EFGH,四边形MNPQ
的形状是(
)
3、如图,在正方形ABCD中,点E,F分别是BC,CD的中点,AF,DE相交于点G,则可得结论:
依次连接矩形四边中点得到的四边形是什么四边形?
H A
E
D G C
F B
问题6:
依次连接怎样一个四边形四边中点的图形是矩形?
连接对角线互相垂直的四边形四条边中点得到 的四边形是矩形
问题7:
依次连接怎样一个四边形四边中点的图形是正方形?
问题8:
依次连接普通平行四边形四边中点得到的四边形是什么四边形?
求证:四边形EFGH是菱形。
连接对角线相等的四边形四条边中点得到的四边形是菱形
平行四边形
问题2:
依次连接矩形四边中点得到的四边形是什么四边形?
已知:如图,E、F、G 、H分别是矩形ABCD四条边AB、 BC、CD、DA的中点, 求证:四边形EFGH是菱形。
A
H
D
E
G
B
F
C
问题3:
依次连接等腰梯形四边中点的四边形是什么四边形?
已知:如图,E、F、G 、H分别是等腰梯形ABCD四 条边AB、BC、CD、DA的中点, 求证:四边形EFGH是菱形。
连接对角线互相垂直的四边形四条边中点得到的四边形是矩形
连接对角线互相垂直的四边形四条边中点得到的四边形是矩形
H 依次连接矩形四边中点得到的四边形是什么四边形? A D 3、如图,在正方形ABCD中,点E,F分别是BC,CD的中点,AF,DE相交于点G,则可得结论:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
其它各种四边形的中点四边形边是何种四
A边矩形形A呢EBC?D 先B观察并菱猜形AD一BCD猜,再证A明.正E方形ABCBD
E
F
H
FA
CH
F
D
G
D
G
C
菱形
矩形B
D 正方G形 C
梯形ABCD
A EB
直角梯形ABCD
A EB
等腰梯形ABCD
AE B
H
FH
F
H
F
D
C
D 平行四G 边形 C 平行四G边形 D 菱形G
“我”的命运谁主宰
——探究中点四边形
知识回顾 1
如下图:在三角形ABC中,点D是AB的中
点,点E是AC的中点。
DE为三角形ABC的 中位线
定理:三角形的中位线平行于第三边,
且等于第三边的一半.
A
∵DE是△ABC的中位线,
D
E
∴DE∥BC, DE 1 BC.
2
B
C
这个定理提供了证明线段平行以及线段成倍分关系
求证:四边形E请FG同H是学菱们形画一画、看一看、 A E 猜一猜并证一证
H
B
F
D
G
C
对角线相等的四边 形的中点四边形为 菱形
我思考,我进步4
A
E
H
B
D
F
G
C
顺次连接菱形各边中点所成的四边
形是什么四边形?
A
E
H
B
D
F
G
C
菱形的中点四边形是矩形。
我思考,我进步5
已顺知次:如连图接,点对E、角F线、G互、相H分垂别直是的四四边形边形 各边A求B中证C:D点各四所边边成中形点的EF,四G且H边是AC形矩⊥形是BD什。么四边形?
C
FG
D
G
C
F
D
“我”的命运由对角线主宰
原四边形的对角线
中点四边形
既不相等又不垂直 相等
平行四边形 菱形
垂直
矩形
相等且垂直
正方形
小组合作交流:
❖ 任意四边形的中点四边形都是平__行__四_边__形_; ❖ 平行四边形的中点四边形是_平__行__四_边__形__; ❖ 矩形的中点四边形是______菱_形_________; ❖ 菱形的中点四边形是________________; ❖ 正方形的中点四边形是______________; ❖ 梯形的中点四边形是________________; ❖ 直角梯形的中点四边形是____________; ❖ 等腰梯形的中点四边形是____________。
任意四边形的中点四 边形都为平行四边形
我思考,我进步2
顺次连接矩形各边中点所成的四边 形是什么四边形?
连结两条对角线
H
A
B
E
G
C
D
F
矩形的中点四边形是菱形。
我思考,我进步3
已顺知次:如连图接,点对E、角F线、G相、等H分的别四是边四形边形各边
中点AB所CD成各的边四中点边,形且是AC什=B么D形。 ?
D
E
H
A
O
C
F
G
B
对角线相等且垂直的四 边形的中点四边形为正 方形
结合刚才的证明过程,小组讨论并思考:
❖ (1)中点四边形的形状与原四边形的什么有着密
切的关系? 对角线
❖ (2)要使中点四边形是菱形,原四边形一定要是 矩形吗?
❖ (3)要使中点四边形是矩形,原四边形一定要是
菱形吗?
B
A
G
E
E
H
AB
C
填空:
❖ (1)中点四边形的形状与原四边形的对角线有 密切关系;
❖ (2)只要原四边形的两条对角线 相等 ,就能 使中点四边形是菱形;
❖ (3)只要原四边形的两条对角线 互相垂直, 就能使中点四边形是矩形;
❖ (4)要使中点四边形是正方形,原四边形要符 合的条件是 对角线相等且互相垂直 。
我思,我进步6
求证:四边形请E同F学GH们为画平一行画四、边看形一。看、
A
E 猜一猜证并明:证连一接证AC
H
D
G
B ∵ E、F是AB、BC边中点
1
F ∴EF∥AC且EF= A2 C
C
同理:HG ∥ AC且HG =
1
AC
2
∴EF ∥ HG且EF = HG
∴四边形EFGH为平行四边形。
(一组对边平行且相等的四边形是平行四边形)
驶向胜
想一想,做一做
利的彼 岸
中点四边形的面积与原四边形的面积的
关系,并说出理由。
举例
A
H
E
D
B
G
F
C
结论:
1. 任意四边形的中点四边形都为平行 四边形。
2. 中点四边形为特殊的平行四边形的 决定因素取决于原四边形对角线是否相 等和垂直。
3.中点四边形的面积总等于原四边形 面积的一半
思考题:
探究四边形中一组对边的中点 和两条对角线的中点构成的四 边形的形状?
D
E
H
A
C O
F
G
B
对角线互相垂直的四 边形的中点四边形为 矩形
我思考,我进步6
顺次连接正方形各边中点所成的四 边形是什么四边形?
A
H
D
E
G
B
C
F
正方形的中点四边形是正方形
我思考,我进步5
已顺知次:如连图接,点对E、角F线、相G、等H且分别互是相四垂边直形 的 四边AB形C各D各边边中中点点,所A成C=的BD四且边AC形⊥是BD什。么 四边求形证:? 四边形EFGH是正方形
的依据.
中点四边形的定义 ❖ 顺次连接四边形各边中点所得的
四边形叫做中点四边形。
B
A C
D
我思,我进步1
驶向胜
想一想,做一做
利的彼 岸
给你一个四边形纸片,你能把它折成平
行四边形吗?
举例
我思考,我进步1
顺已次知:连如接图,任点意E、四F、边G、形H各分边别是中四点边形
所AB成CD的各四边边中形点。是什么形?
