新疆兵团二中2019年中考全疆统一卷预测卷(3)(难度8:1:1)正卷
2019年新疆维吾尔自治区中考语文模拟试题与答案

2019年新疆维吾尔自治区中考语文模拟试题与答案2019年新疆维吾尔自治区中考语文模拟试题与答案考生须知:本试卷满分为120分,考试时间120分钟。
答题前,考生先将自己的“姓名”、“考号”、“考场”、“座位号”在答题卡上填写清楚,将“条形码”准确粘贴在条形码区域内。
保持卡面整洁,不要折叠、不要弄脏、不要弄皱,不准使用涂改液、修正带、刮纸刀。
一、积累与运用(30分)1.下列各组词语中字形和加点字的注音完全正确的一项是()(3分)A.谰语(nán)燥热潜心贯注(qián)低回蜿转B.署名(zhǔ)XXX本色当行(háng)精疲力竭C.虬须(qiú)装饰养精蓄锐(xù)姗姗来迟D.钻探(zuàn)弥散高屋建瓴(líng)崭钉截铁2.下列句子中加点的词语使用不恰当的一项是()(3分)A.作为一名人民教师,他用春风化雨般的教导,培育了无数品学兼优的学生。
B.研究需要沉下心来,贵在持之以恒,重在学懂弄通,不能随随便便、不求甚解。
C.为了在科技比赛中体现创新精神,许多同学处心积虑,设计了各种样式的航空模型。
D.长沙城区内禁止摩托车通行,但仍有很多驾驶员无视交规行车,最后被交警大队扣了车,真是搬起石头砸自己的脚啊!3.下列有关文学、文化常识表述不正确的一项是()。
(3分)A.史书体例有编年体、纪传体、国别体、通史、断代史等,同一史书可以属于不同史书体例,如《史记》属于纪传体、通史。
B.“特别想念那XXX的月光,梦想跟随在放翁的身旁。
就算我没有稼轩同一般的才华,挑灯看剑咱有的是担当”,歌词中涉及到的古人依次是:XXX、XXX、XXX。
“挑灯看剑”让人想起“吹角连营”的一往无前。
C.说,是一种文体,通常借某一事物说明道理,如XXX的《爱莲说》;也可以叙事兼议论,如XXX的《捕蛇者说》。
D.《变色龙》的作者是俄国作家XXX,他的代表作有小说《装在套子里的人》,剧本《万尼亚舅舅》、《樱桃园》等。
新疆维吾尔自治区、新疆生产建设兵团2019年中考语文试题 ( 含答案)

语文试题卷考生须知:1.本试卷分为试题卷和答题卷两部分,试题卷共8页,答题卷共2页。
2.满分150分,考试时间120分钟。
一、基础知识与运用(共20分)1.下列词语中加点字的注音完全正确的一项是(3分)A.诘.问(ji é) 羞怯.(qu è) 悄.然(qi ǎo ) 混.为一谈(h ún ) B.瞥.见(pi ē) 卑鄙.(b ǐ) 两栖.(q ī) 随声附和.(h è) C.贮.蓄(h ù) 迸.溅(b èn ) 拙劣.(li è) 参差.不齐(ch ā) D.恐吓.(i à) 聪颖.(y ǐng ) 倜.傥(h ōu ) 信手拈.(ni ān ) 2.下列词语的书写完全正确的一项是(3分)A.安详 云宵 入目三分 轻歌曼舞B.服侍 帐蓬 语无伦次 眼花潦乱C.震撼 喧闹 重峦叠嶂 持之以恒D.妥帖 狡辨 惊慌失错 神采奕奕3.下列各句中加点成语使用不恰当的一项是(3分)A.中华文明与亚洲众多文明交相辉映,相得益彰....,同时与世界文明交流互鉴,携手前行。
B.当今世界,国际形势风云变幻....,美国挑起的新一轮贸易战将可能抑制全球的经济增长 C.走进温宿大峡谷,奇峰林立,如千年古堡,像巨轮飞渡……全国各地的游客接踵而至....。
D.贝聿铭留给了世人一幢幢栩栩如生....的精美建筑,被誉为“现代主义建筑最后的大师” 4.下列句子中没有语病的一项是(3分)A.能否把爱国主义教育作为永恒主题,是培养青年爱国情怀的重要途径。
B.波澜壮阔的“五四运动”,激发了中国人民和中华民族实现民族复兴。
C.“一带一路”将在非洲这片充满潜力的土地上,结出更多丰硕的果实。
D.许多内地教师心怀理想,奔赴新疆,开创新时代教育援疆的壮丽画卷。
5.填入下列文段横线处的词语,顺序最恰当的一项是(3分)徜徉于宁静之中,人生就多了一份韵律、多了一种意境。
最新新疆维吾尔自治区、新疆生产建设兵团年中考数学试题(图片版,有答案)

2019年新疆生产建设兵团中考数学试卷参考答案一、选择题(本大题共9题,每题5分,共45分)1.A.2.D.3.C.4.B5.D.6.C.7.A.8.B.9.A.二、填空题(本大题共6题,每题5分,共30分)10.(x+1)(x﹣1).11.m>5 .12.17 元.13.1000 元.14.18 cm2.15.①④三、解答题(一)(本大题共4题,共30分)16.【解答】解:原式=2﹣+2+1=3+.17.【解答】解:解不等式①,得:x≤1,解不等式②,得:x<4,则不等式组地解集为x≤1.18.【解答】(1)证明:∵点C是AB地中点,∴AC=BC;在△ADC与△CEB中,,∴△ADC≌△CEB(SSS),(2)证明:连接DE,如图所示:∵△ADC≌△CEB,∴∠ACD=∠CBE,∴CD∥BE,又∵CD=BE,∴四边形CBED是平行四边形.19.【解答】解:如图,过A作AF⊥CD于点F,在Rt△BCD中,∠DBC=60°,BC=30m,∵=tan∠DBC,∴CD=BC•tan60°=30m,∴乙建筑物地高度为30m;在Rt△AFD中,∠DAF=45°,∴DF=AF=BC=30m,∴AB=CF=CD﹣DF=(30﹣30)m,∴甲建筑物地高度为(30﹣30)m.四、解答题(二)(本大题共4题,共45分)20.【解答】解:(1)∵抽取地学生数为6÷0.15=40人,∴a=0.3×40=12人,b=8÷40=0.2,频数分布直方图如下:故答案为:12,0.2,1≤t≤1.5;(2)该校2000名学生中,每周课余阅读时间不足0.5小时地学生大约有:0.15×2000=300人;(3)树状图如图所示:总共有12种等可能地结果,其中刚好是1名男生和1名女生地结果有6种,∴抽取地两名学生刚好是1名男生和1名女生地概率==.21.【解答】解:(1)∵点A地坐标为(1,22),点B地坐标为(3,22),∴活动中心与小宇家相距22千米,小宇在活动中心活动时间为3﹣1=2小时.(22﹣20)÷5=0.4(小时).故答案为:22;2;0.4.(2)根据题意得:y=22﹣5(x﹣3)=﹣5x+37.(3)小宇从活动中心返家所用时间为:0.4+0.4=0.8(小时),∵0.8<1,∴所用小宇12:00前能到家.22.【解答】解:(1)如图所示,连接BO,∵∠ACB=30°,∴∠OBC=∠OCB=30°,∵DE⊥AC,CB=BD,∴Rt△DCE中,BE=CD=BC,∴∠BEC=∠BCE=30°,∴△BCE中,∠EBC=180°﹣∠BEC﹣∠BCE=120°,∴∠EBO=∠EBC﹣∠OBC=120°﹣30°=90°,∴BE是⊙O地切线;(2)当BE=3时,BC=3,∵AC为⊙O地直径,∴∠ABC=90°,又∵∠ACB=30°,∴AB=tan30°×BC=,∴AC=2AB=2,AO=,∴阴影部分地面积=半圆地面积﹣Rt△ABC地面积=π×AO2﹣AB×BC=π×3﹣××3=﹣.23.【解答】解:(1)当y=0时,0=﹣x2+x+2,解得:x1=﹣1,x2=4,则A(﹣1,0),B(4,0),当x=0时,y=2,故C(0,2);(2)①过点D作DE⊥x轴于点E,∵将△ABC绕AB中点M旋转180°,得到△BAD,∴DE=2,AO=BE=1,OM=ME=1.5,∴D(3,﹣2);②∵将△ABC绕AB中点M旋转180°,得到△BAD,∴AC=BD,AD=BC,∴四边形ADBC是平行四边形,∵AC==,BC==2,AB=5,∴AC2+BC2=AB2,∴△ACB是直角三角形,∴∠ACB=90°,∴四边形ADBC是矩形;(3)由题意可得:BD=,AD=2,则=,当△BMP∽△ADB时,==,可得:BM=2.5,则PM=1.25,故P(1.5,1.25),当△BMP∽△ABD时,1(1.5,﹣1.25),P1∽△BDA时,当△BMP2(1.5,5),可得:P2∽△BDA时,当△BMP3可得:P(1.5,﹣5),3综上所述:点P地坐标为:(1.5,1.25),(1.5,﹣1.25),(1.5,5),(1.5,﹣5).。
(附10套中考模拟卷)2019年新疆维吾尔自治区生产建设兵团中考化学试题word含答案
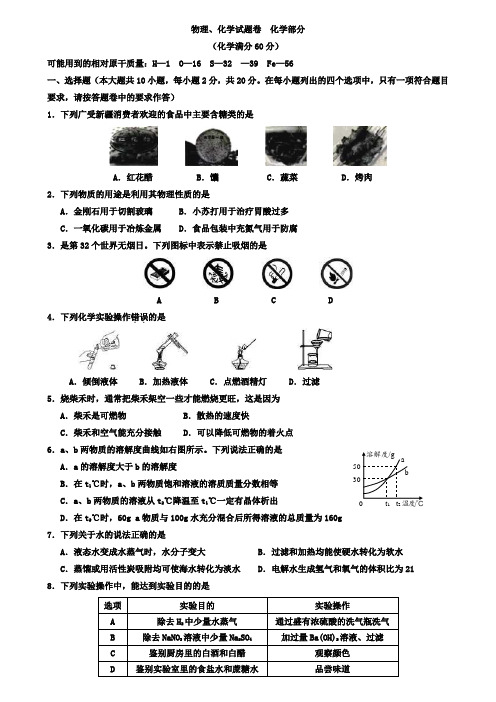
物理、化学试题卷化学部分(化学满分60分)可能用到的相对原干质量:H—1 O—16 S—32 —39 Fe—56一、选择题(本大题共10小题,每小题2分,共20分。
在每小题列出的四个选项中,只有一项符合题目要求,请按答题卷中的要求作答)1.下列广受新疆消费者欢迎的食品中主要含糖类的是A.红花醋 B.馕 C.蔬菜 D.烤肉2.下列物质的用途是利用其物理性质的是A.金刚石用于切割玻璃 B.小苏打用于治疗胃酸过多C.一氧化碳用于冶炼金属 D.食品包装中充氮气用于防腐3.是第32个世界无烟日。
下列图标中表示禁止吸烟的是A B C D4.下列化学实验操作错误..的是A.倾倒液体 B.加热液体 C.点燃酒精灯 D.过滤5.烧柴禾时,通常把柴禾架空一些才能燃烧更旺,这是因为A.柴禾是可燃物 B.散热的速度快C.柴禾和空气能充分接触 D.可以降低可燃物的着火点6.a、b两物质的溶解度曲线如右图所示。
下列说法正确的是A.a的溶解度大于b的溶解度B.在t1℃时,a、b两物质饱和溶液的溶质质量分数相等C.a、b两物质的溶液从t2℃降温至t1℃一定有晶体析出D.在t2℃时,60g a物质与100g水充分混合后所得溶液的总质量为160g7.下列关于水的说法正确的是A.液态水变成水蒸气时,水分子变大 B.过滤和加热均能使硬水转化为软水C.蒸馏或用活性炭吸附均可使海水转化为淡水 D.电解水生成氢气和氧气的体积比为21 8.下列实验操作中,能达到实验目的的是129.对于化学反应2ClO 3=====MnO 2△ 2Cl+3O 2↑,下列说法错误..的是 A .该反应属于分解反应 B .固体减少的质量等于生成O 2的质量C .MnO 2加快了该反应速率D .氯酸钾中、O 元素的质量比是391610.小明将未打磨的铝片和稀盐酸放入密闭容器中,用传感器探究反应过程中温度和压强的变化,如右图所示。
从图中所获信息不正确...的是A .反应过程中有热量放出B .50s 时,溶液中溶质为AlCl 3C .0~50s ,发生Al 2O 3+6HCl===2AlCl 3+3H 2O 反应D .100—140s ,压强减小是因为温度降低二、填空题(本大题共4小题,每空1分,共22分)11.(8分)化学与生活息息相关。
2019年新疆生产建设兵团中考语文试卷以及逐题解析版

2019年新疆生产建设兵团中考语文试卷一、基磁知识与运用(共20分)1.(3分)下列词语中加点字的注音完全正确的一项是()A.诘.问(jié)羞怯.(què)悄.然(qiǎo)混.为一谈(hún)B.瞥.见(piē)卑鄙.(bǐ)两栖.(qī)随声附和.(hè)C.贮.蓄(zhù)迸.溅(bèn)拙劣.(liè)参差.不齐(chā)D.恐吓.(xià)聪颖.(yīng)倜.傥(zhōu)信手拈.来(niān)2.(3分)下列词语的书写完全正确的一项是()A.安详云宵入目三分轻歌曼舞B.服侍帐蓬语无伦次眼花潦乱C.震撼喧闹重峦叠嶂持之以恒D.妥帖狡辩惊慌失错神采奕奕3.(3分)下列各句中加点成语使用不恰当的一项是()A.中华文明与亚洲众多文明交相辉映,相得益彰....,同时与世界文明交流互鉴,携.手前行。
B.当今世界,国际形势风云变幻....,美国挑起的新一轮贸易战将可能抑制全球的经济增长。
C.走进温宿大峡谷,奇峰林立,如千年古堡,像巨轮飞渡……全国各地的游客接踵而至。
.....D.贝聿铭留给了世人一幢幢栩栩如生....的精美建筑,被誉为“现代主义建筑最后的大师”。
4.(3分)下列句子中没有语病的一项是()A.能否把爱国主义教育作为永恒主题,是培养青年爱国情怀的重要途径。
B.波澜壮阔的“五四运动”,激发了中国人民和中华民族实现民族复兴。
C.“一带一路”将在非洲这片充满潜力的土地上,结出更多丰硕的果实。
D.许多内地教师心怀理想,奔赴新疆,开创新时代教育援疆的壮丽画卷。
5.(3分)填入下列文段横线处的同语,顺序最恰当的一项是()徜徉于宁静之中,人生就多了一份的韵律、多了一种意境。
在月下,感受大地之精美,望、揽听天籁之音、赏梅花弄影;在雨中,感受自然之清新,观梧桐细雨、眺、闻、恋雨打琵琶,宁静如诗。
①空中响雷②繁星排空③远山迷蒙④夜风入怀A.②④③①B.③①②④C.①②③④D.③④①②6.(5分)根据要求,回答下列有关文化常识、文学知识及名著的问题。
2019年新疆乌鲁木齐市中考模拟数学试题(附带超详细解析)
装…………○…………订姓名:___________班级:___________考装…………○…………订绝密★启用前2019年新疆乌鲁木齐市中考模拟数学试题注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明 一、单选题1.下列所给的图案中,既是轴对称图形,又是中心对称图形的是( )A .B .C .D .2.下列事件中,属于必然事件的是( ) A .三角形的外心到三边的距离相等 B .某射击运动员射击一次,命中靶心 C .任意画一个三角形,其内角和是 180° D .抛一枚硬币,落地后正面朝上3.二位同学在研究函数2(3)()y a x x a =+-(a 为实数,且0a ≠)时,甲发现当 0<a <1时,函数图像的顶点在第四象限;乙发现方程2(3)()50a x x a+-+=必有两个不相等的实数根,则( ) A .甲、乙的结论都错误 B .甲的结论正确,乙的结论错误 C .甲、乙的结论都正确D .甲的结论错误,乙的结论正确4. 如图,AB 是⊙O 直径,若∠AOC =100°,则∠D 的度数是( )○…………外…○…………装……………订……………………○……※※请※※不※※要※※※线※※内※※答※※题※○…………内…○…………装……………订……………………○……A .50°B .40°C .30°D .45°5.用配方法解一元二次方程2610x x -+=,此方程可化为的正确形式是( ) A .2(3)10x +=B .2(3)8x +=C .2(3)10x -=D .2(3)8x -=6.已知二次函数的图象(0≤x≤4)如图,关于该函数在所给自变量的取值范围内,下列说法正确的是( )A .有最大值 1.5,有最小值﹣2.5B .有最大值 2,有最小值 1.5C .有最大值 2,有最小值﹣2.5D .有最大值 2,无最小值7.如图将OABC 绕点A 逆时针旋转90︒得到相应的,OADE 若点D 恰在线段BC 的延长线上,则下列选项中错误的是( )A .BAD CAE ∠=∠B .120ACB ∠=oC .45ABC ∠=oD .90CDE ∠=o8.如图,AB ,BC 是⊙O 的两条弦,AO ⊥BC ,垂足为D ,若⊙O 的半径为5,BC =8,则AB 的长为( )…………○…………装…………○………学校:___________姓名:___________班级:_____…………○…………装…………○………A .8 B .10C .D .9.某省加快新旧动能转换,促进企业创新发展.某企业一月份的营业额是1000万元,月平均增长率相同,第一季度的总营业额是3990万元.若设月平均增长率是x ,那么可列出的方程是( ) A .1000(1+x )2=3990B .1000+1000(1+x )+1000(1+x )2=3990C .1000(1+2x )=3990D .1000+1000(1+x )+1000(1+2x )=399010.如图四边形ABCD 中,AD ∥BC ,∠A =90°,已知AD =4,AB =,∠C =30°,连接BD ,P 为BD 边上的一个动点.现让P 点从B 点出发沿着B →D (P 不与点B 重合)以1cm /s 的速度运动,Q 为折线BCD 上一动点,现让Q 点从B 出发沿着折线BCD 以3cm /s 的速度运动当其中一个点到达终点时另一点也停止运动.则△PBQ 与△BCD 重合部分的面积S 随时间t )( )A .B .C .D .第II 卷(非选择题)请点击修改第II 卷的文字说明 二、填空题…………装……………订…………○…※请※※不※※要※※在※※装※内※※答※※题※※…………装……………订…………○…11.某班级中有男生和女生各若干,如果随机抽取1人,抽到男生的概率是35,那么抽到女生的概率是_____.12.若关于x的一元二次方程x2-3x+m=0的一个实数根是1,则m的值为_____.13.已知圆锥的底面半径为3,母线长为7,则圆锥的侧面积是_____.14.如图矩形ABCD中,AD=1,CD AC,将线段AC、AB分别绕点A顺时针旋转90°至AE、AF,线段AE与弧BF交于点G,连接CG,则图中阴影部分面积为_____.15.如图,在Rt△ABC中,∠ACB=90°,AC=5cm,BC=12cm,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F,则△ACF与△BDF的周长之和为_______cm.16.已知抛物线y=ax2+bx+c(a≠0)与x轴的两个交点的坐标分别是(﹣3,0),(2,0),则方程ax2+bx+c=0(a≠0)的解是_____.三、解答题17.解方程:x2+x﹣2=0.18.在4×4的方格纸中,△ABC的三个顶点都在格点上.(1)在图①中以点C为对称中心,画出与△ABC成中心对称的图形;(2)将图②中的△ABC绕点C按顺时针方向旋转90°,画出旋转后的图形.外…………○…装…………○………○…………线…………○……学____姓名:___________班级:________内…………○…装…………○………○…………线…………○……19.目前“微信”、“支付宝”、“共享单车“和“网购”给我们的生活带来了很多便利,九年级数学兴趣小组在校内对“你最认可的四大新生事物”进行调查,随机调查了m 人(每名学生必选一种且只能从这四种中选择一种),并将调查结果绘制成如下不完整的统计图. (1)根据图中信息求出m = ,n = ; (2)请你帮助他们将这两个统计图补全;(3)已知A 、B 两位同学都最认可“微信”,C 同学最认可“支付宝”,D 同学最认可“网购”,从这四名同学中抽取两名同学,请你通过树状图或表格,求出这两位同学最认可的新生事物不一样的概率.20.如图,一农户要建一个矩形猪舍,猪舍的一边利用长为15m 的住房墙,另外三边用27m 长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m 宽的门,所围矩形猪舍的长,宽分别为多少米时,猪舍面积为96m 2?21.如图,AB 是⊙O 的直径,弦EF ⊥AB ,垂足为C ,∠A =30°,连结BE ,M 为BE 的中点,连结MF ,过点F 作直线FD ∥AE ,交AB 的延长线于点D . (1)求证:FD 是⊙O 的切线; (2)若MF ,求⊙O 的半径.………○…………装…………线…………○……※※请※※不※※要※答※※题※※………○…………装…………线…………○……22.某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本. (1)当销售单价为70元时,每天的销售利润是多少?(2)求出每天的销售利润y (元)与销售单价x (元)之间的函数关系式,并求出自变量的取值范围;(3)如果该企业每天的总成本不超过7000元,那么销售单价为多少元时,每天的销售利润最大?最大利润是多少?(每天的总成本=每件的成本×每天的销售量) 23.如图,在平面直角坐标系中,抛物线C 1:y =ax 2+bx ﹣1经过点A (﹣2,1)和点B (﹣1,﹣1),抛物线C 2:y =2x 2+x +1,动直线x =t 与抛物线C 1交于点N ,与抛物线C 2交于点M .(1)求抛物线C 1的表达式;(2)直接用含t 的代数式表达线段MN 的长;(3)当△AMN 是以MN 为直角边的等腰直角三角形时,求t 的值.参考答案1.D【解析】【分析】根据中心对称图形与轴对称图形的概念对各选项进行逐一分析即可.【详解】A.不是轴对称图形,是中心对称图形,故本选项错误;B.不是轴对称图形,是中心对称图形,故本选项错误;C.是轴对称图形,但不是中心对称图形,故本选项错误;D. 既是轴对称图形,又是中心对称图形,故本选项正确;故选:D.【点睛】本题考查的是中心对称图形,轴对称图形.熟知中心对称图形与轴对称图形的概念是解答此题的关键.2.C【解析】分析:必然事件就是一定发生的事件,依据定义即可作出判断.详解:A、三角形的外心到三角形的三个顶点的距离相等,三角形的内心到三边的距离相等,是不可能事件,故本选项不符合题意;B、某射击运动员射击一次,命中靶心是随机事件,故本选项不符合题意;C、三角形的内角和是180°,是必然事件,故本选项符合题意;D、抛一枚硬币,落地后正面朝上,是随机事件,故本选项不符合题意;故选C.点睛:解决本题需要正确理解必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件.不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.3.D【解析】【分析】先根据函数的解析式可得顶点的横坐标,结合01a <<判断出横坐标可能取负值,从而判断甲不正确;再通过方程的根的判别式判断其根的情况,从而判断乙的说法. 【详解】0a ≠Q ,∴原函数定为二次函数甲:顶点横坐标为122323132222x x a a a a -+-===-01a <<Q ,13122a ∴->-,所以甲不正确乙:原方程为2(3)()50a x x a+-+=,化简得:2(32)10ax a x +--=22420(32)4(3)039a a a ∆=-+=-+>∴必有两个不相等的实数根,所以乙正确故选:D. 【点睛】本题考查二次函数图象的性质、顶点坐标、一元二次方程的根的判别式,对于一般形式20(a 0)++=≠ax bx c 有:(1)当240b ac ∆=->,方程有两个不相等的实数根;(2)当240b ac ∆=-=,方程有两个相等的实数根;(3)当240b ac ∆=-<,方程没有实数根. 4.B 【解析】 【分析】根据∠AOB=180°,∠AOC=100°,可得出∠BOC 的度数,最后根据圆周角∠BDC 与圆心角∠BOC 所对的弧都是弧BC ,即可求出∠BDC 的度数. 【详解】解:∵AB 是⊙O 直径, ∴∠AOB=180°, ∵∠AOC=100°,∴∠BOC=∠AOB -∠AOC=80°;∵¶BC所对的圆周角是∠BDC ,圆心角是∠BOC ,∴1BDC 402BOC ∠=∠=︒; 故答案选B. 【点睛】本题考查同圆或等圆中,同弧或等弧所对的圆周角是圆心角的一半,在做题时遇到已知圆心角,求圆周角的度数,可以通过计算,得出相应的圆心角的度数,即可得出圆周角的度数. 5.D 【解析】 【分析】方程常数项移到右边,两边加上9变形即可得到结果. 【详解】解:方程移项得:x 2-6x=-1, 配方得:x 2-6x+9=8,即(x-3)2=8, 故选D . 【点睛】本题考查了解一元二次方程-配方法,熟练掌握完全平方公式是解题的关键. 6.C 【解析】 【详解】由图像可知,当x =1时,y 有最大值2;当x =4时,y 有最小值-2.5. 故选C. 7.B 【解析】 【分析】根据题意旋转前后两个三角形全等,根据旋转角为90o 度进而判断出ABD ∆等腰直角三角形,可以得出正确答案. 【详解】解:根据题意可得:90BAD CAE ∠=∠=o , 故A 正确;Q BA AD =,ABD ∴∆为等腰直角三角形,45ABC ∴∠=o ,故C 正确;45ABC ADE ∠=∠=o Q ,454590CDE ADB ADE ∴∠=∠+∠=+=o o o ,故D 正确;∴B 不正确;故答案选B. 【点睛】本题考查的是旋转和三角形结合的综合题,分析清楚题干信息是解题的关键. 8.D 【解析】 【分析】根据垂径定理求出BD ,根据勾股定理求出OD ,求出AD ,再根据勾股定理求出AB 即可. 【详解】解:∵AO ⊥BC ,AO 过O ,BC =8, ∴BD =CD =4,∠BDO =90°,由勾股定理得:OD 3==, ∴AD =OA +OD =5+3=8,在Rt △ADB 中,由勾股定理得:AB = 故选D . 【点睛】本题考查了垂径定理和勾股定理,能根据垂径定理求出BD 长是解此题的关键. 9.B 【解析】 【分析】设月平均增长的百分率是x ,则该超市二月份的营业额为100(1+x )万元,三月份的营业额为100(1+x )2万元,根据该超市第一季度的总营业额是3990万元,即可得出关于x 的一元二次方程,此题得解.【详解】解:设月平均增长的百分率是x ,则该超市二月份的营业额为100(1+x )万元,三月份的营业额为100(1+x )2万元,依题意,得1000+1000(1+x )+1000(1+x )2=3990.故选:B .【点睛】此题主要考查一元二次方程的应用,解题的关键是熟知增长率问题的求解.10.B【解析】【分析】当点Q 在BC 上运动时,211sin 322S BQ BP DBC t t =⨯⨯∠=⨯⨯;当点Q 在CD 上运动时,BCD BCQ BDQ S S S S ∆∆∆=--,即可求解.【详解】解:4=AD ,AB =BD =30ABD ∠=︒,故60DBC ∠=︒,则90BCD ∠=︒,当点Q 在BC 上运动时,211sin 322S BQ BP DBC t t =⨯⨯∠=⨯⨯; 当点Q 在CD 上运动时,如下图:则16CQ t =-,8PQ t =-,16QD t =+,BCD BCQ BDQ S S S S ∆∆∆=--11118(8)(16)16(16)2222t t t =⨯⨯-+-⨯⨯-⨯21(122t t =-++ 故选:B .【点睛】本题考查的是动点图象问题,涉及到二次函数、解直角三角形等知识,此类问题关键是:弄清楚不同时间段,图象和图形的对应关系,进而求解.11.25【解析】【分析】由于抽到男生的概率与抽到女生的概率之和为1,据此即可求出抽到女生的概率.【详解】 解:∵抽到男生的概率是35, ∴抽到女生的概率是1-35=25. 故答案为:25. 【点睛】此题考查的是求概率问题,掌握抽到男生和抽到女生的概率之和等于1是解决此题的关键. 12.2【解析】【分析】将实数根1代入x 2-3x+m=0,计算即可得到答案.【详解】将实数根1代入x 2-3x+m=0得到1-3+m=0,解得m=2.【点睛】本题考查一元二次方程的解,解题的关键是将根代入原方程.13.21π.【解析】【分析】利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式计算.【详解】 解:圆锥的侧面积=12×2π×3×7=21π. 故答案为:21π.【点睛】本题考查圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.14.2π【解析】试题分析:在矩形ABCD 中,∵AD=1,∵AC=2,tan ∠CAB=BC AD AB CD = ∴∠CAB=30°,∵线段AC 、AB 分别绕点A 顺时针旋转90°至AE 、AF ,∴∠CAE=∠BAF=90°,∴∠BAG=60°,∵∴阴影部分面积=S △ABC +S 扇形ABG ﹣S △ACG =12×3×1+﹣12×3×2=2π﹣3. 考点:扇形面积的计算;矩形的性质;旋转的性质.15.42.【解析】试题分析:∵将△ABC 绕点B 顺时针旋转60°,得到△BDE ,∴△ABC ≌△BDE ,∠CBD=60°,∴BD=BC=12cm ,∴△BCD 为等边三角形,∴CD=BC=CD=12cm ,在Rt △ACB 中,AB==13,△ACF 与△BDF 的周长之和=AC+AF+CF+BF+DF+BD=AC+AB+CD+BD=5+13+12+12=42(cm ),故答案为42. 考点:旋转的性质.16..x 1=-3,x 2=2【解析】【详解】解:∵抛物线y =ax 2+bx +c (a ≠0)与x 轴的两个交点的坐标分别是(−3,0),(2,0),∴当x =−3或x =2时,y =0,即方程20ax bx c ++=的解为123 2.x x =-=, 故答案为:123 2.x x =-=, 17.x 1=1,x 2=﹣2.【解析】分析:方程左边利用十字相乘法分解因式后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.本题解析:分解因式得:(x ﹣1)(x+2)=0,可得x ﹣1=0或x+2=0,解得:x 1=1,x 2=﹣2. 18.(1)见解析;(2)见解析【解析】【分析】(1)根据中心对称的性质画出△CA′B′即可得;(2)根据图形旋转的性质画出△CA″B″即可得.【详解】解:(1)如图①,△CA ′B ′即为所求;(2)如图②,△CA ″B ″即为所求.【点睛】本题考查的是作图-旋转变换,熟知图形旋转不变性的性质是解答此题的关键.19.(1)100、35;(2)见解析;(3)5 6【解析】【分析】(1)由共享单车人数及其百分比求得总人数m,用支付宝人数除以总人数可得其百分比n 的值;(2)总人数乘以网购人数的百分比可得其人数,用微信人数除以总人数求得其百分比即可补全两个图形;(3)根据题意画出树状图得出所有等可能结果,从中找到这两位同学最认可的新生事物不一样的结果数,再根据概率公式计算可得.【详解】解:(1)∵被调查的总人数m=10÷10%=100人,∴支付宝的人数所占百分比n%=35100×100%=35%,即n=35,故答案为:100,35;(2)网购人数为100×15%=15人,微信对应的百分比为40100×100%=40%,补全图形如下:(3)根据题意画树状图如下:共有12种情况,这两位同学最认可的新生事物不一样的有10种,所以这两位同学最认可的新生事物不一样的概率为1012=56.【点睛】本题考查的是用列表法或画树状图法求概率以及扇形统计图与条形统计图的知识.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比. 20.所围矩形猪舍的长为12m 、宽为8m【解析】【分析】设矩形猪舍垂直于住房墙一边长为xm 可以得出平行于墙的一边的长为(27﹣2x+1)m .根据矩形的面积公式建立方程求出其解就可以了.【详解】解:设矩形猪舍垂直于住房墙一边长为xm 可以得出平行于墙的一边的长为(27﹣2x+1)m ,由题意得x (27﹣2x+1)=96,解得:x 1=6,x 2=8,当x =6时,27﹣2x+1=16>15(舍去),当x =8时,27﹣2x+1=12.答:所围矩形猪舍的长为12m 、宽为8m .【点睛】本题考查了列一元二次方程解实际问题的运用,矩形的面积公式的运用及一元二次方程的解法的运用,解答时寻找题目的等量关系是关键.21.(1)见解析;(2)⊙O 的半径为2.【解析】【分析】(1)连接OE ,OF ,如图,利用等腰三角形的性质得到DOF DOE =∠∠.而2DOE A =∠∠,所以2DOF α=∠,再根据切线的性质得90OFD ∠=︒即可;(2)连接OM ,如图,利用圆周角定理得到90AEB =︒∠.再证明//OM AE 得到30MOB A ∠=∠=︒.而260DOF A ∠=∠=︒,所以90MOF ∠=︒,设O e 的半径为r ,利用含30度的直角三角形三边的关系得OM ,然后根据勾股定理得到结论.【详解】(1)证明:连接OE ,OF ,如图1,∵EF ⊥AB ,AB 是⊙O 的直径,∴∠DOF =∠DOE ,∵∠DOE =2∠A ,∠A =30°,∴∠DOF =60°,∵∠D =30°,∴∠OFD =90°.∴OF ⊥FD .∴FD 为⊙O 的切线;(2)连接OM .如图2所示:∵AB 为⊙O 的直径,∴O 为AB 中点,∠AEB =90°.∵M 为BE 的中点,∴OM ∥AE ,OM =12AE , ∵∠A =30°,∴∠MOB =∠A =30°.∵∠DOF =2∠A =60°,∴∠MOF =90°,∴OM 2+OF 2=MF 2.设⊙O 的半径为r .∵∠AEB =90°,∠A =30°,∴BE =12AB =r ,AE ,∴OM =12AE ,∵FM ,)2+r 2)2. 解得r =2(舍去负根),∴⊙O 的半径为2.【点睛】本题考查了切线的判定与性质、圆周角定理和垂径定理、直角三角形的性质以及勾股定理等知识;熟练掌握切线的判定与性质和勾股定理是解题的关键.22.(1)4000;(2)y=-52800275000+-=(50≤x≤100);(3)销售单价为82x x元时,每天的销售利润最大,最大利润为4480元.【解析】【分析】(1)根据“利润=(售价-成本)×销售量”即可求解;(2))根据“利润=(售价-成本)×销售量”即可求得函数关系式,根据售价不小于50元即可确定x的取值范围;(3)先由“每天的总成本不超过7000元”列出关于x的不等式50(-5x+550)≤7000,通过解不等式来求x的取值范围,再把(2)中的二次函数解析式转化为顶点式方程,利用二次函数图象的性质进行解答即可.【详解】解:(1)当销售单价为70元时,每天的销售利润是:[50+(100-70)]×(70-50)=4000(元)(2)由题得 y=[50+5(100-x )](x-50)=-5280027500x x +-由x≥50,100-x≥50得50≤x≤100∴y=-5280027500x x +-(50≤x≤100)(3)∵该企业每天的总成本不超过7000元∴50[50+5(100-x )]≤7000解得x≥82由(2)可知50≤x≤100∴82≤x≤100∵抛物线y=-52800275000x x +-=的对称轴为x=80且a =-5<0∴抛物线开口向下,在对称轴右侧,y 随x 增大而减小.∴当x =82时,y 最大=4480,即 销售单价为82元时,每天的销售利润最大,最大利润为4480元.考点:二次函数的应用.23.(1)y =x 2+x ﹣1;(2)MN =t 2+2;(3)t =0或1【解析】【分析】(1)将点A 、B 的坐标代入抛物线表达式,即可求解;(2)点M 、N 的坐标分别为:(t ,2t 2+t+1)、(t ,t 2+t-1),即可求解;(3)分∠ANM=90°、∠AMN=90°两种情况,分别求解即可.【详解】解:(1)将点A 、B 的坐标代入抛物线表达式得:421111a b a b --=⎧⎨--=-⎩,解得:11a b =⎧⎨=⎩, 故抛物线C 1的表达式为:y =x 2+x ﹣1;(2)点M 、N 的坐标分别为:(t ,2t 2+t +1)、(t ,t 2+t ﹣1),则MN=(2t2+t+1)﹣(t2+t﹣1)=t2+2;(3)①当∠ANM=90°时,AN=MN,AN=t﹣(﹣2)=t+2,MN=t2+2,t=t2+2,解得:t=0或1(舍去0),故t=1;②当∠AMN=90°时,AM=MN,AM=t+2=MN=t2+2,解得:t=0或1(舍去1),故t=1;综上,t=0或1.【点睛】本题考查的是二次函数综合运用,涉及到一次函数、等腰三角形的性质等,其中(3),要注意分类求解,避免遗漏.。
新疆兵团二中2019年中考全疆统一卷预测卷(2)(难度8:1:1)解析版
2019年新疆初中学业水平考试预测卷(2)一.选择题(本大题共9小题,每小题5分,共45分) 1. 在0,-1,﹣2,3这四个数中,最小的数是( )A .0B .1C .﹣2D .3 答案:C .【分析】根据有理数大小比较,正数都大于负数,两个负数绝对值大的反而小. 【解答】-1与-2中,-2的绝对值大,所以反而小。
故选:C .2. 中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划,“一带一路”地区覆盖总人口约为4400000000人,这个数用科学记数法表示为( ) A .44×108 B .4.4×109 C .4.4×108 D .4.4×1010 答案:B .【分析】根据科学记数法表示法:对于任意实数有:10na ⨯(n 为整数),且1||10a ≤<.【解答】 4400000000=4.4×109 故选:B .3.某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“国”字所在面相对的面上的汉字是( )A .厉B .害C .了D .我【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答. 【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形, “的”与“害”是相对面,“了”与“厉”是相对面,“我”与“国”是相对面.故选:D.4.如图把一个直角三角尺的直角顶点放在直尺的一边上,若∠1=50°,则∠2=()A.20°B.30°C.40°D.50°【分析】根据两直线平行,同位角相等可得∠3=∠1,再根据平角等于180°列式计算即可得解.【解答】解:∵直尺对边互相平行,∴∠3=∠1=50°,∴∠2=180°﹣50°﹣90°=40°.故选:C.5.若一组数据3、4、5、x、6、7的平均数是5,则x的值是()A.4 B.5 C.6 D.7【分析】根据平均数的定义计算即可;【解答】解:由题意(3+4+5+x+6+7)=5,解得x=5,故选:B.6.篮球比赛规定:胜一场得3分,负一场得1分,某篮球队共进行了6场比赛,得了12分,该队获胜的场数是()A.2 B.3 C.4 D.5【分析】设该队获胜x场,则负了(6﹣x)场,根据总分=3×获胜场数+1×负了的场数,即可得出关于x的一元一次方程,解之即可得出结论.【解答】解:设该队获胜x场,则负了(6﹣x)场,根据题意得:3x+(6﹣x)=12,解得:x=3.答:该队获胜3场.故选:B.7.如图,一个函数的图象由射线BA、线段BC、射线CD组成,其中点A(﹣1,2),B(1,3),C(2,1),D(6,5),则此函数()A.当x<1时,y随x的增大而增大B.当x<1时,y随x的增大而减小C.当x>1时,y随x的增大而增大 D.当x>1时,y随x的增大而减小【分析】根据函数图象和题目中的条件,可以写出各段中函数图象的变化情况,从而可以解答本题.【解答】解:由函数图象可得,当x<1时,y随x的增大而增大,故选项A正确,选项B错误,当1<x<2时,y随x的增大而减小,当x>2时,y随x的增大而增大,故选项C、D错误,故选:A.8.如图,正方形ABCD中,AB=6,G是BC的中点.将△ABG沿AG对折至△AFG,延长GF交DC于点E,则DE的长是()A.1 B.1.5 C.2 D.2.5【分析】根据翻折变换的性质和正方形的性质可证Rt△AFE≌Rt△ADE;在直角△ECG中,根据勾股定理即可求出DE的长.【解答】解:∵AB=AD=AF,∠D=∠AFE=90°,在Rt△ABG和Rt△AFG中,∵AE AE AF AD=⎧⎨=⎩,∴Rt△AFE≌Rt△ADE,∴EF=DE,设DE=FE=x,则EC=6﹣x.∵G为BC中点,BC=6,∴CG=3,在Rt△ECG中,根据勾股定理,得:(6﹣x)2+9=(x+3)2,解得x=2.则DE=2.故选:C.9.如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为()A.5 B.2 C 52.D.2【分析】通过分析图象,点F从点A到D用as,此时,△FBC的面积为a,依此可求菱形的高DE,再由图象可知,BD=,应用两次勾股定理分别求BE和a.【解答】解:过点D作DE⊥BC于点E由图象可知,点F由点A到点D用时为as,△FBC的面积为acm2.∴AD=a ∴12DE AD∴DE=2 当点F从D到B时,用s ∴BD= Rt△DBE中,BE=2222(5)21BD DE BD BE-=-=-=∵ABCD是菱形∴EC=a﹣1,DC=aRt△DEC中,a2=22+(a﹣1)2 解得a=5 2故选:C.二.填空题(本大题共6小题,每小题5分,共30分)10.已知代数式a+b=3,则8-2a-2b=_______【分析】本题考察代数式求值,可用整体代换的思想或特解法.【解答】因为a+b=3,所以:8-2a-2b=8-2(a+b)=8-2×3=6故答案为:611.在平面直角坐标系中,将点(3,﹣2)先向右平移2个单位长度,再向上平移3个单位长度,则所得点的坐标是.【分析】直接利用平移的性质得出平移后点的坐标即可.【解答】解:∵将点(3,﹣2)先向右平移2个单位长度,∴得到(5,﹣2),∵再向上平移3个单位长度,∴所得点的坐标是:(5,1).故答案为:(5,1).12.已知A(﹣4,y1),B(﹣1,y2)是反比例函数y=﹣图象上的两个点,则y1与y2的大小关系为.【分析】根据反比例函数的性质和题目中的函数解析式可以判断y1与y2的大小,从而可以解答本题.【解答】解:∵反比例函数y=4x-,﹣4<0,∴在每个象限内,y随x的增大而增大,∵A(﹣4,y1),B(﹣1,y2)是反比例函数y=4x-图象上的两个点,﹣4<﹣1,∴y1<y2,故答案为:y1<y2.13.如图,在⊙O中,OC⊥AB,∠ADC=32°,则∠OBA的度数是_______【答案】26°【分析】根据垂径定理,可得=,∠OEB=90°,根据圆周角定理,可得∠3,根据直角三角形的性质,可得答案.【解答】解:如图,由OC⊥AB,得=,∠OEB=90°.∴∠2=∠3.∵∠2=2∠1=2×32°=64°.∴∠3=64°,在Rt△OBE中,∠OEB=90°,∴∠B=90°﹣∠3=90°﹣64°=26°,故选:26°.14.如图是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120m,DC=60m,EC=50m,求得河宽AB=m.【答案】100【分析】由两角对应相等可得△BAD∽△CED,利用对应边成比例可得两岸间的大致距离AB.【解答】解:∵∠ADB=∠EDC,∠ABC=∠ECD=90°,∴△ABD∽△ECD,∴,,解得:AB=(米).故答案为:100.15. 如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,连接BQ.若PA=6,PB=8,PC=10,则四边形APBQ的面积为.【答案】24+93.【分析】本题利用旋转不变性,等边三角形性质,勾股定理的逆定理可得; 【解答】解:连接PQ,∵AP=AQ 且∠PAQ =60°, ∴△APQ 是等边三角形, ∴PQ =PA =6 ∵∠BAC =∠PAQ =60°,∴∠CAP =∠BAQ∴△ACP ≌△ABQ(SAS) ∴AB =AC,BQ =CP =10 ∴PB 2+PQ 2=BQ 2, ∴△PBQ 是直角三角形因为四边形APBQ 的面积为△PBQ 与△APQ 面积之和 所以:四边形APBQ 的面积为:213866249324⨯⨯+⨯=+三.解答题(本大题共8小题,共75分)16. (本题6分)计算:101()|3|12(1)2π---++-.【答案】3+3.【解析】实数的运算;零指数幂;负整数指数幂根据负整数指数幂,去绝对值,二次根式的化简以及零指数幂的计算法则计算.【解答】:原式=2.17.(本题6分)解不等式组233(1)(5)0x xx x-<⎧⎨---≥⎩,并把它的解集在数轴上表示出来.【答案】﹣1≤x<3.解集表示见解析.【解析】:首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集.【解答】:解不等式①,得x<3.解不等式②,得x≥﹣1.所以,不等式组的解集是﹣1≤x<3.它的解集在数轴上表示出来为:18.(本题8分)用A、B两种机器人搬运大米,A型机器人比B型机器人每小时多搬运20袋大米,A型机器人搬运700袋大米与B型机器人搬运500袋大米所用时间相等.求A、B型机器人每小时分别搬运多少袋大米.【答案】A型机器人每小时搬大米70袋,则B型机器人每小时搬运50袋.【解析】试题分析:工作效率:设A型机器人每小时搬大米x袋,则B型机器人每小时搬运(x-20)袋;工作量:A型机器人搬运700袋大米,B型机器人搬运500袋大米;工作时间就可以表示为:A型机器人所用时间为:700x,B型机器人所用时间为:50020x-,由所用时间相等,建立等量关系;【解答】:设A型机器人每小时搬大米x袋,则B型机器人每小时搬运(x﹣20)袋,依题意得:700x=50020x-,解这个方程得:x=70经检验x=70是方程的解,所以x﹣20=50.答:A型机器人每小时搬大米70袋,则B型机器人每小时搬运50袋.19.(本题8分)如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC 上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处.(1)求证:四边形AECF是平行四边形;(2)若AB=6,AC=10,求四边形AECF的面积.【答案】(1)证明略.(2)四边形AECF面积为30【解析】(1)首先由矩形的性质和折叠的性质证得AB=CD,AD∥BC,∠ANF=90°,∠CME=90°,易得AN=CM,可得△ANF≌△CME(ASA),由平行四边形的判定定理可得结论;(2)由AB=6,AC=10,可得BC=8,设CE=x,则EM=8﹣x,CM=10﹣6=4,在Rt△CEM 中,利用勾股定理可解得x,由平行四边形的面积公式可得结果.【解答】(1)证明:∵折叠,∴AM=AB,CN=CD,∠FNC=∠D=90°,∠AME=∠B=90°,∴∠ANF=90°,∠CME=90°,∵四边形ABCD为矩形,∴AB=CD,AD∥BC,∴AM=CN,∴AM﹣MN=CN﹣MN,即AN=CM,在△ANF和△CME中,FAN EMC AN CMANF CME ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ANF≌△CME(ASA),∴AF=CE,又∵AF∥CE,∴四边形AECF是平行四边形;(2)解:∵AB=6,AC=10,∴BC=8,设CE=x,则EM=8﹣x,CM=10﹣6=4,在Rt△CEM中,(8﹣x)2+42=x2,解得:x=5,∴四边形AECF的面积的面积为:EC•AB=5×6=30.20.(本题10分)中华文化,源远流长,在文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”,某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题做法全校学生中进行了抽样调查,根据调查结果绘制城如图所示的两个不完整的统计图,请结合图中信息解决下列问题:(1)本次调查所得数据的众数是部,中位数是部,扇形统计图中“1部”所在扇形的圆心角为度.(2)请将条形统计图补充完整;(3)没有读过四大古典名著的两名学生准备从四大固定名著中各自随机选择一部来阅读,则他们选中同一名著的概率为.【答案】(1)1,2,126;(2)作图见解析;(3)14.【解析】(1)先根据调查的总人数,求得1部对应的人数,进而得到本次调查所得数据的众数以及中位数,根据扇形圆心角的度数=部分占总体的百分比×360°,即可得到“1部”所在扇形的圆心角;(2)根据1部对应的人数为40﹣2﹣10﹣8﹣6=14,即可将条形统计图补充完整;(3)根据树状图所得的结果,判断他们选中同一名著的概率;【解答】(1)调查的总人数为:10÷25%=40,∴1部对应的人数为40-2-10-8-6=14∴本次调查所得数据众数是1部,中位数为2部,扇形统计图中“1部”所在扇形的圆心角为:1436012640⨯︒=︒所以答案为:1,2,126(2)条形统计图如图所示:(3)将《西游记》、《三国演义》、《水浒传》、《红楼梦》分别记作A,B,C,D,画树状图可得:共有16种等可能的结果,其中选中同一名著的有4种,故P(两人选中同一名著)=416=14.故答案为:14.21.(本题12分)如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.【答案】两点间的距离为30米.【解析】直接利用等腰三角形的判定与性质得出DE=AE=20,进而求出EF的长,再得出四边形ACDF为矩形,则CD=AF=AE+EF求出答案.【解答】解:过点D作l1的垂线,垂足为F,∵∠DEB=60°,∠DAB=30°,∴∠ADE=∠DEB﹣∠DAB=30°,∴△ADE为等腰三角形,∴DE=AE=20,在Rt△DEF中,EF=DE•cos60°=20×=10,∵DF⊥AF,∴∠DFB=90°,∴AC∥DF,由已知l1∥l2,∴CD∥AF,∴四边形ACDF为矩形,CD=AF=AE+EF=30,答:C、D两点间的距离为30m.22.(本题12分)某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销x件.已知产销两种产品的有关信息如下表:其中a为常数,且3≤a≤5.(1)若产销甲、乙两种产品的年利润分别为y1万元、y2万元,直接写出y1、y2与x的函数关系式;(2)分别求出产销两种产品的最大年利润;(3)为获得最大年利润,该公司应该选择产销哪种产品?请说明理由.【答案】.(1)y1=(6-a)x-20(0<x≤200),y2=-0.05x²+10x-40(0<x≤80)(2)甲种产品的最大年利润为(1180-200a)万元,产销乙种产品的最大年利润为440万元(3)当3≤a<3.7时,生产甲产品的利润高;当a=3.7时,生产甲乙两种产品的利润相同;当3.7<a≤5时,上产乙产品的利润高.【解析】本题考察一次函数、二次函数及最大值.【解答】解:(1)y1=(6-a)x-20(0<x≤200),y2=-0.05x²+10x-40(0<x≤80);(2)甲产品:∵3≤a≤5,∴6-a>0,∴y1随x的增大而增大.∴当x=200时,y1max=1180-200a(3≤a≤5)乙产品:y2=-0.05x²+10x-40(0<x≤80)∴当0<x≤80时,y2随x的增大而增大.当x=80时,y2max=440(万元).∴产销甲种产品的最大年利润为(1180-200a)万元,产销乙种产品的最大年利润为440万元;(3)1180-200>440,解得3≤a<3.7时,此时选择甲产品;1180-200=440,解得a=3.7时,此时选择甲乙产品;1180-200<440,解得3.7<a≤5时,此时选择乙产品.∴当3≤a<3.7时,生产甲产品的利润高;当a=3.7时,生产甲乙两种产品的利润相同;当3.7<a≤5时,上产乙产品的利润高.23.(本题13分)如图,已知抛物线y=﹣14x2﹣12x+2与x轴交于A、B两点,与y轴交于点C(1)求点A,B,C的坐标;(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M 的坐标;若不存在,请说明理由.【答案】A(2,0),B(-4,0),C(0,2)【解析】本题考察二次函数基本性质、二次函数背景下平行四边形、相似三角形点的存在性问题;【解答】(1)令y=0得2112042x x --+=,x=-4或2 所以A (2,0),B (-4,0) 令x=0,得y=2 点 C (0,2) (2)当AB 为平行四边形的边, ∵AB=EF=6,对称轴x=﹣1, ∴点E 的横坐标为﹣7或5, ∴点E 坐标(﹣7,﹣274)或(5,﹣274),此时点F (﹣1,﹣274), ∴以A ,B ,E ,F 为顶点的平行四边形的面积=6×274=812. 当AB 为平行四边形的对角线时,点F 为抛物线的顶点,即F (-1,94),所以点E 的坐标为(-1,-94), ∴以A ,B ,E ,F 为顶点的平行四边形的面积=CN=19276222⨯⨯=, .(3)如图所示,①当C 为顶点时,CM 1=CA ,CM 2=CA ,作M 1N ⊥OC 于N ,在RT △CM 1N 中,=,∴点M1坐标(﹣1,),点M2坐标(﹣1,2. ②当M 3为顶点时,∵直线AC 解析式为y=﹣x+1, 线段AC 的垂直平分线为y=x , ∴点M 3坐标为(﹣1,﹣1). ③当点A 为顶点的等腰三角形不存在.综上所述点M 坐标为(﹣1,﹣1)或(﹣1, 1.2).。
新疆兵团二中2019年中考全疆统一卷预测卷(2)(难度8:1:1)正卷
2019年新疆初中学业水平考试预测卷(2)一.选择题(本大题共9小题,每小题5分,共45分)1. 在0,-1,﹣2,3这四个数中,最小的数是()A .0 B.1 C.﹣2 D .32. 中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划,“一带一路”地区覆盖总人口约为4400000000人,这个数用科学记数法表示为()A .44×108B.4.4×109C.4.4×108D.4.4×10103.某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“国”字所在面相对的面上的汉字是()A .厉B .害C .了D .我4.如图把一个直角三角尺的直角顶点放在直尺的一边上,若∠1=50°,则∠2=()A .20°B .30°C .40°D .50°5.若一组数据3、4、5、x 、6、7的平均数是5,则x 的值是()A .4B.5 C.6 D.76.篮球比赛规定:胜一场得3分,负一场得1分,某篮球队共进行了6场比赛,得了12分,该队获胜的场数是()A .2B.3 C.4 D.57.如图,一个函数的图象由射线BA 、线段BC 、射线CD 组成,其中点A (﹣1,2),B (1,3),C (2,1),D (6,5),则此函数()A .当x <1时,y 随x 的增大而增大B .当x <1时,y 随x 的增大而减小C .当x >1时,y 随x 的增大而增大D .当x >1时,y 随x 的增大而减小8.如图,正方形ABCD 中,AB=6,G 是BC 的中点.将△ABG 沿AG 对折至△AFG ,延长GF 交DC 于点E ,则DE 的长是()A .1B.1.5 C.2D.2.59.如图1,点F 从菱形ABCD 的顶点A 出发,沿A →D →B 以1cm/s 的速度匀速运动到点B ,图2是点F 运动时,△FBC 的面积y (cm 2)随时间x (s )变化的关系图象,则a 的值为()A .B .2C .D.2二.填空题(本大题共6小题,每小题5分,共30分) 10.已知代数式a +b =3,则 8-2a -2b =_______ 11.在平面直角坐标系中,将点(3,﹣2)先向右平移2个单位长度,再向上平移3个单位长度,则所得点的坐标是.12.已知A (﹣4,y 1),B (﹣1,y 2)是反比例函数y=﹣图象上的两个点,则y 1与y 2的大小关系为.13.如图,在⊙O 中,OC ⊥AB ,∠ADC=32°,则∠OBA 的度数是_______第4题第3题第9题第7题第8题第13题14.如图是测量河宽的示意图,AE 与BC 相交于点D ,∠B=∠C=90°,测得BD=120m ,DC=60m ,EC=50m ,求得河宽AB=m .15. 如图,P 是等边三角形ABC 内一点,将线段AP 绕点A 顺时针旋转60°得到线段AQ ,连接BQ .若PA=6,PB=8,PC=10,则四边形APBQ 的面积为.三.解答题(本大题共8小题,共75分) 16. (本题6分)计算:11()|3|12(1)2.17.(本题6分)解不等式组233(1)(5)x xxx,并把它的解集在数轴上表示出来.18.(本题8分)用A 、B 两种机器人搬运大米,A 型机器人比B 型机器人每小时多搬运20袋大米,A 型机器人搬运700袋大米与B 型机器人搬运500袋大米所用时间相等.求A 、B型机器人每小时分别搬运多少袋大米.19.(本题8分)如图,AC 为矩形ABCD 的对角线,将边AB 沿AE 折叠,使点B 落在AC 上的点M 处,将边CD 沿CF 折叠,使点D 落在AC 上的点N 处.(1)求证:四边形AECF 是平行四边形;(2)若AB=6,AC=10,求四边形AECF 的面积.20.(本题10分)中华文化,源远流长,在文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”,某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题做法全校学生中进行了抽样调查,根据调查结果绘制城如图所示的两个不完整的统计图,请结合图中信息解决下列问题:(1)本次调查所得数据的众数是部,中位数是部,扇形统计图中“1部”所在扇形的圆心角为度.(2)请将条形统计图补充完整;(3)没有读过四大古典名著的两名学生准备从四大固定名著中各自随机选择一部来阅读,则他们选中同一名著的概率为.第14题第15题21.(本题12分)如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.22.(本题12分)某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销x件.已知产销两种产品的有关信息如下表:产品每件售价(万元)每件成本(万元)每年其他费用(万元)每年最大产销量(件)甲 6 a 20 200乙20 10 40+0.05x2 80其中a为常数,且3≤a≤5.(1)若产销甲、乙两种产品的年利润分别为y1万元、y2万元,直接写出y1、y2与x的函数关系式;(2)分别求出产销两种产品的最大年利润;(3)为获得最大年利润,该公司应该选择产销哪种产品?请说明理由.23.(本题13分)如图,已知抛物线y=﹣14x2﹣12x+2与x轴交于A、B两点,与y轴交于点C(1)求点A,B,C的坐标;(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M 的坐标;若不存在,请说明理由.2019年新疆初中学业水平考试预测卷(2)答案一.选择题(本题共9小题,每小题5分,共45分)题号 1 2 3 4 5 6 7 8 9答案 C B D C B B A C C 二.填空题(本题共6小题,每小题5分,共30分)10.6 11.(5,1) 12.y1<y2. 13.26° 14.100. 15.24+93.三.解答题16.解:原式=2﹣3+23+1=3+3.17.解:解不等式①,得x<3.解不等式②,得x≥﹣1.所以,不等式组的解集是﹣1≤x<3.它的解集在数轴上表示出来为:18.试题分析:工作效率:设A型机器人每小时搬大米x袋,则B型机器人每小时搬运(x-20)袋;工作量:A型机器人搬运700袋大米,B型机器人搬运500袋大米;工作时间就可以表示为:A型机器人所用时间为:700x,B型机器人所用时间为:50020x,由所用时间相等,建立等量关系;A试题解析:设A型机器人每小时搬大米x袋,则B型机器人每小时搬运(x﹣20)袋,依题意得:700x=50020x,解这个方程得:x=70经检验x=70是方程的解,所以x﹣20=50.答:A型机器人每小时搬大米70袋,则B型机器人每小时搬运50袋.考点:分式方程的应用.19【解答】(1)证明:∵折叠,∴AM=AB,CN=CD,∠FNC=∠D=90°,∠AME=∠B=90°,∴∠ANF=90°,∠CME=90°,∵四边形ABCD为矩形,∴AB=CD,AD∥BC,∴AM=CN,∴AM﹣MN=CN﹣MN,即AN=CM,在△ANF和△CME中,,FAN EMCAN CMANF CME∴△ANF≌△CME(ASA),∴AF=CE,又∵AF∥CE,∴四边形AECF是平行四边形;(2)解:∵AB=6,AC=10,∴BC=8,设CE=x,则EM=8﹣x,CM=10﹣6=4,在Rt△CEM中,(8﹣x)2+42=x2,解得:x=5,∴四边形AECF的面积的面积为:EC?AB=5×6=30.20【解答】(1)调查的总人数为:10÷25%=40,∴1部对应的人数为40-2-10-8-6=14∴本次调查所得数据众数是1部,中位数为2部,扇形统计图中“1部”所在扇形的圆心角为:1436012640所以答案为:1,2,126(2)条形统计图如图所示:(3)将《西游记》、《三国演义》、《水浒传》、《红楼梦》分别记作A,B,C,D,画树状图可得:共有16种等可能的结果,其中选中同一名著的有4种,故P(两人选中同一名著)=416=14.故答案为:14.21.【解答】解:过点D作l1的垂线,垂足为F,∵∠DEB=60°,∠DAB=30°,∴∠ADE=∠DEB﹣∠DAB=30°,∴△ADE为等腰三角形,∴DE=AE=20,在Rt△DEF中,EF=DE?cos60°=20×=10,∵DF⊥AF,∴∠DFB=90°,∴AC∥DF,由已知l1∥l2,∴CD∥AF,∴四边形ACDF为矩形,CD=AF=AE+EF=30,答:C、D两点间的距离为30m.22.【解答】解:(1) y1=(6-a)x-20(0<x≤200),y2=-0.05x2+10x-40(0<x≤80);(2)甲产品:∵3≤a≤5,∴6-a>0,∴y1随x的增大而增大.∴当x=200时,y1max=1180-200a(3≤a≤5)乙产品:y2=-0.05x2+10x-40(0<x≤80)∴当0<x≤80时,y2随x的增大而增大.当x=80时,y2max=440(万元).∴产销甲种产品的最大年利润为(1180-200a)万元,产销乙种产品的最大年利润为440万元;(3)1180-200>440,解得3≤a <3.7时,此时选择甲产品;1180-200=440,解得a=3.7时,此时选择甲乙产品;1180-200<440,解得 3.7<a ≤5时,此时选择乙产品.∴当3≤a <3.7时,生产甲产品的利润高;当a=3.7时,生产甲乙两种产品的利润相同;当3.7<a ≤5时,上产乙产品的利润高.23.【解答】(1)令y=0得2112042xx ,x=-4或2所以A (2,0),B (-4,0)令x=0,得y=2点 C (0,2)(2)当AB 为平行四边形的边,∵AB=EF=6,对称轴x=﹣1,∴点E 的横坐标为﹣7或5,∴点E 坐标(﹣7,﹣274)或(5,﹣274),此时点F (﹣1,﹣274),∴以A ,B ,E ,F 为顶点的平行四边形的面积=6×274=812.当AB 为平行四边形的对角线时,点F 为抛物线的顶点,即F (-1,94),所以点E 的坐标为(-1,-94),∴以A ,B ,E ,F 为顶点的平行四边形的面积=22729621.(3)如图所示,①当C 为顶点时,CM1=CA ,CM2=CA ,作M1N ⊥OC 于N ,在RT △CM1N 中,CN==,∴点M1坐标(﹣1,2+),点M2坐标(﹣1,2﹣).②当M3为顶点时,∵直线AC 解析式为y=﹣x+1,线段AC 的垂直平分线为y=x ,∴点M3坐标为(﹣1,﹣1).③当点A 为顶点的等腰三角形不存在.综上所述点M 坐标为(﹣1,﹣1)或(﹣1,2+)或(﹣1.2﹣).。
2019年新疆生产建设兵团中考数学试卷(含答案与解析)
6.若关于x的一元二次方程以-1)x2+x+l=0有两个实数根,则k的取值范围是()B.k>-44C.且SID.槌。
且5447.在某篮球邀请赛中,参赛的每两个队之间都要比赛一场,共比赛36场.设有尤个队参赛,根据题意,可列方程为() A.尤(尤一1)=36 B.x(x+1)=36C.x(x—1)=36D.x(x+1)=368.如图,在△ABC中,ZC=90°,£4=30。
,以点8为圆心,适当长为半径画弧,分别交BA,BC于点N;再分别以点",N为圆心,大于-MN的长为半径画弧,两孤2交于点P,作射线BF交AC于。
.则下列说法中不正确的是()A.BP是/ABC的平分线B.AD=BDC.S^CBD:S^d=1:3D.CD=BD9.如图,正方形ABC。
的边长为2,点E是BC的中点,AE与交于点P,F是CD上一点,连接AF分别交DE于点M,N,且AF±DE,连接PN,则以下结论中:①S"4Sg;②PN=普;③囱/放弓④△双EA ope,正确的是A.①②③B.①②④C.①③④D.②③④绝密★启用前;;在------此------卷------上------答------题------无------效新疆生产建设兵团2019年初中毕业会考、高级中等学校招生考试数学(本试卷满分150分,考试时间120分钟.)一、选择题(本大题共9小题,每小题5分,共45分,在每小题列出的四个选项中,只有一项符合题目要求,请按答题卷中的要求作答。
)1.-2的绝对值是A.2B.-2C.±2D.-22.下列四个几何体中,主视图为圆的是A B C D3.如图,AB//CD,ZA=50°,则Z1的度数是4.下列计算正确的是A.a2a3=a6B.(-lab)2=4a2b2C. x2+3x2=4x4D.-6a64-2a2=-3a3)))5.甲、乙两人连续5次射击成绩如图所示,下列说法中正确的是()A.甲的成绩更稳定B.乙的成绩更稳定C.甲、乙的成绩一样稳定D.无法判断谁的成绩更稳定17.(8分)解不等式组:2x+3(x-2)<4®<x+32x-5^并把解集在数轴上表示出来.〔2318.(8分)某校为了解九年级学生每天参加体育锻炼的时间,从该校九年级学生中随机抽取20名学生进行调查,得到如下数据(单位:分钟):306070103011570607590157040751058060307045对以上数据进行整理分析,得到下列表一和表二:表一时间〃(单位:分钟)0<f<30303Y6060</<9090v120人数2a10b表二平均数中位数众数60C d 根据以上提供的信息,解答下列问题:(1)填空®a=,b=;®c=,d=;(2)如果该校现有九年级学生200名,请估计该校九年级学生每天参加体育锻炼的时间达到平均水平及以上的学生人数.数学试卷第4页(共22页)二、填空题(本大题共6小题,每小题5分,共30分。
【冲刺实验班】新疆兵团二中2019中考提前自主招生数学模拟试卷(6套)附解析
【冲刺实验班】新疆兵团二中2019中考提前自主招生数学模拟试卷(6套)附解析绝密★启用前重点高中提前招生模拟考试数学试卷(1)学校:___________姓名:___________班级:___________考号:___________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第Ⅰ卷(选择题)一.选择题(共10小题,每题4分)1.下列等式中,不一定成立的是()A.=2B.C.a=﹣D.2.中国人民银行授权中国外汇交易中心公布,2014年1月14日银行间外汇市场人民币汇率中间价为:1美元对人民币6.0930元,某上市公司持有美元资产为980万美元,用科学记数法表示其美元资产折合成人民币为()元(保留两位有效数字)A.5.97×107 B.6.0×107C.5.97×108 D.6.0×1083.如图,一条信息可通过网络线由上(A点)往下(沿箭头方向)向各站点传送,例如信息要到b2点可由经a1的站点送达,也可由经a2的站点送达,共有两条传送途径,则信息由A 点传达到d3的不同途径中,经过站点b3的概率为()A.B.C.D.4.已知x+y=,|x|+|y|=5,则x﹣y的值为()A.B.C.D.5.二次函数y=ax2+bx+c的图象如图所示(a、b、c为常数),则函数y=(4ac﹣b2)x+abc和y=在同一平面直角坐标系中的图象,可能是()A.B.C.D.6.关于x的一元二次方程mx2+x+1=0有两个不相等的同号实数根,则m的取值范围是()A.m且m≠0 B.﹣C.﹣且m≠0 D.07.由于货源紧缺,小王、小李两名商贩连续两次以不同的价格在同一公司购进了A型香米,两次的购买单价分别为a、b(a<b,单位:元/千克),小王的采购方式为:每次购进c 千克大米;小李的采购方式为:每次购进d元的大米(d>c),若只考虑采购单价,下列结论正确的是()A.小王合算 B.小李合算C.一样合算 D.无法确定谁更合算8.函数y=|x2+2x﹣3|图象的草图如图所示,则关于x的方程|x2+2x﹣3|=a(a为常数)的根的情况,描述错误的是()A.方程可能没有实数根B.方程可能有三个互不相等的实数根C.若方程只有两个实数根,则a的取值范围为:a=0D.若方程有四个实数根,记为x1、x2、x3、x4,则x1+x2+x3+x4=﹣49.如图,DE是△ABC的中位线,F为DE上一点,且EF=2DF,BF的延长线交AC于点H,CF的延长线交AB于点G,则S四边形AGFH:S△BFC=()A.1:10 B.1:5 C.3:10 D.2:510.如图,AB是⊙O的直径,AC是⊙O的弦,点D是的中点,弦DE⊥AB,垂足为点F,DE交AC于点G,EH为⊙O的切线,交AC的延长线于H,AF=3,FB=,则tan∠DEH=()A.B.C.D.第Ⅱ卷(非选择题)二.填空题(共10小题,每题4分)11.计算:(π﹣3.14)0﹣2﹣2×+(tan60°﹣2)2013(4sin30°+)2014+=.12.已知实数x,y满足方程(x2﹣4x+6)(9y2+6y+6)=10,则y x=.13.如图,正方体(图1)的展开图如图2所示,在图1中M、N分别是FG、GH的中点,CM、CN、MN是三条线段;请在图2中画出CM、CN、MN这三条线段.14.如图,在正方形ABCD中,E、F分别为AB、BC的中点,连结CE交DB、DF于G、H,则EG:GH:HC=.15.已知直线l1:y=x﹣a﹣3和直线l2:y=﹣2x+5a相交于点A (m,n),其中a为常数,且m>n>0,化简|1﹣a|﹣=.16.在平面直角坐标系内有两点A、B,其坐标为A(﹣1,﹣1),B(2,4),点M为x轴上的一个动点,若要使MB﹣MA的值最大,则点M的坐标为.17.若y关于x的函数y=(a﹣2)x2﹣2(2a﹣1)x+a(a为常数)的图象与坐标轴只有两个不同交点,则a可取的值为.18.如图,已知圆O的面积为3π,AB为圆O的直径,∠AOC=80°,∠BOD=20°,点P为直径AB上任意一点,则PC+PD 的最小值是.19.已知两个反比例函数y=,y=,第一象限内的点P1、P2、P3、…、P2015在反比例函数y=的图象上,它们的横坐标分别为x1、x2、x3、…、x2015,纵坐标分别是1、3、5、…,共2015个连续奇数,过P1、P2、P3、…、P2015分别作y轴的平行线,与y=的图象交点依次为Q1(x'1,y'1)、Q2(x'2,y'2)、…、Q2015(x'2015,y'2015),则P2015Q2015的长度是.20.将连续正整数按以下规律排列,则位于第7行第7列的数x 是.三.解答题(共6小题,共70分)21.若关于x的不等式组只有4个整数解,求a的取值范围.22.跃壮五金商店准备从宁云机械厂购进甲、乙两种零件进行销售.若每个甲种零件的进价比每个乙种零件的进价少2元,且用80元购进甲种零件的数量与用100元购进乙种零件的数量相同.(1)求每个甲种零件、每个乙种零件的进价分别为多少元?(2)若该五金商店本次购进甲种零件的数量比购进乙种零件的数量的3倍还少5个,购进两种零件的总数量不超过95个,该五金商店每个甲种零件的销售价格为12元,每个乙种零件的销售价格为15元,则将本次购进的甲、乙两种零件全部售出后,可使销售两种零件的总利润(利润=售价﹣进价)超过371元,通过计算求出跃壮五金商店本次从宁云机械厂购进甲、乙两种零件有几种方案?请你设计出来.23.如图,OA和OB是⊙O的半径,并且OA⊥OB.P是OA上任意一点,BP的延长线交⊙O于点Q,点R在OA的延长线上,且RP=RQ.(1)求证:RQ是⊙O的切线;(2)当RA≤OA时,试确定∠B的取值范围;(3)求证:OB2=PB?PQ+OP2.24.如图1,在平面直角坐标系中,边长为1的正方形OABC的顶点B在y轴的正半轴上,O为坐标原点.现将正方形OABC绕点O 按顺时针方向旋转,旋转角为θ(0o≤θ≤45o).(1)当点A落到y 轴正半轴上时,求边BC在旋转过程中所扫过的面积;(2)若线段AB与y轴的交点为M(如图2),线段BC与直线y=x的交点为N.当θ=22.5°时,求此时△BMN内切圆的半径;(3)设△MNB的周长为l,试判断在正方形OABC旋转的过程中l值是否发生变化,并说明理由.25.(1)已知n=﹣那么1+2+3+…+n=﹣+﹣+﹣+…+﹣,即1+2+3+…+n=﹣=.模仿上述求和过程,设n2=﹣,确定a与b的值,并计算12+22+32+…+n2的结果.(2)图1中,抛物线y=x2,直线x=1与x轴围成底边长为1的曲边三角形,其面积为S,现利用若干矩形面积和来逼近该值.①将底边3等分,构建3个矩形(见图2),求其面积为S3;②将底边n等分,构建n个矩形(如图3),求其面积和S n并化简;③考虑当n充分大时S n的逼近状况,并给出S的准确值.(3)计算图4中抛物线y=2x2与直线y=2x+4所围成的阴影部分面积.26.如图所示,在平面直角坐标中,四边形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,点P为x轴上的一个动点,点P不与点0、点A重合.连接CP,过点P作PD 交AB于点D.(1)求点B的坐标;(2)当点P运动什么位置时,△OCP为等腰三角形,求这时点P 的坐标;(3)当点P运动什么位置时,使得∠CPD=∠OAB,且,求这时点P的坐标.重点高中提前招生模拟考试数学试卷(1)参考答案与试题解析一.选择题(共10小题)1.下列等式中,不一定成立的是()A.=2B.C.a=﹣D.【考点】65:分式的基本性质;73:二次根式的性质与化简.【分析】根据二次根式的性质对各选项进行逐一分析即可.【解答】解:A、左边==2=右边,故本选项正确;B、当c=0时,无意义,故本选项错误;C、左边=a=a=﹣=右边,故本选项正确;D、左边===右边,故本选项正确.故选:B.【点评】本题考查的是二次根式的性质与化简,熟知二次根式具有非负性是解答此题的关键.2.中国人民银行授权中国外汇交易中心公布,2014年1月14日银行间外汇市场人民币汇率中间价为:1美元对人民币6.0930元,某上市公司持有美元资产为980万美元,用科学记数法表示其美元资产折合成人民币为()元(保留两位有效数字)A.5.97×107 B.6.0×107C.5.97×108 D.6.0×108【考点】1L:科学记数法与有效数字.【分析】根据汇率可求980万美元折合成人民币的钱数,再保留两位有效数字即可求解.【解答】解:980万美元=980000美元,980000×6.0930≈6.0×107元.故选:B.【点评】此题考查了科学记数法与有效数字,对于用科学记数法表示的数,有效数字的计算方法以及与精确到哪一位是需要识记的内容,经常会出错.3.如图,一条信息可通过网络线由上(A点)往下(沿箭头方向)向各站点传送,例如信息要到b2点可由经a1的站点送达,也可由经a2的站点送达,共有两条传送途径,则信息由A点传达到d3的不同途径中,经过站点b3的概率为()A.B.C.D.【考点】X6:列表法与树状图法.【分析】根据题意画出树状图,进而利用概率公式,求出答案.【解答】解:画树状图得:所以共有6种情况,则经过站点b3的概率为:.故选:A.【点评】本题考查树状图法求概率,关键是得到到达目的地应走的路口,列齐所有的可能情况.4.已知x+y=,|x|+|y|=5,则x﹣y的值为()A.B.C.D.【考点】28:实数的性质.【分析】根据绝对值的性质,可得答案.【解答】解:当x>0,y>0时,x+y=5与x+y=2矛盾,当x<0,y<0时,x+y=﹣5与x+y=2矛盾,当x>0,y<0时,x﹣y=5,当x<0,y>0时,x﹣y=﹣5,故选:D.【点评】本题考查了实数的性质,利用绝对值得性质是解题关键,要分类讨论,以防遗漏.5.二次函数y=ax2+bx+c的图象如图所示(a、b、c为常数),则函数y=(4ac﹣b2)x+abc和y=在同一平面直角坐标系中的图象,可能是()A.B.C.D.【考点】F3:一次函数的图象;G2:反比例函数的图象;H2:二次函数的图象.【分析】由抛物线开口方向得到a>0,由抛物线与y轴交于x轴下方得c<0,由抛物线的对称轴得b<0,所以abc>0;根据抛物线与x轴有2个交点可得4ac﹣b2<0,得出一次函数的图象经过第一、二、四象限;利用对称轴的位置和不等式性质即可得到2a+b>0,得出反比例函数的图象位于第一、三象限;即可得出结论.【解答】解:∵抛物线开口向上,∴a>0,∵抛物线与y轴交于(0,c),∴c<0,∵抛物线的对称轴为直线x=﹣>0,∴b<0,∴abc>0;∵抛物线与x轴有2个交点,∴b2﹣4ac>0,∴4ac﹣b2<0;∴函数y=(4ac﹣b2)x+abc经过第一、二、四象限;∵0<﹣<1,而a>0,∴﹣b<2a,即2a+b>0,∴函数y=的图象位于第一、三象限;故选:C.【点评】本题考查了二次函数与系数的关系:二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小.当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置,当a与b同号时(即ab>0),对称轴在y轴左;当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异);常数项c 决定抛物线与y轴交点,抛物线与y轴交于(0,c).当△=b2﹣4ac>0时,抛物线与x 轴有2个交点;△=b2﹣4ac=0时,抛物线与x轴有1个交点;△=b2﹣4ac<0时,抛物线与x轴没有交点.6.关于x的一元二次方程mx2+x+1=0有两个不相等的同号实数根,则m的取值范围是()A.m且m≠0 B.﹣C.﹣且m≠0 D.0【考点】AA:根的判别式.【分析】根据方程有两个不相等的同号实数根结合根的判别式即可得出关于m的一元一次不等式组,解不等式组即可得出结论.【解答】解:∵关于x的一元二次方程mx2+x+1=0有两个不相等的同号实数根,∴,解得:0<m<.故选:D.【点评】本题考查了根的判别式,根据根的判别式结合根与系数的关系找出关于m的一元一次不等式组是解题的关键.7.由于货源紧缺,小王、小李两名商贩连续两次以不同的价格在同一公司购进了A型香米,两次的购买单价分别为a、b(a<b,单位:元/千克),小王的采购方式为:每次购进c千克大米;小李的采购方式为:每次购进d 元的大米(d>c),若只考虑采购单价,下列结论正确的是()A.小王合算 B.小李合算C.一样合算 D.无法确定谁更合算【考点】6C:分式的混合运算.【专题】11:计算题;513:分式.【分析】分别表示出小王与小李两次购买香米的平均价格,利用作差法比较即可.【解答】解:根据题意得:小王两次购买香米的平均价格为=元/千克,小李两次购买香米的平均价格为=元/千克,∴﹣==,∵(a﹣b)2>0,2(a+b)>0,∴﹣>0,即>,则小李的购买方式合算.故选:B.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019年新疆初中学业水平考试预测卷(3) 一.选择题(本大题共9小题,每小题5分,共45分)1.比﹣1小2的数是()A.3 B.1 C.﹣2 D.﹣32.如图是某个几何体的展开图,该几何体是()A.三棱柱B.三棱锥C.圆柱 D.圆锥3.一年之中地球与太阳之间的距离随时间而变化,1个天文单位是地球与太阳之间的平均距离,即1.496亿km,用科学记数法表示1.496亿是()A.1.496×107B.14.96×108C.0.1496×108D.1.496×1084.如图,AB∥CD,点E在线段BC上,CD=CE.若∠ABC=30°,则∠D为()A.85° B.75°C.60° D.30°5.在某次体育测试中,九年级(1)班5位同学的立定跳远成绩(单位:m)分别为:1.8l,1.98,2.10,2.30,2.10.这组数据的众数为()A.2.30 B.2.10 C.1.98 D.1.816.某种商品每件的标价是270元,按标价的八折销售时,仍可获利20%,则这种商品每件的进价为()A.180元 B.200元 C.225元 D.259.2元7.已知点P(1﹣a,2a+6)在第四象限,则a的取值范围是()A.a<﹣3 B.﹣3<a<1 C.a>﹣3 D.a>18.如图,在物理课上,老师将挂在弹簧测力计下端的铁块浸没于水中,然后缓慢匀速向上提起,直至铁块完全露出水面一定高度,则下图能反映弹簧测力计的读数y(单位:N)与铁块被提起的高度x(单位:cm)之间的函数关系的大致图象是()9.如图,将矩形ABCD的四个角向内翻折后,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12厘米,EF=16厘米,则边AD的长是()A.12厘米B.16厘米C.20厘米D.28厘米二.填空题(本大题共6小题,每小题5分,共30分)10.﹣8的立方根为_______.11.将二次函数y=x2﹣1的图象向上平移3个单位长度,得到的图象所对应的函数表达式是_______12.若实数m、n满足等式|m﹣,且m、n恰好是等腰△ABC的两条边的边长,则△ABC的周长是________13.如图,⊙A过点O(0,0),C0),D(0,1),点B是x轴下方⊙A上的一点,连接BO,BD,则∠OBD的度数是()A.15° B.30° C.45° D.60°14.若一个反比例函数的图象经过点A(m,m)和B(2m,﹣1),则这个反比例函数的表达式为.15.如图,在矩形ABCD中,E是边AB的中点,连接DE交对角线AC于点F,若AB=4,AD=3,则CF的长为.三.解答题(本大题共8小题,共75分)16. (本题6分)解方程:53 212 x x=-+17.(本题6分)解不等式组:311442x xx x-≥+⎧⎨+<-⎩18.(本题8分)郴州市正在创建“全国文明城市”,某校拟举办“创文知识”抢答赛,欲购买A、B两种奖品以鼓励抢答者.如果购买A种20件,B种15件,共需380元;如果购买A种15件,B种10件,共需280元.(1)A、B两种奖品每件各多少元?(2)现要购买A、B两种奖品共100件,总费用不超过900元,那么A种奖品最多购买多少件?19.(本题8分)如图,△ABC≌△ABD,点E在边AB上,CE∥BD,连接DE.求证:(1)∠CEB=∠CBE;(2)四边形BCED是菱形.20.(本题10分)某学校为了增强学生体质,决定开放以下体育课外活动项目:A.篮球、B.乒乓球、C.跳绳、D.踢毽子.为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图(如图7(1),图7(2)),请回答下列问题:(1)这次被调查的学生共有多少人?(2)请你将条形统计图补充完整;(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).21.(本题12分)太阳能光伏建筑是现代绿色环保建筑之一,老张准备把自家屋顶改建成光伏瓦面,改建前屋顶截面△ABC如图2所示,BC=10米,∠ABC=∠ACB=36°,改建后顶点D在BA的延长线上,且∠BDC=90°,求改建后南屋面边沿增加部分AD的长.(结果精确到0.1米)(参考数据:sin18°≈0.31,cos18°≈0.95.tan18°≈0.32,sin36°≈0.59.cos36°≈0.81,tan36°≈0.73)22.(本题12分)如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.(1)求证:CD是⊙O的切线;(2)过点B作⊙O的切线交CD的延长线于点E,BC=6,23ADBD=.求BE的长.23. (本题13分)如图,抛物线经过A(﹣1,0),B(5,0),C(0,52-)三点.(1)求抛物线的解析式;(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.2019年新疆初中学业水平考试预测卷(3)答案一.选择题(本大题共9小题,每小题5分,共45分)二.填空题(本大题共6小题,每小题5分,共30分)10.-2 11. y=x2+2 12. 10 13. 30° 14.4yx= 15.103三.解答题(本大题共8小题,共75分)16.(本题6分)解:5(x+2)=3(2x﹣1),解得:x=13,检验:当x=13时,(x+2)≠0,2x﹣1≠0,故x=13是原方程的解.17.(本题6分)解:分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.试题解析:解不等式3x-1≥x+1,得:x≥1,解不等式x+4<4x-2,得:x>2,∴不等式组的解集为x>2.18.(本题8分)解:(1)设A种奖品每件x元,B种奖品每件y元,根据题意得:2015380 1510280x yx y+=⎧⎨+=⎩,解得:164xy=⎧⎨=⎩.答:A种奖品每件16元,B种奖品每件4元.(2)设A种奖品购买a件,则B种奖品购买(100﹣a)件,根据题意得:16a+4(100﹣a)≤900,解得:a≤1253.∵a为整数,∴a≤41.答:A种奖品最多购买41件.19.(本题8分)证明;(1)∵△ABC≌△ABD,∴∠ABC=∠ABD,∵CE∥BD,∴∠CEB=∠DBE,∴∠CEB=∠CBE.(2))∵△ABC≌△ABD,∴BC=BD,∵∠CEB=∠CBE,∴CE=CB,∴CE=BD∵CE∥BD,∴四边形CEDB是平行四边形,∵BC=BD,∴四边形CEDB是菱形.20.(本题10分)解:(1)由扇形统计图可知:扇形A的圆心角是36°,所以喜欢A项目的人数占被调查人数的百分比=36360×100%=10%.由条形图可知:喜欢A类项目的人数有20人,所以被调查的学生共有20÷10%=200(人).(2)喜欢C项目的人数=200-(20+80+40)=60(人),因此在条形图中补画高度为60的长方条,如图所示.(3)画树状图如下:从树状图或表格中可知,从四名同学中任选两名共有12种结果,每种结果出现的可能性相等,其中选中甲乙两位同学(记为事件A)有2种结果,所以P(A)=21 126=.21(本题12分)解:∵∠BDC=90°,BC=10,sinB=CD BC,∴CD=BC•sinB=10×0.59=5.9,∵在Rt△BCD中,∠BCD=90°﹣∠B=90°﹣36°=54°,∴∠ACD=∠BCD﹣∠ACB=54°﹣36°=18°,∴在Rt△ACD中,tan∠ACD=AD CD,∴AD=CD•tan∠ACD=5.9×0.32=1.888≈1.9(米),则改建后南屋面边沿增加部分AD的长约为1.9米.22.(本题12分)(1)证明:连结OD,∵OB=OD,∴∠OBD=∠BDO,∵∠CDA=∠CBD,∴∠CDA=∠ODB,又∵AB是⊙O的直径,∴∠ADB=90°,∴∠ADO+∠ODB=90°,∴∠ADO+∠CDA=90°,即∠CDO=90°,∴OD⊥CD,∵OD是⊙O半径,∴CD是⊙O的切线(2)解:∵∠C=∠C,∠CDA=∠CBD∴△CDA∽△CBD∴CD ADBC BD=∵23ADBD=,BC=6,∴CD=4,∵CE,BE是⊙O的切线∴BE=DE,BE⊥BC∴BE2+BC2=EC2,即BE2+62=(4+BE)2解得:BE=52.23.(本题13分)解:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),∵A (﹣1,0),B (5,0),C (0,52-)三点在抛物线上, ∴0255052a b c a b c c ⎧⎪-+=⎪++=⎨⎪⎪=-⎩, 解得12252a b c ⎧=⎪⎪=-⎨⎪⎪=-⎩. ∴抛物线的解析式为:215222y x x =--;(2)∵抛物线的解析式为:215222y x x =--, ∴其对称轴为直线x=﹣2b a=﹣22122-=⨯,连接BC ,如图1所示, ∵B (5,0),C (0,﹣52), ∴设直线BC 的解析式为y=kx+b (k ≠0),∴5052k b b +=⎧⎪⎨=-⎪⎩, 解得1252k b ⎧=⎪⎪⎨⎪=-⎪⎩, ∴直线BC 的解析式为1522y x =-, 当x=2时,y=1﹣52=﹣32, ∴P (2,﹣32);(3)存在. 如图2所示,①当点N 在x 轴下方时,∵抛物线的对称轴为直线x=2,C (0,﹣52), ∴N 1(4,﹣52); ②当点N 在x 轴上方时,如图,过点N 2作N2D ⊥x 轴于点D , 在△AN 2D 与△M 2CO 中,222222N AD CM O AN CM AN D M CO∠=∠⎧⎪=⎨⎪∠=∠⎩∴△AN 2D ≌△M 2CO (ASA ), ∴N 2D=OC=52,即N 2点的纵坐标为52. ∴215222x x --=52, 解得x 1=2+x 2=2-∴N 2(2+52),N 3(2-52). 综上所述,符合条件的点N 的坐标为(4,﹣52),(252),(2-52).。
