摆小正方体找规律
【单元AB卷】六年级上数学分层训练B卷-第八单元 数学广角——数与形(单元测试) (人教版,含答案)

六年级上册数学分层训练B卷-第八单元数学广角——数与形(满分:100分,完成时间:60分钟)一、选择题(满分16分)1.用火柴棒按下图的方式搭正方形,搭30个这样的正方形需要()根火柴棒。
A.120 B.90 C.912.—列数 1,2,2,3,3,3,4,4,4,4,中的第34个数为()A.6 B.7 C.8 D.93.3×7=21,33×67=2211,333×667=222111,那么3333×6667=()A.222111 B.22221111 C.22211114.2×9=18 22×99=2178 222×9999=221778 2222×9999=22217778 22222×99999=()A.22117788 B.2222177778 C.222221778 D.2222177788 5.猜猜接下来的图形里面有几个圆形()。
A.13 B.14 C.156.如图,下列都是由面积为1的正方形按一定的规律组成,其中,第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的正方形有5个,第(3)个图形中面积为1的正方形有9个,…,按此规律,则第(6)个图形中面积为1的正方形的个数为()A.24 B.25 C.26 D.277.观察下面的图形,想一想,第8个图形有( )个黑点.A.45 B.46 C.47 D.488.下面的三角形是用小棒拼成的,根据图形排列的规律,第100个图形要()根小棒。
A.300 B.299 C.201 D.240二、填空题(满分16分)9.如图,一张桌子可坐4人,2张桌子拼起来可坐6人,3张桌子拼起来可坐8人。
像这样( )张桌子拼起来可坐38人。
10.用圆片摆成这样的图形:。
如果继续摆下去,第8个图形共有( )个圆片。
11.唐唐在桌面上用小正方体按下图方式摆放。
摆1个小正方体有5个面露在外面,摆2个小正方体有8个面露在外面……摆n个小正方体有( )个面露在外面。
找规律例子

例1:盒子里放了一只球,一位魔术师第一次从盒子里将这只球取出,变成4只球后放回盒子里;第二次从盒子里取出2只球,将每只球各变成4只球后,放进盒子里;……;第十次从盒子里取出10只球,将每只球各变成4只球的放回盒子里。
问:这时盒子里共有多少只球?分析:在此题中,变化的量有以下几个:①操作的次数,即取球的次数;②取出的球数;③每次取出球以后,盒中剩余的球数;④每次放回的球数⑤盒中每次增加的球数;⑥每次操作结束后盒子中的球数。
这每一个量都随着操作次数的变化而变化,正因如此,把每次操作的情况列成表格,在表格中的数据上寻找出数据的规律:操作次数1 2 3 (10)取出球数1 2 3 (10)盒中剩球数0 2 7 … A放回的球数4 8 12 … B盒中增加球数3 6 9 … C总球数 4 10 19 … D在上表中,若能把A、B、C、D这四处的数据找到,那么此题也就完成了解题。
从表中容易得到结果的是B为4N、C为3N。
因此对所要求的D的结果就显而易见了:每次变化后的球的数目分别为:1、1+3=4、10=1+3+6、1+3+6+9=19、1+3+6+9+12=31……1+3+6+9+12+15+18+21+24+27+30=166。
即D为166。
说明:解决此类问题时,应将每一过程产生的结果用表格把数据一一列出,再观察数据的变化,从变化的数据中寻找规律,从而得出结论。
例2:有10个朋友聚会,见面时如果每人和其余的每个人只握一次手,那么10个人共握手多少次?若N个朋友呢?分析:学生必须明白:1)每两个人握一次手;2)甲和乙握手的结果与乙和甲握手的结果只能看成是一种结果。
3)若设这10个人为A1、A2、A3、A4、A5、A6、A7、A8、A9、A10。
则A1与其它9个人握9次手;A2则与剩下的8个人握8次手;A3则与剩下的7个人握7次手;……A9与A10握1次手。
因此,所有握手的次数就是9+8+7+6+5+4+3+2+1=45(次)。
初中数学规律题解题基本方法------图形找规律
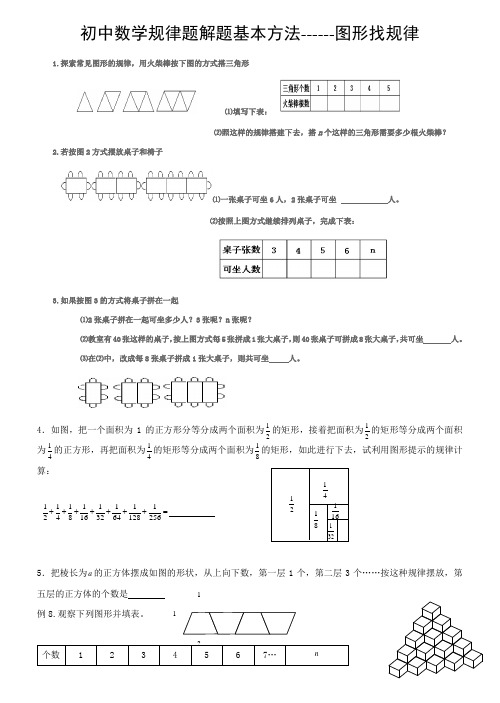
初中数学规律题解题基本方法------图形找规律1.探索常见图形的规律,用火柴棒按下图的方式搭三角形⑴填写下表:⑵照这样的规律搭建下去,搭n 个这样的三角形需要多少根火柴棒? 2.若按图2方式摆放桌子和椅子⑴一张桌子可坐6人,2张桌子可坐 人。
⑵按照上图方式继续排列桌子,完成下表:3.如果按图3的方式将桌子拼在一起⑴2张桌子拼在一起可坐多少人?3张呢?n 张呢?⑵教室有40张这样的桌子,按上图方式每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐 人。
⑶在⑵中,改成每8张桌子拼成1张大桌子,则共可坐 人。
4.如图,把一个面积为1的正方形分等分成两个面积为21的矩形,接着把面积为21的矩形等分成两个面积为41的正方形,再把面积为41的矩形等分成两个面积为81的矩形,如此进行下去,试利用图形提示的规律计算:=+++++++256112816413211618141215.把棱长为a 的正方体摆成如图的形状,从上向下数,第一层1个,第二层3个……按这种规律摆放,第五层的正方体的个数是 例8.观察下列图形并填表。
116.用黑白两颜色的正六边形地面砖按如图所示规律,拼成若干个图案: (1)第4个图案中有白色地面砖 块; (2)第n 个图案中有白色地面砖 块。
……7.下列每个图形都是若干个棋子围成的正方形图案,图案的每条边(包括两个顶点)上都有)2(≥n n 个棋子,每个图案棋子总数为S ,按下图的排列规律推断,S 与n 之间的关系可以用式子 来表示。
……8.观察与分析下面各列数的排列规律,然后填空。
①5,9,13,17, , 。
②4,5,7,11,19, , 。
③10,20,21,42,43, , ,174,175。
④4,9,19,34,54, , ,144。
⑤45,1,43,3,41,5, , ,37,9。
⑥6,1,8,3,10,5,12,7, , 。
⑦0,1,1,2,3,5, , 。
规律题

4.7专题训练(找规律题型)选择题1.为提高信息在传输中的抗干扰能力,通常在原信息中按一定规则加入相关数据组成传输信息.设定原信息为a0a1a2,其中a0a1a2均为0或1,传输信息为h0a0a1a2h1,其中h0=a0+a1,h1=h0+a2.运算规则为:0+0=0,0+1=1,1+0=1,1+1=0,例如原信息为111,则传输信息为01111.传输信息在传输过程中受到干扰可能导致接收信息出错,则下列接收信息一定有误的是()A.11010 B.10111 C.01100 D.00011考点:规律型:数字的变化类。
专题:规律型。
分析:根据题意,只需验证是否满足h0=a0+a1,h1=h0+a2.经验证,A,C,D都符合.B中,h1=h0+a2=1+1=0,故错误.解答:解:∵h1=h0+a2=1+1=0,∴B错误故选B.点评:本题是一道找规律的题目,要求学生通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.此题注意正确理解题意,根据要求进行计算.2.在一列数1,2,3,4,…,200中,数字“0”出现的次数是()A.30个B.31个C.32个D.33个考点:规律型:数字的变化类。
专题:规律型。
分析:根据数的表示方法可知,200中数字“0”出现的次数是11+9+11=31.解答:解:∵100个数字中,只有整十的数字含有0,共11个,101~109中又有9个,110~200中又有11个.∴11+9+11=31.故选B.点评:熟悉数的表示方法:100个数字中,只有整十的数字含有0,共11个,101~109中又有9个,110~200中又有11个.3.把在各个面上写有同样顺序的数字1~6的五个正方体木块排成一排(如图所示),那么与数字6相对的面上写的数字是()X-k-b-1. -c-o-mA.2 B.3 C.5 D.以上都不对考点:规律型:数字的变化类。
分析:首先由五个正方体木块有3个露出了4,可推出4的对面是2;然后由1与4,5,6相邻,可得1的对面是3;故剩下的5与6相对.解答:解:五个正方体木块有3个露出了4,并且4和1,6,5,3相邻,所以4的对面是2;1与4,5,6相邻,因为4与2相对,故1与2也相邻,所以1的对面是3;剩下的5与6相对.故选C.点评:本题考查正方体各个面的相对位置,锻炼了学生的看图能力和空间想象能力.4.意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…,其中从第三个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的长度构造一组正方形(如下图),再分别依次从左到右取2个,3个,4个,5个正方形拼成如下长方形并记为①,②,③,④,相应长方形的周长如下表所示:序号①②③④周长 6 10 16 26若按此规律继续作长方形,则序号为⑧的长方形周长是()A.288 B.178 C.28 D.110考点:规律型:图形的变化类。
3套五年下数学第二单元《长方体》单元测试(附答案)

五年级下册数学第二单元《长方体(一)》单元测试1(附答案)一、细心填空。
(每空1分,共14分)1.长方体和正方体都有( )个面,( )条棱和( )个顶点。
2.至少用( )个相同的小正方体才能拼成一个大正方体。
3.把一个长方体放在桌面上,一次最多能看到它的( )个面,长方体有( )个面露在外面。
4.一个正方体的表面积是2.64dm2,它一个面的面积是( )dm2。
5.一个长方体,长7dm,宽4dm,高2dm,它的棱长总和是( )dm,表面积是( )dm2。
6.把两个棱长为3分米的正方体木块拼成一个长方体,它的棱长减少了( )分米,表面积减少了( )平方分米。
7.用一根长48dm的铁丝焊接成一个最大的正方体框架并糊上纸,这个正方体的棱长是( )dm,表面积是( )dm2。
8.一个无盖的玻璃鱼缸,长6分米,宽和高都是5分米。
制造这个鱼缸至少需要玻璃( )平方分米。
二、认真辨析。
(正确韵打“√”,错误的打“×”)(5分)1.在一个长方体中,最多只能有4条棱的长度相等。
( ) 2.表面积相等的长方体,它们的长、宽、高不一定分别相等。
( ) 3.用3个棱长是1厘米的小正方体粘成一个长方体,这个长方体比原来的小正方体少了3个面。
( ) 4.用个数、大小相同的正方体组合成不同形状的物体,露在外面的面的个数一定相同。
( ) 5.长方体是特殊的正方体。
( ) 三、选择正确答案的序号填在括号里。
(5分)1.用一根60厘米长的铁丝,可以围成一个长5厘米,宽3厘米,高( )厘米的长方体框架。
①9 ②7 ③42.下面是长方体纸盒的展开图的是( )。
① ② ③3.下面的图( )沿虚线折叠能围成正方体。
① ② ③4.一个正方体的棱长扩大2倍,它的表面积扩大( )倍。
①2 ②4 ③125.一个棱长是6厘米的正方体,切成两个相等的长方体,两个长方体的表面积之和比原来正方体的表面积增加了( )。
①18平方厘米②36平方厘米③72平方厘米四、找规律。
初中数学找规律题讲解与总结[1].
![初中数学找规律题讲解与总结[1].](https://img.taocdn.com/s3/m/7a32857cae1ffc4ffe4733687e21af45b307fe73.png)
1、新课引入小时侯我们都玩过搭积木的游戏,今天我们不妨重拾童年趣事,利用手中的火柴棒搭建一些常见的图形,探索规律。
2、合作交流,探索规律:活动一:探索常见图形的规律,用火柴棒按下图的方式搭三角形⑴填写下表:⑵照这样的规律搭建下去,搭n个这样的三角形需要多少根火柴棒?★注意引导学生概括“探索规律”的一般步骤:①寻找数量关系;②用代数式表示规律③验证规律。
★练习:四棱柱有几个顶点、几条棱、几个面?五棱柱呢?十棱柱呢?n棱柱呢?活动二:探索具体情景下事物的规律问题 1.若有两张长方形的桌子,把它们拼成一张大的长方形桌子,有几种拼法?问题 2.若按图2方式摆放桌子和椅子⑴一张桌子可坐6人,2张桌子可坐人。
⑵按照上图方式继续排列桌子,完成下表:问题 3.如果按图3的方式将桌子拼在一起⑴2张桌子拼在一起可坐多少人?3张呢?n张呢?⑵教室有40张这样的桌子,按上图方式每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐人。
⑶在⑵中,改成每8张桌子拼成1张大桌子,则共可坐人。
活动三:探索图表的规律下面是2000年八月份的日历:⑴日历中的绿色方框中的9个数之和与该方框正中间的数有什么关系?⑵这个关系对其它这样的方框成立吗?你能用代数式表示这个关系吗?⑶这个关系对任何一个月的日历都成立吗?为什么?⑷你还能发现这样的方框中9个数之间的其他关系吗?用代数式表示。
⑸你还能提出那些问题?中考数学探索题训练—找规律1、我们平常用的数是十进制数,如2639=2×103+6×102+3×101+9×100,表示十进制的数要用10个数码(又叫数字):0,1,2,3,4,5,6,7,8,9。
在电子数字计算机中用的是二进制,只要两个数码:0和1。
如二进制中101=1×22+0×21+1×20等于十进制的数5,10111=1×24+0×23+1×22+1×21+1×20等于十进制中的数23,那么二进制中的1101等于十进制的数。
2019中考数学规律探索题(中考找规律题目-有答案)
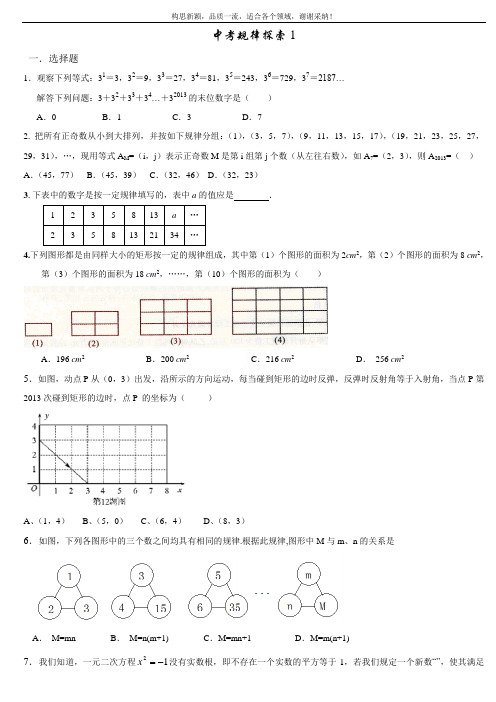
中考规律探索1一.选择题1.观察下列等式:31=3,32=9,33=27,34=81,35=243,36=729,37=2187… 解答下列问题:3+32+33+34…+32013的末位数字是( ) A .0 B .1 C .3 D .72. 把所有正奇数从小到大排列,并按如下规律分组:(1),(3,5,7),(9,11,13,15,17),(19,21,23,25,27,29,31),…,现用等式A M =(i ,j )表示正奇数M 是第i 组第j 个数(从左往右数),如A 7=(2,3),则A 2013=( ) A .(45,77) B .(45,39) C .(32,46) D .(32,23)3.下表中的数字是按一定规律填写的,表中a 的值应是 .1 2 3 5 8 13 a (2)358132134…4.下列图形都是由同样大小的矩形按一定的规律组成,其中第(1)个图形的面积为2cm 2,第(2)个图形的面积为8 cm 2,第(3)个图形的面积为18 cm 2,……,第(10)个图形的面积为( )A .196 cm 2B .200 cm 2C .216 cm 2D . 256 cm 25.如图,动点P 从(0,3)出发,沿所示的方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P 第2013次碰到矩形的边时,点P 的坐标为( )A 、(1,4)B 、(5,0)C 、(6,4)D 、(8,3)6.如图,下列各图形中的三个数之间均具有相同的规律.根据此规律,图形中M 与m 、n 的关系是A . M=mnB . M=n(m+1)C .M=mn+1D .M=m(n+1)7.我们知道,一元二次方程12-=x 没有实数根,即不存在一个实数的平方等于-1,若我们规定一个新数“”,使其满足12-=i (即方程12-=x 有一个根为),并且进一步规定: 一切实数可以与新数进行四则运算,且原有的运算律和运算法则仍然成立,于是有,1i i =12-=i ,,).1(23i i i i i -=-=⋅=.1)1()(2224=-==i i 从而对任意正整数n ,我们可得到,.)(.4414i i i i i i n n n ===+同理可得,1,,143424=-=-=++n n n i i i i 那么,20132012432i i i i i i +⋅⋅⋅++++的值为A .0B .1C .-1D .8.下列图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有1颗棋子,第②个图形一共有6颗棋子,第③个图形一共有16颗棋子,…,则第⑥个图形中棋子的颗数为( )A .51B .70C .76D .81二.填空题1.观察下列图形中点的个数,若按其规律再画下去,可以得到第n 个图形中所有的个数为 (用含n 的代数式表示).2.如图,在直角坐标系中,已知点A (﹣3,0)、B (0,4),对△OAB 连续作旋转变换,依次得到△1、△2、△3、△4…,则△2013的直角顶点的坐标为 .3.如图,正方形ABCD 的边长为1,顺次连接正方形ABCD 四边的中点得到第一个正方形A 1B 1C 1D 1,由顺次连接正方形A 1B 1C 1D 1四边的中点得到第二个正方形A 2B 2C 2D 2…,以此类推,则第六个正方形A 6B 6C 6D 6周长是 .图① 图② 图③···(第8题图)4.直线上有2013个点,我们进行如下操作:在每相邻两点间插入1个点,经过3次这样的操作后,直线上共有个点.5.如图,古希腊人常用小石子在沙滩上摆成各种形状来研究数.例如:称图中的数1,5,12,22…为五边形数,则第6个五边形数是.6 .如图,是用火柴棒拼成的图形,则第n个图形需根火柴棒.7.观察规律:1=12;1+3=22;1+3+5=32;1+3+5+7=42;…,则1+3+5+…+2013的值是.8.如图12,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;……如此进行下去,直至得C13.若P(37,m)在第13段抛物线C13上,则m =_________.9.直线上有2013个点,我们进行如下操作:在每相邻两点间插入1个点,经过3次这样的操作后,直线上共有个点. 10.观察下列各式的计算过程:5×5=0×1×100+25,15×15=1×2×100+25,25×25=2×3×100+25,35×35=3×4×100+25,…………请猜测,第n个算式(n为正整数)应表示为____________________________.11.将连续的正整数按以下规律排列,则位于第7行、第7列的数x是__ __.12、如下图,每一幅图中均含有若干个正方形,第①幅图中含有1个正方形;第②幅图中含有5个正方形;……按这样的规律下去,则第(6)幅图中含有 个正方形;13.将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆, 第2个图形有10个小圆, 第3个图形有16个小圆, 第4个图形有24个小圆, ……,依次规律,第6个图形有 个小圆.14.已知一组数2,4,8,16,32,…,按此规律,则第n 个数是 . 15、我们知道,经过原点的抛物线的解析式可以是y =ax 2+bx (a ≠0) (1)对于这样的抛物线:当顶点坐标为(1,1)时,a =__________;当顶点坐标为(m ,m ),m ≠0时,a 与m 之间的关系式是__________;(2)继续探究,如果b ≠0,且过原点的抛物线顶点在直线y =kx (k ≠0)上,请用含k 的代数式表示b ;(3)现有一组过原点的抛物线,顶点A 1,A 2,…,A n 在直线y =x 上,横坐标依次为1,2,…,n (为正整数,且n ≤12),分别过每个顶点作x 轴的垂线,垂足记为B 1,B 2,…,B n ,以线段A n B n 为边向右作正方形A n B n C n D n ,若这组抛物线中有一条经过D n ,求所有满足条件的正方形边长.16.如图,所有正三角形的一边平行于x 轴,一顶点在y 轴上,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用1A 、2A 、3A 、4A 、…表示,其中12A A 与x 轴、底边12A A 与45A A 、45A A 与78A A 、…均相距一个单位,则顶点3A 的坐标是 ,22A 的坐标是 .xy A 9A 6A 3A 8A 7A 5A 4A 2A 1O第16题图••••••①② ③17.如图,已知直线l :y=33x ,过点A (0,1)作y 轴的垂线交直线l 于点B ,过点B 作直线l 的垂线交y 轴于点A 1;过点A 1作y 轴的垂线交直线l 于点B 1,过点B 1作直线l 的垂线交y 轴于点A 2;……按此作法继续下去,则点A 2013的坐标为 .18、如图,在平面直角坐标系中,一动点从原点O 出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A 1(0,1),A 2(1,1),A 3(1,0),A 4(2,0),…那么点A 4n +1(n 为自然数)的坐标为 (用n 表示)19.当白色小正方形个数n 等于1,2,3…时,由白色小正方形和和黑色小正方形组成的图形分别如图所示.则第n 个图形中白色小正方形和黑色小正方形的个数总和等于_____________.(用n 表示,n 是正整数)20. (2013•衢州4分)如图,在菱形ABCD 中,边长为10,∠A=60°.顺次连结菱形ABCD 各边中点,可得四边形A 1B 1C 1D 1;顺次连结四边形A 1B 1C 1D 1各边中点,可得四边形A 2B 2C 2D 2;顺次连结四边形A 2B 2C 2D 2各边中点,可得四边形A 3B 3C 3D 3;按此规律继续下去….则四边形A 2B 2C 2D 2的周长是 ;四边形A 2013B 2013C 2013D 2013的周长是 .21.一组按规律排列的式子:a2,43a ,65a ,87a ,….则第n 个式子是________ 22.观察下面的单项式:a ,﹣2a 2,4a 3,﹣8a 4,…根据你发现的规律,第8个式子是 .23.如图,已知直线l:y=x,过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1,过点N1作直线l的垂线交x轴于点M2,…;按此作法继续下去,则点M10的坐标为.24.为庆祝“六•一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示:按照上面的规律,摆第(n)图,需用火柴棒的根数为.答案:选择题:1、C 2、C 3、21 4、B 5、D 6、D 7、D 8、 C填空题:1、(n+1)2 2、(8052,0) 3、0.5 4、16097 5、51 6、2n+1 7、1014049 8、 2 9、16097 10、[10(n-1)+5]2=100n(n-1)+25 11、85 12、91 13、46 14、2n 15、(1)-1;a =-1m(或am +1=0); (2)解:∵a ≠0 ∴y =ax 2+bx =a (x +2b a)2-24b a∴顶点坐标为(-2ba ,-24b a )∵顶点在直线y =kx 上∴k (-2ba )=-24b a∵b ≠0∴b =2k(3)解:∵顶点A n 在直线y =x 上 ∴可设A n 的坐标为(n ,n ),点D n 所在的抛物线顶点坐标为(t ,t )由(1)(2)可得,点D n 所在的抛物线解析式为y =-1tx 2+2x∵四边形A n B n C n D n 是正方形∴点D n 的坐标为(2n ,n ) ∴-1t(2n )2+2×2n =n∴4n =3t∵t 、n 是正整数,且t ≤12,n ≤12∴n =3,6或9∴满足条件的正方形边长为3,6或916、(0,31-),(-8,-8). 17、()()201340260,40,2或(注:以上两答案任选一个都对)18、(2n ,1) 19、n 2+4n 20、20;21、221na n (n 为正整数)22、-128a 8 23、(884736,0) 24、6n+2规律探索21、 我们平常用的数是十进制数,如2639=2×103+6×102+3×101+9×100,表示十进制的数要用10个数码(又叫数字):0,1,2,3,4,5,6,7,8,9。
15.【精品】小学数学几何精讲精析专题六 立体图形-类型一 正方体

专题六立体图形类型一正方体【知识讲解】一、正方体的认识:1. 特征:正方体有6个面,每个面都是正方形,所有的面都完全相同,有12条棱,所有的棱都相等,有8个顶点。
2. 正方体的棱长总和=棱长×12用字母表示:12a二、正方体表面积的计算1. 表面积:正方体6个面的总面积叫做它的表面积。
2. 正方体的表面积=棱长×棱长×6用字母表示:S=6a2三、正方体体积的计算1. 物体所占空间的大小叫做物体的体积。
2. 正方体的体积=棱长×棱长×棱长或底面积×高用字母表示: V= a3 或Sh【典例精讲】计算下面图形的表面积和体积。
【答案】表面积是54平方分米,体积是27立方分米.【解析】根据正方体的体积=棱长×棱长×棱长,表面积=棱长×棱长×6,列式计算即可。
解:3×3×6=54(平方分米);3×3×3=27(立方分米);答:正方体的表面积是54平方分米,体积是27立方分米。
【点评】此题主要考查正方体的表面积和体积公式及其计算。
【巩固练习】一、选择题。
1.下列图形中,()是正方体的展开图。
2.正方体的棱长扩大3倍,则体积扩大()倍。
A.2B.4C.27D.83.一个正方体每个面的面积都是9cm2,它的棱长是()cm。
A.9 B.54 C.34.一个正方体的棱长总和是96dm,它的表面积是()dm2。
A.384 B.1536 C.9516 D.5125.一个正方体的棱长是6dm,它的表面积和体积相比较,()A.体积大 B.表面积大 C.同样大 D.无法比较6.用棱长2厘米的正方体木块拼成一个较大的正方体,至少需要()块。
A.4B.8C.9D.647.把一个棱长为6分米的正方体切成棱长为2分米的小正方体,可以得到()小正方体。
A.27个 B.81个 C.9个8.如图是几个相同小正方体拼成的大正方体,由AB向C点斜切,没被切掉的小正方体有()个。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
摆几个棱长为a的正方体,从上向下数,第一层一个,第二层3个,按这种规律摆放,第五层是()个,第n层是()个
分析: 第一层1个
第二层比第一层多2:(1+2)个
第三层比第二层多3:(1+2+3)个
第四层比第三层多4:(1+2+3+4)个
第五层比第四层多5:(1+2+3+4+5)个
解:
∵第二层比第一层多2,故有1+2=3(个)
第三层比第二层多3,故有3+3=6(个)
第四层比第三层多4,故有6+4=10(个)
第五层比第四层多5,故有10+5=15(个)
观察可发现层与层间的规律,而最后提出:第n的立方体个数:(1+2+3+…+n)个
棱长为a的正方体,摆放成如图所示的形状.
(1)如果这一物体摆放三层,试求该物体的表面积;
(2)依图中摆放方法类推,如果该物体摆放了上下20层,求该物体的表面积.考点:几何体的表面积.专题:计算题.分析:由题中图示,从上、下、左、右、前、后等六个方向直视的平面图相同,
(1)每个方向上均有6个等面积的小正方形.
(2)每个方向上均有(1+2+3+…+20)个等面积的小正方形.解答:解:(1)6×(1+2+3)•a2=6a2.
故该物体的表面积为6a2;
(2)6×(1+2+3+…+20)•a2=1260a2.
故该物体的表面积为
1260a2.
点评:本题考查了平面图形的有关知识,关键是要注意立体图形的各个面,及每个面的正方形的个数.
找规律!有一些棱长2厘米的正方体,摆一层是1块,摆二层是4块,摆三层是10块……
第一层:1=(1+1)×1÷2
第二层:3=(1+2)×2÷2
第三层:6=(1+3)×3÷2
第四层:10=(1+4)×4÷2
因此,第n层:(1+n)×n÷2
4层是20块,5层是35块,……,10层是220块……
1层表面积是24cm²,2层是72cm²……
1层体积是8cm³,2层是24cm³……
求表面积的方法是怎样的?
体积与层数之间有着怎样的关系?
设层数为n
第n层个数1/2 n(n+1)
第n层表面积是:1/2n(n+1)×4×6 12n(n+1)
第n层体积是【n(n+1)(2n+1)/12+n(n+1)/4】×8 4n(n+1)
观察下列由棱长为1的小正方体摆成的图形,寻找规律,如图(1)所示共有1个小立方体,其中1个看得见,0个看不见;如图(2)所示:共有8个小立方体,其中7个看得见,1个看不见;如图(3)所示:共有27个小立方体,其中19个看得见,8个看不见…(1)写出第(6)个图中看不见的小立方体有125
125
个;(2)猜想并写出第(n)个图形中看不见的小立方体的个数为
(n-1)3
(n-1)3
个.
考点:立体图形.
专题:规律型.
分析:分别求出排成的立方体的高为1个立方体、2个立方体、3个立方体、4个立方体时看见的正方体与看不见的正方体的个数,找出规律进行解答即可.
解答:解:∵当高有1个立方体时,1=1,0=(1-1)3=03;
当高有2个立方体时,8=23,1=13=(2-1)3;
当高有3个立方体时,27=33,8=(3-1)3=23;
当高有4个立方体时,64=43,27=(4-1)3=33;
当高有5个立方体时,125=53,64=(5-1)3=43;
当高有6个立方体时,216=63,125=(6-1)3=53;
∴当高有n个立方体时,看不见的小立方体的个数为(n-1)3个.
故答案为:125,(n-1)3,.
点评:本题考查的是立体图形,分别根据排成的立方体的高为1个立方体、2个立方体、3个立方体、4个立方体时看见的正方体与看不见的正方体的个数,找出规律即可进行解答.。
