大学物理第六章 气体动理论
大学物理电子教案-气体动理论
气体动理论内容：理想气体模型理想气体的压强和温度理想气体内能麦克斯韦速率分布律范德瓦耳斯方程气体内的输运过程：热传导过程、扩散过程和黏性现象6.1理想气体模型6.1.1气体的分子状况1.分子具有一定的质量和体积宏观物体是由大量分子或原子组成的，物质的量为1mol的任何物质都包含有N0=6.022X1023（N0为阿伏伽德罗常量）个分子。
2.一切物质的分子都在永不停歇地做无规则运动1827年，布朗在显微镜下观察到悬浮在液体中的花粉颗粒分子总是在无规则地、永不停息地运动着。
这就是著名的布朗运动。
它能能够直观的表明：气体、液体、固体中都有扩散现象。
是分子运动的有力证明。
精确的实验表明，在排除一切外界干扰时，布朗运动仍然存在。
对于这种现象，只能用大量无规则热运动的液体分子不断地撞击悬浮微粒来解释。
3.分子间存在分子力在物体的内部，分子与分子之间有着很强的作用力，这个力的大小为r t式中，r是两个分子的中心距，尢、丫、s和t都为正数（这可由相关实验求证）。
在上式中，第一项为正值，表示的是分子间斥力的大小；第二项为负值，表示的是分子间引力的大小。
由于一般情况下，参数s和t的数值都比较大（例如，对于非极性分子s=20，t=9），所以分子力的大小随分子间距的增大而急剧减小。
由分子力F与分子间的距离r的关系曲线可以看出：当r<r0（r0~10-10m）时，斥力大于引力，此时分子间的作用力表现为斥力，并且斥力随r 的减小斥力剧烈增大；当r=r0时，斥力与引力相等，相互抵消，此时分子间的作用力为零；当r>r0时，引力大于斥力，此时分子间的作用力表现为引力，并且引力随r的增大分子力迅速减小。
由于分子力是短程力，它的作用范围极小，在压力不大的情况下，分子间的作用力可以忽略不计。
一般当丫宀10-9m时分子间的作用力就可忽略不计。
4.分子之间以及分子与器壁之间进行着频繁碰撞（1）任意一个分子的速度（包括大小和方向两个方面）都与其它分子不同，并且该分子的运动速度也在时刻发生着变化；（2）对于某一个具体分子而言，它的运动轨迹是没有任何规律的，或者说是随机的，在其轨迹的每个转折点上，它与一个或多个分子发生了碰撞，或与器壁上的固体分子发生了碰撞。
大学物理气体动理论基础
玻尔兹曼方程
玻尔兹曼方程是描述气体分子动理学行为的偏微分方程，它基于分子混沌 近似。
玻尔兹曼方程描述了气体分子速度分布随时间的变化，以及分子与器壁碰 撞后速度的改变。
通过求解玻尔兹曼方程，可以得到气体分子的速度分布、分子碰撞频率、 分子平均自由程等物理量。
输运过程的近似处理
01
输运过程是指气体分子通过器壁的传递过程，包括 扩散、热传导和粘性流动等。
气体动理论在新能源、环保、生物医 学等领域的应用前景广阔，为解决实 际问题提供了重要的理论基础。
THANKS
感谢观看
热传导的应用
在能源、化工、航空航天等领域，利用热传导原 理实现热量传递和热能利用。
气体扩散
扩散现象
气体分子在浓度梯度作用下，通过随机运动传递物质的过程。
扩散定律
扩散通量与浓度梯度成正比，与气体分子的扩散系数有关。
扩散的应用
在环保、化工、生物医学等领域，利用扩散原理实现物质的分离 和传输。
气体粘性
02
在处理输运过程时，可以采用近似方法来简化问题 ，如扩散系数近似、粘性系数近似等。
03
通过这些近似处理，可以得到输运过程的宏观规律 ，如菲克定律、斯托克斯定律等。
04
气体动理论的应用
气体热传导
热传导现象
气体分子在热能作用下，通过碰撞传递能量的过 程。
热传导定律
热能传递速率与温度梯度成正比，与气体分子间 的相互作用力有关。
粘性现象
01
气体分子在相对运动中，由于碰撞产生的阻力。
牛顿粘性定律
02
粘性力与速度梯度成正比，与气体分子的碰撞频率和分子间的
相互作用力有关。
粘性的应用
03
气体动理论
1
追踪每一种分子，不可能，也不必要
微观量：大小、质量、速度、能量
宏观量：如温度、压强、体积
宏观量和微观量必然有着内在联络，尽管个别分 子旳运动是无规律旳，但是就大量分子旳集体体现 来看，却存在着一定旳统计规律，所以能够求出大 量分子旳某些微观量旳统计平均值，用来解释从试 验中直接测得旳物体旳宏观性质。
x
y
z
x
y
z
22
y
四.压强公式
v v l 一种分子与器壁A1碰撞一
y
v 次予以A1 旳冲量为: 2mvx A2
v 连续两次碰A1 所需时间间
z
l x 隔：
2l1
z l vx
单位时间内与A1 碰撞次数：
1 2l1
vx
1
vx 2l
1
y
x A1 2
3
一种分子单位时间内予以A1
旳冲量: 1 2mvx 2l
（2） O2旳质量密度;
（3） 氧分子旳质量;
（4） 分子间旳平均距离；
（5） 分子旳平均平动动能.
解：（1） P nkT
n
P kT
1.38
1.013 105
1023 273
27
2.45
1025
个
m3
（2）
PVMMV RT
P
RT
32 103 1.013105
8.31 273 27
1.30 kg m3
3.将小球看作是完全弹性小球(遵照牛顿力学规律)
自由旳、无规则运动旳弹性球分子旳集合 三.统计规律
1.每个分子处于容器空间内任一点旳几率相同，即任 一点分子数密度均相等
2.每个分子向各个方向运动旳几率相同，即气体分子 旳速度沿各个方向旳分量旳多种平均值相等
大学物理气体动理论
气体分子之间的相互作用力产生的势能， 由于气体分子之间的距离非常大，因此气 体分子的势能通常可以忽略不计。
分子动理论的基本假设
分子之间无相互作用力
气体分子之间不存在相互作用的力，它们之间只 存在微弱的范德华力。
分子运动速度服从麦克斯韦分布
气体分子的运动速度服从麦克斯韦分布，即它们 的速度大小和方向都是随机的。
分子碰撞的统计规律
分子碰撞的随机性
01
气体分子之间的碰撞是随机的，碰撞事件的发生和结果都是随
机的。
分子碰撞频率
02
单位时间内分子之间的碰撞次数与分子数密度、分子平均速度
和分子碰撞截面有关。
碰撞结果的统计规律
03
碰撞后分子的速度方向和大小的变化遵循一定的统计规律，可
以用概率密度函数来描述。
热现象的统计解释
大学物理气体动理论
• 引言 • 气体动理论的基本概念 • 气体动理论的基本定律 • 气体动理论的统计解释 • 气体动理论的应用 • 结论
01Biblioteka 引言主题简介气体动理论
气体动理论是通过微观角度研究气体 运动状态和变化的学科。它以分子运 动论为基础，探究气体分子运动的规 律和特性。
分子模型
气体动理论中，将气体分子视为弹性 小球，相互之间以及与器壁之间发生 弹性碰撞。通过建立分子模型，可以 更好地理解气体分子的运动特性。
对未来研究的展望
随着科学技术的发展，气体动理 论仍有很大的发展空间和应用前
景。
未来研究可以进一步探索气体分 子间的相互作用和气体在极端条 件下的行为，例如高温、高压或
低温等。
气体动理论与其他领域的交叉研 究也将成为未来的一个重要方向， 例如与计算机模拟、量子力学和
大学普通物理学经典课件——气体动理论
出现的可能性大小 .
归一化条件
i
i
Ni iN
1
§7.2 平衡态 理想气体状态方程 一 气体的物态参量及其单位（宏观量）
1 气体压强 p ：作用于容器壁上
单位面积的正压力（力学描述）.
p,V ,T
单位： 1Pa 1N m2
标准大气压：45纬度海平面处, 0 C 时的大气压.
1atm 1.013 105 Pa
~ 107 m; z ~ 1010次 / s
对于由大 量分子组成的 热力学系统从 微观上加以研 究时，必须用 统计的方法 .
小球在伽 尔顿板中的分 布规律 .
............ ........... ............ ........... ............ ........... ............
2mvix
两次碰撞间隔时间
2x vix
单位时间碰撞次数 vix 2x
单个分子单位时间施于器壁的冲量 mvi2x x
y
A2o
z
- mmvvvxx
x
单个分子单位时间 施于器壁的冲量
A1 y
mvi2x x
大量分子总效应
zx
单位时间 N 个粒子
对器壁总冲量
mvi2x ix
m x
i
vi2x
Nm vi2x x iN
pV m RT M
例1 在水面下深为50.0m的湖底处（温度为4.0 ℃ ）， 有一个体积为1.0×10-5m3的空气泡升到湖面上来，若 湖面的温度为17℃，求气泡到达湖面的体积（取大气 压p0=1.013×105Pa）。
§7.3 理想气体压强公式 一 理想气体的微观模型
1）分子本身的线度比起分子之间的距离小 了很多，以至于可以忽略不计（可视为质点）
大学物理《气体动理论(5学时)》课件
特
(1)单一性(各处都有自己的P、V、T )；
p,V ,T
征 (2)状态性质稳定性(与时间无关)；
(3)热动平衡(不同与静力平衡)。 ( p ,V ,T )
p
否则为非平衡态系统。
oV
6/63
【A3.1.2】系统 平衡态 态参量
1 压强 p ： 力学描述
单位: 1 Pa 1 N m2
标准大气压: 45纬度海平面处, 0C 时的 大气压. 1atm 1.01105 Pa
掌 握 麦 克 斯 韦 速 率 分 布律及三种统计速率 了解波尔兹曼分布
氢气分子
vrms 1.93103 m s1
氧气分子
vrms 483m s1
22/63
【A3.11.1】麦克斯韦速率分布律
1 兰媚尔实验 实验装置
接抽气泵
2
l v vl
A
Hg
金属蒸汽 狭 缝
23/63
BC D
显 示
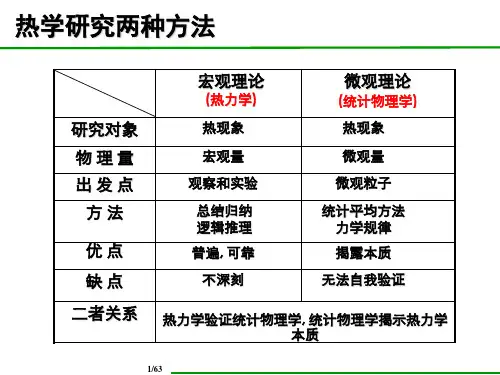
热学研究两种方法
研究对象 物理量 出发点
方法
优点 缺点 二者关系
宏观理论
(热力学)
热现象
宏观量 观察和实验
总结归纳 逻辑推理 普遍, 可靠 不深刻
微观理论
(统计物理学) 热现象
微观量 微观粒子
统计平均方法 力学规律 揭露本质
无法自我验证
热力学验证统计物理学, 统计物理学揭示热力学 本质
1/63
统计规律
(v)dv
3kT
N
N
m
v2 vrms
3kT m
3RT 1.73 kT
m
或
kt
1 2
mv2
3 2
kT ,
v2 3kT / m
大学物理 气体动理论
三、 温 度
决定一个系统是否与其它系统达到热平衡的宏观性质。
处于热平衡的多个系统具有相同的温度
具有相同温度的几个系统放在一起必然处于热平衡。
温度测量
酒精或水银
A
B
A 和 B 热平衡，TA = TB
热胀冷缩特性，标准 状态下，冰水混合， B 上留一刻痕， 水沸 腾，又一刻痕，之间 百等份，就是摄氏温 标（Co）。
生碰撞的�数目为：Ni = nivix dt d A 速度为 vi 分子在 dt 时间对 dA 的冲量为：
�
x
vxi
dA
vidt
nivixdAdt ⋅ (2mvix )
∑ 所有分子在
dt
时间内对
dA 产生的总冲量为：dI = 1 2
i
2mni
v
2
ix
dAdt
∑ ∑ 气体对器壁的宏观压强为：
p=
mni
T0
273.15
= 8.31(Jmol⋅K)
若写成 ν = N NA
N A = 6.023 × 1023 / mol
N为气体分子总数 阿伏伽德罗常量
µN
R
pV = RT = N T
µNA
NA
令
k
≡
R NA
=
1.38 × 10−23
J
K
玻耳兹曼常数
pV = NkT
p = N kT = nkT V
n：气体分子数密度
2
三、气体分子的平均总动能
设分子有： 平动自由度 t 转动自由度 r
分子平均总动能：
1 εk = (t + r) 2 kT
单原子分子 刚性双原子分子
3
大学物理 第六章 气体动理论
6.1 分子运动轮和统计规律
6.1.2 统计规律性
统计规律：大量偶然随机事件的整体具有确定的规律性。
满足统计规律性的前提是必须有大量的事件。参与的事件数目越多，规律性就越明显。
一定量的气体中所包含的分子数是非常大的，虽然每个气体分子可能会以任意数值的速率运动， 但对大量气体分子组成的整体来说，在一定温度下，各种速率的分子数在所有分子中所占的比例却 遵循着确定的统计规律。
但通常分子内部的振动只有在高温下才显著，因此，在常温下，可把气体分子看作是刚性分子， 不考虑其振动自由度。
6.5 能量均分定理
6.5.1 自由度
（1）单原子分子，如He，Ar等，可看作自由运动的质点，有三个平动自由度。
6.5 能量均分定理
6.5.1 自由度
（2）双原子分子，如 O2 ， H2 ，CO 等，其两个原子由一个分子键连接起来。在把气体分子看作 是刚性分子，不考虑其振动自由度的情况下，确定其质心位置需要三个独立坐标（x，y，z）；确定连 线绕质心转动时连线在空间的方位，需用方位角 α，β 两个独立坐标，如图所示。这样，双原子分子 共有五个自由度，其中，三个为平动自由度，两个为转动自由度。
则容器中剩余氧气的质量为 M2
p2V
RT2
5.13 105
8.5 103 32 103 8.31 300
56 (g)
6.4 理想气体的压强和温度
6.4.1 理想气体的微观模型
• 分子本身的线度与分子间平均距离相比，可以忽略不计，故理想气体分子可看
1
作质点，其运动遵循牛顿运动定律。
• 除碰撞的瞬间外，分子之间以及分子与器壁之间都无相互作用，因此，两次碰
大学物理课件 第六章 气体动理论3
v 4 4kT
z d2n d2P
P
4kT d 2
4 1.38 1023 300 3.14 31010 2 105 103
5.85 1010(Pa)
v
vf
v
dv
v
8kT 1.60
kT
0
方均根速率（root-mean-square-speed）：
v 2
v2f vdv(k
1 v2) 2
0
Vp V V2
V2 3kT 1.73 kT
3、玻耳兹曼分布率（Boltzmann distribution） ——有外力场的作用情况下，分子在空间的分布规律
麦克斯韦速率分布函数曲线 f(v)
f(vP)
vP
v
最概然速率vP———与 f ( v ) 极大值对应的速率。
——具有vP的分子数占总分子数的比例最高
——具有vP的分子数最多
最概然速率（most probable speed）：
上页 下页
df 0 vp dv
2kT 1.4：
（2）园柱体的体积为
u t d2
（3）单位体积中的分子数
n
B
D
2d C
d
A
A
ut
上页 下页
（4）碰撞的分子数为 nd2ut 单位时间内的碰撞次数 nd2u
考虑其他分子的运动 u ~ 2v
Z 2nd2v
平均自由程 v 1 Z 2d2n
kT (P nkT) 2d 2 P
上页 下页
计算空气在标准状态下的λ和 Z。 （ d=3.5×10-10m ）
平均自由程 ( mean free path ) 假设： （1）分子的运动是布朗式 （2）分子形状为球体 （3）其他分子不动
(完整版)《大学物理》习题册题目及答案第6单元 气体动理论
第6单元 气体动理论 序号 学号 姓名 专业、班级一 选择题[ C ]1．在标准状态下, 若氧气（视为刚性双原子分子的理想气体）和氦气的体积比2121=V V ，则其内能之比21/E E 为： (A) 1/2 (B) 5/3 (C) 5/6 (D) 3/10[ B ]2．若理想气体的体积为V ，压强为p ，温度为T ，一个分子的质量为m ，k 为玻耳兹曼常量，R 为摩尔气体常量，则该理想气体的分子数为(A) pV/m (B) pV/(kT)(C) pV/(RT) (D) pV/(mT)[ D ]3．若)(v f 为气体分子速率分布函数，N 为分子总数，m 为分子质量，则 )(21221v Nf mv v v ⎰ d v 的物理意义是 (A) 速率为v 2的各分子的总平均动能与速率为v 1的各分子的总平均动能之差。
(B) 速率为v 2的各分子的总平动动能与速率为v 1的各分子的总平动动能之和。
(C) 速率处在速率间隔v 1~ v 2之内的分子的平均平动动能。
(D) 速率处在速率间隔v 1~ v 2之内的分子平动动能之和。
[ D ]4．在一密闭容器中，储有A 、B 、C 三种理想气体，处于平衡状态，A 种气体的分子数密度为 1n ，它产生的压强为 1p ，B 种气体的分子数密度为 12n ，C 种气体的分子数密度为3n 1，则混合气体的压强p 为(A)31p (B)41p(C)51p (D)61p二 填空题1．在定压下加热一定量的理想气体，若使其温度升高1K 时，它的体积增加了0.005倍，则气体原来的温度是_________200k__________。
2．用总分子数N 、气体分子速率v 和速率分布函数f(v)，表示下列各量：(1)速率大于0v 的分子数= ⎰∞0)(v dv v Nf ；(2)速率大于0v 的那些分子的平均速率=⎰⎰∞∞00)()(v v dv v f dv v vf ；(3)多次观察某一分子的速率，发现其速率大于0v 的概率=⎰∞0)(v dv v f 。
大学物理学(第二版)课件：气体动理论
分子的自由度为i，则一个 分子平均能量为ikT/2， 1摩尔理想气体内能
E＝ i 2
kT
NA
i 2
RT
m/M摩尔理想气体内能
说明： •理想气体的内能与温度、分 子数和分子的自由度有关。 •理想气体内能仅是温度的函 数，即E=E(T)。 •理想气体从T1→T2,不论经 过什么过程，内能变化为
E＝ m i RT M2
3. 分子(或原子)之间存在相互作用力
如： 铅柱重新接合、流体很难压缩 吸引力——固、液体聚集在一起 排斥力——固、液体较难压缩
分子力f与分子间距离r的关系
分子力 f 与分子之间的距离r有关 存在一个r0——平衡位置
r= r0≈10-10m时，分子力为零 r < r0分子力表现在排斥力 r > r0分子力表现在吸引力
J z2
t = 3, r = 2, v = 0
i=t+r+v=5
（3）非刚性双原子分子气体，其分子运动比刚性双原子 分子多了一个沿x轴方向的振动
1 2
mvC2x
1 2
mvC2y
1 2
mvC2z
1 2
J
2 y
1 2
J
2 z
1 2
v
2 Rx
1 kx2 2
t = 3, r = 2, v = 2
i=t+r+v=7
t
1 2
mv
2 x
1 2
mv
2 y
1 2
mv
2 z
t = 3, r = 0, v = 0
i=t+r+v=3
（2）刚性双原子分子气体，即分子中两个原子之间的距离 固定不变，只有整体平动和转动，绕x轴的转动惯量近似为 零，没有振动
大学物理(气体动理论)习题答案
大学物理（气体动理论）习题答案8-1 目前可获得的极限真空为Pa 1033.111-⨯，，求此真空度下3cm 1体积内有多少个分子?(设温度为27℃)[解] 由理想气体状态方程nkT P =得 kT V NP =，kT PV N =故 323611102133001038110110331⨯=⨯⨯⨯⨯⨯=---...N (个)8-2 使一定质量的理想气体的状态按V p -图中的曲线沿箭头所示的方向发生变化，图线的BC 段是以横轴和纵轴为渐近线的双曲线。
(1)已知气体在状态A 时的温度是K 300=A T ，求气体在B 、C 、D 时的温度。
(2)将上述状态变化过程在 T V -图(T 为横轴)中画出来，并标出状态变化的方向。
[解] (1)由理想气体状态方程PV /T ＝恒量，可得：由A →B 这一等压过程中BBA A T V T V = 则 6003001020=⋅=⋅=A AB B T V V T (K) 因BC 段为等轴双曲线，所以B →C 为等温过程，则==B C T T 600 (K)C →D 为等压过程，则CCD D T V T V = 3006004020=⋅=⋅=C CD D T V V T (K) (2)8-3 有容积为V 的容器，中间用隔板分成体积相等的两部分，两部分分别装有质量为m 的分子1N 和2N 个, 它们的方均根速率都是0υ，求： (1)两部分的分子数密度和压强各是多少?(2)取出隔板平衡后最终的分子数密度和压强是多少?010203040[解] (1) 分子数密度 VNV N n VN V N n 2222111122====由压强公式：231V nm P =， 可得两部分气体的压强为 VV mN V m n P VV mN V m n P 3231323120220222012011====(2) 取出隔板达到平衡后，气体分子数密度为 VN N V N n 21+==混合后的气体，由于温度和摩尔质量不变，所以方均根速率不变，于是压强为：VV m N N V nm P 3)(31202120+==8-4 在容积为33m 105.2-⨯的容器中，储有15101⨯个氧分子，15104⨯个氮分子，g 103.37-⨯氢分子混合气体，试求混合气体在K 433时的压强。
大学物理第6章气动理论 PPT
用V表示。宏观上讲体积表示容 器的容积。微观上看是容器中分 子所能够到达的区域。
单位：立方米，m3。
2 压强：
用p表示。宏观上看，压强表示容器内的气体对容器壁单位面积 上的压力。微观上看，压强表示容器内分子热运动对容器壁单 位面积上的平均冲力。
单位：帕（斯卡），Pa。1atm=1.013×105Pa。
3.状态方程的其他形式
pV NRTpNRT
NA
VNA
分子数密度 玻尔兹曼常量
n N V
kR1.3810 23JK1 NA
p nkT
当然也可利用摩尔数与气体质量的关系，导出其他形式。
MNmnm
VV
§6.2 理想气体的压强和温度 一、统计规律及其基本特征
孤立系统中，大量分子无休止的运动和彼此频繁的碰撞，使得动量、 能量以及分子自身在系统各处平均化，从而温度、压强等宏观量也趋 于相等，系统自发达到热力学平衡。
大学物理第6章气动理论
汇集全球三分之一智慧的照片: (1927年，第五届索尔维会议，比利时布鲁塞尔， 参加这次会议的29人中有17人获得或后来获得诺贝尔奖)
《大学物理学》 本学期教学内容
热学6-7章 《大学物理学》上册
振动与波动 《大学物理学》下册
光学
《大学物理学》下册
近代物理 《大学物理学》下册
三、理想气体及其状态方程
1.理想气体 热力学系统涉及的几个实验规律
玻意尔定律 盖-吕萨克定律 查里定律
pVConstant
p Constant T V Constant T
我们把严格遵守玻意尔定律、盖-吕萨克定律和查里定律的气体称 为理想气体。
理想气体一般是指密度足够低，温度足够高，压强不太大的气体。
大学物理气体动理论
v v+dv
v
在平衡态下, 设分子总数为N, 速率在v~v+dv区间的 分子数为dN个, 那么 表dN示：
N
——速率在v~v+dv区间的分子数占总分子数的比率。
或一个分子速率处于v~v+dv区间的概率。
dN ~ dv N ~ v f (v)
即 dN f (v)dv N
由 dN f (v)dv N
总之, 理想气体可看作是一群彼此间无相互作用 的无规运动的弹性质点的集合。
二、平衡态的统计假设——等几率原理
1、理想气体处于平衡态时, 分子出现在容器内 各处的几率相等。即分子数密度处处相等, 具 有分布的空间均匀性。
2、分子朝各个方向运动的几率相等, 具有运动 的各向同性。
v 0, vx vy vz 0
（4）粒子的平均速率、方均根速率和最概然速率。
解 (1) 按图所示的速率分布曲线形状, 应有
kv
f
(v)
0
(v v0 ) (v v0 )
由速率分布函数的归一化条件, 可得
f (v)dv
0
v0 0
kvdv
1 2
kv 02
1
故速率分布函数为
2v
f
(v)
v02 0
(v v0 ) (v v0 )
f（v）
得
f (v) dN
Ndv
v v+dv
v
f (v) 称为分子的速率分布函数。
其物理意义是：在速率v附近, 单位速率区间内的分子 数占总分子数的比率。
或一个分子速率出现在v附近单位速率区间内的概率。
所以 f (v) 也称为分子速率分布的概率密度。
3、关于速率分布函数的几点重要讨论：
《大学物理》气体动理论练习题及答案解析
《大学物理》气体动理论练习题及答案解析一、简答题1、你能够从理想气体物态方程出发 ，得出玻意耳定律、查理定律和盖吕萨克定律吗? 答： 方程RT Mm pV '=描述了理想气体在某状态下，p ，V ，T 三个参量所满足的关系式。
对给定量气体（Mm '不变），经历一个过程后，其初态和终态之间有222111T V p T V p =的关系。
当温度不变时，有2211V p V p =，这就是玻意耳定律；当体积不变时，有2211T p T p =，这就是查理定律；当压强不变时，有2211T V T V =，这就是盖吕萨克定律。
由上可知三个定律是理想气体在经历三种特定过程时所表现出来的具体形式。
换句话说，遵从玻意耳定律、查理定律和盖吕萨克定律的气体可作为理想气体。
2、为什么说温度具有统计意义? 讲一个分子具有多少温度，行吗?答：对处于平衡态的理想气体来说，温度是表征大量分子热运动激烈程度的宏观物理量，是对大量气体分子热运动状态的一种统计平均，这一点从公式kT v m 23212=中的2v 计算中就可以看出（∑∑=iii Nv N v22），可见T 本质上是一种统计量，故说温度具有统计意义，说一个分子的T 是毫无意义的。
3、解释下列分子运动论与热力学名词：(1) 状态参量；(2) 微观量；(3) 宏观量。
答：（1）状态参量：在一定的条件下，物质系统都处于一定的状态下，每个状态都需用一组物理量来表征，这些物理量称为状态参量。
（2）微观量：描述个别分子运动状态的物理量。
（3）宏观量：表示大量分子集体特征的物理量。
4、一定量的理想气体处于热动平衡状态时，此热力学系统的不随时间变化的三个宏观量和不随时间变化的微观量分别有哪些？建议：本题“不随时间变化的微观量分别有哪些”不知道通过该设问需要学生掌握什么东西。
其实从微观角度来讲，分子的任何量，如分子速度，动能，动量，严格说来甚至质量也是变化的。
可能会有人回答为平均速度、平均速率、平均自有程等，但那又是一种统计行为，该值对应着某些宏观量，这只能称为统计量，与微观量和宏观量相区别。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
温度T的关系。
（2）求压强为1atm，温度为0o C的情况下
气体分子间的平均距离l。
解：（1）P = nkT
n =
N
⇒1=V
3
=l
V nN
1
l
=
⎛ ⎜
kT
⎞ ⎟
3
⎝P⎠
(2). l =
⎛ ⎜ ⎝
kT P
1
⎞3 ⎟ ⎠
=
1
⎜⎜⎛ ⎝
1.38×10−23 × 273 1.013×105
⎟⎟⎞ ⎠
1038
大爆炸后的宇宙温度
温 度 大 观
109
108 107 106 105 104 103 102
10
1 10−1
10−2 10−3 10−4
10−5
10−6 10−7 10−8
~
宇宙He合成 热核聚变温度（太阳中心温度）
太阳表面温度（6000K） 室温 宇宙微波背景辐射（2.735K） 稀释制冷
解： 设瓶内原装氧气的质量为m,重新充气时瓶内剩余氧气的 质量为m2,每天用氧的质量为m1,则按理想气体的状态方程有：
m
=
PVM RT
, m2
=
P2VM RT
, m1
=
P1V1M RT
,
可用天数：m − m2 = (P − P2 )V = 9(天）
m1
P1V1
[例]：（1）试求气体分子间的平均距离l与压强P、
3
= 3.34×10−9 m (约为分子直径的10倍）
气体动理论 (Kinetic Theory of Gases)
平衡态：系统内部没有宏观的粒子和能量流动，其 宏观性质不随时间改变。是一种动态平衡， 并伴随涨落。布朗运动是可观测的涨落现 象之一。
非平衡态：当处在平衡态的系统受到外界影响时， 内部会出现宏观的粒子和能量流动，此时 系统处在非平衡态。
平衡态
非平衡态
平衡态
平衡态原理：一个孤立的热力学系统，不管它原来 处在什么状态，总会自 发地趋向平衡态， 并保持这个状态不变。
核自旋制冷
失控的温室效应造成 高达4600C的干热金星
高悬天际蔚蓝的地球
地 球 就 是 好 �
失控的冰川效应造成的 零下几十度的冰冷火星
§理想气体状态方程
理想气体在任一平衡态下各宏观量之间的关系称 为理想气体状态方程。
m pV = RT
M
pV =ν ⋅ RT
R为普适气体常数
R
=
p0Vm ,0
1.013 × 105 × 22.4 × 10−3 =
温度
§ 温度 理想气体温标
一、热平衡
A
绝热板
A
A、B两体系互
B 不影响，各自
B
达到平衡态。
二、热力学第零定律
设 A 和 C、B 和 C 分别热平 衡，则 A 和 B 一定热平衡。
导热板
两体系的平衡态有联 系，达到共同的热平 衡状态 (热平衡)。
绝热板
A
B 导热板
C
互为热平衡的热力学体系，必定具有一个共同的宏观物 理性质和相同的宏观参量 ⎯ 温度。
三、平衡态的状态参量
1. 状态参量： 描述系统宏观性质（热学、力学、化 学、电磁等）的宏观量。
2. 气体的状态参量：
体积 V
几何描述 SI 单位：m3
1 l=10-3 m3
压强 p
力学描述
SI 单位：Pa (N/m2)
1 atm=1.01325×105 P来自 = 76 cmHg温度T
热力学描述 反映物质分子运动的剧烈程度。
一、热力学系统与外界
热力学系统：要含有大量原子、分子或其 它微观粒子，体积有限的宏 观物体。热力学研究的对象。
系统
外 界： 热力学系统以外的物体。
系统分类： 1. 孤立系统： 无物质、能量的交换。 2. 封闭系统： 有能量交换，无物质交换。 3. 开放系统： 既有物质交换又有能量交换。
二、平衡态
四、 温 标 温度的数值表示法称为温标。
1. 热力学温标(T):
单位：开[尔文](K)
玻意耳定律： pV = 常数 （温度不变）
参考点： 三相点温度 T3 ≡ 273.15K
2. 摄氏温标 (t)
单位：摄氏度(
�
C
)
t = T − 273.15
五、热力学第三定律
热力学零度是不能达到的。
温度
T K
THERMOTICS
绪论
一、研究对象
热学是研究与热现象有关的规律的科学。 热现象：与温度有关的物理性质的变化统称为
热现象。 微观本质：热现象是物质中大量分子无规则运动
的集体表现(实验证明：布朗运动)。
反映气体分子热运动的特征：小、多、快、乱。
二、热学的研究方法：
宏观法：最基本的实验规律 + 逻辑推理 热力学
m−3
=
2.45 × 1025 m−3
(2)
n
=
p kT
＝ 1.33×10−5 1.38×10−23 × 300
m
−3
=
3.21× 1015m−3
热 学
例：容积V=30L的高压钢瓶内装有P=130atm的氧气， 做实验每天需用P1=1atm和V1=400L的氧气，规定氧气 压强不能降到P2=10atm以下，以免开启阀门时混进空气。 试计算这瓶氧气使用几天后就需要重新充气。
p = nkT
理想气体状态方程
例: 一容器内装有气体，温度为 27 oC，问： (1) 压强为1.013×105 Pa时，在 1 m3 中有多少个分子； (2) 在高真空时，压强为 1.33×10-5 Pa，在 1 m3 中有多
少个分子?
解： 按公式 p = nkT 可知
(1)
n
=
p kT
＝ 1.013×105 1.38×10−23 × 300
三、 温 度
决定一个系统是否与其它系统达到热平衡的宏观性质。
处于热平衡的多个系统具有相同的温度
具有相同温度的几个系统放在一起必然处于热平衡。
温度测量
酒精或水银
A
B
A 和 B 热平衡，TA = TB
热胀冷缩特性，标准 状态下，冰水混合， B 上留一刻痕， 水沸 腾，又一刻痕，之间 百等份，就是摄氏温 标（Co）。
T0
273.15
= 8.31(Jmol⋅K)
若写成 ν = N NA
N A = 6.023 × 1023 / mol
N为气体分子总数 阿伏伽德罗常量
µN
R
pV = RT = N T
µNA
NA
令
k
≡
R NA
=
1.38 × 10−23
J
K
玻耳兹曼常数
pV = NkT
p = N kT = nkT V
n：气体分子数密度
研究热现象的宏观理论(热力学第零、一、 二、三定律)，可靠、普遍。其概念、方 法和结论远远超出物理学范畴。
微观法：物质微观结构假设 + 统计平均方法
+ 与实验事实比较
统计力学
研究热现象的微观理论，揭示了热现象 的微观本质。其初级理论称为气体分子 运动论 (气体动理论).
宏观法与微观法相辅相成。
§ 宏观与微观