2013年高考数学必做客观题——立体几何
2013高考数学 解题方法攻略 立体几何3 理

6 ,则直线 AB 与 CD 所成角的余弦值为( 4
)
-2-
A.
1 2
B. 2
2
C.1 4A NhomakorabeaD. 3 3
F D A D E B B C O C G
【练习 2】若三棱锥 A—BCD 的侧面 ABC 内一动点 P 到棱 AB 的距离与到棱 BC 的距离相等,且 ∠ABC=40°,则 BP 与平面 BCD 所成角θ 的取值范围是 【提示】如图,P 到棱 AB 为距离与到棱 BC 的距离相等, BP 是 PBC 20°,利用最小角定理知:θ ∠PBC=20
,即转化为过空间一点的直线与两异面直线所成角相等的问题。
【考点 3】球与球面距离 S 【例题 5】在半径为 R 的球内有一 都在同一个大圆上, 一个动点从三 过其余三点后返回, 则经过的最短 B A.2π R C. 8 R
立体几何
.专题综述: 立体几何的主要任务是培养学生的空间想像能力,当然推理中兼顾逻辑思维能力的培养, 几何是研究位置关系与数量关系的学科,而位置关系与数量关系可以相互转化,解决立体几 何的基本方法是将空间问题转化为平面的问题,即空间问题平面化,平面化的手法有:平移 (包括线、面、体的平移) 、投影、展开、旋转等变换。 1.考纲要求 (1)掌握平面的基本性质。会用斜二测的画法画水平放置的平面图形的直观图:能够画 出空间两条直线、直线和平面的各种位置关系的图形,能够根据图形想像它们的位置关系。 (2)掌握直线和平面平行的判定定理和性质定理:理解直线和平面垂直的概念,掌握直 线和平面垂直的判定定理:掌握三垂线定理及其逆定理。 (3)理解空间向量的概念,掌握空间向量的加法、减法和数乘。 (4)了解空间向量的基本定理;理解空间向量坐标的概念,掌握空间向量的坐标运算。 (5)掌握空间向量的数量积的定义及其性质:掌握用直角坐标计算空间向量数量积的公 式;掌握空间两点间距离公式。 (6)理解直线的方向向量、平面的法向量、向量在平面内的射影等概念。 (7)掌握直线和直线、直线和平面、平面和平面所成的角、距离的概念,对于异面直线 的距离,只要求会计算已给出公垂线或在坐标表示下的距离掌握直线和平面垂直的性质定理 掌握两个平面平行、垂直的判定定理和性质定量。 (8)了解多面、凸多面体的概念,了解正多面体的概念。 (9)了解棱柱的概念,掌握棱柱的性质,会画直棱柱的直观图。 (10)了解棱锥的概念,掌握正棱锥的性质,会画正棱锥的直观图。 (11)了解球的概念,掌握球的性质,掌握球的表面积、体积公式。 2.考题设置与分值 从近几年各地高考试题分析,立体几何题型一般是 1 至 3 个填空或选择题,1 个解答题, 分值 25 分左右 3.考试重点与难度 (1)空间基本的线、面位置关系。一般以客观题的形式出现,试题很基础,但需要全面、 准确掌握空间线、面位置关系的判断、性质,还需要有好的空间感。 (2)空间距离和角的计算。一般以主观题的形式出现,以棱柱、棱锥或其部分图为试题 背景,其解题方法一般都在二种以上,并且一般都能用空间向量求解(但不一定是最简单的 解法) 。立体几何的解答题一般设置在解答题的前三题之一,所以试题不很难,属中档题。 (3)球的有关问题,特别是球面距离的计算,也是高考的重点考察内容。 (4)平面图形的翻折与空间图形的铺展能很好的考察学生的空间想象能力,这往往作为 立体几何试题的背景。 总之,立体几何试题难度不大,是我们必须抓好的得分点。 二.考点选讲 【考点 1】空间基本的线、面位置关系的判断 【例题 1】设 a、b 是异面直线,给出以下五个命题: ①存在唯一平面 ,使 a、b 与α 距离相等;
2013年高考数学各地名校文科立体几何试题解析汇编

2013年高考数学各地名校文科立体几何试题解析汇编D的外接球表面积,选B.7 【山东省兖州市2013届高三9月入学诊断检测文】设是直线,a,β是两个不同的平面A. 若∥a,∥β,则a∥β B. 若∥a,⊥β,则a⊥βC. 若a⊥β,⊥a,则⊥βD. 若a ⊥β, ∥a,则⊥β【答案】B【解析】根据线面垂直的判定和性质定理可知,选项B正确。
8 【山东省兖州市2013届高三9月入学诊断检测文】某几何体的三视图如下图所示,它的体积为( )A. B. C.D.【答案】C【解析】由三视图可知该组合体是半个球体和一个倒立圆锥体的组合体,球的半径为3,圆锥的底面半径为3,高为4,那么根据体积公式可得组合体的体积为,选C.9 【云南省昆明一中2013届高三新课程第一次摸底测试文】某几何体的三视图如图所示,则该几何体的表面积为A.B.C.D.32【答案】B【解析】根据三视图可知,这是一个四棱台,,,所以表面积为,选B.10 【云南省昆明一中2013届高三新课程第一次摸底测试文】如图,在长方体ABCD—A1B1C1D1中,对角线B1D与平面A1BC1相交于点E,则点E为△A1BC1的A.垂心B.内心C.外心D.重心【答案】D【解析】如图,,所以,且为的中点,选D.11 【山东省烟台市莱州一中20l3届高三第二次质量检测(文)】对于直线m,n和平面,有如下四个命题:(1)若(2)若(3)若(4)若其中真命题的个数是A.1B.2C.3D.4【答案】A【解析】(1)错误。
(2)当时,则不成立。
(3)不正确。
当有,又所以有,所以只有(4)正确。
选A.12 【云南师大附中2013届高三高考适应性月考卷(三)文】一个几何体的三视图如图1所示,其中正视图是一个正三角形,则该几何体的体积为A.1 B.C.D.【答案】B【解析】由三视图可知,此几何体为三棱锥,如图,其中正视图为,是边长为2的正三角形,,且,底面为等腰直角三角形,,所以体积为,故选B.13 【天津市新华中学2012届高三上学期第二次月考文】如图,是一个几何体的正视图、侧视图、俯视图,则该几何体的体积是A. 24B. 12C. 8D. 4【答案】B【解析】由三视图可知,该几何体是有两个相同的直三棱柱构成,三棱柱的高为4,三棱柱的底面三角形为直角三角形,两直角边分别为,所以三角形的底面积为,所以三棱柱的体积为,所以该几何体的体积为,选B.14 【山东省临沂市2013届高三上学期期中考试数学文】某几何体的正视图和侧视图均如右图,则该几何体的俯视图不可能有是【答案】D【解析】因为该几何体的正视图和侧视图是相同的,而选项D的正视图和和侧视图不同。
2013年高考数学试题(8)立体几何

1.(安徽理科第6题、文科第8题)(A ) 48 (B)32+817 (C) 48+8 (C) 48+817 (D) 80解析:由三视图可知几何体是底面是等腰梯形的直棱柱.底面等腰梯形的上底为2,下底为4,高为4,两底面积和为()12244242´+´=,四个侧面的面积为()44221724817++=+,所以几何体的表面积为48817+故选C. 2.(安徽理科第17题,文科第19题,本小题满分13分)分) 如图,A B E D F C 为多面体,平面ABED 与平面A C F D 垂直,点O 在线段A D 上,1O A =,OD =,ODE ODF OAC OAB D D D D ,,,都是正三角形。
都是正三角形。
(Ⅰ)证明直线BC EF ∥;(Ⅱ)求棱锥F OBED -的体积. (1)证明:分别去OA ,OD 的中点M ,N ,连接CM ,BM,BMEN,FN,设EB和DA相交于G,由于OA=1,EN,FN,设EB和DA相交于G,由于OA=1,OD=2,则EN BM //,且EN BM 21=,则M 为GN 的中点,所以GA=1 同理可得:G 为FC 和DA 的交点。
则有C 为FG 的中点,B 为EG 的中点。
所以的中点。
所以BC 是EFG D 的中位线。
故BC EF ∥。
(2)四边形OBED 是梯形,其中OB=1,DE=2,底边上的高为323260sin =×=°OE2333)21(2131331=××+×=×=\-O B E D O B E DF S V3.(北京理科第7题)某四面体的三视图如图所示,该四面体四个面的面积中,最大的是某四面体的三视图如图所示,该四面体四个面的面积中,最大的是某四面体的三视图如图所示,该四面体四个面的面积中,最大的是(A) 8 (B) 62 (C)10 (D) 82解:根据三视图可知,该四面体满足:^SA 平面ABC ,ABC D 中 °=Ð90ABC ,3,4===BC AB SA ,四个三角形都是直角三角形,四个三角形都是直角三角形 6,26,8,10,5,24======D D D D ABC SBC SAB SAC S S S S AC SB4.(北京理科第16题)如图,在四棱锥P ABCD -中,P A ^平面ABCD ,底面ABCD 是菱形,2,60A B B A D =Ð=.(Ⅰ)求证:BD ^平面;P A C(Ⅱ)若,P A A B =求P B 与A C 所成角的余弦值;所成角的余弦值; (Ⅲ)当平面P B C 与平面P D C 垂直时,求P A 的长的长. .解:(1)因为ABCD 是菱形,则对角线互相垂直,BD AC ^\,又^PA 平面ABC所以BD ^平面PAC ,(2)设O BD AC = ,3,1,2,60=====°=ÐCO AO BO AB PA BAD以以O 为坐标原点以OC OB ,所在的直线分别为y x ,轴建立空间直角坐标系xyz O -则)0,3,0(),0,1,1(,0,3,0(),2,3,0(C B A P )--,)2,3,1(-=\PB ,)0,32,0(=AC 设AC PB ,的夹角为q ,则4632226||||cos=´=×=AC PB AC PB q(3)由()由(22)知),0,3,1(-=BC 设)0)(,3,0(>t t P 设平面PBC 的法向量为),,(z y x m =,则0,0=×=×m BP m BC所以ïîïíì=+--=+-0303tz y x y x ,令3=y ,则t z x 6,3==,)6,3,3(t m =\同理,平面PDC 的法向量为)6,3,3(tn -=,因为平面PBC ^平面PDC 所以0=×n m ,即03662=+-t,解得6=t ,6=\PA5.(北京文科第5题)某四棱锥的三视图如图所示,该四棱锥的表面积是锥的表面积是(A)32 (B)16+162 (C)48 (D)16322+6.(北京文科17)如图,在四面体PABC 中,,,P C A B P A B C ^^点,,,D E F G 分别是棱,,,A PA CB C P B的中点。
2013高考数学真题——立体几何分类汇编 2

2013高考数学—导数分类汇编1.(2013山东卷理4)已知三棱柱111C B A ABC -的侧棱与底面垂直,体积为49,底面是边长为3的正三角形,若P 为底面111C B A 的中心,则PA 与平面ABC 所成角的大小为.A π125 .B 3π .C 4π .D 6π2.(2013山东卷理18)如图所示,在三棱锥ABQ P -中,⊥PB 平面ABQ ,BQ BP BA ==,F E C D ,,,分别是BP AP BQ AQ ,,,的中点,BD AQ 2=,PD 与EQ 交于点G ,PC 与FQ 交于点H ,连接GH 。
(1)证明:AB ∥GH ;(2)求二面角E GH D --的余弦值。
3.(2013陕西卷理12)某几何体的三视图如图所示,则其体积为 。
俯视图主视图左视图4.(2013陕西卷理18)如图,四棱柱1111D C B A ABCD -的底面ABCD 是正方形,O 为底面中心,⊥O A 1平面ABCD ,21==AA AB 。
(1) 证明:⊥C A 1平面D D BB 11;(2) 求平面1OCB 与平面D D BB 11的夹角θ的大小。
5.(2013新课标2卷理4)已知n m ,为异面直线,m ⊥平面α,⊥n 平面β,直线l 满足m l ⊥,n l ⊥,βα⊄⊄l l ,,则.A α∥β且l ∥α .B α⊥β且l ⊥β.C α与β相交,且交线垂直于l .D α与β相交,且交线平行于l6.(2013新课标2卷理7)一个四面的顶点在空间直角坐标系xyz O -中的坐标分别是)1,0,1(,)0,1,1(,)1,1,0(,)0,0,0(,画该四面体的正视图时,以zOx 平面为投影面,则得正视图可以为A B C DAB17.(2013新课标2卷理18)如图,直三棱柱111C B A ABC -中,E D ,分别1,BB AB 的中点,AB CB AC AA 221===. (1)证明:1BC ∥平面CD A 1; (2)求二面角E C A D --1的正弦值。
2013年高考名题选编(立体几何)
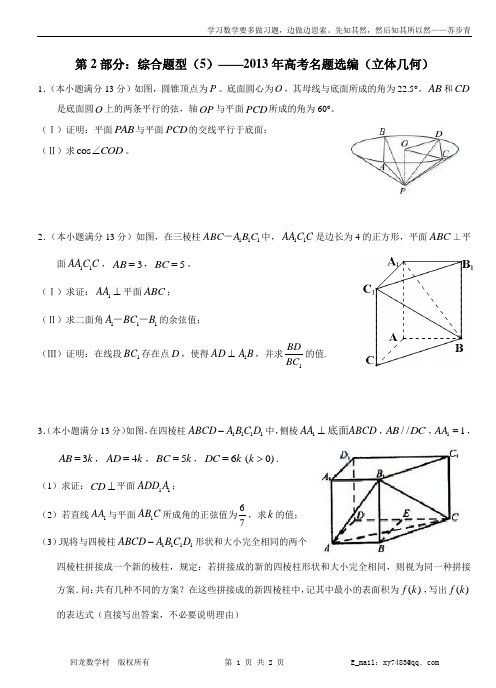
第2部分:综合题型(5)——2013年高考名题选编(立体几何)1.(本小题满分13分)如图,圆锥顶点为P 。
底面圆心为O ,其母线与底面所成的角为22.5°。
AB 和CD是底面圆O 上的两条平行的弦,轴OP 与平面PCD 所成的角为60°。
(Ⅰ)证明:平面PAB 与平面PCD 的交线平行于底面; (Ⅱ)求cos COD ∠。
2.(本小题满分13分)如图,在三棱柱111ABC A B C -中,11AA C C 是边长为4的正方形,平面ABC ⊥平面11AA C C ,3AB =,5BC =。
(Ⅰ)求证:1AA ⊥平面ABC ; (Ⅱ)求二面角111A BC B --的余弦值;(Ⅲ)证明:在线段1BC 存在点D ,使得1AD A B ⊥,并求1BDBC 的值.3.(本小题满分13分)如图,在四棱柱1111ABCD A B C D -中,侧棱1AA ABCD ⊥底面,//AB DC ,11AA =,3AB k =,4AD k =,5BC k =,6DC k =(0)k >.(1)求证:CD ⊥平面11ADD A ;(2)若直线1AA 与平面1AB C 所成角的正弦值为67,求k 的值;(3)现将与四棱柱1111ABCD A B C D -形状和大小完全相同的两个四棱柱拼接成一个新的棱柱,规定:若拼接成的新的四棱柱形状和大小完全相同,则视为同一种拼接方案.问:共有几种不同的方案?在这些拼接成的新四棱柱中,记其中最小的表面积为()f k ,写出()f k 的表达式(直接写出答案,不必要说明理由)4.(本小题满分13分)如图1,在等腰直角三角形ABC 中,90A ∠=︒,6BC =,,D E 分别是,AC AB 上的点,CD BE ==O 为BC 的中点.将ADE ∆沿DE 折起,得到如图2所示的四棱锥A BCDE '-,其中A O '=。
(1)证明:A O '⊥平面BCDE ;(2)求二面角A CD B '--的平面角的余弦值。
2013高考数学试题分类汇编:专题09 立体几何(解析版b)
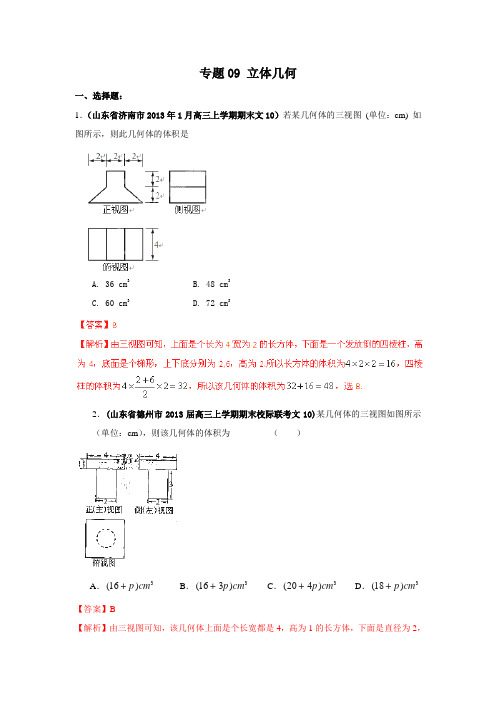
专题09 立体几何一、选择题:1.(山东省济南市2013年1月高三上学期期末文10)若某几何体的三视图 (单位:cm) 如图所示,则此几何体的体积是A. 36 cm 3B. 48 cm 3C. 60 cm 3D. 72 cm 32.(山东省德州市2013届高三上学期期末校际联考文10)某几何体的三视图如图所示(单位:cm ),则该几何体的体积为 ( )A .3(16)cm p +B .3(163)cm p +C .3(204)cm p +D .3(18)cm p + 【答案】B【解析】由三视图可知,该几何体上面是个长宽都是4,高为1的长方体,下面是直径为2,高为3的圆柱。
所以长方体的体积为314416()cm ⨯⨯=,圆柱的体积为333()cm ππ⨯=,所以该几何体的体积为3(163)cm p +,选B.3. (山东省济宁市2013届高三1月份期末测试文7)下列命题中错误..的是 A.如果平面α⊥平面β,那么平面α内一定存在直线平行于平面βB.如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面βC.如果平面α⊥平面γ,平面β⊥平面γ,l αβ⋂=,那么直线l ⊥平面γD.如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β4. (山东省烟台市2013届高三上学期期末文6)右图是底面半径为1,母线长均为2的圆锥和圆柱的组合体,则该组合体的侧视图的面积为A.8πB.6πC.4+D.2+5. (山东省烟台市2013届高三上学期期末文10)已知直线a 和平面,,l a a αβαβαβ=⊄⊄I 、,,且a 在αβ、内的射影分别为直线b 和c ,则b 和c 的位置关系是A.相交或平行B.相交或异面C.平行或异面D.相交、平行或异面6.(山东省潍坊市2013年1月高三上学期期末考试A 卷文7)设m ,n 是两条不同直线,βα,是两个不同的平面,下列命题正确的是(A )βα//,//n m 且,//βα则n m //(B ) βα⊥⊥n m ,且 βα⊥,则 n m ⊥(C ),,,n m n m ⊥⊂⊥βα 则βα⊥(D ),//,//,,ββααn m n m ⊂⊂则βα//7. (山东省潍坊市2013年1月高三上学期期末考试A 卷文10)一个几何体的三视图如图所示,其中主视图和左视图是腰长为4的两个全等的等腰直角三角形,若该几何体的所有顶点在同一球面上,则该球的表面积是(A )π12(B )π24 (C )π32 (D )π48【答案】D 【解析】该几何体的直观图如图1所示,它是有一条侧棱垂直于底面的四棱锥.其中底面ABCD 是边长为4的正方形,高为CC 1=4,该几何体的所有顶点在同一球面上,则球的直径为D.8.(山东省泰安市2013届高三上学期期末文2)如图,若一个空间几何体的三视图中,正视图和侧视图都是直角三角形,其直角边均为1,则该几何体的体积为A.13B.12C.16D.19.(山东省泰安市2013届高三上学期期末文8)下列命题正确的是A.若两条直线和同一个平面所成的角相等,则这两条直线平行B.若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行C.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D.若两个平面都垂直于第三个平面,则这两个平面平行10. (山东省青岛即墨市2013届高三上学期期末考试文7)设a,b 是不同的直线,βα、是不同的平面,则下列命题:①若βα//,//,b a b a 则⊥ ②若ββαα⊥⊥a a 则,,//③若αβαβ//,,a a 则⊥⊥ ④若βαβα⊥⊥⊥⊥则,,,b a b a 其中正确命题的个数是 A.0 B.1 C.2 D.311.(山东省潍坊一中2013届高三12月月考测试文)已知直线a 和平面,,,,l a a a b a ba b ?怂,且a 在,a b 内的射影分别为直线b 和c ,则b 和c 的位置关系是 A.相交或平行 B.相交或异面 C.平行或异面 D.相交、平行或异面12.(山东省潍坊一中2013届高三12月月考测试文)四棱锥P ABCD -的三视图如右图所示,四棱锥P ABCD -的五个顶点都在一个球面上,E 、F 分别是棱AB 、CD 的中点,直线EF 被球面所截得的线段长为 A.12pB.24pC.36pD.48p【答案】A13.(山东省师大附中2013届高三第四次模拟测试1月文)已知两条直线 a ,b 与两个平面α、αβ⊥b ,,则下列命题中正确的是①若α//a ,则b a ⊥;②若b a ⊥,则α//a ; ③若β⊥b ,则βα//;④若βα⊥,则β//b .A .①③B .②④C .①④D .②③14.(山东省师大附中2013届高三第四次模拟测试1月文)若一个底面为正三角形的几何体的三视图如右图所示,则这个几何体的体积为A .. C . . 615.(山东省青岛一中2013届高三1月调研考试文)已知某几何体的侧视图与其正视图相同,相关的尺寸如下图所示,则这个几何体的体积是( )A. 8πB. 7πC. 2π `D. 74π16.(山东省聊城市东阿一中2013届高三上学期期初考试)设直线m 、n 和平面βα、,下列四个命题中,正确的是 ( )A. 若n m n m //,//,//则ααB. 若βαββαα//,//,//,,则n m n m ⊂⊂C. 若βαβα⊥⊂⊥m m 则,,D. 若ααββα//,,,m m m 则⊄⊥⊥【答案】D【解析】因为选项A 中,两条直线同时平行与同一个平面,则两直线的位置关系有三种,选项B 中,只有Mm,n 相交时成立,选项C 中,只有m 垂直于交线时成立,故选D17.(山东省烟台市莱州一中20l3届高三第二次质量检测文)一个简单几何体的主视图,左视图如图所示,则其俯视图不可能为①长方形;②直角三角形;③圆;④椭圆.其中正确的是A.①B.②C.③D.④18.(山东省烟台市莱州一中20l3届高三第二次质量检测文)对于直线m ,n 和平面,,αβγ,有如下四个命题:(1)若//,,m m n n αα⊥⊥则(2)若,,//m m n n αα⊥⊥则 (3)若,,//αβγβαγ⊥⊥则(4)若,//,,m m n n αβαβ⊥⊂⊥则其中真命题的个数是A.1B.2C.3D.419.(山东省临沂市2013届高三上学期期中考试文)某几何体的正视图和侧视图均如右图,则该几何体的俯视图不可能有是二、填空题:20. (山东省济宁市2013届高三1月份期末测试文14)已知一个空间几何体的三视图如图所示,其中正视图、侧视图都是由半圆和矩形组成,根据图中标出的尺寸,可得这个几何体的体积是.21.(山东省潍坊一中2013届高三12月月考测试文)已知正四棱柱ABCD-A1B1C1D1的高为323p,则A、B两点的球面距离为____________.22.(山东省烟台市莱州一中20l3届高三第二次质量检测文)在正三棱锥S-ABC中,侧面-外接球的表SAB、侧面SAC、侧面SBC两两垂直,且侧棱SA=,则正三棱锥S ABC面积为____________.23.(山东省临沂市2013届高三上学期期中考试文)如图,正方体ABCD—A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=1,则四面体A—EFB的体积V等于。
2013年高考真题理科数学解析分类汇编7-立体几何 2范文
2013年高考真题理科数学解析分类汇编7 立体几何一选择题1.[湖南]7.已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能...等于A .1 B.C.D2.陕西12. 某几何体的三视图如图所示, 则其体积3π. 3.安徽理(3)在下列命题中,不是公理..的是 (A )平行于同一个平面的两个平面相互平行(B )过不在同一条直线上的三点,有且只有一个平面(C )如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内 (D )如果两个不重合的平面有一个公共点, 那么他们有且只有一条过该点的公共直线 4.广东5.某四棱台的三视图如图1所示,则该四棱台的体积是图1A. 4B.143 C.163D. 6 5.广东6.设m ,n 是两条不同的直线,,αβ是两个不同的平面,下列命题中正确的是 A.若,,m n αβαβ⊥⊂⊂,则m ⊥n ; B. 若//,,m n αβαβ⊂⊂,则//m nC. 若,,m n m n αβ⊥⊂⊂,则αβ⊥;D. 若,//,//m m n n αβ⊥,则αβ⊥6.新课标I ,6、如图,有一个水平放置的透明无盖的正方体容器,容器高8cm ,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm ,如果不计容器的厚度,则球的体积为 ( ) A 、500π3cm 3B 、866π3cm 3C 、1372π3cm 3D 、2048π3cm 37.新课标II 4、已知m ,n 为异面直线,m ⊥平面α,n ⊥平面β,直线l 满足l ⊥m ,l ⊥n ,l ⊄α, l ⊄β,则( )(A ) α∥β且l ∥α (B )α⊥β且l ⊥β (C )α与β相交,且交线垂直于l (D )α与β相交,且交线平行于l8、新课标II 7、一个四面体的顶点在空间直角坐标系O xyz -中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为投影面,则得到正视图可以为( )(A)(B)(C)(D)9.江西8.如图,正方体的底面与正四面体的底面在同一平面α上,且AB CD ,正方体的六个面所在的平面与直线CE ,EF 相交的平面个数分别记为,m n ,那么m n +=A.8B.9C.10D.11 10.辽宁(10)已知三棱柱1116.34ABC A BC O AB AC -==的个顶点都在球的球面上若,, ,AB AC ⊥112AA O =,则球的半径为A B .C .132D .11.全国(10)已知正四棱柱1111112,ABCD A BC D AA AB CD BDC -=中,则与平面所成角的正弦值等于(A )23(B )3 (C )3(D )1312.山东4、已知三棱柱111-ABC A B C 的侧棱与底面垂直,体积为94若P 为底面111A B C 的中心,则PA 与平面ABC 所成角的大小为(A)512π (B)3π (C) 4π (D) 6π 13.四川3、一个几何体的三视图如图所示,则该几何体的直观图可以是( )14.重庆5、某几何体的三视图如题()5图所示,则该几何体的体积为( )A 、5603B 、5803C 、200D 、240二填空题15.[江苏] 8.如图,在三棱柱ABC C B A -111中,F E D ,,分别是1AA AC AB ,,的中点,设三棱锥ADE F-的体积为1V ,三棱柱ABC C B A -111的体积为2V ,则=21:V V .【答案】1:2416.[全国] (16)已知圆O和圆K是球O的大圆和小圆,其公共弦长等于球O的半径,3602OK O K =,且圆与圆所在的平面所成角为,则球O 的表面积等于 . 答案16π17.辽宁(13)某几何体的三视图如图所示,则该几何体的体积是1616π-.三解答题18.广东18.如图5,在等腰直角三角形ABC 中,∠A=90°,BC=6,D 、E 分别是AC ,AB 上的点,O 是BC 的中点,将△ADE 折起得到如图6所示的四棱锥'ABCDE -,其中'A O =(1)证明'A O ⊥平面BCDE ;(2)求二面角'A CD B --的平面角的余弦值。
2013年立体几何 高考题汇总
立体几何一、选择题1 .(2013年高考四川卷(文))一个几何体的三视图如图所示,则该几何体可以是 ( )A .棱柱B .棱台C .圆柱D .圆台 2 .(2013年高考湖南(文))已知正方体的棱长为1,其俯视图是一个面积为1的正方形,侧视图是一个面积为的矩形,则该正方体的正视图的面积等于______( )A B .1 C D3.(2013年高考浙江卷(文))设m.n 是两条不同的直线,α.β是两个不同的平面,( ) A .若m∥α,n∥α,则m∥nB .若m∥α,m∥β,则α∥βC .若m∥n,m⊥α,则n⊥αD .若m∥α,α⊥β,则m⊥β4.(2013年高考广东卷(文))设l 为直线,,αβ是两个不同的平面,下列命题中正确的是 ( )A .若//l α,//l β,则//αβB .若l α⊥,l β⊥,则//αβC .若l α⊥,//l β,则//αβD .若αβ⊥,//l α,则l β⊥5.(2013年高考山东卷(文))一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如右图所示该四棱锥侧面积和体积分别是( )A .B .83C .81),3D .8,86.(2013年高考江西卷(文))一几何体的三视图如右所示,则该几何体的体积为( ) A .200+9π B .200+18π C .140+9π D .140+18π二、填空题7.(2013年高考课标Ⅱ卷(文))已知正四棱锥O-ABCD 的体积为,底面边长为,则以O 为球心,OA 为半径的球的表面积为________.8.(2013年高考湖北卷(文))我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水. 天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸. 若盆中积水深九寸,则平地降雨量是__________寸.(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸)9.(2013年高考北京卷(文))某四棱锥的三视图如图所示,该四棱锥的体积为__________.10.(2013年高考天津卷(文))已知一个正方体的所有顶点在一个球面上. 若球的体积为92π, 则正方体的棱长为 ______.三、解答题11.(2013年高考辽宁卷(文))如图,.AB O PA O C O 是圆的直径,垂直圆所在的平面,是圆上的点(I)求证:BC PAC ⊥平面;(II)设//.Q PAG AOC QG PBC ∆为的中点,为的重心,求证:平面12.(2013年高考陕西卷(文))如图, 四棱柱ABCD-A1B1C1D1的底面ABCD是正方形, O为底面中心, A1O⊥平面ABCD,1AB AA=1A(Ⅰ) 证明: A1BD // 平面CD1B1;(Ⅱ) 求三棱柱ABD-A1B1D1的体积.13.(2013年高考福建卷(文))如图,在四棱锥P ABCD-中,PD ABCD⊥面,//AB DC,AB AD⊥,5BC=,3DC=,4AD=,60PAD∠=.(1)当正视图方向与向量AD的方向相同时,画出四棱锥P ABCD-的正视图.(要求标出尺寸,并画出演算过程);(2)若M为PA的中点,求证://DM PBC面;(3)求三棱锥D PBC-的体积.14.(2013年高考湖南(文))如图2.在直菱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=,AA1=3,D是BC的中点,点E在菱BB1上运动.(I) 证明:AD⊥C1E;(II) 当异面直线AC,C1E 所成的角为60°时,求三棱柱C1-A2B1E的体积.15.(2013年高考北京卷(文))如图,在四棱锥P ABCD -中,//AB CD ,AB AD ⊥,2CD AB =,平面PAD ⊥底面ABCD ,PA AD ⊥,E 和F 分别是CD 和PC 的中点,求证:(1)PA ⊥底面ABCD ;(2)//BE 平面PAD ;(3)平面BEF ⊥平面PCD16.(2013年高考课标Ⅰ卷(文))如图,三棱柱111ABC A B C -中,CA CB =,1AB AA =,160BAA ∠=.(Ⅰ)证明:1AB AC ⊥; (Ⅱ)若2AB CB ==,1AC =,求三棱柱111ABC A B C -的体积. C 1B 1A A 1B C 17.(2013年高考山东卷(文))如图,四棱锥P ABCD -中,,AB AC AB PA ⊥⊥,,2AB CD AB CD =∥,,,,,E F G M N 分别为 ,,,,PB AB BC PD PC 的中点(Ⅰ)求证:CE PAD ∥平面;(Ⅱ)求证:EFG EMN ⊥平面平面18.(2013年高考课标Ⅱ卷(文))如图,直三棱柱ABC-A 1B 1C 1中,D,E 分别是AB,BB 1的中点.(1) 证明: BC 1//平面A 1CD;(2) 设AA 1= AC=CB=2,AB=2,求三棱锥C 一A 1DE 的体积.19.(2013年高考大纲卷(文))如图,四棱锥902,P ABCD ABC BAD BC AD PAB PAD -∠=∠==∆∆中,,与都是边长为2的等边三角形.(I)证明:;PB CD ⊥ (II)求点.A PCD 到平面的距离20.(2013年高考安徽(文))如图,四棱锥P ABCD -的底面ABCD 是边长为2的菱形,60BAD ∠=.已知2,PB PD PA === .(Ⅰ)证明:PC BD ⊥(Ⅱ)若E 为PA 的中点,求三棱锥P BCE -的体积.21.(2013年上海高考数学试题(文科))如图,正三棱锥O ABC 底面边长为2,高为1,求该三棱锥的体积及表面积.第19题图B22.(2013年高考江西卷(文))如图,直四棱柱ABCD – A 1B 1C 1D 1中,AB//CD,AD ⊥AB,AB=2,AD=,AA 1=3,E 为CD 上一点,DE=1,EC=3(1) 证明:BE ⊥平面BB 1C 1C;(2) 求点B1 到平面EA1C 1 的距离。
2013年高考数学试题分类汇编——立体几何
2013高考数学试题分类汇编——立体几何一、选择题1、(2010浙江理数)(6)设l ,m 是两条不同的直线,α是一个平面,则下列命题正确的是 (A )若l m ⊥,m α⊂,则l α⊥ (B )若l α⊥,l m //,则m α⊥ (C )若l α//,m α⊂,则l m // (D )若l α//,m α//,则l m //解析:选B ,可对选项进行逐个检查。
本题主要考察了立体几何中线面之间的位置关系及其中的公理和判定定理,也蕴含了对定理公理综合运用能力的考察,属中档题2、(2010全国卷2理数)(11)与正方体1111ABCD A B C D -的三条棱AB 、1CC 、11A D 所在直线的距离相等的点(A )有且只有1个 (B )有且只有2个 (C )有且只有3个 (D )有无数个 【答案】D【解析】直线上取一点,分别作垂直于于则分别作,垂足分别为M ,N ,Q ,连PM ,PN ,PQ ,由三垂线定理可得,PN ⊥PM ⊥;PQ ⊥AB ,由于正方体中各个表面、对等角全等,所以,∴PM=PN=PQ ,即P 到三条棱AB 、CC 1、A 1D 1.所在直线的距离相等所以有无穷多点满足条件,故选D.3、(2010全国卷2理数)(9)已知正四棱锥S ABCD -中,SA =,那么当该棱锥的体积最大时,它的高为(A )1 (B (C )2 (D )3 【答案】C【命题意图】本试题主要考察椎体的体积,考察告辞函数的最值问题.【解析】设底面边长为a ,则高所以体积,设,则,当y 取最值时,,解得a=0或a=4时,体积最大,此时,故选C.4、(2010陕西文数) 8.若某空间几何体的三视图如图所示,则该几何体的体积是 [B](A )2 (B )1(C )23(D )13解析:本题考查立体图形三视图及体积公式 如图,该立体图形为直三棱柱所以其体积为122121=⨯⨯⨯5、(2010辽宁文数)(11)已知,,,S A B C 是球O 表面上的点,SA ABC ⊥平面,AB BC ⊥,1SA AB ==,BC =O 的表面积等于(A )4π (B )3π (C )2π (D )π解析:选A.由已知,球O 的直径为22R SC ==,∴表面积为244.R ππ=6、(2010辽宁理数)(12) (12)有四根长都为2的直铁条,若再选两根长都为a 的直铁条,使这六根铁条端点处相连能够焊接成一个三棱锥形的铁架,则a 的取值范围是(A)((B)(1,(D) (0,221【答案】A【命题立意】本题考查了学生的空间想象能力以及灵活运用知识解决数学问题的能力。
2013高考数学真题——立体几何分类汇编
2013高考数学—导数分类汇编1.(2013山东卷理4)已知三棱柱111C B A ABC -的侧棱与底面垂直,体积为49,底面是边长为3的正三角形,若P 为底面111C B A 的中心,则PA 与平面ABC 所成角的大小为.A π125 .B 3π .C 4π .D 6π2.(2013山东卷理18)如图所示,在三棱锥ABQ P -中,⊥PB 平面ABQ ,BQ BP BA ==,F E C D ,,,分别是BP AP BQ AQ ,,,的中点,BD AQ 2=,PD 与EQ 交于点G ,PC 与FQ 交于点H ,连接GH 。
(1)证明:AB ∥GH ;(2)求二面角E GH D --的余弦值。
3.(2013陕西卷理12)某几何体的三视图如图所示,则其体积为 。
俯视图主视图左视图4.(2013陕西卷理18)如图,四棱柱1111D C B A ABCD -的底面ABCD 是正方形,O 为底面中心,⊥O A 1平面ABCD ,21==AA AB 。
(1) 证明:⊥C A 1平面D D BB 11;(2) 求平面1OCB 与平面D D BB 11的夹角θ的大小。
5.(2013新课标2卷理4)已知n m ,为异面直线,m ⊥平面α,⊥n 平面β,直线l 满足m l ⊥,n l ⊥,βα⊄⊄l l ,,则.A α∥β且l ∥α .B α⊥β且l ⊥β.C α与β相交,且交线垂直于l .D α与β相交,且交线平行于l6.(2013新课标2卷理7)一个四面的顶点在空间直角坐标系xyz O -中的坐标分别是)1,0,1(,)0,1,1(,)1,1,0(,)0,0,0(,画该四面体的正视图时,以zOx 平面为投影面,则得正视图可以为A B C DA17.(2013新课标2卷理18)如图,直三棱柱111C B A ABC -中,E D ,分别1,BB AB 的中点,AB CB AC AA 221===. (1)证明:1BC ∥平面CD A 1; (2)求二面角E C A D --1的正弦值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013年高考数学必做客观题——立体几何作者:余飞宏来源:《数学金刊·高考版》2013年第08期空间几何体的直观图与三视图(★★★★)必做1 图1是一个空间几何体的三视图,则该几何体的体积是________.[4][6][2][2][俯视图] [2][正视图][侧视图]图1[牛刀小试] [牛刀小试]精妙解法由三视图可以构造出空间图形(直观图)如图2所示. 在计算体积时,把左侧面看成底面,长为6的底棱看成高,这样就易得该几何体的体积为36.极速突击此类试题的突破点在于观察三视图,还原几何体. 如果几何体为锥体,那么只需将锥体的顶点从俯视图中拉起还原就行;如果几何体不是锥体,那么通常先找一个基本几何体,然后将它削出来,我们通常称之为“寄居法”,这个基本几何体就是我们所研究几何体“寄居”的壳.误点警示注意对得到的直观图,要“压扁”还原检验,看看其三视图是否符合要求.(★★★)必做2 若某多面体的三视图(单位: cm)如图3所示,则此多面体外接球的表面积是()A. 18π cm2B. 24π cm2C. 27π cm2D. 36π cm2[牛刀小试] [牛刀小试]精妙解法先还原出该几何体的直观图形. 该题所表达的几何体是一个棱长为3的正方体截去一个正三棱锥剩下的部分(如图4所示),所以这个几何体的外接球与(母体)正方体的外接球是一致的. 正方体的体对角线就是球的一直径. 答案选C.极速突击在正方体ABCD-A1B1C1D1中(如图5),各棱长为a,一个考生应该具备下面几个知识点:(1)正方体中有两个重要关系的截面,如截面A1C1B与截面AD1C,两个都是正三角形,且相互平行,都垂直于体对角线B1D,并且三等分B1D.(2)正方体的体对角线长相等且交于一点,互相平分,交点为O,它到正方体八个顶点的距离相等,所以正方体的外接球(过正方体的八个顶点的球)的球心就是O,直径等于正方体的体对角线的长.(3)正方体中如A1,C1,B,D四点构成一个正四面体,因此任何一个确定的正方体对应于一种大小确定的正四面体;反过来,任何一个正四面体,只能扩张为一个确定的正方体. 从而在解决正四面体的许多数量关系时可以考虑外延到正方体中进行思考(这种方法容易记忆),如正四面体的高就等于正方体的体对角线长的,正四面体相对棱之间的距离等于正方体的棱长,正四面体的外接球就是正方体的外接球等.(4)正方体可以分解为所需要的若干几何体,反过来,许多几何体也可以扩展回归到正方体中进行考虑(包括正方体的棱长、对角线以及各种截面等问题).以上知识绝大多数都可以推广到长方体中去.三视图的正(主)视图、侧(左)视图、俯视图分别是从几何体的正前方、正左方、正上方正投影得到的,重叠的线只画一条,挡住的线要画成虚线. 基本原则是“长对正、高平齐、宽相等”.空间几何体的表面积与体积(★★★★)必做3 如图6,四边形ABCD中,AB=AD=CD=1,BD=,BD⊥CD,将其沿对角线BD折成四面体A1-BCD,使平面A1BD⊥平面BCD,若四面体A1-BCD的顶点都在同一个球面上,则该球的体积为()A. πB. 3πC. πD. 2π[D][A][B][C][A1][B][C][D]图6[牛刀小试] [牛刀小试]精妙解法由四面体A1-BCD可以延伸为一个棱长为1的正方体(如图7),其中△A1BD 为正方体一个底面的一部分(刚好是底面正方形的一半),CD为正方体的侧棱. 故选A.极速突击高考试题中,解决多面体的外接球问题,大多要依据正方体、长方体以及正四面体等特殊几何体与它们的外接球的关系,但这些关系最后都要归结到正方体与其外接球的关系上去.(★★★★)必做4 如图8所示,正四面体ABCD的外接球的体积为4π,则正四面体的体积是_____.[牛刀小试] [牛刀小试]精妙解法法1:由已知πR3=4π,所以R=.设AE为球的直径. 故AD⊥DE,AE⊥O1D.设AD=a,所以O1D=·a=a,所以AO1=a,O1E=2R-AO1=2-a.由射影定理知,O1D2=AO1·O1E,解得a=2. 故V=·a2·AO1=.法2:正四面体的外接球即为正方体的外接球,正方体的对角线长为球的直径.由πR3=4π,所以R=,所以正方体棱长为2,所以AB=2,S△BCD=×2×2sin60°=2.点A到平面BCD的距离h=×2R=,所以VA-BCD=S△BCD×h=.极速突击方法1设法寻求正四面体的棱长与球的半径之间的关系;方法2将正四面体ABCD置于正方体中.空间的平行关系(★★★★)必做5 用a,b,c表示三条不同的直线,γ表示平面,给出下列命题:①若a∥b,b∥c,则a∥c;②若a⊥b,b⊥c,则a∥c;③若a∥γ,b∥γ,则a∥b;④若a⊥γ,b⊥γ,则a∥b.其中真命题的序号是()A. ①②B. ②③C. ①④D. ③④[牛刀小试] [牛刀小试]精妙解法①平行关系的传递性. ②举反例:在正方体ABCD-A1B1C1D1中,AB⊥AD,AB⊥AA1,但AD不平行AA1. ③a与b可能相交. ④垂直于同一平面的两直线互相平行. 故①④正确,选C.极速突击本题的入手点是借助实体模型进行排除验证,同时也要求我们必须熟练记住关于平行的一些常见结论.(★★★)必做6 如图10,在三棱柱ABC-A′B′C′中,点E,F,H,K分别为AC′,CB′,A′B,B′C′的中点,G为△ABC的重心. 从K,H,G,B′中取一点作为P,使得该棱柱恰有2条棱与平面PEF平行,则P为()[B][A][C][G][H][E][F][K][B′][C′][A′]图10A. KB. HC. GD. B′[牛刀小试] [牛刀小试]精妙解法假如平面PEF与侧棱BB′平行,则和三条侧棱都平行,不满足题意,而FK∥BB′,排除A;假如P为B′点,则平面PEF即平面A′B′C,此平面只与一条侧棱AB平行,排除D. 若P为H点,则HF为△BA′C′的中位线,所以HF∥A′C′;EF为△ABC′的中位线,所以EF∥AB;HE为△AB′C′的中位线,所以HE∥B′C′,显然不合题意,排除B,故选C.极速突击本题主要考查“线面平行”的判定,“线面平行”可由“线线平行”或“面面平行”进行转化. 一般地,我们习惯选择降维处理,即选择用“线线平行”来推出“线面平行”,所以思维的落脚点应该在寻找“线线平行”. 所以在此题中,也可这样考虑,因为EF是△ABC′的中位线,所以EF∥AB∥A′B′,故点P只要使得平面PEF与其他各棱均不平行即可,故选G点.空间的垂直关系(★★★★)必做7 如图11,在直三棱柱A1B1C1-ABC中,∠BAC=90°,AB=AC=AA1=1,已知G与E分别为线段A1B1和CC1的中点,点D和F分别是线段AC和AB上的动点(不包括端点),若GD⊥EF,则线段DF的长度的取值范围为()[D][A][B][C][E][F][G][A1][B1][C1]图11A.,1B.,2C. [1,)D.,[牛刀小试]精妙解法由题所揭示的几何体,可以按图所示,以A为原点,AB为x轴、AC为y轴,建立空间直角坐标系,则B(1,0,0),C(0,1,0),G,0,1,E0,1,,D(0,y,0),F(x,0,0). 所以=x,-1,-,=-,y,-1,由GD⊥EF得x+2y=1. 结合x∈(0,1),y∈(0,1),得y∈0,;又DF===∈,1. 故选A.[A][B][C][E][F(x,0,0)][G][A1][B1][C1][z][x][y][D(0,y,0)]图12极速突击本题应从垂直、平行关系入手,寻找垂直、平行成立的充分条件. 另外,本题有三个明显特征,启发我们使用空间直角坐标系解题:①有运动的背景;②有长度的取值范围(即函数的值域意义);③有“空间直三面角”条件.误点警示该题中,容易忽略求变量y的取值范围,导致所求的取值范围偏大.(★★★)必做8 棱长为1的正方体ABCD-A1B1C1D1中,平面α与体对角线BD垂直,则正方体在平面α上的射影面积为__________.精妙解法如图13,在正方体ABCD-A1B1C1D1中,体对角线BD1与截面正三角形AB1C、正三角形A1C1D垂直,即这两个三角形所在的平面与平面α是平行的,两个三角形的六个顶点到直线BD1的距离都等于··AB1=,这六个点的分布是均匀的,所以,正方体ABCD-A1B1C1D1在平面α上的射影为正六边形,边长就是前面求得的距离(即正六边形外接圆的半径),所以正方体ABCD-A1B1C1D1在平面α上的射影的面积为6··=.极速突击能正确作出相应图形是解题的关键,因此要注意结合图形解题的方法.空间的角(★★★★)必做9 在正四棱锥S-ABCD中,侧棱与底面所成的角为α,侧面与底面所成的二面角为β,侧棱SB与底面的正方形ABCD的对角线AC所成角为γ,相邻两侧面所成二面角为θ,则α,β,γ,θ之间的大小关系是()A. αC. α[S][A][E][D][C][O][B][F]图14[牛刀小试]精妙解法作底面的垂线SO,交底面于点O,则O为AC和BD的交点,BO是侧棱SB在底面ABCD上的射影,而BO垂直AC,因此,γ=;过O作OE⊥AD交AD于点E,连结SE,则sinα=,sinβ=,且SA>SE,故α. 故有α极速突击本题采用“几何法”求解,其步骤一般为“找角→找角所在的三角形→求三角形各边的长→利用余弦定理(三角函数)求解”.误点警示做这类试题要杜绝凭感觉胡乱选择,注意异面直线所成角的取值范围为0,,所以其余弦值为正值.(★★★★)必做10 已知正四棱锥P-ABCD的侧棱与底面所成角为60°,M为PA中点,连结DM,则DM与平面PAC所成角的大小是__________.[P][C][A][B][D][M]图15[牛刀小试]精妙解法:法1:取AC中点O,连结DO,PO,MO,则DO⊥平面PAC,所以∠DMO是DM与平面PAC所成角.因为PB与底面所成角为60°,所以∠PBO=60°,记AB=a,则BO=a,所以cos∠PBO===,所以PB=a. 在△PAC中,MO=PC=a,所以tan∠DMO==1,所以DM与平面PAC所成角为45°.法2:如图16建立空间直角坐标系,则平面PAC的法向量为n=(1,0,0),D-a,0,0,M0,-a,a,=a,-a,a,所以sinφ=cosθ==,所以DM与平面PAC所成角为45°.极速突击本题采用两种方法求解,方法1为“几何法”,可按照“一找、二证、三算”的步骤进行;方法2为“向量法”,先建立空间直角坐标系,再求解“斜线与平面法向量所成角的余弦值”,最后由“斜线与平面法向量所成角的余弦值的绝对值”等于“斜线与平面所成角的正弦值”得出答案.误点警示本题易错在采用向量法计算时,没有正确理解“斜线与平面法向量所成的角”和“斜线与平面所成的角”的关系,误以为它们是相等的,实则不然.找异面直线所成的角,一般可以采用平移的方法,把其中一条异面直线平移至与另一条异面直线相交,然后在某个三角形中解他们的夹角;当然,也可以建立空间直角坐标系,然后利用空间向量的方法进行求解.利用平面法向量求直线与平面的夹角时,应注意直线与平面的夹角θ和两向量夹角(锐角)是互为余角的关系,即sinθ=cosα;利用平面法向量求二面角的平面角时,应注意法向量的方向,或直接从图形中观察出其是钝(或锐)二面角,再利用向量夹角与平面角的互补关系而得.空间的距离(★★★)必做11 若正四棱锥P-ABCD的底面边长为2,高为3,E,F分别为PC,PD的中点,则异面直线AC与EF的距离为()A. B.C. D.[牛刀小试]精妙解法法1:因为EF∥CD,则异面直线AC与EF的距离即为E到平面ABCD的距离,因为E为PC中点,所以E到平面ABCD的距离为P到平面ABCD的距离的一半,所以d=. 故选B.法2:以正方形ABCD的中心为原点,与边BC,CD垂直的直线分别为x轴、y轴,OP 为z轴建立空间直角坐标系,则由条件知:C(1,1,0),D(-1,1,0),P(0,0,3),所以E,,,F-,,,所以=(1,1,0),=(-1,0,0). 设n=(x,y,z),则n·=0,n·=0,所以x+y=0,-x=0,所以x=y=0,取n=(0,0,1),又=-,-,,所以d==,故选B.极速突击求异面直线间的距离时,可以作出两异面直线的公垂线段,然后再求其长度;也可以采用上述的向量方法;有时也可以转化为直线与平面的距离,或者点到平面的距离再求解. 运用向量法求解点A到平面α的距离时,可以采用如下的方法:建立适当的空间直角坐标系→确定点A的坐标→在平面α内取一点B→求出向量→求出平面α的一个法向量n→求出点A到平面α的距离. 运用几何法求点A到平面α的距离时,可以先作平行线或平行平面,将A 点到平面α的距离转移到点B到平面α的距离,或者利用中位线及线段长度的比例关系,将A 点到平面α的距离转移到其他点到平面α的距离,再利用等积变换或直接法求之.点A(x,y)到平面α距离: d= (P为平面α上任一点,n为平面α的法向量),而线面距离、面面距离都可以转化成点面距离,当题目中的距离难以找出来时,应采用空间向量进行求解,避免耗时过多.a。
