弯曲的内力与强度计算 习题
8章弯曲应力及弯曲强度

x
Fs<0 M
递增函数
x
x
递减函数
Fs1–Fs2=F 由左到右的折角
Fs2
x
斜直线
曲线
M x
递增函数
M x
M
M
x
隆起 与 F相同
以轴线变弯为主要特征 的变形形式。 a) 外力特征: 受横向载荷的作用,即外 力或外力偶的矢量方向垂 直于杆轴. b) 变形特征: 杆件的轴线由直线变为曲线. 梁:以弯曲变形为主要变形的杆件.
8.1 平面弯曲的概念和实例
对称面
c) 平面弯曲: 如果作用于杆件上的所有外力都在同一平面内,并 且弯曲变形后的轴线也位于这个平面内,则梁必关于 此平面对称,这类弯曲称为平面弯曲。
1 a y qL M x 1 M1 x1 Fs1 2 b FR MR
2 用截面法计算Fs1和M1 取1-1截面左边的梁段,根据平衡条件计算 Fs1和M1 .
1 2 M R M qL(a b) qb 2
FR qL qb
F
Y
0
ql FS1 0
M
c1
0
FS1 ql
FS 2 q( x2 a l )
M
c2
0
1 M ql x2 M 2 q( x2 a) 2 0 2
1 M 2 M qlx 2 q( x2 a) 2 2
8.2 剪力和弯矩与剪力图和弯矩图
qL M 1 1 a y x 2
q
若取2-2截面右边的梁段,计算FQ2 FR qL qb 和M2.
F
y
0; ( FS ( x) dFs ( x) Fs ( x) q( x)dx 0
弯曲(1)

a
A
b F
C
B
b M FA x1 Fx1 l 0 x1 a
x1 0 时 M 0 x1 a 时 M ab F
x1 x2
ab M F l
a M =- l FX2 +aF a x2 l
直线
ab x2 a 时 M F l x2 l 时 M 0
l
(4). 简支梁受集中力偶 例4:如图所示的简支梁AB,在点C处受集中力偶M0作用, 尺寸a、b和L均为已知,试作此梁的弯矩图。 解: 1.求约束反力 x2
使微段梁两相邻截面发生左上右下的相对错动时,横截面 上的剪力为正 使微段梁弯曲成凹形时的弯矩为正,弯曲成凸形时的弯矩 为负
课本P39
二. 内力分析结果
内力名称:剪力Q和弯矩M 内力计算:
内力数值—剪力数值上等于所求截面任一侧所有 外力的代数和;弯矩数值上等于所求截面任一侧所有 外力对该截面形心力矩的代数和(包括外力偶) 内力符号—左上右下,剪力为正;左顺右逆,弯 矩为正
a M M0 l
M0 M M 0 FA x2 M 0 x2 l
a x2 l
x2 a
x2 l
b M M0 l M 0
剪力和弯矩的规律
剪力和弯矩的规律
弯矩图的规律
1.梁受集中力或集中力偶作用时,弯矩图 为直线,并且在集中力作用处,弯矩发生转 折;在集中力偶作用处,弯矩发生突变,突 变量为集中力偶的大小。 2.梁受到均布载荷作用时,弯矩图为抛物 线,且抛物线的开口方向与均布载荷的方向 一致。 3.梁的两端点若无集中力偶作用,则端点 处的弯矩为0;若有集中力偶作用时,则弯 矩为集中力偶的大小。
变形量 强度计算
《材料力学》弯曲计算-习题

②无均布载荷段弯矩图均为直线。有均布载荷段,弯矩图为
抛物线,其开口与均布载荷方向相同。
(3)弯矩、剪力、载荷集度的关系
①
M '(x) F S (x) F S'(x) q(x)
② FS=0的点是M图的取极值的点,FS=0的段M图是平行
于轴线的直线。
注意: 内力图上要注明控制面值、特殊点纵坐标值。
利用微分关系绘内力图
y
B截面 30.3 +
z
C截面 15.1 z
-
+
69
34.5
(d) 单位:MPa
Engineering Mechanics
四、弯曲 弯曲强度计算
例3 之二
解:(1)求截面形心轴,即中性轴z轴。
yC
( yi Ai ) Ai
170 30 170 30 200 (170 30)
2
2
17030 30 200
解:(1)外力分析,判变形。
10kN
50kN
(a) A
CD
B
z
4m
2m
4m
求得支坐反力
FA 26kN ,FB 34kN
荷载与梁轴垂直,梁将发
26kN 26 16
34kN
生平面弯曲。中性轴z过形心
+ (b)
与载荷垂直,沿水平方向。
FQ(kN)
104 136
34
(2)内力分析,判危险面。剪力
+
(c)
⑤解题步骤:
1)外力分析,判变形、中性轴,求截面的几何性质、支反力。 2)内力分析,判危险面,画剪力图、弯矩图(可只画弯矩图)
3)应力分析,判危险点。 4)强度计算。
最新弯曲的内力与强度计算习题

弯曲的内力与强度计算一、判断题1.如图1示截面上,弯矩M和剪力Q的符号是:M为正,Q为负。
()图12.取不同的坐标系时,弯曲内力的符号情况是M不同,Q相同。
()3、在集中力作用的截面处,Q图有突变,M连续但不光滑。
()4、梁在集中力偶作用截面处,M图有突变,Q图无变化。
()5.梁在某截面处,若剪力Q=0,则该截面的M值一定为零值。
()6.在梁的某一段上,若无荷载作用,则该梁段上的剪力为常数。
()7.梁的内力图通常与横截面面积有关。
()8.应用理论力学中的外力定理,将梁的横向集中力左右平移时,梁的Q 图,M图都不变。
()9.将梁上集中力偶左右平移时,梁的Q图不变,M图变化。
()10.图2所示简支梁跨中截面上的内力为M≠0,Q=0。
()图 2 图 311.梁的剪力图如图3所示,则梁的BC段有均布荷载,AB段没有。
()12.上题中,作用于B处的集中力大小为6KN,方向向上。
()13.右端固定的悬臂梁,长为4m,M图如图示,则在x=2m处,既有集中力又有集中力偶。
()图 4 图 514.上题中,作用在x=2m处的集中力偶大小为6KN·m,转向为顺时针。
()15.图5所示梁中,AB跨间剪力为零。
()16.中性轴是中性层与横截面的交线。
()17.梁任意截面上的剪力,在数值上等于截面一侧所有外力的代数和。
()18.弯矩图表示梁的各横截面上弯矩沿轴线变化的情况,是分析梁的危险截面的依据之一。
()19.梁上某段无荷载作用,即q=0,此段剪力图为平行x的直线;弯矩图也为平行x轴的直线。
()20.梁上某段有均布荷载作用,即q=常数,故剪力图为斜直线;弯矩图为二次抛物线。
()21.极值弯矩一定是梁上最大的弯矩。
()22.最大弯矩Mmax只可能发生在集中力F作用处,因此只需校核此截面强度是否满足梁的强度条件。
()23.截面积相等,抗弯截面模量必相等,截面积不等,抗弯截面模量必不相等。
()24.大多数梁都只进行弯曲正应力强度核算,而不作弯曲剪应力核算,这是因为它们横截面上只有正应力存在。
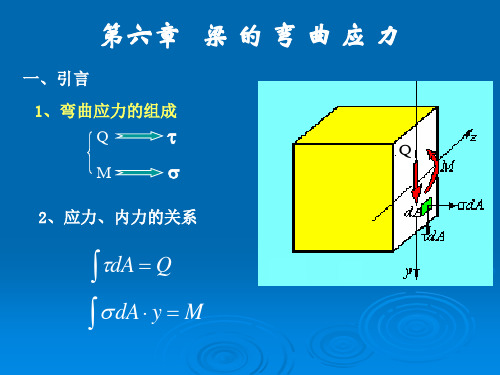
第九章第六节梁弯曲时的应力及强度计算(上课用)

m
V
( Stresses in Beams)
m
m
M
V
m m
只有与剪应力有关的切向内力元素 d V = dA 才能合成剪力
只有与正应力有关的法向内力元素 d FN = dA 才能合成弯矩
剪力V 内力 弯矩M 正应力 剪应力
所以,在梁的横截面上一般
既有 正应力, 又有 剪应力
先观察下列各组图
所以,可作出如下 假设和推断:
1、平面假设:
2.单向受力假设: 各纵向纤维之间互不挤压,纵向纤维均处于单向受拉或受压的状态。 因此梁横截面上只有正应力σ而无剪应力τ
各横向线代表横截面,实验表 明梁的横截面变形后仍为平面。
梁在弯曲变形时,上面部分纵向纤维缩短,下面部分纵向纤维伸长,必 有一层纵向纤维既不伸长也不缩短,保持原来的长度,这一纵向纤维层称为 中性层. 中性层与横截面的交线称为中性轴,中性轴通过截面形心,是一条形心轴。 且与截面纵向对称轴y垂直,将截面分为受拉区及受压区。梁弯曲变形时, 各横截面绕中性轴转动。
(3)横截面上任一点处的剪应力计算公式(推导略)为
V S I zb
Z
V——横截面上的剪力
Iz——整个横截面对中性轴的惯性矩
b——需求剪应力处的横截面宽度 S*Z——横截面上需求剪应力处的水平线 以外(以下或以上)部分面积A*(如图 )对 中性轴的静矩
V
3V 4 y2 (1 2 ) 2bh h
应力状态按主应力分类:
(1)单向应力状态。在三个相对面上三个 主应力中只有一个主应力不等于零。 (2)双向应力状态。在三个相对面上三个 主应力中有两个主应力不等于零。
(3)三向应力状态。其三个主应力都不等于零。例 如列车车轮与钢轨接触处附近的材料就是处在三向应 力状态下.
建筑力学与结构5

f y max f l l l
上式就是梁的刚度条件。 【例6-11】
子情境四 单跨静定梁的刚度计算
•四、提高梁刚度的措施
1)提高梁的抗弯刚度EIZ 2)减改善荷载的分布情况 3)改善荷载的分布情况
想一想
1、P76页,习题6-7
子情境二 单跨静定梁弯曲时的内力图绘制方法
•三、轴绘制内力图的第三种方法——叠加法和区段叠加法
(二)叠加法绘制弯矩图
子情境二 单跨静定梁弯曲时的内力图绘制方法
•三、轴绘制内力图的第三种方法——叠加法和区段叠加法
(二)叠加法绘制弯矩图
子情境二 单跨静定梁弯曲时的内力图绘制方法
•三、轴绘制内力图的第三种方法——叠加法和区段叠加法
(二)剪力图和弯矩图 【6-5】
从剪力图和弯矩图中可得结论: 在无荷载梁段剪力图为平行线,弯矩 图为斜直线。在集中力作用处,左右 截面上的剪力图发生突变,其突变值 等于该集中力的大小,突变方向与该 集中力的方向一致;而弯矩图出现转 折,即出现尖点,尖点方向与该集中 力方向一致。
子情境二 单跨静定梁弯曲时的内力图绘制方法
(二)单跨静定梁的类型 1)悬臂梁:梁的一端为固定端,另一端为自由端
子情境一 单跨静定梁弯曲时的内力计算
• 一、平面弯曲
(二)单跨静定梁的类型 2)简支梁:梁的一端为固定铰支座,另一端为可动铰支座
子情境一 单跨静定梁弯曲时的内力计算
• 一、平面弯曲
(二)单跨静定梁的类型 3)外伸梁:梁的一端或两端伸出支座的简支梁
•二、轴绘制内力图的第二种方法——微分关系法
想一想
1、P75页,习题6-2(a)、(b)。
子情境二 单跨静定梁弯曲时的内力图绘制方法
梁的弯曲应力和强度计算
88
7.5 106 7.6 106
88 86.8MPa
弯曲正应力计算
三、计算题
27.一矩形截面简支梁,梁上荷载如图所示.已知P=6kN、 l=4m、b=0.1m、h=0.2m,试画出梁的剪力图和弯矩图并求 梁中的最大正应力. 解:(1) 作剪力图、弯矩图
(2)求最大正应力
Mmax 6kN m
横向线:仍为直线,仍与纵向线正交,相对转动了一个角度 纵向线:曲线,下部伸长,上部缩短
(2)假设 平面假设:横截面在变形前为平面,变形后仍为平面,且仍
垂直于变形后梁的轴线,只是绕横截面上某个轴 旋转了一个角度。 单向受力假设:梁由无数根纵向纤维组成,之间无横向挤压,
只受轴向拉伸与压缩。
中性层
3、正应力计算公式 〖1〗几何变形关系
内容回顾
弯曲正应力 1. 基本假设:
(1)平面假设:变形前为平面的横截面,变形后仍为平面,但转动了一角度。 (2)单向受力假设:杆件的纵截面(与杆轴平行的截面)上无正应力。
2.中性轴Z:
中性层与横截面的交线,平面弯曲时中性轴过形心且与对称轴垂直。
3.正应力计算公式:
中性层
4.正应力分布规律:沿截面高度呈线性分布。
4、正负号确定 1)M、y 符号代入公式
2)直接观察变形
5、适用范围及推广
〖1〗适用范围: 平面弯曲(平面假设、单向受力假设基础上)、 线弹性材料
〖2〗推广: ① 至少有一个对称轴的截面; ② 细长梁 (l/h>5);
6、最大正应力
工程上关心的是极值应力:
只与截面形状、尺寸有关
抗弯截面模量
对剪切(横力)弯曲: 矩形:
解:(1)作弯矩图,
求最大弯矩
第八章 弯曲内力、应力及强度计算

例8-3 如图所示的悬臂梁上作用有均布载荷q,试画出该梁的 剪力图和弯矩图。
解:(1) 列剪力方程和弯矩方程,
将梁左端A点取作坐标原点。
剪力方程和弯矩方程
FQ (x) qx (0 x l) M (x) 1 qx2 (0 x l)
2
(2) 画剪力图和弯矩图
剪力图是一倾斜直线
弯矩图是一抛物线
解 (1)计算1-1截面上弯矩
M1 P 200 1.5103 200103 300N m
(2) 计算 1-1 截面惯性矩
Ix
bh2 12
1.8 32 12
4.05 10 3 m4
(3) 计算1-1截面上各指定点的正应力
A
M1 yA Ix
300 1.5 102 4.05102
111106 N/m2
拉应力
B
M1 yB Ix
300 1.5 102 4.05102
111106 N/m2
压应力
A
M1 yC Ix
M1 0 0N/m 2 Ix
D
M1 yD Ix
3001.5102 4.05102
74.1106 N/m2
压应力
例8-9 一简支木梁受力如图(a)所示。已知q=2kN/m,l=2m。试比 较梁在竖放(图(b))和平放(图(c))时横截面C处的最大正应力。
3、 画剪力图和弯矩图
FQ FQ
FQ
max
ql 2
ql 2 M max 8
例 4 简支梁AB,在C 点处受集中力P 作用, 如图所示。 试作此梁的弯矩图。
解 (1)求支座反力
M B 0 Pb FAl 0
FY 0 FA FB P 0
(2) 列弯矩方程
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
弯曲的内力与强度计算一、判断题1.如图1示截面上,弯矩M和剪力Q的符号是:M为正,Q为负。
()图12.取不同的坐标系时,弯曲内力的符号情况是M不同,Q相同。
()3、在集中力作用的截面处,Q图有突变,M连续但不光滑。
()4、梁在集中力偶作用截面处,M图有突变,Q图无变化。
()5.梁在某截面处,若剪力Q=0,则该截面的M值一定为零值。
()6.在梁的某一段上,若无荷载作用,则该梁段上的剪力为常数。
()7.梁的内力图通常与横截面面积有关。
()8.应用理论力学中的外力定理,将梁的横向集中力左右平移时,梁的Q图,M图都不变。
()9.将梁上集中力偶左右平移时,梁的Q图不变,M图变化。
()10.图2所示简支梁跨中截面上的内力为M≠0,Q=0。
()图 2 图 311.梁的剪力图如图3所示,则梁的BC段有均布荷载,AB段没有。
()12.上题中,作用于B处的集中力大小为6KN,方向向上。
()13.右端固定的悬臂梁,长为4m,M图如图示,则在x=2m处,既有集中力又有集中力偶。
()图 4 图 514.上题中,作用在x=2m处的集中力偶大小为6KN·m,转向为顺时针。
()15.图5所示梁中,AB跨间剪力为零。
()16.中性轴是中性层与横截面的交线。
()17.梁任意截面上的剪力,在数值上等于截面一侧所有外力的代数和。
()18.弯矩图表示梁的各横截面上弯矩沿轴线变化的情况,是分析梁的危险截面的依据之一。
()19.梁上某段无荷载作用,即q=0,此段剪力图为平行x的直线;弯矩图也为平行x轴的直线。
()20.梁上某段有均布荷载作用,即q=常数,故剪力图为斜直线;弯矩图为二次抛物线。
()21.极值弯矩一定是梁上最大的弯矩。
()22.最大弯矩Mmax只可能发生在集中力F作用处,因此只需校核此截面强度是否满足梁的强度条件。
()23.截面积相等,抗弯截面模量必相等,截面积不等,抗弯截面模量必不相等。
()24.大多数梁都只进行弯曲正应力强度核算,而不作弯曲剪应力核算,这是因为它们横截面上只有正应力存在。
()25.对弯曲变形梁,最大挠度发生处必定是最大转角发生处。
()26.两根不同材料制成的梁,若截面尺寸和形状完全相同,长度及受力情况也相同,那么对此两根梁弯曲变形有关量值,有如下判断:(1)最大正应力相同;()(2)最大挠度值相同;()(3)最大转角值不同;()(4)最大剪应力值不同;()(5)强度相同。
()27.两根材料、截面形状及尺寸均不同的等跨简支梁,受相同的荷载作用,则两梁的反力与内力相同。
()28.梁内最大剪力的作用面上必有最大弯矩。
()29.梁内最大弯矩的作用面上剪力必为零。
()30.图(a)、(b)中,m-m截面上的中性轴分别为通过截面形心的水平轴与铅垂轴。
()图 1331.在匀质材料的等截面梁中,最大拉应力必出现在弯矩值M最大的截面上。
()32.对于等截面梁,最大拉应力与最大压应力在数值上必定相等。
()33.对于矩形截面的梁,出现最大正应力的点上,剪应力必为零。
()34.弯曲应力公式σ=MY/IZ 适用于任何截面的梁。
()35.在梁的弯曲正应力公式σ= 中,Iz为梁截面对于形心轴的惯性矩。
()36.一悬臂梁及其T形截面如图示,其中c为截面形心,该截面的中性轴Z0,最大拉应力在上边缘处。
()图 1437.T形截面梁受矩为负值,图示应力分布图完全正确。
()图 1538.匀质材料的等截面梁上,最大正应力∣σ∣max必出现在弯矩M最大的截面上。
()39.对于等截面梁,最大拉应力与最大压应力在数值上必定相等。
()40.对于矩形截面的梁,出现最大正应力的点上,剪应力必为零。
()41.矩形截面梁发生剪切弯曲时,其横截面的中性轴处,σ=0,τ最大。
()42.T形梁在发生剪切弯曲时,其横截面上的σmax发生在中性轴上,τmax 发生在离中性轴最远的点处。
()43.图16所示T形截面外伸梁的最大拉应力发生在A截面处。
()图 1644.T截面铸铁梁,当梁为纯弯曲时,其放置形式最合理的方式是A。
()图 1745.大多数梁都只进行弯曲正应力强度校核,而不作弯曲剪应力校核,这是因为它们横截面上只有正应力存在。
()46.截面积相等的抗弯截面模量必相等,截面积不等的抗弯截面模量必不相等。
()47.梁弯曲时最合理的截面形状,是在横截面积相同条件下,获得W2/A值最大的截面形状。
()48.矩形截面梁,若其截面高度和宽度都增加一倍,则其强度提高到原来的16倍。
()49.弯曲变形梁,最大挠度发生处,必定是最大转角发生处。
()50.图18所示脆性材料⊥形截面外伸梁,若进行正应力强度校核,应校核D.B点下边缘。
()51.图19示悬臂梁,其最大挠度处,必定是最大转角发生处。
()图 18 图 1952.不同材料制成的梁,若截面尺寸和形状完全相同,长度及受力情况也相同,那么对此两根梁弯曲变形时,它们的最大挠度值相同。
()53.EI是梁的抗弯刚度,提高它的最有效,最合理的方法是改用更好的材料。
()二、选择题1.图6所示B截面的弯矩值为()。
图 6A.PL B.–Pa C.Pa D.–PL2.图7所示简支梁剪力图正确的为()。
图 73.应用截面法计算横截面上的弯矩,其弯矩等于()。
A.梁上所有外力对截面力矩的代数和B.该截面左段梁(或右段梁)上所有外力对任何矩心的代数和C.该截面左段梁(或右段梁)所有外力(包括力偶)对该截面形心力矩的代数和D.截面一边所有外力对支座的力矩代数和4.在集中力作用处剪力图()。
A.发生转折 B.发生突变C.无影响D.发生弯曲5.在弯曲的正应力公式σ=中,I Z为梁截面对于()的惯性矩。
A.任一轴Z B.形心轴 C.对称轴D.中性轴6.梁的截面为T型,z轴通过横截面形心,弯矩图如图示,则有()。
A.最大拉应力与最大压应力位于同一截面c或dB.最大抗应力位于截面c,最大压应力位于截面dC.最大拉应力位于截面d,最大压应力位于截面cD.以上说法都不正确图 207.最大弯矩截面最大拉应力等于最大压应力的条件是()。
A.梁材料的拉压强度相等B.截面形状对称于中性轴C.同时满足以上两条D.截面形状不对称于中性轴6、两根荷载、长度、支座相同的梁横截面上最大正应力值相等的条件是()。
A.Mmax与截面积分别相等B.Mmax与WZ分别相等C.Mmax与WZ分别相等,且材料相同D.两梁的许用应力相等8.直梁弯曲强度条件σmax=≤[σ]中,σmax应是()上的最大正应力。
A.最大弯矩所在截面 B.梁的最大横截面C.梁的最小横截面 D.梁的危险截面9.EI是梁的抗弯刚度,提高它的最有效、最合理的方法是()A.改用更好的材料 B.增加横截面面积C.采用惯性矩大的截面形状D.以上作法都不合理10.由叠加法作图示简支梁的弯矩图,则下述正确的是图()。
图 2111.跨中受集中荷载P作用的圆截面简支梁,它的θA= ,yc = 。
若将L变为2L,d变为2d时,它的,yc之比为()。
A. B.C. D.三、分析题1.绘出图示梁横截面上的正应力分布图(假定此截面上的弯矩为正值)。
图 22四、计算题1.作下列各梁的剪力图和弯矩图,并求出Qmax和Mmax。
图 82.试作梁的剪力图和弯矩图,并确定M MAX,Q MAX的值;已知V A=8KN(↑),V B=12KN(↑)。
图 93.画出下图梁的内力图。
图 104.作图示多跨静定梁的内力图。
图 115.求静定多跨梁的弯矩图图 126.求图23所示梁的最大正应力及其所在位置。
图237.简支梁受均布荷载作用,已知L=4m,截面为矩形如图24所示。
材料的许用应力[σ]=10Mpa,试求梁的许可荷载q。
图 248.图25所示矩形截面外伸梁,截面高宽比h/b=1.5,材料的许用应力[σ]=10Mpa,试求b和h。
图 259.图26所示T形截面铸铁梁,Z轴为通过截面形心的中性轴,惯性矩Iz=4.0X107mm4,铸铁的许用应力〔σ+〕=35 Mpa,〔σ-〕=140 Mpa,试校核梁的强度。
图 2610.图27所示结构,AB为矩形截面木梁,截面尺寸如图,DE为直径d=30mm 的圆截面刚杆,AB的[σ]1=10Mpa,DE的[σ]2=160Mpa,试确定F的容许值[F]图 2711.图28所示矩形截面外伸木梁,材料的许用正应力[σ]=10Mpa,许用剪应力[τ]=1Mpa,试校核该梁的强度。
图 2812.图29所示梁,已知矩形截面尺寸的比例为b:h=3:4,梁的许用正应力[σ]=15.6Mpa,许用正应力[τ]=1.7Mpa,试确定截面尺寸。
图 2913.图30所示外伸梁,已知Wz=截面面积A=材料的[σ]=170Mpa,[τ]=100Mpa,试求许可荷载[F]。
图 3014.图31所示为20b工字钢制成的外梁,已知L=6m,P=30KN,q=6KN/m,[σ]=160MPa梁的弯矩图如图示,试校核梁的强度。
提示:20b工字钢 Iz=。
图 3115.图32所示T型截面铸铁梁,已知P1 =10.8KN,P2 =4.8KN,a = 1m,,y1 =5.2cm,=8.8cm,弯矩图已绘出。
试求梁中最大拉应力的数值及其所在位置。
