弯曲强度计算
理论力学10弯曲的应力分析和强度计算
解 绘制弯矩图，得 M B = 10kN ⋅ m M C = 7.5kN ⋅ m
Q = Q(x)
--剪力方程
M = M (x)
--弯矩方程
梁的剪力和弯矩随截面位置的变化关系，常用图形来 表示，这种图形称为剪力图和弯矩图。
14
例2
如图所示为一受集中力作用的简支梁。设P、l及a均为 已知，试列出剪力方程和弯矩方程，并画出剪力图和弯矩图。
解 1、求支座约束力
l−a
a
RA =
RB = P
火车轮轴简化为外伸梁
8
弯曲的应力分析和强度计算
二、剪力与弯矩
截面法求内力
∑F y =0 RA − P − Q = 01
∑M c = 0 M + P ( x − a ) − RA x =
01
Q = RA − P1
剪力
M = RA x − P ( x − a ) 弯矩1
9
弯曲的应力分析和强度计算
剪力符号规定：当剪力使微段梁绕微段内任一点沿顺时针 转动时为正，反之为负。
横截面对y，z的惯性积，由于y轴为对称轴，故 惯性积为零。
34
弯曲的应力分析和强度计算
} 1 M
=
ρ EI xz
σ =E y ρ
M
σ=y
IZ
--纯弯曲梁横截面正应力计算公式
横截面上的最大正应力发生在离中性轴最远点。
σ max M
=
σ max M
=
ymax
WZ
IZIZ WZ =
弯曲截面系数
ymax 35
σa
−
σb
⊕
σc
−
石材弯曲强度计算公式
石材弯曲强度计算公式石材弯曲强度计算公式石材是一种常用的建筑材料，具有美观、耐久、防火等优点。
在建筑和装饰中，常常需要使用到弯曲形状的石材。
因此石材弯曲强度的计算变得十分重要。
本文将介绍石材弯曲强度的计算公式和相关知识点。
一、石材的基本力学性质首先，石材的力学性质是研究石材弯曲强度的前提。
石材的力学性质主要包括弹性模量、剪切模量、泊松比等。
其中，弹性模量是指石材在受到外力作用后产生的变形量和受力面积之比。
剪切模量是指石材的抗剪能力大小。
泊松比则是描述了石材在受力过程中其沿自身垂直方向的体积收缩量与其沿水平方向的体积膨胀量之比。
二、石材弯曲强度的基本知识石材的抗弯强度是指在石材的纤维方向上承受强制弯曲时，其所能继续承受的最大弯曲强度或称曲率极限的大小。
获得石材抗弯强度的最通用方法是三点弯曲试验和四点弯曲试验。
三、石材弯曲强度计算石材弯曲强度的计算公式如下：S=6M/bd^2其中，S为石材的弯曲强度，M是施加于试块上的弯矩，b表示试块的宽度，d表示试块的高度。
这里需要注意的是，该计算公式只适用于矩形截面的试块，在实际使用过程中，需要根据试块的不同截面形状进行相应的修正。
四、石材弯曲强度的影响因素石材的弯曲强度受到如下因素的影响：1. 石材的品种和种类；2. 石材的质量；3. 石材的备品率；4. 石材的截面形状；5. 石材在弯曲时的水平和竖直形变量。
五、结语石材是一种被广泛应用在建筑和装饰领域的材料，它具有种类繁多、坚固耐用、美观大方等优点。
弯曲形状是极其常见的石材使用形态，因此本文深入介绍了石材弯曲强度的计算公式和相关知识点。
希望读者能从中深入了解石材的力学性质，更好地应用于实际生产和工程设计中。
弯曲变形的强度条件和强度计算
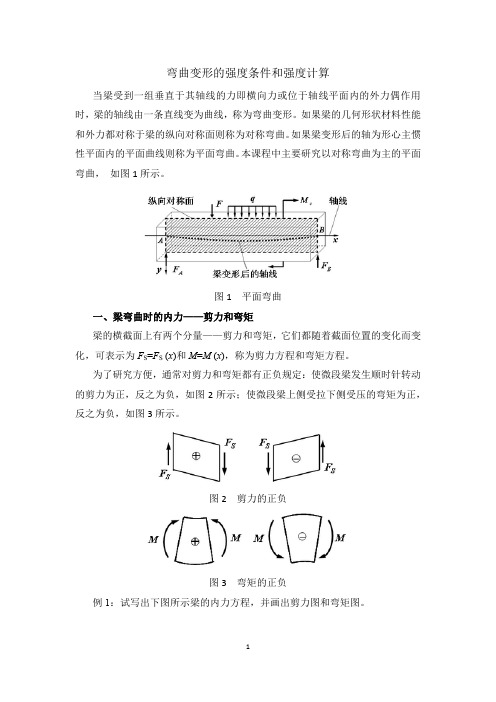
弯曲变形的强度条件和强度计算当梁受到一组垂直于其轴线的力即横向力或位于轴线平面内的外力偶作用时，梁的轴线由一条直线变为曲线，称为弯曲变形。
如果梁的几何形状材料性能和外力都对称于梁的纵向对称面则称为对称弯曲。
如果梁变形后的轴为形心主惯性平面内的平面曲线则称为平面弯曲。
本课程中主要研究以对称弯曲为主的平面弯曲，如图1所示。
图1 平面弯曲一、梁弯曲时的内力——剪力和弯矩梁的横截面上有两个分量——剪力和弯矩，它们都随着截面位置的变化而变化，可表示为F S=F S(x)和M=M (x)，称为剪力方程和弯矩方程。
为了研究方便，通常对剪力和弯矩都有正负规定：使微段梁发生顺时针转动的剪力为正，反之为负，如图2所示；使微段梁上侧受拉下侧受压的弯矩为正，反之为负，如图3所示。
图2 剪力的正负图3 弯矩的正负例1：试写出下图所示梁的内力方程，并画出剪力图和弯矩图。
解：（1）求支反力=∑C M：0310126=⨯--⋅AyF，kN7=AyF=∑Y：010=-+ByAyFF，kN3=ByF（2）列内力方程剪力：⎩⎨⎧<<-<<=63kN33kN7)(S xxxF弯矩：⎩⎨⎧≤≤≤≤⋅-⋅-=633mkN)6(3mkN127)(xxxxxM（3）作剪力图和弯矩图二、梁弯曲时的正应力在一般情况下，梁的横截面上既有弯矩又有剪力。
若梁上只有弯矩没有剪力，称为纯弯曲。
本讲主要讨论纯弯曲时横截面上的应力——正应力。
梁横截面上的正应力大小与该点至中性轴的距离成正比，即正应力沿截面宽度均匀分布，沿高度呈线性分布，如图4所示。
图4 梁弯曲时的正应力分布图即有yIxMz)(=σ（1）中性轴把截面分成受拉区和受压区两部分，且最大拉应力和最大压应力发生在上下边缘处，其值为max max y I Mz=σ。
令max y I W z z=，即有：zW M =max σ （2）式中，W z 称为抗弯截面系数，它与横截面的几何尺寸和形状有关，量纲为[长度]3，常用单位为mm 3或m 3。
梁的应力及强度计算
梁的应力及强度计算梁是一种常见的结构元件，用于承受或分配荷载。
在设计和分析梁的过程中，计算梁的应力及强度是非常重要的。
本文将详细介绍梁的应力及强度计算方法。
首先，梁的应力定义为单位面积上的力，用公式表示为：σ=M*y/I其中，σ表示梁的应力，M表示梁的弯矩，y表示距离中性轴的垂直距离，I表示梁的截面惯性矩。
梁的应力通常包括弯曲应力、剪切应力和轴向应力。
弯曲应力是由于弯曲力引起的应力，计算公式为：σ_b=M*y/I其中，σ_b表示弯曲应力。
剪切应力是由于纵向剪力引起的应力，计算公式为：τ=V*Q/(b*t)其中，τ表示剪切应力，V表示纵向剪力，Q为形状系数，b为梁的宽度，t为梁的厚度。
轴向应力是由于轴向力引起的应力，计算公式为：σ_a=N/A其中，σ_a表示轴向应力，N表示轴向力，A表示梁的截面积。
梁的强度是指在给定的荷载下梁能够承受的最大应力。
在计算梁的强度时，通常需要将不同种类的应力进行合并。
弯曲强度是指梁在弯曲荷载下的抗弯矩能力。
根据材料的弯曲性能和形状，可以采用破坏理论或变形理论计算梁的弯曲强度。
剪切强度是指梁在剪切荷载下的抗剪切能力。
根据材料的剪切性能和梁的几何形状，可以计算出梁的剪切强度。
轴向强度是指梁在轴向荷载下的抗轴向力能力。
轴向强度的计算通常基于材料的抗拉性能。
在进行梁的应力及强度计算时，还需要考虑其他因素，如材料的弹性模量、断裂韧性和安全系数等。
总之，梁的应力及强度计算是结构设计和分析中必不可少的一部分。
通过合理的计算方法，可以确保梁在荷载下的正常工作和安全使用。
学习任务6 弯曲强度计算
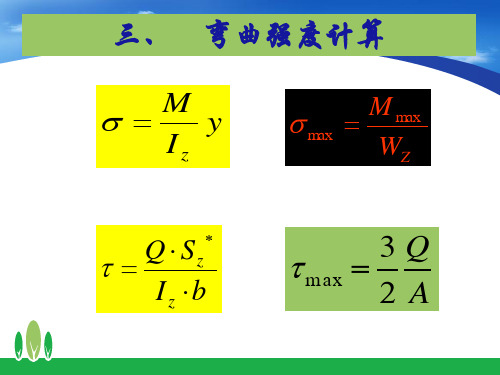
例2 已知悬臂梁如图，l 1.5m ，P=32kN，梁由22a工字
钢制成，自重按 q 0.33kN / m ，材料的 160 MPa
140 MPa 校核粱强度。
q
p
A
B
z
l
例3 矩形截面松木梁如图，已知 q 3.6kN / m ，材料的
10MPa 2MPa l 4m
计算：1）若截面高宽比h/b=2，设计木梁尺寸b、h。 2）若木梁采用b=140mm，h=210mm的矩形截面，计算
z
Wz1
D13
32
max
1.33 m
4Q 3A
D1
As D12 a2 , a
4
R; (R D1 / 2)
a
z
Wz 2
bh2 6
(
R)3
6
1.18Wz1
a
max 1.5 m
当 D12
4
[D2
(0.8D)2 ]时, D 4
1.67 D1
Wz3
D3
32
(1 -
0.8
4
)
2.75Wz1
z
max 2 m
0.8D D
2a1
当 D12
4
2a12时, a1
2 D1 / 4
Wz 4
bh2 6
4a13 6
1.67Wz1
max 1.5 m
z a1
2a2 1.6a2
当 D12
4
2a22
0.81.6a22时, a2
1.05D1
z 0.8a2
a2
Wz5 4.57Wz1
max 2.3 m (= Q Af )
求最大应力并校核强度
max
钢板验证强度计算公式
钢板验证强度计算公式钢板是工程中常见的材料，其强度计算是工程设计中的重要一环。
在设计过程中，需要对钢板的强度进行验证，以确保其在使用过程中能够承受所受力的作用而不发生破坏。
钢板的强度计算公式是验证钢板强度的重要工具，本文将对钢板强度计算公式进行详细的介绍和分析。
首先，钢板的强度计算公式一般包括以下几个方面，拉伸强度、屈服强度、压缩强度、剪切强度和弯曲强度。
这些强度计算公式是根据钢板的材料性质和受力情况而确定的。
在实际工程设计中，需要根据具体的工程要求和使用条件选择合适的强度计算公式进行验证。
钢板的拉伸强度是指在拉伸作用下钢板所能承受的最大应力。
拉伸强度计算公式一般为，σt = P/A，其中σt为拉伸应力，P为受力，A为受力面积。
在实际工程设计中，需要根据受力情况和材料性质确定合适的拉伸强度计算公式，并进行验证。
屈服强度是指在受拉作用下材料开始发生塑性变形的应力值。
屈服强度计算公式一般为，σy = Fy/A，其中σy为屈服应力，Fy为屈服强度，A为受力面积。
在实际工程设计中，需要根据钢板的材料性质和受力情况选择合适的屈服强度计算公式进行验证。
压缩强度是指在受压作用下材料所能承受的最大应力。
压缩强度计算公式一般为，σc = P/A，其中σc为压缩应力，P为受力，A为受力面积。
在实际工程设计中，需要根据受力情况和材料性质选择合适的压缩强度计算公式进行验证。
剪切强度是指在受剪作用下材料所能承受的最大应力。
剪切强度计算公式一般为，τ= P/A，其中τ为剪切应力，P为受力，A为受力面积。
在实际工程设计中，需要根据受力情况和材料性质选择合适的剪切强度计算公式进行验证。
弯曲强度是指在受弯作用下材料所能承受的最大应力。
弯曲强度计算公式一般为，σb = M/S，其中σb为弯曲应力，M为弯矩，S为截面模量。
在实际工程设计中，需要根据受力情况和材料性质选择合适的弯曲强度计算公式进行验证。
除了上述几种强度计算公式外，还有一些特殊情况下的强度计算公式，如冲击强度、疲劳强度等。
轴抗弯强度计算公式12则
轴抗弯强度计算公式12则抗弯强度计算公式(一)工字钢抗弯强度计算方法一、梁的静力计算概况1、单跨梁形式: 简支梁2、荷载受力形式: 简支梁中间受集中载荷3、计算模型基本参数:长 L =6 M4、集中力:标准值Pk=Pg+Pq =40+40=80 KN设计值Pd=Pg*γG+Pq*γQ =40*1.2+40*1.4=104 KN工字钢抗弯强度计算方法二、选择受荷截面11、截面类型: 工字钢:I40c2、截面特性: Ix= 23850cm4 Wx= 1190cm3 Sx= 711.2cm3 G= 80.1kg/m翼缘厚度 tf= 16.5mm 腹板厚度 tw= 14.5mm工字钢抗弯强度计算方法三、相关参数1、材质:Q2352、x轴塑性发展系数γx:1.053、梁的挠度控制〔v〕:L/250工字钢抗弯强度计算方法四、内力计算结果1、支座反力 RA = RB =52 KN2、支座反力 RB = Pd / 2 =52 KN3、最大弯矩 Mmax = Pd * L / 4 =156 KN.M工字钢抗弯强度计算方法五、强度及刚度验算结果21、弯曲正应力ζmax = Mmax / (γx * Wx),124.85 N/mm22、A处剪应力ηA = RA * Sx / (Ix * tw),10.69 N/mm23、B处剪应力ηB = RB * Sx / (Ix * tw),10.69 N/毫米为单位，直接把数值代入上述公式，得出即为每米方管的重量，以克为单位。
如30x30x2.5毫米的方管，按上述公式即可算出其每米重量为:4x2.5x(30-2.5)x7.85=275x7.85=2158.75克，即约2.16公斤矩管抗弯强度计算公式1、先计算截面模量WX=(a四次方-b四次方)/6a2、再根据所选材料的强度，计算所能承受的弯矩3、与梁上载荷所形成的弯矩比对，看看是否在安全范围内参见《机械设计手册》机械工业出版社2007年12月版第一卷第1-59页玻璃的抗弯强度计算公式锦泰特种玻璃生产的玻璃的抗弯强度一般在60~220Mpa之间，玻璃样品的形式和表面状态对测试的结果影响较大，3通常采用万能压力测试仪测试。
螺杆的抗弯曲强度计算公式
螺杆的抗弯曲强度计算公式引言。
螺杆是一种常见的机械零部件，广泛应用于工程领域中。
在使用过程中，螺杆可能会受到弯曲力的作用，因此了解螺杆的抗弯曲强度是非常重要的。
本文将介绍螺杆的抗弯曲强度计算公式及其应用。
螺杆的抗弯曲强度计算公式。
螺杆的抗弯曲强度可以通过以下公式进行计算：\[σ=\frac{M\cdot c}{I}\]其中，σ为螺杆的抗弯曲应力，M为作用在螺杆上的弯矩，c为螺杆的截面中性轴到最外纤维的距离，I为螺杆的截面惯性矩。
螺杆的截面惯性矩可以通过以下公式进行计算：\[I=\frac{πd^4}{64}\]其中，d为螺杆的直径。
螺杆的抗弯曲强度计算实例。
假设有一根直径为10mm的螺杆，作用在其上的弯矩为100N·m，求螺杆的抗弯曲应力。
首先计算螺杆的截面惯性矩：\[I=\frac{π\cdot(10\times10^{-3})^4}{64}≈4.91\times10^{-8}m^4\]然后根据抗弯曲强度计算公式计算螺杆的抗弯曲应力：\[σ=\frac{100\times10^{-3}\cdot c}{4.91\times10^{-8}}\]假设螺杆的截面中性轴到最外纤维的距离为5mm，则。
\[σ=\frac{100\times10^{-3}\cdot5\times10^{-3}}{4.91\times10^{-8}}≈1.02\times10^8Pa\]因此，螺杆的抗弯曲应力为1.02×10^8Pa。
螺杆的抗弯曲强度计算公式的应用。
螺杆的抗弯曲强度计算公式可以帮助工程师们在设计和选择螺杆时进行合理的计算和评估。
通过计算螺杆的抗弯曲应力，工程师可以确定螺杆是否能够承受特定的弯曲力，从而保证螺杆在使用过程中不会发生弯曲变形或破裂。
此外，螺杆的抗弯曲强度计算公式还可以用于优化螺杆的设计。
通过调整螺杆的直径、截面形状和材料等参数，工程师可以提高螺杆的抗弯曲强度，从而提高螺杆的使用寿命和安全性。
工程力学：第9章 弯曲应力及强度计算(新)
P1
例如：
P2
纵向对称面
aP
Pa
A
P FS P
B P
x
P Pa M
x
3、纯弯曲(Pure Bending): 某段梁的内力只有弯矩
没有剪力时，该段梁的变 形称为纯弯曲。
纯弯曲：AB段
三.两个概念 中性层：梁内一层纤维既不伸长也不缩短，因而纤维不
受拉应力和压应力，此层纤维称中性层。 中性轴：中性层与横截面的交线。
x
t max
1.5
FS max A
1.5 5400 0.12 0.18
qL
2
0.375MPa 0.9MPa [t ]
应力之比
x
s max M max 2 A L 16.7
t max Wz 3FS h
P1=9kN
A
C
P2=4kN
B
D
1m RA
1m 1m RB
2.5kNm
x
4
例3 T 字形截面的铸铁梁受力如
(sdA)z
A
Eyz dA E
A
yzdA EI yz 0
A
（对称面）
M z
(sdA) y
A
Ey 2 dA E
A
y2dA
A
EI z
MZ
A y2dA I Z
• IZ—横截面对中性轴的惯性矩
1 Mz
EI z
… …(3) EIz 杆的抗弯刚度。
sx
M y Iz
...... (4)
M(x)+d M(x) 在梁上取微段如图b；
z
t1
x
在微段上取一块如图c，平衡
sI
t
花岗石弯曲强度计算方法
花岗石弯曲强度计算方法花岗石是一种硬质的岩石，其弯曲强度可以通过不同的方法计算。
在以下文章中，将简要介绍两种常用的计算花岗石弯曲强度的方法。
方法一：根据应力-应变关系计算弯曲强度在花岗石材料的弯曲试验中，通过施加一定的力使花岗石板材产生弯曲，并测量弯曲前后的应变，从而得到应力-应变的关系。
弯曲强度可以通过该关系计算得出。
1.弯曲试验准备：-准备一块符合标准尺寸的花岗石板材。
-使用弯曲试验机，按照标准要求施加力使花岗石板材产生弯曲。
-在试验过程中，记录施加在花岗石板材上的力以及产生的应变。
2.弯曲应力-应变计算：-根据弯曲试验的数据，计算花岗石板材在弯曲过程中的应力和应变。
-应力可以通过施加在花岗石板材上的力除以板材的截面积得到。
-应变可以通过测量花岗石板材上的变形程度除以板材的初始长度得到。
3.构建应力-应变曲线：-将弯曲试验中得到的应力和应变数据进行绘图，得到应力-应变曲线。
-曲线的斜率表示花岗石板材在不同应力水平下的弯曲刚度。
4.弯曲强度计算：-弯曲强度等于应力-应变曲线中的最大应力。
-可以通过测量弯曲点的位置或者绘制应力-应变曲线来确定最大应力。
方法二：基于静力学条件计算弯曲强度此方法通过对花岗石板材上的应力和力的平衡进行分析，计算弯曲强度。
1.弯曲试验准备：-准备一块符合标准尺寸的花岗石板材。
-在板材上施加一定的力产生弯曲。
-记录施加在花岗石板材上的力以及板材的几何参数。
2.静力学分析：-分析弯曲过程中的力平衡关系。
-根据材料力学性质和几何参数，计算板材上的应力分布。
3.弯曲强度计算：-弯曲强度等于花岗石板材上的最大应力。
-可以通过应力分布图或者静力学计算公式来确定最大应力。
两种方法各有优缺点，可以根据具体情况选择适合的方法计算花岗石的弯曲强度。
在进行弯曲试验时，应严格按照标准操作，并注意考虑各种因素对试验结果的影响，如温度、湿度等。
同时，需要注意花岗石材料的不均匀性可能影响试验结果，因此应尽可能选择均匀的花岗石样品进行试验。
工程力学弯曲强度2(应力分析与强度计算
max
y
2
当中性轴是横截面的对称轴时：
IZ
max
IZ
y
y1 y2 y max
1
即对称截 面梁
max max max
y
Iz 简单截面的抗弯截面系数 Wz＝ ymax y
h z
y z
bh Iz bh 2 Wz＝ 12 h h 6 2 2
3
max - max -
i max
M z max max i = Wz i
一般非等直梁
M z x y x max = max x = I z x max
可利用函数求导的方法得到最大正应力数值
固定端处梁截面上的弯矩: M＝Me 。 且这一梁的所有横截面上的弯矩都 等于外加力偶的力偶矩Me
中性轴通过 截面形心，因此z 轴就是中性轴。 据弯矩方向可知中性 轴以上均受压应力，以下 均受拉应力。 根据正应力公式，横截面上正应力沿截面高度（y） 按直线分布，在上、下边缘正应力最大。可画出固定 端截面上的正应力分布图。
M max y 2 0.253N m 10 3 15 10 3 m 2 0.842 10 3 Pa 84.2MPa Iz 4.5 10 -8 m 4
例题
C
FRA FRB
T形截面简支梁在中点承受集中力 FP ＝32kN， l=2m。 T形截面的形心坐标yC=96.4mm，横截面对于z 轴的惯性矩Iz =1.02108 mm4。求：弯矩最大截面上的 最大拉应力和最大压应力。 解： 根据静力学平衡可求得支座A和B处的约束力分别 为FRA＝FRB＝16 kN。据内力分析，知梁中点截面 上弯矩最大
钢梁的抗弯强度计算公式中,当 rx取大于1.0数时表示
钢梁的抗弯强度计算公式中,当rx取大于1.0数时表示
摘要：
1.钢梁的抗弯强度计算公式
2.rx 的含义
3.当rx 大于1.0 时的表示
正文：
一、钢梁的抗弯强度计算公式
钢梁的抗弯强度计算公式是结构工程师在设计钢梁时必须掌握的重要公式。
这个公式可以帮助他们确定钢梁在承受弯曲负荷时的强度。
这个公式为：
F = M*W*L^2/8*rx
其中，F 是抗弯强度，M 是弯矩，W 是钢梁的截面模量，L 是钢梁的长度，rx 是弯曲半径。
二、rx 的含义
rx，也称为弯曲半径，是指钢梁在承受弯曲负荷时，梁的弯曲部分中心线到梁的边缘的距离。
它是一个重要的参数，会影响到钢梁的抗弯强度和弯曲变形。
三、当rx 取大于1.0 数时表示
当rx 的值大于1.0 时，这表示钢梁的弯曲半径大于1，也就是说，钢梁在承受弯曲负荷时，弯曲的部分的中心线到梁的边缘的距离大于1。
这种情况下，钢梁的抗弯强度会增大，因为弯曲半径的增大会降低弯曲应力，从而提高钢梁的抗弯强度。
材料力学课件—— 弯曲强度计算
q Ba YB QB左 B MB左
B左截面
C YA - QB左 0
qa 2 YAa - M B左 0
Q B左
YA
3 qa 2
M B左
1 qa2 2
（2）计算各截面内力（续）
qa 2
A
a
YA
q
Ba C YB
QB右 q
MB右B
aC
B右截面
QB右 - qa 0
M B右
qa
1 2
a
0
Q
B右
第五章 弯曲强度计算
第一部分 弯曲内力 (Bending forces)
第一节 概述 第二节 静定梁的基本形式 第三节 平面弯曲时梁横截面上的内力 第四节 剪力图和弯矩图 第五节 剪力、弯矩和分布载荷间的关系 第六节 用叠加法作剪力图和弯矩图 第七节 刚架的弯矩图、轴力图
第一节 概述
构件 （Component, Structural member） 杆 （bar） 梁 （beam）
RB
r
M0b/l M0a/l
m0/l
aM0= Par b
Ax C
B
RA
l
RB
Q
(+)
x
M
(+)
(-)
x
例 为一直齿圆柱齿轮传动轴。该轴可简化为简支梁，当仅考 虑齿轮上的径向力P对轴的作用时，其计算简图如图所示。试 作轴的剪力图和弯矩图。
a
b
aP b
A
C
RA x
l
RB
aP b
A
C
RA x
l
RB
Q
(+)
qa
M B右
1 qa 2 2
抗弯强度计算公式
抗弯强度计算公式
抗弯强度是指材料在弯曲作用下所能承受的最大应力或最大弯曲应变。
抗弯强度是材料的重要力学性能指标之一，用于评估材料的弯曲性能和抗
弯能力。
常见的抗弯强度计算公式有以下几种。
1.弯矩与截面惯性矩之比法（弯矩法）：
抗弯强度（σ）=弯矩（M）/截面惯性矩（I）
弯矩和截面惯性矩之间的关系可以通过受弯构件的几何形状和边界条
件来计算。
其中弯矩是由外力和支座反力引起的，截面惯性矩则与截面形
状有关。
这种方法适用于均匀截面和直线弯曲构件。
2.应变能法：
抗弯强度（σ）=弯矩（M）/弯曲半径（ρ)
其中弯曲半径是指受弯构件上任意一点处的弯曲曲率半径，可以通过
应变能原理进行求解。
3.钢筋计算法：
抗弯强度（σ）=弯矩（M）/距离钢筋所在中和轴的距离（c）
这种计算方法主要适用于钢筋混凝土梁，通过将梁截面划分为钢筋区
和混凝土区，并根据不同材料的应力-应变关系进行计算。
4.极限平衡法：
抗弯强度（σ）=弯矩（M）/节点的抗弯强度
这种计算方法适用于结构的极限状态设计，通过平衡力矩和力的作用力进行计算，要求加强截面到极限荷载的耐久性。
以上是常见的抗弯强度计算公式，不同的计算方法适用于不同的材料和构件形状。
在计算过程中，需要准确的构件尺寸和截面特性参数，以及材料的力学性能参数。
此外，还需要根据具体工程需求和设计规范进行计算，确保结构的安全性和可靠性。
齿轮弯曲强度计算
齿轮弯曲强度计算齿轮弯曲强度计算是齿轮设计的重要环节，它直接关系到齿轮的耐用性和可靠性。
本文将详细介绍齿轮弯曲强度的计算方法，包括对齿轮的基本参数、弯曲力矩、弯曲应力等方面的讨论。
一、齿轮的基本参数在进行齿轮弯曲强度计算之前，我们需要了解齿轮的基本参数，包括模数、齿数、压力角、齿宽等。
模数是齿轮设计和制造中的基本单位，它表示齿轮的轮齿尺寸和强度。
齿数是齿轮的齿数，它直接影响到齿轮的传动能力和弯曲强度。
压力角是指齿轮轮齿上的齿廓与分度圆交点的切线与齿廓方向之间的夹角，它对齿轮的传动性能和强度有一定的影响。
齿宽是指齿轮轮齿的宽度，它对齿轮的弯曲强度和稳定性有一定的影响。
二、弯曲力矩的计算弯曲力矩是导致齿轮弯曲的主要因素，它的大小直接影响到齿轮的弯曲强度。
根据弯曲力矩的计算公式，可以得出弯曲力矩与齿轮的基本参数之间的关系。
一般来说，弯曲力矩的计算公式如下：M = F * d其中，M是弯曲力矩，F是作用在齿轮上的名义应力，d是齿轮的分度圆直径。
根据这个公式，我们可以得出以下结论：1.弯曲力矩与名义应力成正比，与分度圆直径成反比。
因此，在设计齿轮时，可以通过降低名义应力和增加分度圆直径来提高齿轮的弯曲强度。
2.在相同的名义应力和分度圆直径下，齿数越少，弯曲力矩越大。
因此，在保证齿轮传动能力和强度的前提下，可以适当减少齿数来降低弯曲力矩的影响。
三、弯曲应力的计算弯曲应力是衡量齿轮弯曲强度的关键指标，它的大小直接影响到齿轮的使用寿命和可靠性。
根据材料力学的基本理论，可以得出弯曲应力的计算公式：σ = M / W其中，σ是弯曲应力，M是弯曲力矩，W是抗弯截面系数。
根据这个公式，我们可以得出以下结论：1.弯曲应力与弯曲力矩成正比，与抗弯截面系数成反比。
因此，在设计齿轮时，可以通过增加材料的抗弯截面系数来提高齿轮的弯曲强度。
常用的增加抗弯截面系数的措施包括增加齿高、增加齿宽等。
2.在相同的弯曲力矩和抗弯截面系数下，模数越小，弯曲应力越大。
杆件的强度计算公式
杆件的强度计算公式1.应力：应力是杆件内部单位面积上的力，通常以帕斯卡（Pa）为单位。
应力被定义为负载除以横截面积。
在强度计算中，应力是一个重要的参数，用于评估杆件是否能够承受给定的负载。
2.截面形状：截面形状指的是杆件横截面的形状，如圆形、矩形、梯形等。
截面形状对杆件的强度计算有很大影响，因为不同的形状在承载能力方面具有不同的特点。
3.材料性质：杆件的材料性质包括弹性模量、屈服强度、抗拉强度等。
这些参数用于计算杆件在受力情况下的应力和应变，并评估其强度。
根据杆件的受力类型和计算方法的不同，强度计算公式可以有很多种形式。
以下是几个常见的强度计算公式示例：1.杆件的拉伸强度计算公式：拉伸强度=屈服强度/安全系数这个公式适用于纯拉伸情况下的杆件强度计算。
通常，设计中会采用一个安全系数，以确保杆件在实际应用中不会超过其屈服强度。
2.杆件的压缩强度计算公式：压缩强度=屈服强度/安全系数这个公式适用于纯压缩情况下的杆件强度计算。
与拉伸情况类似，设计中也会采用一个安全系数。
3.杆件的弯曲强度计算公式：弯曲强度=弯矩/抗弯矩弯曲强度计算涉及到杆件的几何形状和截面惯性矩等参数，以及杆件的材料性质。
通过计算弯矩和抗弯矩的比值，可以评估杆件在受弯应力作用下的强度。
此外，还有一些特殊情况下的杆件强度计算公式，如扭转、剪切、冲击等。
这些公式通常相对复杂，需要更详细的材料性质和截面形状参数。
需要注意的是，强度计算公式只是一种初步评估杆件承载能力的方法，它没有考虑杆件的缺陷、损伤和非均匀加载等因素。
因此，在实际工程中，还需要进行更为详细的强度分析和安全性评估，以确保杆件的可靠性和安全性。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
3.88MPa
6
正应力强度满足。
（3） 校核切应力强度
max
3FQ m ax 2A
3 4103 2140 210
0.20 MPa
切应力强度满足。
练习：
例2. 一简支梁如下图示。梁由两根工字钢组 成，[σ]=170MPa，选择工字钢的型号。
❖解
10KN 50KN
（a）
C
z
A
B
12kN
2m
1m
8KN·m
a b
A截面
M B 12KN m, M A 8KN m
M图
A截面最大拉应力
12kN·m
c
max
M A y2 Iz
8106 200 1108
16MPa
B截面最大拉应力
d B截面
max
MB Iz
y1
12106 100 1108
max
将此式改写为
max
I y 令
Wz
Байду номын сангаас
Iz ymax
则
z max
max
M Wz
式中 Wz——抗弯截面系数。在M相同的情况
下，Wz 愈大， max就愈小，梁便不容易破坏。可见
，抗弯截面系数反映截面抵抗弯曲破坏的能力。
（2） 脆性材料杆件和中性轴不在对称轴的 截面，最大拉应力和最大压应力不一定发生
例1 下图所示木梁，已知[σ]=10MPa，
[τ]=2MPa，b=140mm，h=210mm，校核梁
强度。
❖解
q=2kN/m
z
h
=4m
b
4kN
FQ图
4kN
M图
作 FQ 和 M图
4kN·m
FQmax 4KN
M max 4KN m
（2）校核正应力强度
max
M max Wz
4 106 1 140 2102
❖ 1. 强度校核
max
M max Wz
2. 设计截面
max
FQ
S* z max
Iz b
Wz M max
圆截面：
Wz
Iz ymax
d 4
d
64 2
d3
32
矩形截面：
Wz
Iz ymax
bh3 12 h2
bh2 6
3. 确定许用荷载 M max Wz
复习：
弯曲杆件正应力计算公式：
M y
I
弯曲切应力计算公式：
FQ Sz
Iz b
第五节 弯曲杆件的强度计算
❖ 一、强度条件
❖ 1. 正应力强度条件 ❖ （1） 横截面上的最大正应力 ❖ 对整个等截面杆件来说，最大正应力发生
在弯矩最大的截面上，其值为
M max
M max Iz
ymax
在同一截面，所以，最大正应力公式表示为
mmaxaxMM2I1Iyzyzmmaaxx
y max yymax
z 图8-30
σymax M
σ max
例8.12 悬臂梁受力如下图所示，已知
I z 1108 mm 4 试求梁的最大拉应力。
22kN
解：画M图。
100 200 (y1) (y2)
A
B
CD
z
4m 2m 4m
RA 26 KN
RB 34 KN
M max 136 KN m
Wz
M max
2
136 106 2 170
400 cm3
2.切应力强度条件
❖ 对于等截面直梁，全梁的最大切应力发生在FQmax 所在截面的中性轴处。
max
FQ
S* z max
Iz b
当杆件出现以下情况之一时，必须校核切应
力强度，甚至由切应力强度条件来控制：
（1）梁的跨度较小或荷载作用在支座附时。
（2）某些组合截面梁（如焊接的工字形钢板
梁），当腹板厚度与高度之比小于相应型钢的相
应比值时。
（3）木梁或玻璃等复合材料梁。
3.主应力强度条件
❖ 当截面为三块矩形钢板 焊接而成的工字形：
1
2
2
2
2
3
2
2
2
2
a z
b
y
M
τmin
τmax τmin
二、强度计算
12MPa
（2）.强度条件
产生最大弯矩的截面称为危险截面，危险
截面上产生最大应力的点称为危险点。
max
M max ymax IZ
M max Wz
对于脆性材料
max
M
ym ax Iz
max
M
ym ax Iz
式中各量计算均用绝对值。