齿根强度计算
标准直齿圆柱齿轮传动的强度计算
标准直齿圆柱齿轮传动的强度计算一、轮齿的受力分析图6-6所示为齿轮啮合传动时主动齿轮的受力情况，不考虑摩擦力时，轮齿所受总作用力f n将沿着啮合线方向，f n称为法向力。
f n在分度圆上可分解为切于分度圆的切向力f t和沿半径方向并指向轮心的径向力f r 。
圆周力f t=n径向力 f r= f t tg n (6-1)法向力 f n=n式中:d1为主动轮分度圆直径,mm；为分度圆压力角，标准齿轮=20°。
设计时可根据主动轮传递的功率p1（kw）及转速n1(r/min)，由下式求主动轮力矩t1=9.55×106×（n mm）（6-2）根据作用力与反作用力原理，f t1=-f t2，f t1是主动轮上的工作阻力，故其方向与主动轮的转向相反，f t2是从动轮上的驱动力，其方向与从动轮的转向相同。
同理，f r1=-f r2，其方向指向各自的轮心。
二、载荷与载荷系数由上述求得的法向力f n 为理想状况下的名义载荷。
由于各种因素的影响，齿轮工作时实际所承受的载荷通常大于名义载荷，因此，在强度计算中，用载荷系数k 考虑各种影响载荷的因素，以计算载荷f nc 代替名义载荷f n 。
其计算公式为(6-3)式中：k 为载荷系数，见表6-3。
表6-3 载荷系数k二、齿根弯曲疲劳强度计算齿根处的弯曲强度最弱。
计算时设全部载荷由一对齿承担，且载荷作用于齿顶，将轮齿看作悬臂梁，其危险截面可用30o 切线法确定，即作与轮齿对称中心线成30o 夹角并与齿根过渡曲线相切的两条直线，连接两切点的截面即为齿根的危险截面，如图6-7所示。
运用材料力学的方法，可得轮齿弯曲强度校核的公式为= ≤或σf =≤（6-4）或由上式得计算模数m的设计公式m≥ (6-5)式中:=b/d1称齿宽系数（b为大齿轮宽度），由表6-4查取；称为齿形系数，由图6-8查取；[]为弯曲许用应力，由式6-8计算。
表6-4齿宽系数=b/d1三、齿面接触疲劳强度计算齿面接触疲劳强度计算是为了防止齿间发生疲劳点蚀的一种计算方法，它的实质是使齿面节线处所产生的最大接触应力小于齿轮的许用接触应力，齿面接触应力的计算公式是以弹性力学中的赫兹公式为依据的，对于渐开线标准直齿圆柱齿轮传动，其齿面接触疲劳强度的校核公式为≤或≤ (6-6)将上式变换得齿面接触疲劳强度的设计公式d1≥ (6-7)式中：“±”分别用于外啮合、内啮合齿轮；z e为齿轮材料弹性系数，见表6-5；z h为节点区域系数，标准直齿轮正确安装时z h =2.5；[σh]为两齿轮中较小的许用接触应力，由式6-9计算；u为齿数比，即大齿轮齿数与小齿轮齿数之比。
标准直齿圆柱齿轮传动强度
标准直齿圆柱齿轮传动的强度可以根据以下步骤进行计算：
1.确定齿轮上所受的力。
这包括圆周力（Ft）、径向力（Fr）和法向力
（Fn）。
2.根据圆周力和齿轮的节圆直径（d1），计算出转矩（T1）。
转矩可以用公
式T1 = 2 × Ft × tanα来表示，其中α是啮合角，通常取值为20°。
3.根据转矩和齿宽，计算出弯曲应力。
弯曲应力可以用公式σ= Ft/Wb来表
示，其中Wb是齿宽。
4.根据齿根处的弯曲应力，计算出弯曲疲劳强度系数。
这个系数通常由实验
确定，也可以通过查阅相关设计手册获得。
5.根据弯曲疲劳强度系数和弯曲应力，计算出弯曲疲劳极限。
弯曲疲劳极限
可以用公式σHlim = k × Wb × Ft来表示，其中k是弯曲疲劳强度系数。
6.根据弯曲疲劳极限，计算出安全系数。
安全系数可以用公式H=σHlim/σH
来表示，其中σH是工作应力。
7.根据安全系数和弯曲应力，计算出许用弯曲应力。
许用弯曲应力可以用公
式σH=σHlim/S来表示，其中S是安全系数。
以上是标准直齿圆柱齿轮传动强度的计算步骤，希望能对您有所帮助。
圆柱齿轮传动强度的计算
圆柱齿轮传动的强度计算1 直齿圆柱齿轮传动的强度计算1.齿面接触疲劳强度计算为了保证在预定寿命内齿轮不发生点蚀失效，应进行齿面接触疲劳强度计算。
因此，齿轮接触疲劳强度计算准则为：齿面接触应力σH小于或等于许用接触应力σHP，即σH≤σHP赫兹公式由于直齿轮在节点附近往往是单对齿啮合区，轮齿受力较大，故点蚀首先出现在节点附近。
因此，通常计算节点的接触疲劳强度。
图a表示一对渐开线直齿圆柱齿轮在节点接触的情况。
为了简化计算，用一对轴线平行的圆柱体代替它。
两圆柱的半径ρ1、ρ2分别等于两齿廓在节点处的曲率半径，如图b所示。
由弹性力学可知，当一对轴线平行的圆柱体相接触并受压力作用时，将由线接触变为面接触，其接触面为一狭长矩形，在接触面上产生接触应力，并且最大接触应力位于接触区中线上，其数值为式中σH-接触应力（Mpa）Fn-法向力（N）L-接触线长度（mm）rS-综合曲率半径（mm）；±-正号用于外接触，负号用于内接触ZE-材料弹性系数（），，其中E1、E2分别为两圆柱体材料的弹性模量（MPa）；m1、m2分别为两圆柱体材料的泊松比。
上式表明接触应力应随齿廓上各接触点的综合曲率半径的变化而不同，且靠近节点的齿根处最大（图c、d）。
但为了简化计算，通常控制节点处的接触应力。
节点处的参数（1）综合曲率半径由图可知，，代入rE公式得式中：，称为齿数比。
对减速传动，u=i；对增速传动，u=1/i。
因，则有（2）计算法向力（3）接触线长度L引入重合度系数Ze，令接触线长度将上述参数代入最大接触应力公式得接触疲劳强度计算公式令，称为节点区域系数。
则得(1) 齿面接触疲劳强度的校核公式齿面接触疲劳强度的校核公式为(2) 齿面接触疲劳强度设计公式设齿宽系数，并将代入上式，则得齿面接触疲劳强度的设计公式式中:d1-小齿轮分度圆直径（mm）；ZE-材料弹性系数()，按下表查取；注：泊松比m1＝m2＝0.3Z H-节点区域系数，考虑节点处轮廓曲率对接触应力的影响，可由下左图查取。
齿轮齿面接触强度及齿根弯曲强度核算
齿面接触强度及齿根弯曲强度核算在设计产品过程中，经常会选用齿轮作为传动力及扭矩的原件。
在大部分成型产品改造或调整过程中，关于齿轮的强度校核这一步骤就可以用类比法代替，从而节省设计人员的精力，缩短了设计周期。
但得出的结果没有书面依据以及理论方面的支持。
所以当进行多次类比之后，所设计出来的齿轮与理论计算得出的齿轮偏差会较大。
其原理类似于累计偏差。
所以应该进行强度校核方面的计算。
齿轮强度校核计算，在实际应用中，主要是两方面的核算：1、齿面接触强度的核算。
2、齿根弯曲强度的核算。
1.齿面接触强度核算-分度圆直径计算参考文献：在初步设计齿轮时，根据齿面接触强度，可按照下列公式估算齿轮传动的尺寸。
(机械设计手册P14-133)a≥A a(μ±1)·√KT1ψaσHP23①d1≥A d·√KT1ψdσHP2·μ±1μ3②公式①为两齿轮中心距的计算；公式②为齿轮分度圆直径的计算。
由于本次计算的是齿轮齿条传动。
所以，中心距a= d1/2其中：d1为齿轮分度圆直径，只需要核算齿轮分度圆直径d1首先，要确定公式②中各个符号代表的含义及数值选取。
d1—齿轮分度圆直径；A d—常系数；K—载荷系数；μ—齿数比；σHP—许用接触应力；ψd—齿宽系数；T1—电机减速机输出扭矩；d1：齿轮分度圆直径，待求；A d：常系数值；A d值在表14-1-65中，通过螺旋角角度β的数值求得。
齿轮的螺旋角β=11.655°,则A d = 756。
载荷系数K，常用值K=1.2～2（机械设计手册P14-133），当载荷平稳，齿宽系数较小，轴承对称布置，轴的刚性较大，齿轮精度较高（6级以上），以及齿轮的螺旋角较大时取较小值；反之取较大值。
根据对比后的结果在K的常用范围内选取。
此次选择K=1.8（载荷平稳，齿宽系数较小，轴为非对称分布，轴的刚性不大，齿轮精度不高）u：传动比。
当齿轮之间为外啮合的时候，选取“+”；当齿轮之间为内啮合的时候，选取“-”，本次计算为齿轮齿条，不影响计算结果。
齿顶高和齿根高计算公式
齿顶高和齿根高计算公式齿顶高和齿根高是在齿轮设计和制造过程中非常重要的参数，它们直接影响着齿轮的传动性能和使用寿命。
本文将介绍齿顶高和齿根高的计算公式及其意义。
一、齿顶高齿顶高是齿轮齿面上凸起部分的高度，它由齿轮轮齿间隔（模数）m和齿轮的分度圆直径d决定。
齿顶高的计算公式为：h_a = 2m + c其中，h_a表示齿顶高，m表示齿轮轮齿间隔（模数），c表示齿顶高工作系数。
齿顶高工作系数c的取值范围一般在0.25~0.4之间。
当传动功率较大或工作环境恶劣时，可以适当增大齿顶高工作系数，以增强齿轮的承载能力和使用寿命。
计算齿顶高时，需要根据齿轮的模数和分度圆直径来确定齿距（即两个相邻齿顶之间的距离），然后再根据齿距和齿顶高工作系数来计算出齿顶高。
二、齿根高齿根高是齿轮齿面下凹部分的高度，它直接影响着齿轮的强度和刚度。
齿根高的计算公式为：h_f = 2.2m + c_f其中，h_f表示齿根高，m表示齿轮轮齿间隔（模数），c_f表示齿根高工作系数。
齿根高工作系数c_f的取值范围一般在0.3~0.5之间。
当传动功率较大或工作环境恶劣时，可以适当增大齿根高工作系数，以提高齿轮的强度和刚度。
计算齿根高时，同样需要根据齿轮的模数和分度圆直径来确定齿距，然后再根据齿距和齿根高工作系数来计算出齿根高。
三、齿顶高与齿根高的意义齿顶高和齿根高是齿轮齿面的重要尺寸。
它们的大小直接影响着齿轮的使用寿命、载荷能力、传动效率等性能指标。
较大的齿顶高可以提供更大的接触面积，减小齿轮的载荷集中程度，从而增强了齿轮的承载能力和使用寿命。
然而，齿顶高过大会增加齿面接触应力和摩擦损失，降低传动效率。
因此，在设计齿轮时需要在承载能力和传动效率之间进行权衡。
较大的齿根高可以提高齿轮的强度和刚度，增强了齿轮的抗弯挠性和抗疲劳性能。
然而，齿根高过大会增加齿轮的体积和重量，降低传动效率。
因此，在设计齿轮时也需要在强度和刚度之间进行权衡。
总之，齿顶高和齿根高是齿轮设计中需要考虑的重要参数，它们的计算公式可以通过模数和工作系数进行计算。
机械设计(6.6.1)--标准直齿圆柱齿轮齿根弯曲疲劳强度计算
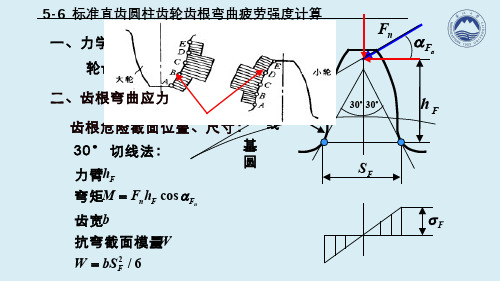
5-6 标准直齿圆柱齿轮齿根弯曲疲劳强度计算 Fh FS 30o 30oaF a nF 基圆过渡曲线Fs 一、力学模型轮齿悬臂梁，F n 作用于齿顶齿根危险截面位置、尺寸：30°切线法：2cos /6n Fn F F F h M F h bWW bS a ==力臂弯矩齿宽抗弯截面模量二、齿根弯曲应力二、齿根弯曲应力12216cos cos 2/6cos aaF F nc F F F F F h F h KT M m W bS bd m S m a a s a ������===������齿根弯曲应力：26cos ,514,cos aa F F F F h mY mS m a a ⎛⎫⎪⎝⎭=-⎛⎫⎪⎝⎭齿形系数图与齿廓形状有关，与模数无关(515)0.750.25sa Y Y e ae -=+应力修正系数图重合度系数2112N/mm a F F sa KT Y Y Y bd mes =齿根弯曲应力：三、标准直齿圆柱齿轮齿根弯曲疲劳强度112:aF F sa F KT Y Y Y bd me s s =≤⎡⎤⎣⎦1.齿根弯曲疲劳强度条件2.分别校核大小齿轮根齿弯曲疲劳强度11111112222122F Fa sa F F Fa sa F KT Y Y Y bd mKT Y Y Y bd me e s s s s =ﾣ����=ﾣ����3.按齿根弯曲疲劳强度设计三、标准直齿圆柱齿轮齿根弯曲疲劳强度()3121312d 14mm12 mm Fa sa a F Fa sa F Y Y Y KT m u z Y Y Y KT m z e eϕs ϕs ≥±⎡⎤⎣⎦≥⎡⎤⎣⎦或1a a 1d 1(1);2d mz u b a b d mz f f f f ﾣ====1122121max ,(2)0.8~1.4,()Fa sa Fa sa Fa sa F F F t ttY Y Y Y Y Y KY KY KY KY m m KY e e ee e s s s ����=����������������==4.设计式的有关说明（）设计式中，设计时，试选。
齿根弯曲强度校核公式
齿根弯曲强度校核公式
齿根弯曲强度校核公式是用于评估齿轮传动系统中齿根的强度的重要公式。
在
设计和制造齿轮时，确保齿根弯曲强度满足要求是至关重要的。
齿轮传动系统中，齿根弯曲强度是指齿根在受到负载时的能力，即齿根是否能
够承受负载而不发生弯曲破坏。
为了确保齿根弯曲强度充分满足工作条件，我们需要校核其强度。
根据国际标准，可以使用以下公式来计算齿根弯曲强度校核：
YB = YB1 * YB2 * YB3 * YB4 * YB5
其中，YB表示齿根弯曲强度系数，YB1表示弯曲强度系数，YB2表示几何弯
曲系数，YB3表示应力集中系数，YB4表示表面弯曲系数，YB5表示温度弯曲系数。
弯曲强度系数YB1与齿轮材料弯曲强度有关，根据材料的弯曲强度来确定。
几何弯曲系数YB2与齿轮模数、齿轮系数和齿宽有关，根据设计参数确定。
应力
集中系数YB3与齿轮齿型有关，在计算过程中考虑齿形修正因素。
表面弯曲系数YB4与表面处理有关，可以通过热处理等表面处理手段来提高强度。
最后，温度
弯曲系数YB5与齿轮工作温度有关，一般通过实验数据或工程经验确定。
通过计算并比较齿根弯曲强度系数YB与要求的设计系数YB0，可以评估齿根
弯曲强度是否满足要求。
如果YB≥YB0，则齿根弯曲强度校核通过；反之，则需
要重新设计或采取强化措施。
总之，齿根弯曲强度校核公式是评估齿轮传动系统中齿根弯曲强度的重要工具。
根据公式中各个系数的计算和比较，我们可以判断齿根是否满足弯曲强度要求，并采取相应的措施来确保齿轮传动系统的可靠性和安全性。
齿轮强度计算公式
齿轮强度计算公式在计算齿轮的强度时，需要考虑以下几个因素：齿轮的材料、齿轮的几何参数、齿轮的载荷等。
下面将详细介绍一些常用的齿轮强度计算公式。
1.根弯曲强度计算：齿轮的根弯曲强度是指齿轮齿根部分在受载条件下的强度。
根据弯曲强度理论，可以得到如下公式：σb=(Ks⋅M)/(Z⋅Y)其中，σb为齿轮的根弯曲应力，Ks是安全系数，M为齿轮的弯矩，Z为齿轮的模数，Y为齿轮的几何弯曲系数。
2.接触疲劳强度计算：接触疲劳强度是指齿轮齿面在接触运动中的承载能力。
根据接触疲劳强度理论，可以得到如下公式：σH=(Z⋅v⋅Kv⋅Kσ)/(b⋅Y)其中，σH为齿轮的接触疲劳应力，v为齿轮的线速度，Kv为速度系数，Kσ为安全系数，b为齿宽，Y为齿轮的几何弯曲系数。
3.齿侧面强度计算：齿侧面强度是指齿轮齿面在受载条件下的强度。
根据齿侧面强度理论，可以得到如下公式：σH=(Ks⋅Mt)/(Z⋅m⋅Y)其中，σH为齿轮的齿侧面应力，Mt为齿轮的扭矩，m为齿数比，Ks为安全系数，Z为齿轮的模数，Y为齿轮的几何弯曲系数。
以上三个公式是常用的齿轮强度计算公式，通过对这些公式的计算，可以得到齿轮在不同工况下的强度情况。
需要注意的是，齿轮的强度计算还需要考虑其他因素，比如表面强度、温度影响等，以得到更准确的结果。
在实际应用中，为了确保齿轮的安全可靠性，通常要选择合适的安全系数，并进行必要的强度验证。
此外，还需要根据实际情况对齿轮的几何参数进行优化，以提高其强度和可靠性。
齿轮的强度计算是齿轮设计中的重要环节，通过合理计算齿轮的强度，可以确保齿轮在使用过程中能够承受合适的载荷，提高齿轮的使用寿命和可靠性。
齿啮式卡箍连接件强度计算
93414.01485 N
0.081402224 MPa
548
mm
100
mm
20
1.578473006
1.943649724
1.74522293 93.98414995 MPa
应 力 校 核 序 号
卡箍材料
项目
卡箍材料许用应力
符号
[σ]t S1 S2 S3 S4 S5
公式或数据来源 ZG-270-500
齿 啮 式 卡 箍 连 接 件 应 力 计 算
卡 箍 和 卡 箍 齿 部 应 力 计 算
序 号
项目
总轴向力 法兰齿外径 法兰齿顶处圆弧半径 法兰齿和卡箍齿相接触时的有效外径 卡箍齿长度 卡箍齿顶处圆弧半径 卡箍齿有效长度 卡箍体厚度 卡箍齿内径 法兰齿和卡箍齿相接触时的有效内径 钢材的泊松比 卡箍高度 卡箍开口间隙 和卡箍结构尺寸有关的参数 系数 系数 系数 系数 系数 卡箍体和卡箍环连接处的边缘力矩 卡箍体的轴向弯曲应力 卡箍体的轴向拉伸应力 6 卡箍体的轴向总应力 计及安装偏差引入的载荷修正系数 齿数 卡箍齿在根部的弧长 7 卡箍齿根轴向剪切应力 8 卡箍齿根的弯曲应力
SBC+STC 标准给定 设计图纸 设计图纸 3Hf1/(nL(Cw-Cg)) 24HCmf1/(nL(Cw-Cg)2)
1/4
数值
数值
单位
38220000 4886.5 20 4846.5 100 20 80 110 4706.5 4746.5 0.3 1183 783
0.002447356 327396.2962 0.074121372 6.010518407 1.04483848 1.244735589 267219.836 132.5057038 22.04688863 154.5525924
齿轮副的齿形设计和强度计算
齿轮副的齿形设计和强度计算齿轮副是机械传动中最常用的一种传动方式，其基本构成单元是齿轮。
齿轮的齿形设计和强度计算则是齿轮副设计中的重要内容。
本文将从齿形设计和强度计算两个方面来探讨齿轮副的设计。
一、齿形设计齿形是齿轮副中最基本的构成单元，它直接影响着齿轮副传动的精度和效率，因此齿形设计是齿轮副设计中不可忽视的一个环节。
1.基本概念齿形设计的基本概念包括齿形参数和齿形尺寸。
齿形参数是指齿轮齿形的一些几何参数，包括齿高、齿顶高、齿根高等。
齿形尺寸则是指齿轮齿形的具体大小，包括齿轮的模数、齿数、齿顶径、齿宽等。
2.齿形设计原则齿形设计的原则是在保证齿轮副传动精度和效率的前提下，尽量减小齿轮与齿轮之间的啮合震动和噪音。
在齿形设计中，需要注意以下几点：（1）齿轮与齿轮之间的啮合面要尽量光滑且呈流线型，以减小摩擦损失和噪音。
（2）齿形设计应合理安排齿数、齿高、齿顶高和齿根高等参数，使得齿轮副的啮合角度和齿数比适当，减小啮合震动和噪音。
（3）齿形设计应根据齿轮的使用环境和要求进行调整，如要求传动效率高，应尽量减小齿形参数；要求传动平稳，应适当增大齿形参数。
二、强度计算齿轮副的强度计算是齿轮副设计中的关键环节，是确保齿轮副传动稳定和长久使用的保障。
1.强度设计基础强度计算的基础是齿轮的材料强度和齿面接触应力。
齿轮的材料强度是指齿轮的材料在受力时所能承受的最大应力，而齿面接触应力则是指齿轮齿面之间接触所产生的应力。
2.计算方法强度计算方法主要有两种，一种是按ISO齿轮标准计算；另一种是按照AGMA齿轮标准计算。
两种计算方法各有优缺点，具体的计算方法应根据齿轮的实际情况来确定。
ISO计算方法适用于齿轮模数在3mm及以下的小模数齿轮。
ISO计算方法的优点是计算简单、公式标准，容易掌握，不需要复杂的CAD软件支持。
但缺点是计算精度偏低，不适用于高精度齿轮的设计。
AGMA计算方法适用于所有模数的齿轮。
AGMA计算方法的优点是计算精度高，可以用CAD软件进行辅助计算，适合精密齿轮的设计。
锥度齿轮齿根计算公式
锥度齿轮齿根计算公式锥度齿轮是一种常见的传动装置，它通过齿轮的啮合来传递动力和转矩。
在设计和制造锥度齿轮时，齿根的计算是非常重要的一步，因为它直接关系到齿轮的强度和耐久性。
本文将介绍锥度齿轮齿根的计算公式及其应用。
锥度齿轮齿根计算公式是根据齿轮的模数、齿数、齿轮厚度等参数来确定的。
在计算齿根时，需要考虑齿轮的载荷、材料强度、齿轮的设计寿命等因素。
下面将介绍锥度齿轮齿根计算公式的具体内容。
首先，我们来看一下锥度齿轮齿根计算公式的基本形式：h = m (1 + cosα) / 2。
其中，h为齿根高度，m为模数，α为压力角。
在实际应用中，还需要考虑齿轮的齿数、齿轮厚度等参数。
根据这些参数，可以得到更为精确的齿根计算公式。
一般来说，齿根的计算公式可以表示为：h = m (1 + cosα) / 2 + c。
其中，c为齿根间隙。
通过这个公式，可以计算出锥度齿轮的齿根高度。
在实际应用中，还需要根据具体的工程要求和设计条件来确定齿根的具体数值。
例如，如果齿轮的载荷较大，需要考虑增加齿根高度以提高齿轮的强度和耐久性。
除了齿根高度的计算，还需要考虑齿根的形状和加工工艺。
在实际制造中，需要根据计算得到的齿根高度来确定齿根的具体形状和加工工艺。
这些都需要考虑到齿轮的实际使用条件和工程要求。
在实际应用中，锥度齿轮齿根的计算是一个复杂的工程问题。
需要考虑到多个因素的影响，包括载荷、材料强度、齿轮的设计寿命等。
因此，在进行齿根计算时，需要进行详细的分析和计算，以确保齿轮的强度和耐久性。
总之，锥度齿轮齿根的计算是一个重要的工程问题，它直接关系到齿轮的强度和耐久性。
通过合理的计算和分析，可以确定锥度齿轮的齿根高度，从而保证齿轮的正常工作和长期使用。
希望本文对锥度齿轮齿根的计算有所帮助。
齿根弯曲疲劳强度计算公式
齿根弯曲疲劳强度计算公式
其中，S_H表示齿根弯曲疲劳强度；K_M表示材料强度系数；K_N 表示载荷系数；K_R表示可靠度系数；K_A表示表面硬度系数；K_V
表示材料体积系数；S_Hlim表示材料疲劳极限。
具体计算方法如下：
1. 确定齿轮材料的弹性模量E和泊松比v。
2. 根据齿轮的材料，查阅相应的材料疲劳极限表，得到材料疲
劳极限S_Hlim。
3. 计算载荷系数K_N。
根据齿轮的传动比i、输入功率P、齿轮系数Y和齿轮转速n，可以得到载荷系数K_N。
4. 计算表面硬度系数K_A。
根据齿轮的齿面硬度、齿疲劳极限
和齿根圆角半径，可以得到表面硬度系数K_A。
5. 计算材料体积系数K_V。
根据齿轮的模数m和齿轮宽度b，可以得到材料体积系数K_V。
6. 计算材料强度系数K_M。
根据齿轮所采用的材料，可以得到
相应的材料强度系数K_M。
7. 计算可靠度系数K_R。
根据齿轮的工作条件、工作寿命和可
靠度等级，可以得到可靠度系数K_R。
8. 将以上计算结果代入公式中，即可得到齿根弯曲疲劳强度S_H。
- 1 -。
标准齿轮计算公式
标准齿轮计算公式1. 齿轮基本参数的计算。
在进行齿轮设计和计算时，首先需要确定一些基本参数，包括模数、齿数、齿宽等。
这些参数的计算可以通过以下标准公式进行：（1）模数的计算公式：\[ m = \frac{d}{z} \]其中，m为模数，d为齿轮的分度圆直径，z为齿数。
（2）齿宽的计算公式：\[ b = m \times z \]其中，b为齿宽。
（3）齿顶高和齿根高的计算公式：\[ h_t = m \]\[ h_f = 1.25 \times m \]其中，h_t为齿顶高，h_f为齿根高。
2. 齿轮传动比的计算。
齿轮的传动比是指两个齿轮的齿数之比，一般用i表示。
齿轮传动比的计算公式为：\[ i = \frac{z_2}{z_1} \]其中，z_1为驱动齿轮的齿数，z_2为被动齿轮的齿数。
3. 齿轮啮合角的计算。
齿轮啮合角是指齿轮啮合时齿廓线与径向的夹角，它的大小对齿轮传动的平稳性和噪音有着重要影响。
齿轮啮合角的计算公式为：\[ \alpha = \arccos \left( \frac{m}{d} \right) \]其中，α为齿轮啮合角，m为模数，d为齿轮的分度圆直径。
4. 齿轮齿形修形系数的计算。
齿轮齿形修形系数是用来修正齿轮齿形的参数，它的大小对齿轮的传动效率和运行平稳性有着重要影响。
齿轮齿形修形系数的计算公式为：\[ x = 0.5 \times \left( \frac{1}{\cos \alpha} \frac{1}{\cos^3 \alpha} \right) \]其中，x为齿形修形系数，α为齿轮啮合角。
5. 齿轮齿面接触疲劳强度的计算。
齿轮齿面接触疲劳强度是指齿轮齿面在啮合过程中所承受的接触应力，它的大小对齿轮的使用寿命有着重要影响。
齿轮齿面接触疲劳强度的计算公式为：\[ \sigma_H = \frac{2 \times P}{\pi \times m \times b \times J} \]其中，σ_H为齿面接触疲劳强度，P为传动功率，m为模数，b为齿宽，J为齿形修形系数。
齿根弯曲疲劳强度计算-机械设计
2 1
4 ×
靠近转矩输入端，轮齿所受载荷较大。
× × 差
3
好
×
例： 图示减速器哪端输入更好？ 综合考虑a、b两因素。
机械设计
措施：
第 6章
齿轮传动
28
1）↑齿轮及支承刚度； 2）合理选择齿轮布置形式 （对称、非对称、悬臂） 3）合理选择齿宽； 4）↑制造安装精度； 5）采用鼓形齿； 6）齿轮位于远离转矩输入端。
计算载荷 Pca K p
K K A Kv K K
使用系数
动载系数
机械设计
第 6章
齿轮传动
24
1、使用系数KA 考虑原动机、工作机、联轴器等外部因素引起的动载荷而 引入的系数。（P100 表6.2） 2、动载系数Kv 考虑齿轮啮合过程中因啮合误差和运转速度引起的内部附加 动载荷系数。 基节误差、齿形误差、轮齿变形等
机械设计
第 6章
齿轮传动
10
点蚀机理
点蚀实例
机械设计
第 6章
齿轮传动
11
传动失效
后果：齿廓表面破坏，振动↑，噪音↑，传动不平稳
接触面↓，承载能力↓ 软齿面齿轮：收敛性点蚀，相当于跑合；
跑合后，若σH仍大于[σH]，则成为扩展性点蚀。 硬齿面齿轮：点蚀一旦形成就扩展，直至齿面完全破坏。 ——扩展性点蚀 开式传动：无点蚀（∵v磨损>v点蚀） 改善措施： 1）HB↑——[σH] ↑ 3）↑润滑油粘度 （↑接触强度） 2）↓表面粗糙度，↑加工精度
常出现在润滑良好的闭式软齿面传动中。 现象：节线靠近齿根部位出现麻点状小坑。
原因：σH＞[σH]
脉动循环应力 1）齿面受多次交变应力作用，产生接触疲劳裂纹； 2）节线处常为单齿啮合，接触应力大；
齿根强度计算
FnsinFa
h Fa
30° 30°
S Fa
2.齿根弯曲应力的计算
按悬臂梁理论，当载 荷作用于齿顶时，在 齿根危险截面上存在 三种应力：弯曲应力 σb、压应力σP 、切 应力τ。
FncosFa
Fa
FnsinFa
Fn
30°30°
h Fa
略去压应力σP 和切
S Fa
应力τ的影响，只按弯 曲应力σb进行计算。
24 2.67
25 2.64
Y sa 1.52 1.53 1.54 1.55 1.56 1.57 1.575 1.58 1.59
Z 26 27 28 29 30 35 40 … ∞
（z v）
Y Fa 2.63 2.60 2.58 2.56 2.54 2.46 2.41 … 2.06
Y sa 1.595 1.60 1.61 1.62 1.625 1.65 1.67 … 1.97
b b
Ft Ft
2T1
b
d1
b 2T1
d1
T1 T1
955nP 011 955P 01 n1
n1 n1
Ft Ft
b b
nn11
9604 720 3
b 4 b 3
由齿轮尺寸关系可知， hFa，SFa与模数m成正比。
因此YFa仅与齿廓形状有关而与模数无关。
当Z ↗、变位系数X↗ 、压力角α ↗时，齿根厚度↗
， YFa↘，从而使齿根弯曲应力降低。
Z=10 Z=25 Z=∞
α =20° α =25°
公式的修正
•引入应力修正系数Ysa可得齿根弯曲强度 校核公式：
R/min；试问要改变那个参数，并使该参数现用值与原来的值
直齿圆柱齿轮的齿根弯曲强度计算
接触疲劳极限Hlim
表14－6安全系数
可靠程度 高可靠性
SH 1.25
一般可靠性 1.00
低可靠性 0.80
SF 1.50 1.00 0.70
对于高速重载或重要的齿轮传动，应按 高可靠性选取，一般传动齿轮可适当降 低可靠性要求。
接触寿命系数ＺＮ
齿轮的弯曲疲劳极限Flim 当齿根弯曲应力为对称循环时，将查出的Flim乘以 0.7
齿形系数Yfa
应力修正系数YSa
重合度系数Y
齿宽系数d
表14-4
齿轮相对于轴承
齿面硬度
的位置
软齿面 硬齿面
对称布置
0.8 ~ 1.4 0.4 ~ 0.9
非对称布置 0.6 ~ 1.2 0.3 ~ 0.6
悬臂布置
0.3 ~ 0.4 0.2 ~ 0.25
直齿轮取表中的小值，斜齿轮取大值。
2、许用弯曲应力
e<1.6m时，将齿轮与 轴做成一体，称为齿 轮轴。
齿轮轴 直齿轮的齿轮轴
锥齿轮的Байду номын сангаас轮轴
2、实心齿轮
当齿轮的齿根圆直径与轴的直径相差较 大时，应分开制造。
当da<=180 mm 时，齿轮做成实心结构。
3、腹板式结构 当180 < = da<=500mm时，齿轮做成腹板式结构
二、铸造齿轮 当齿顶圆直径 da>=500mm时，齿轮锻造困难， 采用铸造的轮辐式结构。
FPFliSm F YNYx (MPa)
Flim－试验齿轮的弯曲疲劳极限，
YＮ－弯曲寿命系数
由图14-25查得
横坐标为实际应力循环系数 N
SF－弯曲疲劳安全系数
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Fa
Fn
Fn sin Fa
30°30°
hFa
S Fa
KFt F YFa bm
3 齿形系数YFa
齿形系数，表示由于齿轮齿廓形状不同对其弯曲强 度影响的系数。
由齿轮尺寸关系可知， hFa，SFa与模数m成正比。 因此YFa仅与齿廓形状有关而与模数无关。
当Z ↗、变位系数X↗ 、压力角α ↗时，齿根厚度 ↗， YFa↘，从而使齿根弯曲应力降低。
F
bm
F
解：若使改变转速前后传动的弯曲强度不变： F F
F
KFt K Ft YF F YF bm bm
K K
Ft Ft b b
YF Y F
m m
Ft b b Ft
Ft Ft
d1 T1 b 2T1 b T1 P 9550 1 d1 n1
u
σF
2 KT1 YFaYsa [σ F ] 2 bm z1
d 2 z2 1 d , 则a (d1 d 2 ) 1 ( u 1) d1 z1 2 2
a b a b / 0.5d1(u 1)
2 KT1 σF Y Y [σ F ] 3 2 Fa sa 0.5(u 1) a m z1
Fn
Fn sin Fa hFa
S Fa
确定危险截面位置 常用方法： 30°切线法
Fn cos Fa
Fa
Fn
Fn sin Fa hFa
30° 30°
S Fa
2.齿根弯曲应力的计算
按悬臂梁理论，当载 荷作用于齿顶时，在 齿根危险截面上存在 三种应力：弯曲应力 σb、压应力σP 、切 应力τ。
Fn cos Fa
Fa
Fn
Fn sin Fa
30°30°
hFa
略去压应力σP 和切 应力τ的影响，只按弯 曲应力σb进行计算。
S Fa
σb σP
τ
弯曲应力的计算
M 6 KFn cos Fa .hFa F 2 W bSFa
hFa 6 cos Fa KFt m F . 2 bm sFa cos m
Байду номын сангаас为计算悬臂梁危险截面的应力就需要确定力F、 力臂长L和梁截面尺寸b、t。
Ｆ
Ｌ
ｂ
ｔ
确定载荷作用点位置
Fn
Fn cos Fa
Fa
Fn sin Fa
Fn cos Fa
问题：αFa是 否为齿轮齿顶 圆与渐开线交 点的压力角？
Fa
Fn
确定危险截面位置 常用方法：抛物线法
Fn cos Fa
Fa
标准直齿圆柱齿轮传动
齿根弯曲疲劳强度的计算
1、齿根弯曲力学模型
针对轮齿折断失效，需进行齿根弯曲 疲劳强度的计算。
计算准则： F [ F ]
假设：
考虑到轮齿的制造误差和安装误差，通常假 定全部载荷由一对轮齿全部承担，并且作用在 一对轮齿上。 轮齿视为宽度为b的悬臂梁。
悬臂梁应力分析
得到设计公式：
YFaYsa 4 KT1 m . 2 ( u 1) a .z1 [ F ]
3
mm
讨论： F 1 ？ F 2
齿根弯曲疲劳强度计算
齿根弯曲的力学模型 齿根弯曲应力的计算 齿形系数 设计计算公式
例题分析:
1、有一标准直齿圆柱齿轮传动，若配对齿轮材料及齿 面硬度、齿数Z1 和Z2 ，中心距a、传动功率P，载荷系数 K 均保持不变，而把小轮的转速从n1=960 r/min降到n1′= 720 R/min；试问要改变那个参数，并使该参数现用值与原来的值 之比等于多少才能使该传动具有原来的弯曲强度（ KFt Y ）
Z
（z v）
Fa及应力修正系数Y sa
17 2.96 1.52
18
19
20
21
22
23
24
25
Y Y
Fa
2.91 2.85 2.82 2.77 2.74 2.70 2.67 2.64 1.53 1.54 1.55 1.56 1.57 1.575 1.58 1.59
sa
Z
（z v）
26 2.63
27
28
Z=10 Z=25 Z=∞
α =20° α =25°
公式的修正 •引入应力修正系数Ysa可得齿根弯曲强度 校核公式：
F
KFt YFa bm
Ft 2T1 d1
KFt F YFaYsa bm
d1 mz1
2KT 1 Y Y [σ ] σ F Fa sa F bm2 z 1
表 10-4 齿形系数Y
29
30
35
40
… …
…
∞ 2.06
1.97
Y
Y
Fa
2.60 2.58 2.56 2.54 2.46 2.41
sa
1.595 1.60 1.61 1.62 1.625 1.65 1.67
注：基准齿形的参数α=20˚，ha*=1，c*=0.25；ρ=0.38 m
4、设计公式
根据校核公式： 引入齿数比： 引入齿宽系数：
Ft b n 960 4 1 b 720 3 Ft n1
b 4 b 3
2T1
P 9550 1 n1
n1 n1