计算机控制系统实验(最少拍、大林算法)
计算机控制工程实验报告

计算机控制工程实验一 实验目的 试验目的:1了解计算机控制系统的基本构成结构和掌握计算机控制系统的原理;熟悉计算机控制系统的设计过程。
2掌握控制器的设计方法;能够利用最小拍有纹波,最小拍无纹波,大林算法,数字PID 四种方法设计数字控制器。
并体会四种算法设计的不同。
比较不同控制器的设计方法的区别,在编程和仿真的过程中,学习MATLAB 软件的使用,通过Matlab 工具仿真控制效果,掌握不同控制器的特点;3 通过本实验积累在具体控制工程中分析与解决具体问题的能力,并熟悉设计控制系统的过程。
4 对仿真结果进行分析,体会不同的设计思想,加深对计算机控制系统设计的理解 二 实验任务 实验对象结构:D(z)是待设计的数字控制器,G(s)是被控对象的连续传递函数,G h (s)是零阶保持器,T 为采样周期G(s)有两种:传函G 1:()Se s G S S s G Tsh --=+=1)(,)2(2传函G 2:()Se s G S e s G Tsh S ---=+=1)(,22 T=0.5 试分别设计控制算法(D(z))使输出Y(t)能够跟踪v(t)参考输入,v (t )有三种:1单位阶跃 2单位速度3随动信号:设输入信号包含上升、平顶和下降阶段或改用加速度信号设计4种控制器:1数字PID2大林算法3最小拍(最速跟踪) 4最小拍无纹波三 数字控制器的设计、实验设计与仿真结果 1 有纹波的最小拍控制器(1)传函G 1的最小有纹波控制器设计广义对象的Z 传递函数为:故输入阶跃信号时被控对象为G 1(s)的控制器设计对单位阶跃信号,1=q 所以,因为, 且)('1z F 的首项为1,所以有,)('1z F =1, 即则数字控制器为: 输入阶跃信号时被控对象为G 1(s)的控制器设计:)368.01)(1()717.01(184.0)2(21)(1111-------+=⎥⎦⎤⎢⎣⎡+⋅-=z z z z s s s e Z z G Ts 11111=-===---j z N M d ,,,)()('1z F z z -=φ)()1()('11z F z z e --=φ01)(deg '1=-+=-m d z F )1()(1--=z z e φ1)(1)(-=-=z z z e φφ)717.01()368.01(43.5)()()(1)(11--+-=⋅=z z z z z G z D eφφ输入阶跃信号时被控对象为G 1(s)的仿真结果:输入速度信号时被控对象为G 1(s)的控制器设计对单位速度信号,2=q 所以,因为, 且)('1z F 的首项为1,所以有,)('1z F =1, 即则数字控制器为:输入速度信号时被控对象为G 1(s)的控制器设计:)()('1z F z z -=φ)()1()('121z F z z e --=φ01)(deg '1=-+=-m d z F 21)1()(--=z z e φ212)(1)(---=-=z z z z e φφ)717.01)(1()368.01)(5.01(86.10)()()(1)(1111----+---=⋅=z z z z z z z G z D e φφ输入速度信号时被控对象为G 1(s)的仿真结果:输入随动信号时被控对象为G 1(s)的控制器设计设计的随动信号是有单位速度信号叠加而成的,最高阶次为2,设计的控制器与单位速度信号相同。
计算机控制系统作业参考答案
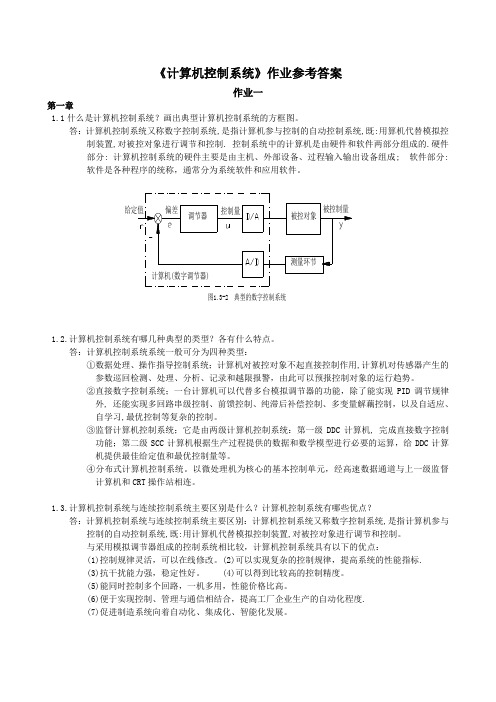
《计算机控制系统》作业参考答案作业一第一章1.1什么是计算机控制系统?画出典型计算机控制系统的方框图。
答:计算机控制系统又称数字控制系统,是指计算机参与控制的自动控制系统,既:用算机代替模拟控制装置,对被控对象进行调节和控制. 控制系统中的计算机是由硬件和软件两部分组成的.硬件部分: 计算机控制系统的硬件主要是由主机、外部设备、过程输入输出设备组成; 软件部分: 软件是各种程序的统称,通常分为系统软件和应用软件。
图1.3-2 典型的数字控制系统1.2.计算机控制系统有哪几种典型的类型?各有什么特点。
答:计算机控制系统系统一般可分为四种类型:①数据处理、操作指导控制系统;计算机对被控对象不起直接控制作用,计算机对传感器产生的参数巡回检测、处理、分析、记录和越限报警,由此可以预报控制对象的运行趋势。
②直接数字控制系统;一台计算机可以代替多台模拟调节器的功能,除了能实现PID调节规律外, 还能实现多回路串级控制、前馈控制、纯滞后补偿控制、多变量解藕控制,以及自适应、自学习,最优控制等复杂的控制。
③监督计算机控制系统;它是由两级计算机控制系统:第一级DDC计算机, 完成直接数字控制功能;第二级SCC计算机根据生产过程提供的数据和数学模型进行必要的运算,给DDC计算机提供最佳给定值和最优控制量等。
④分布式计算机控制系统。
以微处理机为核心的基本控制单元,经高速数据通道与上一级监督计算机和CRT操作站相连。
1.3.计算机控制系统与连续控制系统主要区别是什么?计算机控制系统有哪些优点?答:计算机控制系统与连续控制系统主要区别:计算机控制系统又称数字控制系统,是指计算机参与控制的自动控制系统,既:用计算机代替模拟控制装置,对被控对象进行调节和控制。
与采用模拟调节器组成的控制系统相比较,计算机控制系统具有以下的优点:(1)控制规律灵活,可以在线修改。
(2)可以实现复杂的控制规律,提高系统的性能指标.(3)抗干扰能力强,稳定性好。
17大林算法控制器的设计——【东北大学 计算机控制系统】

Wd
(
z
)
Z
1
eTs s
Ke NTs T1s 1
K
(1 eT /T1 )z(N 1) 1 eT /T1 z1
得到控制器传递函数为:
D(z)
(1 eT /T1 z1)(1 eT /T0 ) K (1 eT /T1 )[1 eT /T0 z1 (1 eT /T0 )z(N 1) ]
大林算法设计原理
思考:给定的闭环系统传递函数WB(s)的增益为何为1?
整个系统的闭环脉冲传递函数为:
大林算法设计原理
WB (z)
Y (z) R(z)
Z
1 eTs
s
eNTs T0s 1
z(N 1) (1 eT /T0 1 eT /T0 z1
)
为什么加零阶保持器?
原因: (1)加入零阶保持器:保证离散前后的阶跃 响应相等 (2)不加零阶保持器:保证离散前后的脉冲 响应相等
效果:消除了振铃现象 出现了超调,过渡过程时间变长
·教学单元四结束·
本节内容结束
W (s) K es , NT
T1s 1
W (s)
K
e s , NT
(T1s 1)(T2s 1)
大林算法设计原理
大林算法的设计目标是设计一个合适的数字控制器,使整个闭环系统的 传递函数相当于一个带有纯滞后的一阶惯性环节,即:
滞后与被控对象相同
WB
(s)
e s 和T2中最小的还要小。
大林算法设计原理
解:系统广义被控对象传递函数为
Wd
(s)
1
e sT s
W
(s)
(1 e0.5s )es s(s 1)
大林算法设计原理
系统控制实验报告(3篇)

第1篇一、实验目的1. 掌握系统控制的基本原理和方法。
2. 熟悉最少拍控制系统的分析方法。
3. 了解输入信号对最小拍控制系统的影响及其改进措施。
4. 培养实验操作能力和数据分析能力。
二、实验原理最少拍控制系统是一种直接数字设计方法,其目的是使闭环系统对于某种特定的输入在最少个采样周期内达到无静差的稳态,使系统输出值尽快地跟踪期望值的变化。
其闭环传递函数具有形式:\[ G(s) = \frac{1}{(z-1)^N} \]其中,N是可能情况下的最小正整数。
这一传递形式表明闭环系统的脉冲响应在N个采样周期后变为零,从而意味着系统在N拍之内到达稳态。
三、实验设备1. 硬件环境:- 微型计算机一台,Pentium 4以上各类微机2. 软件平台:- 操作系统:Windows 2000- 仿真软件:MATLAB6.0四、实验内容与步骤1. 计算控制器:- 按照系统要求计算最少拍有纹波控制器。
2. 构造系统结构图模型:- 在Simulink下构造系统结构图模型。
- 取输入信号为单位阶跃信号和单位速度信号。
3. 设计控制器:- 设计控制器,观察输入输出波型,标明参数,打印结果。
4. 观察系统输出波形:- 观察系统输出波形在采样点以外的波形。
五、实验结果与分析1. 单位阶跃输入下的最少拍有纹波控制系统:- 通过仿真,可以得到单位阶跃输入下的最少拍有纹波控制系统的输出波形,如图1-2所示。
- 从图中可以看出,系统在3个采样周期内达到稳态,且稳态误差较小。
2. 单位速度输入下的最少拍有纹波控制系统:- 通过仿真,可以得到单位速度输入下的最少拍有纹波控制系统的输出波形。
- 从图中可以看出,系统在3个采样周期内达到稳态,且稳态误差较小。
3. 输入信号对系统的影响:- 通过改变输入信号,可以观察到输入信号对系统输出波形的影响。
- 例如,当输入信号为单位阶跃信号时,系统输出波形呈现出明显的纹波现象;而当输入信号为单位速度信号时,系统输出波形则较为平滑。
微型计算机控制技术实验1-4(8学时)

%Linear model yout(k)=-den(2)*y_1-den(3)*y_2-den(4)*y_3+num(2)*u_1+num(3)*u_2+num(4)*u_3; error(k)=rin(k)-yout(k);
r_1=rin(k);
u_3=u_2;u_2=u_1;u_1=u(k); y_3=y_2;y_2=y_1;y_1=yout(k);
仿真程序:ex3.mdl
图 1-1 离散 PID 控制的 Simulink 主程序
图 1-2 离散 PID 控制的 Simulink 控制器程序
图 1-3 离散 PID 控制的封装界面 位置式 PID 控制算法的缺点是,由于采用全量输出,所以每次输出均与过去的状态有关,计算时要对 e(k)量进行累加,计算机输出控制量 u(k)对应的是执行机构的实际位置偏差,如果位置传感器出现故障,u(k) 可能会出现大幅度变化。u(k)大幅度变化会引起执行机构未知的大幅度变化,这种情况在生产中是不允 许的,在某些重要场合还可能造成重大事故。为了避免这种情况的发生,可采用增量式 PID 控制算法。 三、增量式 PID 控制算法及仿真 当执行机构需要的是控制量的增量(例如驱动步进电机)时,应采用增量式 PID 控制,根据递推原理可
求出 G(s)对应的离散形式 G(z) Y (z) ,其中 Y(z)和 U(z)是关于 z 的多项式,则可以得到其对应的差 U (z)
yout(k) den(2) y(k 1) den(3) y(k 2) den(4) y(k 3)
分表达式
num(2)u(k 1) num(3)u(k 2) num(4)u(k 3)
end end plot(time,rin,'r',time,yout,'b'); xlabel('time(s)');ylabel('rin,yout');
计控实验3 大林算法

2. 接收模块库(Sinks) 接收模块是用来接收模 块信号的。 主要有:
Scope(示波器) Display(数字显示) XY Graph(信号关系图) To File(数据保存) To Workspace(写成矩阵) Stop Simulation(终止) Out(输出)
3. 连续系统模块库 (Continuous) 连续系统模块是构成连续 系统的环节 。 主要有: Integrator(积分) Derivative(微分) State-Space(状态方程) Transfer Fcn(传递函数) Zero-Pole(零极点) Transport Delay(延时)
1、启动MATLAB
下载软件或用光盘进行MATLAB的安装。
点击 图标 ,启动MATLAB,出现操作窗口:
操作界面分为以下几部分: (1)菜单 (2)工具栏 (3)工作空间窗口
(4)命令窗口 (5)历史命令窗口 (6)开始按钮
菜单 工具栏
工作空 间窗口
命令 窗口
历史 命令 窗口 开始按钮
2、进入Simulink 在命令窗口输入 “Simulink”,或 单击工具栏中 的 图标,打开 Simulink模块库浏 览器。 图中左边为模块 库和工具栏,右边 是子模块库
实验三:大林算法
一、实验目的:
1、对应纯滞后的被控对象,应采用大林算法。 (1)大林算法的设计准则:对于一阶或二阶滞后系 统,设计数字控制器D(z),使整个闭环系统的滞后与 被控对象的滞后相同,消除滞后环节对系统稳定性的 s Ke 影响。 G( s ) 1 T 1s 一阶滞后系统可表示为: e s Gc (s) 1 THS 闭环系统的传递函数:
式中T1为被控对象的时间常数,τ为纯滞后时间,一般取采 样周期T的整数τ =NT。TH为惯性时间常数。
计算机控制09.大林控制算法

常用控制算法>>大林控制算法
大林控制算法控制器D(z)的基本形式 的基本形式 大林控制算法控制器
Simulink仿真结构图为 仿真结构图为
Scope2 1-0.779z-1 1-0.607z-1 +-0.393z-3 controller
Scope1 1 4s+1 Zero-Order Hold Transfer Fcn Transport Delay Scope
其与零阶保持器相串联的的脉冲传递函数为: 其与零阶保持器相串联的的脉冲传递函数为:
1 − e −Ts K (C1 + C2 z −1 ) z − N −1 Ke − NTs G( z) = Z ⋅ = s (1 + T1s )(1 + T2 s ) (1 − e −T T1 z −1 )(1 − e −T T2 z −1 ) 1 C1 = 1 + (T1e−T / T1 − T2e−T / T2 ) T2 − T1 1 1 −T + C = e T1 T2 + 1 (T e −T / T2 − T e −T / T1 ) 1 2 2 T2 − T1
0.1493z−2(1+0.733z−1) G(z) = 1−0.7413z−1
选取φ(z),时间常数为 τ=2s,纯滞后时间为 时间常数为T 纯滞后时间为τ=1s。则N=1,于是 选取 时间常数为 纯滞后时间为 。 于是
−1/ 2 (1−e−T/Tτ )z−1 )z−1 0.3935z−2 −1 (1−e ⋅ =z ⋅ = −T /T -1 −1/2 -1 τ 1−e z 1−e z 1−0.6065z−1
计算机控制系统实验报告

计算机控制系统实验报告学院机电工程学院专业电气工程及其自动化姓名__________________学号__________________实验一已知闭环Z 传递函数321() 1.40.070.26W z z z z =+-- (1) 判定系统的稳定性。
一、实验目的1、掌握离散系统稳定的充要条件;2、掌握稳定的物理意义;a. 有界输入得到有界输出;b. 李雅普诺夫稳定判据;3、熟悉matlab 以及simulink 的基本应用。
二、实验设备计算机、matlab2012a 软件三、实验理论分析判断系统的稳定性,可以通过分析闭环传递函数的极点分布情况判定。
如果系统极点都在z 平面内单位圆内,则系统稳定,否者,系统不稳定。
另外,也可以通过matlab 软件仿真系统在阶跃函数下的输出波形,来判定系统是否稳定。
四、实验内容及步骤 1、实验内容:(1)计算系统的极点分布,据此判断系统的稳定性;(2)给出系统在特定输入作用的输出波形,并据此判断系统的稳定性。
2、实验步骤:(1)用MATLAB 求出系统闭环传递函数的极点分布,算法及结果如下: >> a=1;>> b=[1 1.4 -0.07 -0.26]; >> G=tf(a,b); >> G1=zpk(G) G1 =1----------------------- (s+1.3) (s+0.5) (s-0.4)(2)用simulink 模块仿真单位阶跃信号下系统输出,结构框图及输出波形分别如下图a 和b 。
图a图b(3)根据李雅普诺夫判据验证系统抗干扰的能力,结构框图及系统输出如下图c,d所示。
图C图 D五、实验数据分析(1) 由matlab 计算的系统闭环传递函数极点分布为-1.3、-0.5、0.4,由于存在z 平面内单位圆外的极点z=-1.3,所以该系统不稳定。
(2) 由simulink 仿真的系统单位阶跃信号作用下输出结果,以及李雅普诺夫判据可得,该系统输出不稳定,即该系统不稳定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四、实验内容
考虑图中所示的采样数字控制系统,被控对象的脉冲传递函数为
e 2 s Go ( s ) s ( s 1)
数字控制系统 设采样周期 T=1s,要求利用大林算法设计数字控制器 D(z)。
五、 实验数据及结果分析
分析、计算系统的控制特性,将所得结果用Matlab中的Simulink 工具箱进行仿真,分 析信号U(z)及Y(z),假设输入为阶跃信号。
检验误差:
1
1
E( z) [1 Gc ( z)]R( z) z
1
从 E ( z ) 看出, 按单位速度输入设计的系统, 当 k 2 之后, 即二拍之后, 误差 e(k ) 0。 控制系统Simulink 框图如下图所示:
单位速度信号输入时最少拍控制系统
实验二
一、实验目的
基于 Matlab 的大林算法设计
五、实验总结
附录:
设采样周期 T=1s ,首先求取广义被控对象的脉冲传递函数。 广义被控对象:
对于单位速度信号,我们可以得到:
0.5434(1 0.5 z )(1 0.3679 z ) Gc ( z ) D( Z ) 1 1 G ( z )(1 Gc ( z )) (1 z )(1 0.718 z )
实验一
一、 实验目的
基于 Matlab 的最少拍控制系统设计
学习使用 Matlab 设计最少拍系统的方法。
二、 实验器材
x86 系列兼容型计算机,Matlab 软件。
三、 实验原理
最少拍设计,是指系统在典型输入信号(如阶跃信号、速度信号、加速度信号等)作用 下,经过最少拍(有限拍)使系统输出的系统稳态误差为零。因此,最少拍控制系统也称最 少拍无差系统或最少拍随动系统, 它实质上是时间最优控制系统, 系统的性能指标就是系统 调节时间最短或尽可能短,即对闭环 Z 传递函数要求快速性和准确性。
学习使用 Matlab 设计大林算法, 掌握大林控制算法的基本概念和实现方法; 观
察振铃现象,并且尝试消除振铃现象 二、实验器材
x86 系列兼容型计算机,Matlab 软件。
三、实验原理
大林算法的主要目标是设计一个数字控制器组成计算机控制系统, 使闭环系统的纯滞后 时间等于被控对象的纯滞后时间,从而消除纯滞后环节对系统稳定性的影响。
四、实验内容
考虑图中所示的采样数字控制系统,被控对象的脉冲传递函数为
Go (s)
10 s( s 1)
最少拍采样数字控制系统 设采样周期 T=1s,要求研究当输入信号为单位斜坡信号时,系统的跟随特性。
四、 实验数据及结果分析
分析、 计算系统的控制特性, 将所得结果分别用Matlab中的Simulink 工具箱进行仿真, 并将输入、输出和误差三条曲线放置在同一图像内,分析系统的跟随特性。
六、实验总结
