分段函数完整ppt课件
合集下载
函数的表示图像分段函数省公开课一等奖全国示范课微课金奖PPT课件

三.翻折变换
1、上翻
保留f(x)在x轴上方图象,
y=f(x)图象
y= f(x) 图象
将x轴下方图象翻到x轴上方
2、左翻
保留f(x)在y轴右边图象,
y=f(x)图象
y=f( x ) 图象
将y轴右边图象翻到y轴左边
f (x) x2 2x 3, f ( x ) x 2 2 x 3
第13页
例5.请画出下列函数的图像:y 1 , y x 1, y 1 , y x . x x x 1 x 1
如,坐标平面内的所有点组成的集合为 A,所有 的有序数对组成的集合为
B x, y | x R, y R.
让每一点与其坐标对应,则 A中每一个元素 点, 在B中都有惟一元素 有序数对 与之对应.
函数是映射, 但映射不一定是函数 .
第15页
例1 下图所示的对应中, 哪些是A到B的映射 ?
a1
1.2.2 函数表示 阅读书本第21页例5与例6. 一.分断函数定义:
一个函数在自变量不一样取值范围内 对应法则有所不一样(解析式不一样).
分段函数不能认为是几个函数合并.
例题巩固
例1.已知函数f
(x)
x,
x2
x 0, , x 0,
试求f
(2)与f
(
f
(2))的值.
f (2) 2, f ( f (2)) 4.
1
o
1
x
一、平移变换 1、左右平移:
y=f(x)图象
a>0时,向左平移 a 个单位
y=f(x+a)图象
a<0时,向右平移 a 个单位
第9页
例2.已知函数y f (x) x2请画出它的图像, 并用它的图像进行变换得出下列函数的图像:
高中数学必修一(人教版)《3.1.2 第二课时 分段函数》课件

题型一 分段函数求值问题
【学透用活】
[典例 1]
已知函数 f(x)=xx+ 2+12,x,x≤--2<2x,<2, 2x-1,x≥2.
(1)求 f(-5),f(- 3),ff-52的值; (2)若 f(a)=3,求实数 a 的值; (3)若 f(x)>2x,求 x 的取值范围.
[解] (1)由-5∈(-∞,-2],- 3∈(-2,2),-52∈(-∞,-2], 知 f(-5)=-5+1=-4,
【课堂思维激活】 一、综合性——强调融会贯通 1.下面是解“已知实数 a≠0,函数 f(x)=2-x+x-a,2ax,<x1≥,1. 若 f(1-a)=f(1+
a),求 a 的值”的过程:
解:由 f(1-a)=f(1+a),得 2(1-a)+a=-(1+a)-2a,即 2-a=-1- 3a,∴a=-32. 上述解题过程是否正确?请说明理由.
[解] 如图,过点 A,D 分别作 AG⊥BC,DH⊥BC, 垂足分别是 G,H.
因为四边形 ABCD 是等腰梯形,底角为 45°,AB= 2 2 cm,所以 BG=AG=DH=HC=2 cm.又 BC=7 cm,所以 AD=GH=3 cm.
①当点 F 在 BG 上,即 x∈[0,2]时,y=12x2; ②当点 F 在 GH 上,即 x∈(2,5]时,y=x+x2-2×2=2x-2;
(2)问:该企业选择哪家俱乐部比较合算?为什么?
解:(1)由题意得 f(x)=6x,x∈[12,30], g(x)=920x, +1520≤ ,x2≤ 0<20x, ≤30. (2)①当 12≤x≤20 时,令 6x=90,解得 x=15. 即当 12≤x<15 时,f(x)<g(x);当 x=15 时,f(x)=g(x);当 15<x≤20 时,f(x) >g(x). ②当 20<x≤30 时,f(x)>g(x). 综上,当 12≤x<15 时,选 A 俱乐部合算;当 x=15 时,两家俱乐部一样合算; 当 15<x≤30 时,选 B 俱乐部合算.
3 第3课时 分段函数ppt课件

PPT素材:./sucai/
PPT背景:./beijing/
PPT图表:./tubiao/
PPT下载:./xiazai/
PPT教程: ./powerpoint/
资料下载:./ziliao/
范文下载:./fanwen/
试卷下载:./shiti/
教案下载:./jiaoan/
PPT论坛:
范文下载:./fanwen/
试卷下载:./shiti/
教案下载:./jiaoan/
PPT论坛:
PPT课件:./kejian/
语文课件:./kejian/yuwen/ 数学课件:./kejian/shuxue/
英语课件:./kejian/yingyu/ 美术课件:./kejian/meishu/
PPT素材:./sucai/
PPT背景:./beijing/
PPT图表:./tubiao/
PPT下载:./xiazai/
PPT教程: ./powerpoint/
资料下载:./ziliao/
范文下载:./fanwen/
试卷下载:./shiti/
教案下载:./jiaoan/
PPT论坛:
资料下载:./ziliao/
范文下载:./fanwen/
试卷下载:./shiti/
教案下载:./jiaoan/PPT论坛:PPT课件:./kejian/
语文课件:./kejian/yuwen/ 数学课件:./kejian/shuxue/
英语课件:./kejian/yingyu/ 美术课件:./kejian/meishu/
范文下载:./fanwen/
试卷下载:./shiti/
教案下载:./jiaoan/
PPT论坛:
分段函数(共9张PPT)

(1)写出每户每月用水量不超过6米3和每户每月用 水量超过6米3时,y与x之间的函数关系式,并判 断它们是否为一次函数。
(2)已知某户5月份的用水量为米3,求该用户5月 份的水费。
生活中的数学
【例 3】某医药研究所开发了一种新药,在实际验药时
发现,如果成人按规定剂量服用,那么每毫升血液中含
药量y(微克)随时间x(时)的变化情况如图所示 ,当成年人按规定剂量服药后。
Y(元) 跑步速度 y与时间 x的函数关系式是
例2、某供电公司为了鼓励居民用电,采用分段计费的方法来计算电费,月用电x(度)与相应电费y(元)之间的函数的 图象如图所示。 例1 小芳以200米/分的速度起跑后,先匀加速跑5分钟,每分提高速度20米/分,又匀速跑10分钟, 试写出这段时间里她的跑步速度y(米/分)随跑步时间 x(分)变化的函数关系式,并画出函数图象. (2)已知某户5月份的用水量为米3,求该用户5月份的水费。
例2、某供电公司为了鼓励居民用电,采用分段计费的方法来计算电费,月用电x(度)与相应电费y(元)之间的函数的 图象如图所示。
解:依题意得 { 例1 小芳以200米/分的速度起跑后,先匀加速跑5分钟,每分提高速度20米/分,又匀速跑10分钟, 试写出这段时间里她的跑步速度y(米/分)随跑步时间
s=10+6(x-5) (5<x≤10) x(分)变化的函数关系式,并画出函数图象.
化情况如图所示,当成年人按规定剂量服药后。
1 例2、某供电公司为了鼓励居民用电,采用分段计费的方法来计算电费,月用电x(度)与相应电费y(元)之间的函数的 图象如图所示。
(3)月用电量为260度时,应交电费多少元?
(2)当x≥100时求y与x之间的函数关系式; Y= x+20 3.写出每一段的函数解析式 5 例1 小芳以200米/分的速度起跑后,先匀加速跑5分钟,每分提高速度20米/分,又匀速跑10分钟, 试写出这段时间里她的跑步速度y(米/分)随跑步时间
(2)已知某户5月份的用水量为米3,求该用户5月 份的水费。
生活中的数学
【例 3】某医药研究所开发了一种新药,在实际验药时
发现,如果成人按规定剂量服用,那么每毫升血液中含
药量y(微克)随时间x(时)的变化情况如图所示 ,当成年人按规定剂量服药后。
Y(元) 跑步速度 y与时间 x的函数关系式是
例2、某供电公司为了鼓励居民用电,采用分段计费的方法来计算电费,月用电x(度)与相应电费y(元)之间的函数的 图象如图所示。 例1 小芳以200米/分的速度起跑后,先匀加速跑5分钟,每分提高速度20米/分,又匀速跑10分钟, 试写出这段时间里她的跑步速度y(米/分)随跑步时间 x(分)变化的函数关系式,并画出函数图象. (2)已知某户5月份的用水量为米3,求该用户5月份的水费。
例2、某供电公司为了鼓励居民用电,采用分段计费的方法来计算电费,月用电x(度)与相应电费y(元)之间的函数的 图象如图所示。
解:依题意得 { 例1 小芳以200米/分的速度起跑后,先匀加速跑5分钟,每分提高速度20米/分,又匀速跑10分钟, 试写出这段时间里她的跑步速度y(米/分)随跑步时间
s=10+6(x-5) (5<x≤10) x(分)变化的函数关系式,并画出函数图象.
化情况如图所示,当成年人按规定剂量服药后。
1 例2、某供电公司为了鼓励居民用电,采用分段计费的方法来计算电费,月用电x(度)与相应电费y(元)之间的函数的 图象如图所示。
(3)月用电量为260度时,应交电费多少元?
(2)当x≥100时求y与x之间的函数关系式; Y= x+20 3.写出每一段的函数解析式 5 例1 小芳以200米/分的速度起跑后,先匀加速跑5分钟,每分提高速度20米/分,又匀速跑10分钟, 试写出这段时间里她的跑步速度y(米/分)随跑步时间
人教版高中必修一数学课件:3.2分段函数fine (共39张PPT)

并集
1.6x, 0≤x≤10 f ( x) = 2.8x 12, x 10.
求分段函数 的函数值时,首 先判断自变量 所属的取值范 围,再把自变量 的值代入相应 取值范围的表 达式中进行计 算.
追加任务2 求出某户用水12m3应交的 水费f(12).
因为12>10, 所以利用 f ( x) 2.8 x 12 计算,得
追加任务2 求出某户用水12m3应交的 水费f(12).
因为12>10, 所以利用 f ( x) 2.8 x 12 计算,得
函 数 值
f (12) 2.8 12 12 21.6 (元).
1.6x, 0≤x≤10 f ( x) = 2.8x 12, x 10.
1.6x, 0≤x≤10 f ( x) = 2.8x 12, x 10.
追加任务2 追加任务1 求出某户用水12m3应交的 该函数的定义域是什么? 水费f(12).
分段函数的 定义域是自变 量的各个不同 取值范围的并 集.
该函数的定义域为
定 义 域
. 0, 0,10 ∪ 10,
函 数 值
f (12) 2.8 12 12 21.6 (元).
1.6x, 0≤x≤10 f ( x) = 2.8x 12, x 10.
求分段函数 的函数值时,首 先判断自变量 所属的取值范 围,再把自变量 的值代入相应 取值范围的表 达式中进行计 算.
追加任务2 求出某户用水12m3应交的 水费f(12).
用水量 用水费(元/m3) 污水处理费(元/m3) 不超过10m3 部分 1.30 0.30 超过10 m3部分 2.00 0.80
试写出每户每月用水量x(m3 )与应交水费 y(元) 之间的函数解析式. 综合以上两种情况,函数写作
分段函数 ppt课件

小结:(1)求分段函数的函数值时,一般先
确定自变量的数值属于哪个区间段,然后选取相 应的对应法则来求函数值.
(2)解决此类问题应自内向外依次求值.
分段函数
2x+3, x<-1, 已知函数f (x)= x2, -1≤x<1,
x-1, x≥1 .
当f (x)=-7时,求x 。
解:若x<-1 , 2x+3 <1,
分段函数
陈锦云 分段函数
1、函数的定义:
设A,B是非空数集,如果按照某种确定的对 应关系f,使对于集合A中的任意一个数x,在集合 B中都有确定的数f(x)和它相对应,那么f : A→B为从集合A到B的一个函数,记作: y=f(x),x∈A。
2、函数的表示法:
解析法、图像法、列表法
分段函数
例5 画出函数y= x 的图像。
分段函数
解:设票价为y,里程为x,则根据题意,自变量x的 取值范围是(0,20] 由公交车票价的规定,可得到以下函数解析式:
2, 0<x ≤ 5 3, 5< x ≤ 10 y= 4, 10<x ≤ 15 5, 15<x ≤ 20
分段函数
根据函数解析式,可画出函数图象,如下图
y
5
○
4
○
3○
2○
1
0 5 10 15 20
x
分段函数
已知函数f (x)= 求(1)求f(-2);
2x+3, x<-1, x2, -) 求 f{f[f(-2)]} 。
分段函数
解: ( 1 )f( 2 ) 2 ( 2 ) 3 1
(2) f{f[f(-2)]} = f{f[-1]}
= f{1} =0
与f (x)=-7相符,
确定自变量的数值属于哪个区间段,然后选取相 应的对应法则来求函数值.
(2)解决此类问题应自内向外依次求值.
分段函数
2x+3, x<-1, 已知函数f (x)= x2, -1≤x<1,
x-1, x≥1 .
当f (x)=-7时,求x 。
解:若x<-1 , 2x+3 <1,
分段函数
陈锦云 分段函数
1、函数的定义:
设A,B是非空数集,如果按照某种确定的对 应关系f,使对于集合A中的任意一个数x,在集合 B中都有确定的数f(x)和它相对应,那么f : A→B为从集合A到B的一个函数,记作: y=f(x),x∈A。
2、函数的表示法:
解析法、图像法、列表法
分段函数
例5 画出函数y= x 的图像。
分段函数
解:设票价为y,里程为x,则根据题意,自变量x的 取值范围是(0,20] 由公交车票价的规定,可得到以下函数解析式:
2, 0<x ≤ 5 3, 5< x ≤ 10 y= 4, 10<x ≤ 15 5, 15<x ≤ 20
分段函数
根据函数解析式,可画出函数图象,如下图
y
5
○
4
○
3○
2○
1
0 5 10 15 20
x
分段函数
已知函数f (x)= 求(1)求f(-2);
2x+3, x<-1, x2, -) 求 f{f[f(-2)]} 。
分段函数
解: ( 1 )f( 2 ) 2 ( 2 ) 3 1
(2) f{f[f(-2)]} = f{f[-1]}
= f{1} =0
与f (x)=-7相符,
高一数学必修一--分段函数(课件)
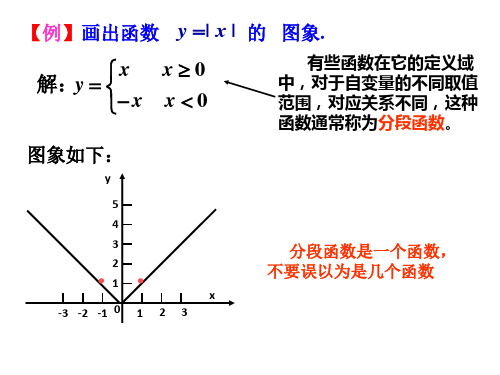
【例】画出函数 y | x | 的 图象.
x0 x 解:y x x 0
图象如下:
y
有些函数在它的定义域 中,对于自变量的不同取值 范围,对应关系不同,这种 函数通常称为分段函数。
5
4 3 2
..
1 -3 -2 -1 0 1
2 3
分段函数是一个函数, 不要误以为是几个函数
x
例2: 某市“招手即停”公共汽车的票价按下列规则制定
Y=
2, 3, 4, 5,
0<x≤5, 5<x≤10, 10<
x
y
5 4
3
2 1 -3 -2 -1 0 1 2 3 x
作函数y=|x-2|+1的图像
y 5 4 3 2 1 -3 -2 -1 0 1 2 3 x
2 x 2 1 (1)设f ( x ) x 2 3 f (1) __
(1)5公里以内(含5公里),票价2元。 (2) 5公里以上,每增加5公里,票价增加1元(不
足5公里的按5公里计算)。
如果某条路线的总里程为20公里,请根据题意,写出票价与里程 之间的函数解析式,并用图象法表示这函数。
y 解:设票价为y,里程为x,由题意可知, 5 自变量的取值范围是(0,20】由 “招手即停”的票价制定规则,可得 4 函数的解析式: 3 2 1 0 5
-1 x 0 3 0 x 2 ,则f ( )= ______, 4 x2
f ( x )的定义域是 ______
x0 x 解:y x x 0
图象如下:
y
有些函数在它的定义域 中,对于自变量的不同取值 范围,对应关系不同,这种 函数通常称为分段函数。
5
4 3 2
..
1 -3 -2 -1 0 1
2 3
分段函数是一个函数, 不要误以为是几个函数
x
例2: 某市“招手即停”公共汽车的票价按下列规则制定
Y=
2, 3, 4, 5,
0<x≤5, 5<x≤10, 10<
x
y
5 4
3
2 1 -3 -2 -1 0 1 2 3 x
作函数y=|x-2|+1的图像
y 5 4 3 2 1 -3 -2 -1 0 1 2 3 x
2 x 2 1 (1)设f ( x ) x 2 3 f (1) __
(1)5公里以内(含5公里),票价2元。 (2) 5公里以上,每增加5公里,票价增加1元(不
足5公里的按5公里计算)。
如果某条路线的总里程为20公里,请根据题意,写出票价与里程 之间的函数解析式,并用图象法表示这函数。
y 解:设票价为y,里程为x,由题意可知, 5 自变量的取值范围是(0,20】由 “招手即停”的票价制定规则,可得 4 函数的解析式: 3 2 1 0 5
-1 x 0 3 0 x 2 ,则f ( )= ______, 4 x2
f ( x )的定义域是 ______
3.1.2 第2课时 分段函数课件ppt

综上可知 y≥2 6或 y≤-2 6,
即函数的值域为(-∞,-2 6]∪[2 6,+∞).
3
时,等号成
2
(3)已知函数式可变形为:yx2+2yx+3y=2x2+4x-7.
(y-2)x2+2(y-2)x+3y+7=0,
当y≠2时,将上式视为关于x的一元二次方程.
∵x∈R,∴Δ≥0,即[2(y-2)]2-4(y-2)(3y+7)≥0.
(1)因为分段函数在定义域的不同区间内解析式不一样,所以它的图象也由
几部分构成,有的可以是光滑的曲线段,有的也可以是一些孤立的点或几段
线段,画图时要特别注意区间端点处对应点的实虚之分.
(2)对含有绝对值的函数,要作出其图象,首先根据绝对值的意义去掉绝对
值符号,将函数转化为分段函数来画图象.
变式训练1已知函数f(x)=|x-1|-2.
每个站点之间的距离为1千米,如果某空调公共汽车运行路线中设20个站
点,求票价y(单位:元)关于里程x(单位:千米)的函数解析式,并画出图象.
解 根据题意,
如果某空调汽车运行路线中设20个站点(包括起点站和终点站),那么汽车
行驶的里程约为19千米,所以自变量x的取值范围是{x∈N*|x≤19}.
由空调汽车票价制定的规则,
选取相应的对应关系.要注意写解析式时各区间的端点能否取到,做到不重
复、不遗漏.
(3)分段函数的定义域是各段定义域的并集,值域是分别求出各段上的值域
后取并集.
微练习
-x,x ≤ 0,
f(x)= 2
x ,x > 0.
(1)求f(f(-2))的值;
(2)若f(a)=4,求实数a的值.
即函数的值域为(-∞,-2 6]∪[2 6,+∞).
3
时,等号成
2
(3)已知函数式可变形为:yx2+2yx+3y=2x2+4x-7.
(y-2)x2+2(y-2)x+3y+7=0,
当y≠2时,将上式视为关于x的一元二次方程.
∵x∈R,∴Δ≥0,即[2(y-2)]2-4(y-2)(3y+7)≥0.
(1)因为分段函数在定义域的不同区间内解析式不一样,所以它的图象也由
几部分构成,有的可以是光滑的曲线段,有的也可以是一些孤立的点或几段
线段,画图时要特别注意区间端点处对应点的实虚之分.
(2)对含有绝对值的函数,要作出其图象,首先根据绝对值的意义去掉绝对
值符号,将函数转化为分段函数来画图象.
变式训练1已知函数f(x)=|x-1|-2.
每个站点之间的距离为1千米,如果某空调公共汽车运行路线中设20个站
点,求票价y(单位:元)关于里程x(单位:千米)的函数解析式,并画出图象.
解 根据题意,
如果某空调汽车运行路线中设20个站点(包括起点站和终点站),那么汽车
行驶的里程约为19千米,所以自变量x的取值范围是{x∈N*|x≤19}.
由空调汽车票价制定的规则,
选取相应的对应关系.要注意写解析式时各区间的端点能否取到,做到不重
复、不遗漏.
(3)分段函数的定义域是各段定义域的并集,值域是分别求出各段上的值域
后取并集.
微练习
-x,x ≤ 0,
f(x)= 2
x ,x > 0.
(1)求f(f(-2))的值;
(2)若f(a)=4,求实数a的值.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2. 分段函数的定义域是各个部分定义域 的并集,值域也是各个部分值域的并集。
.
例6 某市公交车的票价按下列规则制定: (1)5公里以内(含5公里),票价2元; (2)5公里以上,每增加5公里,票价增
加1元(不足5公里的按5公里计算)。 如果某条线路的总里程为20公里,请根 据题意,写出票价y与里程x之间的函数解析 式,并画出函数的图象。
确定自变量的数值属于哪个区间段,然后选取相 应的对应法则来求函数值.
(2)解决此类问题应自内向外依次求值.
.
2x+3, x<-1, 已知函数f (x)= x2, -1≤x<1,
x-1, x≥1 .
当f (x)=-7时,求x 。
解:若x<-1 , 2x+3 <1,
与f (x)=-7相符,
由2x+3 =-7得x=-5
x
.
已知函数f (x)= 求(1)求f(-2);
2x+3, x<-1, x2, -1≤x<1, x-1, x≥1 .
(2) 求 f{f[f(-2)]} 。
.
解: ( 1 )f( 2 ) 2 ( 2 ) 3 1
(2) f{f[f(-2)]} = f{f[-1]}
= f{1} =0
小结:(1)求分段函数的函数值时,一般先
.
解:设票价为y,里程为x,则根据题意,自变量x的 取值范围是(0,20] 由公交车票价的规定,可得到以下函数解析式:
2, 0<x ≤ 5 3, 5< x ≤ 10 y= 4, 10<x ≤ 15 5, 15<x ≤ 20
.
根据函数解析式,可画出函数图象,如下图
y
5
○
4
○
3○
2○
1
0 5 10 15 20
.
作业:
x+2, (x≤-1)
1 已知函数 f (x)= x2, (-1<x<2)
2x, ( x≥2 )
若f(x)=3, 则x的值是(
)
A. 1
B.
1或
3 2
C. 1, 3 , 3 D. 3
2
2 教材24页A组第7.题
.
陈锦云 .
1、函数的定义:
设A,B是非空数集,如果按照某种确定的对 应关系f,使对于集合A中的任意一个数x,在集合 B中都有确定的数f(x)和它相对应,那么f : A→B为从集合A到B的一个函数,记作: y=f(x),x∈A。
2、函数的表示法:
解析法、图像法、列表法
.
例5 画出函数y= x 的图像。
易知其他二段均不符合f (x)=-7 。
故 x=-5
.
1、定义:在定义域的不同部分,有不同 的对应法则的函数称为分段函数。 2、分段函数是一个函数,分段函数的定 义域是各个部分定义域的并集,值域也是 各个部分值域的并集。
3、处理分段函数问题时,首先要确定自 变量的数值属于哪个区间段从而选取相应 的对应法则。
解:由绝对值
ห้องสมุดไป่ตู้
的概念,我们
y
有
x , x≥0
y=
-x, x<0
所以函数图像如图示
o
x
.
画出y=|x-2|的图像
解:由绝对值 y
的概念,我们
有
x-2 x≥2
y=
-x+2 x<2
o
2
x
.
定义:在定义域的不同部分,有不同的
对应法则的函数称为分段函数。
注意
1. 分段函数是一个函数,不要把它误 认为是“几个函数”;
.
例6 某市公交车的票价按下列规则制定: (1)5公里以内(含5公里),票价2元; (2)5公里以上,每增加5公里,票价增
加1元(不足5公里的按5公里计算)。 如果某条线路的总里程为20公里,请根 据题意,写出票价y与里程x之间的函数解析 式,并画出函数的图象。
确定自变量的数值属于哪个区间段,然后选取相 应的对应法则来求函数值.
(2)解决此类问题应自内向外依次求值.
.
2x+3, x<-1, 已知函数f (x)= x2, -1≤x<1,
x-1, x≥1 .
当f (x)=-7时,求x 。
解:若x<-1 , 2x+3 <1,
与f (x)=-7相符,
由2x+3 =-7得x=-5
x
.
已知函数f (x)= 求(1)求f(-2);
2x+3, x<-1, x2, -1≤x<1, x-1, x≥1 .
(2) 求 f{f[f(-2)]} 。
.
解: ( 1 )f( 2 ) 2 ( 2 ) 3 1
(2) f{f[f(-2)]} = f{f[-1]}
= f{1} =0
小结:(1)求分段函数的函数值时,一般先
.
解:设票价为y,里程为x,则根据题意,自变量x的 取值范围是(0,20] 由公交车票价的规定,可得到以下函数解析式:
2, 0<x ≤ 5 3, 5< x ≤ 10 y= 4, 10<x ≤ 15 5, 15<x ≤ 20
.
根据函数解析式,可画出函数图象,如下图
y
5
○
4
○
3○
2○
1
0 5 10 15 20
.
作业:
x+2, (x≤-1)
1 已知函数 f (x)= x2, (-1<x<2)
2x, ( x≥2 )
若f(x)=3, 则x的值是(
)
A. 1
B.
1或
3 2
C. 1, 3 , 3 D. 3
2
2 教材24页A组第7.题
.
陈锦云 .
1、函数的定义:
设A,B是非空数集,如果按照某种确定的对 应关系f,使对于集合A中的任意一个数x,在集合 B中都有确定的数f(x)和它相对应,那么f : A→B为从集合A到B的一个函数,记作: y=f(x),x∈A。
2、函数的表示法:
解析法、图像法、列表法
.
例5 画出函数y= x 的图像。
易知其他二段均不符合f (x)=-7 。
故 x=-5
.
1、定义:在定义域的不同部分,有不同 的对应法则的函数称为分段函数。 2、分段函数是一个函数,分段函数的定 义域是各个部分定义域的并集,值域也是 各个部分值域的并集。
3、处理分段函数问题时,首先要确定自 变量的数值属于哪个区间段从而选取相应 的对应法则。
解:由绝对值
ห้องสมุดไป่ตู้
的概念,我们
y
有
x , x≥0
y=
-x, x<0
所以函数图像如图示
o
x
.
画出y=|x-2|的图像
解:由绝对值 y
的概念,我们
有
x-2 x≥2
y=
-x+2 x<2
o
2
x
.
定义:在定义域的不同部分,有不同的
对应法则的函数称为分段函数。
注意
1. 分段函数是一个函数,不要把它误 认为是“几个函数”;
