2021西南大学附中数学七年级周末全真试题及答案分析下载
2021-2022学年重庆市北碚区西南大学附中七年级上学期期末数学训练卷(含解析)

2021-2022学年重庆市北碚区西南大学附中七年级上学期期末数学训练卷一、选择题(本大题共12小题,共36.0分)1. 下列式子中,与2x 2y 不是同类项的是( )A. −3x 2yB. 4xy 2C. yx 2D. x 2y 3 2. 下列方程中是一元一次方程的是( )A. 2x −1=3yB. 7x +5=6(x −1)C. x 2+12(x −1)=1D. 1x −2=x 3. 将一个正方体的表面沿它的某些棱剪开,展成一个平面图形,则下面各图中不可能是正方体的展开图的是( )A. B. C. D.4. 若a <b ,则下列结论中,不成立的是( )A. a +3<b +3B. −2a >−2bC. 3a <3bD. a −2>b −25. 不等式组{12x −2≥−38−2x >4的解集在数轴上表示为( ) A. B.C.D. 6. 某同学用剪刀沿直线将一片平整的银杏叶剪掉一部分(如图),发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是( )A. 两点之间线段最短B. 两点确定一条直线C. 垂线段最短D. 经过直线外一点,有且只有一条直线与这条直线平行7. 已知关于x 的不等式组{3x +5a >4(x +1)+3a 12x +13>−13x 的整数解只有三个,则a 的取值范围是( )A. a >3或a <2B. 2<a <52C. 3<a ≤72D. 3≤a <72 8. 已知A 、B 两地相距126 km ,一辆小汽车和一辆货车分别从A 、B 两地同时出发,相向而行,经过45分钟相遇,相遇时小汽车比货车多行6 km ,设小汽车和货车的速度分别为xkm/ℎ,ykm/ℎ,则下列方程组正确的是A. B.C. D.9. 三元一次方程组{a −b +c =04a +2b +c =32a +b −3c =19消去一个未知数后,所得二元一次方程组是( )A. {a +b =12a +b =4B. {3a +b =32a +b =4C. {a +b =13a −2c =19D. {5a −2b =193a +b =310. 已知点M(5−m,m +3)在第一象限,则下列关系式正确的是( )A. 3<m <5B. −3<m <5C. −5<m <3D. −5<m <−311. 王芳同学到文具店购买中性笔和笔记本,中性笔每支1元,笔记本每本3元,王芳同学现有10元钱,则可供她选择的购买方案的个数为(两样都买,余下的钱少于1元)( )A. 2B. 3C. 4D. 5 12. 若数m 使关于x 的不等式组{3+x2−1≤3m −2x ≤−2有解且至多有3个整数解,且使关于y 的分式方程3y 2y−4=m−2y−2+12的解满足−3≤y ≤4,则满足条件的所有整数m 的个数是( )A. 6B. 5C. 4D. 3二、填空题(本大题共8小题,共24.0分)13. −(−223)的相反数是______.14. 如果方程组{3x −5y =2a 2x −7y =a −18的解互为相反数,那么a =______. 15. 时钟指向2时30分时,这时时针与分针所成的锐角是 度.16. 某水池有甲进水管和乙出水管,已知单开甲注满水池需6ℎ,单开乙管放完全池水需要9ℎ,当同时开放甲、乙两管时需要______ℎ水池水量达全池的一半.17. 若线段AB =a ,点C 为线段AB 上一点,点M 、N 分别在线段AC 、BC 上,且CM =2AM ,CN =2BN ,则MN 的长为______.18. 已知方程组{x +y =3ax +y =4和{x −2y =6x +by =1有相同的解,则a 的值为______ . 19. 若关于x 的方程5x−16=73与8x−52=x +2m 的解相同,则m 的值为______.20. 为深入践行”绿水青山就是金山银山”的发展理念,我国生态文明建设不断迈出坚实步伐,绿色发展成就举世瞩目.在今年的植树造林活动期间,某苗圃园第一天卖出一批雪松收款11000元;第二天又卖出一批雪松收款23000元,所卖数量是第一天的2倍,售价比第一天每棵多了5元.第二天每棵雪松售价______元.三、解答题(本大题共7小题,共60.0分)21. 解方程:x−42−(3x +4)=−152.22. 解方程组:{3x −2y =−8x +2y =0.23. (1)计算:|−4|−20190+(12)−1−(√3)2;(2)解不等式组:{x −1>4x +22x+13>2x .24. 直角三角板ABC 的直角顶点C 在直线DE 上,CF 平分∠BCD .(1)图中若∠BCE =40°,则∠ACF =______.(2)图中若∠BCE =a ,求∠ACF 的度数(用含a 的式子表示).25. 如图是一段火车路线图,图中字母所示的6个点表示6个车站.图中有几条线段?在这段路线上往返行车,需要印制几种车票(每种车票都要印出上车站和下车站)?26. 如图,等腰梯形OBCD 中,DC//OB ,OD =CB ,∠DOB =∠CBO ,BD ⊥OD ,在平面直角坐标系中,等腰梯形OBCD 的下底OB 在x 轴正半轴上,O 为坐标原点,点B 的坐标为(√5a,0),C 、D 两点落在第一象限,且BD=2a.点P以每秒1个单位长度的速度在对角线BD上由点B向点D运动(点P不与点B、点D重合),过点P作PE⊥BD,交下底OB于点E,交腰BC(或上底CD)于点F.(1)线段BC的长是______(用含a的代数式表示);(2)已知直线PE经过点C时,直线PE的解析式为y=2x−6√5,求a的值,并直接写出点B、C、D的5坐标;(3)在(2)的条件下,设动点P运动时间为t(秒),在点P运动过程中,请直接写出△BEF为等腰三角形时t的值(或取值范围),并直接写出等腰△BEF面积的最大值.27.中国研制的高速磁悬浮列车时速可达600km/ℎ,比目前高铁列车的最高时速还快5,目前高铁列7车的最高时速为多少km/ℎ?参考答案及解析1.答案:B解析:解:与2x2y不是同类项的是4xy2,故选:B.所含字母相同且相同字母的指数也相同的项是同类项.此题考查同类项,关键是根据同类项定义中的两个“相同”解答:(1)所含字母相同;(2)相同字母的指数相同2.答案:B解析:解:A、本方程中含有两个未知数,所以它不是一元一次方程,故本选项不符合题意;B、本方程符合一元一次方程的定义,所以它是一元一次方程.故本选项符合题意;C、本方程的未知数的最高次数是2,不是一元一次方程,故本选项不符合题意;D、本方程不是整式方程,故本选项不符合题意;故选:B.只含有一个未知数(元),并且未知数的指数是1(次)的方程叫做一元一次方程.它的一般形式是ax+ b=0(a,b是常数且a≠0).本题主要考查了一元一次方程的定义,一元一次方程首先是整式方程,即等号左右两边的式子都是整式,另外把整式方程化简后,只含有一个未知数(元),并且未知数的指数是1(次).3.答案:D解析:解:由四棱柱四个侧面和上下两个底面的特征可知,A,B,C选项可以拼成一个正方体,而D 选项,是田字格,故不是正方体的展开图.故选D.由平面图形的折叠及正方体的展开图解题.解题时勿忘记四棱柱的特征及正方体展开图的各种情形.4.答案:D解析:解:∵a<b,∴a+3<b+3,∴选项A成立;∵a<b,∴−2a>−2b,∴选项B成立.∵a<b,∴3a<3b,∴选项C成立;∵a<b,∴a−2<b−2,∴选项D不成立;故选:D.根据不等式的性质逐一判断,判断出结论不成立的是哪个即可.此题主要考查了不等式的性质,要熟练掌握,特别要注意在不等式两边同乘以(或除以)同一个数时,不仅要考虑这个数不等于0,而且必须先确定这个数是正数还是负数,如果是负数,不等号的方向必须改变.5.答案:Ax−2≥−3,得:x≥−2,解析:解:解不等式12解不等式8−2x>4,得:x<2,则不等式组的解集为−2≤x<2,故选:A.分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.6.答案:A解析:解:某同学用剪刀沿直线将一片平整的银杏叶剪掉一部分(如图),发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是两点之间线段最短.故选:A.根据两点之间,线段最短进行解答.此题主要考查了线段的性质,关键是掌握两点之间,线段最短.7.答案:C解析:解:解不等式3x+5a>4(x+1)+3a,得:x<2a−4,解不等式3x+5a+4>4(x+1)+3a,得:x>−2,5∵不等式组的整数解只有三个,∴这三个整数解为0、1、2,∴2<2a−4≤3,解得3<a≤7,2故选:C.先求出不等式组的解集,再根据不等式组的整数解只有三个,求出实数a的取值范围.此题考查的是一元一次不等式的解法和特殊解,求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.8.答案:D解析:本题根据两车相距126km可以得到:两车的路程之和是126km;根据相遇时小汽车比货车多行6km,可得:小汽车的路程减去货车的路程等于6km找到相等关系,根据相等关系列出方程组.解:45分钟=小时,因为两车经过小时相遇,所以可得:,因为相遇时,小汽车比货车多行6km,所以可得:,所以可列方程组,故应选D.9.答案:A解析:解:{a −b +c =0①4a +2b +c =3②2a +b −3c =19③②−①,得a +b =1④,②×3+③,得2a +b =4⑤,由④⑤可知,选项A 正确,故选A .根据解三元一次方程组的方法可以解答本题.本题考查解三元一次方程组,解题的关键是明确题意,会用消元法解方程.10.答案:B解析:解:∵点M(5−m,m +3)在第一象限,∴{5−m >0m +3>0, 解得−3<m <5,故选:B .根据第一象限内点的坐标符号特点得出关于m 的不等式组,解之可得.本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.11.答案:B解析:解:设购买x 支中性笔,y 本笔记本,根据题意得出:9<x +3y ≤10,当x =1时,y =3,当x =4时,y =2,当x =7时,y =1,故一共有3种方案.故选:B .设购买x 支中性笔,y 本笔记本(x 、y 均为正整数),根据总价=单价×数量结合余下的钱少于1元,即可得出关于x 、y 的二元一次不定方程,再结合x 、y 值均为正整数,即可找出各购买方案. 此题主要考查了二元一次方程的应用,得出不等关系是解题关键.12.答案:C解析:本题考查学生的计算能力以及推理能力,解题的关键是根据不等式组以及分式方程求出m 的范围,本题属于中等题型.根据不等式组有解且至多有3个整数解求出m 的范围,然后再根据分式方程求出m 的范围,从而确定的m 的可能值.解:由不等式组可知:x ≤5且x ≥m+22, ∵有解且至多有3个整数解,∴2<m+22≤5,∴2<m ≤8由分式方程可知:y =m −3,将y =m −3代入y −2≠0,∴m ≠5,∵−3≤y ≤4,∴−3≤m −3≤4,∴0≤m ≤7,综上,2<m ≤7,∵m 是整数,∴所有满足条件的整数m 有:3、4、6、7,4个,故选:C .13.答案:−223解析:解:−(−223)=223的相反数是:−223.故答案为:−223.直接利用相反数的定义进而得出答案.此题主要考查了相反数,正确把握定义是解题关键. 14.答案:−725解析:解:由方程组的解互为相反数,得到x +y =0,即x =−y ,代入方程组得:{−3y −5y =2a ①−2y −7y =a −18 ②, 由①得:y =−14a ,由②得:y =−a−189, 可得−14a =−a−189,即9a =4a −72,解得:a =−725,故答案为:−725由方程组的解互为相反数,得到x +y =0,即x =−y ,代入方程组求出a 的值即可.此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值. 15.答案:105.解析:计算钟面角的度数,一般先从钟面上找出某一时刻分针与时针所处的位置,确定其夹角,再根据表面上每一格30°的规律,计算出分针与时针的夹角的度数.2时30分时,钟面上时针指向数字2与3的中间,分针指向数字6,∴钟表上2点30分,时针与分针的夹角是:3×30°+0.5×30°=105°.故答案为:105.16.答案:9解析:解:设x 小时水池水量达全池的一半,甲的工作效率是16,乙的工作效率是19,由题意可知:x 6−x 9=12,解得:x =9,答:当同时开放甲、乙两管时需要9ℎ水池水量达全池的一半.故答案为:9设x 小时水池水量达全池的一半,甲的工作效率是16,乙的工作效率是19,根据等量关系列出方程即可. 本题考查一元一次方程,解题的关键正确找出题中的等量关系,本题属于基础题型. 17.答案:23a解析:解:因为CM =2AM ,CN =2BN ,所以CM =23AC 、CN =23BC ,所以MN =MC +CN =23AC +23BC =23(AC +BC)=23AB ,因为AB =a ,所以MN =23a.由CM =2AM ,CN =2BN 得CM =23AC 、CN =23BC ,根据MN =MC +CN =23AC +23BC =23(AC +BC)可得答案.本题主要考查两点间的距离,掌握线段之间的关系、线段的和差运算是解题的关键. 18.答案:54解析:解:解方程组{x +y =3x −2y =6, 解得{x =4y =−1, 代入ax +y =4得,4a −1=4,解答a =54.故答案为:54.因为方程组有相同的解,所以只需求出一组解代入另一组,即可求出未知数的值.本题主要考查了二元一次方程的解及二元一次方程组的解法,正确理解题意,然后根据题意得到关于待定系数的方程组,解方程组是解答此题的关键. 19.答案:134解析:解:5x−16=73, 3(5x −1)=6×7,15x −3=42,15x =45,x =3,把x =3代入方程8x−52=x +2m 得:8×3−52=3+2m , m =134,故答案为:134.先求出方程5x−16=73的解,再把x 的值代入方程8x−52=x +2m ,即可解答.本题考查了同解方程,解答本题的关键是能够求解关于x 的方程,要正确理解方程解的含义. 20.答案:115解析:解:设第一天每棵雪松售价x 元,则第二天每棵雪松售价(x +5)元,由题意得:23000x+5=2×11000x ,解得:x =110,经检验,x =110是原方程的解,则x +5=115,即第二天每棵雪松售价115元,故答案为:115.设第一天每棵雪松售价x 元,则第二天每棵雪松售价(x +5)元,由题意:某苗圃园第一天卖出一批雪松收款11000元;第二天又卖出一批雪松收款23000元,所卖数量是第一天的2倍,列出分式方程,解方程即可.本题考查了分式方程的应用;找准等量关系,正确列出分式方程是解题的关键.21.答案:解:去分母得,(x −4)−2(3x +4)=−15,去括号得,x −4−6x −8=−15,移项得,x −6x =−15+4+8,合并同类项得,−5x =−3,系数化为1得,x =35.解析:这是一个带分母的方程,所以要先去分母,再去括号,最后移项,合并同类项,系数化为1,从而得到方程的解.本题主要考查了解一元一次方程,注意在去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号. 22.答案:解:{3x −2y =−8 ①x +2y =0 ②, ①+②得:4x =−8,解得:x =−2,将x =−2代入②得:−2+2y =0,解得:y =1,所以原方程组的解为{x =−2y =1. 解析:①+②得出4x =−8,求出x ,再把x =−2代入②求出y 即可.本题考查了解二元一次方程组,能把二元一次方程组转化成一元一次方程是解此题的关键. 23.答案:解:(1)原式=4−1+2−3=2;(2){x −1>4x +2①2x+13>2x②, 由①可得:x <−1;由②可得:x <14;所以不等式组的解集为:x <−1.解析:(1)根据实数的混合计算解答即可;(2)先求出两个不等式的解集,再求其公共解.本题主要考查了一元一次不等式组解集的求法,其简便求法就是用口诀求解.求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解). 24.答案:20°解析:解:(1)∵∠ACB =90°,∴∠BCD =180°−∠BCE =180°−40°=140°,∠BCE +∠ACD =90°,∴∠ACD =90°−∠BCE =90°−40°=50°,∵CF 平分∠BCD ,∴∠DCF =12∠BCD =70°,∴∠ACF =∠DCF −∠ACD =20°,故答案为:20°(2)∵∠ACB =90°,∠BCE =a ,∴∠ACD =180°−90°−a°=90°−a ,∠BCD =180°−a ,又∵CF 平分∠BCD ,∴∠DCF =∠BCF =12∠BCD =12(180°−a)=90°−12α,∴∠ACF =∠DCF −∠ACD =90°−12α−(90°−a)=12α. (1)由已知得出∠BCD =180°−∠BCE =140°,∠BCE +∠ACD =90°,得出∠ACD =90°−∠BCE =50°,由角平分线定义得出∠DCF =12∠BCD =70°,即可得出答案;(2)由已知得出∠ACD=180°−90°−a°=90°−a,∠BCD=180°−a,由角平分线定义得出∠DCF=∠BCF=12∠BCD=12(180°−a)=90°−12α,即可得出答案.本题考查了角的计算、平角的定义和角平分线的定义等知识;熟练掌握平角定义和角平分线定义是解题的关键.25.答案:解:图中线段有:AE、AC、AD、AF、AB,EC、ED、EF、EB,CD、CF、CB,DF、DB,FB,共5+4+3+2+1=15条,∵每条线段应印2种车票,∴共需印15×2=30种车票.解析:根据线段的定义找出线段的条数,再根据车票的起始站的不同,乘以2即可得到车票的种数.本题考查了线段条数的计算,应按照一定的顺序,才能做到不遗漏,不重复,还需注意每条线段应印2种车票.26.答案:a解析:解:(1)如图1中,∵BD⊥OD,∴∠BDO=90°,∵BD=2a,AB=√5a,∴OD=√AB2−BD2=a,∵四边形ODCB是等腰梯形,∴BD=OD=a.故答案为a.(2)如图2中,作DM⊥OB于M,CN⊥OB于N.∵∠DOB=∠CBO,BC=a,∴sin∠CBO=sin∠DOB=2a√5a =2√55a=CNBC,∴CN=2√55a,BN=√BC2−CN2=√55a,∴ON=OB−BN=4√55a,∴C(4√55a,2√55a),∵直线y=2x−65√5经过点C,∴2√55a=8√55a−6√55,∴a=1.(3)如图3−1中,当点F在线段BC上时,∵EF⊥BD,OD⊥BD,∴EF//OD,∴∠FEB=∠DOB,∵∠DOB=∠CBO,∴FEB=∠FBE,∴FE=FB,∴△FEB是等腰三角形,如图2中,当直线EF经过点C时,E(3√55,0),此时EB=2√55,∴PB=EB⋅cos∠EBP=2√55⋅2√55=45,共线图形可知当0<t≤45时,△BFE是等腰三角形.如图3−2中,当点F在线段CD上,EF=BE时,1=√52t,∴t=2√55.如图3−3中,当点F在线段CD上,BF=BE时,易证:PE=PF,∴12t=12,∴t=1,综上所述,t的值为0<t≤45或2√55或1时,△BEF是等腰三角形.当t=1时,△BEF的面积最大,最大值=12×√55×4√55=25.(1)在Rt△BOD中,求出OD,再根据等腰梯形的性质解决问题即可.(2)如图2中,作DM ⊥OB 于M ,CN ⊥OB 于N.由a 表示出点C 坐标,利用待定系数法即可解决问题.(3)分三种情形分别求解:①如图3−1中,当点F 在线段BC 上时,②如图3−2中,当点F 在线段CD 上,EF =BE 时,③如图3−3中,当点F 在线段CD 上,BF =BE 时.本题属于一次函数综合题,考查了等腰梯形的性质,一次函数的应用,等腰三角形的性质等知识,解题的关键是熟练掌握基本知识,学会用分类讨论的思想思考问题,属于中考压轴题. 27.答案:解:根据题意可得,600÷(1+57)=600÷127=350( km/ℎ).答:目前高铁列车的最高时速为350 km/ℎ. 解析:把目前高铁列车的最高时速看作单位“1”,根据题意可知,中国研制的高速磁悬浮列车时速是目前高铁列车最高时速的(1+57)倍,用高速磁悬浮列车时速÷(1+57)即可求解.本题考查了有理数混合运算的应用,找准单位“1”,得出中国研制的高速磁悬浮列车时速是目前高铁列车最高时速的(1+57)倍是解题的关键.。
1_精品解析:重庆市西南大学附属中学校2021-2021学年七年级上学期期末数学试题(原卷版)

度上期期末考试初一数学试题一、选择题1.下列各数中,倒数是3-的数是( ) A. 3B. 3-C.13D. 13-2.方程3(1)6x -=的解是( ). A. 1B. 1-C. 2D. 2-3.已知a b >,则下列各式不正确的是( ). A. 33a b +>+B. 33a b ->-C. 33a b >D. 33a b ->-4.下列各数是不等式271x -≥的解的是( ). A. 4B. 3C. 2D. 15.方程834x ax -=-的解是3x =,则a 的值是( ). A. 1B. 1-C. 3-D. 36.下列说法错误的是( ). A. 两个负数,绝对值大的反而小B. 数轴上右边的点表示的数总是比左边的点表示的数大C. 等式两边除以同一个数等式仍然成立D. 一元一次不等式组的解集是不等式组中各不等式解集的公共部分 7.按如图所示的运算程序,能使输出结果的值为11的是( )A. x =3,y =1B. x =2,y =2C. x =2,y =3D. x =0,y =1.58.若不等式(2)2m x m +>+的解集是1x <,则m 的取值范围是( ). A 0m >B. 0m <C. 2m >-D. 2m <-9.《九章算术》有题曰:“今有五雀,六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平.并燕雀重一斤.问燕雀一枚各重几何?”其大意是:“现在有5只雀,6只燕,分别集中放在天平上称重,聚在一起的雀重燕轻.将一只雀一只燕交换位置而放,重量相等.5只雀、6只燕重量共一斤,问雀和燕各重多少?”古代记1斤为16两,则设1只雀x 两一只燕y 两,可列出方程( ).A. 561645x y x y y x +=⎧⎨+=+⎩B. 561056x y x y +=⎧⎨=⎩C. 561045x y x y y x+=⎧⎨+=+⎩D. 561656x y x y+=⎧⎨=⎩10.若30x y -=且0y ≠,则2525x yx y-+的值为( ).A. 11B. 111-C. 111D. 11-11.有不足30个苹果分给若干个小朋友,若每个小朋友分3个,则剩2个苹果;若每个小朋友分4个,则有一个小朋友没分到苹果,且最后一个分到苹果的小朋友分得的苹果数不足3个,已知小朋友人数是偶数个,那么苹果的个数是( ) A .25B. 26C. 28D. 2912.已知关于x 的方程123x m x m+--=的解不大于1,且关于x 的不等式组36043x m x -≤⎧⎨-+>-⎩有且只有3个整数解,则符合条件的所有整数m 的和为( ). A. 2B. 3C. 5D. 6二、填空题13.2019年下半年猪肉价格一路上涨,为平抑猪肉价格,商务部会同国家发展委员会、财政部自9月19日以来累计向市场投放中央储备猪肉31000吨,请将31000用科学记数法表示为__________. 14.单项式3a 2b 3的次数是_____.15.计算:22(9)|4|3π⎛⎫-⨯-+-= ⎪⎝⎭__________.16.若||1(2)26k k x-+-=是关于x 的一元一次方程,则k =__________. 17.甲仓库的货物是乙仓库货物的2倍,从甲仓库调5吨到乙仓库,这时甲仓库的货物恰好比乙仓库的一半多3吨,设乙仓库原有x 吨,则x =__________.18.如果方程组233x y mx y m +=⎧⎨+=+⎩的解满足12x y +=,求m 的值为__________. 19.已知325x y -=,若x 满足61511x ≤-<,那么y 的取值范围是__________.20.某超市销售糖果,将A 、B 、C 三种糖果搭配成甲、乙、丙三种礼盒方式销售,每个礼盒的成本分别为礼盒中A 、B 、C 糖果的成本之和,礼盒成本忽略不计.甲种礼盒每盒分别装有A 、B 、C 三种糖果7kg 、2kg 、1kg ,乙种礼盒每盒分别装有A 、B 、C 三种糖果1kg 、6kg 、3kg ,每盒甲的成本是每千克A 成本的12倍,每盒甲的销售利润率为25%,每盒甲的售价比每盒乙的售价低16,丙每盒在成本上提高30%标价后打九折销售获利为每千克A 成本的1.7倍,当销售甲、乙、丙三种礼盒的数量之比为2:1:4时,销售的总利润率为__________.(用百分数表示)三、计算题21.解方程组:(1)2236x y x y =⎧⎨+=⎩(2)534231232x y x y +=⎧⎪+-⎨-=⎪⎩22.解不等式(组)并把解集在数轴上表示出来: (1)83(3)5(1)x x --≤+(2)312(1)1132x x x x +>-⎧⎪⎨-≥-⎪⎩①②23.先化简再求值:已知a ,b 满足2(2)|1|0a b b -++=,求()22223232a b ab ab a b ⎡⎤-++-⎣⎦的值.24.列方程(组)或不等式(组)解应用题:(1)甲工人接到240个零件的任务,工作1小时后,因要提前完成任务,调来乙和甲合作,合做了5小时完成.已知甲每小时比乙少做4个,那么甲、乙每小时各做多少个?(2)某工厂准备购进A 、B 两种机器共20台用于生产零件,经调查2台A 型机器和1台B 型机器价格为18万元,1台A 型机器和2台B 型机器价格为21万元. ①求一台A 型机器和一台B 型机器价格分别多少万元?②已知1台A型机器每月可加工零件400个,1台B型机器每月可加工零件800个,经预算购买两种机器的价格不超过140万元,每月两种机器加工零件总数不低于12400个,那么有哪几种购买方案,哪种方案最省钱?25.阅读理解:材料一:对于一个两位数M,交换它的个位和十位数字得到的新数N叫这个两位数M的“倒序数”.如:23的倒序数是32,50的倒序数是05.材料二:对于一个两位数M,若它的个位数字与十位数字的和小于等于9,则把个位数字与十位数字的和插入到这个两位数中间得到的新数叫这个两位数M的“凸数”.如23的凸数是253.(1)请求出42的“倒序数”与“凸数”;38有“凸数”吗?为什么?(2)若一个两位数与它的“倒序数”的和的4倍比这个两位数的“凸数”小132,请求出这个两位数. 26.已知在数轴上A,B两点对应数分别为-3,20.(1)若P点为线段AB的中点,求P点对应的数.(2)若点A以每秒3个单位,点B以每秒2个单位的速度同时出发向右运动多长时间后A,B两点相距2个单位长度?(3)若点A,B同时分别以2个单位长度秒的速度相向运动,点M(M点在原点)同时以4个单位长度/秒的速度向右运动.①经过t秒后A与M之间的距离AM(用含t的式子表示)②几秒后点M到点A、点B的距离相等?求此时M对应的数.登录组卷网可对本试卷进行单题组卷、细目表分析、布置作业、举一反三等操作。
重庆市西南大学附中2020-2021学年七年级上半期数学试题

西南大学附中2020-2021学年度上期期中考试初一教学试题(满分:120分考试时间:100分钟)一、选择题:本大题12个小题,每小题3分,共36分.1、在0, -3, 3.14,加中,不是有理数的是()A. 0B.—3C. 3.14D. n2、某品牌大米包装袋上的质量标识为“50±0.5的",则下列四袋大米中,质量不合格的是()A. 49.4 kgB. 49.7 kgC. 50.1 kgD. 50.4 kg3、下列几组数中,相等的是( )A.23和32B.(—3)2和-32C.(—1)2022和—12022 万+(-5)和—| —5|4、按如图程序输入一个数x,若输入的数X=-1,则输出的结果为()B.—2/xy3z2的系数和次数分别是—2/和6C.2机2 —3771+ 45是五次三项式D.2—1 = 3是一元一次方程x6、如果—"mTy,zB与3/y2-3”3是同类项,那么7n和"的值分别为()DA.等不是整式A. 5 和 4B. 6 和|7、下列等式的变形中,正确的是(A.如果那么a = b C CC.如果ax = ay9那么x = yC. 6和一2D. 5和一三 3 3)B.如果|a| = |b|,那么a = b。
.如果m = 〃,那么登=£c2-4c2-45、下列说法正确的是()8、若。
、b互为相反数,c、d互为倒数,m的倒数是它本身,则加2 +。
+ /)+ 2的值为A. 2 3. 2或0 C. 3或2 D.不确定£9、已知K —1| = 2, (y —1)2 = 4, -< 0,则x — y 的值为( )A. -4B. 0C. 4D. ±4 10、已知关于」的方程3y+2m-5 =0的解比y — 3(?n —2) = 2的解大1,则桁的值为( )n 10D. -----1111、若代数式2血%2 + 4% - 2y2 - 3(/一的值为() 12、下列说法正确的是(①已知〃、b 是不为0的有理数,则叫+ =一餐的值为1或-3; a \b\ \ab\a + b(a > b)②如果定义{a,b } = < 0(a = b),当ab < 0, Q + b < 0, |a| > |b|时,{。
重庆市西南大学附属中学校2022-2023学年七年级下学期期末数学试题(含答案)

初2025届初一下数学期末试卷一、选择题:1.四个大小完全相同的正方体搭成的几何体如图所示,从正面看得到的平面图形是( )A .B .C .D .2.下列计算正确的是()A .B .C .D .3.如图,,下列条件中不能保证的是()A . B .C .D .4.下列说法不正确的是()A .三角形的三条角平分线交于一点B .全等三角形对应角相等C .过一点有且只有一条直线与已知直线平行D .连接直线外一点与直线上各点的所有线段中,垂线段最短5.已知,则代数式的值为()A .B .0C .3D .26.用大小完全相同的圆点按如图所示的规律拼图案,其中第①个图案中有5个圆点,第②个图案中有9个圆点,第③个图案中有13个圆点,第④个图案中有17个圆点,…,按此规律排列下去,则第⑨个图案中圆点的个数为()22422x x -=22(2)(2)4x y x y x y +-=-()33628a a -=-222()a b a b +=+,ABC DEF BE CF ∠=∠=ABC DEF △≌△A D ∠=∠ACB DFE ∠=∠AB DE =AC DF =3,2ab a b =+=223ab a b ab +-3-① ② ③ ④A .29B .33C .37D .407.西南大学附属中学某校区本学期组织学生参加春游活动,在欢乐谷的某个对抗项目中,安排人员时发现,若每只飞船坐6人,则有15人无飞船可坐:若每只飞船坐10人,则其中一只飞船只坐了5人,其余的飞船均坐满.设乘坐的飞船有x 只,本次参加活动的学生有y 人,根据题意,所列方程组正确的是()A . B . C . D .8.如图,在中,,平分交于点,若的面积为10,的面积为6,则的面积为( )A .2B .2.5C .3D .49.已知关于y的方程的解为整数,且关于x 的不等式组有解且至多有2个整数解,则满足条件的所有整数a 的和是()A .8B .11C .13D .1910.如果代数式(均为非0常数),(均为非0常数),且满足,则称这两个代数式A 与B 互为“相反式”,对于上述“相反式”A 与B ,下列结论正确的有()个.①若,则;②若为常数,,则A 的值为1;③若关于x ,y 的代数式(k 为正整数)不含一次项,则的最大值为2;④若关于x 、y 的两个方程(k 、t 均为常数)有相同的解,则.A .1B .2C .3D .4二、填空题:11.2023年5月28日上午,国产客机执行首个商业航班,的单架采购价格为9900万美元,折合61510(1)5x y x y -=⎧⎨+=-⎩61510(1)5x y x y +=⎧⎨+=+⎩61510(1)5x y x y -=⎧⎨-=+⎩61510(1)5x y x y +=⎧⎨-=-⎩ABC △90ABC ∠=︒AD BAC ∠BC ,D DE DC =ADC △AED △DBE △(2)32a y y -+=-123231x x x a x +⎧>-+⎪⎨⎪-<-⎩111A a x b y c =++111,,a b c 222B a x b y c =++222,,a b c 1212120,0,0a a b b c c +=+=+=222023,20233A x ayB bx by =-+-=++2023()1a b +=-,()p q p q ≠pA qB p q +=-2()A B kA B -+⋅1c 12,A kc B tc ==0k t +=C919C919人民币约为6.53亿元,把653000000用科学记数法表示为__________.12.计算:__________.13.已知,则__________.14.如图,正六边形与正五边形位置如图所示,则的度数为__________.15.已知的三边分别为a 、b 、c ,化简:__________.16.已知实数x ,y 满足,则__________17.如图,将沿翻折,顶点A 、B 均落在点G 处,若,则__________°.18.如图,四边形中,与相交于点O ,且,点E 是和平分线的交点,连接,给出下列结论:①;②;③;④;其中正确结论的序号为__________.三、解答题:19.计算:(2023)|1|ππ---=226,3x y x y +=+=xy =ABCDEF EFGHI AFG ∠ABC △||||||a b c a b c c b a +---++---=221454x xy y y -+-=-2x y +=ABC △DE EF 、58CDG CFG ∠-∠=︒C ∠=ABCD AC BD ,AC BD AC AB BD ⊥==BAC ∠ABD ∠,ED EC 135AEB ∠=︒AD DC =BE EC ⊥AEB EDC S S =△△(1);(2).20.因式分解:(1); (2).21.先化简,再求值:,其中.22.请在下列解题过程的空白处填上恰当的内容(推理的理由或数学表达式):如图,在中,于点D ,E 、F 分别是上的一点,且,延长交于点G ,若,求证:.证明:(___________________________)在和中,(__________)(_______________________)(_________________)∴__________∴__________(____________________)(____________________)23.如图,,点E 为上一点,且,延长交于点F.(2)(3)(1)x x x x ++--2(2)(3)(3)x y x y x y ---+3228a ab -224()8()4()a b x xy b a y a b ---+-22(2)(2)4()(2)(2)x y x y x y y y ⎡⎤+--+--÷-⎣⎦2|2|(3)0x y ++-=ABC △AD BC ⊥BD AD 、EF AC =EF AC ,180DF DC B BEG =∠+∠=︒AB AC ⊥AD BC⊥ 90EDF ADC ∴∠=∠=︒Rt EDF △Rt ADC △EF AC DF DC=⎧⎨=⎩Rt Rt EDF ADC ∴△≌△12∴∠=∠1180C ADC ∠+∠+∠=︒ 190C ∴∠+∠=︒90C +∠=︒(180)290EGC C ∴∠=︒-∠+∠=︒180B BEG ∠+∠=︒90BAC EGC ∴∠=∠=︒AB AC∴⊥,BC BD BC AD =∥BD ABD BCE ∠=∠CE AB(1)求证:;(2)若,,求的度数.24.又是一年端阳至,绿杨带雨垂垂重,五色新丝缠角粽,吃粽子是端午节的习俗.某糕点店推出的“鲜肉粽”和“蛋黄粽”深受顾客喜欢.已知3个“鲜肉粽”、2个“蛋黄粽”的售价之和为46元,5个“鲜肉粽”、1个“蛋黄粽”的售价之和为58元.(1)求“鲜肉粽”和“蛋黄粽”的售价各是多少元?(2)糕点店在今年端午节前夕,购进了3000个“鲜肉棕”,2500个“蛋黄粽”.适逢店庆,为答谢新老顾客,糕点店对两种粽子都展开了降价促销活动,其中“鲜肉粽”按售价打折(a 为整数)出售,“蛋黄棕”每个让利元,且保证降价后“鲜肉棕”的售价低于“蛋黄粽”售价的1.5倍,最终两种棕子全部销售出去,且总销售额不低于39000元,求a 的值.25.对任意一个四位数m ,如果m 各个数位上的数字都不为零且互不相同,满足个位数字与千位数字的和等于十位数字与百位数字的和,那么称这个数为“和平数”,将一个“和平数”个位数字与千位数字对调,十位数字与百位数字对调后得到另一个新四位数,记.例如,因为,所以3456是一个“和平数”,将3456个位数字与千位数字对调,十位数字与百位数字对调得到,所以.(1)请判断1234、3669是否是“和平数”?如果是,请求出的值;(2)已知s 、t 均为“和平数”,(其中且a 、b 、c 、d 均为整数),若能被11整除,26.在中,;在中,,.(1)如图1,若,点E 在线段上,且,求的度数.图1(2)如图2,若,点E 在外部,连接交于点F ,连接,已知F 是中点,求证:.ABD ECB △≌△25BCE ∠=︒100CFA ∠=︒BDC ∠()4a +0.4a 1m 1()1111m m F m +=3456m =3645+=+16543m =34566543(3456)91111F +==()F m 5030100,704100010s a b t c d =++=++19,17,39,19a b c d ≤≤≤≤≤≤≤≤()2()F s F t +ABC △90ABC ∠=︒BDE △90BDE ∠=︒DB DE =BA BC =AC 2CBD CBE ∠=∠AEB ∠BA BC =ABC △AD EB CD AD ACD CBD ∠=∠图2(3)如图3,点E 在线段上,且平分,过点D 作交线段于点M 线段C 于点水连接,当时,请直接写出的周长.图3AC CD ACB ∠45MDN ∠=︒AB BD AD MN 、、68,,255BC AB AC ===BMN △初2025届初一下数学期末试卷评讲一、选择题:1.D 2.B 3.D 4.C 5.A 6.C 7.D 8.A 9.D 10.C二、填空题:11. 12. 13.1.5 14.132 15. 16.2 17.61 18.①③④三、解答题:(1)解:原式 3分5分(2)解:原式 3分5分20.因式分解:(1)解:原式 3分5分(2)解:原式 3分5分21.解:原式 2分4分6分∴原式 7分8分22.垂直的定义 全等三角形对应角相等 三角形内角和为或或 同旁内角互补,两直线平行 两直线平行,同位角相等23.(1) 1分在和中86.5310⨯2π-a b c --22326x x x x x =+++-+66x =+()2222449x xy y x y =-+--2222449x xy y x y =---+2413xy y =-+()2224a a b =-2(2)(2)a a b a b =+-()224()2a b x xy y =-++24()()a b x y =-+()222224424(2)x y x xy y y y ⎡⎤=--++-÷-⎣⎦942x y =+2|2|(3)0x y ++-= 2,3x y ∴=-=94(2)32=⨯-+⨯112=HL 180︒2∠AB EG ∥AB EF ∥AB FG ∥BC AD∥CBE BDA ∴∠=∠ABD △ECB △3分4分(未写判定依据扣1分)(2) 7分10分24.(1)设“鲜肉棕”的售价为x 元/个;“蛋黄粽”售价为y 元/个,则2分解得: 3分答:“鲜肉粽”的售价为10元/个;“蛋黄粽”售价为8元/个.4分(2)由题意得7分解得: 8分为整数 9分答:a 的值为4. 10分25.(1)1234是“和平数”;3669不是“和平数” 2分 4分(2)ABD ECBBD CB BDA CBE∠=∠⎧⎪=⎨⎪∠=∠⎩(ASA)ABD ECB ∴△≌△,25ABD ECB ECB ∠=∠∠=︒25ABD ∴∠=︒,100CFA BCE CBF CFA ∠=∠+∠∠=︒75CBF ∴∠=︒50CBD CBF ABD ∴∠=∠-∠=︒BC BD= BCD BDC∴∠=∠180BCD BDC CBD ∠+∠+∠=︒65BDC ∴∠=︒3246558x y x y +=⎧⎨+=⎩108x y =⎧⎨=⎩410 1.5(80.4)1043000102500(80.4)390010a a a a +⎧⨯<-⎪⎪⎨+⎪⨯⨯+-≥⎪⎩ 3.55a ≤<a 4a ∴=12344321(1234)51111F +==5030100,19,17s a b a b =++≤≤≤≤为“和平数”为“和平数”(6分)能被11整除(k 为整数)(7分)(8分)①当即时(舍)(舍)②当即时或或(舍)(10分,多写扣1分)26.(1)53s a b∴=s 2,()5a b F s b ∴-==+704100010,39,19t c d c d =++≤≤≤≤ 74t c d ∴=t 3,()4c d F t c ∴-==+()2()F s F t + 52(4)11b c k ∴+++=2211c b k ∴++=39,17c b ≤≤≤≤ 92227c b ∴≤++≤2211,22c b ∴++=2211c b ++=29c b +=33c b =⎧⎨=⎩41c b =⎧⎨=⎩2222c b ++=220c b +=92c b =⎧⎨=⎩84c b =⎧⎨=⎩76c b =⎧⎨=⎩9764,8754t ∴=DB DE= DBE DEB∴∠=∠180DBE DEB BDE ∠+∠+∠=︒ 90BDE ∠=︒45DBE DEB ∴∠=∠=︒2CBD CBE∠=∠ CBD CBE DBE∠+∠=∠15CBE ∴∠=︒90BA BC ABC =∠=︒,45C ∴∠=︒(3分)(2)在上截取一点M ,使,连接为的中点在和中5分在和中8分. 9分(3) 12分60AEB C CBE ∴∠=∠+∠=︒BF FM EF =AM A AD AF DF∴=AFM △DFE △AF DFAFM DFEFM FE=⎧⎪∠=∠⎨⎪=⎩()SAS AFM DFE ∴△≌△,AMF E AM DE∴∠=∠=,90DB DE BDE =∠=︒45E DBE ∴∠=∠=︒,45BD DE AM AMF E ∴==∠=∠=︒AMF BAM ABM∠=∠+∠ 45BAM ABM ∴∠+∠=︒90ABM DBE CBD ABC ∠+∠+∠=∠=︒ 45ABM CBD ∴∠+∠=︒BAM CBD∴∠=∠BAM △CBD △AM BDBAM CBD AB BC=⎧⎪∠=∠⎨⎪=⎩(SAS)BAM CBD ∴△≌△,45ABM CBD CBD BCD ∴∠=∠∴∠+∠=︒,45ACD BCD ACB ACB ∠+∠=∠∠=︒ 45ACD BCD ∴∠+∠=︒ACD CBD ∴∠=∠45。
2021-2022学年重庆市北碚区西南大学附中初一数学第一学期期末试卷及解析

2021-2022学年重庆市北碚区西南大学附中初一数学第一学期期末试卷一、选择题:本大题12小题,每小题4分,共48分.1.下列各数中,是不等式12x +>的解的是( )A .7-B .1-C .0D .92.下列计算中正确的是( )A .11||33--=B .22256x y x y x y -=-C .257a b ab +=D .224-= 3.下列说法正确的是( )A .2mn π的系数是2πB .228ab -的次数是5次C .3234xy x y +-的常数项为4D .21165x x -+是三次三项式4.已知2224x x --=,则代数式2639x x --的值是( )A .3-B .3C .9D .185.若关于x ,y 的方程||7(1)6m x m y +-=是二元一次方程,则m 的值为( )A .1-B .0C .1D .26.下列说法中错误的是( )A .若a b <,则11a b +<+B .若22a b ->-,则a b <C .若a b <,则ac bc <D .若22(1)(1)a c b c +<+,则a b <7.今年,网络购物已经成为人们生活中越来越常用的购物方式.元旦期间,某快递分派站有包裹若干件需快递员派送,若每个快递员派送7件,还剩6件;若每个快递员派送8件,还差1件,设该分派站有x 名快递员,则可列方程为( )A .7681x x -=+B .7681x x +=-C .6178x x -+=D .6178x x +-= 8.已知21x =,||2y =,且x y >,则x y -的值为( )A .1或3B .1或3-C .1-或3-D .1-或39.观察下列图形:它们都是由同样大小的圆圈按一定的规律组成,其中第1个图形有5个圆圈,第2个图形有9个圆圈,第3个图形有13个圆圈,⋯,按此规律,第7个图形中圆圈的个数为( )A .21B .25C .28D .2910.若关于x 的不等式组231232x m x x-⎧⎪⎨⎪->-⎩无解,则m 的取值范围是( )A .1m >B .1mC .1m <D .1m11.已知关于x ,y 的方程组3424x y ax by -=⎧⎨-=-⎩和2593x y bx ay +=⎧⎨+=⎩的解相同,则2021(3)a b +的值为( ) A .1 B .1- C .0 D .202112.若关于x 的不等式组2123342x x a x x -⎧-<⎪⎨⎪--⎩有且仅有3个整数解,且关于y 的方程2135a y a y --=+的解为负整数,则符合条件的整数a 的个数为( )A .1个B .2个C .3个D .4个二、填空题:本大题4个小题,每小题4分,共16分.13.将数据“4570000”用科学记数法表示为 .14.已知关于x ,y 的二元一次方程组2586235x y a x y a +=+⎧⎨-=-⎩的解x ,y 互为相反数,则a 的值为 . 15.已知x 为不等式组212(1)1x x x -<⎧⎨-<+⎩的解,则|3||1|x x -+-的值为 . 16.某水果基地为提高效益,对甲、乙、丙三种水果品种进行种植对比研究.去年甲、乙、丙三种水果的种植面积之比为5:3:2,甲、乙、丙三种水果的平均亩产量之比为6:3:5.今年重新规划三种水果的种植面积,三种水果的平均亩产量和总产量都有所变化.甲品种水果的平均亩产量在去年的基础上提高了50%,乙品种水果的平均亩产量在去年的基础上提高了20%,丙品种的平均亩产量不变.其中甲、乙两种品种水果的产量之比为3:1,乙、丙两种品种水果的产量之比为6:5,丙品种水果增加的产量占今年水果总产量的587,则三种水果去年的种植总面积与今年的种植总面积之比为 . 三、计算题:本大题共4个小题,共40分.解答时每小题必须给出必要的演算过程或推理步骤.17.计算:(1)2(5)(6)3|1|-⨯-+-÷--;(2)22020202112(4)(21)(1)4-÷-⨯--+--. 18.解方程(组):(1)3122123m m -+-=;(2)323123m n m n m n m n +-⎧+=⎪⎪⎨+-⎪-=-⎪⎩. 19.(16分)解下列不等式(组),并把解集在数轴上表示出来:(1)733(5)x x --;(2)211134x x x ---<-; (3)314232x x x ->-⎧⎨-⎩;(4)2(2)3(8)43310.20.5x x x x ->+⎧⎪+-⎨+-⎪⎩. 20.先化简,再求值.(1)已知2|2|(3)0a b -+-=,求多项式3[2()][2()]a b ab a b ab +--+-的值;(2)已知23212A nx x =--,21243B x mx =-+,当23A B -的值与x 的取值无关时,求多项式2222(32)(24)m mn n m mn n -+-+-的值.四、解答题:本大题共5小题,21题8分,22题8分,23题10分,24题10分,25题10分,共46分.解答应写出必要的文字说明、证明过程或演算步骤.21.定义一种新运算“⊗”,规定:23a b a b =-⊗.等式右边的运算就是加、减、乘、除四则运算,例如:2(3)223(3)4913-=⨯-⨯-=+=⊗,122132264=⨯-⨯=-=-⊗.(1)求(2)[5(1)]--⊗⊗的值;(2)若(32)(1)2x x -+=⊗,求x 的值.22.一艘轮船在相距120千米的甲、乙两地之间匀速航行,从甲地到乙地顺流航行用6小时,从乙地到甲地逆流航行用10小时.(请列方程或方程组解答)(1)求该轮船在静水中的速度和水流速度;(2)若在甲、乙两地之间的丙地新建一个码头,使该轮船从甲地到丙地和从乙地到丙地所用的航行时间相同,问甲、丙两地相距多少千米?23.永辉超市计划购进甲、乙两种体育器材,若购进甲器材3件,乙器材6件,需要480元,购进甲器材2件,乙器材3件,需要280元,销售每件甲器材的利润率为37.5%,销售每件乙器材的利润率为30%.(1)甲、乙两种体育器材进价分别为多少元/件?(列方程或方程组解答)(2)该超市决定购进甲、乙体育器材100件,并且考虑市场需求和资金周转,用于购进这些体育器材的资金不少于6300元,同时又不能超过6430元,则该超市有哪几种进货方案?哪种方案获利最大?最大利润是多少元?24.对任意一个三位数(19M abc a =,19b ,09c ,a ,b ,c 为整数),如果其个位上的数字与百位上的数字之和等于十位数上的数字,则称M 为“万象数”,现将“万象数” M 的个位作为十位,十位作为百位,百位作为个位,得到一个数N ,并规定()K M N M =-,我们称新数()K M 为M 的“格致数”. 例如154是一个“万象数”,将其个位作为十位,十位作为百位,百位作为个位,得到一个541N =,(154)541154387K =-=,所以154的“格致数”为387.(1)填空:当132M =时,N = ;当495M =时,(495)K = ;(2)求证:对任意的“万象数” M ,其“格致数” ()K M 都能被9整除;(3)已知某“万象数” M 的“格致数”为()K M ,()K M 既是72的倍数又是完全平方数,求出所有满足条件的“万象数” M .(完全平方数:如200=,211=,242=,293=,2164=⋯,我们称0、1、4、9、16⋯叫完全平方数)25.如图,已知数轴上两点A ,B 表示的数分别为2-,6,用符号“||AB ”来表示点A 和点B 之间的距离.(1)如图1,若点C 为点A 、B 的中点,则点C 表示的数为 ;(2)如图2,若点C 对应数为4.点E 以1个单位/秒的速度从点A 出发沿着数轴的正方向运动,2秒后点F 以2个单位/秒的速度从点C 出发也沿着数轴的正方向运动,点F 到达B 点处立刻按原速返回沿着数轴的负方向运动,直到点E 到达点B ,两个点同时停止运动.设点E 运动的时间为(0)t t >,在此过程中存在t 使得||3||EF BE =成立,求t 的值;(3)如图3,若点C 对应数为4.长度均为1个单位的电子虫MN 和电子虫PQ ,其中MN 从点A 出发(点N 与点A 重合)以1个单位/秒的速度沿着数轴的正方向运动,同时PQ 从点C 出发(点P 与点C 重合)以2个单位/秒的速度沿着数轴的负方向运动,当PQ 运动到点P 与点A 重合时,PQ 保持速度不变,反向沿着数轴正方向运动,当点Q 运动到与点M 重合时,两电子虫都停止运动.在运动过程中,如果出现两条电子虫有重叠的时候,它们各自运动方向不变但速度会减半,重叠结束速度立即恢复.设电子虫MN 运动时间为t 秒,是否存在(0)t t >,使两电子虫上的点N 和点P 刚好相距3个单位长度,若存在,请直接写出t 的值.若不存在,请说明理由.答案与解析一、选择题:本大题12小题,每小题4分,共48分.1.解:解不等式12x +>,得1x >.故选:D .2.解:A .11||33--=-,故A 不符合题意; 222.56B x y x y x y -=-,故B 符合题意;.2C a 与5b 不能合并,故C 不符合题意;D .224-=-,故D 不符合题意;故选:B .3.解:A 、2mn π的系数是2π,故A 符合题意.B 、228ab -的次数是3次,故B 不符合题意.C 、3234xy x y +-的常数项为4-,故C 不符合题意.D 、21165x x -+是二次三项式,故D 不符合题意.故选:A .4.解:2224x x --=,226x x ∴-=,∴原式23(2)93699x x =--=⨯-=.故选:C .5.解:由题意得:||1m =,且10m -≠,解得:1m =-,故选:A .6.解:A .a b <,11a b ∴+<+,故本选项不符合题意;B .22a b ->-,a b ∴<,故本选项不符合题意;C .当0c 时,由a b <不能推出ac bc <,故本选项符合题意;D .22(1)(1)a c b c +<+,a b ∴<,故本选项不符合题意;故选:C .7.解:设该分派站有x 名快递员,则可列方程为:7681x x +=-.故选:B .8.解:21x =,||2y =且x y >,1x ∴=±,2y =-,当1x =,2y =-时,则3x y -=,当1x =-,2y =-时,则1x y -=.故选:A .9.解:第1个图形有5个圆圈,第2个图形有9个圆圈,第3个图形有13个圆圈,⋯,∴第n 个图形中圆圈的个数为:41n +,∴第7个图形中圆圈的个数为:47129⨯+=(个),故选:D .10.解:由23x m -,得:32x m +, 解不等式1232x x ->-,得:5x >,不等式组无解,325m ∴+,解得1m ,故选:D .11.解:关于x ,y 的方程组3424x y ax by -=⎧⎨-=-⎩和2593x y bx ay +=⎧⎨+=⎩的解相同, ∴342259x y x y -=⎧⎨+=⎩, 解得:21x y =⎧⎨=⎩,把21x y =⎧⎨=⎩代入43ax by bx ay -=-⎧⎨+=⎩中可得: 2423a b b a -=-⎧⎨+=⎩, 解得:12a b =-⎧⎨=⎩, 20212021(3)(32)1a b ∴+=-+=-,故选:B .12.解:不等式组2123342x x a x x -⎧-<⎪⎨⎪--⎩整理得227x a x <⎧⎪+⎨⎪⎩, 不等式组有且仅有3个整数解,2217a +∴-<-,169a ∴-<-,2135a y a y --=+, 方程的两边同时乘以15得556315a y a y -=-+,移项、合并同类项得,215y a =--,解得152a y +=-, 方程的解为负整数,a ∴是奇数,a ∴的值为13-、11-、9-,∴符合条件的所有整数a 的个数为3个,故选:C .二、填空题:本大题4个小题,每小题4分,共16分.13.解:根据科学记数法的定义,64570000 4.5710=⨯,故答案为:64.5710⨯.14.解:由题意得:0x y +=,y x ∴=-,把y x =-代入原方程组可得:386335x a x a -=+⎧⎨=-⎩①②, ①+②可得:390a +=,解得3a =-,故答案为:3-.15.解:由21x -<,得:1x >,由2(1)1x x -<+,得:3x <,则不等式组的解集为13x <<,∴原式31x x =-+-2=,故答案为:2.16.解:去年甲、乙、丙三种水果的种植面积之比为5:3:2,甲、乙、丙三种水果的平均亩产量之比为6:3:5. ∴设去年的甲的种植面积为5a ,则乙的种植面积为3a ,丙的种植面积为2a .设去年甲种水果的平均亩产量为6b ,则乙种水果的平均亩产量为3b ,丙种水果的平均亩产量为5b . ∴今年甲种水果的平均亩产量为6(150%)9b b +=,则乙种水果的平均亩产量为3(120%) 3.6b b +=,丙种水果的平均亩产量为5b .设今年甲、乙、丙三种水果的种植面积之比为::x y z ,∴今年甲种水果的总产量为9bx ,乙种水果的总产量为3.6by ,丙种水果的总产量为5bz , 依题意得,93 3.6bx by =⨯①,5 3.665by bz ⨯=⨯②,分别整理①、②得, 1.2x y =,0.6z y =,::6:5:3x y z ∴=,∴可设今年甲的种植面积为6c ,乙的种植面积为5c ,丙的种植面积为3c ,今年水果总产量为541815bc bbc bc ++,丙水果增加的总产量为5(541815)587bc bbc bc bc ++⨯=, 依题意得,52553b a bc b c ⋅+=⋅,整理得,a c =, ∴三种水果去年的种植总面积53210a a a a ++=,今年的种植总面积为6531414c c c c a ++==, 10:145:7a a =.故答案为:5:7.三、计算题:本大题共4个小题,共40分.解答时每小题必须给出必要的演算过程或推理步骤.17.解:(1)原式1021=--7=;(2)原式2020114()(1)(1)44=-⨯-⨯---- 1114=-+ 14=. 18.解:(1)3122123m m -+-=, 去分母,得3(31)62(22)m m --=+, 去括号,得93644m m --=+,移项,得94364m m -=++,合并同类项,得513m =,系数化为1,得135m =; (2)323123m n m n m n m n +-⎧+=⎪⎪⎨+-⎪-=-⎪⎩, 设2m n x +=,3m n y -=, 则原方程组化为31x y x y +=⎧⎨-=-⎩①②, ①+②,得22x =,解得1x =,把1x =代入①,得2y =, ∴12m n +=,23m n -=, 故26m n m n +=⎧⎨-=⎩, 解得42m n =⎧⎨=-⎩. 19.解:(1)去括号,得:73315x x --, 移项,得:73153x x --+,合并,得:412x -,系数化为1,得:3x -,将不等式解集表示在数轴上如下:(2)去分母,得:124(21)123(1)x x x --<--,去括号,得:12841233x x x -+<-+,移项,得:12831234x x x --<--,合并,得:5x <,将不等式解集表示在数轴上如下:;(3)314232x x x ->-⎧⎨-⎩①②, 解不等式①得:1x >-,解不等式②得:2x ,则不等式组的解集为12x -<,将不等式组的解集表示在数轴上如下:;(4)()()223843310.20.5x x x x ⎧->+⎪⎨+-+-⎪⎩①②, 解不等式①得:4x <-,解不等式②得:10x -,则不等式组的解集为10x -,将不等式组的解集表示在数轴上如下:.20.解:(1)原式2[2()]a b ab =+-2(22)a b ab =+-442a b ab =+-,2|2|(3)0a b -+-=,20a ∴-=,30b -=,2a ∴=,3b =,∴原式4243223812128=⨯+⨯-⨯⨯=+-=.(2)23212A nx x =--,21243B x mx =-+, 2231232(21)3(24)23A B nx x x mx ∴-=----+ 22342612nx x x mx =---+-2(36)(4)14n x m x =-+--,23A B -的值与x 的取值无关,360n ∴-=,40m -=,2n ∴=,4m =,2222(32)(24)m mn n m mn n ∴-+-+-22223224m mn n m mn n =-+--+2246m mn n =--+22444262=--⨯⨯+⨯163224=--+24=-.四、解答题:本大题共5小题,21题8分,22题8分,23题10分,24题10分,25题10分,共46分.解答应写出必要的文字说明、证明过程或演算步骤.21.解:(1)根据题中的新定义得:5(1)253(1)10313-=⨯-⨯-=+=⊗,则原式(2)132(2)31343943=-=⨯--⨯=--=-⊗;(2)已知等式利用题中的新定义化简得:2(32)3(1)2x x --+=,去括号得:64332x x ---=,移项得:63243x x -=++,合并得:39x =,系数化为1,得:3x =.22.解:(1)设该轮船在静水中的速度是x 千米/时,水流速度是y 千米/时,依题意,得:6()12010()120x yx y+=⎧⎨-=⎩,解得:164xy=⎧⎨=⎩.答:该轮船在静水中的速度是16千米/时,水流速度是4千米/时.(2)设甲、丙两地相距a千米,则乙、丙两地相距(120)a-千米,依题意,得:120 164164a a-=+-,解得:75a=.答:甲、丙两地相距75千米.23.解:(1)设甲种体育器材进价x元/件,乙种体育器材进价y元/件,依题意,得:36480 23280x yx y+=⎧⎨+=⎩,解得:8040xy=⎧⎨=⎩.答:甲种体育器材进价80元/件,乙种体育器材进价40元/件.(2)设购甲种体育器材a件,则乙种体育器材(100)a-件,依题意,得:8040(100)6300 8040(100)6430a aa a+-⎧⎨+-⎩,解得:13 576024a,a为整数,58a∴=或59或60,∴该商场共有3种进货方案,方案1:购进甲种体育器材58件,乙种体育器材42件;方案2:购进甲种体育器材59件,乙种体育器材41件;方案3:购进甲种体育器材60件,乙种体育器材40件.24.(1)解:由新定义可得:321N=,当495M=时,954N=,()954495459K M N M∴=-=-=.故答案为:321,459;(2)证明:设“万象数”M为abc,则N为bca,则10010M a b c=++,10010N b c a=++,a c b+=,∴其“格致数” ()1001010010909999(1011)9(11)K M N M b c a a b c b c a b c a c a =-=++---=+-=+-=-. ∴其“格致数” ()K M 都能被9整除;(3)解:()9(11)K M c a =-是72的倍数,1183c a c c a ∴-=+-是8的倍数,3c a ∴-是8的倍数,19a ,19b ,09c ,a ,b ,c 为整数,9326c a ∴--,a cb +=,19a c ∴+,38c a ∴-=-或30c a -=或38c a -=或316c a -=或324c a -=,8a ∴=,0c =或6a =,2c =或4a =,4c =或3a =,1c =或2a =,6c =或1a =,3c =, ()9(11)K M c a =-,()K M ∴的值为72-或144或360或72或576或270,()K M 是完全平方数,()K M ∴的值为144或576,M ∴的值为682或286.25.解:(1)A ,B 表示的数分别为2-,6,点C 为点A 、B 的中点,∴点C 表示的数为2622-+=, 故答案为:2;(2)F 未到达B ,即3t <时,F 表示的数是42(2)2t t +-=,E 表示的数是2t -+, 2(2)2EF t t t ∴=--+=+,6(2)8BE t t =--+=-,||3||EF BE =,23(8)t t ∴+=-,解答 5.5t =(不小于3,舍去),F 到达B 后沿着数轴的负方向运动,即3t >时,F 表示的数是62(3)122t t --=-,E 表示的数是2t -+,|(2)(122)||314|EF t t t ∴=-+--=-,6(2)8BE t t =--+=-,||3||EF BE =,|314|3(8)t t ∴-=-, 解得193t =,答:t的值是193;(3)存在(0)t t>,使两电子虫上的点N和点P刚好相距3个单位长度,①在N、P未相遇时,N表示的数是2t-+,P表示的数是42t-,根据题意得42(2)3t t---+=,解得1t=,1t∴=时,点N和点P刚好相距3个单位长度,②若242t t-+=-,则2t=,2t∴=时,点N和点P相遇,此时开始速度会减半,即MN的速度变为0.5个单位/秒,PQ的速度变为1个单位/秒,而电子虫MN和电子虫PQ的长度都是1个单位,∴经过1140.513+=+秒电子虫MN和电子虫PQ才完全离开(没有重叠部分),此时410233t=+=,P表示的数是44422133-⨯-⨯=-,N表示的数是422210.533-+⨯+⨯=,当101133t<时,P表示的数是410162()2333t t---=-+,N表示的数是2108()333t t+-=-,根据题意得:816(2)333t t---+=,解得113t=,113t∴=时,点N和点P刚好相距3个单位长度,此时P到达点(2)A-,N到达表示1的点,当PQ运动到点P与点A重合时,PQ保持速度不变,反向沿着数轴正方向运动,当点Q运动到与点M 重合时,两电子虫都停止运动,∴当PQ反向沿着数轴正方向运动时,不存在点N和点P相距3个单位长度,综上所述,t的值是1或113.。
重庆市西南大学附属中学2020-2021学年下学期期中考试七年级数学试题
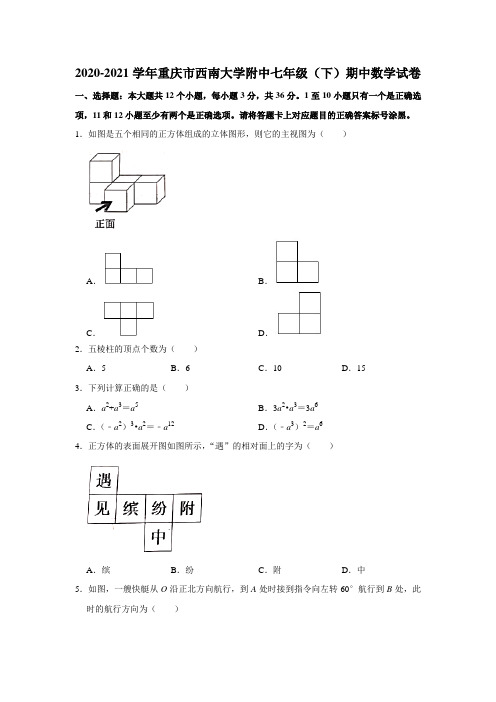
2020-2021学年重庆市西南大学附中七年级(下)期中数学试卷一、选择题:本大题共12个小题,每小题3分,共36分。
1至10小题只有一个是正确选项,11和12小题至少有两个是正确选项。
请将答题卡上对应题目的正确答案标号涂黑。
1.如图是五个相同的正方体组成的立体图形,则它的主视图为()A.B.C.D.2.五棱柱的顶点个数为()A.5B.6C.10D.153.下列计算正确的是()A.a2+a3=a5B.3a2•a3=3a6C.(﹣a2)3•a2=﹣a12D.(﹣a3)2=a64.正方体的表面展开图如图所示,“遇”的相对面上的字为()A.缤B.纷C.附D.中5.如图,一艘快艇从O沿正北方向航行,到A处时接到指令向左转60°航行到B处,此时的航行方向为()A.北偏东40°B.北偏东50°C.南偏西40°D.南偏西50°6.要使(2x2﹣x+3)(3x2+ax﹣2)的展开式中不含x2项,则a的值为()A.5B.﹣5C.13D.﹣137.如图,OD平分∠AOB,OC⊥OD,若∠BOE=15°,则∠AOD的度数为()A.18°B..20°C..22°D..30°8.点C为线段AB的三等分点,D为射线BA上一点,若AB=6,则CD的长为()A.4B.4或6C.12D.10或129.古希腊毕达哥拉斯学派的“三角形数”是一列点(或圆球)在等距的排列下可以形成正三角形的数,如1,3,6,15,…….我国宋元时期数学家朱世杰心在《四元玉鉴》中所记载的“垛积术”其中的“落一形”堆垛就是每层为“三角形数”的三角锥的锥垛(如图所示顶上一层1个球,下一层3个球,再下一层6个球),则该堆垛球的总个数为()A.55B.220C.285D.38510.若关于x的不等式组至多2个整数解,且关于y的方程8﹣2a=(a﹣1)(y﹣2),则符合条件的所有整数a的和为()A.﹣3B.1C.7D.911.下列说法错误的是()A.在同一平面内,若P A=PB,则P是线段AB的中点B.两直线平行,同旁内角相等C.过一点,有且只有一条直线与已知直线垂直D.两点之间,线段最短12.如图,△OAB为等腰直角三角形(∠A=∠B=45°,∠AOB=90°),△OCD为等边三角形(∠C=∠D=∠C0D=60°),△OCD绕点O从射线OC与射线OA重合的位置开始,逆时针旋转(0°<α<360°),下列说法正确的是()A.当α=15°时,DC∥ABB.当OC⊥AB时,α=45°C.当边OB与边OD在同一直线上时,直线DC与直线AB相交形成的锐角为15°D.整个旋转过程,共有10个位置使得△OAB与△OCD有一条边平行二、填空题:本大题共6个小题,每小题3分,共18分。
2022-2023学年重庆市北碚区西南大学附中七年级(下)入学数学试卷及答案解析

2022-2023学年重庆市北碚区西南大学附中七年级(下)入学数学试卷一、选择题:本大题12个小题,每小题4分,共48分.在每个小题的下面,都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的.请将答题卡上对应题目的正确答案标号涂黑.1.(4分)的倒数是()A.2B.C.D.﹣22.(4分)下列说法正确的是()A.π是有理数B.x2+2xy+y2是二次三项式C.单项式﹣x3y的系数是﹣1,次数是3D.近似数23.0是精确到个位3.(4分)下列变形正确的是()A.由a=b,得a+5=b﹣5B.由x=y,得C.如果2x=3y,那么2x+2=3y+2D.如果3a=6b﹣1,那么a=2b﹣1 4.(4分)关于x的方程3x+2m=4的解是x=2,则m的值是()A.1B.﹣1C.5D.﹣55.(4分)一个多项式与x2﹣3x+2的和是2x+5,则这个多项式为()A.x2﹣x﹣7B.﹣x2﹣x﹣3C.﹣x2+5x+3D.x2﹣5x﹣3 6.(4分)按照如图所示的计算程序,若x=2,则输出的结果是()A.16B.﹣16C.26D.﹣267.(4分)若m﹣x=3,n+y=7,则(m﹣n)﹣(x+y)=()A.﹣10B.﹣4C.4D.108.(4分)“今有人盗库绢,不知所失几何.但闻草中分绢,人得六匹,盈六匹;人得七匹,不足七匹,问人、绢各几何?(选自《孙子算经》)”.大意为:有盗贼窃去库存的绸缎,不知究竟窃去多少.有人在草丛中听到这帮盗贼分赃的情况.如果每个盗贼分得6匹,就多出6匹;如果每个盗贼分得7匹,就缺少7匹.盗贼有几人?失窃的绸缎有几匹?设盗贼有x人,失窃的绸缎有y匹,根据题意可列方程组为()A.B.C.D.9.(4分)下列图形都是由同样大小的小圆圈按一定规律所组成,其中第①个图形中一共有4个小圆圈,第②个图形中一共有10个小圆圈,第③个图形中一共有19个小圆圈,……按此规律排列,则第⑧个图形中小圆圈的个数为()A.96B.100C.109D.11410.(4分)一家商店将某种服装按成本价提高40%后标价,又以8折优惠卖出,结果每件服装仍可获利24元,则这种服装每件的成本是()A.100元B.180元C.200元D.205元11.(4分)关于x的方程的解为整数,则符合条件的正整数m的值之和为()A.19B.18C.8D.412.(4分)对x、y定义一种新运算T,规定:T(x,y)=axy+bx﹣4(其中a、b均为非零常数),这里等式右边是通常的四则运算.例如:T(0,1)=a×0×1+b×0﹣4=﹣4,若T(2,1)=2,T(﹣1,2)=﹣8,则下列结论正确的个数为()(1)a=1,b=2;(2)若T(m,n)=0(n≠﹣2),则;(3)若T(m,n)=0,则m、n有且仅有3组整数解;(4)若无论k取何值时,T(kx,y)的值均不变,则y=﹣2;(5)若T(kx,y)=T(ky,x)对任意有理数x、y都成立,则k=0.A.2个B.3个C.4个D.5个二、填空题:本大题6个小题,每小题4分,共24分.请将每小题的答案直接填在答题卡中对应的横线上.13.(4分)2022年12月,西南大学附中第二十二届缤纷节“和你一起”云端晚会在网络平台累计共有283000点击量,将283000用科学记数法表示为.14.(4分)方程2x m﹣1+3y2n﹣1=7是关于x,y的二元一次方程,则m﹣2n的值为.15.(4分)若x2=9,|y|=5,且满足x﹣y<0,则x+y的值为.16.(4分)关于x,y的方程组的解满足x﹣2y=﹣1,则a的值为.17.(4分)一艘轮船航行在嘉陵江两个码头之间,顺水航行用了3小时,逆水航行比顺水航行多用20分钟,已知轮船在静水中的速度是19千米/时,则水流速度为千米/时.18.(4分)新春佳节享团圆,吉祥如意在兔年!新年将至,某商场推出了甲、乙、丙三种新春大礼包,第一周销售甲、乙、丙三种新春礼包的数量之比为2:1:5,甲、乙、丙三种新春礼包的单价之比为3:4:1.第二周商场开展了春节促销活动,把乙礼包的单价在第一周的基础上降低25%,丙礼包的单价打八折,甲礼包的单价保持不变,第二周新春礼包的销售总额比第一周有所增加,其中甲礼包和乙礼包的销售额之比是8:5,丙礼包增加的销售额占第二周总销售额的,且三种礼包的数量之和比第一周增加,则甲礼包第一周与第二周的销售额之比为.三、计算题:本大题共2个小题,共28分.解答时每小题必须给出必要的演算过程或推理步骤,请将解答过程书写在答题卡中对应的位置上.19.(8分)计算(1)﹣3+12÷+3×(﹣4);(2)×[﹣8+(﹣4)2]÷(﹣4).20.(20分)解下列各方程(组)(1)4﹣2x=3x﹣6;(2);(3);(4).四、解答题:本大题共5小题,共50分。
2021重庆西南大学附中七年级上册思维训练试卷及答案分析下载

2021重庆西南大学附中七年级上册思维训练试卷及答案分析下载第Ⅰ卷选择题(共30分)一、选择题(本大题共10个小题,每小题3分,共30分.在每个小题给出的四个选项中,只有一项符合题目要求,请选出并在答题卡上将该项涂黑)1.在0, -1, -x, x^2, 3-x, 5x, 1中,是单项式的有()A.1个B.2个C.3个 D.4个2.据报道,我省西环高铁预计2015年底建成通车,计划总投资27100000000元,数据27100 000000用科学记数法表示为( )A.271×108B.2.71×109C.2.71×1010 D.2.71×10113.在数轴上与-3的距离等于4的点表示的数是().A.1B.-7C.1或-7D.无数个4.数据1600万用科学记数法表示为()A.1.6×108B.1.6×107C.16×102D.1.6×1065. 一种面粉的质量标识为“25±0.25千克”,则下列面粉中合格的是( )A.24. 70千克B.25.30千克C.24.80千克D.25.51千克6.延长线段AB到C,下列说法正确的是()A.点C在线段AB上B.点C在直线AB上C.点C不在直线AB上D.点C在直线BA的延长线上7.已知2是关于x的方程3x+a=0的解.那么a的值是( )A.-6 B.-3 C.-4 D.-58.如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点.若青蛙从数1这点开始跳,第1次跳到数3那个点,如此,则经2013次跳后它停的点所对应的数为……………………………………………………………………………………()A.1 B.2 C.3 D.59.据报道,5月28日参观2010上海世博会的人数达35.6万﹒用科学记数法表示数35.6万是( ) A .3.56×101 B .3.56×104 C .3.56×105 D .35.6×10410.若﹣3x 2m y 3与2x 4y n 是同类项,则|m ﹣n|的值是( ) A .0 B .1 C .7 D .﹣1第Ⅱ卷 非选择题(共90分)二、填空题(本大题共5个小题,每小题3分,共15分)11. -8的绝对值是 ,-8的倒数是 . 12、如果a 与1互为相反数,则︱a+2︱= .13.国家体育场“鸟巢”的建筑面积达258000m 2,用科学记数法表示为____________ m 2.14.现定义某种运算“*”,对任意两个有理数a ,b ,有a*b=a b ,则(﹣3)*2= .15.漳州市某校在开展庆“六•一”活动前夕,从该校2015~2016学年度七年级共400名学生中,随机抽取40名学生进行“你最喜欢的活动”问卷调查,调查结果如下表: 你最喜欢的活动 猜谜 唱歌 投篮 跳绳 其它人 数6 8 16 8 2 请你估计该校2015~2016学年度七年级学生中,最喜欢“投篮”这项活动的约有 人.三、解答题 (本大题共8个小题,共75分.解答应写出文字说明、证明过程或演算步骤)16.计算(1)(-8)+(+0.25)-(-9)+(-14) (2)-14÷(-32)+8×(-23)(3)(34-56+712)÷(-136) (4) -14-16×[2-(-3)2]17.计算:(满分6分,每小题3分)(1)2a -5b +3a +b (2)3(2a 2b -ab 2)-4(ab 2-3a 2b )18.在数轴上画出表示下列5个数的点,并用..“.<.”.把.它.们连接起来.....:-(-4),-||-3.5,+(-12) ,+(+2.5),11219.下表为国外几个城市与北京的时差(正数表示同一时刻比北京时间早的时数,负数表示同一时刻比北京时间晚的时数):城市东京巴黎伦敦纽约莫斯科悉尼时差(时)+1 ﹣7 ﹣8 ﹣13 ﹣5 +2(1)北京6月11日20时是巴黎的什么时间?(2)北京6月11日20时是悉尼的什么时间?(3)小莹的爸爸于6月11日20时从北京乘飞机,经过16小时的航行到达纽约,到达纽约时北京时间是多少?20.已知数轴上点A、B、C所表示的数分别是-3,+7,.(1)求线段AB的长;(2)若AC=4,点M、N分别是AB、AC的中点,求线段MN的长度.21.在边长为16cm的正方形纸片的四个角上各剪去一个同样大小的正方形,折成一个无盖的长方体(如图) .(1)如果剪去的小正方形的边长为x cm,请用x表示这个无盖长方体的容积;(2)当剪去的小正方形的边长x的值分别为3cm和3.5cm时,比较折成的无盖长方体的容积的大小.22. 仔细观察下面的日历,回答下列问题:-4 -3 -2 2⑴在日历中,用正方形框圈出四个日期(如图)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021西南大学附中数学七年级周末全真试题及答案分析下载
第Ⅰ卷 选择题(共30分)
一、选择题(本大题共10个小题,每小题3分,共30分.在每个小题给出的四个选项中,只有一项符合题目要求,请选出并在答题卡上将该项涂黑)
1.用一个平面去截一个几何体,得到的截面是四边形,这个几何体可能是( ) A.圆锥 B.圆柱 C.球体 D.以上都有可能
2.(2015·浙江丽水中考)在数-3,-2,0,3中,大小在-1和2之间的数是( ) A.-3 B.-2 C. 0 D. 3
3.如下图,下列图形属于柱体的有( )个
A.4
B.5
C.2
D.1
4.有理数a 、b 在数轴上表示的点如图所示,则a 、-a 、b 、-b 的大小关系是 ( )
A .-b >a >-a >b
B .-b <a <-a <b
C .b >-a >-b >a
D .b >a >-b >-a
5.如图,数轴上的点A 和点B 分别表示数a 与数b , 下列结论中正确的是……………………………(
)
A .a >b
B .|a |>|b |
C .-a <b
D . a +b <0
6.-2+5的值等于( )
A .3
B .2
C .-2
D .4
7.如图,数轴上每相邻两点之间相距1个单位长度,点A 对应的数为a ,B 对应的数为b ,且b
-2a =7,那么数轴上原点的位置在…………………………………………( ) A.点A B .点B C.点C D.点D
a b
8.a为有理数,定义运算符号“※”:当a>-2时,※a=-a;当a<-2时,※a=a;
当a=-2时,※a=0.根据这种运算,则※[4+※(2-5)]的值为--------------()
A.1 B.-1 C.7 D.-7
9.已知x=1是关于x的方程2-ax=x+a的解,则a的值是()
A.B.C.D.1
10、地球绕太阳每小时转动经过的路程约为110000千米,用科学记数法记为()
A.1.1×105米 B. 1.1×106米 C. 1.1×107米 D. 1.1×108米
第Ⅱ卷非选择题(共90分)
二、填空题(本大题共5个小题,每小题3分,共15分)
11、x^2=64,则x= ____________。
12.绝对值最小的数是______;倒数等于它本身的数是______.
13.数轴上点M表示有理数-3,将点M向右平移2个单位长度到达点N,点E到点N的距离为4,则点E表示的有理数为__________.
14.规定符号※的意义为:a※b=ab-a+b+1,那么(-2)※5=.
15.将连续的正整数按以下规律排列,则位于第6行、第六列的数是______.
三、解答题(本大题共8个小题,共75分.解答应写出文字说明、证明过程或演算步骤)
16.计算
(1)÷(﹣+)
(2)﹣14﹣(1﹣0.5)÷(﹣)×[﹣1﹣(﹣3)2]
(3)﹣[2m﹣3(m﹣n+1)].
17.计算:(满分6分,每小题3分)
(1)2a-5b+3a+b(2)3(2a2b-ab2)-4(ab2-3a2b)
18.如图,所有小正方形的边长都为1,A、B、C都在格点上.
(1)过点C画直线AB的平行线(不写画法,下同);
(2)过点A画直线BC的垂线,并注明垂足
..为G;
过点A画直线AB的垂线,交BC于点H.
(3)线段的长度是点A到直线BC的
距离;
(4)线段AG、AH的大小
..关系为
AG AH.(填写下列符号>,<,之一)
19.你能在3,4,5,6,7,8,9,10的前面添加“+”或“—”号,使它们的和为0吗?若能,请写出三个式子;若不能,请说明理由.
20.甲、乙两家体育用品商店出售同样的乒乓球拍和乒乓球,乒乓球拍每副定价20元,乒乓球每盒定价5元.现两家商店搞促销活动,甲店的优惠办法是:每买一副乒乓球拍赠一盒乒乓
球;乙店的优惠办法是:全部商品按定价的9折出售.某班需购买乒乓球拍4副,乒乓球若干盒(不少于4盒).
(1)当购买乒乓球的盒数为x 盒时,在甲店购买需付款 元; 在乙店购买需付款 元.(用含x 的代数式表示)
(2)当购买乒乓球盒数为10盒时,去哪家商店购买较合算?请说明理由.
21.)如图,半径为1个单位的圆片上有一点A 与数轴上的原点重合,AB 是圆片的直径. (注:结果保留 )
(1)把圆片沿数轴向右滚动半周,点B 到达数轴上点C 的位置,点C 表示的数是 数(填“无理”或“有理”),这个数是 ;
(2)把圆片沿数轴滚动2周,点A 到达数轴上点D 的位置,点D 表示的数是 ; (3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负 数,依次运动情况记录如下:+2,-1,+3,-4,-3
①第 次滚动后,A 点距离原点最近,第 次滚动后,A 点距离原点最远. ②当圆片结束运动时,A 点运动的路程共有 ,此时点A 所表示的数是 .
22、规定一种新运算:a*b=(a+1) -(b -1),例如(-6)* (-3)=(-6+1) -(-3-1)=-5+4=-1。
试计算:(0*1)+ (1*2)+ (2*3) +(3*4)+…+ (2012*2013)的值
B
A 0
-5
-4
-3
-2
-1
4
3
2
1
23.如图,已知A、B、C是数轴上三点,点C表示的数为8,BC=6,AB=14.
(1)写出数轴上点A表示的数________,B表示的数_________;
(2)动点P、Q分别从A、C同时出发,点P以每秒4个单位长度的速度沿数轴向右匀速运动,到达原点O立即掉头,按原来的速度运动,点Q以每秒1个单位长度的速度沿数轴向左匀速运动,P、Q两点到点A 停止运动,设运动时间为t(t>0)秒.
①当0<t≤3时,求数轴上点P、Q表示的数(用含t的式子表示);
②t为何值时,点O为线段PQ的中点.。
