工程数学第四章 概率统计模型
合集下载
数学建模第四章 概率统计模型.ppt
在这里，小说使用“快乐”“强壮”“勇敢” 这样三个形容词是否有深意？
答：①“快乐、强壮、勇敢”原指一个人乐 观，身体强健，能从容面对困难。这里写出这些 身体强壮的人平素貌似快乐和勇敢，实则在关键 时刻缺乏挑战困难、拯救族群的勇气，（内容角 度）②这与后来他们在遇到困难后的恐惧和伤心 形成鲜明对比。（结构和情节角度）
英雄！
作品主题是由作者和读者共同创造的！
小说主 读者的人
题的基 本把握 补充
多元化、 个性化的 主题解读 和感悟
没有伟大的人物出现的民族，是世 界上最可怜的生物之群；有了伟大的人 物，而不 知拥护，爱戴，崇仰的国家， 是没有希望的奴隶之邦。因鲁迅的一死， 使人自觉出了民 族的尚可以有为，也 因鲁迅之一死，使人家看出了中国还是 奴隶性很浓厚的半绝望的国 家。
《伊则吉尔老婆子》是高尔基早期浪漫主义代表 作。
“ 读伟大的小说，捧起前 与放下后你已判若两人”
为什么小说有如此大的作用？ 主要是因为伟大的小说有着博大 深邃的思想内涵、深刻的主题， 它能丰富我们的思想情感，提升 我们的人生境界。
小说主题哪里去找？
1.故事情节 2.人物分析 3.环境描写
一、情节：写了哪几个场景，试加以概 括。
1.族人陷于困境，彷徨失措，丹柯挺身而出 引导鼓舞族人。
2.族人途中遭险，围攻诋毁，丹柯不计得失， 拯救族人。
3.丹柯抓开胸膛，高举心脏，引领大家走出 困境，燃烧的心最后化为草原上蓝色火星。
故事在一开头就为丹柯的出现拉开了序幕：一群 生活在草原上，快乐、强壮、勇敢的人被另一凶残的 种族赶到不宜生存的林子深处去了，惟一的出路是穿 越森林到另一片草原上寻找生机。
提示：悲剧将人生中有价值的东西毁灭给 人看。（鲁迅）
答：①“快乐、强壮、勇敢”原指一个人乐 观，身体强健，能从容面对困难。这里写出这些 身体强壮的人平素貌似快乐和勇敢，实则在关键 时刻缺乏挑战困难、拯救族群的勇气，（内容角 度）②这与后来他们在遇到困难后的恐惧和伤心 形成鲜明对比。（结构和情节角度）
英雄！
作品主题是由作者和读者共同创造的！
小说主 读者的人
题的基 本把握 补充
多元化、 个性化的 主题解读 和感悟
没有伟大的人物出现的民族，是世 界上最可怜的生物之群；有了伟大的人 物，而不 知拥护，爱戴，崇仰的国家， 是没有希望的奴隶之邦。因鲁迅的一死， 使人自觉出了民 族的尚可以有为，也 因鲁迅之一死，使人家看出了中国还是 奴隶性很浓厚的半绝望的国 家。
《伊则吉尔老婆子》是高尔基早期浪漫主义代表 作。
“ 读伟大的小说，捧起前 与放下后你已判若两人”
为什么小说有如此大的作用？ 主要是因为伟大的小说有着博大 深邃的思想内涵、深刻的主题， 它能丰富我们的思想情感，提升 我们的人生境界。
小说主题哪里去找？
1.故事情节 2.人物分析 3.环境描写
一、情节：写了哪几个场景，试加以概 括。
1.族人陷于困境，彷徨失措，丹柯挺身而出 引导鼓舞族人。
2.族人途中遭险，围攻诋毁，丹柯不计得失， 拯救族人。
3.丹柯抓开胸膛，高举心脏，引领大家走出 困境，燃烧的心最后化为草原上蓝色火星。
故事在一开头就为丹柯的出现拉开了序幕：一群 生活在草原上，快乐、强壮、勇敢的人被另一凶残的 种族赶到不宜生存的林子深处去了，惟一的出路是穿 越森林到另一片草原上寻找生机。
提示：悲剧将人生中有价值的东西毁灭给 人看。（鲁迅）
概率与统计第4章 ——概率论课件PPT
定理 4.1： 设 =g(X), g(X) 是连续函数， 若 X的分布律为 pk P{ X xk }
且 pk g( xk ) 绝对收敛，则 k 1
E() g( xk ) pk k 1 14
定理4.1的重要性在于计算随机变量的函数 Y=g(X)的数学期望E[g(X)]时，不必求出随 机变量Y的分布律，可由随机变量X的分布 律直接计算E(Y)，应用起来比较方便。
随机变量的概率分布完整地描述了随机变量 的统计规律，但是在实际问题中求得随机变量 的概率分布并不容易，而且对某些问题来说， 只需要知道它的某些特征就够了，不一定非要 求出概率分布。
我们把刻画随机变量某些方面特征的数值 称为随机变量的数字特征。本章主要有： 数学期望，方差，协方差，相关系数和矩。
2
4.1 数学期望
0
1 20
1
2 20
9 2 10 20
1 20
10 i0
xi
fi
以频率为权数的加权平均
3
引例 2：某班有 N 个人，其中有 ni 个人为 ai
k
分， i 1,2,k ， ni N ， 求平均成绩。
i 1
解： 平均成绩为:
1 N
k
ai ni
i 1
k
ai
i 1
ni N
若用 X 表示成绩，则
设连续型随机变量X的概率密度为f(x)，
若积分 xf (x)dx 绝对收敛，则称积分
xf ( x)dx 的值为X的数学期望。
记为E(X) = xf ( x)dx
数学期望也称为均值。
19
例4.4 设随机变量X 的密度函数为
f
x
x
2
e
x2 2 2
且 pk g( xk ) 绝对收敛，则 k 1
E() g( xk ) pk k 1 14
定理4.1的重要性在于计算随机变量的函数 Y=g(X)的数学期望E[g(X)]时，不必求出随 机变量Y的分布律，可由随机变量X的分布 律直接计算E(Y)，应用起来比较方便。
随机变量的概率分布完整地描述了随机变量 的统计规律，但是在实际问题中求得随机变量 的概率分布并不容易，而且对某些问题来说， 只需要知道它的某些特征就够了，不一定非要 求出概率分布。
我们把刻画随机变量某些方面特征的数值 称为随机变量的数字特征。本章主要有： 数学期望，方差，协方差，相关系数和矩。
2
4.1 数学期望
0
1 20
1
2 20
9 2 10 20
1 20
10 i0
xi
fi
以频率为权数的加权平均
3
引例 2：某班有 N 个人，其中有 ni 个人为 ai
k
分， i 1,2,k ， ni N ， 求平均成绩。
i 1
解： 平均成绩为:
1 N
k
ai ni
i 1
k
ai
i 1
ni N
若用 X 表示成绩，则
设连续型随机变量X的概率密度为f(x)，
若积分 xf (x)dx 绝对收敛，则称积分
xf ( x)dx 的值为X的数学期望。
记为E(X) = xf ( x)dx
数学期望也称为均值。
19
例4.4 设随机变量X 的密度函数为
f
x
x
2
e
x2 2 2
大学概率统计教程第四章
例4.1.4.一 工 厂 生 产 的 某 种 产 寿 品命 （ 以 年 1 计算） X ~ e( ), 工 厂 规 定 ， 产 品 售 出 一 后年 5 内 若 损 坏 则 可 以 更 换若 ，售 出 一 件 产 品 赢 利 200元 ， 更 换 一 个 产 品 亏 300 损 元，求工厂售 一 件 产 品 赢 利 的 数 学望 期。
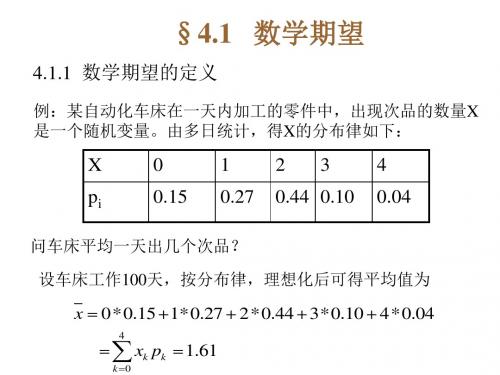
§4.1 数学期望
4.1.1 数学期望的定义
例：某自动化车床在一天内加工的零件中，出现次品的数量X 是一个随机变量。由多日统计，得X的分布律如下：
X pi
0 0.15
1 0.27
2
3
4 0.04
0.44 0.10
问车床平均一天出几个次品？ 设车床工作100天，按分布律，理想化后可得平均值为
x 0*0.15 1*0.27 2*0.44 3*0.10 4*0.04 xk pk 1.61
这表明积分 xf (x )dx 不绝对收敛，因而 EX 不存在．
离 散 型 随 机 变 量 无 数期 学望 的 例 子 ：
k 2 随机变量 X取 值x k ( 1)k , k 1,2, 对 应 的 k 1 概 率p k P( X x k ) k 2
1/ 2 由pk 0, pk 1, 因 此 它是 概 率 分 布 1 1/ 2 k 1
求随机变量Y=X2的数学期望 解: Y Pk 1
2 3
0
1 3
2 1 2 E (Y ) 1 0 3 3 3
定理4.1.1 P(108) 设X为随机变量，Y=g(X)是X的函数 (1)若离散型随机变量X～P{X=xk}=pk, k=1,2,…, 如果级数 绝对收敛，则
概率论与数理统计第四章
上述定理还可以推广到两个或两个以上随 机变量的函数的情况。
02
该公式的重要性在于: 当我们求E[g(X)]时, 不必知道g(X)的分布，而只需知道X的分布就可以了. 这给求随机变量函数的期望带来很大方便.
01
例6
例 7
解：
设(X,Y)在区域A上服从均匀分布，其中A为x轴，y轴和直线x+y+1=0所围成的区域。 求EX，E(-3X+2Y)，EXY。
例5
若将这两个电子装置串联连接组成整机,求整机
寿命(以小时计) N 的数学期望.
的分布函数为
三、随机变量函数的数学期望
1. 问题的提出：
设已知随机变量X的分布，我们需要计算的不是X的期望，而是X的某个函数的期望，比如说g(X)的期望. 那么应该如何计算呢？
一种方法是，因为g(X)也是随机变量，故应有概率分布，它的分布可以由已知的X的分布求出来. 一旦我们知道了g(X)的分布，就可以按照期望的定义把E[g(X)]计算出来.
若设
i=1,2，…，n
则 是n次试验中“成功” 的次数
解
X~B(n,p),
“成功” 次数 .
则X表示n重努里试验中的
于是
i=1,2，…，n
由于X1,X2,…, Xn 相互独立
= np(1- p)
E(Xi)= p,
D(Xi)=
p(1- p) ,
例7
解
1
展开
2
证：D(X)=E[X-E(X)]2
3
=E{X2-2XE(X)+[E(X)]2}
4
=E(X2)-2[E(X)]2+[E(X)]2
5
=E(X2)-[E(X)]2
第二版 工程数学-概率统计简明教程-第四章随机变量及其分布
P( X
1)
27 64
27 64
27 32
.
30
例7 已知一批螺丝钉的次品率为0.01，且每个螺丝 钉是相互独立的，现将这批螺丝钉没10个宝成一包 出售，并保证若每包发现多于一个次品则课退款。 问卖出的某包螺丝钉被退回的概率多大？
解 设X表示每包中的次品数，则X～B(10,0.01)
退回 ↔ 次品多于一个 ↔ X＞1
取球结果为:红或者白，是定性的描述。可这样量化： 用X表示抽得的结果， 则X只有两种结果， 每一种结果分别对应一个数，如 X=1表示取到红球, X=0表示取到白球
特点：试验结果数量化了，试验结果与数建立了
一个对应关系
随机变量的定义
随机变量
设随机试验的样本空间为Ω ，如果对于每一个 样本点w∈Ω ，均有唯一的实数X(w)与之对应， 称X(w)为样本空间Ω 上的随机变量。
则X服从0-1分布，其分布律为:
X
0
1
P
7
3
10
10
二项分布
在n重伯努利试验中,若以X表示事件A发生的次数, 则X可能的取值为0,1,2,3,…,n.
随机变量X的分布律为
P X k Cnk pk (1 p)nk
k 0,1, 2..., n; 其中0< p <1, 则称X服从参数为 n, p 的二 项分布(也称Bernoulli 分布）,记为
k 0
15 15 15 15 15
即 10 5c 1 15
c 1
例5 袋中有5个球，分别编号1,2,3,4,5.从中同时取出3个
球，以X表示取出的球的最小号码，求X的分布律与分布函数. 解 由于X表示取出的3个球中的最小号码， 因此X的所有可
概率统计模型决策模型教学课件
THANKS FOR WATCHING
感谢您的观看
过程能力分析
通过概率统计模型分析生产过程中的能力指数，评估生产 过程的稳定性和可靠性，为生产计划的制定提供依据。
故障模式分析
使用概率统计模型对生产过程中出现的故障模式进行分析 ，找出故障原因和解决方法，提高生产效率和产品质量。
在医疗诊断中的应用
疾病预测
基于大数据和概率统计模型，可以对患者的疾病风险进行预测和分 析，为医生提供更加准确的诊断依据。
不确定决策模型
不确定决策模型的概述
不确定决策模型是指在决策过程中，各种因素的发生概率是未知的，决策者需要 根据历史数据和经验进行推断。
不确定决策模型的应用场景
不确定ห้องสมุดไป่ตู้策模型广泛应用于风险管理、预测等领域，如天气预报、市场预测等。
基于偏好关系的决策模型
基于偏好关系的决策模型的概述
基于偏好关系的决策模型是指在决策过程中，决策者根据自身偏好进行决策，这些偏好关系可以用数学模型表示 。
02
概率统计模型在科学、工程、医 学等领域有广泛的应用，为决策 提供科学依据。
概率统计模型的基本概念
01
02
03
04
随机试验
指可能出现不同结果的事件， 且每个结果的出现具有不确定
性。
随机事件
指随机试验中可能出现的观察 结果，如扔硬币的正面或反面
。
概率
指随机事件发生的可能性，用 介于0和1之间的实数表示。
平均数
所有变量值的和除以变量值的 个数，反映变量的集中趋势。
标准差
衡量变量值离散程度的指标， 反映变量的波动大小。
推论性统计模型
参数估计
根据样本数据推断总体参数的方法， 如点估计和区间估计。
工程数学第四章 随机事件及其概率
样本空间，记为 .如例 2 中的 {A, B,C}就是样本空间.于是任意一个事件
都可看成样本空间的一个子集.特别地，必然事件就是样本空间，不可能事件就是
空集 .
上页
下页
返回
结束
定义 2 事件发生是指该事件中的一个或多个基本事件发生，即如果某事件中 的一个或多个基本事件发生，则认为该事件发生．
到一个白球和一个红球”， D 表示“取到白球”，则 A, B,C, D 都为随机事件.
上页
下页
返回
结束
若令 表示“取到的两球不同色”， 表示“取到的两球同色”，这两个事件具 有确定性， 一定发生， 一定不发生．
实际上， 和 不是随机事件，但为了研究方便，我们仍将它们称之为特
殊的随机事件，即必然事件与不可能事件.所谓必然事件是指在试验中必然发生的
随机试验的每一个可能结果称为随机事件,简称事件.一般用 A, B,C,L 表示.
例 1 掷一枚硬币， A {正面朝上}， B {反面朝上}，显然，对“掷一枚硬 币”的观察为随机试验， A ,B 为随机事件.
例 2 从一个装有红、白、黄球各一个的盒中任取两个球，若令 A 表示结果 “取到一个黄球和一个白球”，B 表示“取到一个黄球和一个红球”，C 表示“取
(4)若 B {A1, A2 ,L , An} ，则 A1, A2 ,L An 至少有一个发生的充要条件是 B 发
生.
上页
下页
返回
结束
三、事件的关系与运算
我们已经知道任一事件都是样本空间的一个子集，因此事件之间的关系与运 算与集合间的关系与运算相似.
1.包含与相等
定义 3 设 A 与 B 是试验 E 的两个事件，若 A 发生必然有 B 发生，则称 A 包 含于 B ，记为 A B ．此时 A 的每一个样本点都包含在 B 中.若还有 B A ，则
都可看成样本空间的一个子集.特别地，必然事件就是样本空间，不可能事件就是
空集 .
上页
下页
返回
结束
定义 2 事件发生是指该事件中的一个或多个基本事件发生，即如果某事件中 的一个或多个基本事件发生，则认为该事件发生．
到一个白球和一个红球”， D 表示“取到白球”，则 A, B,C, D 都为随机事件.
上页
下页
返回
结束
若令 表示“取到的两球不同色”， 表示“取到的两球同色”，这两个事件具 有确定性， 一定发生， 一定不发生．
实际上， 和 不是随机事件，但为了研究方便，我们仍将它们称之为特
殊的随机事件，即必然事件与不可能事件.所谓必然事件是指在试验中必然发生的
随机试验的每一个可能结果称为随机事件,简称事件.一般用 A, B,C,L 表示.
例 1 掷一枚硬币， A {正面朝上}， B {反面朝上}，显然，对“掷一枚硬 币”的观察为随机试验， A ,B 为随机事件.
例 2 从一个装有红、白、黄球各一个的盒中任取两个球，若令 A 表示结果 “取到一个黄球和一个白球”，B 表示“取到一个黄球和一个红球”，C 表示“取
(4)若 B {A1, A2 ,L , An} ，则 A1, A2 ,L An 至少有一个发生的充要条件是 B 发
生.
上页
下页
返回
结束
三、事件的关系与运算
我们已经知道任一事件都是样本空间的一个子集，因此事件之间的关系与运 算与集合间的关系与运算相似.
1.包含与相等
定义 3 设 A 与 B 是试验 E 的两个事件，若 A 发生必然有 B 发生，则称 A 包 含于 B ，记为 A B ．此时 A 的每一个样本点都包含在 B 中.若还有 B A ，则
《概率统计模型》课件
回归分析在市场预测中的应用还包括价 格分析、消费者行为分析等方面。
在市场营销领域，回归分析可以用于预 测产品需求、销售量、市场份额等方面 。
通过回归分析，企业可以了解市场趋势 ，制定有针对性的营销策略，提高市场 竞争力。
THANKS FOR WATCHING
感谢您的观看
03
统计方法在医学领域的应用还包括疾病预测、诊断和治疗效果评估等 方面。
04
统计方法在医学领域的应用有助于提高医学研究的准确性和可靠性。
回归分析在市场预测中的应用
回归分析是一种常用的统计分析方法， 用于探索变量之间的关系，并对未来趋 势进行预测。
回归分析在市场预测中的应用有助于企 业做出科学合理的决策，提高市场占有 率和盈利能力。
详细描述
时间序列分析涉及对按时间顺序排列的数据 进行统计处理，以揭示其内在的规律和特性 。这种方法广泛应用于金融、气象、医学等 领域，用于预测未来趋势和进行决策分析。
06 案例研究
概率论在金融中的应用
概率论在金融领域中有着 广泛的应用，如风险评估 、投资组合优化、期权定 价等。
概率论在金融领域的应用 还包括信用评级、保险精 算、风险管理等方面。
描述随机变量取值的平均水平和分散程度。
常见的随机变量分布
二项分布、泊松分布、正态分布等。
02 统计推断
参数估计
参数估计的概念
参数估计是用样本信息来估计总体参 数的过程，是统计推断的重要内容之 一。
点估计
点估计是指用一个单一的数值来估计 总体参数，常用的方法有矩估计和极 大似然估计。
区间估计
区间估计是指用一个区间范围来估计 总体参数，常用的方法有置信区间和 预测区间。
假设检验的步骤
在市场营销领域，回归分析可以用于预 测产品需求、销售量、市场份额等方面 。
通过回归分析，企业可以了解市场趋势 ，制定有针对性的营销策略，提高市场 竞争力。
THANKS FOR WATCHING
感谢您的观看
03
统计方法在医学领域的应用还包括疾病预测、诊断和治疗效果评估等 方面。
04
统计方法在医学领域的应用有助于提高医学研究的准确性和可靠性。
回归分析在市场预测中的应用
回归分析是一种常用的统计分析方法， 用于探索变量之间的关系，并对未来趋 势进行预测。
回归分析在市场预测中的应用有助于企 业做出科学合理的决策，提高市场占有 率和盈利能力。
详细描述
时间序列分析涉及对按时间顺序排列的数据 进行统计处理，以揭示其内在的规律和特性 。这种方法广泛应用于金融、气象、医学等 领域，用于预测未来趋势和进行决策分析。
06 案例研究
概率论在金融中的应用
概率论在金融领域中有着 广泛的应用，如风险评估 、投资组合优化、期权定 价等。
概率论在金融领域的应用 还包括信用评级、保险精 算、风险管理等方面。
描述随机变量取值的平均水平和分散程度。
常见的随机变量分布
二项分布、泊松分布、正态分布等。
02 统计推断
参数估计
参数估计的概念
参数估计是用样本信息来估计总体参 数的过程，是统计推断的重要内容之 一。
点估计
点估计是指用一个单一的数值来估计 总体参数，常用的方法有矩估计和极 大似然估计。
区间估计
区间估计是指用一个区间范围来估计 总体参数，常用的方法有置信区间和 预测区间。
假设检验的步骤
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
0 n
n
n
d 2G 又 (c a) p(n) 0，所以确实为极大值点。 2 dn
结果解释
n
p ( r ) dr a b p ( r ) dr b c
0 n
n
p(r )dr P , p(r )dr P
0 1 n
2
P a b 1 取 n使 P2 bc
dG ? (a b)np(n) n (b c) p(r )dr 0 dn (a b)np(n) (a b) p(r )dr
n
n
(b c) p(r )dr (a b) p(r )dr
0
dG 0 dn
p ( r ) dr a b p ( r ) dr b c
z
z
0 t (t )dt t (t )dt 0.4
1 pq z t (t )dt 0 第 3项 2 m g ( z ) g b n=300, p=0.05, b/g=0.2, 计算得 m=319
思考：还可以 对第3项做更精 细的估计，从 而得到更高精 度结果。
模型求解
方法三：Monte Carlo模拟（不求数学期望，从最原始 的随机数开始模拟，忽略r）
clear;n=300;p=0.05;g=1000;b=200; for i=0:50; m=n+i; K=binornd(m,p,1,10000); ES(i+1)=mean(g*(m-K).*(m-K<=n)+(n*g-b*(m-K-n)).*(mK>n)); end [maxES,id]=max(ES) m=n+id %计算结果m=321
模型求解
ES0=ES-1; while ES>ES0 m=m+1;ES0=ES; for k=0:(m-n-1) P(k+1)=nchoosek(m,k)*p^k*q^(m-k); end ES=q*m*g-(g+b)*(m-n-(0:(m-n-1)))*P'; end m,ES0 %计算结果m=321(但计算有溢出警告)
来源变量也可以考虑多个，但是如果他们不独 立，是很难处理的。
算例
若每份报纸的购进价为0.75元，售出价为 1元，退回 价为0.6元，需求量服从均值500份，均方差50份的 正 态分布，报童每天应购进多少份报纸才能使平均收入 最高？
P1 a b 1 0.75 5 5 3 P2 b c 0.75 0.6 3 P1 ，P 2 8 8 P1 P2 1
4.2 机票超售(overbook )策略
2013-10-21 《北京晚报》：三天前，徐先生网上 为朋友订购了大新华航空公司于昨天下午3点55 分从北京飞往哈尔滨的机票。昨天下午，朋友两 点多就来到了机场，却在换登机牌时被工作人员 告知，登机牌已经换完，飞机上“满座”，已无 空位置。“为什么我买了票却不让我上去？”由 于着急赶时间，徐先生的朋友急切地与工作人员 交涉，结果被告知，“很多航班都会这样售票， 防止有人买票后临时有事退票或改签，导致飞机 坐不满人，浪费资源。”
z
qg 1 pq z q ( z ) t (t )dt 0 g b 2 m mq n 这里z , ( z )和 (t )为N (0,1)分布和密度 mpq
模型求解
由于(-t)= (t) ，所以 可以证明zR
z 0
z 0时, t (t )dt 0
a-b ~售出一份赚的钱
b-c ~退回一份赔的钱
p
P1 0
P2 n r
通常，a-b>b-c, R接近正态分布，n>E(R)
为什么用随机分布模型?
需求R是随机的 由于收入是需求的非线性函数，日平均收入 ES(n)不是简单地由日平均需求E(R)决定
G(n) E (S (n)) [(a b)r (b c)(n r )] f (r )
第四章
概率统计模型
4.1 报童的诀窍（随机分布）
4.2 机票超售策略（随机模拟）
4.3 牙膏的销售量（多元线性回归）
4.4 教学评估（逐步回归）
4.5 Logistic回归
4.6 判别与聚类
确定性因素和随机性因素
确定性是理想化的，随机性是现实中必然存在的 1. 随机因素可以忽略 2. 随机因素影响可以简单 地以平均值的作用出现 3. 随机因素影响必须考虑 确定性模型
F '( y ) f (b( y ), y )b( y ) f (a ( y ), y )a( y )
b( y ) a( y)
f y ( x, y )dx
为简化计算
求解
n
将r视为连续变量
f (r ) p(r ) (概率密度）
G(n) 0 [( a b)r (b c)( n r )] p(r )dr n (a b)np(r )dr
应根据需求确定购进量 每天需求量是随机的
存在一个合 适的购进量
每天收入是随机的
优化问题的目标函数应是长期的日平均收入 等于每天收入的数学期望
准 备 建 模
随机因素的主要来源——每天需求量 为 R ，概率 P(R=r)=f(r), r=0,1,2… • 设每天购进 n 份(不随机)，日平均收入为 G(n) • 已知售出一份赚 a-b；退回一份赔 b-c, 日收入为 (a b) R (b c)(n R), R n S (n) (a b)n Rn
随机性模型
4.1
报童的诀窍
假设《新民晚报》 平均每天零售 500份，报亭每 天应该预定多 少份？
4.1 报童的诀窍
报童售报： a (零售价) > b(购进价) > c(退回价)
问 售出一份赚 a-b；退回一份赔 b-c 题
购进太多卖不完退回赔钱
每天购进多少份可使收入最大？
分 购进太少不够销售赚钱少 析
5 R 500 x 500 5 P P ( R x ) ＝ P ( ) ， 1 8 50 50 8 查标准正态分布表： 1 e 2 x 500 0.32 50 516份
0.32 t2 2
5 x 500 dt ， 0.32 8 50
r 0 n r n 1
(a b)nf (r )
R的随机分布对最优决策有影响 若收入是需求的线性函数，日平均收入可用日 平均需求来表示，就不必用随机模型。
怎样运用随机分布模型？
关键：搞清楚随机性的主要来源是什么？ 这个主要来源设为一个随机变量(如报童模型中 每天的需求量R)
这个随机变量的分布是容易得到的； 其他随机变量(如收入)可以写成它的函数。
mnx ( x mp ) 2 exp( )dx 2mpq 2 mpq mq n t mpq 2 t2 exp( )dt 2
mq n mpq
模型求解
令dE(S)/dm=0得
1 pq z qg ( g b)q (t )dt ( g b) t (t )dt 0 2 m
考虑不同客源的模型
第一类顾客(no show概率大)：后付费，高票价。 第二类顾客：先付费，低票价。设打折，打折 票t张，第二类顾客no show概率=0. no show K~B(m-t, p)
k 0
qmg r ( g b)
(m n k ) p
k
(q=1-p).
求m使E(S(m))最大
模型求解
方法一：数值模拟(实际计算适用)
对m=n, n+1, n+2, …., 计算E(S(m)), 求得最优m 注意到最优解与r无关 Matlab程序
n=300;p=0.05;q=1-p;g=1000;b=200; m=n+1; for k=0:(m-n-1) P(k+1)=nchoosek(m,k)*p^k*q^(m-k); end ES=q*m*g-(g+b)*(m-n-(0:(Байду номын сангаас-n-1)))*P'
基本模型
利润
订票数m, 容量n, no-show人数 K~B(m,p)
到来(on-show)人数m-K
(m K ) g r mK n S K n)b m K n ng r (m m m 期望利润 p 1, kp mp
E ( S (m))
n r 0 r n 1
G(n) E (S (n)) [(a b)r (b c)(n r )] f (r )
(a b)nf (r )
求 n 使 G(n) 最大
n=E(R) ？？？
变限积分求导公式
F ( y)
b( y ) a( y)
f ( x, y )dx
问题的推广
现实情况：每天的需求并不完全是随机的，如 周末或重大事件期间销量会上升，天气不好时 销量会下降。 解决途径一：利用历史数据； 解决途径二：利用时间序列分析方法； 解决途径三：利用Monte Carlo数值模拟。
Monte Carlo模拟
若明天需求量依赖于气温T, R=500+-|T-20|, N(0,50^2), U(5,15), 与独立 Matlab程序(明天T=5)求得n0=371(近似). a=1;b=0.75;c=0.6; T=5; N=1000; e=normrnd(0,50,1,N); d=unifrnd(5,15,1,N); R=500+e-d*abs(T-20); S0=0;for n=100:800, S=mean(((a-b)*R-(b-c)*(n-R)).*(R<=n)+(a-b)*n*(R>n)); if S>S0, S0=S;n0=n;end; end;n0,S0
n
n
d 2G 又 (c a) p(n) 0，所以确实为极大值点。 2 dn
结果解释
n
p ( r ) dr a b p ( r ) dr b c
0 n
n
p(r )dr P , p(r )dr P
0 1 n
2
P a b 1 取 n使 P2 bc
dG ? (a b)np(n) n (b c) p(r )dr 0 dn (a b)np(n) (a b) p(r )dr
n
n
(b c) p(r )dr (a b) p(r )dr
0
dG 0 dn
p ( r ) dr a b p ( r ) dr b c
z
z
0 t (t )dt t (t )dt 0.4
1 pq z t (t )dt 0 第 3项 2 m g ( z ) g b n=300, p=0.05, b/g=0.2, 计算得 m=319
思考：还可以 对第3项做更精 细的估计，从 而得到更高精 度结果。
模型求解
方法三：Monte Carlo模拟（不求数学期望，从最原始 的随机数开始模拟，忽略r）
clear;n=300;p=0.05;g=1000;b=200; for i=0:50; m=n+i; K=binornd(m,p,1,10000); ES(i+1)=mean(g*(m-K).*(m-K<=n)+(n*g-b*(m-K-n)).*(mK>n)); end [maxES,id]=max(ES) m=n+id %计算结果m=321
模型求解
ES0=ES-1; while ES>ES0 m=m+1;ES0=ES; for k=0:(m-n-1) P(k+1)=nchoosek(m,k)*p^k*q^(m-k); end ES=q*m*g-(g+b)*(m-n-(0:(m-n-1)))*P'; end m,ES0 %计算结果m=321(但计算有溢出警告)
来源变量也可以考虑多个，但是如果他们不独 立，是很难处理的。
算例
若每份报纸的购进价为0.75元，售出价为 1元，退回 价为0.6元，需求量服从均值500份，均方差50份的 正 态分布，报童每天应购进多少份报纸才能使平均收入 最高？
P1 a b 1 0.75 5 5 3 P2 b c 0.75 0.6 3 P1 ，P 2 8 8 P1 P2 1
4.2 机票超售(overbook )策略
2013-10-21 《北京晚报》：三天前，徐先生网上 为朋友订购了大新华航空公司于昨天下午3点55 分从北京飞往哈尔滨的机票。昨天下午，朋友两 点多就来到了机场，却在换登机牌时被工作人员 告知，登机牌已经换完，飞机上“满座”，已无 空位置。“为什么我买了票却不让我上去？”由 于着急赶时间，徐先生的朋友急切地与工作人员 交涉，结果被告知，“很多航班都会这样售票， 防止有人买票后临时有事退票或改签，导致飞机 坐不满人，浪费资源。”
z
qg 1 pq z q ( z ) t (t )dt 0 g b 2 m mq n 这里z , ( z )和 (t )为N (0,1)分布和密度 mpq
模型求解
由于(-t)= (t) ，所以 可以证明zR
z 0
z 0时, t (t )dt 0
a-b ~售出一份赚的钱
b-c ~退回一份赔的钱
p
P1 0
P2 n r
通常，a-b>b-c, R接近正态分布，n>E(R)
为什么用随机分布模型?
需求R是随机的 由于收入是需求的非线性函数，日平均收入 ES(n)不是简单地由日平均需求E(R)决定
G(n) E (S (n)) [(a b)r (b c)(n r )] f (r )
第四章
概率统计模型
4.1 报童的诀窍（随机分布）
4.2 机票超售策略（随机模拟）
4.3 牙膏的销售量（多元线性回归）
4.4 教学评估（逐步回归）
4.5 Logistic回归
4.6 判别与聚类
确定性因素和随机性因素
确定性是理想化的，随机性是现实中必然存在的 1. 随机因素可以忽略 2. 随机因素影响可以简单 地以平均值的作用出现 3. 随机因素影响必须考虑 确定性模型
F '( y ) f (b( y ), y )b( y ) f (a ( y ), y )a( y )
b( y ) a( y)
f y ( x, y )dx
为简化计算
求解
n
将r视为连续变量
f (r ) p(r ) (概率密度）
G(n) 0 [( a b)r (b c)( n r )] p(r )dr n (a b)np(r )dr
应根据需求确定购进量 每天需求量是随机的
存在一个合 适的购进量
每天收入是随机的
优化问题的目标函数应是长期的日平均收入 等于每天收入的数学期望
准 备 建 模
随机因素的主要来源——每天需求量 为 R ，概率 P(R=r)=f(r), r=0,1,2… • 设每天购进 n 份(不随机)，日平均收入为 G(n) • 已知售出一份赚 a-b；退回一份赔 b-c, 日收入为 (a b) R (b c)(n R), R n S (n) (a b)n Rn
随机性模型
4.1
报童的诀窍
假设《新民晚报》 平均每天零售 500份，报亭每 天应该预定多 少份？
4.1 报童的诀窍
报童售报： a (零售价) > b(购进价) > c(退回价)
问 售出一份赚 a-b；退回一份赔 b-c 题
购进太多卖不完退回赔钱
每天购进多少份可使收入最大？
分 购进太少不够销售赚钱少 析
5 R 500 x 500 5 P P ( R x ) ＝ P ( ) ， 1 8 50 50 8 查标准正态分布表： 1 e 2 x 500 0.32 50 516份
0.32 t2 2
5 x 500 dt ， 0.32 8 50
r 0 n r n 1
(a b)nf (r )
R的随机分布对最优决策有影响 若收入是需求的线性函数，日平均收入可用日 平均需求来表示，就不必用随机模型。
怎样运用随机分布模型？
关键：搞清楚随机性的主要来源是什么？ 这个主要来源设为一个随机变量(如报童模型中 每天的需求量R)
这个随机变量的分布是容易得到的； 其他随机变量(如收入)可以写成它的函数。
mnx ( x mp ) 2 exp( )dx 2mpq 2 mpq mq n t mpq 2 t2 exp( )dt 2
mq n mpq
模型求解
令dE(S)/dm=0得
1 pq z qg ( g b)q (t )dt ( g b) t (t )dt 0 2 m
考虑不同客源的模型
第一类顾客(no show概率大)：后付费，高票价。 第二类顾客：先付费，低票价。设打折，打折 票t张，第二类顾客no show概率=0. no show K~B(m-t, p)
k 0
qmg r ( g b)
(m n k ) p
k
(q=1-p).
求m使E(S(m))最大
模型求解
方法一：数值模拟(实际计算适用)
对m=n, n+1, n+2, …., 计算E(S(m)), 求得最优m 注意到最优解与r无关 Matlab程序
n=300;p=0.05;q=1-p;g=1000;b=200; m=n+1; for k=0:(m-n-1) P(k+1)=nchoosek(m,k)*p^k*q^(m-k); end ES=q*m*g-(g+b)*(m-n-(0:(Байду номын сангаас-n-1)))*P'
基本模型
利润
订票数m, 容量n, no-show人数 K~B(m,p)
到来(on-show)人数m-K
(m K ) g r mK n S K n)b m K n ng r (m m m 期望利润 p 1, kp mp
E ( S (m))
n r 0 r n 1
G(n) E (S (n)) [(a b)r (b c)(n r )] f (r )
(a b)nf (r )
求 n 使 G(n) 最大
n=E(R) ？？？
变限积分求导公式
F ( y)
b( y ) a( y)
f ( x, y )dx
问题的推广
现实情况：每天的需求并不完全是随机的，如 周末或重大事件期间销量会上升，天气不好时 销量会下降。 解决途径一：利用历史数据； 解决途径二：利用时间序列分析方法； 解决途径三：利用Monte Carlo数值模拟。
Monte Carlo模拟
若明天需求量依赖于气温T, R=500+-|T-20|, N(0,50^2), U(5,15), 与独立 Matlab程序(明天T=5)求得n0=371(近似). a=1;b=0.75;c=0.6; T=5; N=1000; e=normrnd(0,50,1,N); d=unifrnd(5,15,1,N); R=500+e-d*abs(T-20); S0=0;for n=100:800, S=mean(((a-b)*R-(b-c)*(n-R)).*(R<=n)+(a-b)*n*(R>n)); if S>S0, S0=S;n0=n;end; end;n0,S0