2011年云南会考数学试题
往届云南普通高中会考数学真题及答案

正视图侧视图1 252 23 5 6 31(第4题)往届云南普通高中会考数学真题及答案选择题(共51分)一、选择题:本大题共17个小题,每小题3分,共51分。
在每小题给出的四个选项中,只有一项符合题目要求,请在答题卡相应的位置上填涂。
1. 设集合1,2,3M,1N ,则下列关系正确的是( )A.N M ∈B. N M ∉C. N M =D. N M ≠⊂2. 有一个几何体的三视图如下图所示,这个几何体是一个( )A.棱台B.棱锥C.棱柱D.圆柱3. 已知向量=(1,0)OA ,OB 则AB 等于( )4.如图是某运动员在某个赛季得分的茎叶统计图,A.2 B.3C.22D.23 5.函数1+=x y 的零点是( )A.0B.1-C. )0,0( D .0,1(-6.已知一个算法,其流程图右图,则输出的结果是( )A.10B.11C.8D.9 7.在ABC ∆中,M 是BC 的重点,则+等于( )A.AM 21B. AMC. 2 D . 8.如图 ,在边长为2的正方形内有一内切圆,现从正方形内取一点P,则点P 在圆内的概率为( )A.44π- B. π4C.4πD. π 9.下列函数中,以2π为最小正周期的是( )A. 2sin xy = B. x y sin = C. x y 2sin = D .x y 4sin =10. 在ABC ∆中,内角A 、B 、C 的对边分别为a 、b 、c ,若︒=135A ,︒=30B ,2=a ,则b 等于( )A.1B.2C. 3D.211.同时抛投两枚质地均匀的硬币,则两枚硬币均正面向上的概率为( )A.41 B. 21 C. 43D. 1 12.直线210x y -+=与直线12(1)y x -=+的位置关系是( )A.平行B. 垂直C. 相交但不垂直D.重合 13.不等式(3)0x x -<的解集是( )A.{}|0x x <B. {}|3x x <C. {}|03x x <<D. {}|03x x x <>或 14.已知5432()1f x x x x x x =+++++,用秦九韶算法计算(3)f 的值时,首先计算的最内层括号内一次多项式1v 的值是( )A. 1B. 2C. 3D. 4 15. 已知函数3()f x x =-,则下列说法中正确的是( )A. ()f x 为奇函数,且在()0,+∞上是增函数B. ()f x 为奇函数,且在()0,+∞上是减函数C. ()f x 为偶函数,且在()0,+∞上是增函数D. ()f x 为偶函数,且在()0,+∞上是减函数16. 已知数列{}n a 是公比为实数的等比数列,且11a =,59a =,则3a 等于( )A.2B. 3C. 4D. 517.已知直线l过点P ,圆C :224x y +=,则直线l 与圆C 的位置关系是( ) A.相交B. 相切C.相交或相切D.相离非选择题(共49分)二、 填空题:本大题共5个小题,每小题3分,共15分。
2011年云南省昆明市初中毕业暨高中招生考试

2011年云南省昆明市初中毕业暨高中招生考试数学试卷1.昆明小学1月份某天的气温为5℃,最低气温为﹣1℃,则昆明这天的气温差为( ) A .4℃ B .6℃ C .﹣4℃ D .﹣6℃ 2.如图是一个由相同的小正方体组成的立体图形,它的主视图是( )A .B .C .D .3.据2010年全国第六次人口普查数据公布,云南省常住人口为45966239人,45966239用科学记数法表示且保留两个有效数字为( ) A .4.6×107 B .4.6×106 C .4.5×108 D .4.5×107 4.小明在九年级进行的六次数学测验成绩如下(单位:分):76.82.91.85.84.85,则这次数学测验成绩的众数和中位数分别为( ) A .91,88 B .85,88 C .85,85 D .85,84.55.若x 1,x 2是一元二次方程2x 2﹣7x+4=0的两根,则x 1+x 2与x 1•x 2的值分别是( )A .﹣72,﹣2 B .﹣72,2 C .72,2 D .72,﹣26.列各式运算中,正确的是( )A .3a•2a=6aB .22=- C 2-= D .(2a+b )(2a ﹣b )=2a 2﹣b 27.(2011•昆明)如图,在□ABCD 中,添加下列条件不能判定□ABCD 是菱形的是( )A .AB=BCB .AC ⊥BD C .BD 平分∠ABC D .AC=BD 8.抛物线y=ax 2+bx+c (a≠0)的图象如图所示,则下列说法正确的是( )A .b 2﹣4ac <0B .abc <0C .12b a-<- D .a ﹣b+c <09.如图,在Rt △ABC 中,∠ACB=90°,BC=3,AC=,AB 的垂直平分线ED 交BC 的延长线与D 点,垂足为E ,则sin ∠CAD=( ) A .14B .13C .4D .15二、填空题(每题3分,满分18分.)10.当x 时,二次根式11.如图,点D 是△ABC 的边BC 延长线上的一点,∠A=70°,∠ACD=105°,则∠B= .13.计算:2()ab a b a a ba b++÷--= .14.如图,在△ABC 中,∠C=120°,AB=4cm ,两等圆⊙A 与⊙B 外切,则图中两个扇形(即阴影部分)的面积之和为 cm 2.(结果保留π).15.某公司只生产普通汽车和新能源汽车,该公司在去年的汽车产量中,新能源汽车占总产量的10%,今年由于国家能源政策的导向和油价上涨的影响,计划将普通汽车的产量减少10%,为保持总产量与去年相等,那么今年新能源汽车的产量应增加的百分数为 . 三.简答题(共10题,满分75.)161020111()1)(1)2--+-. 17.解方程:31122x x+=--.18.在□ABCD 中,E ,F 分别是BC 、AD 上的点,且BE=DF 。
2011年云南省昭通市数学试题(word版含答案)

昭通市 2011 年初中毕业生升学考试数 学 试 题 卷(全卷三个大题,共 30 个小题,共 6 页;满分 150 分,考试用时 150 分钟)注意事项: 1.本卷为试题卷,考生必须在答题卷上解题作答,答案书写在答题卷相应位置上,在 试题卷、草稿纸上作答无效. 2.考试结束后,请将试题卷和答题卷一并交回. 一、选择题(本大题共 10 小题,每小题只有一个正确选项,每小题 3 分,满分 30 分) 1.下列结论正确的是( )3a 2a 5a A.2B. 9 3C. (a b)(a b) a2 b2 )x x x D.6 232.下列图形中既是中心对称图形,又是轴对称图形的图形有(A.1 个 B.2 个 C.3 个 D .4 个 3.一组数据 2、1、5、4 的方差和中位数分别是( ) A.2.5 和 2 B.1.5 和 3 C.2.5 和 3 D.1.5 和 2 4.图 1 所示是一个由 4 个相同的正方体组成的立体图形,它的三视图为()A. B. C. 5.下列说法中正确的是( ) A. “打开电视,正在播放《新闻联播》 ”是必然事件. B.某次抽奖活动中奖的概率为D.1 ,说明每买 100 张奖券,一定有一次中奖. 100C.某地明天下雨的概率是 80%,表示明天有 80%的时间下雨. D.想了解某地区城镇居民人均年收入水平,宜采用抽样调查. 6.将一副直角三角板如图 2 所示放置,使含 30 ° 角的三角板的一条直角边和含 45° 角的三角板的 一条直角边重合,则 1 的度数为( ) 85 ° A.45° B.60 ° C.75 ° D. 7.由于国家出台对房屋的限购令,我省某地的房 屋价格原价为 2400 元/ 米 2 ,通过连续两次降价 a % 后,售价变为 2000 元/ 米 2 ,下列方程中正确 的是( )2A. 2400(1 a ) 2000B. 2000(1 a) 24002C. 2400(1 a)2 2000D. 2400(1 a)2 20008.如图 3 所示,将矩形纸片 ABCD 折叠,使点 D 与点 B 重合,点 C 落在点 C 处,折痕为 EF ,若 EFC 125° ,那么 ABE 的度数 为( ) A. 15 ° B. 20° C. 25° D. 30 ° 9.已知两圆的半径 R 、 r 分别为方程 x 3x 2 0 的两根,这两2圆的圆心距为 3,则这两圆的位置关系是( ) A.外切 B.内切 C.相交 D.外离 10.函数 y mx m 与 y m ( m 0) 在同一直角坐标系中的图象可能是( x)A. B. C. D. 二、填空题(本大题共 10 小题,每小题 3 分,满分 30 分) 11. 2 的倒数是_____________. 12.分解因式: 3a 27 _____________.213. 如图 4 所示, 已知点 A 、D 、B 、F 在一条直线上,AC EF , AD FB ,要使 △ ABC ≌△FDE ,还需添加一个 条件,这个条 .. 件可以是_____________. (只需填一个即可) 14.使 x 2 有意义的 x 的取值范围是_____________. 15.如图 5 所示, AB 是 ⊙O 的直径,弦 DC 与 AB 相交于点 E ,若 ACD 50° ,则 DAB _____________.16.不等式 3x 1 4 的解集是_____________. 17.如图 6 所示,某班上体育课,甲、乙两名同学分别站在 C 、 D 的位置时,乙的影子恰 好在甲的影子里边,已知甲身高 1.8 米,乙身高 1.5 米,甲的影长是 6 米,则甲、乙同学相 距_____________米. 18.地球与太阳之间的距离约为 149 600 000 千米,用科学记数法表示(保留 2 个有效数字) 约为_____________千米. 19.已知圆锥的母线长是 12cm,它的侧面展开图的圆心角是 120° ,则它的底面圆的直径为 _____________cm.20.把抛物线 y x2 bx 4 的图象向右平移 3 个单位,再向上平移 2 个单位,所得图象的 解析式为 y x2 2x 3 ,则 b 的值为_____________. 三、解答题(本大题共 10 小题,满分 90 分)1 21. (6 分)计算: 2 2cos 60° (3 2π)0 . 2122. (7 分)解分式方程:3 x 1 . 2x 4 x 2 21) , 23. (8 分)如图 7 所示,在平面直角坐标系中, △ ABC 的三个顶点的坐标分别为 A(0, 3) . B(11) , , C (1,(1)画出 △ ABC 关于 x 轴对称的图形 △A1B1C1 ,并写出点 C1 的坐标; (2)画出 △ ABC 绕原点 O 顺时针方向旋转 90 ° 后得到的图形 △A2 B2C2 ,并求出点 C 所 走过的路径的长.24. (9 分)老张进行苹果树科学管理试验.把一片苹果林分成甲、乙两部分,甲地块用新 技术管理,乙地块用老方法管理,管理成本相同.在甲、乙两地块上各随机选取 20 棵苹果 树,根据每棵树产量把苹果树划分成 A , B , C , D , E 五个等级(甲、乙的等级划分标 准相同,每组数据包括左端点不包括右端点)画出统计图 8:(1)认真阅读图 8 补齐直方图,求 a 的值及相应扇形的圆心角度数; (2)选择合适的统计量,比较甲乙两地块的产量水平,并说明试验结果.25. (9 分)如图 9 所示, AECF 的对角线相交于点 O ,DB 经过点 O ,分别与 AE ,CF 交于点 B , D . 求证:四边形 ABCD 是平行四边形.26. (9 分)如图 10 所示,若河岸的两边平行,河宽为 900 米,一只船由河岸的 A 处沿直线 方向开往对岸的 B 处, AB 与河岸的夹角是 60 ° ,船从 A 到 B 处需时间 2 3 分钟.求该船 的速度.27. (10 分)某校初三(5)班同学利用课余时间回收饮料瓶,用卖得的钱去购买 5 本大小 不同的两种笔记本,要求共花钱不超过 28 元,且购买的笔记本的总页数不低于 340 页,两种笔记本的价格和页数如下表. 大笔记本 价格(元/本) 页数(页/本) 6 100 小笔记本 5 60根据上述相关数据,请你设计一种节约资金的购买方案,并说明节约资金的理由.28. (10 分) 某校举办艺术节, 其中 A 班和 B 班的节目决赛总成绩并列第一, 学校决定从 A 、 B 两班中选派一个班代表学校参加全省比赛,B 班班长想法是: 用八张扑克牌, 将数字为 1, A 2,3,5 的四张牌给 班班长,将数字为 4,6,7,8 的四张牌留给自己,并按如下游戏规 则进行: A 班班长和 B 班班长从各自的四张牌中随机抽出一张,然后将抽出的两张扑克牌 数字相加,如果和为偶数,则 A 班去;如果和为奇数,则 B 班去. (1)请用树状图或列表的方法求 A 班去参赛的概率; (2) B 班班长设计的游戏规则公平吗?若公平,请说明理由;若不公平,请你设计一种公 平的游戏规则.29. (10 分) 如图 11 (1) 所示, AB 是 ⊙O 的直径,AC 是弦, 直线 EF 和 ⊙O 相切于点 C , AD EF ,垂足为 D . (1)求证: DAC BAC ; (2)若直线 EF 向上平行移动,如图 11(2)所示, EF 交 ⊙O 于 G 、 C 两点,若题中的 其他条件不变,这时与 DAC 相等的角是哪一个?为什么?30 . ( 12 分)如图 12 所示,二次函数 y ax2 bx1( a 0) 的图像与 x 轴分别交于 1 0) 两点,且与 y 轴交于点 C ; A , 0 、 B(2, 2 (1)求该抛物线的解析式,并判断 △ ABC 的形状; (2)在 x 轴上方的抛物线上有一点 D ,且以 A 、 C 、 D 、 B 四点为顶点的四边形是等腰 梯形,请直接写出 D 点的坐标; (3)在此抛物线上是否存在点 P ,使得以 A 、 C 、 B 、 P 四点为顶点的四边形是直角梯 形?若存在,求出 P 点的坐标;若不存在,说明理由.昭通市 2011 年初中毕业生升学考试数学参考答案一、选择题(本大题共 10 小题,每小题只有一个正确选项,每小题 3 分,满分 30 分) 题号 答案 11. 1 C 2 A 3 C 4 B 5 D 6 C 7 D 8 B 9 A 10 D二、填空题(本大题共 10 题,每小题 3 分,满分 30 分)1 12. 3(a 3)(a 3) 2 13. A F 或 AC ∥ EF 或 BC DE (答案不惟一) 14. x ≥ 2 15. 40° 16. x 1 17. 118. 1.5 10819. 820. 4 三、解答题(本大题共 10 小题,满分 90 分) 21. (6 分) 解:原式 2 2 2 1 1 2 4.22. (7 分) 解:去分母,得 整理,得 解得 经检验, x 3 2x x 2 , 3x 5 , 5 x , 35 是原方程的解 3 5 所以,原方程的解是 x . 323. (8 分) 答案: (图形略) (1) C1 (1 , 3) . (2)10 π. 224. (9 分) 解: (1) (画直方图略) a 10 ,相应扇形的圆心角: 360°10% 36° . (2) x甲 95 5 85 6 75 5 65 3 55 1 80.5 , 20 95 3 85 2 75 9 65 4 55 2 x乙 75 , 20x甲 x乙 ,由样本估计总体的思想,说明通过新技术管理甲地块苹果产量高于乙地块苹果产量. 25. (9 分) 证明: 四边形 AECF 是平行四边形, OE OF,OA OC, AE ∥ CF , DFO BEO , FDO EBO , △FDO ≌△EBO , OD OB , OA OC , 四边形 ABCD 是平行四边形. 26. (9 分)解:如图,过点 B 作 BC 垂直河岸,垂足为 C , 则在 Rt△ ACB 中,有 BC 900 AB 600 3 , sin BAC sin 60°因而速度 v 600 3 300 , 2 3答:该船的速度为 300 米/分钟. 27. (10 分) 解:设购买大笔记本为 x 本,则购买小笔记本为 (5 x) 本, 依题意,得 6 x 5(5 x) ≤ 28, 100 x 60(5 x) ≥ 340.解得, 1 ≤ x ≤ 3 . x 为整数, x 的取值为 1,2,3; 当 x 1 时,购买笔记本的总金额为 6 1 5 4 26 (元) ; 当 x 2 时,购买笔记本的总金额为 6 2 5 3 27 (元) ; 当 x 3 时,购买笔记本的总金额为 6 3 5 2 28 (元) . 应购买大笔记本 1 本,小笔记本 4 本,花钱最少. 28. (10 分) 解: (1)所有可能的结果如下表: A 1 2 3 5 B 4 (1,4) (2,4) (3,4) (5,4) 6 (1,6) (2,6) (3,6) (5,6) 7 (1,7) (2,7) (3,7) (5,7) 8 (1,8) (2,8) (3,8) (5,8)一共有 16 种结果,每种结果出现的可能性相同.P(和为偶数的概率) 6 3 16 8 3 . 8 3 5 , B 班去的概率为 ,所以游戏不公平, 8 8所以 A 班去参赛的概率为(2)由(1)列表的结果可知: A 班去的概率为对 B 班有利. 注:第(2)小题规则修改不惟一,只要使得 A 、 B 两班的概率相等即可. 29. (10 分)证明: (1)连接 OC , EF 与 ⊙O 相切, OC EF .AD EF AD ∥ OC , OCA DAC , OA OC , OCA BAC , DAC BAC . (2) BAG 与 DAC 相等.理由如下: 连接 BC , B AGD AB 是直径, AD EF , BCA GDA 90° B BAC 90° , AGD DAG 90° . BAC DAG , BAC CAG DAG CAG , 即 BAG DAC .30. (12 分)0) 代入 y ax bx 1 解: (1) 根据题意, 将 A , 0 ,B(2,2 1 2 中,得1 1 3 a b 1 0, 解这个方程,得 a 1,b , 2 4 2 4a 2b 1 0.3 该抛物线的解析式为 y x 2 x 1 , 2当 x 0 时, y 1 ,1) . 点 C 的坐标为 (0,5 1 . 在 Rt△ AOC 中, AC OA2 OC 2 12 2 22在 Rt△BOC 中, BC OB2 OC 2 22 12 5 .AB OA OB 1 5 2 , 2 2AC 2 BC 2 5 25 5 AB 2 , 4 4△ ABC 是直角三角形.(2)点 D 的坐标为 , 1 . (3)存在. 由(1)知, AC BC .3 2 1 ① 若以 BC 为底边, 则 BC ∥ AP , 如图 1 所示, 可求得直线 BC 的解析式为 y x 1 , 2 1 直线 AP 可以看作是由直线 BC 平移得到的,所以设直线 AP 的解析式为 y x b1 ,把 2点 A , 0 代入直线 AP 的解析式,求得 b1 1 2 1 , 41 1 直线 AP 的解析式为 y x . 2 4点 P 既在抛物线上,又在直线 AP 上,3 1 1 点 P 的纵坐标相等,即 x 2 x 1 x , 2 2 4 5 1 解得 x1 , x2 (舍去) . 2 2 5 3 当 x 时, y , 2 2 5 3 . 点 P , 2 2② 若以 AC 为底边, 则 BP ∥ AC , 如图 2 所示. 可求得直线 AC 的解析式为 y 2 x 1 . 直线 BP 可以看作是由直线 AC 平移得到的,所以设直线 BP 的解析式为 y 2 x b2 ,把点B(2, 0) 代入直线 BP 的解析式,求得 b2 4 , 直线 BP 的解析式为 y 2 x 4 .点 P 既在抛物线上,又在直线 BP 上, 点 P 的纵坐标相等, 即 x 23 5 x 1 2 x 4 ,解得 x1 , x2 2 (舍去) . 2 2 5 5 时, y 9 , 点 P 的坐标为 , 9 . 2 2 当x综上所述,满足题目条件的点P为5322⎛⎫-⎪⎝⎭,或592⎛⎫--⎪⎝⎭,.图2。
2011-2017年云南省学业水平考试真题+直线与圆

1.(2011.1)经过直线20x y -=与直线60x y +-=的交点,且与直线210x y +-=垂直的直线方程是A. 260x y -+=B. 260x y --=C. 2100x y +-=D. 280x y +-=2.(2011.1)圆心(3,2--),且过点(1,1)的圆的标准方程为A. ()()22325x y -+-=B. ()()223225x y -+-=C. ()()22325x y +++=D. ()()223225x y +++= 3.(2011.1)过点P(-2,-3)向圆2284110x y x y +--+=引两条切线,切点是T 1、T 2,则直线T 1T 2的方程是A. 65250x y ++=B. 65250x y +-=C. 1210250x y ++=D. 1210250x y +-=4.(2011.7)两条直线210x y ++=与210x y -+=的位置关系是A. 平行B. 垂直C. 相交且不垂直D. 重合5.(2011.7)已知直线的点斜式方程是21)y x -=+,那么此直线的倾斜角为A. 6πB. 3πC. 23πD. 56π6.(2011.7)若一个圆的圆心在直线2y x =上,在y 轴上截得的弦的长度等于2,且与直线0x y -相切,则这个圆的方程可能..是 A. 2220x y x y +--= B. 22240x y x y +++= C. 2220x y +-= D. 2210x y +-=7.(2012.1)过点P (-1,3),且平行于直线24+10x y -=的直线方程为A. 2+-50x y =B. 2+10x y -=C. -2+70x y =D. -250x y -= 8.(2012.1)已知直线的点斜式方程是12y x +=-,那么此直线的斜率为A. 14B. 13C.12D. 19.(2012.1)过点M(2,-2)以及圆2250x y x +-=与圆222x y +=交点的圆的方程是A. 22151042x y x +--=B. 22151042x y x +-+=C. 22151042x y x ++-=D. 22151042x y x +++= 10.(2012.7)点到直线的距离为11.(2012.7)圆心为,半径为5的圆的标准方程为12.(2012.7)已知,直线,则被所截得的弦长为13.(2013.1)圆224690x y x y ++-+=的圆心坐标是( )A.(2,3)B.(-2,-3)C. (2,-3)D. (-2,3)14.(2013.1)已知圆C 的圆心为(2,0),且圆C 与直线20x -+=相切,则圆C 的方程为_________. 15.(2013.7)直线x + y + 1= 0的倾斜角是( )A .-1B . 4π- C . 4π D . 43π 16.(2013.7)斜率为-2,在y 轴的截距为3的直线方程是( )A .2 x +y +3=0B .2 x -y +3=0C .2 x -y -3=0D .2 x +y -3=017.(2013.7)已知直线l 过点P (4,3),圆C :2225x y +=,则直线l 与圆的位置关系是( )A .相交B .相切C .相交或相切D .相离18.(2014.1)直线210x y -+=与直线12(1)y x -=+的位置关系是( )A.平行B. 垂直C. 相交但不垂直D.重合19.(2014.1)已知直线l 过点P ,圆C :224x y +=,则直线l 与圆C 的位置关系是( )A.相交 B . 相切 C.相交或相切 D.相离20.(2014.1)直线10x y ++=的纵截距是 。
云南省2011-2014普通高中学业水平考试+数学+立体几何真题及答案
A F
E
C
16.(2014.7)(本小题满分 8 分)
如图,在正方体 ABCD A1 B1C1 D1 中, E 、 F 分别为 DD1 、 CC1 的中点。 D1 (1)求证: AC BD1 ; (2) AE //平面 BFD 1. C1
A1 E
B1
F
D
C
A
B
云南省 2011 年-2014 年普通高中学业水平考试·数学·立体几何
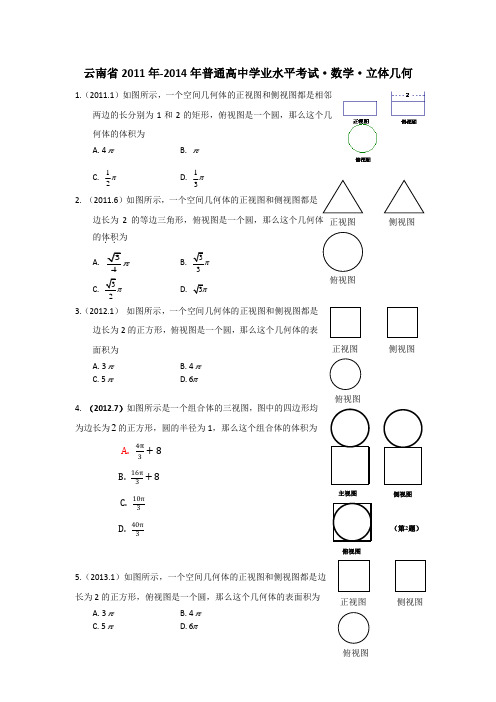
1.(2011.1)如图所示,一个空间几何体的正视图和侧视图都是相邻 两边的长分别为 1 和 2 的矩形,俯视图是一个圆,那么这个几 何体的体积为 A. 4 C.
1 2
B. D.
1 3
2. (2011.6)如图所示,一个空间几何体的正视图和侧视图都是 边长为 2 的等边三角形,俯视图是一个圆,那么这个几何体 正视图 的体积 为 .. A. C.
E F/ / A C ,
又 EF 平面ABCD, AC 平面ABCD ,
EF / /平面ABCD. ………………4 分
A
(2)连接 A 1B , A 1BCD 1 是平行四边形, A 1B / / D 1C , 1 D ,容易证明四边形 A
两异面直线 BD 与 CD1 所成角为 A1BD ,易知 V A1 BD 是等边三角形, A1BD 60.
在直角三角形 ACC1 中, tan∠C1AC=
C1C 2 2 AC 2
即 AC1 与底面 ABCD 所成角的正切值为 2 。 。 。 。 。 。 。 。 。 。 。 。 。8 分
S
15.(2014.1)(本小题满分 8 分) 如图所示,在三棱锥 P-ABC 中,E、F 分别为 AC、BC 的中点。 (1)证明: EF / /平面PAB ; (2)若 PA PB , CA CB ,求证: AB PC 。
2011—2017年云南省学业水平真题及高考真题训练+数列学案

1(2016.1)已知数列{}n a 中,13a =,1n n a ca m +=+(c ,m 为常数)(1) 当1c =,1m =时,求数列{}n a 的通项公式n a ; (2) 当2c=,1m =-时,证明:数列{}1n a -为等比数列;(3) 在(2)的条件下,记11n n b a =-,12n n S b b b =+++ ,证明:1n S <.2. (2017.1)已知C 是常数,在数列{}n a 中,21=a ,28321+++=+n n n n a ca a a(1) 设{}n a 是递增数列,求c 的取值范围 (2)若c =4,数列⎭⎬⎫⎩⎨⎧n a 1的前n 项和为n s ,求证:nn n S 311321-32-<≤⨯3. (2017.7)已知n S 是等差数列{}n a 的前n 项和,且39S =,749S =。
(1)求数列{}n a 的通项公式;(2)设11n n n b a a +=,求数列{}n b 的前n 项和n T 。
4.(2015.1)5.(2014.7)已知递增等比数列{}n a 满足:14432=++a a a ,且13+a 是2a ,4a 的等差中项. (1)求数列{}n a 的通项公式;(2)若数列{}n a 的前n 项和为n S ,求使63<n S 成立的正整数n 的最大值.6.(2014.1)已知正项数列{}n a 的前n 项和为n S ,且2*1(1)().4n n S a n N =+∈ (1)求1a 、2a ; (2)求证:数列{}n a 是等差数列; (3)令19n n b a =-,问数列{}n b 的前多少项的和最小?最小值是多少?7.(2013.7)已知数列{}n a 满足:111,41(2)2n n a a a n -==+?。
(1)求123a a a ++; (2)令13n n b a =+,求证数列{}n b 是等比数列; (3)求数列{}n b 的前n 项和n T .8.(2013.1)已知等差数列{}n a 满足12341,9a a a a =++=。
云南高中数学会考试题分类汇编
【2016.1】已知集合 M {0, 1, 2, 3} , N {1,3, 4} ,那么 M N 等于( A. {0}
Y
A. 单调递增,且有最小值 f (1) C. 单调递减,且有最小值 f ( 2)
B. {0,1}
C. {1,3}
—1—
D. {0,1, 2,3, 4}
—2—
【2014.7】15. 已知函数 f ( x ) x ,则下列说话正确的是( A. f ( x ) 为奇函数,且在 0, 上是增函数 C. f ( x ) 为偶函数,且在 0, 上是增函数 17. 函数 f ( x )
3
)
【2016.7.17】 定义: 对于函数 f ( x ) , 在使 f ( x ) M 成立的所有常数 M 中, 我们把 M 的最大值叫做函数 f ( x ) 的下确界.例如函数 f ( x ) x 4 x 的下确界是-4,则函数的下确界是( A. -2 (三)指数和对数的运算 【2015.18】 log 5 5 _________ . D.非奇非偶函数 【2015.7.6】 log 2 三、零点 【2011.1】函数 f x log 2 x 2 x 6 的零点所在的大致区间是( A. ,1 2
云南省高中历年学业水平考试数学试卷考点、考题分类汇编
必修模块一 一、集合 【2011.1】设集合 M {1} , N {1,2} , P {1,2,3} ,则 ( M N ) P ( A. {1} 【2011.7】 A. {2} B. {3} C. {1,2} )
【2016.7】设集合 M {1, 2, 3, 4,5, 6} , N {2, 4, 6} ,则 M N 等于( A. {2, 4,5, 6} 二、函数 B. {4,5, 6}
云南省2011年6月普通高中学业水平考试试卷(数学)解析版
云南省2011年6月普通高中学业水平考试试卷(数学)解析版(考试用时100分钟,满分100分)选择题(共54分)一、选择题,本大题共18个小题,每小题3分,共54分.在第小题给出的四个选项中,只有一项是符合要求的,请在答题卡相应的位置上填涂. 1.已知集合{1,2,3,4}M =,集合{1,3,5}N =,则M N 等于.{2}A .{2,3}B .{1,3}C .{1,2,3,4,5}D[答案] C[解析] {1,2,3,4}{1,3,5}{1,3}M N M N =−−−−→= 取公共元素,故选C .2.如图所示,一个空间几何体的正视图和侧图都是边长为2的等边三角形,俯视图是一个圆,那么这个几何体的体积..为.A .B.2C [答案] B[解析]该几何体是底面直径和母线都为2的圆锥,其高为22=212()32π⋅=,故选B . 3.在平行四边形ABCD 中,AB AD +等于.A AC .B BD .C DB.D AC[答案] A[解析] AB AD AB BC AC +=+=,故选A .4.已知向量a 、b ,2a = ,(3,4)b =,a 与b 夹角等于30︒,则a b ⋅ 等于.5A .B .C .D [答案] D[解析] (3,4)5b b =⇒= ,cos ,252a b a b a b ⋅=⋅⋅=⨯⨯= ,故选D .5.为了得到函数1cos3y x =,只需要把cos y x =图象上所有的点的 .A 横坐标伸长到原来的3倍,纵坐标不变.B 横坐标缩小到原来的13倍,纵坐标不变.A 纵坐标伸长到原来的3倍,横坐标不变.D 纵坐标缩小到原来的13倍,横坐标不变[答案] A[解析]观察周期26ππ−−−→变化到,所以横坐标伸长到原来的3倍,又值域没变,所以纵坐标不变,故选A .6.已知一个算法,其流程图如右图所示,则输出的结果是.3A .9B .27C .81D[答案] D[解析] 27271133339<<→⨯=−−−→⨯=−−−→循环循环303093272738181<>⨯=−−−→⨯=−−−−→循环执行输出故选D .7.两条直线210x y ++=与210x y -+=的位置关系是.A 平行 .B 垂直 .C 相交且不垂直 .D 重合[答案] B[解析] 因为对应系数的积和:122(1)0⨯+⨯-=,所以这两条直线是垂直的,故选B .8.若AD 为ABC ∆的中线,现有质地均匀的粒子散落在ABC ∆内,则粒子在ABD ∆内的概率等于4.5A 3.4B 1.2C 2.3D [答案] C [解析] 12ABD ABC S P S ∆∆==,故选C . 9.计算sin 240︒的值为.A 1.2B - 1.2CD[答案] A[解析]sin 240sin(18060)sin 60︒=︒+︒=-︒=A . ⒑在ABC ∆中,A ∠、B ∠、C ∠所对的边长分别是2、3、4,则cos B ∠的值为7.8A 11.16B 1.4C 1.4D - [答案] B[解析]由余弦定理得:22224311cos 22416B +-∠==⨯⨯,故选B . ⒒同时掷两个骰子,则向上的点数之积是3的概率是1.36A 1.21B 2.21C 1.18D [答案] D[解析] 因为两个骰子掷出的点数是相互独立的,给两个骰子编号为甲、乙,甲向上的点数是1乙向上的点数是3和甲向上的点数是3乙向上的点数是1是两之积是3,所以概率是11111666618⨯+⨯=,故选D . ⒓已知直线的点斜式方程是21)y x -=-,那么此直线的倾斜角为.6A π.3B π2.3C π 5.6D π [答案] C[解析]tan k α== 233ππαπ∴=-=,故选C . ⒔函数3()2f x x =-的零点所在的区间是.(2,0)A - .(0,1)B .(1,2)C .(2,3)D [答案] C[解析] 3(1)(1)210f =-=-< ,3(2)(2)260f =-=>,故选C .⒕已知实数x 、y 满足04x y x y ⎧⎪⎨⎪+⎩≥≥0≥.0A .1B .4C .5D[答案] B[解析]行域,如图,可知目标z x =+经过点(0,1)时,z 011z ∴=+=,故选B .⒖已知函数()f x 是奇函数,是.A 单调递减函数,且有最小值(2)f - .B 单调递减函数,且有最大值(2)f -.C 单调递增函数,且有最小值(2)f .D 单调递增函数,且有最大值(2)f [答案] B[解析] 因为函数()f x 是奇函数,所以(2)(2)f f -=-,(1)(1)f f -=-又,()f x 在区间[1,2]单调递减,所以12(1)(2)(1)(2)(1)(2)()f f f f f f f x ->->⇒-<-⇒-<-−−−→在区间[2,1]--上是单调递减函数,且有最大值(2)f -,故选B . ⒗已知等差数列{}n a 中,22a =,46a =,则前4项的和4S 等于.8A .10B .12C .14D [答案] C[解析] 设等差数列{}n a 的公差为d ,则4262(42)22a a d d -=+-⇒==,12220a a d =-=-=,所以1444()2(06)122a a S +==+=,故选C . ⒘当输入a 的值为2,b 的值为3-时,右边程序运行的结果是.2A - .1B - .1C .2D[答案] B[解析] 程序运行的结果是输入两数的和,2(3)1+-=-,故选B .⒙ 若一个圆的圆心在直线2y x =上,在y 轴上截得的弦的长度等于2,且与直线0x y -=相切,则这个圆的方程可能..是 22.20A x y x y +--= 22.240B x y x y +++= 22.20C x y +-= 22.10D x y +-=[答案] D[解析]选项D 表示的圆的圆心(0,0)在直线2y x =上,到直线0x y -=的1==半径,即相切,在y 轴上截得的弦的长度是圆的直径等于2,所以这个圆的方程只可能是2210x y +-=,故选D .非选择题(共46分)二、填空题,本大题共4个小题,每小题4分,共16分.请把答案写在答题卡的位置上.⒚ 某校有老师200名,男生1200,女生1000名,现用分层抽样的方法从所有师生中抽取一个容量为240的样本,则从女生中抽取的人数为 . [答案] 100 [解析]24024010001000100()200120010002400⨯=⨯=++人⒛如图是某中学高二年级举办的演讲比赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的中位数为 .[答案] 85[解析] 去掉一个最高分93分和一个最低分79分后,余下的五个分数依次是:84,84,85,86,87,中位数是85. 21.计算1222log 8log +的值是 . [答案] 2[解析] 21122222222log 8log log 8log 4log 22log 2212+=⨯====⨯= 22.已知2()(1)(1)f x x m x m =++++的图象与x 轴没有..公共点,则m 的取值范围是(用区间表示). [答案] (1,3)-[解析]依题意2(1)4(1)(1)(3)013m m m m m ∆=+-+=+-<⇒-<<, 故m 的取值范围用区间表示为(1,3)-三、解答题,本大题共4个小题,第23、24题各7分,第25、26题各8分,共30分.解答应写出文字说明、证明过程或演算步骤. 23.(本小题满分7分,其中第⑴问4分,第⑵问3分)已知函数2(sin cos )y x x =+ ⑴求它的最小正周期和最大值; ⑵求它的递增区间. [答案] ⑴,2π;⑵[]44k k ππππ-+,[解析] ⑴222(sin cos )sin cos 2sin cos 1sin 2y x x x x x x x =+=++=+22T ππ∴==,112y =+=最大值 ⑵由2222244k x k k x k ππππππππ-+⇒-+≤≤≤≤得要求的递增区间是[]44k k ππππ-+,24.(本小题满分7分,其中第⑴问4分,第⑵问3分)在正方体1111ABCD A BC D -中 ⑴求证:1AC BD ⊥⑵求异面直线AC 与1BC 所成角的大小.[答案] ⑴略;⑵60︒[解析]⑴连结BD ,由正方体性质,得111111AC BDAC D DAC D DB AC BD BD D D D BD D DB ⎫⊥⎫⎪⎪⊥⇒⊥⎬⎪⇒⊥⎬⎪=⎭⎪⎪⊂⎭ 平面平面⑵连结1AD 、1D C ,由111A D B CDA C ⇒∠∥是异面直线AC 与1BC 所成的角,又1ACD ∆是正三角形,所以160D AC ∠=︒,即异面直线AC 与1BC 所成的角是60︒25.(本小题满分8分,其中第⑴问4分,第⑵问4分)已知函数1()lg1xf x x-=+ ⑴求函数()f x 的定义域; ⑵证明()f x 是奇函数. [答案] ⑴{11}x x -<<;⑵略[解析] ⑴函数1()lg1xf x x-=+有意义,即101x x ->+,且10x +≠ 10(1)(1)0111x x x x x->−−−→-+>⇒-<<+同解于所以,函数()f x 的定义域是{11}x x -<<;⑵因为,11()111()lglg lg()lg ()1()111x x x xf x f x x x x x---+-+-====-=-+--+-所以,函数()f x 是奇函数.26. (本小题满分8分,其中第⑴问2分,第⑵问3分,第⑶问3分) 已知数列{}n a 中,11a =,23a =,1232(3)n n n a a a n --=-≥. ⑴ 求3a 的值;⑵ 证明:数列1{}(2)n n a a n --≥是等比数列; ⑶ 求数列{}n a 的通项公式.[答案] ⑴37a =;⑵略;⑶21n n a =-()n N *∈. [解析]⑴由已知3213233217a a a =-=⨯-⨯=⑵112112121232222()2n n n n n n n n n n n n n a a a a a a a a a a a a a -----------=-⇒-=-=-⇒=-所以,1{}(2)n n a a n --≥是首项为312-=,公比也为2的是等比数列; ⑶由⑵可知,2n ≥时,(1)111222n n n n a a -----=⋅=所以:112n n n a a ---=2122n n n a a ----= 3232n n n a a ----=3432a a -= 2322a a -= 1212a a -=∴,13212222n n a a --=++++112(12)2(21)2212n n n ---==-=--所以,21n n a =-(2)n ≥,又已知11a =,11211a =-=,即,21n n a =-对于1n =也成立。
云南数学文试卷解析-2011年普通高等学校招生全国统一考试(精)
2011年普通高等学校招生全国统一考试文科数学(必修+选修I)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至2页。
第Ⅱ卷3至4页。
考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷注意事项:1.答题前,考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚,并贴好条形码。
请认真核准条形码上的准考证号、姓名和科目。
2.每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,在试题卷上作答无效。
..........3.第Ⅰ卷共l2小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
一、选择题(1)设集合U={}1,2,3,4,{}1,2,3,M ={}2,3,4,N =则075,2,A b a c ==求与=⋂(M N )ð (A ){}12, (B ){}23, (C ){}2,4 (D ){}1,4【思路点拨】解决本题的关键是掌握集合交并补的计算方法,易求{2,3}MN =, 进而求出其补集为{}1,4.【精讲精析】选D. {2,3},(){1,4}U M N M N =∴=ð.(2)函数0)y x =≥的反函数为(A )2()4x y x R =∈ (B )2(0)4x y x =≥ (C )24y x =()x R ∈ (D )24(0)y x x =≥【思路点拨】先反解用y 表示x,注意要求出y 的取值范围,它是反函数的定义域。
【精讲精析】选B.在函数0)y x=≥中,0y≥且反解x得24yx=,所以0)y x=≥的反函数为2(0)4xy x=≥(3)权向量a,b满足a=b=12-,则2a b+=(A(B(C(D【思路点拨】本题要把充要条件的概念搞清,注意寻找的是通过选项能推出a>b,而由a>b 推不出选项的选项.【精讲精析】选A.即寻找命题P使P,a b a b⇒>>推不出P,逐项验证可选A。
云南省2011届高三第二次毕业生复习统一检测(word版):数学文
2011年云南省第二次高中毕业生复习统一检测文科数学本试卷分第I卷(选择题)和第II卷(非选择题)两部分。
第I卷I至3页,第II卷4至6页。
考试结束后,将本试卷和答题卡一并交回。
满分150分,考试用时120分钟。
第I卷 (选择题,共60分)注意事项:1. 答题前,考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚,并认真核准条形码上的准考证号、姓名、考场号、座位号及科目,在规定的位置贴好条形码。
2. 每小题选出答案后,用2B铅笔把答题卡h对应题0的答案标号涂黑。
如需改动,用橡皮擦擦干净后,再选涂其它答案标号。
答在试卷上的答案无效。
参考公式:如果事件A、B互斥,那么球的表面积公式P{A+B) = P(A) + P(B)如果事件A、B相互独立,那么其中表示球的半径P(A • B) = P(A) • P(B) 球的{本积公式如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中亊件A恰好发生k次的概率其中表示球的半径本卷共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
一.选择题(1)已知函数的定义域为实数集如果,那么=(A) 4 (B) 2(C) 4x (D) 2x(2) 在的展开式中,的系数等于(A) – 80 (B) 80(C) – 40 (D) 40(3) 已知数列是公差等于2的等差数列,如果a4是a2与a5的等比中项,那么a1的值(A) 2 (B) -4(C) -10 (D) -16(4) 如果将抛物线沿平面向量平移得到抛物线,那么平面向量的坐标为(A) (-1,2) (B) (-4,2)(C)(1,-2) (D) ( 4 , - 2)(5) 曲线在点(-1,-)处的切线的倾斜角等于(A) (B)(C) (D) 1(6>如果点在椭圆上,那么椭圆的离心率等于(A) (B)(C) (D)(7)如果,那么等于(A) —2 (B) -1(C) 1 (D) 2(8)已知直线把圆分成两段弧,这两段弧长之差的绝对值等于(A) (B)(C) (D)(9)在下列给出的四个函数中,与互为反函数的是(A) (B)(C) (D)(10)以抛物线上的一点M为圆心作圆M,如果圆M经过抛物线的顶点和焦点,那么圆M的半径等于(A) (B) 2(C) (D) 3(11)己知球O在一个棱长为的正四面体内,如果球O是该正四面体内的最大球,那么球O的表面积等于(A) ( B)(C) (D)(12)已知N是自然数集,常数a,b都是自然数,集合,集合.如果,那么以(a,b)为坐标的点一共有(A) 20 个 (B) 25个(C) 30个(D) 42 个2011年云南省第二次高中毕业生复习统一检测文科数学第II卷(非选择题,共90分)注意事项:本卷共3页,10小题,用黑色碳素笔将答案答在答题卡上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正视图侧视图俯视图【考试时间:2011年7月1日上午8:30 — 10:10,共100分钟】云南省2011年6月普通高中学业水平考试数学试卷【考生注意】 考试用时100分钟,必须在答题卡上指定位置按规定要求作答,答在试卷上一律无效。
参考公式: 如果事件A 、B 互斥,那么()()()P A B P A P B +=+. 球的表面积公式:24S R π=,其中R 表示球的半径.柱体的体积公式:V Sh =,其中是柱体的底面积,h 是柱体的高.锥体的体积公式:13V Sh =,其中是锥体的底面积,h 是锥体的高.选择题(共54分)一、选择题:本大题共18个小题,每小题3分,共54分。
在每小题给出的四个选项中,只有一项符合题目要求,请在答题卡相应的位置上填涂。
1. 已知集合{}{}1,2,3,4,1,3,5,M N M N ==集合则等于IA. {2}B. {2,3}C. {1,,3 }D. {1,2,3,4,5}2. 如图所示,一个空间几何体的正视图和侧视图都是边长为2的等边三角形,俯视图是一个圆,那么这个几何体的体积..为 A. 34π B.33πC.32π D. 3π3. 在平行四边形ABCD 中, AB AD +等于uu u ruuu rA.ACuuu rB. BD uuu rC. DB uuu rD.ACuuu r4. 已知向量 a b 、r r,=2, (3,4)a b =rr, a r与b r的夹角等于30︒,则a b ⋅r r等于 A. 5B.1033C. 52D. 535. 为了得到函数cos3x y =的图象,只需把函数cos y x=图象上所有的点的A. 横坐标伸长到原来的3倍,纵坐标不变B. 横坐标缩小到原来的13倍,纵坐标不变C. 纵坐标伸长到原来的3倍,横坐标不变D. 纵坐标缩小到原来的13倍,横坐标不变6. 已知一个算法,其流程图如右图所示,则输出结果是 A. 3 B. 9C. 27D. 817. 两条直线210x y ++=与210x y -+=的位置关系是A. 平行B. 垂直C. 相交且不垂直D. 重合8. 若AD 为∆ABC 的中线,现有质地均匀的粒子散落在∆ABC 内,则粒子落在△ABD 内的概率等于A.45B.34C.12D.239. 计算sin 240︒的值为A.32-B.12-C.12D.3210. 在△ABC 中,A B C ∠∠∠、、所对的边分别是2、3、4,则cos B ∠的值为A.78B.1116C.14D.14-11. 同时掷两个骰子,则向上的点数之积是3的概率是A.136B.121C.221D.11812. 已知直线的点斜式方程是23(1)y x -=-+,那么此直线的倾斜角为A.6πB.3πC.23π D.56π13. 函数()32f x x =-的零点所在的区间是A. ()2,0-B. (0,1)C. (1,2)D. (2,3)14. 已知实数x 、y 满足0044x y x y ≥⎧⎪≥⎨⎪+≥⎩,则z x y =+的最小值等于A. 0B. 1C. 4D. 515. 已知函数()f x 是奇函数,且在区间[]1,2上单调递减,则()[]2,1f x --在区间上是A. 单调递减函数,且有最小值()2f -B. 单调递减函数,且有最大值()2f -a=3aa =1 输出a a>30?是 否(第6题)开始 结束C. 单调递增函数,且有最小值()2fD. 单调递增函数,且有最大值()2f16. 已知等差数列{}n a 中,242,6a a ==,则前4项的和4S 等于 A. 8B. 10C. 12D. 14 17. 当输入a 的值为2,b 的值为3-时,右边的程序运行的结果是 A .-2 B .-1 C .1 D .218. 若一个圆的圆心在直线2yx=上,在y 轴上截得的弦的长度等于2,且与直线20x y -+=相切,则这个圆的方程可能..是 A. 2220x y x y +--=B. 22240x y x y +++=C.2220x y +-=D.2210x y +-=非选择题(共46分)二、 填空题:本大题共4个小题,每小题4分,共16分。
请把答案写在答题卡相应的位置上。
19. 某校有老师200名,男生1200名,女生1000名,现用分层抽样的方法从所有师生中抽取一个容量为240的样本,则从女生中抽取的人数为_________。
20. 如图是某中学高二年级举办的演讲比赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和最低分后,所剩数据的中位数为_________。
21. 计算221log 8log 2+的值是_________。
22. 已知函数()2()1(1)f x x m x m =++++的图像与x 轴没有..公共点,则m 的取值范围是__________(用区间表示)。
三、 解答题:本大题共4小题,23、24各7分,25、26各8分,共30分。
解答应写出文字说明、证明过程或演算过程。
23. (本小题满分7分,其中第(1)问4分,第(2)问3分) 已知函数2(sin cos ).y x x =+ (1)求它的最小正周期和最大值;(2)求它的递增区间。
INPUT ,a ba ab =+PRINT a END7 98 4 5 6 4 7 9 324. (本小题满分7分,其中第(1)问4分,第(2)问3分) 如图,在正方体1111ABCD A B C D -中. (1)求证:AC 1BD ⊥;(2)求异面直线AC 与1BC 所成角的大小。
25. (本小题满分8分,其中第(1)问4分,第(2)问4分)已知函数1()lg.1x f x x-=+(1)求()f x 的定义域; (2)证明函数()f x 是奇函数。
。
26. (本小题满分8分,其中第(1)问2分,第(2)问3分,第(3)问3分) 已知数列{}n a 中,()12121,3,323n n n a a a a a n --===-≥。
(1)求3a 的值;(2)证明:数列{}()12n n a a n --≥是等比数列; (3)求数列{}n a 的通项公式。
ABC C 1DD 1A 1B 1云南省2011年6月普通高中学业水平考试数学参考答案一、选择题(每小题3分,共54分) 题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 答案CBADADBCABDCCABCBD二、填空题(每小题4分,共16分)题号 19 20 21 22 答案1008521,3-()三、解答题23.(1)2()(sin cos )2sin cos 1sin 21f x x x x x x =+=+=+∴()f x 的最小正周期T=π,max ()2f x =………..…………………………….4分(2)由222()22k x k k Z ππππ-≤≤+∈得,44k x k ππππ-≤≤+()f x ∴的递增区间是,()44k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦………………………………..7分 24. (1)连结BD ,ABCD 为正方形,∴AC ⊥BD ,1111ABCD A B C D -为正方体,∴DD 1⊥平面ABCD , ∴ DD 1⊥AC,又 BD DD 1=D ,∴AC ⊥平面BDD 1, 又 BD 1⊂平面BDD 1, ∴ AC 1BD ⊥。
…………………………………………....4分(2)连结AD 1,CD 1, 易证四边形ABC 1D 1是平行四边形,11//AD BC ∴∴异面直线AC 与1BC 所成的角即为1C AD ∠。
易证1AC AD ==1C D 1ACD ∴∆是等边三角形,ABC C 1DD 1A 1B 1160C AD ∴∠=︒∴异面直线AC 与1BC 所成角的大小等于60︒。
……………………..……..8分25. (1)由101x x->+得(1)(1)0(-1)(1)0x x x x -+>+<即11x ∴-<<所以()f x 的定义域为(-1,1). …………………………………………………4分(2)因为1()lg .1xf x x -=+ 所以1111()lglg()lg()111x x x f x f x xxx-+---===-=--++故函数()f x 是奇函数。
…………………………………………………8分26.(1)()12121,3,323n n n a a a a a n --===-≥取3n =得321327a a a =-=,………2分(2)在()12323n n n a a a n --=-≥两端同时减去1n a -,整理得1122()n n n n a a a a ----=-2120a a -=≠,则1122n n n n a a a a ----=-,故数列{}1(2)n n a a n --≥是首项等于2且公比等于2的等比数列。
………….5分(3)由(2)知,211222(2)n n n n a a n ----=⨯=≥ 所以:212a a -=2322a a -= 3432a a -=……112n n n a a ---=把上述1n -个式子相加得:12112(12)22 (22212)n n nn a a ----=+++==--又11,21nn a a =∴=-Q (2)n ≥ 经验证知,上式对1n =也成立,故该数列的通项公式是:*21()n n a n N =-∈………………………….8分。
