面板数据分析方法步骤全解
面板数据分析简要步骤与注意事项(面板单位根—面板协整—回归分析)(2)
面板数据分析简要步骤与注意事项（面板单位根—面板协整—回归分析）步骤一：分析数据的平稳性（单位根检验）按照正规程序，面板数据模型在回归前需检验数据的平稳性。
李子奈曾指出，一些非平稳的经济时间序列往往表现出共同的变化趋势，而这些序列间本身不一定有直接的关联，此时，对这些数据进行回归，尽管有较高的R平方，但其结果是没有任何实际意义的。
这种情况称为称为虚假回归或伪回归（spurious regression）。
他认为平稳的真正含义是：一个时间序列剔除了不变的均值（可视为截距）和时间趋势以后，剩余的序列为零均值，同方差，即白噪声。
因此单位根检验时有三种检验模式：既有趋势又有截距、只有截距、以上都无。
因此为了避免伪回归，确保估计结果的有效性，我们必须对各面板序列的平稳性进行检验。
而检验数据平稳性最常用的办法就是单位根检验。
首先，我们可以先对面板序列绘制时序图，以粗略观测时序图中由各个观测值描出代表变量的折线是否含有趋势项和（或）截距项，从而为进一步的单位根检验的检验模式做准备。
单位根检验方法的文献综述：在非平稳的面板数据渐进过程中,LevinandLin(1993) 很早就发现这些估计量的极限分布是高斯分布,这些结果也被应用在有异方差的面板数据中,并建立了对面板单位根进行检验的早期版本。
后来经过Levin et al. (2002)的改进,提出了检验面板单位根的LLC 法。
Levin et al. (2002) 指出,该方法允许不同截距和时间趋势,异方差和高阶序列相关,适合于中等维度(时间序列介于25～250 之间,截面数介于10～250 之间) 的面板单位根检验。
Im et al. (1997) 还提出了检验面板单位根的IPS 法,但Breitung(2000) 发现IPS 法对限定性趋势的设定极为敏感,并提出了面板单位根检验的Breitung 法。
Maddala and Wu(1999)又提出了ADF-Fisher和PP-Fisher面板单位根检验方法。
面板数据分析简要步骤与注意事项面板单位根—面板协整—回归分析
面板数据分析简要步骤与注意事项面板单位根—面板协整—回归分析 SANY标准化小组 #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#面板数据分析简要步骤与注意事项（面板单位根—面板协整—回归分析）步骤一：分析数据的平稳性（单位根检验）按照正规程序，面板数据模型在回归前需检验数据的平稳性。
李子奈曾指出，一些非平稳的经济时间序列往往表现出共同的变化趋势，而这些序列间本身不一定有直接的关联，此时，对这些数据进行回归，尽管有较高的R平方，但其结果是没有任何实际意义的。
这种情况称为称为虚假回归或伪回归（spurious regression）。
他认为平稳的真正含义是：一个时间序列剔除了不变的均值（可视为截距）和时间趋势以后，剩余的序列为零均值，同方差，即白噪声。
因此单位根检验时有三种检验模式：既有趋势又有截距、只有截距、以上都无。
因此为了避免伪回归，确保估计结果的有效性，我们必须对各面板序列的平稳性进行检验。
而检验数据平稳性最常用的办法就是单位根检验。
首先，我们可以先对面板序列绘制时序图，以粗略观测时序图中由各个观测值描出代表变量的折线是否含有趋势项和（或）截距项，从而为进一步的单位根检验的检验模式做准备。
单位根检验方法的文献综述：在非平稳的面板数据渐进过程中,LevinandLin(1993) 很早就发现这些估计量的极限分布是高斯分布,这些结果也被应用在有异方差的面板数据中,并建立了对面板单位根进行检验的早期版本。
后来经过Levin et al. (2002)的改进,提出了检验面板单位根的LLC 法。
Levin et al. (2002) 指出,该方法允许不同截距和时间趋势,异方差和高阶序列相关,适合于中等维度(时间序列介于25～250 之间,截面数介于10～250 之间) 的面板单位根检验。
Im et al. (1997) 还提出了检验面板单位根的IPS 法,但Breitung(2000) 发现IPS 法对限定性趋势的设定极为敏感,并提出了面板单位根检验的Breitung 法。
5分钟搞定Stata面板数据分析
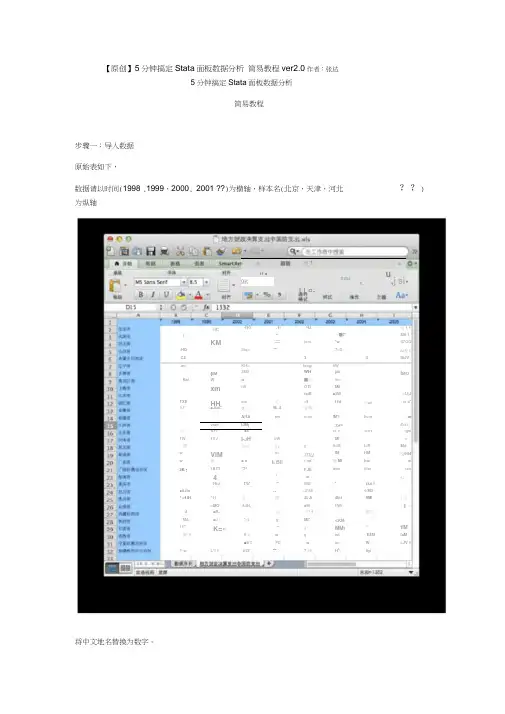
【原创】5分钟搞定Stata面板数据分析简易教程ver2.0作者：张达5分钟搞定Stata面板数据分析简易教程步骤一：导入数据原始表如下，数据请以时间(1998 ,1999，2000, 2001 ??)为横轴，样本名(北京，天津，河北？？) 为纵轴1 裁*■■別1A I11 ■u 9K ILEXxl-V,j si aoLL B-iic190 ..1( HJ曲1 1g力«r4 々■l* Mfl 1KM J| JgRi MM3icm*w II7QQ-HQ Siq<XM3 7>D tuff 1'C4 3 4 IftJV-mi KH>loogi liW(0M 3M9WH jaii I MOKai W w ■齐itmxm fill OTI MiltaiK ■5W»U|JTXE HH sia心«9 f Id 叼m in a*ft I*■JtaC如M~4 気HiA|$A rm inoo IM? livra.wvtatr1IJMj X#*4>t1|筑・BF7 ■«|!N I9*V1IRV gw1W1VJ I-J H itW Ml «稠申审砂y li>M l>R Mdw VIM e> mu IM HM 內)944w 命■ n I L BII i mi 靜Ml hw w3K：1ST? *7^ FJE inm ifini uni4 5w 心HtJ TW JTfl 9MI*HAS■ilJto KO >4*461/M31 <141*11诃却4LJt 4ktt VM匸F<MO 4dN,■M I!Wi・】•\ 4 ■R- 呵鬥1皑用MA■J广*»i g Ml* <KM11*K=« 1 31 1MM I“tlM韓!1fi >w g ivt E4M laM■ii T PD w im W i.JV 1P w L*l 1tiZF MM7 <1 H1! liyi将中文地名替换为数字。
面板数据分析方法步骤全解
面板数据分析方法步骤全解面板数据分析是一种常用的统计方法，可用于研究面板数据。
面板数据是指在一定时间内，对多个个体或单位进行反复观测的数据。
面板数据的特点是具有跨个体和跨时间的变异性，可以更好地捕捉个体变量和时间变量的相关性。
本文将详细介绍面板数据分析的方法步骤。
步骤一：数据准备面板数据分析的第一步是准备数据。
首先，需要收集面板数据，包括个体的观测值和时间变量。
然后，对数据进行清洗和整理，包括处理缺失值、异常值和重复值。
此外，还要对变量进行命名和编码，以便后续分析使用。
步骤二：面板数据的描述性统计分析在进行面板数据分析之前，通常需要对数据进行描述性统计分析。
这可以帮助我们了解数据的基本特征和变化趋势。
常用的描述性统计方法包括计算平均数、标准差、最大值、最小值和分位数等。
此外，还可以使用图表和图表来可视化数据的分布和变化情况。
步骤三：面板数据的平稳性检验面板数据在进行进一步分析之前，需要进行平稳性检验。
平稳性是指面板数据的统计特性在时间和个体之间保持不变。
常用的平稳性检验方法包括单位根检验和平稳均值假设检验。
如果数据不平稳，可以通过差分或其他方法进行处理，以实现平稳性。
步骤四：面板数据的固定效应模型估计面板数据分析的核心是建立面板数据模型并进行参数估计。
其中，固定效应模型是最常用的面板数据模型之一。
固定效应模型假设个体效应是固定的，与个体的观测值无关。
通过固定效应模型，可以估计个体效应和其他变量的影响。
常用的估计方法包括最小二乘法、广义最小二乘法和联合估计法等。
步骤五：面板数据的随机效应模型估计除了固定效应模型外，还可以使用随机效应模型进行面板数据分析。
随机效应模型假设个体效应是随机的，与个体的观测值相关。
通过随机效应模型，可以同时估计个体效应和其他变量的影响。
常用的估计方法包括广义最小二乘法和极大似然估计法等。
步骤六：面板数据的混合效应模型估计混合效应模型是固定效应模型和随机效应模型的组合，既考虑了个体效应的固定性，又考虑了个体效应的随机性。
stata分析面板数据
引言概述面板数据（Paneldata）是一种特殊类型的数据，它同时包含了横向和纵向的信息。
对于研究人员来说，面板数据的分析具有重要的意义，因为它可以对个体、时间和个体在不同时间上的变异进行深入研究。
Stata是一种流行的统计软件，具备强大的面板数据分析功能，可以处理各种面板数据相关的统计问题。
本文将介绍Stata分析面板数据的方法与技巧。
正文内容一、数据准备与导入1.定义面板变量：在Stata中，我们需要先将面板数据转换为面板变量。
可以使用“xtset”命令来定义面板变量，并指定个体和时间的标识变量。
例如，命令“xtsetidyear”可以将变量“id”作为个体标识变量，“year”作为时间标识变量。
2.导入面板数据：Stata支持多种数据格式的导入，如Excel、CSV等。
可以使用“importdelimited”命令导入CSV格式的面板数据。
命令格式如下：“importdelimitedfilename,varnames(1)”.其中，filename是文件名，varnames(1)表示将第一行作为变量名。
二、面板数据的描述统计分析1.描述性统计：在面板数据分析中，我们首先需要对数据进行描述性统计。
可以使用“summarize”命令计算平均值、标准差、最小值、最大值等统计指标。
例如，“summarizevarname”可以计算变量varname的平均值、标准差等。
2.变量相关分析：面板数据中的变量通常具有时间序列的特征，因此，变量之间的相关性也具有时间相关性。
可以使用“xtcorr”命令来计算面板数据中变量的相关系数矩阵。
命令格式如下：“xtcorrvar1var2,pwcorr”.其中，var1和var2是需要计算相关系数的变量。
三、面板数据的固定效应模型分析1.固定效应模型简介：固定效应模型是一种常见的面板数据分析方法，它考虑了个体固定效应，并通过个体虚拟变量来捕捉个体固定效应对因变量的影响。
《面板数据分析》课件
面板数据分析的步骤
1
数据描述
对数据进行描述性统计，确定数据在时间和个体方面的特征。
2
ห้องสมุดไป่ตู้
分类讨论
分析不同情况下个体间行为的差异和影响因素，如何影响个体行为的内部因素和外部 环境。
3
建模和估计
根据分类讨论的结论，运用面板数据模型建立样本分布，通过极大似然法和广义矩估 计法进行参数估计。
4
结果解释
对估计的结果进行解释，如何分析因素对个体行为的影响和相关关系等。
生产领域
跟踪生产的进度和效果，寻找 提高生产效率的方法。
总结和展望
总结
面板数据分析是一种高通量数据分析方法，通 过对个体间微观差异的捕捉和分析，提高了分 析数据的精确性，研究结果更具有真实性和普 遍性。
展望
随着数据分析和研究技术的不断发展，面板数 据分析将进一步被广泛接受和使用，为各行各 业的发展与创新提供支持。
《面板数据分析》PPT课 件
欢迎各位来到《面板数据分析》课件。本课程将向大家介绍如何运用面板数 据分析各种数据，并运用不同的分析方法提升数据的价值。
面板数据的定义和特点
什么是面板数据？
面板数据指的是在一定时间内，对相同个体做重复观测所得到的数据。
面板数据的特点
相对于横截面数据和时间序列数据，面板数据能够更精确地反映个体间的差异和发展。
面板数据模型的建立
线性回归模型
用于研究数值型因变量和数值 型自变量之间的关系。
逻辑回归模型
用于研究分类因变量和数值型 自变量之间的关系。
混合效应模型
考虑组间差异和个体内部差异， 更为精确地分析面板数据的特 点。
面板数据分析的常用方法
1 固定效应模型
面板数据分析
面板数据分析面板数据分析是一种常见的经济学和社会科学研究方法，用于研究在一定时间内观察到的个体或单位的变化。
面板数据可以提供比横截面数据或时间序列数据更多的信息，因为它同时考虑了个体之间的差异和时间的变化。
面板数据通常由两个维度构成：个体维度和时间维度。
个体维度可以是个人、家庭、企业、国家等，而时间维度可以是天、月、年等。
面板数据的独特之处在于可以观察到个体内部的变化和个体之间的差异，这为研究人员提供了更准确的分析和推断能力。
面板数据分析可以用于多种目的，例如，研究个体间的经济行为、评估政策措施的效果、预测未来发展趋势等。
它可以帮助研究人员更好地理解经济和社会现象，并为政策制定者提供有力的决策依据。
具体而言，面板数据分析可以包括以下几个步骤：1. 数据准备：收集和整理面板数据。
这包括选择适当的个体和时间维度，并确保数据的质量和完整性。
在进行面板数据分析之前，还需要对数据进行清洗和处理，以确保数据的可靠性和可用性。
2. 描述性统计：对面板数据进行基本的描述性统计分析，如均值、标准差和相关性等。
这有助于了解数据的总体特征和个体之间的关系。
3. 面板数据模型建立：建立适当的面板数据模型来解释个体和时间维度的变化。
常用的面板数据模型包括固定效应模型、随机效应模型和混合效应模型等。
选择适当的模型是关键，需要根据具体研究问题和数据特征来确定。
4. 参数估计和推断：利用面板数据模型进行参数估计和推断，以获得对个体和时间变化的准确描述。
这可以通过最大似然估计、广义矩估计等统计方法来实现。
5. 模型诊断和策略分析：对建立的面板数据模型进行诊断检验，评估模型的拟合度和稳健性。
然后，可以利用模型的结果进行策略分析和政策评估，以指导实际决策和干预措施。
面板数据分析在实证经济学、社会科学和市场研究等领域具有广泛的应用。
它可以应用于各种问题和场景，例如研究教育投资对学生表现的影响、评估医疗政策对健康结果的影响、分析企业之间的竞争关系等。
5分钟搞定Stata面板数据分析小教程实用
如图： 至此，使用 stata 进行面板数据回归分析完成。
口令： reshape long var, i (样本名 )
例如： reshape long var, i(province) 其中 var 代表的是所有的年份（ var2,var3,var4 ） 转化后的格式如图：
转化成功后继续重命名，其中 _j 这 里代表原始表中的年份， var 代表该变量的名 称 口令例如： rename _j year rename var taxi 也可直接在需要修改的名称处双击，在弹出的窗口中修改 如图：
步骤三：排序
口令： sort 变 量名
例如： sort province year 意思为将 province 按升序排列，然后再根据排好的 列 如图：
province 数列排 year 这一
（虽然很多时候在执行 sort 前数据就已经符合要求了，但以防万一请务期数据处理就完成了，请如法炮制的处理所有的变量。在 处理新变量前请使用
5 分钟搞定 Stata 面板数据分析 简易教程
步骤一：导入数据
口令： insheet using 文 件路径
例如： insheet using C:\STUDY\paper\taxi.csv 其中 csv 格式可用 excel 的“另存为 ”导出 数据请以时间（ 1999， 2000 ，2001 ）为横轴，样本名（ 1，2，3 ）为 纵轴 请注意：表中不能有中文字符，否则会出现错误。面板数据中不能有空值，没 有数据的位置请以 0 代替。 如图：
也可直接将数据复制粘贴到 stata 的 data editor 中 如图：
步骤二：调整格式
首先请将代表样本的 var1 重命名
口令： rename v ar1 样 本名
(完整word版)面板数据分析简要步骤与注意事项(面板单位根—面板协整—回归分析)
面板数据分析简要步骤与注意事项（面板单位根检验—面板协整—回归分析）面板数据分析方法：面板单位根检验—若为同阶—面板协整—回归分析—若为不同阶—序列变化—同阶建模随机效应模型与固定效应模型的区别不体现为R2的大小，固定效应模型为误差项和解释变量是相关，而随机效应模型表现为误差项和解释变量不相关。
先用hausman检验是fixed 还是random，面板数据R-squared值对于一般标准而言，超过0.3为非常优秀的模型。
不是时间序列那种接近0.8为优秀。
另外，建议回归前先做stationary。
很想知道随机效应应该看哪个R方？很多资料说固定看within，随机看overall，我得出的overall非常小0.03，然后within是53%。
fe和re输出差不多，不过hausman检验不能拒绝，所以只能是re。
该如何选择呢？步骤一：分析数据的平稳性（单位根检验）按照正规程序，面板数据模型在回归前需检验数据的平稳性。
李子奈曾指出，一些非平稳的经济时间序列往往表现出共同的变化趋势，而这些序列间本身不一定有直接的关联，此时，对这些数据进行回归，尽管有较高的R平方，但其结果是没有任何实际意义的。
这种情况称为称为虚假回归或伪回归（spurious regression）。
他认为平稳的真正含义是：一个时间序列剔除了不变的均值（可视为截距）和时间趋势以后，剩余的序列为零均值，同方差，即白噪声。
因此单位根检验时有三种检验模式：既有趋势又有截距、只有截距、以上都无。
因此为了避免伪回归，确保估计结果的有效性，我们必须对各面板序列的平稳性进行检验。
而检验数据平稳性最常用的办法就是单位根检验。
首先，我们可以先对面板序列绘制时序图，以粗略观测时序图中由各个观测值描出代表变量的折线是否含有趋势项和（或）截距项，从而为进一步的单位根检验的检验模式做准备。
单位根检验方法的文献综述：在非平稳的面板数据渐进过程中,Levin andLin(1993) 很早就发现这些估计量的极限分布是高斯分布,这些结果也被应用在有异方差的面板数据中,并建立了对面板单位根进行检验的早期版本。
面板数据分析方法步骤全解
面板数据分析方法步骤全解面板数据分析方法步骤全解步骤一：分析数据的平稳性(单位根检验)按照正规程序，面板数据模型在回归前需检验数据的平稳性。
李子奈曾指出，一些非平稳的经济时间序列往往表现出共同的变化趋势，而这些序列间本身不一定有直接的关联，此时，对这些数据进行回归，尽管有较高的R平方，但其结果是没有任何实际意义的。
这种情况称为称为虚假回归或伪回归(spurious regression)。
他认为平稳的真正含义是：一个时间序列剔除了不变的均值(可视为截距)和时间趋势以后，剩余的序列为零均值，同方差，即白噪声。
因此单位根检验时有三种检验模式：既有趋势又有截距、只有截距、以上都无。
因此为了避免伪回归，确保估计结果的有效性，我们必须对各面板序列的平稳性进行检验。
而检验数据平稳性最常用的办法就是单位根检验。
首先，我们可以先对面板序列绘制时序图，以粗略观测时序图中由各个观测值描出代表变量的折线是否含有趋势项和(或)截距项，从而为进一步的单位根检验的检验模式做准备。
单位根检验方法的文献综述：在非平稳的面板数据渐进过程中,Levin andLin(1993) 很早就发现这些估计量的极限分布是高斯分布,这些结果也被应用在有异方差的面板数据中,并建立了对面板单位根进行检验的早期版本。
后来经过Levin et al. (2002)的改进,提出了检验面板单位根的LLC 法。
Levin et al. (2002) 指出,该方法允许不同截距和时间趋势,异方差和高阶序列相关,适合于中等维度(时间序列介于25～250 之间,截面数介于10～250 之间) 的面板单位根检验。
Im et al. (1997) 还提出了检验面板单位根的IPS 法,但Breitung(2000) 发现IPS 法对限定性趋势的设定极为敏感,并提出了面板单位根检验的Breitung 法。
Maddala and Wu(1999)又提出了ADF-Fisher和PP-Fisher面板单位根检验方法。
面板数据回归分析步骤(一)2024
面板数据回归分析步骤（一）引言概述：面板数据回归分析是一种常用的经济学和统计学方法，用于研究面板数据的相关性、影响因素和趋势。
本文将详细介绍面板数据回归分析的步骤和方法，帮助读者更好地理解和应用这一方法。
正文：一、数据准备1. 收集面板数据：通过调查、观测或公共数据库来获得所需的面板数据。
2. 确定面板数据的类型：面板数据可以是平衡面板数据（每个交叉单元的观测次数相等）或非平衡面板数据（每个交叉单元的观测次数不相等）。
3. 检查数据的完整性和准确性：对面板数据进行缺失值和异常值的处理，确保数据的可靠性。
二、建立模型1. 确定因变量和自变量：根据研究目的和问题，确定面板数据中的因变量和自变量。
2. 选择适当的回归模型：根据变量的特点和关系，选择合适的面板数据回归模型，如随机效应模型、固定效应模型或混合效应模型。
3. 进行模型检验和诊断：对所选的面板数据回归模型进行统计检验，检查模型的拟合度和假设的成立情况。
三、估计回归系数1. 选择估计方法：根据面板数据的性质，选择合适的估计方法，如最小二乘法、广义最小二乘法或仪器变量法。
2. 进行回归系数估计：根据选择的估计方法，对面板数据回归模型进行回归系数估计，得到对各个自变量的系数估计值。
四、解释结果1. 解释回归系数：根据回归系数的估计结果，解释自变量对因变量的影响程度和方向。
2. 进行统计推断：对回归系数进行假设检验和置信区间估计，判断回归系数的显著性和可靠性。
五、结果分析与应用1. 分析回归结果：综合考虑回归系数的解释和统计推断结果，分析面板数据回归分析的整体效果和相关性。
2. 制定政策建议：通过分析回归结果，得出结论并提出政策建议，为决策者提供参考和借鉴。
总结：本文系统介绍了面板数据回归分析的步骤和方法，包括数据准备、模型建立、回归系数估计、结果解释和分析以及应用。
通过学习和应用面板数据回归分析，可以更好地理解和分析面板数据的相关性和趋势，从而为决策者提供有力的支持。
面板数据的分析步骤
面板数据的分析方法或许我们已经了解许多了，但是到底有没有一个基本的步骤呢？那些步骤是必须的？这些都是我们在研究的过程中需要考虑的，而且又是很实在的问题。
面板单位根检验如何进行？协整检验呢？什么情况下要进行模型的修正？面板模型回归形式的选择？如何更有效的进行回归？诸如此类的问题我们应该如何去分析并一一解决？以下是我近期对面板数据研究后做出的一个简要总结，和大家分享一下，也希望大家都进来讨论讨论。
步骤一：分析数据的平稳性（单位根检验）按照正规程序，面板数据模型在回归前需检验数据的平稳性。
李子奈曾指出，一些非平稳的经济时间序列往往表现出共同的变化趋势，而这些序列间本身不一定有直接的关联，此时，对这些数据进行回归，尽管有较高的R平方，但其结果是没有任何实际意义的。
这种情况称为称为虚假回归或伪回归（spurious regression）。
他认为平稳的真正含义是：一个时间序列剔除了不变的均值（可视为截距）和时间趋势以后，剩余的序列为零均值，同方差，即白噪声。
因此单位根检验时有三种检验模式：既有趋势又有截距、只有截距、以上都无。
因此为了避免伪回归，确保估计结果的有效性，我们必须对各面板序列的平稳性进行检验。
而检验数据平稳性最常用的办法就是单位根检验。
首先，我们可以先对面板序列绘制时序图，以粗略观测时序图中由各个观测值描出代表变量的折线是否含有趋势项和（或）截距项，从而为进一步的单位根检验的检验模式做准备。
单位根检验方法的文献综述：在非平稳的面板数据渐进过程中,Levin andLin(1993) 很早就发现这些估计量的极限分布是高斯分布,这些结果也被应用在有异方差的面板数据中,并建立了对面板单位根进行检验的早期版本。
后来经过Levin et al. (2002)的改进,提出了检验面板单位根的LLC 法。
Levin et al. (2002) 指出,该方法允许不同截距和时间趋势,异方差和高阶序列相关,适合于中等维度(时间序列介于25～250 之间,截面数介于10～250 之间)的面板单位根检验。
面板数据分析方法
面板数据分析方法面板数据分析方法是一种使用面板数据（panel data）进行统计分析的方法。
面板数据是指在一段时间内对多个个体进行观测得到的数据，例如对同一组个体在多个时间点上的经济数据、社会调查数据等。
面板数据分析方法可用于研究个体间的动态变化和个体间的差异，对于探索个体特征、推断因果关系以及进行政策评估具有重要的意义。
面板数据分析方法的主要步骤包括面板数据的描述、面板数据的平稳性检验、面板数据的估计以及面板数据的推断等。
首先，在进行面板数据分析前，需要对面板数据进行描述性分析。
可以通过计算面板数据的平均值、标准差、最大值、最小值等统计量来描述面板数据的整体情况，以及通过绘制各个个体在不同时间点上的散点图和折线图等图表来观察面板数据的变化趋势和个体间的差异。
其次，为了能够进行面板数据的分析，需要对面板数据的平稳性进行检验。
平稳性是指面板数据中个体和时间之间的变化趋势是稳定的，如果面板数据不满足平稳性前提，则可能会导致估计结果的偏误。
一种常用的平稳性检验方法是基于单位根检验，例如ADF检验和PP检验，这些检验方法可以检验面板数据中的个体序列和时间序列是否是平稳的。
然后，在对面板数据进行估计时，可以使用固定效应模型（Fixed Effects，FE）和随机效应模型（Random Effects，RE）等方法。
固定效应模型假设个体间的差异是固定的，只有个体内部的变化是随时间变动的，可以通过引入个体固定效应来控制个体间的不可观测因素。
随机效应模型则假设个体间的差异是随机的，无法通过个体固定效应来完全控制。
FE模型和RE模型的选择可以基于Hausman检验等方法进行。
最后，面板数据分析方法可以用于面板数据的推断。
例如，可以通过FE模型和RE模型的估计结果进行个体间的差异比较，判断不同因素对个体间差异的影响是否显著。
此外，还可以使用面板数据进行因果推断，如Granger因果检验和差分GMM模型等方法，用于探索个体特征之间的因果关系。
面板数据分析的流程
面板数据分析的流程下载温馨提示:该文档是我店铺精心编制而成，希望大家下载以后，能够帮助大家解决实际的问题。
文档下载后可定制随意修改，请根据实际需要进行相应的调整和使用，谢谢!并且，本店铺为大家提供各种各样类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，如想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by theeditor. I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!面板数据分析是一种常用的数据分析方法，它可以同时分析多个个体在多个时间点上的数据。
面板数据分析方法步骤全解
面板数据分析方法步骤全解yonglee , May 5 16:16 , 文档资料»数据挖掘, 评论(0) , 引用(0) , 阅读(35079) , 本站原创面板数据分析方法步骤全解(2009-11-07 11:50:38)转载标签：面板数据步骤一：分析数据的平稳性（单位根检验）按照正规程序，面板数据模型在回归前需检验数据的平稳性。
李子奈曾指出，一些非平稳的经济时间序列往往表现出共同的变化趋势，而这些序列间本身不一定有直接的关联，此时，对这些数据进行回归，尽管有较高的R平方，但其结果是没有任何实际意义的。
这种情况称为称为虚假回归或伪回归（spurious regression）。
他认为平稳的真正含义是：一个时间序列剔除了不变的均值（可视为截距）和时间趋势以后，剩余的序列为零均值，同方差，即白噪声。
因此单位根检验时有三种检验模式：既有趋势又有截距、只有截距、以上都无。
因此为了避免伪回归，确保估计结果的有效性，我们必须对各面板序列的平稳性进行检验。
而检验数据平稳性最常用的办法就是单位根检验。
首先，我们可以先对面板序列绘制时序图，以粗略观测时序图中由各个观测值描出代表变量的折线是否含有趋势项和（或）截距项，从而为进一步的单位根检验的检验模式做准备。
单位根检验方法的文献综述：在非平稳的面板数据渐进过程中,Levin andLin(1993) 很早就发现这些估计量的极限分布是高斯分布,这些结果也被应用在有异方差的面板数据中,并建立了对面板单位根进行检验的早期版本。
后来经过Levin et al. (2002)的改进,提出了检验面板单位根的LLC 法。
Levin et al. (2002) 指出,该方法允许不同截距和时间趋势,异方差和高阶序列相关,适合于中等维度(时间序列介于25～250 之间,截面数介于10～250 之间) 的面板单位根检验。
Im et al. (1997) 还提出了检验面板单位根的IPS 法,但Breitung(2000) 发现IPS 法对限定性趋势的设定极为敏感,并提出了面板单位根检验的Breitung 法。
面板数据分析方法步骤全解
面板数据分析方法步骤全解面板数据分析是一种重要的统计分析方法，广泛应用于经济、金融、社会科学等领域。
它可以有效地处理多个观测单位在不同时间点上的数据，提供了更为精确和全面的分析结果。
本文将介绍面板数据分析的基本概念、步骤和常见方法。
一、面板数据的基本概念面板数据也被称为追踪数据、长期数据或纵向数据，它是一种将多个观测单位在不同时间点上的数据进行整合的方式。
面板数据分为两种类型：平衡面板和非平衡面板。
平衡面板是指每个观测单位在每个时间点上都有完整的数据，而非平衡面板则允许观测单位在某些时间点上缺失数据。
面板数据的优势在于可以充分利用时间序列和截面数据的信息，提供更为准确和有力的分析结果。
然而，面板数据的分析往往需要解决一些特殊的问题，比如异质性、序列相关性和观测单位间的相关性等。
二、面板数据分析的步骤1. 数据准备：面板数据分析的第一步是准备好所需的数据。
这包括收集和整理各个观测单位在不同时间点上的数据，并进行数据清洗和处理。
在数据准备阶段，需要注意保持数据的一致性和完整性，排除异常值和缺失数据等。
2. 描述性统计：在面板数据分析中，描述性统计是了解数据特征和趋势的基础。
通过计算各个变量的均值、标准差、最大值、最小值等统计量，可以对数据的分布和变化进行初步分析。
此外，还可以绘制折线图、柱状图等图表，直观地展示数据的变化趋势。
3. 模型选择：选择适当的模型是面板数据分析的核心步骤。
常见的面板数据分析模型包括固定效应模型、随机效应模型和混合效应模型。
固定效应模型假设每个观测单位的效应是固定的，而随机效应模型假设每个观测单位的效应是随机的。
混合效应模型则将两者结合起来，既考虑了固定效应，又考虑了随机效应。
4. 假设检验：在面板数据分析中，假设检验是判断模型的显著性和一致性的重要方法。
通过假设检验可以判断各个变量之间的关系是否显著，以及模型的拟合程度如何。
常用的假设检验方法包括t检验、F检验等，可以用于检验模型参数的显著性和方差的平稳性。
面板数据分析方法 ppt课件
' 其中： 为 k 1的矩阵，xit 为k个解释变量的第i个个体在
第t时期的观测值，为 1 k 的矩阵。zi为不随时间
而变的个体特征，即 zit zi , t 。扰动项由 (ui it )
两部分构成，被称为“复合扰动项”。
ppt课件 35
个体效应模型
' yit xit zi' ui it
ppt课件
7
一、面板数据的定义
面板数据（panel data）是指由变量y关于N个不 同对象的T个观测期所得到的二维结构数据，记为yit， 其中，i表示N个不同对象（如国家、地区、行业、企 业或消费者等，一般称之为第i个个体），t表示T个观 测期。
ppt课件
8
面板数据是二维结构数据
时间序列数据或截面数据都是一维数据。时间序列 数据是变量按时间得到的数据；截面数据是变量在固定
27安徽河北江苏内蒙古山西1996199920020200040006000800010000120001400019961997199819992000200120021996199820002002安徽福建黑龙江江苏辽宁山东山西浙江02000400060008000100001200014000安徽北京福建河北黑龙江吉林江苏江西辽宁内蒙古山东上海山西天津浙江安徽河北江苏内蒙古山西19961998200020020200040006000800010000120001996199719981999200020012002199619992002安徽河北江苏内蒙古山西020004000600080001000012000安徽北京福建河北黑龙江吉林江苏江西辽宁内蒙古山东上海山西天津浙江例案例1file
12
ppt课件
面板数据回归分析步骤(二)2024
面板数据回归分析步骤（二）引言概述：面板数据回归分析是一种经济学和社会科学中常用的统计方法，用于探究个体间和时间间的关系。
本文将介绍面板数据回归分析的具体步骤，以帮助读者理解和运用这一方法。
正文：一、数据准备阶段1. 收集面板数据：收集涉及多个个体和多个时间点的数据，确保数据的质量和可靠性。
2. 数据清洗和处理：对数据进行处理，包括去除缺失值、删除离群值等，以保证数据的准确性和一致性。
3. 数据转换：如果有需要，对数据进行转换，如对变量进行标准化或对数化处理，以符合回归模型的要求。
二、模型设定阶段1. 选择回归模型类型：根据研究问题和数据特点，选择适合的回归模型类型，如固定效应模型、随机效应模型等。
2. 确定自变量和因变量：根据研究目的，选择适当的自变量和因变量，并进行变量的定义和测量。
3. 添加控制变量：根据理论知识和实际需求，添加可能的控制变量，以控制其他因素对因变量的影响。
三、模型估计阶段1. 估计模型参数：利用面板数据回归模型进行参数估计，得到各个自变量对因变量的影响程度。
2. 检验模型的拟合程度：通过计算回归模型的拟合度指标，如R方、调整R方等，评估模型对数据的拟合情况。
3. 分析模型的显著性：利用t检验或F检验等方法，对模型的显著性进行检验，以确定模型是否有效。
四、模型解释和分析阶段1. 解释回归系数：分析估计得到的回归系数的意义，解释自变量对因变量的影响方式和程度。
2. 检验假设：根据回归系数的显著性检验结果，检验研究假设是否被支持。
3. 进行敏感性分析：对模型的稳健性进行检验，进行不同假设和规范性分析，以确保结论的稳健性。
五、结果报告和讨论阶段1. 结果呈现：将回归模型的结果呈现出来，包括回归系数、显著性检验结果等，以清晰地展示研究结果。
2. 结果解读：解读回归结果的含义，并与相关的理论框架和研究背景进行对比和讨论。
3. 结论总结：总结回归分析的结果和发现，提出可能的政策建议或进一步研究的方向。
面板数据分析
面板数据分析面板数据分析是一种常见的数据分析方法，通过对不同类型的面板数据进行统计和分析，可以帮助我们了解数据之间的关系和趋势。
面板数据通常指的是具有时间序列和横截面维度的数据，这种数据结构在经济学、社会学、医学等领域都有广泛的应用。
本文将介绍面板数据分析的基本概念和方法，并结合实例进行演示和说明。
面板数据的基本特征面板数据是一种既有时间序列又有横截面维度的数据结构，通常用于描述多个个体（如个人、家庭、公司等）在不同时间点上的变化。
面板数据可以分为平衡面板数据和非平衡面板数据两种类型。
平衡面板数据指的是在每个时间点上都有完整数据的面板，而非平衡面板数据则是在某些时间点上个体缺失数据的情况。
面板数据分析的基本方法面板数据分析通常涉及到固定效应模型、随机效应模型、面板数据单位根检验、汇总单位根检验等方法。
固定效应模型假设个体间的差异是固定的，而随机效应模型则假设个体间的差异是随机的。
面板数据单位根检验用于检验数据的平稳性，汇总单位根检验则是对所有面板单位进行单位根检验并进行拒绝或接受零假设。
面板数据分析的实例分析下面我们通过一个实例来演示面板数据分析的具体步骤。
假设我们有一个包含多个公司在不同时间点上销售额和成本数据的面板数据集，我们想要分析销售额和成本之间的关系。
首先，我们可以通过描述性统计分析来了解数据的基本特征，包括平均值、标准差、相关系数等。
然后，我们可以建立一个固定效应模型来分析销售额和成本之间的关系，控制个体特征和时间效应。
最后，我们可以进行假设检验来验证我们的模型是否显著，并通过模型拟合的结果来解释销售额和成本之间的关系。
总结面板数据分析是一种重要的数据分析方法，通过对具有时间序列和横截面特征的数据进行统计和建模，可以更好地了解数据的特性和规律。
在实际应用中，面板数据分析可以帮助我们进行效果评估、政策分析、市场预测等工作。
希望本文对你了解面板数据分析有所帮助。
详细的EVIEWS面板数据分析操作
第一步 录入数据 第二步 分析数据的平稳性（单位根检验） 第三步 平稳性检验后分析路径选择 第四步 协整检验` 第五步 回归模型
1
第一步 录入数据 一 请点 实例数据 二 请点 录入数据软件操作
2
实例数据
录入企业投资需求模型数据：五家企业和三个变量的20个年度 （1935-1954年）观测值的时间序列 （数据略）
65.74 (0.2266)
注：加“*”表示在5%的显著性水平下拒绝原假设而接受备择假设。
上述检验结果检验的样本区间为1991-2003年，从表10.8和 表10.9的检验结果可以看出，我国29个省市的城镇居民消费和 收入的面板数据之间存在协整关系。
17
因果分析
格兰杰因果检验（因果检验的前提是变量协整）。 Eviews好像没有在POOL窗口中提供Granger causality test，如果想对面板数据中的某些合成序列 做因果检验的话，不妨先导出相关序列到一个组中 (POOL窗口中的Proc/Make Group)，再来试试
5家企业： GM：通用汽车公司 CH：克莱斯勒公司 GE：通用电器公司
3个变量： I ：总投资 M ：前一年企业的市场价值 （反映企业的预期利润）
WE：西屋公司 US：美国钢铁公司
K ：前一年末工厂存货和设备的价值
（反映企业必要重置投资期望值）
3录入 数据软件操Fra bibliotek（EVIEW6.0） 方式一
File/New/ Workfile Workfile structure type ： Dated-regular frequency
18
回归模型
一 确定影响形式 固定影响 随机影响
二 确定模型形式 形式一 形式二 形式三
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
面板数据分析方法步骤全解面板数据的分析方法或许我们已经了解许多了，但是到底有没有一个基本的步骤呢？那些步骤是必须的？这些都是我们在研究的过程中需要考虑的，而且又是很实在的问题。
面板单位根检验如何进行？协整检验呢？什么情况下要进行模型的修正？面板模型回归形式的选择？如何更有效的进行回归？诸如此类的问题我们应该如何去分析并一一解决？以下是我近期对面板数据研究后做出的一个简要总结，和大家分享一下，也希望大家都进来讨论讨论。
步骤一：分析数据的平稳性（单位根检验）按照正规程序，面板数据模型在回归前需检验数据的平稳性。
李子奈曾指出，一些非平稳的经济时间序列往往表现出共同的变化趋势，而这些序列间本身不一定有直接的关联，此时，对这些数据进行回归，尽管有较高的R平方，但其结果是没有任何实际意义的。
这种情况称为称为虚假回归或伪回归（spurious regression）。
他认为平稳的真正含义是：一个时间序列剔除了不变的均值（可视为截距）和时间趋势以后，剩余的序列为零均值，同方差，即白噪声。
因此单位根检验时有三种检验模式：既有趋势又有截距、只有截距、以上都无。
因此为了避免伪回归，确保估计结果的有效性，我们必须对各面板序列的平稳性进行检验。
而检验数据平稳性最常用的办法就是单位根检验。
首先，我们可以先对面板序列绘制时序图，以粗略观测时序图中由各个观测值描出代表变量的折线是否含有趋势项和（或）截距项，从而为进一步的单位根检验的检验模式做准备。
单位根检验方法的文献综述：在非平稳的面板数据渐进过程中,Levin andLin(1993) 很早就发现这些估计量的极限分布是高斯分布,这些结果也被应用在有异方差的面板数据中,并建立了对面板单位根进行检验的早期版本。
后来经过Levin et al. (2002)的改进,提出了检验面板单位根的LLC 法。
Levin et al. (2002) 指出,该方法允许不同截距和时间趋势,异方差和高阶序列相关,适合于中等维度(时间序列介于25～250 之间,截面数介于10～250 之间) 的面板单位根检验。
Im et al. (1997) 还提出了检验面板单位根的IPS 法,但Breitung(2000) 发现IPS 法对限定性趋势的设定极为敏感,并提出了面板单位根检验的Breitung 法。
Maddala and Wu(1999)又提出了ADF-Fisher和PP-Fisher面板单位根检验方法。
由上述综述可知，可以使用LLC、IPS、Breintung、ADF-Fisher 和PP-Fisher5种方法进行面板单位根检验。
其中LLC-T 、BR-T、IPS-W 、ADF-FCS、PP-FCS 、H-Z 分别指Levin, Lin & Chu t* 统计量、Breitung t 统计量、lm Pesaran & Shin W 统计量、ADF- Fisher Chi-square统计量、PP-Fisher Chi-square统计量、Hadri Z 统计量，并且Levin, Lin & Chu t* 统计量、Breitung t统计量的原假设为存在普通的单位根过程，lm Pesaran & Shin W 统计量、ADF- Fisher Chi-square统计量、PP-Fisher Chi-square统计量的原假设为存在有效的单位根过程，Hadri Z统计量的检验原假设为不存在普通的单位根过程。
有时，为了方便，只采用两种面板数据单位根检验方法，即相同根单位根检验LLC（Levin-Lin-Chu）检验和不同根单位根检验Fisher-ADF 检验（注：对普通序列（非面板序列）的单位根检验方法则常用ADF 检验），如果在两种检验中均拒绝存在单位根的原假设则我们说此序列是平稳的，反之则不平稳。
如果我们以T（trend）代表序列含趋势项，以I（intercept）代表序列含截距项，T&I代表两项都含，N（none）代表两项都不含，那么我们可以基于前面时序图得出的结论，在单位根检验中选择相应检验模式。
但基于时序图得出的结论毕竟是粗略的，严格来说，那些检验结构均需一一检验。
具体操作可以参照李子奈的说法：ADF检验是通过三个模型来完成，首先从含有截距和趋势项的模型开始，再检验只含截距项的模型，最后检验二者都不含的模型。
并且认为，只有三个模型的检验结果都不能拒绝原假设时，我们才认为时间序列是非平稳的，而只要其中有一个模型的检验结果拒绝了零假设，就可认为时间序列是平稳的。
此外，单位根检验一般是先从水平（level）序列开始检验起，如果存在单位根，则对该序列进行一阶差分后继续检验，若仍存在单位根，则进行二阶甚至高阶差分后检验，直至序列平稳为止。
我们记I(0)为零阶单整，I(1)为一阶单整，依次类推，I(N)为N阶单整。
步骤二：协整检验或模型修正情况一：如果基于单位根检验的结果发现变量之间是同阶单整的，那么我们可以进行协整检验。
协整检验是考察变量间长期均衡关系的方法。
所谓的协整是指若两个或多个非平稳的变量序列，其某个线性组合后的序列呈平稳性。
此时我们称这些变量序列间有协整关系存在。
因此协整的要求或前提是同阶单整。
但也有如下的宽限说法：如果变量个数多于两个，即解释变量个数多于一个，被解释变量的单整阶数不能高于任何一个解释变量的单整阶数。
另当解释变量的单整阶数高于被解释变量的单整阶数时，则必须至少有两个解释变量的单整阶数高于被解释变量的单整阶数。
如果只含有两个解释变量，则两个变量的单整阶数应该相同。
也就是说，单整阶数不同的两个或以上的非平稳序列如果一起进行协整检验，必然有某些低阶单整的，即波动相对高阶序列的波动甚微弱（有可能波动幅度也不同）的序列，对协整结果的影响不大，因此包不包含的重要性不大。
而相对处于最高阶序列，由于其波动较大，对回归残差的平稳性带来极大的影响，所以如果协整是包含有某些高阶单整序列的话（但如果所有变量都是阶数相同的高阶，此时也被称作同阶单整，这样的话另当别论），一定不能将其纳入协整检验。
协整检验方法的文献综述：(1)Kao(1999)、Kao and Chiang(2000)利用推广的DF和ADF检验提出了检验面板协整的方法,这种方法零假设是没有协整关系,并且利用静态面板回归的残差来构建统计量。
(2)Pedron(1999)在零假设是在动态多元面板回归中没有协整关系的条件下给出了七种基于残差的面板协整检验方法。
和Kao的方法不同的是,Pedroni的检验方法允许异质面板的存在。
(3)Larsson et al(2001)发展了基于Johansen(1995)向量自回归的似然检验的面板协整检验方法，这种检验的方法是检验变量存在共同的协整的秩。
我们主要采用的是Pedroni、Kao、Johansen的方法。
通过了协整检验，说明变量之间存在着长期稳定的均衡关系，其方程回归残差是平稳的。
因此可以在此基础上直接对原方程进行回归，此时的回归结果是较精确的。
这时，我们或许还想进一步对面板数据做格兰杰因果检验（因果检验的前提是变量协整）。
但如果变量之间不是协整（即非同阶单整）的话，是不能进行格兰杰因果检验的，不过此时可以先对数据进行处理。
引用张晓峒的原话，“如果y和x不同阶，不能做格兰杰因果检验，但可通过差分序列或其他处理得到同阶单整序列，并且要看它们此时有无经济意义。
”下面简要介绍一下因果检验的含义：这里的因果关系是从统计角度而言的，即是通过概率或者分布函数的角度体现出来的：在所有其它事件的发生情况固定不变的条件下，如果一个事件X的发生与不发生对于另一个事件Y的发生的概率（如果通过事件定义了随机变量那么也可以说分布函数）有影响，并且这两个事件在时间上又有先后顺序（A 前B后），那么我们便可以说X是Y的原因。
考虑最简单的形式，Granger 检验是运用F-统计量来检验X的滞后值是否显著影响Y（在统计的意义下，且已经综合考虑了Y的滞后值；如果影响不显著，那么称X不是Y的“Granger原因”（Granger cause）；如果影响显著，那么称X 是Y的“Granger原因”。
同样，这也可以用于检验Y是X的“原因”，检验Y的滞后值是否影响X（已经考虑了X的滞后对X自身的影响）。
Eviews好像没有在POOL窗口中提供Granger causality test，而只有unit root test和cointegration test。
说明Eviews是无法对面板数据序列做格兰杰检验的，格兰杰检验只能针对序列组做。
也就是说格兰杰因果检验在Eviews中是针对普通的序列对(pairwise)而言的。
你如果想对面板数据中的某些合成序列做因果检验的话，不妨先导出相关序列到一个组中(POOL窗口中的Proc/Make Group)，再来试试。
情况二：如果如果基于单位根检验的结果发现变量之间是非同阶单整的，即面板数据中有些序列平稳而有些序列不平稳，此时不能进行协整检验与直接对原序列进行回归。
但此时也不要着急，我们可以在保持变量经济意义的前提下，对我们前面提出的模型进行修正，以消除数据不平稳对回归造成的不利影响。
如差分某些序列，将基于时间频度的绝对数据变成时间频度下的变动数据或增长率数据。
此时的研究转向新的模型，但要保证模型具有经济意义。
因此一般不要对原序列进行二阶差分，因为对变动数据或增长率数据再进行差分，我们不好对其冠以经济解释。
难道你称其为变动率的变动率？步骤三：面板模型的选择与回归面板数据模型的选择通常有三种形式：一种是混合估计模型（Pooled Regression Model）。
如果从时间上看，不同个体之间不存在显著性差异；从截面上看，不同截面之间也不存在显著性差异，那么就可以直接把面板数据混合在一起用普通最小二乘法（OLS）估计参数。
一种是固定效应模型（Fixed Effects Regression Model）。
如果对于不同的截面或不同的时间序列，模型的截距不同，则可以采用在模型中添加虚拟变量的方法估计回归参数。
一种是随机效应模型（Random Effects Regression Model）。
如果固定效应模型中的截距项包括了截面随机误差项和时间随机误差项的平均效应，并且这两个随机误差项都服从正态分布，则固定效应模型就变成了随机效应模型。
在面板数据模型形式的选择方法上，我们经常采用F检验决定选用混合模型还是固定效应模型，然后用Hausman检验确定应该建立随机效应模型还是固定效应模型。
检验完毕后，我们也就知道该选用哪种模型了，然后我们就开始回归：在回归的时候，权数可以选择按截面加权（cross-section weights）的方式，对于横截面个数大于时序个数的情况更应如此，表示允许不同的截面存在异方差现象。