实验4 Mamdani型模糊推理系统的设计与仿真
模糊控制系统课件4.4(FIS的设计与仿真)

坐标区
网格,可 填入3-100 之间的数 字
主菜单Options之下有两个子菜单:Plot(画图) 和Color Map(填色),都是关于绘图的。
实验一:用GUI设计Mamdani型FIS
洗衣机利用分光光度计传感器,通过检测洗涤液的
透明程度等方法,测出洗涤液中的污泥含量x∈[0,100]% 和油脂含量y∈[0,100]%。模糊控制规则根据x和y的数 据,选定洗涤时间t∈[0,60](分钟)。因为只考虑洗涤时 间,可以用双输入-单输出模糊控制器完成任务。
4.4 FIS的设计与仿真
启动MATLAB后,在主窗口键入fuzzy,回车。
模糊子集
把模糊推理系统改成T-S(Sugeno)型: File→New FIS…→Sugeno
线性函数
这两个编辑 框不允许填 入内容
相当于Mamdani推理中的蕴涵、综合、清晰化 三者的综合结果
模糊规则编辑器
以液位控制系统为例。
④if level is okay and rate is positive then valve is close slow
⑤if level is okay and rate is negative then valve is open slow 根据上述模糊规则,编辑这个“液位模糊控制器” 的仿真模型。
实验二:用GUI设计Sugeno型FIS
例:双输入(x和y)、单输出(u)系统,四条 模糊规则。
R1 : if R2 : if R3 : if R4 : if
x is x1 then u1 x 1; x is x2 and y is y1 then u 2 0.1x 4 y 1.2; x is x2 and y is y2 then u3 0.9 x 0.7 y 9; x is x3 and y is y2 then u4 0.2 x 0.1 y 0.2
mamdani查表法

Mamdani查表法
Mamdani模糊逻辑系统中使用的查表法(Look-up Table, LUT)是一种实现模糊推理
的有效方法。
在模糊控制和模糊系统设计中,Mamdani模型通常包括模糊化、模糊推
理以及去模糊化三个主要步骤。
1.模糊化:将精确的输入变量通过模糊化 membership 函数转化为模糊集中的隶属度
值。
2.模糊推理:基于预定义的模糊规则集合,进行模糊推理过程。
在Mamdani系统中,
这常常涉及到利用“IF-THEN”形式的模糊规则来生成结论。
例如,“如果温度是冷且湿度是高,则舒适度是不适”。
3.查表法:
o在此阶段,为了简化计算过程并提高处理速度,可以预先根据模糊规则生成一个模糊推理表或查找表(LUT)。
这个表通常包含每一对模糊输入变量所有可能
的组合及其对应的模糊输出变量的结论集。
o每当系统接收到新的输入数据时,可以直接从该表中查找相应的模糊输出结果,而无需实时重新计算所有的模糊逻辑推理过程。
4.去模糊化:得到模糊输出后,通过合适的去模糊化方法(如重心法、最大隶属度法
等)将其转化为清晰的输出值以指导系统的实际操作。
因此,在Mamdani模糊逻辑控制系统中使用查表法,可以在保证推理正确性的前提下,显著地减少实时计算量,提高系统的实时响应性能。
在Matlab中,可以通过构造合适的矩阵来实现这样的模糊推理查表功能。
实验报告
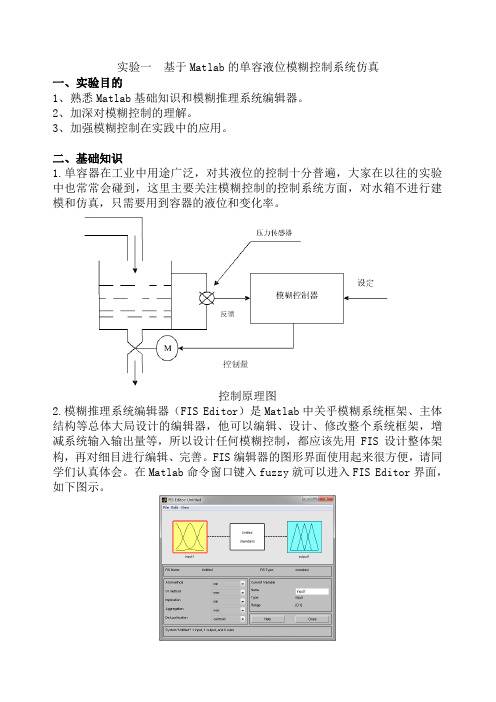
实验一基于Matlab的单容液位模糊控制系统仿真一、实验目的1、熟悉Matlab基础知识和模糊推理系统编辑器。
2、加深对模糊控制的理解。
3、加强模糊控制在实践中的应用。
二、基础知识1.单容器在工业中用途广泛,对其液位的控制十分普遍,大家在以往的实验中也常常会碰到,这里主要关注模糊控制的控制系统方面,对水箱不进行建模和仿真,只需要用到容器的液位和变化率。
控制原理图2.模糊推理系统编辑器(FIS Editor)是Matlab中关乎模糊系统框架、主体结构等总体大局设计的编辑器,他可以编辑、设计、修改整个系统框架,增减系统输入输出量等,所以设计任何模糊控制,都应该先用FIS设计整体架构,再对细目进行编辑、完善。
FIS编辑器的图形界面使用起来很方便,请同学们认真体会。
在Matlab命令窗口键入fuzzy就可以进入FIS Editor界面,如下图示。
图1三、实验内容1.打开模糊逻辑工具箱的图形界面,新建一个Mamdani模糊推理模型。
键入fuzzy打开图形界面,默认即为Mamdani模型。
2.增加一个输入变量,将输入变量命名为level、rate,输出变量为valve,这样就定义了两输入单输出模糊推理系统,保存为tank0.fis。
3.设计模糊化模块:将输入变量rate的论域设为[-0.1,0.1],另外两个变量采用默认论域[-1,1]不变。
通过增加隶属度函数来划分模糊空间:(1)输入变量level划分三个模糊集:low、okay和high,隶属度函数均为高斯函数,参数分别为[0.3 -1]、[0.3 0]、[0.3 1]。
(2)输入变量rate划分三个模糊子集:negative、zore和positive,隶属度函数均为高斯函数,参数分别[0.03 -0.1]、[0.03 0]、[0.03 1]。
(3)输出变量valve划分为五个模糊集:close_fast、close_slow、no_change、open_slow和open_fast,隶属度函数均为三角形函数,参数分别为[-1 -0.9-0.8]、[-0.6 -0.5 -0.4]、[-0.1 0 0.1]、[0.2 0.3 0.4 ]、[0.8 0.9 1]。
Mamdani与Sugeno型模糊推理的应用研究_钟飞

第20卷第2期湖 北 工 业 大 学 学 报2005年04月Vol.20No.2 Journal of Hubei University of Technology Apr.2005[收稿日期]2004-11-11[基金项目]国家自然科学基金项目(50375047).[作者简介]钟 飞(1970-),男,湖北武汉人,湖北工业大学讲师,工学硕士,研究方向:智能控制与检测.[文章编号]1003-4684(2005)04 0028 03M amdani 与Sugeno 型模糊推理的应用研究钟 飞,钟毓宁(湖北工业大学机械工程学院,湖北武汉430068)[摘 要]从模糊控制系统中M amdani 和Sug eno 两种模糊推理模型的结构着手,对其输入输出变量的形式和在模糊控制中的作用,以及两种模糊推理的推理结果和适用范围进行比较和分析.利用M atlab 中Fuzzy 工具箱的计算和图形化功能,通过实例进一步验证两种系统的优缺点和适用范围,为模糊控制器设计的模糊推理类型的选用提供方法.[关键词]模糊控制;M amdani 模糊推理;Sugeno 模糊推理;隶属函数[中图分类号]T P 13[文献标识码]:A模糊推理是指根据模糊输入和模糊规则,按照确定好的推理方法进行推理,得到模糊输出量.其本质上就是将一个给定输入空间通过模糊逻辑的方法映射到一个特定的输出空间的计算过程.最常见的模糊推理系统有3类:纯模糊逻辑系统、高木关野(Takagi Sugeno)型和迈达尼(M amdani)型.由于纯模糊逻辑系统的输入和输出均为模糊集合,而现实世界大多数工程系统的输入与输出都是精确的,因此纯模糊逻辑系统不能直接应用于实际工程中.为解决这一问题,有关学者在纯模糊逻辑系统的基础上提出了具有模糊产生器和模糊消除器的M am dani 型模糊推理系统,而日本学者T akagi 和Suge no 则提出了模糊规则的后项结论为精确值的模糊逻辑系统,称为Sugeno 型模糊逻辑系统.1 Mamdani 模糊推理模型Mamdani 型的模糊推理方法最先将模糊集合的理论用于控制系统.它是由Ebrahim Mamdani 在1975年为了控制蒸汽发动机提出来的.这种方法源于Zadeh 关于模糊算法在复杂系统和决策处理中应用的思想[1],按照综合一系列有经验的操作者提供的线性控制规律来控制锅炉,M amdani 型模糊推理算法采用极小运算规则定义模糊蕴含表达的模糊关系,如规则R:If x is A then y is B.式中:x 为输入语言变量;A 为推理前件的模糊集合;y 为输出语言变量;B 模糊规则的后件.用Rc 表示模糊关系:Rc =A B =X YA (x )B (y )f (x ,y ).(1)当x 为A ,且模糊关系的合成运算采用 极大 极小 运算时,模糊推理的结论计算如下[2]:B =A Rc =Yx X( A (x ) ( A (x ) B (y )))/y.(2)工程应用中,往往期待推理输出的是一个确定的控制量或其他的确定数值,而应用M amdani 型的模糊推理系统,每一条规则推理后得到的输出是变量的分布隶属度函数或离散的模糊集合.在将多条规则的结果合成以后,对每一个输出变量模糊集合都需要进行解模糊化处理,以得到实际问题期望的输出.2 Sugeno 模糊推理模型Sugeno 模糊模型也称TSK 模糊模型,旨在开发从给定的输入输出数据集产生模糊规则的系统化方法.Sug eno 型模糊推理将去模糊化也结合到模糊推理中,其输出为精确量.这是由Sug eno 模糊规则的形式所决定的.在Sugeno 型模糊规则的后件部分讲述储量表示为输入量的线性组合.Sug eno 型模糊推理算法是最常用的模糊推理算法.Sug eno 型模糊推理算法与Mamdani 型类似,其中,输入量模糊化和模糊逻辑运算过程完全相同,主要差别在于输出隶属函数的形式.典型的零阶Sug eno 型模糊规则的形式如下:If x is A and y is B then z =k.式中:x 和y 为输入语言变量;A 和B 为推理前件的模糊集合;z 为输出语言变量;k 为常数.更为一般的一阶Sug eno 模型规则的形式为:if x is A and y is B then z =p x +qy +r.式中:x 和y 为输入语言变量;A 和B 为推理前件的模糊集合;z 为输出语言变量;p ,q,r 为常数.对于一个由n 条规则组成的Sug eno 型模糊推理系统,设每条规则具有下面的形式:Ri :If x is A i and y is B i then z =z i(i =1,2, ,n).则系统总的输出y =ni=1Ai(x ) Bi (y )z i /ni=1Ai(x ) Bi (y ).(3)由于高阶数的Sug eno 模型增加了复杂性,性能却改善不大,故很少使用.在M amdani 型模糊推理算法中,输出隶属函数是模糊集合,经过模糊合成处理,即得到一个需要逆模糊化的输出变量.当采用尖峰脉冲形隶属函数替代分布形隶属函数时,往往能使模糊推理过程有效简化,这就是所谓的单元素隶属函数.单元素隶属函数可以看作已预先逆模糊化处理的模糊集合.由于不需要像Mamdani 型模型那样计算二维函数的形心,可以极大地提高逆模糊化处理过程的效率[3].Sugeno 模型中即采用单元素输出隶属函数,其模糊蕴含即是简单的乘法,模糊合成即是各单元属输出隶属函数的简单包涵.3 Mamdani 和Sugeno 型模糊推理系统的仿真利用M ATLAB 提供的模糊工具箱,可以方便地实现M amdani 和Sugeno 型的模糊推理系统的设计.M amdani 型模糊系统的每一条推理规则的结论都是一个分布的模糊集合,但在许多问题中,如果每一条模糊规则的结论部分是论域上一个确定的单点而不是分布的模糊集合,可能会更加有效.这种单点可以看作是一个已经预先经过清晰化的模糊集合.因为这种方法可以提高清晰化的效率,极大地简化了通常Mamdani 型系统中的计算量.它采用部分数据点的加权平均求和代替二维的积分计算来求取二维函数的质心.而这种单点模型是Sugeno 型系统所支持的.通常,Sugeno 型系统推理规则的结论部分是关于输入的线性函数或常值函数的[4].下面对具有相同输入和不同输出的M amdani 和Sugeno 模糊模型进行仿真比较.一个具有4条规则的两输入单输出M amdani 模糊模型的例子可以表示为:如果x 小,且y 小则z 小;如果x 小,且y 大则z 较小;如果x 大,且y 小则z 较大;如果x 大,且y 大则z 大.一个具有四条规则的两输入单输出Sug eno 模糊模型的例子可以表示为:如果x 小,且y 小则z =-x +y +2;如果x 小,且y 大则z =y -3;如果x 大,且y 小则z =-x +1;如果x 大,且y 大则z =x -y +1.采用Matlab 的Fuzzy 工具箱进行仿真,其中两种推理模型的输入相同,其隶属度函数见图1和图2.由于M amdani 模糊模型为模糊输出,其输出的隶属度函数见图3.根据给出规则建立规则库,图4和图5为两种模糊推理的规则库图解.图6和图7为两种模糊推理的输入输出曲面.第20卷第2期 钟 飞等 M4 结论以上的仿真可见Mam dani 型模糊推理和Sug eno 型模糊推理各有优缺点.M amdani 型模糊推理,由于其规则的形式符合人们思维和语言表达的习惯,因而能够方便地表达人类的知识,但存在计算复杂、不利于数学分析的缺点;而Sugeno 型模糊推理则具有计算简单,利于数学分析的优点,易于与PID 控制方法以及优化、自适应方法结合,是具有优化与自适应能力的控制器或模糊建模工具,是基于样本的模糊建模中最常选用的方法.[ 参 考 文 献 ][1] 刘曙光.模糊控制技术[M ].北京:中国纺织出版社,2001.[2] 诸 静.模糊控制原理与应用[M ].北京:机械工业出版社,2001.[3] 边润强.一种基于Sigeno 模糊模型的测量数据处理方法[J].2001,22(3):318-320.[4] 徐 昕.M atL ab 工具箱应用指南:控制工程篇[M ].北京:电子工业出版社,2000.The Application Research of Mamdani andSugeno Style Fuzzy InferenceZH ONG Fei,ZH ONG Yu ning(S chool of Mechanical Eng ine.,H ubei Univ.of Technology ,Wuhan 430068,China)Abstract:Beg inning w ith the structur es o f Mamdani and Sug eno fuzzy inference modeling in fuzzy contro l system ,the com pariso n is m ade in the fo rm of their input and output var iables,their function in fuzzy con tro l,and their inference results and application fields.By m eans of the computation and g raphics function of the Fuzzy too lbox in Matlab,the tw o systems'advantages and disadvantag es and application scope are further validated.T his ar ticle presents the method of choosing the ty pe of fuzzy inference designed by fuzz y contr oller.Keywords:fuzzy contr ol;mamdani fuzzy infer ence;sugeno fuzzy inference;membership function[责任编辑:张 众]30湖 北 工 业 大 学 学 报2005年第2期。
matlab mamdani模糊推理

matlab mamdani模糊推理摘要:一、引言二、MATLAB 简介三、Mamdani 模糊推理简介四、MATLAB 实现Mamdani 模糊推理五、案例应用六、总结正文:一、引言MATLAB 是一种广泛应用于科学计算和工程设计的编程语言,其强大的数值计算和图形绘制功能,使得其在各个领域都有着广泛的应用。
在人工智能领域,MATLAB 也有着广泛的应用,例如,在模糊推理方面的应用。
二、MATLAB 简介MATLAB 是一种由美国MathWorks 公司开发的数学软件,其具有强大的数值计算、数据分析、可视化等功能,广泛应用于科学计算、工程设计、数据分析等领域。
三、Mamdani 模糊推理简介Mamdani 模糊推理是一种基于Mamdani 规则的模糊推理方法。
Mamdani 规则是一种基于IF-THEN 规则的推理方法,其基本思想是,如果某个条件命题(例如:温度高于30 度)成立,那么结论命题(例如:打开空调)就一定成立。
四、MATLAB 实现Mamdani 模糊推理在MATLAB 中,可以通过编写代码来实现Mamdani 模糊推理。
具体的实现过程如下:1.定义模糊集合:在MATLAB 中,可以通过fuzzy 函数来定义模糊集合。
例如,定义一个温度模糊集合,可以写成:```matlabT = fuzzy(30:100, 50:150);```其中,30:100 表示温度的上界和下界,50:150 表示温度的不确定性。
2.定义Mamdani 规则:在MATLAB 中,可以通过fuzzy rulebook 函数来定义Mamdani 规则。
例如,定义一个关于温度的Mamdani 规则,可以写成:```matlabR = [T>30, T<100, T>50, T<150];```其中,T>30 表示温度高于30 度,T<100 表示温度低于100 度,以此类推。
3.进行模糊推理:在MATLAB 中,可以通过fuzzy 推理函数来进行模糊推理。
基于Mamdani型直觉模糊推理的图像融合算法

基于Mamdani型直觉模糊推理的图像融合算法孙祺;那彦;刘波【摘要】提出了一种基于Mamdani型直觉模糊推理的图像融合算法,该算法首先根据融合目标设定推理规则,并根据推理规则建立直觉模糊推理系统,并将待融合图像的每个像素点直觉模糊化并输入系统,经过推理得到输出图像每个像素点的隶属、非隶属程度,最后通过解模糊计算输出图像的灰度值得到融合图像.实验结果证明,该算法的有效性,且由于直觉模糊集更加精确地描述了客观事物的不确定性,其融合结果优于基于模糊推理系统图像融合算法得到的结果.【期刊名称】《电子科技》【年(卷),期】2014(027)005【总页数】4页(P193-196)【关键词】直觉模糊集;Mamdani模型;直觉模糊推理;图像融合【作者】孙祺;那彦;刘波【作者单位】西安电子科技大学电子工程学院,陕西西安710071;西安电子科技大学电子工程学院,陕西西安710071;西安电子科技大学电子工程学院,陕西西安710071【正文语种】中文【中图分类】TP391.41图像融合是将不同传感器对同一场景的成像融合成一幅新的图像,以获得更多信息的过程。
融合后的图像可信度更高、模糊较少,为计算机视觉检测、分类、识别等提供必要的准备,具有重要的意义[1]。
1986年K.T.Atanassov教授在模糊理论的基础上提出直觉模糊理论[2],创造性地引入了“非隶属度”这一参数,使直觉模糊集不仅可以描述对象“亦此亦彼”的模糊概念,还可以描述其“非此非彼”的中立概念,具有良好的应用前景。
最早将模糊理论引入图像融合的是加拿大的A Nejatali和 IR Ciric[3],随着近年来的发展,基于模糊理论的图像融合算法得到了广泛的研究[4-5],也出现了少量基于直觉模糊理论的图像融合算法[6]。
但这些算法只引入了直觉模糊逻辑,算法复杂、不灵活,针对这些问题本文提出一种基于Mamdani型直觉模糊推理的图像融合算法,通过制定合理的融合规则确定直觉模糊推理系统,将待融合图像作为系统输入即可得到融合图像,操作简便、效果良好,通过改变推理规则可完成不同的融合目标。
模糊推理的Mamdani算法及其Matlab实现

然后将各推理结 果以 “ 的方式 聚合 为一个最终的结果 B , u” ‘
B- - …口 .B』 2 uB U () 4
这样得到多重 F z 推理模 型的 M m a i uz y a dn 算法
()( U 2 y= l U… y= V f‘c\ ) ( ) A。yB y】 5
‘ e. I
于CI R 方案 的 F z , 理算法 , uz 推 ) 被称为 M m ai 法 , a dn 算 至今仍是一 种被广泛使用的有效算法 。
取模糊关系生成算法为 “ 运算 ’
Rx )(- B xy= (, =A + X , - )A缸NB c )mif ( } t 。, = nA扛 By y ) 1)
文献标识码 : A 文章编号 :6 2 7 9 ( 0 8) 0 2 9 0 17 — 8 4 20 1— 6 — 1
Al Bl
制 工 具 箱进 行 算 法的 上 机 实现 。
中图分类号 : P 0 . T 3 16
一
、
引 言
目前 , 模糊推 理系统 已经成 功应用 于 自动控 制、 数据分 类 、 决
A _ ÷ A
—
其 中A A ・A , ∈ ( )B B …B , F Y 。 b a・ A F X . b ∈ ( ) . B
先分别按简单 F zy推理模 型处理 如下 uz
A J A _÷ B2 2 A _+ B _ A‘ A B , , … ’
刘 恒
( 淮南师范学院数 学与计算科学系 安徽 ・ 淮南 220 ) 30 1
通过一般 F zy推理模型的 Ma ai uz mdn 算法 , 推导 多维 F zy推理模 型的 Ma ai uz md n 算法 , 并运用 Maa tb的模糊控 l
基于Mamdani型模糊推理的电压暂降源识别

则实现从输入到输 出的推理计算 ,从 而建立准确的辨识 系统 。通过仿真验证 ,该方法能够较好地对 电压 暂降
源进 行 准 确 辨 识 。
关 键 词 : 电压 暂 降 ;暂 降 源识 别 ;Ma a i 糊 推 理 ;仿 真 mdn 模
中图分类号 : M74 T 1
文献标识码 :A
文章编号 :10 —2 9 2 1 )0 —0 4 —0 0 7 6 1(00 2 0 3 6
第3 7卷第 2 期
21 0 0年 3月
华 北 电 力 大 学 学 报
J un l f rhChn lcrcP we iest or a t iaE eti o rUnv riy o No
Vl . 7.No 2 o 3 J . Ma. 2 1 r, 00
基 于 Ma a i md n 型模 糊 推 理 的 电压 暂 降源 识别
,
( . i j l t c o r c ne& R s rhIstt,Taj 0 0 2 hn ;2 S ho o l tcl n 1Ta i Ee r we S i c nn c P i e ee c tue i i 3 02 ,C i a ni nn a . ol f e r aa d c Ec i
mo o tr i g we e a ay e .Th r r o i e e t p e o n u n h o tg g u e y d f r n t rsa t r n lz n d e e a e s me df rn h n me a d r g t e v l e s s c s d b i e e t f i a a a f o re .Th h r c eso h aa c ft et e h s s h h gn r n ft e v l g e h g e d n s u cs e c a a tr ft eb ln eo h h e p a e ,t e c a i g te d o h o t e wh n t e s n sa d r n a a v l g a mo i r t u i g t es g we ec n ie e e t e c tr f e o nzn h i e e t ot g g s u c ot e h r n c a i d r h a r o sd r t b h r e i o c g iig t ed f r n l es r e a o n d o i a r f v a a o s b sn md n u z fr n e y u ig Ma a i z y i e e c .M a a i u z fr n e u e h u e ih a eara y k o o c ry o tt e f n md z y i e e c ss t e r l wh c l d n wn t a r u h n f n s r e ra o ig c mp tt n r m p tt u p t esnn o u a i sfo i u oo t u .Th o r c in o hs me h sp v d b me s o n e c r e t ft i t o wa r e y s o d o o i l in a e mu a o st k n i t n
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验四 Mamdani 型模糊推理系统的设计与仿真
一、 目的和要求 1. 目的
(1) 通过本次综合设计,进一步了解模糊控制的基本原理、模糊模型的建立和模
糊控制器的设计过程。
(2) 提高控制系统的仿真能力
(3) 熟悉MATLAB 在模糊控制系统仿真中的应用。
2. 要求
(1) 充分理解实验内容,并独立完成实验报告。
(2) 实验报告要求:实验题目、实验具体内容及实验功能、结果分析、收获或不
足、程序清单。
二、 实验内容
完成对给定的对象的模糊控制仿真:
(1)自选控制对象,比如传递函数()s
s Ke s G ts +=-2
067.0。
(2)确定模糊控制论域和参数。
(3)在MATLAB 中输入fuzzy( ),设计模糊控制隶属度函数和控制规则。
(4)运行SIMULINK 仿真程序,绘制仿真图。
(5)运行仿真,记录实验数据和控制曲线。
(6)并分析结果。
三、 实验步骤
1)确定模糊规则
误差E 、误差变化EC 及控制量U 的模糊集定义如下:
EC 和U 的模糊集均为:{NB,NM,NS,ZO,PS,PM,PB } E 的模糊集为:{NB,NM,NS,NO,PO,PS,PM,PB } 确定模糊控制规则:一般如表2所示:
表2 模糊控制规则表
2)设计模糊逻辑控制器
模糊逻辑控制系统的参数对控制性能影响很大,因此参数设置是实验的重点内容,具体步骤如下:
a.打开Matlab的FIS编辑器(双击Fuzzy logic toolbox下的FIS Editor
Viewer),确定模糊推理输入变量和输出变量的个数、名字。
b.打开隶属函数编辑器,选定变量的论域和显示范围,选择隶属函数的形
状和参数。
c. 打开模糊规则编辑器,编辑模糊规则。
d. 重新回到FIS编辑器界面,选择模糊算子,推理方法,聚类方法,解模糊的方法等(centroid,bisector,middle of maximum,largest of maximum,smallest of maximum)。
e. 用模糊规则观察器或输出曲面观察器,观看模糊推理情况。
f. 将建立的FIS保存到磁盘,文件名后缀为.fis。
g. 进行模糊控制仿真时,首先要将FIS发送到Matlab工作空间(workspace)中,用FIS窗口下File/Export/to workspace实现,用户建立一个工作空间变量名(例如fuzzycontrol),这个变量将FIS系统作为Matlab的一个结构进行工作。
仿真时,打开fuzzy logic controller ,输入FIS变量名,就可以进行
仿真了。
3)建立SIMULINK仿真模型
在MATLAB的simulink仿真环境中建立模糊控制系统的方框图。
如图1所示。
其中有信号发生器,比较器,放大器(Gain),零阶保持器,多路混合器(Mux),模糊逻辑控制器(FIS)(在Simulink Library Browser/Fuzzy Logic Toolbox下添加),控制对象,示波器(scope)。
图1 在线推理方式模糊控制仿真模型
4)调整Ke,Kec ,Ku的值的大小(二阶系统模糊控制参考数据是100, 1, -150),得到系统适合的输出曲线直到符合要求(如误差小于1%或者超调量小于5%)为止,观察输出曲线。
四、实验结果
五、总结。
